| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.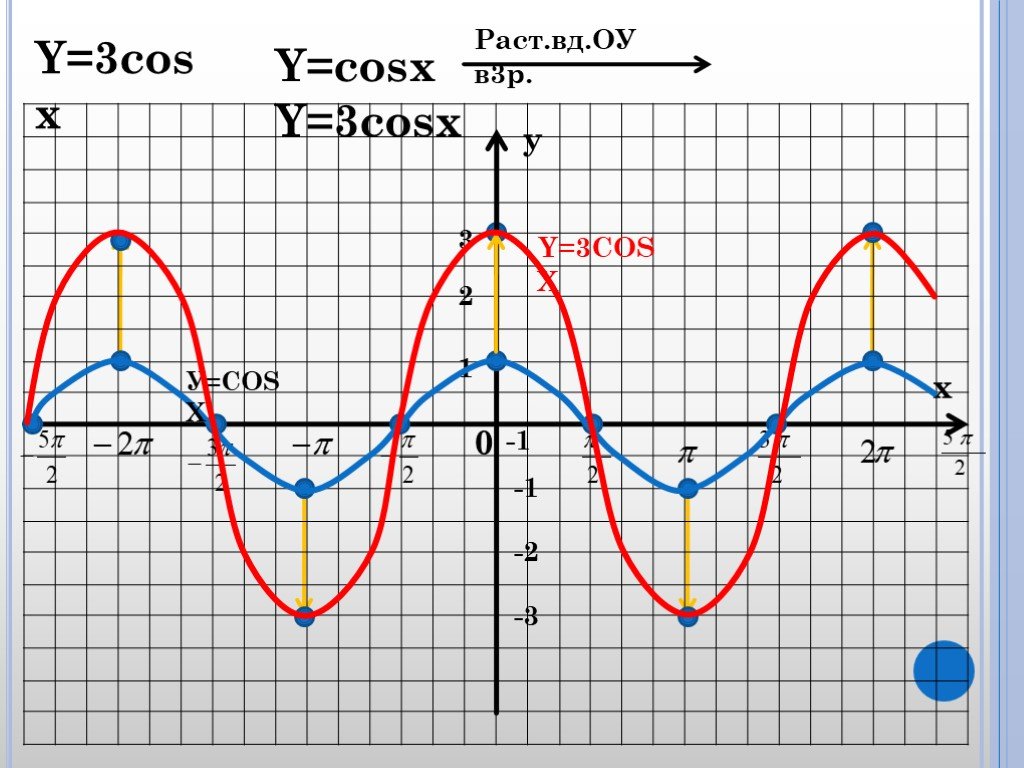 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.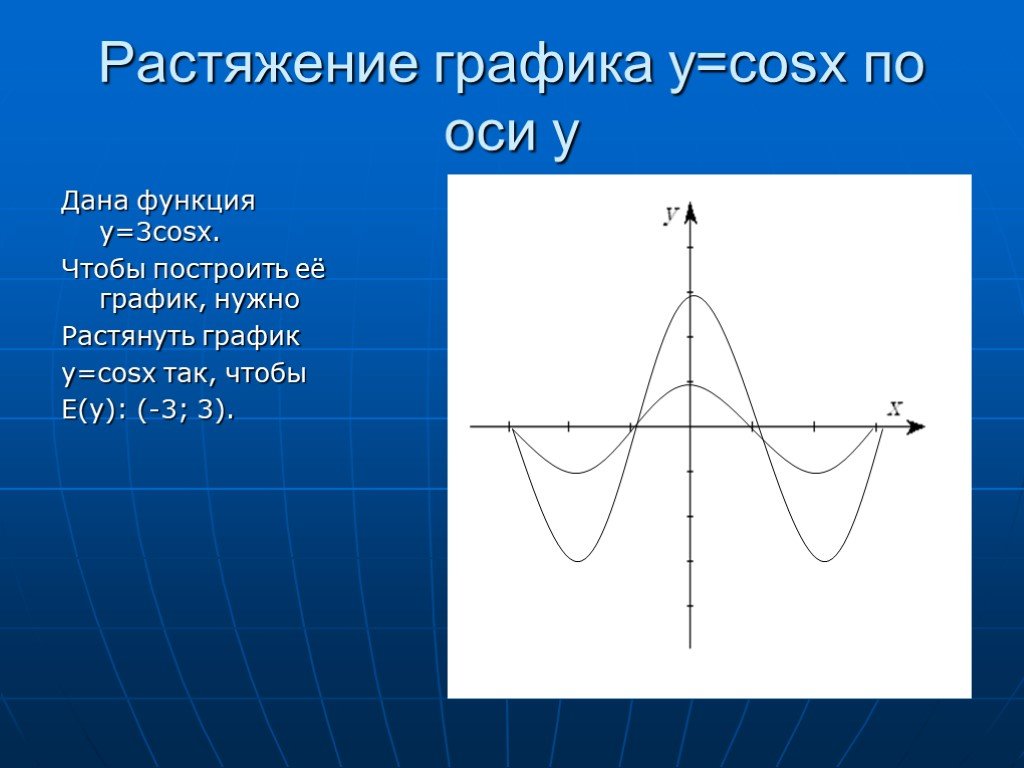 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.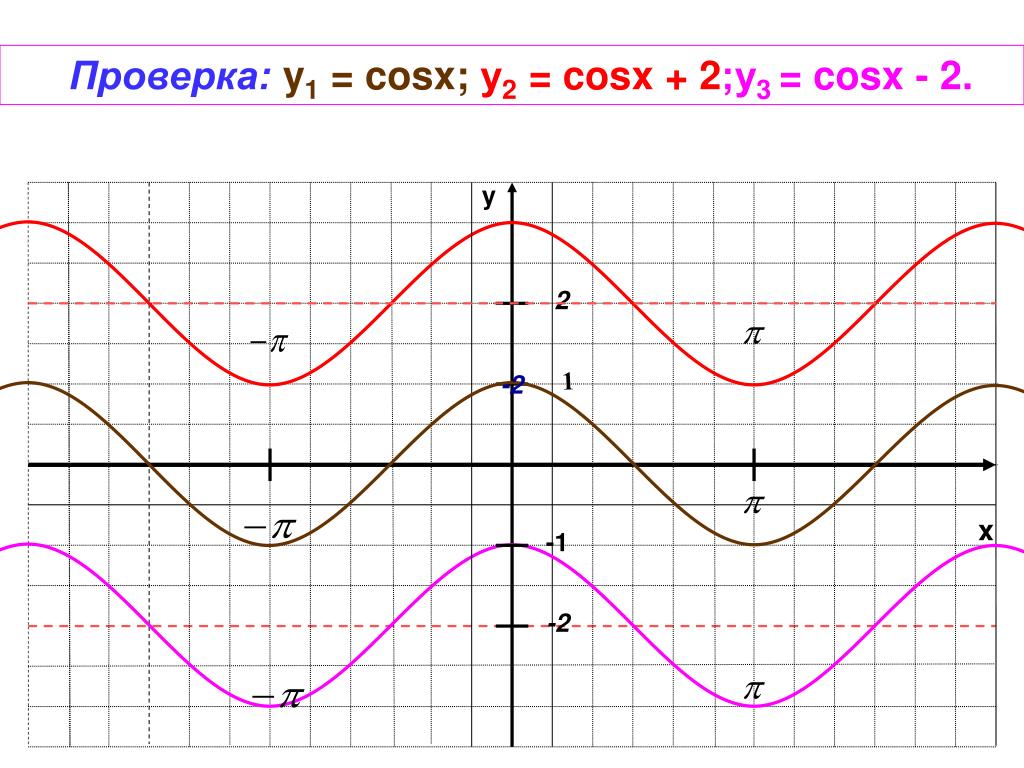 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.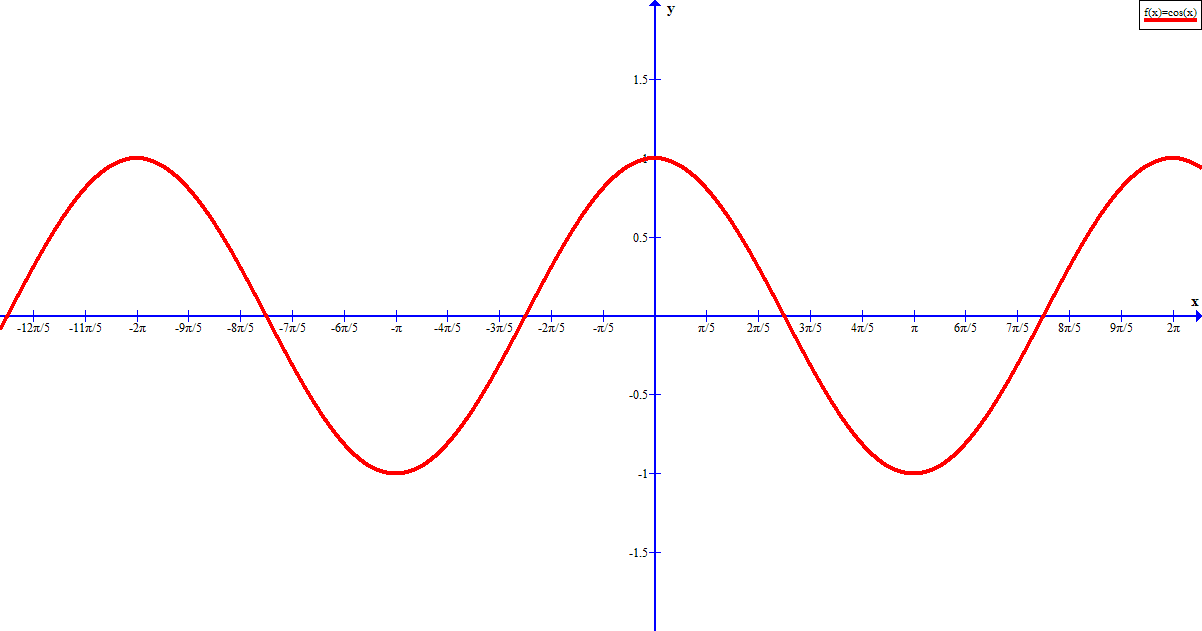 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.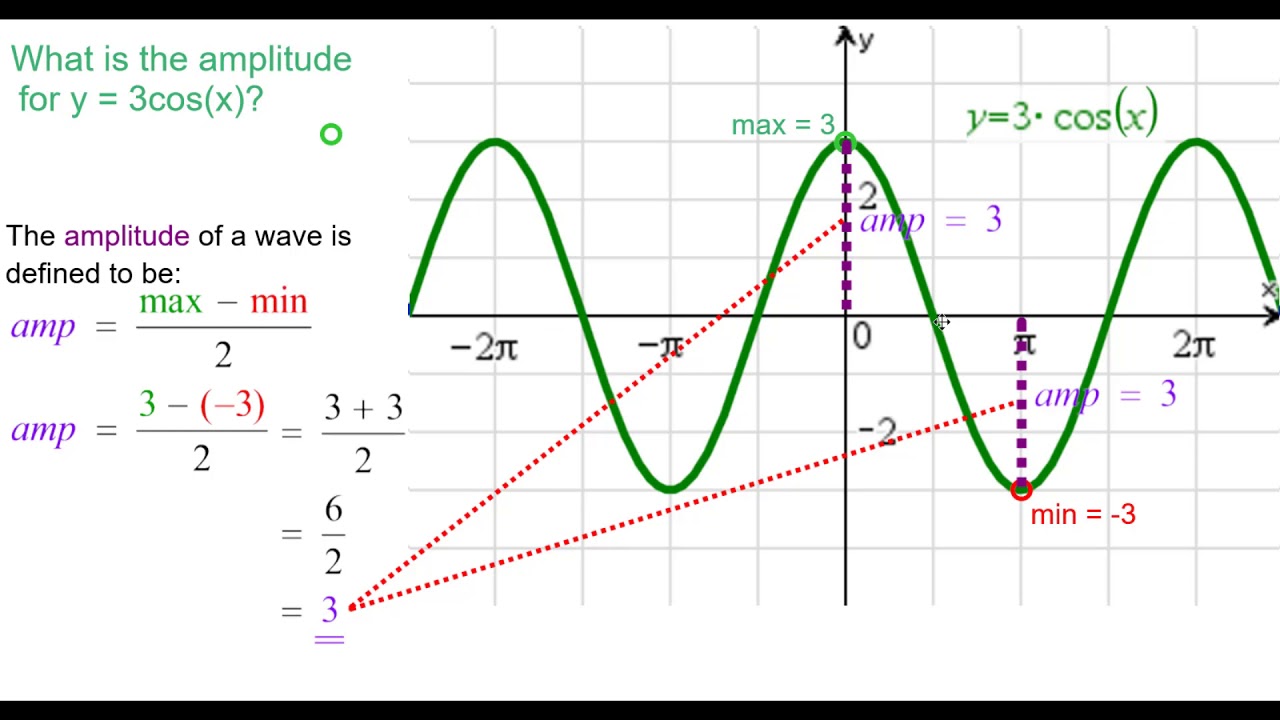 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Глава 7. Использование сценариев в KmPlot
Для KmPlot возможно писать сценарии с помощью D-Bus. Например, чтобы определить функцию f(x)=2sin x+3cos x, установить толщину её линии равной 20 единицам и построить эту функцию, наберите в консоли:
qdbus org.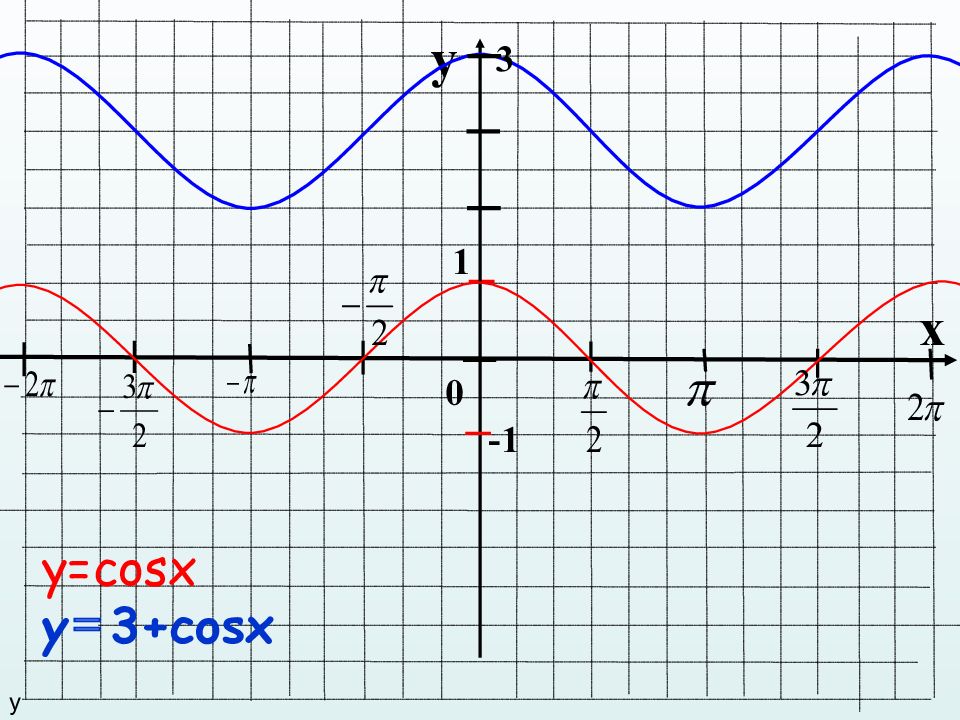 kde.kmplot-PID /parser org.kde.kmplot.Parser.addFunction «f(x)=2sin x+3cos x» «» После этого будет возвращён номер-идентификатор новой функции или -1 в случае ошибки.
kde.kmplot-PID /parser org.kde.kmplot.Parser.addFunction «f(x)=2sin x+3cos x» «» После этого будет возвращён номер-идентификатор новой функции или -1 в случае ошибки.
qdbus org.kde.kmplot-PID /parser org.kde.kmplot.Parser.setFunctionFLineWidth ID 20 Эта команда изменяет толщину линии графика функции с номером-идентификатором ID на 20.
qdbus org.kde.kmplot-PID /view org.kde.kmplot.View.drawPlot Эта команда перерисовывает окно, чтобы график функции стал видимым.
Список доступных функций:
- /kmplot org.kde.kmplot.KmPlot.fileOpen url
Загрузить файл
url.- /maindlg org.kde.kmplot.MainDlg.isModified
Возвращает true, если изменения сделаны после последнего сохранения.
- /maindlg org.kde.kmplot.MainDlg.checkModified
Если имеются несохранённые изменения, появляется диалог, с помощью которого возможно сохранить, сбросить изменения в графиках или отменить выход.

- /maindlg org.kde.kmplot.MainDlg.editAxes
Открывает диалог координатной системы.
- /maindlg org.kde.kmplot.MainDlg.toggleShowSlider
Показать/скрыть окно с ползунком для смены параметра.
- /maindlg org.kde.kmplot.MainDlg.slotSave
Сохранить функции (открыть диалог сохранения, если это новый файл).
- /maindlg org.kde.kmplot.MainDlg.slotSaveas
Аналогично выбору пункта меню Файл → Сохранить как….
- /maindlg org.kde.kmplot.MainDlg.slotPrint
Открывает диалог печати.
- /maindlg org.kde.kmplot.MainDlg.slotResetView
Аналогично выбору пункта меню Вид → Сбросить масштаб.
- /maindlg org.kde.kmplot.MainDlg.slotExport
Открывает диалог экспорта.
- /maindlg org.kde.kmplot.MainDlg.slotSettings
Открывает диалог настройки.
- /maindlg org.kde.kmplot.MainDlg.slotNames
Выводит список предопределённых математических функций в руководстве.

- /maindlg org.kde.kmplot.MainDlg.findMinimumValue
Аналогично выбору пункта меню Сервис → Минимальное значение….
- /maindlg org.kde.kmplot.MainDlg.findMaximumValue
Аналогично выбору пункта меню Сервис → Максимальное значение….
- /maindlg org.kde.kmplot.MainDlg.graphArea
Аналогично выбору пункта меню Сервис → Площадь под графиком….
- /maindlg org.kde.kmplot.MainDlg.calculator
Аналогично выбору пункта меню Сервис → Калькулятор.
- /parser org.kde.kmplot.Parser.addFunction f_str0 f_fstr1
Добавить функцию, определяемую выражениями
f_str0иf_str1. Если выражение не содержит имени функции, оно будет сгенерировано автоматически. После этого будет возвращён номер-идентификатор функции или -1 в случае ошибки.- /parser org.kde.kmplot.Parser.removeFunction id
Удалить функцию по её номеру
id. В случае ошибки возвращается false, иначе — true.
- /parser org.kde.kmplot.Parser.setFunctionExpression id eq f_str
Изменить выражение функции с номером-идентификатором
idнаf_str. В случае ошибки возвращается false, иначе — true.- /parser org.kde.kmplot.Parser.countFunctions
Возвращает число функций (параметрические считаются за две).
- /parser org.kde.kmplot.Parser.listFunctionNames
Возвращает список всех функций.
- /parser org.kde.kmplot.Parser.fnameToID f_str
Возвращает номер
f_strили -1, если функции с именемf_strнет.- /parser org.kde.kmplot.Parser.functionFVisible id
Возвращает true, если функция с номером-идентификатором
idвидима.- /parser org.kde.kmplot.Parser.functionF1Visible id
Возвращает true, если видима производная первого порядка функции с номером-идентификатором
id.
- /parser org.kde.kmplot.Parser.functionF2Visible id
Возвращает true, если видима производная второго порядка функции с номером-идентификатором
id.- /parser org.kde.kmplot.Parser.functionIntVisible id
Возвращает true, если видима первообразная функции с номером-идентификатором
id.- /parser org.kde.kmplot.Parser.setFunctionFVisible id visible
Отображает график функции с идентификатором
id, если параметрvisibleустановлен в значение true. Если параметрvisibleустановлен в значение false, эта функция будет скрыта. Возвращает true, если функция существует, в ином случае — false.- /parser org.kde.kmplot.Parser.setFunctionF1Visible id visible
Отображает или скрывает первую производную функции с номером-идентификатором
id. Возвращает false, если функция не существует.- /parser org.
 kde.kmplot.Parser.setFunctionF2Visible id visible
kde.kmplot.Parser.setFunctionF2Visible id visible Отображает или скрывает вторую производную функции с номером-идентификатором
id. Возвращает false, если функция не существует.- /parser org.kde.kmplot.Parser.setFunctionIntVisible id visible
Отображает или скрывает первообразную функции с номером-идентификатором
id. Возвращает false, если функция не существует.- /parser org.kde.kmplot.Parser.functionStr id eq
Возвращает выражение функции с номером-идентификатором
id. Возвращает false, если функция не существует.- /parser org.kde.kmplot.Parser.functionFLineWidth id
Возвращает толщину линии графика функции с номером-идентификатором
id. Возвращает 0, если функция не существует.- /parser org.kde.kmplot.Parser.functionF1LineWidth id
Возвращает толщину линии графика первой производной функции с номером-идентификатором
id. Возвращает 0, если функция не существует.
Возвращает 0, если функция не существует.- /parser org.kde.kmplot.Parser.functionF2LineWidth id
Возвращает толщину линии графика второй производной функции с номером-идентификатором
id. Возвращает 0, если функция не существует.- /parser org.kde.kmplot.Parser.functionIntLineWidth id
Возвращает толщину линии графика первообразной функции с номером-идентификатором
id. Возвращает 0, если функция не существует.- /parser org.kde.kmplot.Parser.setFunctionFLineWidth id linewidth
Установить толщину линии графика функции с номером-идентификатором
idвlinewidth. Возвращает false, если функция не существует.- /parser org.kde.kmplot.Parser.setFunctionF1LineWidth id linewidth
Установить толщину линии графика первой производной функции с номером-идентификатором
idвlinewidth. Возвращает false, если функция не существует.
- /parser org.kde.kmplot.Parser.setFunctionF2LineWidth id linewidth
Установить толщину линии графика второй производной функции с номером-идентификатором
idвlinewidth. Возвращает false, если функция не существует.- /parser org.kde.kmplot.Parser.setFunctionIntLineWidth id linewidth
Установить толщину линии графика первообразной функции с номером-идентификатором
idвlinewidth. Возвращает false, если функция не существует.- /parser org.kde.kmplot.Parser.functionParameterList id
Возвращает список всех значений параметра функции с номером-идентификатором
id.- /parser org.kde.kmplot.Parser.functionAddParameter id new_parameter
Добавить значение параметра
new_parameterфункции с номеромid. Возвращает false в случае ошибки.- /parser org.kde.
 kmplot.Parser.functionRemoveParameter id remove_parameter
kmplot.Parser.functionRemoveParameter id remove_parameter Удалить значение параметра
remove_parameterфункции с номеромid. Возвращает false в случае ошибки.- /parser org.kde.kmplot.Parser.functionMinValue id
Возвращает минимум диапазона построения функции с номером-идентификатором
id. Если функция не существует или минимум не определён, возвращается пустая строка.- /parser org.kde.kmplot.Parser.functionMaxValue id
Возвращает максимум диапазона построения функции с номером-идентификатором
id. Если функция не существует или максимум не определён, возвращается пустая строка.- /parser org.kde.kmplot.Parser.setFunctionMinValue id min
Устанавливает минимум области построения функции с номером-идентификатором
idвmin. Если функция не существует или выражение недопустимо, возвращается false.
- /parser org.kde.kmplot.Parser.setFunctionMaxValue id max
Устанавливает максимум области построения функции с номером-идентификатором
idвmin. Если функция не существует или выражение недопустимо, возвращается false.- /parser org.kde.kmplot.Parser.functionStartXValue id
Возвращает начальную абсциссу для первообразной функции с номером-идентификатором
id. Если функция не существует или выражение абсциссы не определено, возвращается пустая строка.- /parser org.kde.kmplot.Parser.functionStartYValue id
Возвращает начальную ординату для первообразной функции с номером-идентификатором
id. Если функция не существует или выражение ординаты не определено, возвращается пустая строка.- /parser org.kde.kmplot.Parser.setFunctionStartValue id x y
Устанавливает начальную абсциссу и ординату для первообразной функции с идентификатором
idвxиy. Возвращает true, если функция существует и выражение допустимо, в ином случае — false.
Возвращает true, если функция существует и выражение допустимо, в ином случае — false.- /view org.kde.kmplot.View.stopDrawing
Если KmPlot в данный момент рисует график функции, это будет остановлено.
- /view org.kde.kmplot.View.drawPlot
Перерисовать все графики функций.
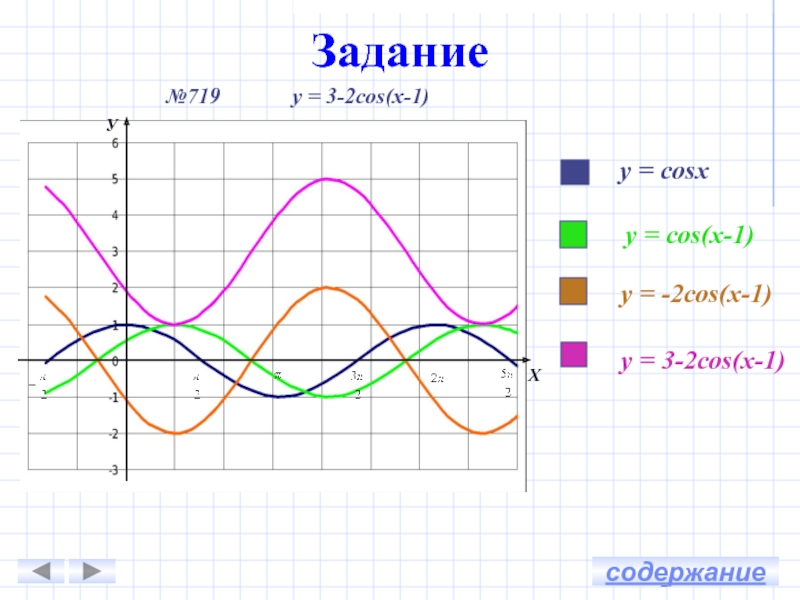
Постройте график функции y=3 cos x-sqrt3 sin x, преобразовав кривую косинуса.
- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8 900 03 Класс 7
- Класс 6
- NCERT
- IIT JEE
- Экзамен
- JEE MAINS
- JEE ADVANCED
- X BOARDS
- XII BOARDS
- NEET
- Neet Предыдущий год (по годам)
- Физика Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Нет Все образцы работ
- Образцы работ Биология
- Образцы работ Физика
- Образцы работ Химия 900 08
- Скачать PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- Экзаменационный уголок
- Онлайн-класс
- Викторина
- Задать вопрос в Whatsapp
- Поиск Doubtnut
- Английский словарь
- Toppers Talk
- Блог
- О нас Us
- Карьера
- Скачать
- Получить приложение
Вопрос
Обновлено: 26/04/202 3 9(- 1) x)
34764
09:58
Если x в [0,2 pi], то y=(sin x)/(|sin x|),y=(|cos x|)/ (cos x) идентичны функции для x в
63512
04:56
Максимальное расстояние точки на графике функции y=sqrt(3)sin x+cos x от оси X равно
4735251
02:54
Нарисуйте график функций на тех же осях: y=sinx и y=cosx,0≤x≤2π
8494050
02:11
Нарисуйте график y=|| |х|−2|−3| путем преобразования графика y=|x|
41927258
Текст Решение
Из кривой y=sin x постройте график функций.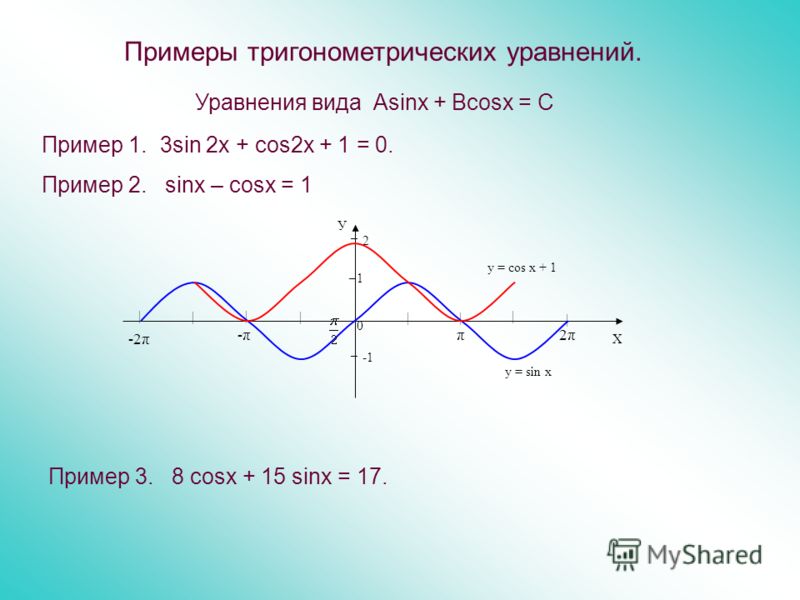
y=sin (-x)
168314155
02:33
Из кривой y=sin x постройте график функций.
y= -sin (-x),
168314156
01:18
Из кривой y=sin x постройте график функций.
y=sin(π2+x), что равно cos x.
168314159
02:56
Из кривой y=sin x постройте график функций.
y= sin(π2−x), что также является cos x.
168314161
03:30
Обозначим график функции
f(x)=|sinx|+|cosx|
248387130
02:59
Из кривой y= sinx постройте график функции
(i) y=sin(-x)
(ii) y=-sin(-x)
(iii) y=sin (π2+x), что равно cos x
(iv) y=sin(π2−x), что также равно cos x (см. тригонометрию)
508113401
Текстовое решение
Максимальное расстояние точки на графике функция y=√3sinx+cosx от оси X равна
642506151
02:58
Нарисуйте график y=|||x|−2|−3| путем преобразования графика y=|x|
642547550
09:21
फलन y=√3sinx+cosxके आलेख पर स्थित क
642887923
05:03
Если sin x+sin y=3(cos y -cos x) тогда значение sin 3 x+sin 3 y=
644182422
03:59
РЕКЛАМА
И.
 А. SIS-графическое представление функций
А. SIS-графическое представление функцийНарисуйте график следующих функций: (a) y=cos x+|cos x|, …
04:19
Нарисуйте график функции y=2|x-2| -|х+1|+х.
03:41
Нарисуйте график функции Y=sin x.
02:09
График функции y=3 cos x-sqrt3 sin x путем преобразования косинуса cu…
03:46
- Ask Unlimited Сомнения
- Видеорешения на нескольких языках ( включая хинди)
- Видеолекции экспертов
Doubtnut хочет отправлять вам уведомления. Разрешите получать регулярные обновления!
Прослушивание…
Cos3x — формула, вывод, примеры, тождество
Cos3x представляет собой тождество тройного угла в тригонометрии. Это частный случай идентичности составных углов функции косинуса. Cos3x дает значение тригонометрической функции косинуса для тройного угла. Расширение cos3x может быть получено с использованием идентичности сложения углов косинуса, и оно включает термин cos куб x (cos ^ 3x).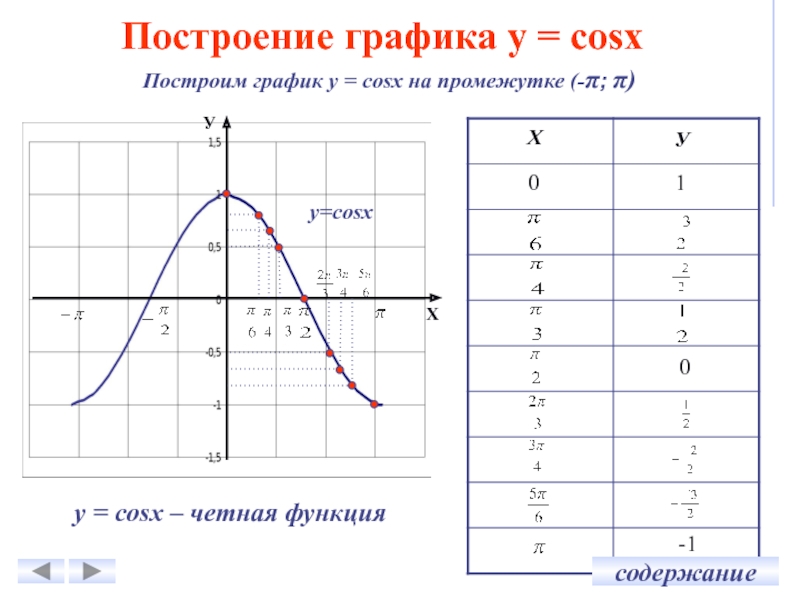 3x помогают решать различные тригонометрические задачи. 93x, их вывод и применение вместе с решенными примерами для лучшего понимания. Мы также изучим график функции cos3x, чтобы понять ее поведение.
3x помогают решать различные тригонометрические задачи. 93x, их вывод и применение вместе с решенными примерами для лучшего понимания. Мы также изучим график функции cos3x, чтобы понять ее поведение.| 1. | Что такое Cos3x в тригонометрии? |
| 2. | Формула Cos3x |
| 3. | Получение формулы Cos3x |
| 4. | График Cos3x 93x Формула |
| 7. | Как применять формулу Cos3x? |
| 8. | Часто задаваемые вопросы по Cos3x |
Что такое Cos3x в тригонометрии?
Cos3x — важное тождество в тригонометрии, которое используется для определения значения функции косинуса для угла, который в три раза больше угла x. Его можно выразить через cos x. Поведение функции cos3x аналогично поведению cos x. Поскольку период cos x равен 2π, период cos3x равен 2π/3, то есть цикл cos3x повторяется через каждые 2π/3 радиана. Теперь давайте посмотрим на формулу для cos3x. 93x — 3cos x = 4 cos 3 x — 3 cos x . Теперь мы рассмотрим вывод формулы cos3x в следующем разделе, используя формулу суммы углов функции косинуса.
Теперь давайте посмотрим на формулу для cos3x. 93x — 3cos x = 4 cos 3 x — 3 cos x . Теперь мы рассмотрим вывод формулы cos3x в следующем разделе, используя формулу суммы углов функции косинуса.
Получение формулы Cos3x
Мы будем использовать формулу сложения углов функции косинуса, чтобы вывести формулу cos3x. Мы знаем, что угол 3x можно записать как 3x = 2x + x. Мы будем использовать следующие тригонометрические тождества для вывода cos3x:
- cos (a + b) = cos a cos b — sin a sin b
- sin 2x = 2 sin x cos x
- cos 2x = 1 — 2sin 2 x
- sin 2 х + cos 2 х = 1
Мы будем использовать приведенные выше тождества для доказательства тождества cos3x. Используя формулу сложения углов для функции косинуса, мы имеем
cos3x = cos (2x + x)
= cos 2x cos x — sin 2x sin x [Потому что cos (a + b) = cos a cos b — sin a sin б]
93x — 3cosx Следовательно, мы получили cos3x = 4 cos 3 x — 3 cos x , используя тождество сложения углов для функции косинуса.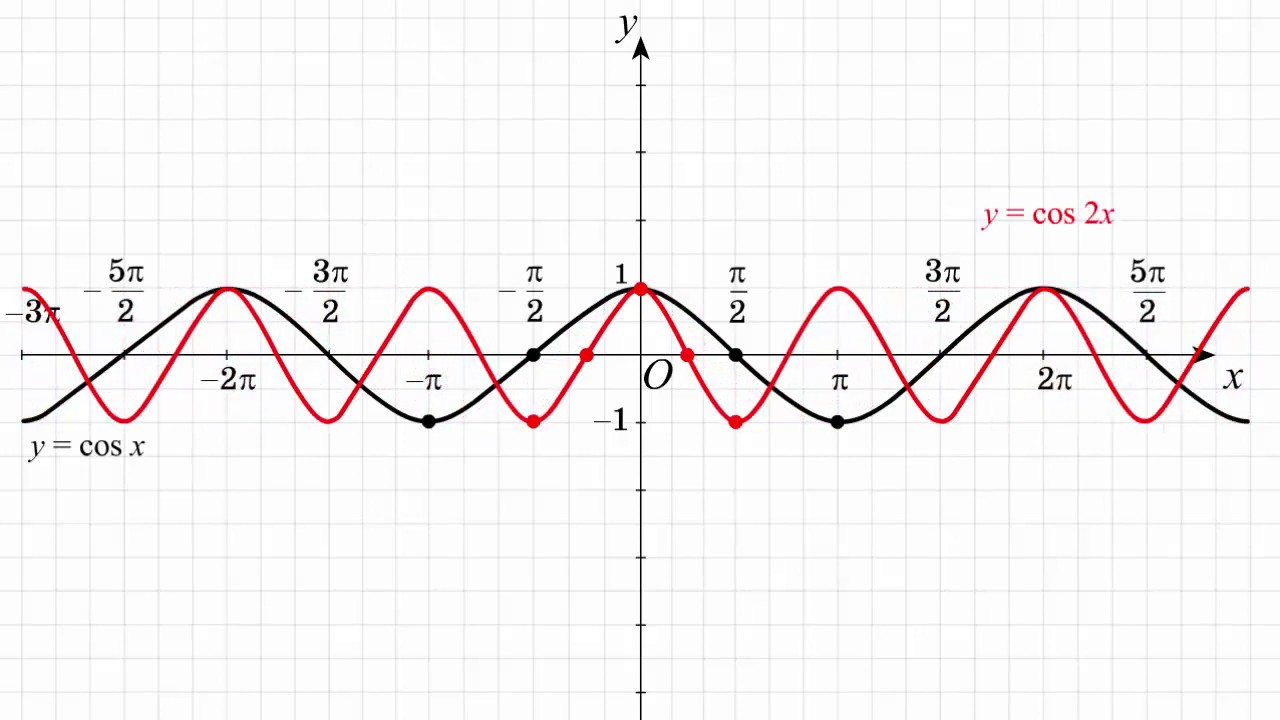
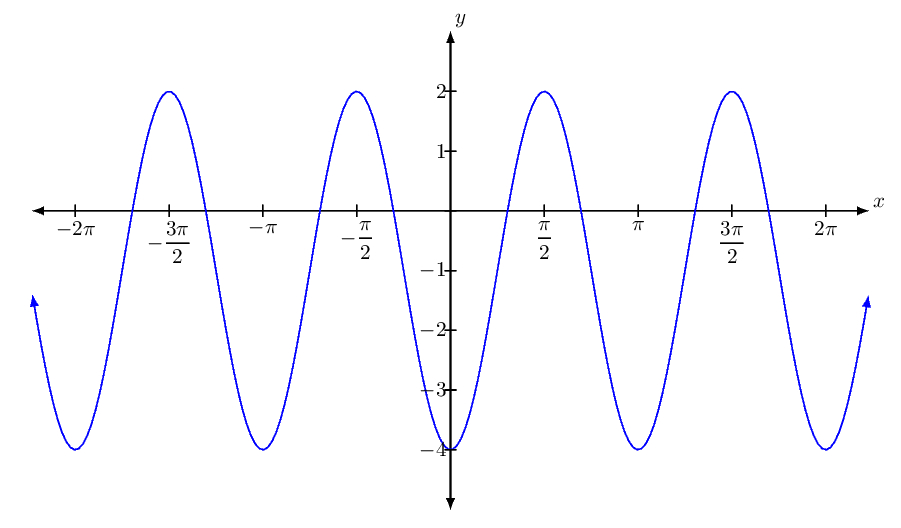
График Cos3x
График cos3x аналогичен графику cos x. Поскольку угол в cos3x в три раза больше угла в cos x, график cos3x уже, чем cos x, и, следовательно, период cos3x также составляет одну треть периода функции cos x. Кроме того, для функции cos bx период равен 2π/|b|. Следовательно, период cos3x равен 2π/3. Мы можем построить график cos 3x, взяв несколько точек на графике и соединив их. Рассмотрим несколько точек для y = cos3x и y = cos x и нанесем их на график. 93x ⇒ cos 3 x = 1/сек 3 x
Как применять формулу Cos3x?
Чтобы понять применение cos3x, рассмотрим пример. Изучаем и запоминаем значение функции косинуса для некоторых конкретных углов, таких как 0°, 30°, 45°, 60°, 90° и т. д. Теперь определим значение cos 135° по формуле cos3x. Если 3x = 135°, x = 135°/3 = 45°. Следовательно, используя формулу cos3x, мы имеем
cos 135° = cos (3 × 45°) = 4 cos 93x = (1/4) cos3x + (3/4) cosx, который используется для упрощения сложных задач интеграции.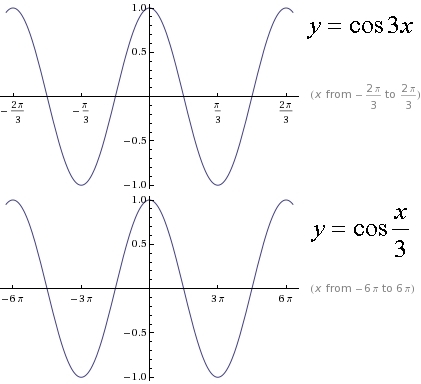
☛ Статьи по теме:
- Грех греха Инверсия
- грех 2 Пи
- соз а сос б
- sin3x
Часто задаваемые вопросы по Cos3x
Что такое Cos3x в тригонометрии?
Cos3x — тождество тройного угла в тригонометрии. Его можно получить, используя тождество сложения углов функции косинуса. Идентичность cos3x задается как cos3x = 4 cos 3 х — 3 cos х.
Что такое Период cos3x?
Поскольку угол в cos3x в три раза больше угла в cos x, период cos3x также составляет одну треть периода функции cos x. Для функции cos bx период равен 2π/|b|. Следовательно, период cos3x равен 2π/3.
Как построить график cos3x?
Поскольку угол в cos3x в три раза больше угла в cos x, график cos3x уже, чем cos x. Мы можем рассмотреть несколько точек для y = cos3x и y = cos x и соединить их, чтобы построить график.
- Когда x = 0, 3x = 0 ⇒ cos x = 1, cos3x = 1
- Когда x = -π/3, 3x = -π ⇒ cos x = 1/2, cos3x = -1
- Когда x = π/3, 3x = π ⇒ cos x = 1/2, cos3x = -1
- Когда x = 2π/3, 3x = 2π ⇒ cos x = -1/2, cos3x = 1
- Когда x = -2π/3, 3x = -2π ⇒ cos x = -1/2, cos3x = 1
Какая формула для Cos3x?
Тригонометрическая формула для cos3x: cos3x = 4 cos 3 x — 3 cos x.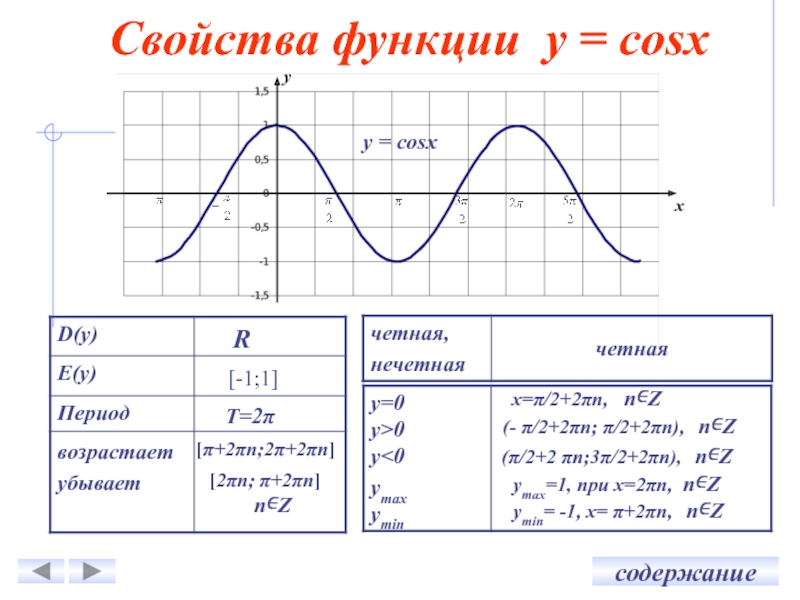



 kde.kmplot.Parser.setFunctionF2Visible id visible
kde.kmplot.Parser.setFunctionF2Visible id visible Возвращает 0, если функция не существует.
Возвращает 0, если функция не существует.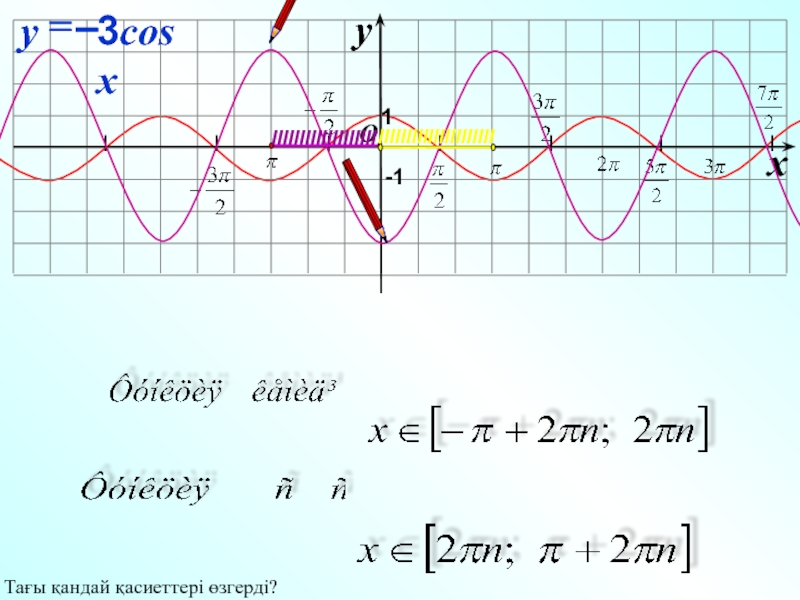
 kmplot.Parser.functionRemoveParameter id remove_parameter
kmplot.Parser.functionRemoveParameter id remove_parameter
 Возвращает true, если функция существует и выражение допустимо, в ином случае — false.
Возвращает true, если функция существует и выражение допустимо, в ином случае — false. А. SIS-графическое представление функций
А. SIS-графическое представление функций