График функции — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Как построить график
функции у=f(х)+m,
если известен график
функции у=f(х).
у
Сдвиг на 1
единицу вверх
вдоль оси у
у=х²+1
у=х²
у=х²+1
+1
5
4
у=х²
Постройте
график
функции:
10
9
2
1
-3 -2 -1 0
х 0
0 11
У 1
0 21
54
х
1 2 3
-1 -2
33 -1
-2 -3
-3
10
9 21 54 10
9
у
у=х²
9
Сдвиг на 4
единицы вниз
вдоль оси у
5
4
у=х²-4
-4
1
-3 -2 -1 0
Постройте
график
функции:
у=х²-4
1 2 3
х
-3
-4
х 0 1
У -4 -3
2
0
3
5
-1 -2 -3
-3 0 5
АЛГОРИТМ 1.
Чтобы построить график функции
y=f(x)+m, где m – заданное
положительное число, нужно сдвинуть
график функции y=f(x) вдоль оси y на m
единиц масштаба вверх.
Чтобы построить график функции
y=f(x)-m, где m – заданное положительное
число, нужно сдвинуть график функции
y=f(x) вдоль оси y на m единиц масштаба
вниз.
Постройте график
функции:
y х 2
2
1.Вспомогательная
система
координат:
х= 0
у= -2
х=0 у
4
3
2
1
y х 2
-3 -2 -1 0 1 2 3
-1
-2
-3
2. Привязываем к
-4
ней график функции
у=х²
Х 0
У 0
±1 ±2
-1 -4
2
х
у=-2
АЛГОРИТМ 2 (экономичный).
Чтобы построить график функции
y=f(x)+m нужно:
1. Перейти к вспомогательной системе
координат, проведя пунктиром
вспомогательные прямые х= 0, y=m, т. е.
выбрав в качестве начала новой системы
координат точку (0, m)
2. К новой системе координат привязать
график функции у=f(х).
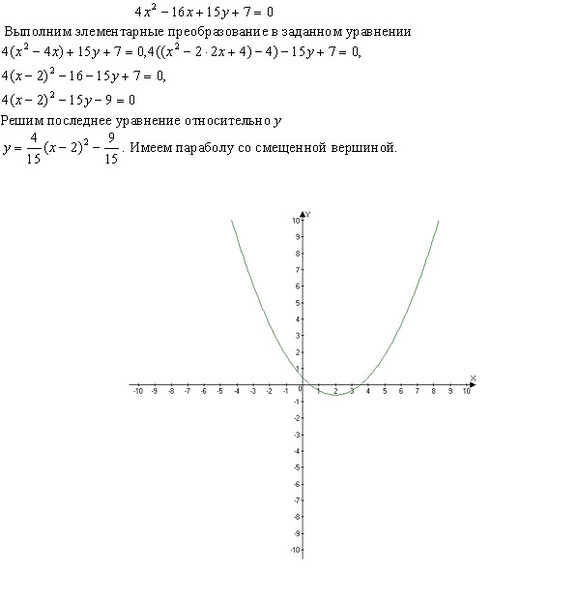
Постройте график
функции:
y 3х 2
2
1.Вспомогательная
система
координат:
х=0 у
2
1
у=2
-4 -3 -2 -1 0 1 2 3 4 5 6 7
-1
-2
2
y
3
х
2
-3
-4
-5
2. Привязываем к
-6
ней график функции
-7
-8
х= 0
у= 2
у=-3х²
Х 0
У 0
±1
-3
х
Постройте график
функции:
y 4х 5
2
1.Вспомогательная
система
координат:
х= 0
х=0 у
5
4
3
2
1
y 4 х2 5
-3 -2 -1 0 1 2 3
-1
-2
-3
2. Привязываем к
-4
ней график функции
-5
у=4х²
Х 0 ±1
У 0 4
х
у=-5
Постройте график
функции:
х=05
3
y 1
х
1.Вспомогательная
у
4
3
2
система
координат:
1
у=1
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
3
-2
у 1
-3
х
-4
2. Привязываем к
-5
ней график функции
х= 0
у= 1
3
y
х
Х
1
У
-3
3
6 -1
-1 -0,5 3
-3
-6
1
0,5
х
Постройте график
функции:
у
5
4
3
2
1
2
y 2
х
1.
Вспомогательнаясистема
координат:
х=0
2
y 2
х
-4 -3 -2 -1 0 1 2 3 4 5
х
-1
-2
у=-2
-3
-4
х= 0
у= -2
2. Привязываем к
ней график функции
2
y
х
Х
1
У
2
2
4 -1 -2 -4
1 0,5 -2 -1 -0,5
Найдите
унаиб. и унаим.
функции
у=-3х²+4
на отрезке
1; 0
Унаиб.= 4
Унаим.= 1
х=0 у
4
3
2
1
у=2
-4 -3 -2 -1 0 1 2 3 4 5 6 7
-1
-2
у=-3х²+4
-3
-4
-5
-6
х
Найдите
унаиб. и унаим.
2 -2
функции У= х
на отрезке
2 ; 2
Унаиб.=НЕТ
Унаим.=НЕТ
у
5
4
3
2
1
х=0
2
y 2
х
-4 -3 -2 -1 0 1 2 3 4 5
х
-1
-2
у=-2
-3
-4
8
Решить графически уравнение:
7
х²-3=2х
1
у=х²-3
Построим в одной системе
координат графики функций:
6 у
х=0 5
4
3
2
1
х
у=х²-3
В.С.К. х=0, у=-3
-4 -3 -2 -1 0 1 2 3 4
-1
у=х²
-2
Х 0 ±1±2±3
-3
у=-3
у=2х -4
У 0 1 4 9
у=2х
Найдём абсциссы точек
Х 0 2
2 пересечения графиков
ОТВЕТ: х=-1, х=3
3
Решить графически систему уравнений:
у=3х²+2
у=х+1
1
х=0 у
2
y 3х 2 4
Построим в одной системе
координат графики функций:
у=3х²+2
В.
С.К. х=0, у=2у=3х²
Х 0 ±1
У 0 3
Х 0 3
у=х+1
У 1 4
у=2
х
-3 -2 -1 0 1 2 3
-1
-2
у=х-3-3
-4
Найдём
координаты
точек 3
2 Нет
точек
пересечения
пересечения графиков
3
2
1
ОТВЕТ:
Нет решений
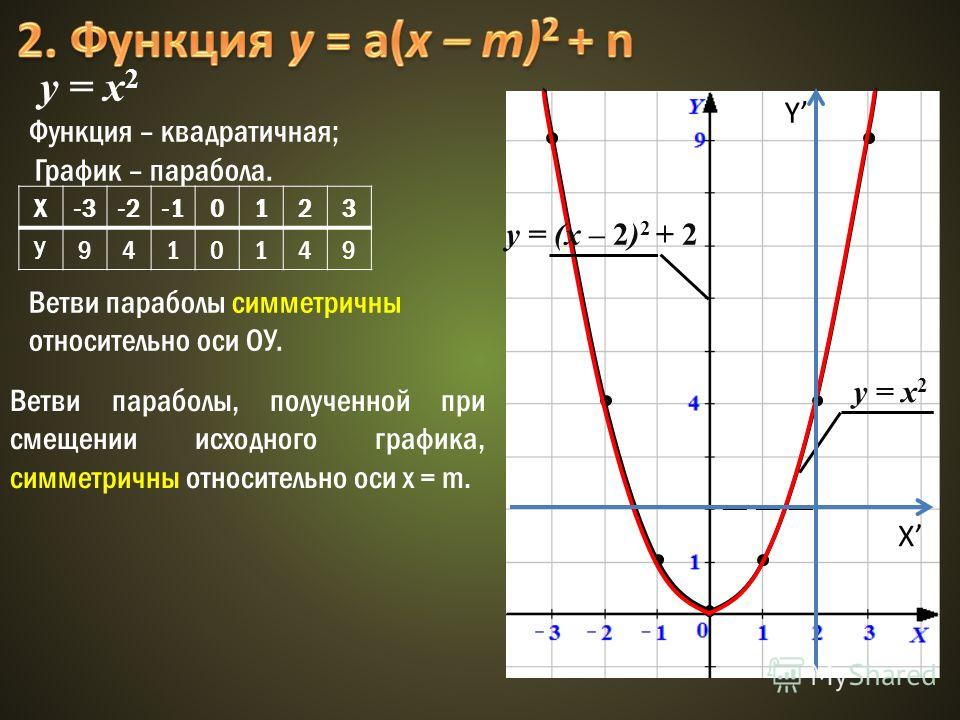
Постройте график функции
(x+2)²,если -4≤х≤0
f(x)= 4-х²,если х>0
и опишите её свойства.
(x+2)²,если -4≤х≤0
f(x)= 4-х²,если х>0
у=(х+2)²
у
у=х²
4
Х 0 ±1 ±2
У 0 1 4
-4 ≤ х ≤ 0
у= 4-х²=-х²+4
1
-4 -3 -2 -1 0 1 2 3
-1
у=-х²
Х 0 ±1 ±2
У 0 -1 -4
-4
х>0
х
Свойства функции:
1.Область
1. D ( f ) 4 ;
определения
E ( f ) ; 4
у
f(x)=
4
(x+2)²,если -4≤х≤0
4-х²,если х>0
2.
2.Область
значений
3. у=0, если х= -2 ; 2
у>0, если
х 4; 2 2; 2
1
х
у<0, если х 2;
4. Функция убывает
при х 4; 2 0;
Функция возрастает
при х 2 ; 0
ограничена сверху, но не ограничена
5.
ФункцияОграниченность
снизу.
унаиб.= 4
6. унаим.= НЕТ
7. Непрерывность
Непрерывна.
-4 -3 -2 -1 0 1 2 3 4
-2
Постройте графики функций:
у=2х²-5
у=х²+3
у=-0,5х²-1
у=3х²+2
у
у=3х²
у=2х²
4
3
2
1
у=х²+3
у=3х²+2
у=х²
х
-5 -4 -3 -2 -1 0 1 2 3 4 5
-1
у=-0,5х²-1
-2
-3
у=2х²-5
у=-4х²-3
-4
-5
у=-0,5х²
у=-4х²
у=-4х²-3
Для вывода на экран построений, нужно сделать клики на соответствующих
прямоугольниках (4 раза на каждом)
1
у 3
х
4
у 2
х
2
у 2
х
3
у 4
х
у
2
у3
у у 14х
х х
5
4
3
2
1
1 3
у y 3
х х
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2
-3
-4
-5
х
44
у y 2
хх
2
у 2
х
Для вывода на экран построений, нужно сделать клики на соответствующих
прямоугольниках (4 раза на каждом)
English Русский Правила
3-8Видеоурок: построение графиков квадратичных функций
Стенограмма видео
В этом видео мы научимся
построить график любой квадратичной функции, заданной в стандартной и вершинной формах, используя и
изучение его превращений.
Квадратные уравнения используются в повседневная жизнь. Они используются в науке, бизнесе, и машиностроение. Они могут помочь нам смоделировать пути движущиеся объекты, от прыгающих мячей до траекторий полета пчел. Предприятия используют их для прогнозирования доходы и дизайн упаковки для минимизации отходов. Далее, мы можем использовать квадратное уравнения для определения минимальных и максимальных значений множества различных переменных, включая скорость, стоимость и площадь.
Итак, давайте начнем с того, что вспомним, что мы
означает, когда мы говорим, что уравнение является квадратным. Квадратное уравнение – это уравнение, которое
можно записать в виде 𝑦 равно 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐. Теперь важно, чтобы 𝑎 не было
равны нулю, а 𝑎, 𝑏 и 𝑐 — действительные константы. На самом деле слово «квадратичный» происходит
от латинского «квадрат».
Это все уравнения, в которых
высшая степень 𝑥 равна двум; это в квадрате. Итак, как мы рисуем эти
графики? Начнем с того, что напомним себе
как выглядит график 𝑦 равно 𝑥 в квадрате. У него типичная парабола
форма. Он проходит через начало. А это, собственно, место
его вершины или точки поворота.
График 𝑦 равен отрицательному 𝑥
квадрат находится путем отражения этого графика по оси 𝑥. Итак, это перевернутая парабола с
его вершина в той же точке. Но что, если мы применим дальше
преобразования? Например, представьте, что мы хотим
нарисуйте график 𝑦 равно 𝑥 плюс четыре в квадрате. По сути, это горизонталь.
перевод. График сдвинется на четыре
остались единицы. И так мы видим вершину этого
график лежит в минус четыре, ноль. Тогда как насчет графика 𝑦
равно 𝑥 плюс четыре в квадрате плюс два? Ну, на этот раз, это вертикаль
перевод нашего предыдущего графика 𝑦 равен 𝑥 плюс четыре в квадрате.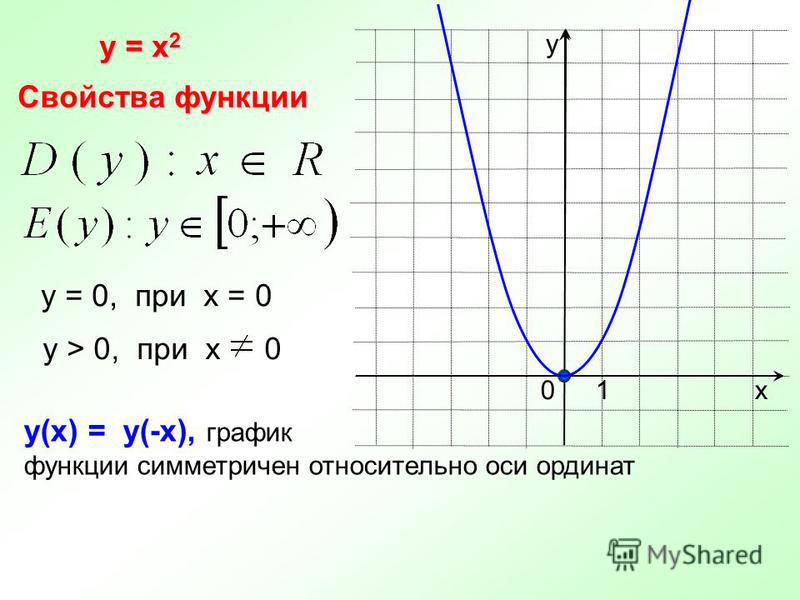
Как это поможет? Мы не хотим применять
ряд преобразований каждый раз, когда мы рисуем график. Ну, это означает, что если мы можем переписать
наше квадратное уравнение в форме 𝑎 умножить на 𝑥 плюс 𝑘 все в квадрате плюс ℎ, где 𝑘
и ℎ — действительные числа, можно сказать, что этот граф имеет вершину в точке
отрицательный 𝑘, ℎ. Это, конечно, в завершенном
квадратная форма. Итак, объединив это с тем, что мы знаем
о наброске любого графика, и у нас есть удобное руководство, мы начинаем, как и раньше. Мы просто проверяем форму
парабола. Если 𝑎 больше нуля — в
Другими словами, если коэффициент при квадрате 𝑥 положителен — мы имеем стандарт
форма параболы, где ее вершина является минимумом. Это самая низкая точка на
график.
Если же 𝑎 меньше нуля —
другими словами, коэффициент при квадрате 𝑥 отрицателен — мы имеем перевернутую
парабола. Таким образом, вершина на самом деле является
максимальная точка. Тогда так же, как если бы мы были
рисуя график линейной функции, находим 𝑦-перехват, полагая 𝑥
равный нулю и решающий для 𝑦. Точно так же мы можем найти место
любых 𝑥-перехватов, приравняв 𝑦 к нулю. Конечно, с этими графиками
очень возможно, что 𝑥-перехватов вообще нет. В этом случае, установив 𝑦 равным
ноль, и решение для 𝑥 не приведет к реальным решениям. Мы можем найти местонахождение
вершину, записав в виде заполненного квадрата. Итак, 𝑎 скобки 𝑥 плюс 𝑘 все
квадрат плюс ℎ имеет отрицательную вершину 𝑘, ℎ. Итак, с этими четырьмя шагами мы
затем может рисовать или даже распознавать графики квадратичных функций. Давайте продемонстрируем это в нашем первом
пример.
Какой график представляет функцию 𝑦 равно минусу 0,5𝑥 в квадрате плюс четыре?
Здесь квадратичный
уравнение. Мы можем идентифицировать его график по
выполнение ряда действий. Начнем с простого определения
правильная форма. Мы знаем, что если коэффициент
𝑥 квадрат положителен, то у нас есть стандартная парабола. Но если коэффициент 𝑥
квадрат отрицателен, у нас есть перевернутая парабола. В этом случае 𝑎 коэффициент
𝑥 в квадрате, минус 0,5. А это меньше нуля. Итак, у нас есть перевернутый
парабола. Это означает, что мы не можем выбрать (а) или
б) потому что они имеют стандартную форму параболы. Далее мы можем найти местоположение
𝑦-перехват, установив 𝑥 равным нулю. Когда мы это делаем, мы обнаруживаем, что
уравнение становится 𝑦 равным минусу 0,5, умноженным на ноль в квадрате, плюс четыре. А это равно четырем.
Итак, мы знаем, что 𝑦-перехват
в ноль, четыре. Это означает, что мы можем очень быстро
вариант (d) также не учитывать; у которого есть 𝑦-перехват в минус четыре.
Так что нам остается только с одним вариантом, вариант (c). Мы проверим это, позволив 𝑦 равен нулю и решение для 𝑥. И это скажет нам местоположение любых 𝑥-перехватов. Это ноль равняется минус 0,5𝑥 в квадрате плюс четыре. Добавление 0,5𝑥 в квадрате к обеим сторонам дает нам 0,5𝑥 в квадрате равно четырем. И затем, когда мы разделим на 0,5, получаем 𝑥 в квадрате равно восьми. Тогда мы можем извлечь квадратный корень из обе части этого уравнения. И мы должны помнить, чтобы взять оба положительный и отрицательный квадратный корень из восьми. Итак, 𝑥-перехваты или корни этого уравнения положительный и отрицательный корень восемь.
Тогда мы можем оценить стоимость
корень восемь, узнав, что он находится между квадратным корнем из четырех и квадратом
корень из девяти.
Так что, на самом деле, это между двумя и
три. И так как восемь ближе к девяти
чем к четырем, решение, скорее всего, будет ближе к трем, чем к
два. Ну, мы можем видеть 𝑥-перехваты
на нашей диаграмме чуть больше отрицательной тройки и чуть меньше
чем три. Итак, график, представляющий
задана функция (с).
В нашем следующем примере мы рассмотрим как манипулировать квадратным уравнением, чтобы найти его график.
Какой из следующих графиков представляет уравнение 𝑦 равно 𝑥 в квадрате минус пять 𝑥 плюс восемь?
Это квадратное уравнение. Итак, есть несколько вещей, которые мы можем сделать.
чтобы помочь нам идентифицировать его график. Во-первых, для квадратного уравнения
форма 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐, если коэффициент 𝑥 в квадрате 𝑎 равен
больше нуля, то это обычная форма параболы, которую мы ожидаем.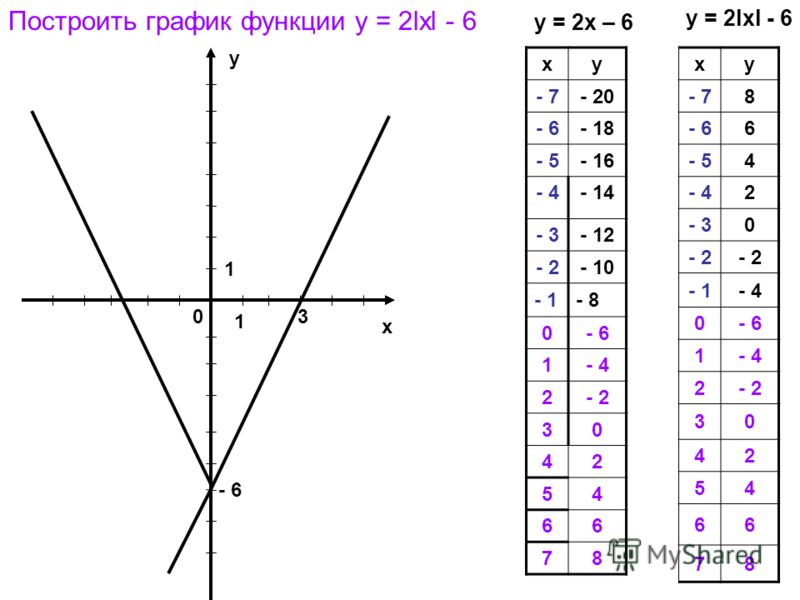
Но если 𝑎 меньше нуля, то
это перевернутая парабола. Ну, в нашем случае 𝑎 это просто
равен единице. У нас есть один 𝑥 в квадрате. Значит больше нуля. значит это не инвертор
парабола. И поэтому мы можем игнорировать варианты (C)
и (Д). Мы удалим их с экрана, чтобы
сделать больше места.
Далее мы можем найти местоположение
𝑦-перехват, приравняв 𝑥 к нулю. Когда мы это делаем, наше уравнение становится 𝑦
равно нулю в квадрате минус пять раз ноль плюс восемь, что равно восьми. Мы видим, что и (А), и (В) имеют
𝑥-перехват в восемь. Итак, давайте избавимся от варианта (E). Теперь нашим следующим шагом может быть поиск
расположение любых 𝑥-перехватов, приравняв 𝑦 к нулю. Но на самом деле ни то, ни другое
графы имеют 𝑥-перехваты. И мы проверим это в
немного больше подробностей в данный момент. Поэтому вместо этого мы напишем
наше уравнение в форме заполненного квадрата, другими словами, в виде 𝑎 𝑥 плюс 𝑘 все
в квадрате плюс ℎ.
Если мы можем записать в такой форме, то
мы знаем, что у него есть отрицательная вершина 𝑘, ℎ.
Теперь коэффициент 𝑥 в квадрате
здесь один, поэтому заполнить квадрат относительно просто. Начнем с уменьшения вдвое коэффициента
из 𝑥, так что половина минус пять. Это минус пять больше двух. Поэтому в скобках мы пишем 𝑥
минус пять больше двух, и все в квадрате. Затем мы вычитаем квадрат этого
ценность. Итак, мы вычитаем минус пять из всех
в квадрате. И тогда мы добавляем восемь. Это то же самое, что вычесть 25
более четырех. И если мы напишем восемь как 32 над
четыре, то мы можем сложить эти две дроби. Минус 25 больше четырех плюс 32 больше
четыре семь больше четырех. И так в завершенном квадратном виде,
наше уравнение 𝑥 минус пять на два в квадрате плюс семь на четыре. Значит, его вершина имеет координаты
пять больше двух, семь больше четырех.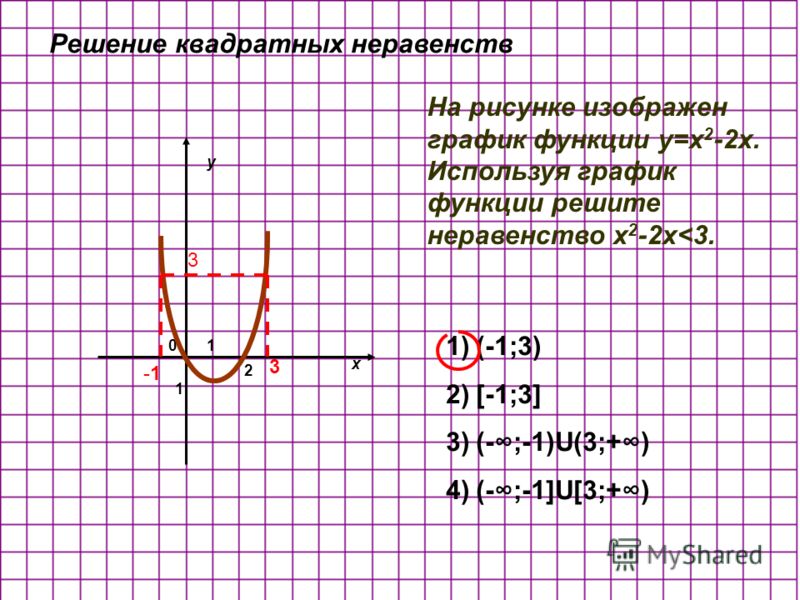
Поскольку и 𝑥-, и 𝑦-координата здесь положительна, вершина нашего графа должна лежать в первой квадрант. Итак, ответ (А), а не вариант (В). И в этот момент мы можем перепроверьте, что происходит с 𝑥-перехватами. Мы находим их, полагая 𝑦 равным нуль. И один из способов решения уравнения затем использовать заполненную квадратную форму. Мы вычитаем семь на четыре из обе стороны, и тогда мы замечаем, что нашим следующим шагом будет взятие квадрата корень. Но, конечно, квадратный корень из отрицательное число не является реальным значением. Так что нет реальных решений, когда мы принимаем 𝑦 равным нулю, что означает отсутствие 𝑥-перехватов. И ответ поэтому вариант (А).
Что если нам дан график
функции и попросили найти ее квадратное уравнение? Это очень похожий процесс. мы по сути работаем
назад.
Итак, в нашем следующем примере давайте посмотрим
как бы это выглядело.
Напишите квадратное уравнение представлена показанным графиком. Дайте ответ с учетом форма.
Начнем с изучения графика нам дали. Мы могли бы сначала заметить, что вершина или точка поворота этого графика имеет координаты один минус девять. Это дает нам некоторое представление о том, что может выглядеть законченное уравнение квадратной формы этого графика. Уравнение вида 𝑎 𝑥 плюс 𝑘 квадрат плюс ℎ имеет отрицательную вершину 𝑘, ℎ. Итак, пусть отрицательный 𝑘 будет равен единица и ℎ равны минус девяти. И мы видим, что уравнение нашего график 𝑦 равен некоторой константе 𝑎, умноженной на 𝑥 минус единица в квадрате минус девять.
Так как же нам найти значение
𝑎? Ну, на самом деле, мы можем выбрать
координаты любой точки, лежащей на этой кривой, и подставьте ее.
координата четыре, ноль. 𝑥-координата равна четырем, а
𝑦-координата равна нулю. И поэтому наше уравнение становится равным нулю
равно 𝑎, умноженное на четыре минус один в квадрате минус девять. Ну, четыре минус один в квадрате
три в квадрате, что девять. Таким образом, наше уравнение становится равным нулю
девять 𝑎 минус девять. Мы добавляем девять к обеим сторонам этого
уравнение. И, наконец, мы разделим
к девяти. И когда мы это делаем, мы обнаруживаем, что 𝑎
равен единице. Подставив это обратно в
уравнение 𝑎 умножить на 𝑥 минус один все в квадрате минус девять, и мы находим, что уравнение
этого квадратного числа 𝑦 равно 𝑥 минус один в квадрате минус девять.
Теперь, по сути, нам говорят дать
это в факторизованной форме. Так, что дальше? Ну, мы просто собираемся
распределите скобки, упростите, а затем разложите.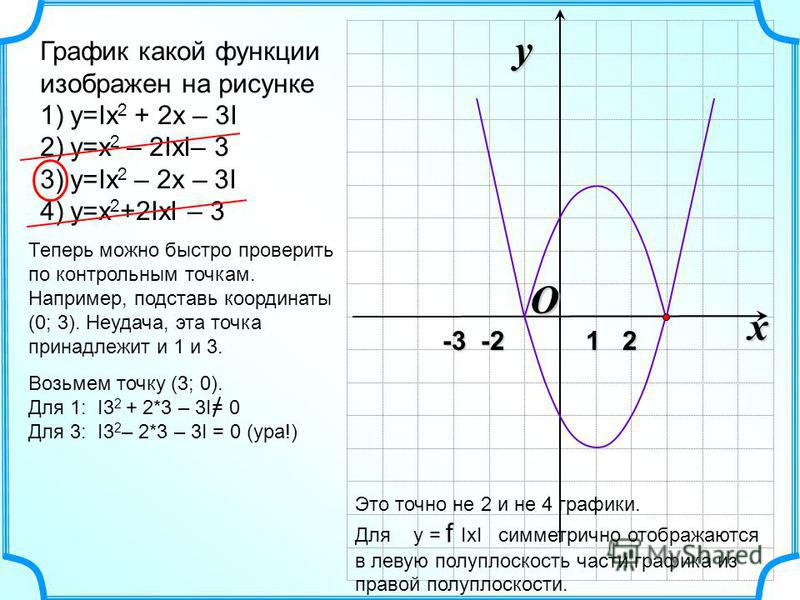
𝑥 минус один в квадрате равно 𝑥
минус один раз 𝑥 минус один. Распределение скобок и
мы получаем 𝑥 в квадрате минус 𝑥 минус 𝑥 плюс один. Итак, наше уравнение становится 𝑦
равно 𝑥 в квадрате минус два 𝑥 минус восемь. Чтобы учесть это, мы просто находим
пара чисел, у которых есть произведение отрицательной восьмерки и сумма, чтобы сделать отрицательным
два. Это минус четыре и два. Итак, в факторизованной форме
квадратное уравнение, представленное показанным графиком, равно 𝑦 равно 𝑥 минус четыре раза
𝑥 плюс два.
Давайте вспомним ключевые понятия из
этот урок. Мы можем нарисовать график
квадратное уравнение в форме 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐, сначала взглянув на
коэффициент 𝑥 в квадрате. Если он положительный, то график представляет собой
парабола. А если отрицательный, то
перевернутая парабола.