| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.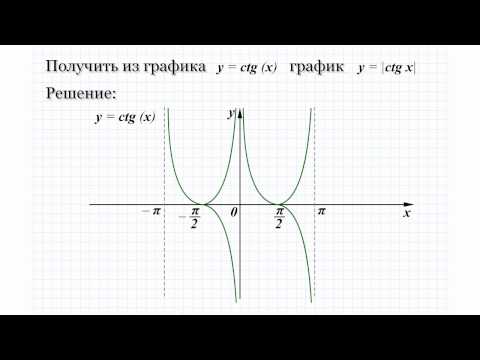 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.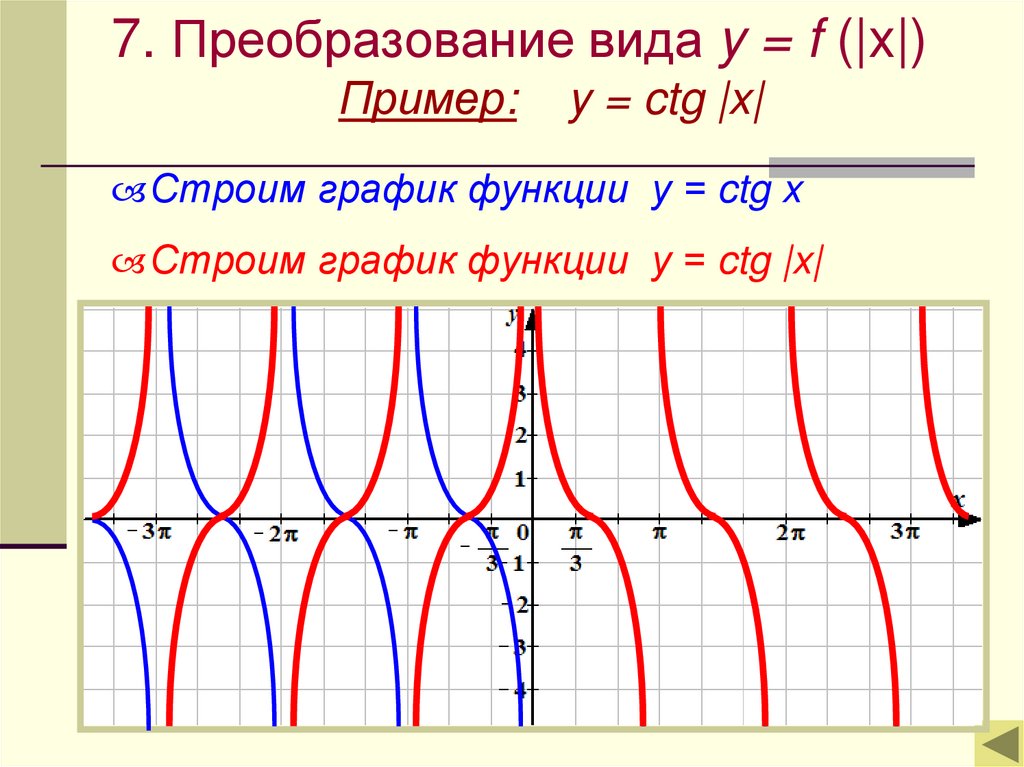 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.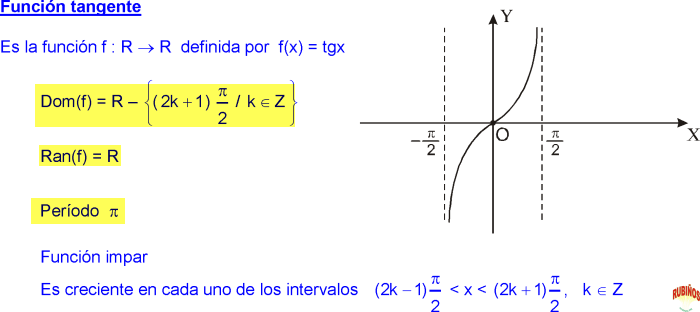 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.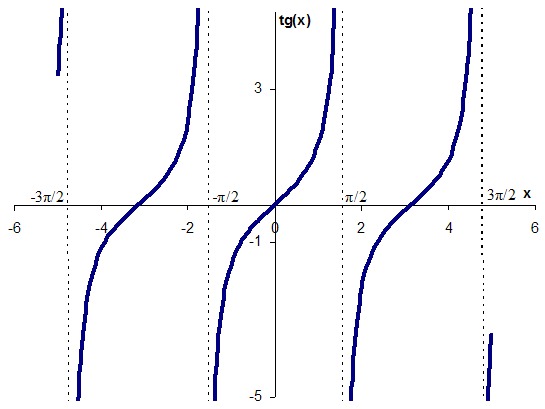 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | ||
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.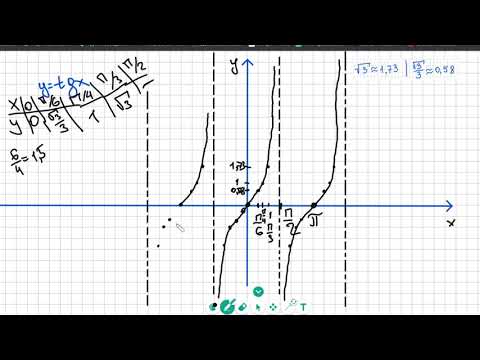 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | arcsin(-1/2) | ||
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.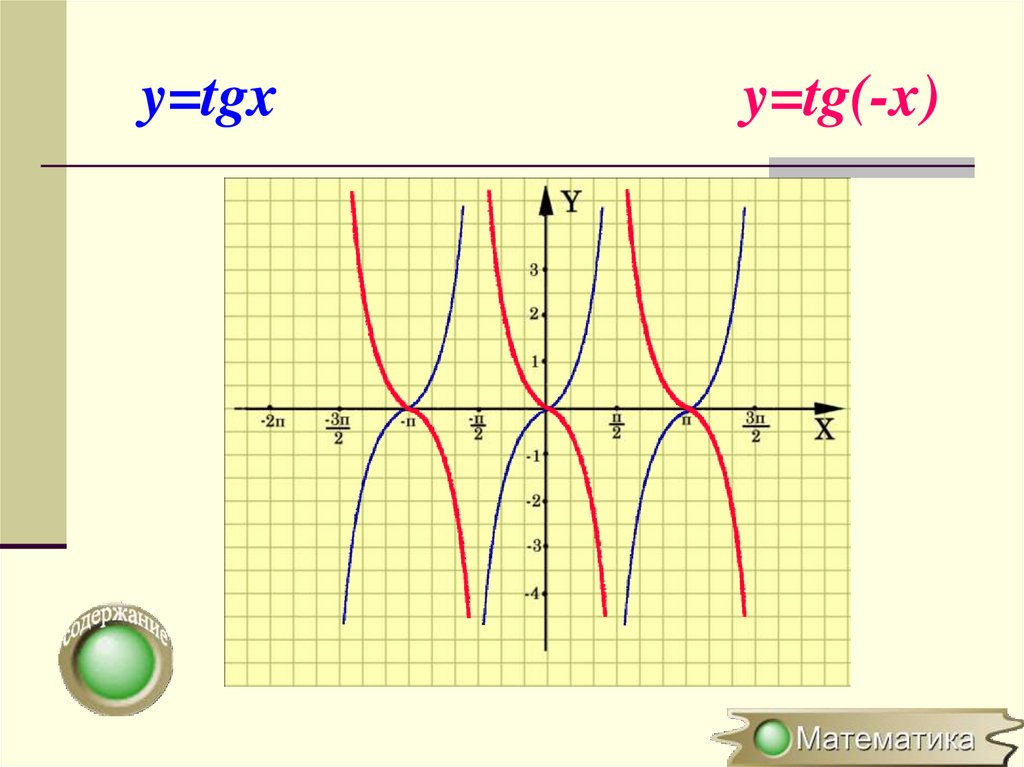 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | ||
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.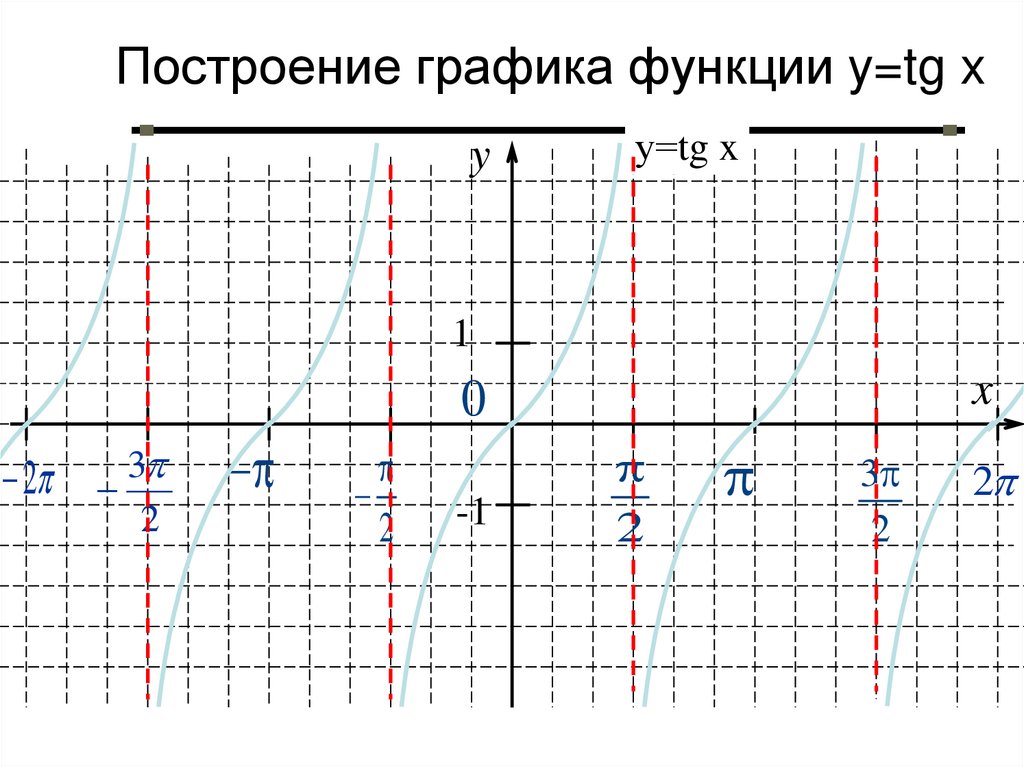 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
Точка движется в плоскости XOY. 2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные
2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные
Построить график функции y=2x-2 и определить проходит ли график через точку:A(10;-20)
Пользуйтесь нашим приложением
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Тригонометрические функции и их графики: тангенс
Со-функции синусов и косинусов
Purplemath
На предыдущей странице мы рассмотрели, как отношения синусов и косинусов для прямоугольных треугольников могут быть расширены с помощью единичного круга до полноценных графических функций.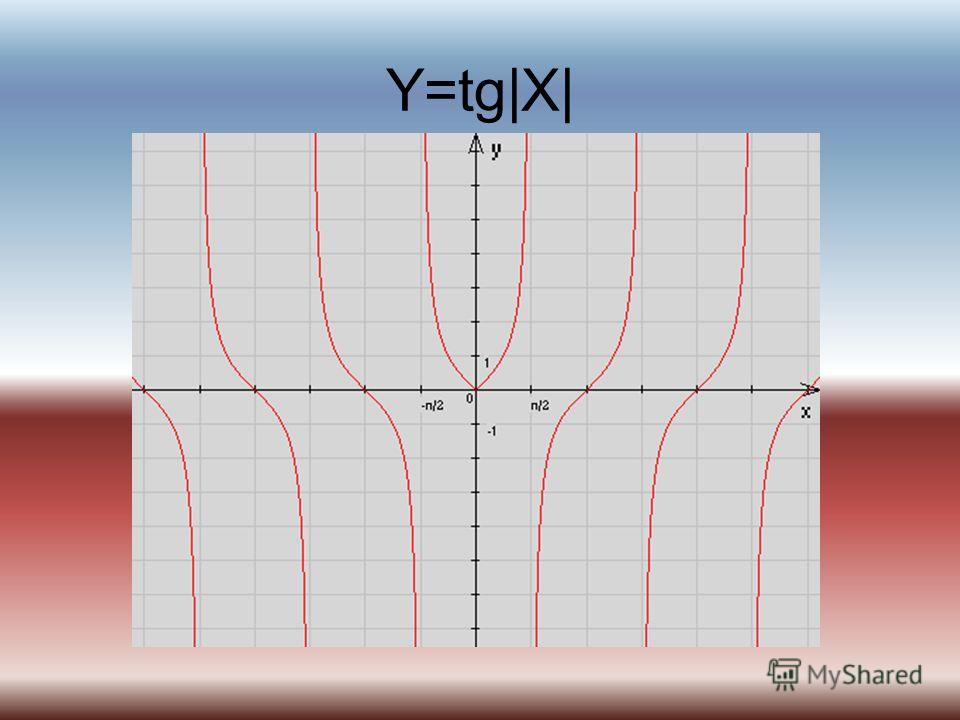 Следующее тригонометрическое соотношение, которое мы рассмотрим, — это отношение тангенса. Но значения касательной трудно отобразить на единичной окружности. Это связано с тем, что тангенс формируется путем деления значения единичного круга для синуса на его значение для косинуса, каждое из которых иногда равно нулю, а мы не можем делить на ноль.
Следующее тригонометрическое соотношение, которое мы рассмотрим, — это отношение тангенса. Но значения касательной трудно отобразить на единичной окружности. Это связано с тем, что тангенс формируется путем деления значения единичного круга для синуса на его значение для косинуса, каждое из которых иногда равно нулю, а мы не можем делить на ноль.
Итак, вместо этого давайте подробнее рассмотрим графики синусов и косинусов, помня о том, что tan(θ) равен этому делению: sin(θ) ÷ cos(θ).
Содержимое продолжается ниже. Синус равен нулю в точках 0, π, 2π, 3π и т. д., а также в точках −π, −2π, −3π и т. д.; то есть тангенс будет иметь нулевое значение при каждом кратном π. Давайте пока рассмотрим только область от −π до 2π. Таким образом, касательная будет равна нулю (то есть пересечет x -ось) при -π, 0, π и 2π.
Тангенс, будучи дробью, будет неопределенным , где бы его знаменатель (то есть значение косинуса для этой меры угла) не равнялся нулю. И, возвращаясь к тому времени, когда вы узнали о построении графиков рациональных функций, вы знаете, что ноль в знаменателе функции означает, что у вас будет вертикальная асимптота.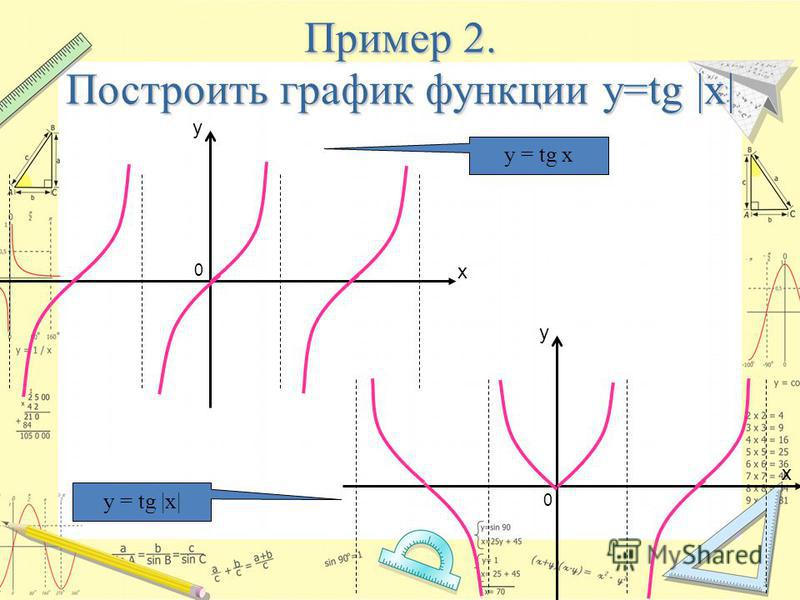 Таким образом, тангенс будет иметь вертикальные асимптоты везде, где косинус равен нулю. Придерживаясь того же интервала от -π до 2π, вертикальные асимптоты будут при -π/2, π/2 и 3π/2. Другими словами, между каждым числом, кратным π, будет вертикальная асимптота.
Таким образом, тангенс будет иметь вертикальные асимптоты везде, где косинус равен нулю. Придерживаясь того же интервала от -π до 2π, вертикальные асимптоты будут при -π/2, π/2 и 3π/2. Другими словами, между каждым числом, кратным π, будет вертикальная асимптота.
Точно так же, как отношения синуса и косинуса были преобразованы в функции, мы также можем преобразовать отношение тангенса в функцию. Тангенс неявно будет чем-то вроде рациональной функции, за исключением того, что его отношение образуется путем деления двух тригонометрических функций (а не двух многочленов). Эта функция обозначается как tan() или просто [TAN] на вашем калькуляторе. Эта функция периодична, как и синус и косинус, образующие тангенс. Но график не может быть хорошей простой волной, не в последнюю очередь из-за вертикальных асимптот.
График функции тангенса
Чтобы построить график тангенса, начнем с «интересных» точек, то есть с нулей и асимптот. Поставьте точки вместо нулей и пунктирные вертикальные линии для асимптот:
← смахните , сколько нужно, чтобы просмотреть полное изображение →
Но куда же идет функция от этих нулей? Здесь мы используем то, что знаем о синусе, косинусе и асимптотах, чтобы заполнить остальную часть графика касательной. Рассмотрим интервал между нулем в точке 0π и асимптотой в точке ½π.
Рассмотрим интервал между нулем в точке 0π и асимптотой в точке ½π.
- Мы знаем, что график никогда не коснется и не пересечет вертикальные асимптоты
- Мы знаем, что между нулем и асимптотой график будет либо ниже оси (и скользить вниз по асимптоте до отрицательной бесконечности), либо выше оси (и тоньше вверх по асимптоте до положительной бесконечности).
- Между нулем и π/2 и синус, и косинус положительны.
- Тогда тангенс, являющийся их частным, также должен быть положительным, поэтому график скользит вверх по асимптоте. 909:40
Имея эту информацию, мы можем начать наш график:
← пролистните сколько нужно, чтобы просмотреть полное изображение →
Теперь давайте рассмотрим следующий интервал. Между π/2 и π синус положительный, а косинус отрицательный. Эти противоположные знаки означают, что тангенсное частное будет отрицательным, поэтому оно будет скользить вверх по правой стороне асимптоты снизу, изгибаться и встречаться с осью x в точке x = π.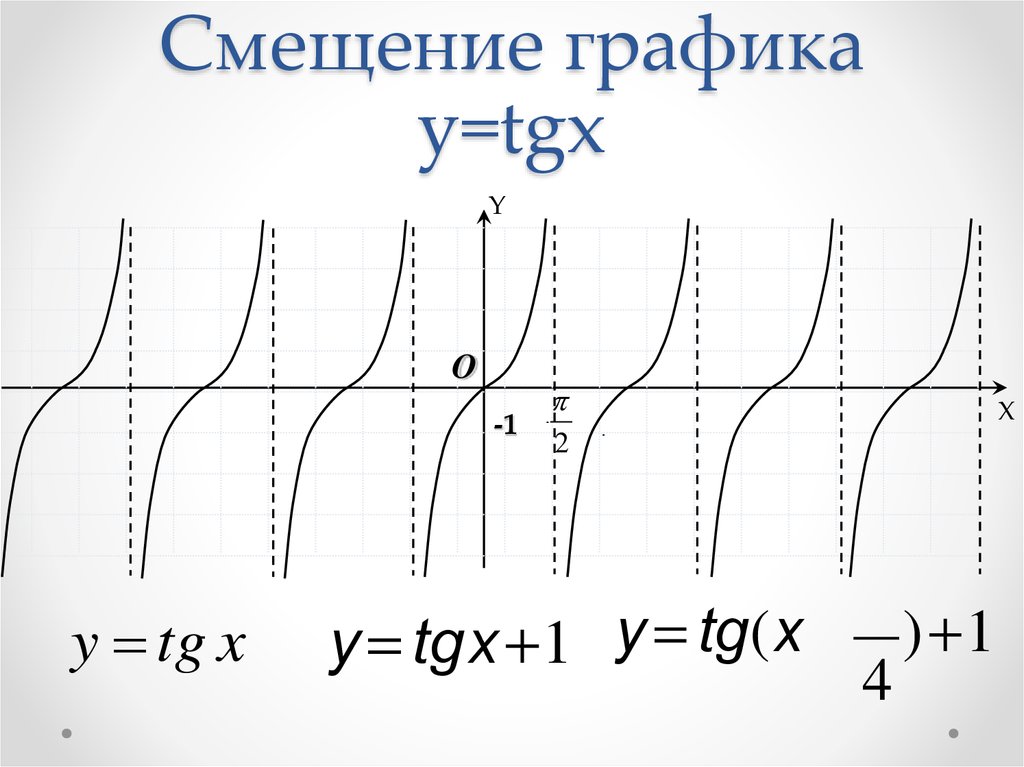 Давайте нарисуем этот бит:
Давайте нарисуем этот бит:
← смахните , чтобы просмотреть полное изображение →
Поскольку синус и косинус являются периодическими, то тангенс также должен быть периодическим. Быстрая проверка знаков подсказывает нам, как заполнить остальную часть графика:
- от −π до −π/2: синус отрицательный, а косинус отрицательный, поэтому тангенс положительный; эта часть графика должна дублировать график между 0 и ½π
- от −π/2 до 0: синус отрицательный, а косинус положительный, поэтому тангенс отрицательный; эта часть графика должна дублировать график между ½π и π 909:40
- π в 3π/2: синус отрицательный, а косинус отрицательный, поэтому тангенс положительный; часть графика должна дублировать график между 0 и ½π
- От 3π/2 до 2π: синус отрицательный, но косинус положительный, поэтому тангенс отрицательный; эта часть графика должна дублировать график между ½π и π
Используя эту периодичность (повторяющуюся для каждого числа, кратного π), теперь мы можем завершить наш график:
← смахните , чтобы просмотреть полное изображение →
Как видите, тангенс имеет период π, причем каждый период отделен вертикальной асимптотой.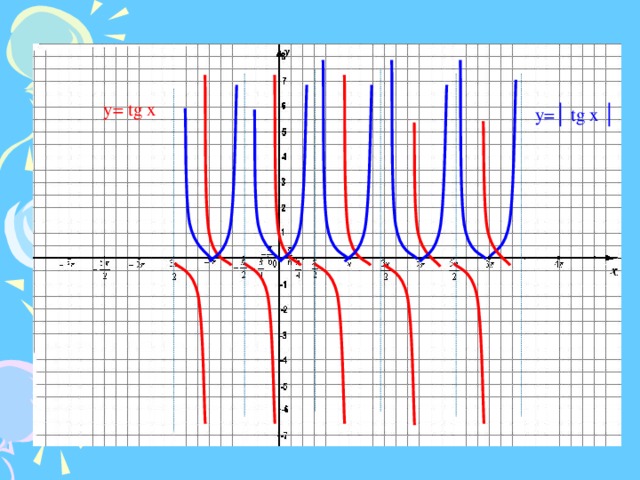 Понятие «амплитуда» действительно не применяется. Благодаря асимптотам значения тангенса не ограничены; то есть значения изменяются от -∞ до +∞; диапазон вывода y -значения «все».
Понятие «амплитуда» действительно не применяется. Благодаря асимптотам значения тангенса не ограничены; то есть значения изменяются от -∞ до +∞; диапазон вывода y -значения «все».
При построении графика придерживайтесь «интересных» точек. Нарисуйте нули на x = 0, π, 2π и т. д. (они совпадают с нулями синуса), а затем прочеркните вертикальные асимптоты посередине между каждым нулем. Затем нарисуйте кривую. Вы можете нанести еще несколько точек, если хотите, но обычно от этого мало что выигрывают.
Если вы предпочитаете запоминать графики, запомните интервал по вашему выбору из графика выше. Вы можете предпочесть интервал 0 и π или, возможно, −½π и асимптоту при ½π. Все, что вам покажется полезным, является «правильной» вещью для запоминания. Что касается меня лично, у меня всегда были проблемы с поддержанием прямолинейности чего-либо, выходящего далеко за пределы синуса и косинуса, поэтому я использовал рассуждения, продемонстрированные выше, чтобы выяснить графики тангенса (и кофункции).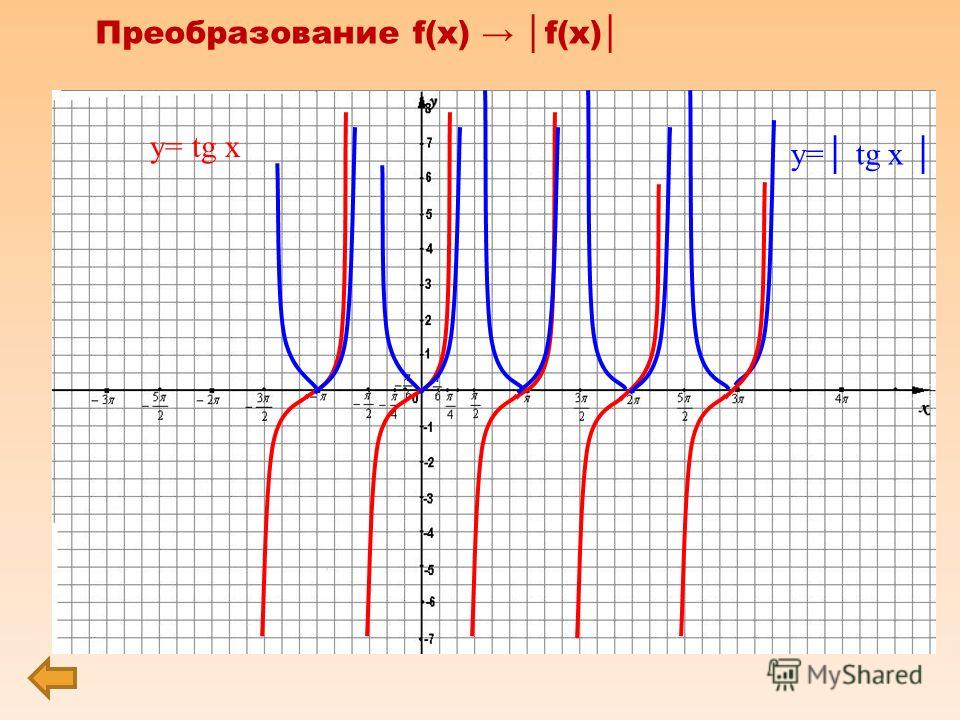

 09.17
09.17