404 — Страница не найдена
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
by/algebra/funkcii/funkcija-ysinx] не найдена.
05.13 
by 2013-2016Функции и Графики — сайт по математике и не только!!! Всё о Математических функциях и их графиках…
Функции и Графики — сайт по математике и не только!!! Всё о Математических функциях и их графиках…
|
Используются технологии uCoz |
Нарисовать график y = sin x
- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10
- Класс 9 9000 3 Класс 8
- Класс 7
- Класс 6
- NCERT
- IIT JEE
- Exam
- JEE MAINS
- JEE ADVANCED
- ПЛАТЫ X
- ПЛАТЫ XII
- NEET 9004 0
- Новый предыдущий год (по годам)
- Физика Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Нет Все образцы работ
- Образцы работ Биология
- Образцы работ Физика
- Образцы работ Химия
- Скачать PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- Экзаменационный уголок
- Онлайн-класс
- Викторина
- Задать вопрос в Whatsapp
- Поиск Сомнения
- 900 03 Английский словарь
- Toppers Talk
- Блог
- О нас
- Карьера
- Скачать
- Получить приложение
Вопрос
Обновлено: 26/04/2023
Рекомендуемые вопросы
9 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Видео по теме
Нарисуйте график зависимости y=xsinx.
642540663
04:55
Нарисуйте график зависимости y=sinxx.
642540699
02:26
Нарисуйте график y=sin−1(sinx)
642542767
04:38
Нарисуйте график y=sinx и y=sin.x2.
644016228
01:37
Нарисуйте график зависимости y=sin|x| .
645278574
01:42
Нарисуйте график зависимости y = x sin x.
645279450
06:19
Нарисуйте график y = (sin x)/(x) .
645279486
01:42
Нарисуйте график зависимости y=sin|x| .
646278291
03:10
РЕКЛАМА
Рекомендуемые вопросы
Нарисуйте график y = sin x
04:34 9(-1)(sin x)
Текст Решение
y =sin x ग्राफ खींचिए|
02:42
Нарисуйте график зависимости y=sin x и y=sin . (х)/(2).
03:16
Нарисуйте график зависимости y=sin|x|.
02:19
- Ask Unlimited Doubts
- Видео решения на нескольких языках (включая хинди)
- Видео лекции экспертов
Doubtnut хочет отправлять вам уведомления.
Разрешите получать регулярные обновления!
Слушаю…
Тригонометрия — Интуитивное объяснение графика $y = \sin x$
спросил
Изменено 11 лет, 4 месяца назад
Просмотрено 2к раз
$\begingroup$
Возможный дубликат:
Intuition для построения графика синуса/косинуса
Мы все видели график $y = \sin x$
(я не могу опубликовать изображение из-за репутации, поэтому я разместил ссылку на график)
Синусоидальный график Изображение
Сейчас выключено , единственные определения синуса, которые я понимаю, — это определение «отношения в треугольнике» и определение «единичного круга».
Поэтому я надеюсь, что можно ответить на мой вопрос, используя одно из этих определений.
Из этого определения легко понять, почему при ($0,5\pi$) радианах значение $y$ равно $1$, легко понять, почему при пи радианах значение $y$ равно $0$, и я, конечно, понимаю, почему функция повторяется каждые $2 \pi$ радиан, используя определение единичного круга.
Чего я не понимаю, так это почему он имеет именно такую форму, почему он выглядит так, как будто он находится между 0 и 0,5 Пи, почему он имеет именно такую вогнутость?
- У этого есть интуитивное объяснение?
- Как первые математики рисовали эту функцию, действительно ли они измеряли синус всех углов линейкой, а потом рисовали график?
- тригонометрия
- функции
- графические функции
$\endgroup$
1
$\begingroup$
Эта анимация скорее всего вам поможет! Ваше здоровье! 🙂
$\endgroup$
$\begingroup$
Вы спрашиваете, почему график $\sin$ выглядит именно так, как на $[0,\pi/2]$.
Вы можете легко (с помощью некоторых тригонометрических формул) вычислить значения $\sin x$ для $x=0,\pi/6,\pi/3,\pi/4,\pi/2, \pi/ 12,\пи/5$. Постройте эти значения.
Имейте в виду, что $\sin$ непрерывна как отношение двух непрерывных функций (противоположная сторона/гипотенуза). Он возрастает, так как при увеличении угла увеличивается и синус. Попробуйте сейчас и начертите $\sin$, зная только вышеупомянутые факты. Вы увидите, что это приближение графика похоже на приближение вогнутой функции. Конечно, вогнутость можно доказать с помощью тригонометрической формулы. Вы просили что-то более интуитивное.
[Могу я спросить, почему вы задали этот вопрос? Мне просто интересно. Не поймите неправильно, но спрашивать, почему $\sin$ вогнута между $0$ и $\pi/2$, все равно что спрашивать, почему буква $A$ выглядит именно так. Это один из элементарных блоков математики. Нет правильного ответа, почему график выглядит именно так. Это выглядит так из-за свойств функции $\sin$.]
$\endgroup$
3
$\begingroup$
Представьте себе точку, движущуюся по единичной окружности, начиная с $(1,0)$ и двигаясь против часовой стрелки.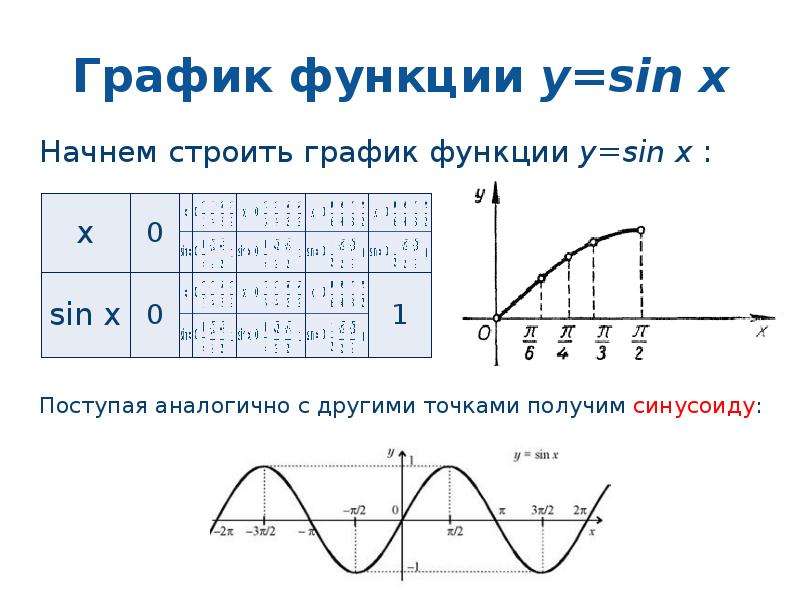
Координата $y$ точки равна $\sin\theta$, где $\theta$ – угол между точкой, началом координат и точкой $(1,0)$ (и, конечно, измеренный положительный в направлении против часовой стрелки с положительной осью $x$, соответствующей $\theta=0$).
Теперь, когда точка перемещается из $(1,0)$ в $(0,1)$, что происходит с координатой точки $y$? Что ж, оно возрастает от 0 до 1. Итак, график $\sin\theta$ (с $\theta$ в качестве горизонтальной оси) возрастает по $[0,\pi/2]$ от 0 до 1.
Если вы представите точку, пересекающую всю единичную окружность, вы должны быть в состоянии убедить себя, что, по крайней мере, с точки зрения «возрастания или убывания» и с точки зрения того, где находятся нули и максимумы/минимумы, график $\sin$ как есть. 9\circ$, с помощью элементарной геометрии легко понять, почему значения синуса должны быть именно такими, какие они есть ($1/2$ и $\sqrt{3}/2$. Для других нужно действовать тоньше.
$\endgroup$
$\begingroup$
- 1.
Я изучил функцию sin как качающийся объект. Вы увидите $y$ как расстояние от центра и $x$ как прошедшее время. Обратите внимание, что качающийся объект дольше всего остается сбоку ($x = k*π$, $y = 0$) и быстро проходит через центр ($x = (k+1/2)*π$, $у = 1$).
Это также объясняет производную от $sin x$, которая равна $cos x$. Производная от позиции — это скорость, которая отображается на графике $cos x$. Объект проходит через центр с максимально возможной скоростью и останавливается на очень короткое время в самой удаленной от центра точке.
Попробуйте сами, просто качайте что-нибудь (например, часы на цепочке) и представьте себе функцию $sin x$.
2.
(Чисто предположение, у меня нет источника)
Лично я думаю, что ранние математики тянули «бумагу» под качающийся объект, оставляющий за собой след. Вы получите синусоидальную функцию, если будете тянуть бумагу с обычной скоростью.
Может быть, у них не было ни бумаги, ни ручки, но это самый естественный способ нарисовать такой график.
$\endgroup$
$\begingroup$
Функции $\sin$ и $\cos$ являются результатом функции, которая экспоненциально проецирует прямую (числовую прямую $\mathbb{R}$) на окружность с радиусом $r=1$. Вот определение функции:
$E: \mathbb{R} \mapsto k$
для $t \in [0, 2\pi\rangle, E(t)=T$, так что $|IT|$( это арка )=t и эта арка $IT$ положительно ориентирована ( против часовой стрелки )
для $t \in \mathbb{R}\backslash [0, 2\pi\rangle, E(t)=E(t_0) $ где $t=t_0 +2k\pi,k\in \mathbb{Z},t_{0}=[0, 2\pi\rangle$
Точка I расположена на $(1,0)$.
Из этого определения теперь ясно видно, что то, что вы в основном делаете, это, неформально говоря, «рисование» $\mathbb{R}$ в круг, а круг может иметь значения только в диапазоне $t[0, 2\pi \rangle$. Вот кое-что интересное происходит. Поскольку вы представляете числа на круге, вам легче определить, где находится $\pi$ (трансцендентное число), чем число $1$, например.