Графики функции, производной, первообразной — Умскул Учебник
На этой странице вы узнаете- Где проходит граница между теплом и холодом?
- Почему успех фильма не всегда зависит от наличия экшн-сцен?
- Чем кофе похож на функцию, ее первообразную и производную?
Многие из нас чем-то похожи на родителей. Не являясь их точной копией, мы перенимаем определенные черты. То же самое происходит и с графиками. О том, какие особенности “наследуют” друг у друга графики функции, производной и первообразной, поговорим в статье.
Связь графика функции и производнойПодготовим карандаши и линейки, мы начинаем погружение в мир графиков. Почему графики — это круто? Они дают нам наглядное представление о функции. Мы можем проанализировать ее, не прибегая к сложным формулам и трудоемким вычислениям.
Воспринимать визуальную информацию всегда легче. А графики — это как раз визуальное описание функции.
Возьмем график произвольной функции.
Прежде чем приступать к дальнейшему изучению материала, рекомендуем ознакомиться с «Определением и графиком функции», а также «Производной».
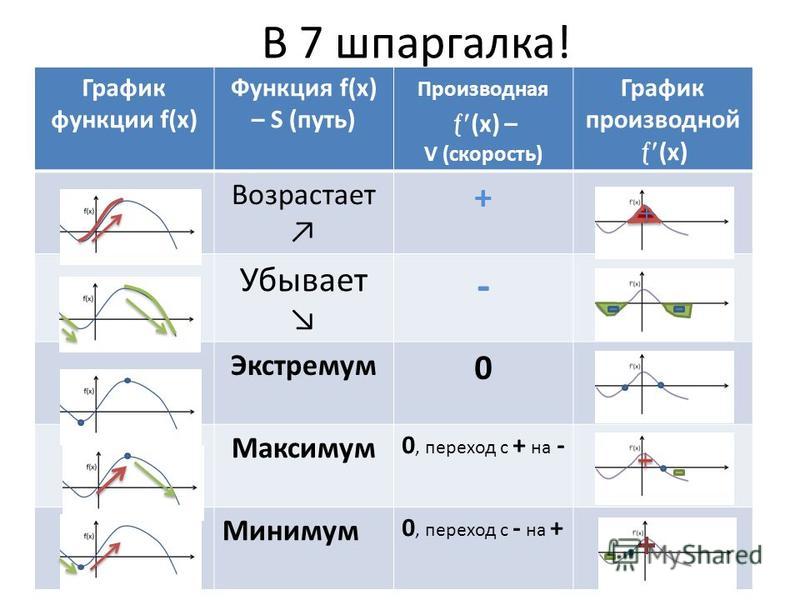
Мы точно видим, на каких промежутках график будет возрастать, а на каких убывать. Если представить, что мы пойдем по направлению оси х, то график будет возрастать на подъемах в горку и убывать на спусках с нее. Отметим промежутки возрастания зеленым фоном, а промежутки убывания красным.
В зеленых промежутках производная будет положительна, а в красных отрицательна. Пока что просто запомним этот факт.
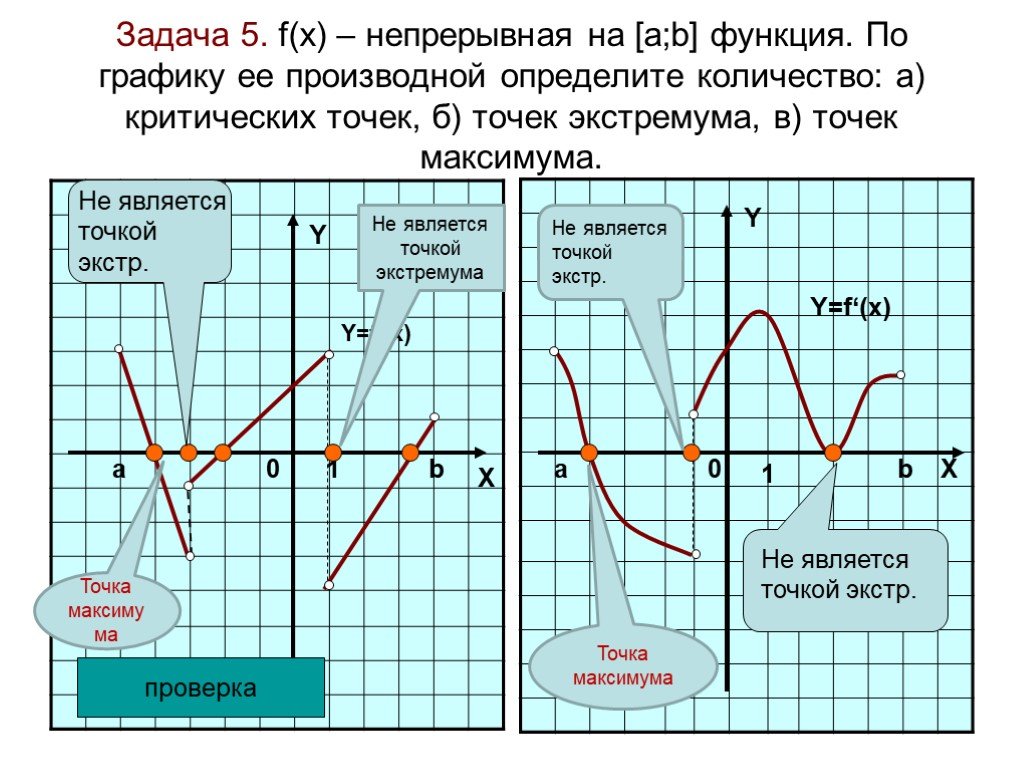
Обратим внимание на границы между зелеными и красными зонами. В этих точках функция будет менять свой знак с положительного на отрицательный или обратно. Такие точки называются точками экстремума.
Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.
Точки экстремума — точки, в которых достигается экстремум.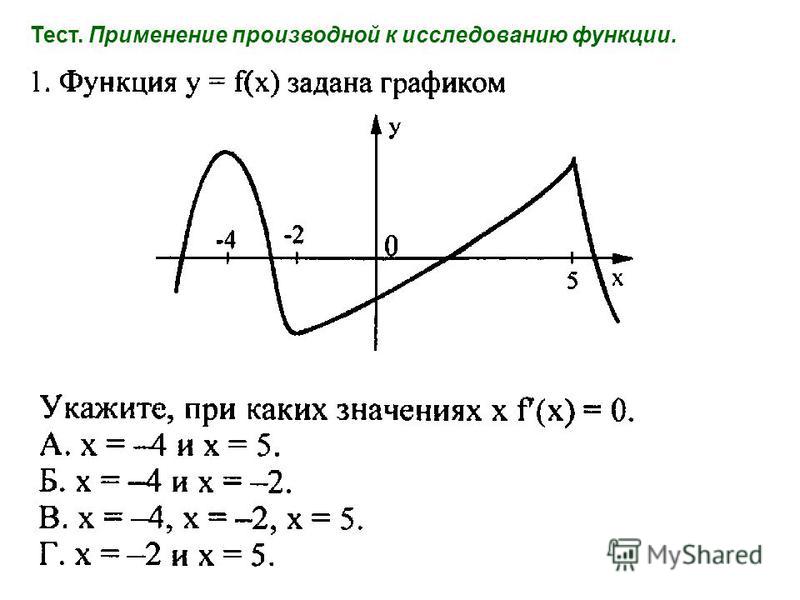
В точках экстремума производная равна 0.
Теперь попробуем построить примерный график производной. Для начала опустим точки экстремума. Где они будут лежать на графике производной? На оси х.
Вспомним, что в точках экстремума производная функции будет равна 0. Пусть график будет задан
y = f'(x), тогда в точках экстремума получаем y = 0. Это и есть ось х.
Так мы получили целых 9 точек, через которые пройдет производная. Осталось провести через них примерный график.
Вспомним, что:
- производная положительна на промежутках возрастания функции;
- производная отрицательна на промежутках убывания функции.
Как понять, что все точки на графике производной будут положительны или отрицательны? Достаточно посмотреть на то, с какой стороны от оси х они располагаются.
Положительные значения всегда будут лежать выше оси х. Это связано со значением y: значения функции будут положительны при положительных значениях у, и отрицательны при отрицательных значениях у.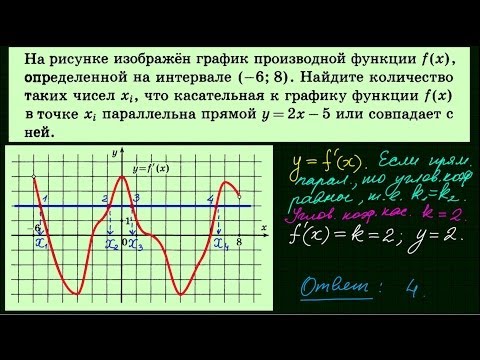
| Где проходит граница между теплом и холодом? Можно представить, что ось х — это полюс, который разделяет тропики и льды. Над осью х всегда будет светить солнце, а температура будет положительной. А вот под осью х всегда будут льды и снега, и температура — отрицательной. Следовательно, знак производной на ее графике будет совпадать со знаком температуры в тропиках или льдах. |
Итак, как нам нарисовать график производной? На зеленых участках ее график будет лежать над осью х, а на красных участках — под ней.
Подведем итоги:
- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.

Эти зависимости можно отследить на любых графиках функции и ее производной.
Если провести обратные рассуждения, то по графику производной можно восстановить примерный график функции. В этом случае:
- В точках, где график производной пересекает ось х, будут лежать точки экстремума. При этом если в точке производная меняет значение с положительного на отрицательное, то это точка максимума, а если с отрицательного на положительное, то это точка минимума.
- На промежутках, где график производной будет лежать выше оси х, функция будет возрастать.
- На промежутках, где график производной будет лежать ниже оси х, функция будет убывать.
Разберем несколько примеров, где можно применить эти знания.
Пример 1. На рисунке изображен график функции f(x) и отмечены пять точек на оси абсцисс: x1, x2, x3, x4, x5. В скольких из этих точек производная функции отрицательна?
В скольких из этих точек производная функции отрицательна?
Решение. Производная отрицательна на промежутках убывания функции. Отметим такие промежутки.
В точках, которые попали в эти промежутки, производная отрицательная. Всего таких точек 2.
Ответ: 2
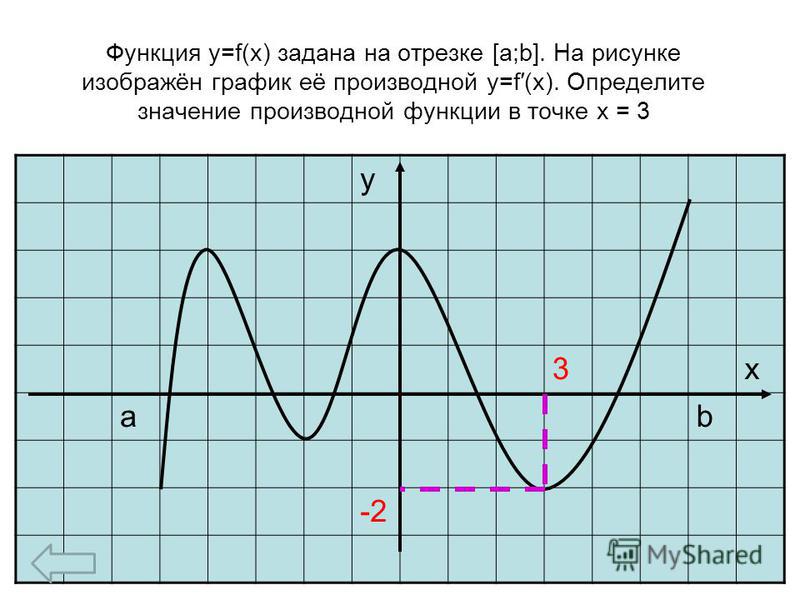
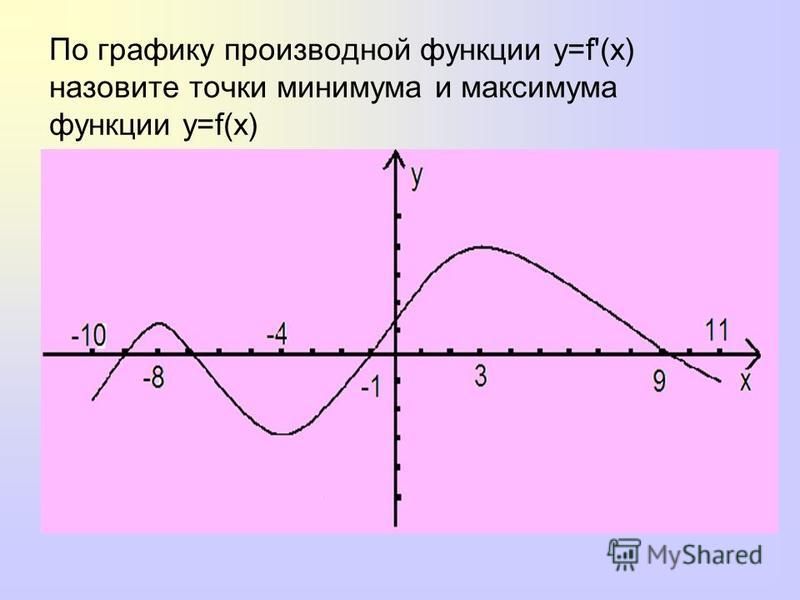
Пример 2. На рисунке изображен график функции y = f'(x) — производной функции f(x), определенной на интервале (-5; 3). Найдите точку максимума функции f(x).
Решение. Точки экстремума на графике производной лежат на оси х. На данном графике таких точки две: x = -2, x = 2.
Точка максимума — это точка, в которой производная меняет знак с положительного на отрицательный. По графику определяем, что это точка x = -2.
Ответ: -2
| Почему успех фильма не всегда зависит от наличия экшн-сцен? Представим, что мы составили графики “Заинтересованность зрителей фильмом” и “Наличие в фильме экшн-сцен”. Экшн-сцены могут вызывать интерес у зрителей, равно как и романтические сцены или смешные повороты сюжета. Получается, что наличие экшн-сцен и заинтересованность фильмом — это разные величины в кинематографе, хотя и связаны между собой. Также и графики производной и функции: они зависят друг от друга, но иллюстрируют совсем разные свойства функции, поэтому сильно отличаются. |
Мы разобрались, как связаны графики функции и ее производной. Есть ли связь между графиком функции и «Первообразной»?
Вспомним один важный факт: если взять производную от первообразной, то получим функцию.
F'(x) = f(x)
Похоже на функцию и ее производную, верно? На самом деле, ситуации ничем не отличаются.
В этом случае изначальной функцией будет первообразная, а ее производной — функция. Для наглядности составим таблицу.
| Было | Взяли производную | Стало | |
| Функция и производная | f(x) | f'(x) | f'(x) |
| Функция и первообразная | F(x) | F'(x) | f(x) |
Получается, для функции и первообразной будут действовать почти те же правила, что и для функции и ее производной.
При решении заданий с графиками первообразной достаточно проанализировать уравнение F'(x) = f(x). Рассмотрим несколько примеров.
Пример 3. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x) и отмечены шесть точек на оси абсцисс x1, x2, x3, x4, x5, x6. В скольких из этих точек функция f(x) отрицательна?
Решение. Поскольку F'(x) = f(x), то функция f(x) будет отрицательна в тех же точках, в которых будет отрицательна F'(x).
Поскольку на графике изображена функция y = F(x), то ее производная будет отрицательна на промежутках убывания функции. Отметим их красным.
В эти промежутки попадают 3 из 6 точек.
Ответ: 3.
Пример 4. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x), определенной на интервале (-6; 7). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-5; 4].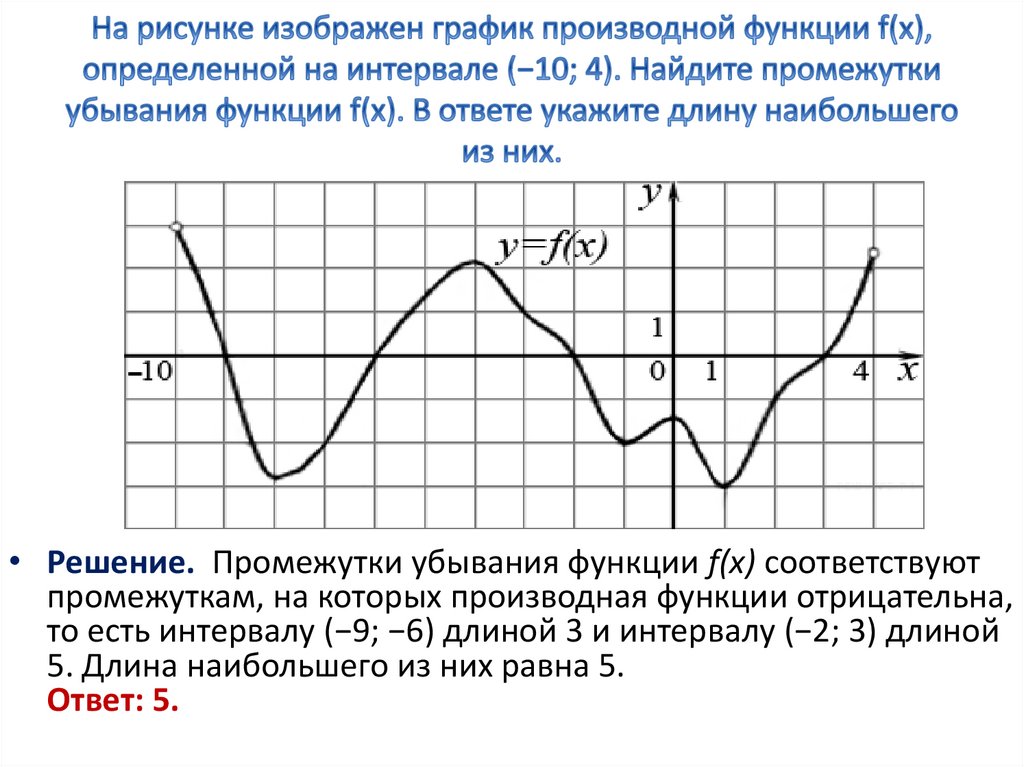
Решение. Вспомним, что F'(x) = f(x). Тогда если f(x) = 0, то и F'(x) = 0. Следовательно, на заданном промежутке нужно найти точки экстремума.
Отметим заданный промежуток красными линиями. На промежутке всего 9 точек экстремума, значит, в 9 точках f(x) будет равна 0.
Ответ: 9
| Чем кофе похож на функцию, ее первообразную и производную? Представим, что в качестве функции у нас выступают кофейные зерна. Тогда производная — то, что мы получаем в результате их переработки — это вкусный напиток. Из чего получаются сами кофейные зерна? Их собирают с кофейного дерева. То есть зерна будут производной от кофейного дерева, а кофейное дерево — это первообразная. Так мы можем отследить следующую цепочку: кофейное дерево → кофейные зерна → кофе. И эта цепочка наглядно иллюстрирует связь первообразной, функции и ее производной. |
- Графики функции, производной и первообразной связаны между собой.

- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
- Для решения задач с первообразной необходимо вспомнить, что F'(x) = f(x). Любой график можно проанализировать с помощью этого уравнения также, как анализируются графики функции и ее производной.
Задание 1.
На каких промежутках будет производная функции будет положительна?
- На промежутках убывания функции.
- На промежутках возрастания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 2.
На каких промежутках производная функции будет отрицательна?
- На промежутках возрастания функции.

- На промежутках убывания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 3.
На рисунке изображен график производной функции f(x), на котором отмечена точка. Чем будет являться эта точка для функции f(x)?
- Точка максимума функции.
- Точка минимума функции.
- Любая произвольная точка на функции.
- Невозможно определить по графику.
Задание 4.
Выберите верный вариант:
- F(x) = f'(x)
- F(x) = f(x)
- F'(x) = f'(x)
- F'(x) = f(x)
Ответы: 1. — 2 2. — 2 3. — 1 4. — 4
описание, свойства, значение, отличие от графика функции
Содержание:
- График производной функции — описание
- Свойства графика
- Знак производной на интервалах возрастания
- Знак производной на интервалах убывания
- Производная и угловой коэффициент касательной
- В каких точках производная равна нулю
- Примеры производной на графике функции
- График производной функции — описание
- Свойства графика
- Знак производной на интервалах возрастания
- Знак производной на интервалах убывания
- Производная и угловой коэффициент касательной
- В каких точках производная равна нулю
- Примеры производной на графике функции
График производной функции — описание
Производная функции — это скорость изменения у при изменении х. При этом одна и та же функция может иметь разное значение производной в разных точках. Обозначается производная следующим образом: \(f'(x)\).
При этом одна и та же функция может иметь разное значение производной в разных точках. Обозначается производная следующим образом: \(f'(x)\).
Зависимость производной функции от скорости изменения y заключается в том, что они прямо пропорциональны. Значение производной может быть как больше, так и меньше нуля. Производную функции используют для нахождения точек максимума и минимума функций, а также промежутков их возрастания и убывания.
При помощи вычисления производной и приравнивания её к нулю, возможно найти точки, разбивающие числовую ось на интервалы. Знак производной будет определяться на каждом из найденных интервалов, что позволит сделать в дальнейшем сделать вывод о возрастании или убывании функции.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Производная функции \(f(x)\) в точке \(x_0\) эквивалентна тангенсу угла наклона касательной к графику функции в \(x_0\).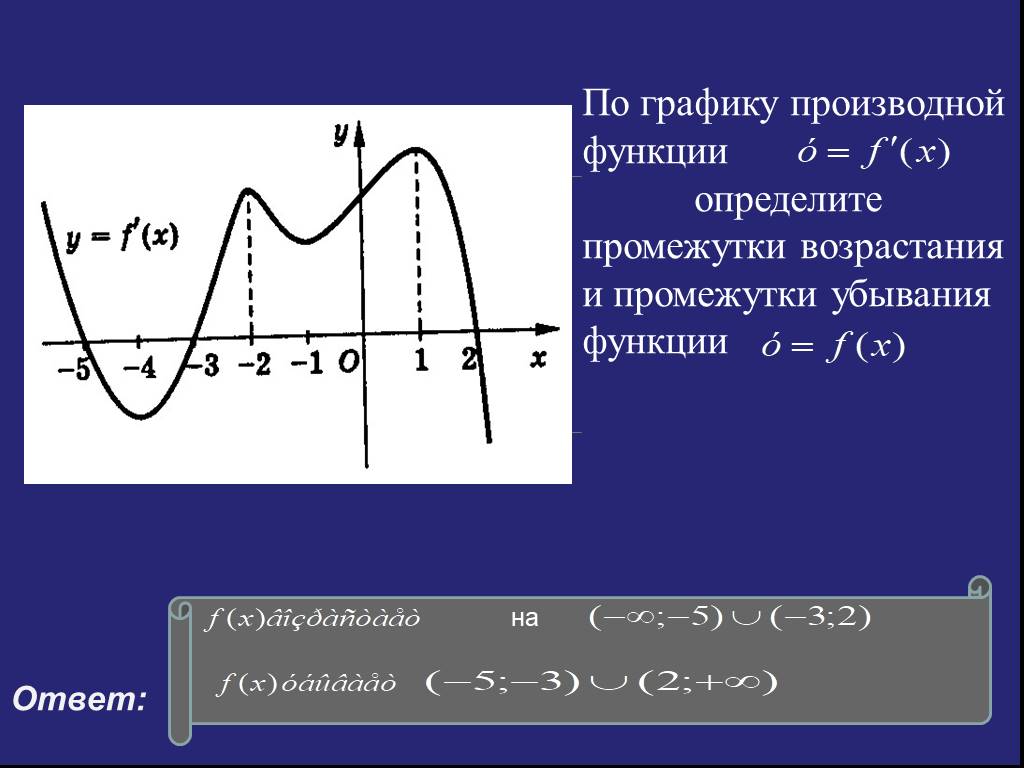
\(f'(x_0)\;=\;tg\alpha\)
Свойства графика
- Производная будет положительной на интервалах возрастания функции. Таким образом, в случае если производная в определенной точке некоего интервала обладает положительным значением, график функции возрастает в обозначенном интервале.
- Производная будет отрицательной на интервалах убывания функции. Таким образом, в случае если производная в определенной точке некоего интервала обладает отрицательным значением, график функции убывает в обозначенном интервале.
- В точке х производная будет равняться угловому коэффициенту касательной к графику функции в обозначенной точке.
- Производная равняется нулю в точках максимума и минимума функции, в тех же случаях параллельности касательной к графику функции и оси \(ОХ\).
Знак производной на интервалах возрастания
Определим, какая функция называется возвращающей.
\(y = f(x)\) будет возрастать на интервале \(X\), если для любых \(x_1\;\in\;X\) и \(x_2\;\in\;X\), где \(x_2\;>\;x_1\), справедливо неравенство \(f(x_2)\;\geq\;f(x_1)\).
В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть иметь вид \(f(x_1) < f(x_2)\), функция \(y = f(x)\) будет называться строго возрастающей на интервале \((a, b)\).
На интервалах возрастания производная будет иметь положительный знак. То есть при подстановке значения из интервала в производную, получившееся число будет положительным.
В тех случаях, когда производная функции \(y = f(x)\) положительна для любого x из интервала \(X\), функция возрастает на \(X\).
Знак производной на интервалах убывания
Определим, какая функция называется убывающей.
\(y = f(x)\) будет убывать на интервале \(X\), если для любых \(x_1\;\in\;X\) и \(x_2\;\in\;X\), где \(x_2\;>\;x_1\) справедливо неравенство \(f(x_2)\;\leq\;f(x_1).\)
В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть имеет вид \(f(x_1) < f(x_2)\), функция \(y = f(x)\) будет называться строго убывающей на интервале \((a, b)\).
На интервалах убывания производная будет иметь отрицательный знак. То есть при подстановке значения из интервала в производную, получившееся число будет отрицательным.
В тех случаях, когда производная функции \(y = f(x)\) отрицательна для любого x из интервала \(X\), функция убывает на \(X\).
Производная и угловой коэффициент касательной
Касательная — прямая, которая имеет на определенном участке единственную общую точку с графиком.
В случае, когда при \(x_1\;\rightarrow\;x_0\) имеется предельное положение секущей графика функции \(y = f(x)\), оно будет носить название касательной к графику функции \(y = f(x)\) в точке \(A\;=\;((x_0;\;f(x_0))\). А значение производной в точке касания \(x_0\) будет эквивалентно угловому коэффициенту касательной.
Угловой коэффициент касательной равен значению производной в точке касания \(x_0\). И в соответствии с тем, что касательная параллельна прямой \(y = -x\), ее угловой коэффициент равен -1.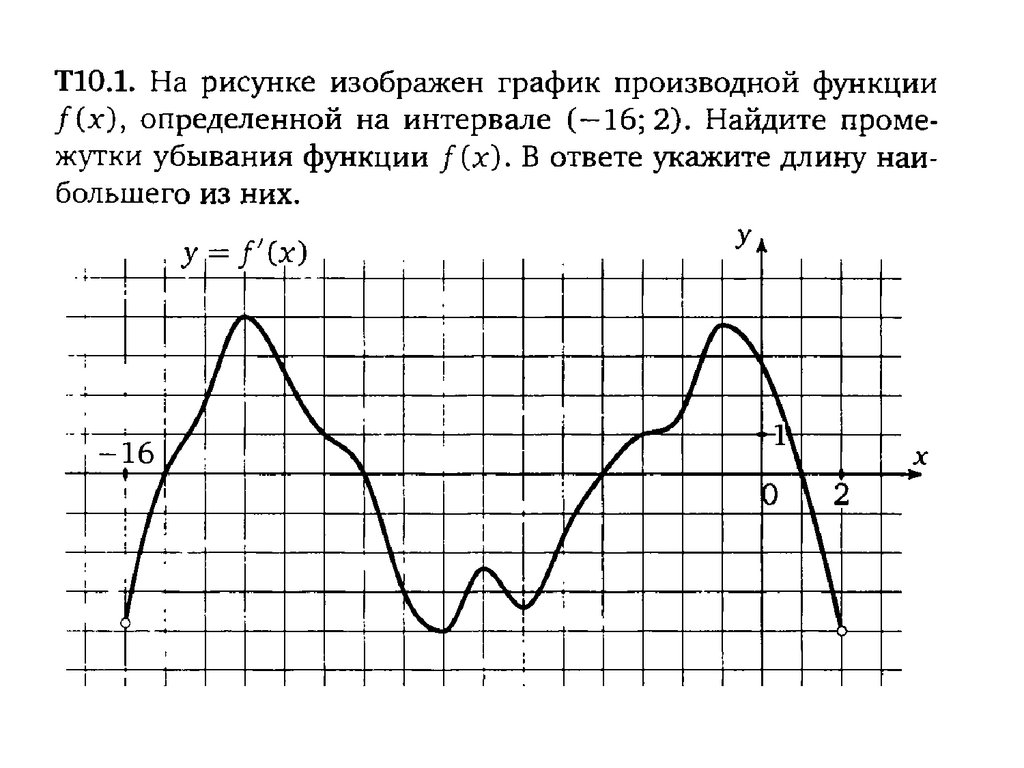
Геометрический смысл производной состоит в том, что производная в точке \(x_0\) равна угловому коэффициенту касательной к графику функции \(y = f(x)\) в этой точке.
Формула уравнения касательной к графику функции \(y = f(x)\) в точке \(x_0\) выглядит следующим образом:
\(y\;=\;f(x_0)\;+\;f'(x_0)(x\;-\;x_0)\)
Рассмотрим рисунок графика функции \(y = f(x)\). Очевидно, что для каждой из точек \(A\) и \(B\) графика функции справедливо следующее разностное отношение:
\(\frac{f(x_0+\triangle x)}{f(x_0)\triangle x}=tg\alpha\)
Здесь \(\alpha\) — угол между прямой и осью \(ОХ\), а предел разностного отношения эквивалентен угловому коэффициенту касательной в точке \(A\).
Зафиксируем точку \(A\) и будем продвигать точку \(B\) в направлении к ней. Тогда \(\triangle x\) бесконечно уменьшается и приближается к 0, а секущая \(АВ\) приближается к касательной \(АС\).
Пример
Необходимо записать уравнение касательной к графику функции \(y=x+e^{-2x}\), если эта функция параллельна прямой \(y = -x.
Используем уравнение касательной
\(y\;=\;f(x_0)\;+f'(x_0)(x\;-\;x_0)\\x_0\;=\;0;\;f'(x_0)\;=\;-1;\;f(x_0)\;=\;1\\y\;=\;1\;-\;1(x-0)\;=\;1\;-\;x\)
В каких точках производная равна нулю
Производная будет эквивалентна нулю в точках минимума, максимума и перегиба, при параллельной оси \(ОX\) касательной. Рассмотрим следующий рисунок:
Очевидно, что в точках \(C\) и \(D\) касательная горизонтальна, тогда тангенс угла ее наклона будет равняться 0. Отсюда можно сделать вывод, что и производная равна 0. Точка C здесь будет являться точкой максимума. В этой точке возрастание функции изменяется на убывание, как меняется и знак производной — с плюса на минус. Точка \(D\) здесь — точка минимума. В это случае также происходят изменения, но в обратном порядке.
Примечание
Важно отметить, что производная может не существовать в точке максимума. Такое происходит, если на графике изображен резкий излом, к которому невозможно провести касательную.
Рассмотрим еще одно изображение функции:
В данном случае производная будет эквивалентна нулю в точке перегиба, так как в точке \(E\) касательная к функции параллельна оси \(ОX\). В этом случае знак производной не будет изменяться, потому что до точки перегиба и после функция возрастает. Знак был и остается положительным.
Пример
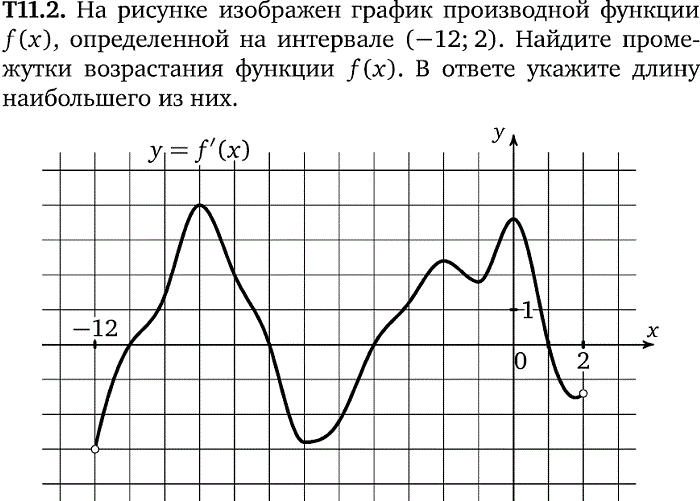
Рассмотрим рисунок, на котором начерчен график функции \(y = f(x)\). График определен на интервале (−3; 9). Необходимо определить количество точек, где производная функции \(f(x)\) эквивалентна 0.
На данном рисунке очевидно, что производная функции f(x) эквивалентна нулю в точках максимума и минимума, то есть в точках −2; −1; 1; 4 и 6. Таким образом производная равна нулю в 5 точках.
Примеры производной на графике функции
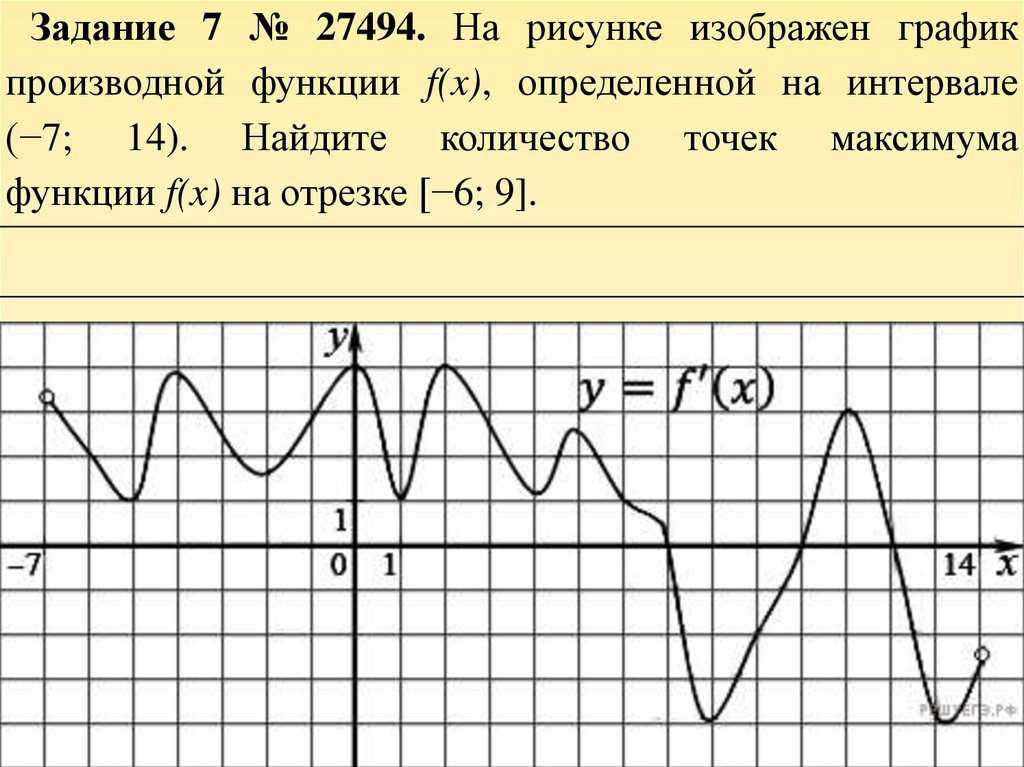
Задача №1
Рассмотрим рисунок.
Рисунок изображает график производной функции \(f(x)\). Функция определена на интервале (-10; 2). Необходимо найти, в скольких точках касательная к графику функции \(f(x)\) будет параллельна прямой \(y = -2x — 11\) или совпадать с ней.
Функция определена на интервале (-10; 2). Необходимо найти, в скольких точках касательная к графику функции \(f(x)\) будет параллельна прямой \(y = -2x — 11\) или совпадать с ней.
Решение
Используем правило о значении производной, которое в точке касания эквивалентно угловому коэффициенту касательной. Тогда, зная, что касательная параллельна прямой \(y = -2x — 11\) или идентична с ней, можно утверждать, что угловые коэффициенты равны \(-2\).
Теперь необходимо найти число точек, в которых \(f'(x)\;=\;-2\). Искомое значение соответствует числу точек, где график производной пересекается с прямой \(y = -2\). На заданном интервале 5 таких точек.
Ответ: 5.
Задача №2
Первый рисунок изображает график функции \(y = f(x)\) и касательную к нему в точке с абсциссой \(x_0\). Необходимо установить значение производной функции \(f(x)\) в точке \(x_0\).
Решение
Используем правило, гласящее, что угловой коэффициент касательной эквивалентен значению производной в точке касания, который в свою очередь эквивалентен тангенсу угла наклона данной касательной к оси абсцисс.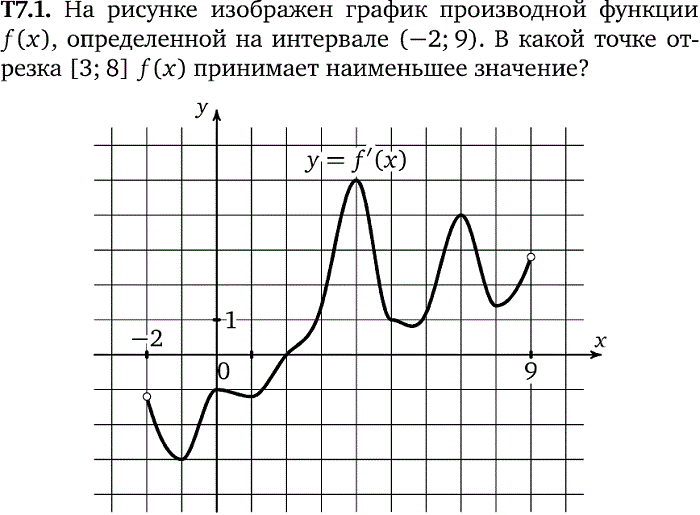 На втором рисунке показано, что решить задачу можно с помощью построения треугольника, вершины которого соответствуют точкам A (1; 2), B (1; -4), C(-2; -4). Тогда угол наклона касательной к оси абсцисс можно найти через угол \(ACB\), которому он будет равен:
На втором рисунке показано, что решить задачу можно с помощью построения треугольника, вершины которого соответствуют точкам A (1; 2), B (1; -4), C(-2; -4). Тогда угол наклона касательной к оси абсцисс можно найти через угол \(ACB\), которому он будет равен:
\(y'(x_0)\;=\;tg\angle ABC\;=\;\frac{AB}{BC}\;=\;\frac{2+4}{1+2}\;=\;2\)
Ответ: 2.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
AC Производная функция
Мотивирующие вопросы
Как предельное определение производной функции \(f\) приводит к совершенно новой (но родственной) функции \(f’\text{?}\)
В чем разница между написанием \(f'(a)\) и \(f'(x)\text{?}\)
Как график производной функции \(f'(x)\) связан с графиком \(f(x)\text{?}\)
Приведите примеры функций \(f\), для которых \(f’\) не определена в одной или нескольких точках?
Теперь мы знаем, что мгновенная скорость изменения функции \(f(x)\) в точке \(x = a\text{,}\) или, что то же самое, наклон касательной к графику \(y = f(x)\) at \(x = a\text{,}\) задается значением \(f'(a)\text{.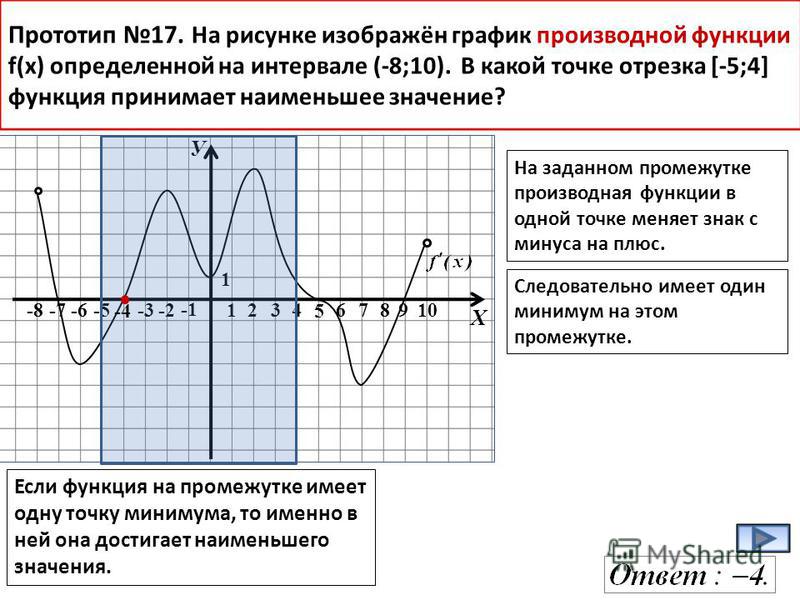 }\) Во всех наших примерах до сих пор мы идентифицировали конкретное значение \(a\) в качестве нашего интереса: \(a = 1\text{,}\) \(a = 3\text{,}\) и т. д. Но нетрудно представить, что мы часто будет интересоваться значением производной для более чем одного \(a\)-значения и, возможно, для многих из них. В этом разделе мы исследуем, как мы можем перейти от вычисления производной в одной точке к вычислению формулы для \(f'(a)\) в любой точке \(a\text{.}\). Действительно, процесс «взятие производной» порождает новую функцию, обозначаемую \(f'(x)\text{,}\), производную от исходной функции \(f(x)\text{.}\) 92\текст{.}\)
}\) Во всех наших примерах до сих пор мы идентифицировали конкретное значение \(a\) в качестве нашего интереса: \(a = 1\text{,}\) \(a = 3\text{,}\) и т. д. Но нетрудно представить, что мы часто будет интересоваться значением производной для более чем одного \(a\)-значения и, возможно, для многих из них. В этом разделе мы исследуем, как мы можем перейти от вычисления производной в одной точке к вычислению формулы для \(f'(a)\) в любой точке \(a\text{.}\). Действительно, процесс «взятие производной» порождает новую функцию, обозначаемую \(f'(x)\text{,}\), производную от исходной функции \(f(x)\text{.}\) 92\текст{.}\)
Используйте определение предела для вычисления производных значений: \(f'(0)\text{,}\) \(f'(1)\text{,}\) \(f'(2)\text {,}\) и \(f'(3)\text{.}\)
Обратите внимание, что работа по нахождению \(f'(a)\) одинакова, независимо от значения \(a\text{.}\) Основываясь на вашей работе в (a), что вы предполагаете значение \(f'(4)\text{?}\) Как насчет \(f'(5)\text{?}\) (Примечание: вы должны , а не использовать предельное определение производной, чтобы найти любое значение.
 ) 92\text{,}\) возможно, вы нашли несколько шаблонов. Один исходит из наблюдения, что \(f'(0) = 4\text{,}\) \(f'(1) = 2\text{,}\) \(f'(2) = 0\text{, }\) и \(f'(3) = -2\text{.}\). Эта последовательность значений естественным образом приводит нас к предположению, что \(f'(4) = -4\) и \(f'(5 ) = -6\text{.}\) Мы также замечаем, что конкретное значение \(a\) очень мало влияет на процесс вычисления значения производной через определение предела. Чтобы увидеть это более ясно, мы вычисляем \(f'(a)\text{,}\), где \(a\) представляет собой число, которое будет названо позже. Следуя теперь уже стандартному процессу использования предельного определения производной, 92}{ч}\\
=\mathstrut \amp \lim_{h \to 0} \frac{h(4 — 2a — h)}{h} = \lim_{h \to 0} (4 — 2a — h)\text{.}
\конец{выравнивание*}
) 92\text{,}\) возможно, вы нашли несколько шаблонов. Один исходит из наблюдения, что \(f'(0) = 4\text{,}\) \(f'(1) = 2\text{,}\) \(f'(2) = 0\text{, }\) и \(f'(3) = -2\text{.}\). Эта последовательность значений естественным образом приводит нас к предположению, что \(f'(4) = -4\) и \(f'(5 ) = -6\text{.}\) Мы также замечаем, что конкретное значение \(a\) очень мало влияет на процесс вычисления значения производной через определение предела. Чтобы увидеть это более ясно, мы вычисляем \(f'(a)\text{,}\), где \(a\) представляет собой число, которое будет названо позже. Следуя теперь уже стандартному процессу использования предельного определения производной, 92}{ч}\\
=\mathstrut \amp \lim_{h \to 0} \frac{h(4 — 2a — h)}{h} = \lim_{h \to 0} (4 — 2a — h)\text{.}
\конец{выравнивание*}Здесь мы видим, что ни \(4\), ни \(2a\) не зависят от значения \(h\text{,}\), так что \(h \to 0\text{,}\) \(( 4 — 2a — h) \to (4 — 2a)\text{.}\) Таким образом, \(f'(a) = 4 — 2a\text{.}\)
Этот результат согласуется с конкретными значениями, которые мы нашли выше: например, \(f'(3) = 4 — 2(3) = -2\text{.
 2\text{,}\) следует, что \(f'(x) = 4 — 2x\text{.}\) 92\) вместе с набором касательных в точках, которые мы рассмотрели выше. Справа мы показываем график \(f'(x) = 4 — 2x\) с акцентом на высотах графика производной при том же выборе точек. Обратите внимание на связь между цветами на левом и правом графиках: зеленая касательная на исходном графике связана с зеленой точкой на правом графике следующим образом: наклон касательной в точке на левом графике такой же, как высота в соответствующей точке на правом графике. То есть при каждом соответствующем значении \(x\text{,}\) наклон касательной к исходной функции равен высоте производной функции. Обратите внимание, однако, что единицы измерения на вертикальных осях разные: на левом графике вертикальные единицы — это просто выходные единицы \(f\text{.}\). На правом графике \(y = f’ (x)\text{,}\) единицы измерения по вертикальной оси представляют собой единицы \(f\) на единицу \(x\text{.}\)
2\text{,}\) следует, что \(f'(x) = 4 — 2x\text{.}\) 92\) вместе с набором касательных в точках, которые мы рассмотрели выше. Справа мы показываем график \(f'(x) = 4 — 2x\) с акцентом на высотах графика производной при том же выборе точек. Обратите внимание на связь между цветами на левом и правом графиках: зеленая касательная на исходном графике связана с зеленой точкой на правом графике следующим образом: наклон касательной в точке на левом графике такой же, как высота в соответствующей точке на правом графике. То есть при каждом соответствующем значении \(x\text{,}\) наклон касательной к исходной функции равен высоте производной функции. Обратите внимание, однако, что единицы измерения на вертикальных осях разные: на левом графике вертикальные единицы — это просто выходные единицы \(f\text{.}\). На правом графике \(y = f’ (x)\text{,}\) единицы измерения по вертикальной оси представляют собой единицы \(f\) на единицу \(x\text{.}\)Отличный способ изучить, как график \(f(x)\) порождает график \(f'(x)\), — это использовать апплет.
 См., например, апплеты по адресу gvsu.edu/s/5C или gvsu.edu/s/5D на сайтах Дэвида Остина 1 и Марка Рено 2 .
См., например, апплеты по адресу gvsu.edu/s/5C или gvsu.edu/s/5D на сайтах Дэвида Остина 1 и Марка Рено 2 .В разделе 1.3, когда мы впервые определили производную, мы записали определение в терминах значения \(a\), чтобы найти \(f'(a)\text{.}\) Как мы видели выше, буква \ (a\) — это просто заполнитель, и часто имеет смысл использовать вместо него \(x\). Для справки, здесь мы повторяем определение производной.
Определение 1.4.2.
Пусть \(f\) — функция, а \(x\) — значение в области определения функции. Мы определяем производную \(f\) , новую функцию, называемую \(f’\text{,}\) по формуле \(f'(x) = \lim_{h \to 0} \frac{ f(x+h)-f(x)}{h}\text{,}\) при условии, что этот предел существует.
Теперь у нас есть два разных взгляда на производную функцию:
задан график \(y = f(x)\text{,}\) как этот график приводит к графику производной функции \(y = f'(x)\text{?}\) и
учитывая формулу для \(y = f(x)\text{,}\) как предельное определение производной порождает формулу для \(y = f'(x)\text{?}\)
Оба этих вопроса исследуются в ходе следующих занятий.

Мероприятие 1.4.2.
Для каждого заданного графика \(y = f(x)\text{,}\) начертите приблизительный график его производной функции \(y = f'(x)\text{,}\) на осях непосредственно ниже. Масштаб сетки для графика \(f\) равен \(1 \times 1\text{;}\) предположим, что горизонтальный масштаб сетки для графика \(f’\) идентичен масштабу для \(f\text{.}\) При необходимости отрегулируйте и обозначьте вертикальный масштаб на осях для \(f’\text{.}\)
Когда вы закончите со всеми 8 графиками, напишите несколько предложений, описывающих общий процесс построения графика производной функции, учитывая, что график исходной функции. Какие значения производной функции вы обычно идентифицируете в первую очередь? Что вы делаете после этого? Как ключевые черты графика производной функции иллюстрируют свойства графика исходной функции?
Для динамического исследования, которое позволяет вам экспериментировать с графическим отображением \(f’\) при заданном графике \(f\text{,}\), см.

В следующем упражнении мы дополнительно исследуем более алгебраический подход к нахождению \(f'(x)\text{:}\) по формуле для \(y = f(x)\text{,}\) предела определение производной будет использовано для разработки формулы для \(f'(x)\text{.}\)
Мероприятие 1.4.3.
Для каждой из перечисленных функций определите формулу производной функции. Для первых двух определите формулу производной, размышляя о характере данной функции и ее наклоне в различных точках; не используйте определение предела.
 Для последних четырех используйте определение предела. Обратите особое внимание на имена функций и независимых переменных. Важно уметь использовать буквы, отличные от \(f\) и \(x\text{.}\). Например, для данной функции \(p(z)\text{,}\) мы называем ее производной \(p'(z)\text{.}\) 93\)
Для последних четырех используйте определение предела. Обратите особое внимание на имена функций и независимых переменных. Важно уметь использовать буквы, отличные от \(f\) и \(x\text{.}\). Например, для данной функции \(p(z)\text{,}\) мы называем ее производной \(p'(z)\text{.}\) 93\)\(\displaystyle F(t) = \frac{1}{t}\)
\(\displaystyle G(y) = \sqrt{y}\)
Подраздел 1.4.2 Резюме
Предельное определение производной, \(f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\text{,}\ ) дает значение для каждого \(x\), при котором определяется производная, и это приводит к новой функции \(y = f'(x)\text{.}\). Особенно важно отметить, что взятие производная — это процесс, который начинается с заданной функции (\(f\)) и производит новую связанную функцию (\(f’\)).
По сути, нет никакой разницы между записью \(f'(a)\) (как мы регулярно делали в разделе 1.3) и записью \(f'(x)\text{.}\). В любом случае переменная просто заполнитель, который используется для определения правила для производной функции.

Имея график функции \(y = f(x)\text{,}\), мы можем начертить приблизительный график ее производной \(y = f'(x)\), заметив, что высот на график производной соответствует наклонам на графике исходной функции.
В упражнении 1.4.2 мы столкнулись с некоторыми функциями, у которых на графиках были острые углы, например, функция сдвинутого абсолютного значения. В таких точках производная не существует, и мы говорим, что \(f\) там не дифференцируема. Пока достаточно понимать это как следствие скачка, который должен произойти в производной функции на остром углу графика исходной функции.
Упражнения 1.4.3 Упражнения
1. Производная функция графически.
Рассмотрим функцию \(f(x)\), показанную на графике ниже.
(Обратите внимание, что вы можете нажать на график, чтобы получить его увеличенную версию, и что может быть полезно распечатать эту увеличенную версию, чтобы иметь возможность работать с ней вручную. )
)
Тщательно нарисуйте производную функцию данной функции (при этом вы захотите оценить значения производной функции при разных значениях \(x\)). Используйте график производной функции, чтобы оценить следующие значения производной функции. 9{2}-8\) с использованием коэффициентов разности:
\(g'(x) = \lim\limits_{h\to0}\, [(\) \() / h]\)
\(\qquad «=»
(В первом поле ответа укажите числитель разностного отношения, которое вы используете для оценки производной. Во втором поле введите производную, полученную после завершения расчета предела.)
3. Зарисовка производной.
Для функции \(f(x)\), показанной на графике ниже, нарисуйте график производной. Затем вы будете выбирать, какой из следующих графиков является правильным графиком производной, но обязательно сначала нарисуйте производную самостоятельно.
Какой из следующих графиков является производным от \(f(x)\text{?}\)
1
2
3
4
5
6
7
8
(Нажмите на график, чтобы увеличить его)
1. | 2. | 3. | 4. |
| 5. | 6. | 7. | 8. |
4. Сравнение значений функции и производной.
График функции \(f\) показан ниже.
При каком из помеченных \(x\)-значений
\(f(x)\) наименьшее? \(х =\)
x1
x2
x3
x4
x5
x6
\(f(x)\) наибольший? \(х =\)
x1
x2
x3
x4
x5
x6
\(f'(x)\) меньше всего? \(х =\)
x1
x2
x3
x4
x5
x6
\(f'(x)\) наибольший? \(х =\)
x1
x2
x3
x4
x5
x6
5.
 Предельное определение производной рациональной функции.
Предельное определение производной рациональной функции.Пусть
\begin{equation*} е (х) = \ гидроразрыва {1} {х — 4} \end{уравнение*}
Найти
(i) \(f'(3)\)
(ii) \(f'(5)\)
(iii) \(f'(6)\)
(iv) \ (f'(8)\)
6.
Пусть \(f\) — функция со следующими свойствами: \(f\) дифференцируема при каждом значении \(x\) (то есть \(f\) имеет производную в каждой точке), \( f(-2) = 1\text{,}\) и \(f'(-2) = -2\text{,}\) \(f'(-1) = -1\text{,}\ ) \(f'(0) = 0\text{,}\) \(f'(1) = 1\text{,}\) и \(f'(2) = 2\text{.}\)
На осях слева на рисунке 1.4.3 нарисуйте возможный график \(y = f(x)\text{.}\) Объясните, почему ваш график соответствует указанным критериям. 92 — 4x + 12\текст{.}\)
Сравните найденные вами формулы для \(g'(x)\) и \(p'(x)\). Как константы 5, 4, 12 и 3 влияют на результаты?
8.
Пусть \(g\) — непрерывная функция (то есть функция без скачков и дыр в графике) и предположим, что график \(y = g'(x)\) задается графиком справа на рисунке 1.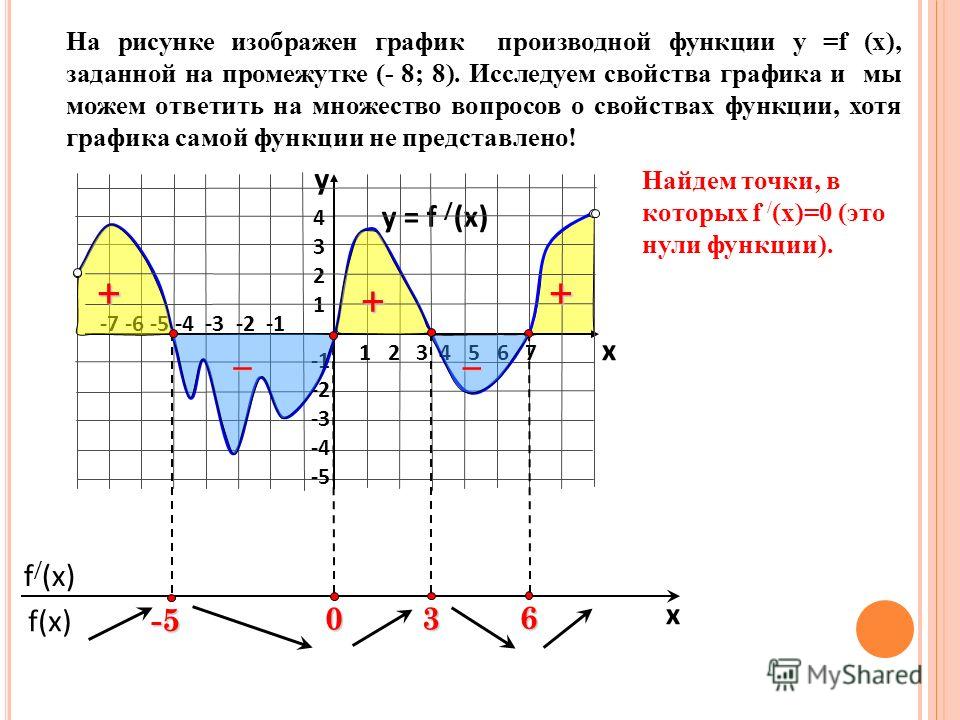 4.4.
4.4.
Обратите внимание, что для каждого значения \(x\), удовлетворяющего условию \(0 \lt x \lt 2\text{,}\), значение \(g'(x)\) является постоянным. Что это говорит вам о поведении графика \(y = g(x)\) на этом интервале?
На каких интервалах, кроме \(0 \lt x \lt 2\), вы ожидаете, что \(y = g(x)\) будет линейной функцией? Почему?
При каких значениях \(x\) \(g'(x)\) не определено? Какое поведение вы ожидаете увидеть на графике \(y=g(x)\text{?}\)
Предположим, что \(g(0) = 1\text{.}\) На осях, указанных слева на рисунке 1.4.4, нарисуйте точный график \(y = g(x)\text{.}\ )
9.
Для каждого графика, представляющего исходную функцию \(y = f(x)\) на рис. 1.4.5, ваша задача состоит в том, чтобы начертить приближенный график ее производной функции, \(y = f'(x)\text{ ,}\) на осях непосредственно ниже.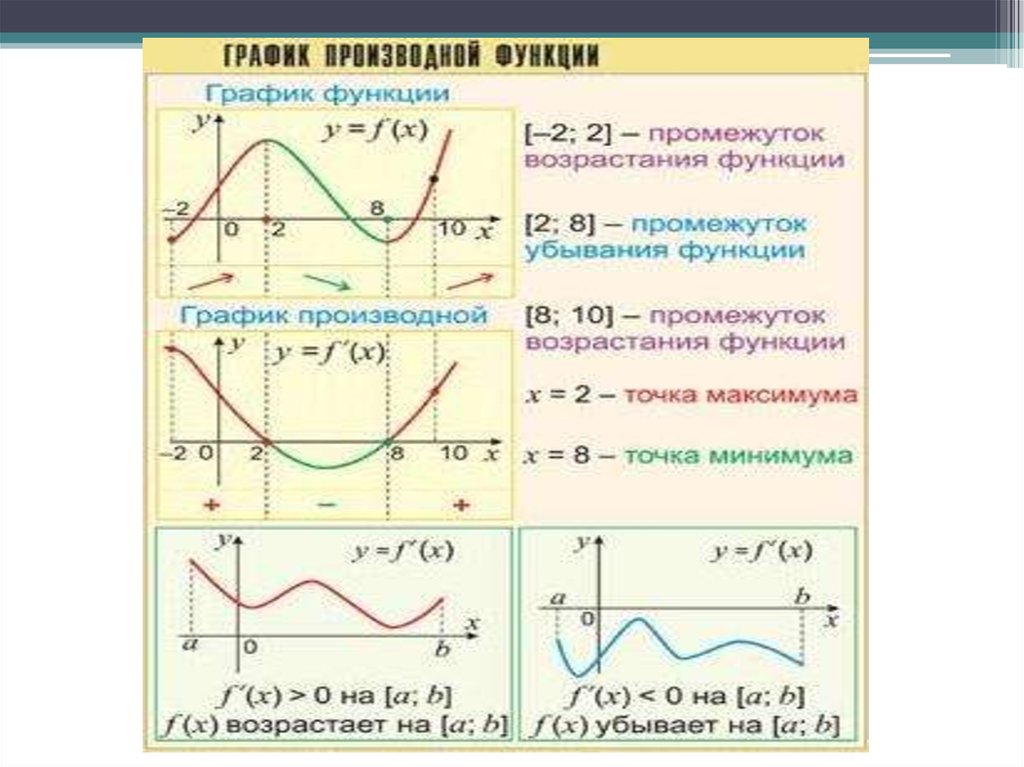 Просмотрите масштаб сетки для графика \(f\) как \(1 \times 1\text{,}\) и предположите, что горизонтальный масштаб сетки для графика \(f’\) идентичен к тому, что для \(f\text{.}\) Если вам нужно настроить вертикальный масштаб по осям для графика \(f’\text{,}\), вы должны пометить это соответствующим образом.
Просмотрите масштаб сетки для графика \(f\) как \(1 \times 1\text{,}\) и предположите, что горизонтальный масштаб сетки для графика \(f’\) идентичен к тому, что для \(f\text{.}\) Если вам нужно настроить вертикальный масштаб по осям для графика \(f’\text{,}\), вы должны пометить это соответствующим образом.
gvsu.edu/s/5r
gvsu .edu/s/5p
gvsu.edu/s/8y
Производные и графики – неформальное исчисление
35 Производные и графики
его производная состоит в том, что положительная производная означает, что количество увеличивается, а отрицательная производная означает, что количество уменьшается.
Возрастание и убывание
Наружная температура имеет положительную производную от 3:00 до 15:00 и отрицательную производную от 15:00 до 3:00.
 Нарисуйте график этого и обозначьте каждую часть графика как «возрастающую» или «убывающую».
Нарисуйте график этого и обозначьте каждую часть графика как «возрастающую» или «убывающую».При положительной производной с 3:00 до 15:00 это значение должно повышаться и обозначаться как «возрастающее». С 15:00 до 3:00 график идет вниз и помечен как «убывающий».
На границе между увеличением и уменьшением, в 3 часа дня, температура самая высокая. Это ключ к одному из самых полезных приложений исчисления: оптимизации! Оптимизация заключается в том, чтобы либо выяснить, когда количество максимально или максимально возможно, либо выяснить, когда количество минимизируется или как можно меньше. Часто это происходит на границе возрастания и убывания, то есть там, где функция переходит от положительной производной к отрицательной. Отсюда одно из важнейших правил исчисления: оптимизация происходит, когда производная равна нулю! Мы вернемся к этому в следующем разделе.
А пока, используя представление о положительной, отрицательной или нулевой производной, мы можем нарисовать грубый набросок производной на основе графика функции.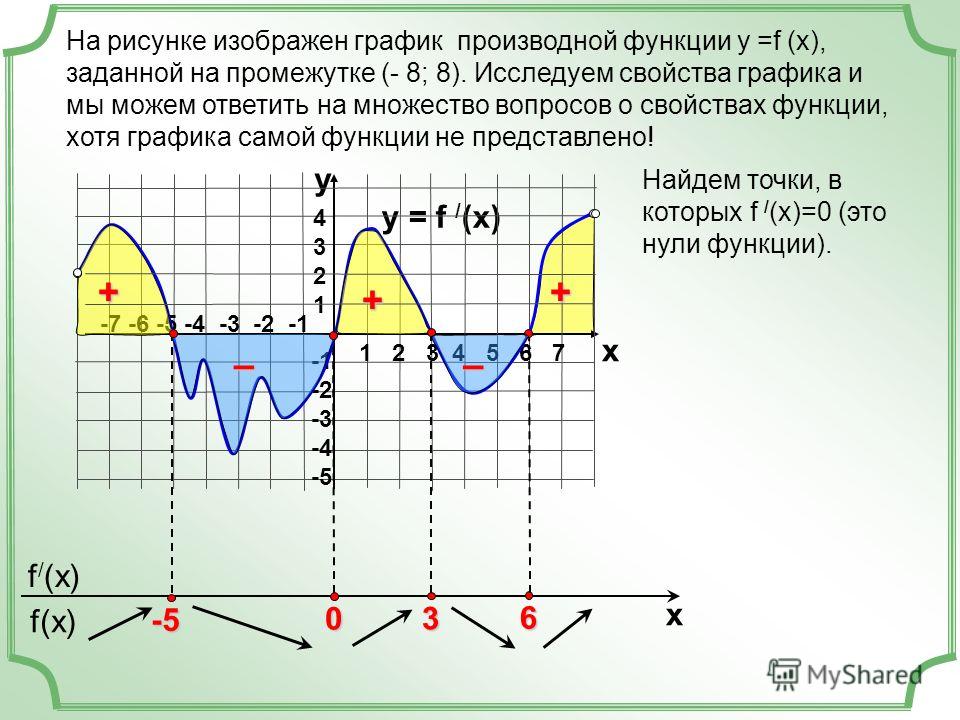 Давайте посмотрим пример
Давайте посмотрим пример
Эскиз производной
Нарисуйте производную следующей функции.
При наброске производной помните об этой идее: наклонов становятся [латексными]y[/латексными] значениями . Во-первых, давайте отметим, где производная равна нулю:
Это места, которые на графике производной имеют нулевое значение для [latex]y[/latex]-значения. Это означает, что это [latex]x[/latex]-перехваты!
Теперь отметим, где производная положительная, а где отрицательная.
Наконец, мы можем использовать это как приблизительное руководство для скетча, опять же помня, что наклон становится [латекс]y[/латекс]-значениями. Здесь производная выделена черным цветом, а исходная функция — серым.
Давайте посмотрим на другой пример.
Эскиз производной 2
Эскиз производной
В этом случае график всегда идет вниз, поэтому производная всегда отрицательна.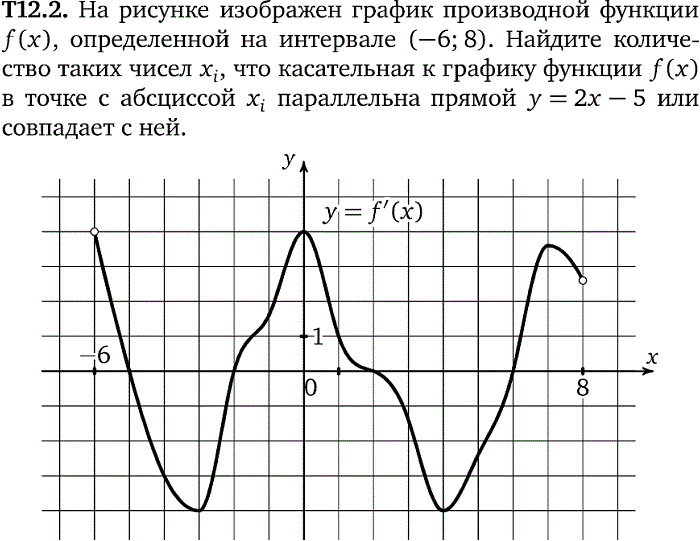

 Совпадут ли эти графики? Скорее всего, нет.
Совпадут ли эти графики? Скорее всего, нет. 
 ) 92\text{,}\) возможно, вы нашли несколько шаблонов. Один исходит из наблюдения, что \(f'(0) = 4\text{,}\) \(f'(1) = 2\text{,}\) \(f'(2) = 0\text{, }\) и \(f'(3) = -2\text{.}\). Эта последовательность значений естественным образом приводит нас к предположению, что \(f'(4) = -4\) и \(f'(5 ) = -6\text{.}\) Мы также замечаем, что конкретное значение \(a\) очень мало влияет на процесс вычисления значения производной через определение предела. Чтобы увидеть это более ясно, мы вычисляем \(f'(a)\text{,}\), где \(a\) представляет собой число, которое будет названо позже. Следуя теперь уже стандартному процессу использования предельного определения производной, 92}{ч}\\
=\mathstrut \amp \lim_{h \to 0} \frac{h(4 — 2a — h)}{h} = \lim_{h \to 0} (4 — 2a — h)\text{.}
\конец{выравнивание*}
) 92\text{,}\) возможно, вы нашли несколько шаблонов. Один исходит из наблюдения, что \(f'(0) = 4\text{,}\) \(f'(1) = 2\text{,}\) \(f'(2) = 0\text{, }\) и \(f'(3) = -2\text{.}\). Эта последовательность значений естественным образом приводит нас к предположению, что \(f'(4) = -4\) и \(f'(5 ) = -6\text{.}\) Мы также замечаем, что конкретное значение \(a\) очень мало влияет на процесс вычисления значения производной через определение предела. Чтобы увидеть это более ясно, мы вычисляем \(f'(a)\text{,}\), где \(a\) представляет собой число, которое будет названо позже. Следуя теперь уже стандартному процессу использования предельного определения производной, 92}{ч}\\
=\mathstrut \amp \lim_{h \to 0} \frac{h(4 — 2a — h)}{h} = \lim_{h \to 0} (4 — 2a — h)\text{.}
\конец{выравнивание*}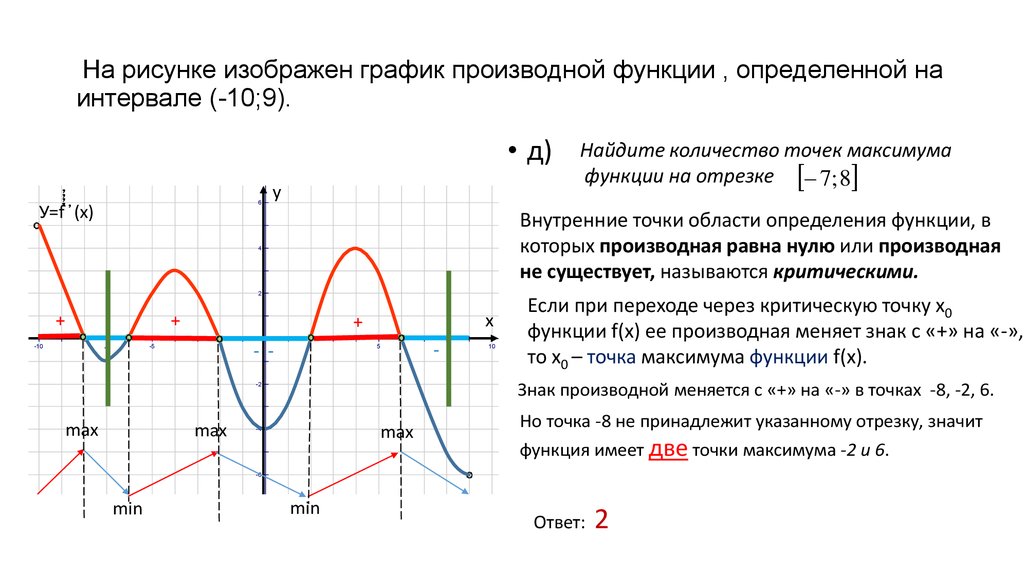 2\text{,}\) следует, что \(f'(x) = 4 — 2x\text{.}\) 92\) вместе с набором касательных в точках, которые мы рассмотрели выше. Справа мы показываем график \(f'(x) = 4 — 2x\) с акцентом на высотах графика производной при том же выборе точек. Обратите внимание на связь между цветами на левом и правом графиках: зеленая касательная на исходном графике связана с зеленой точкой на правом графике следующим образом: наклон касательной в точке на левом графике такой же, как высота в соответствующей точке на правом графике. То есть при каждом соответствующем значении \(x\text{,}\) наклон касательной к исходной функции равен высоте производной функции. Обратите внимание, однако, что единицы измерения на вертикальных осях разные: на левом графике вертикальные единицы — это просто выходные единицы \(f\text{.}\). На правом графике \(y = f’ (x)\text{,}\) единицы измерения по вертикальной оси представляют собой единицы \(f\) на единицу \(x\text{.}\)
2\text{,}\) следует, что \(f'(x) = 4 — 2x\text{.}\) 92\) вместе с набором касательных в точках, которые мы рассмотрели выше. Справа мы показываем график \(f'(x) = 4 — 2x\) с акцентом на высотах графика производной при том же выборе точек. Обратите внимание на связь между цветами на левом и правом графиках: зеленая касательная на исходном графике связана с зеленой точкой на правом графике следующим образом: наклон касательной в точке на левом графике такой же, как высота в соответствующей точке на правом графике. То есть при каждом соответствующем значении \(x\text{,}\) наклон касательной к исходной функции равен высоте производной функции. Обратите внимание, однако, что единицы измерения на вертикальных осях разные: на левом графике вертикальные единицы — это просто выходные единицы \(f\text{.}\). На правом графике \(y = f’ (x)\text{,}\) единицы измерения по вертикальной оси представляют собой единицы \(f\) на единицу \(x\text{.}\) См., например, апплеты по адресу gvsu.edu/s/5C или gvsu.edu/s/5D на сайтах Дэвида Остина 1 и Марка Рено 2 .
См., например, апплеты по адресу gvsu.edu/s/5C или gvsu.edu/s/5D на сайтах Дэвида Остина 1 и Марка Рено 2 .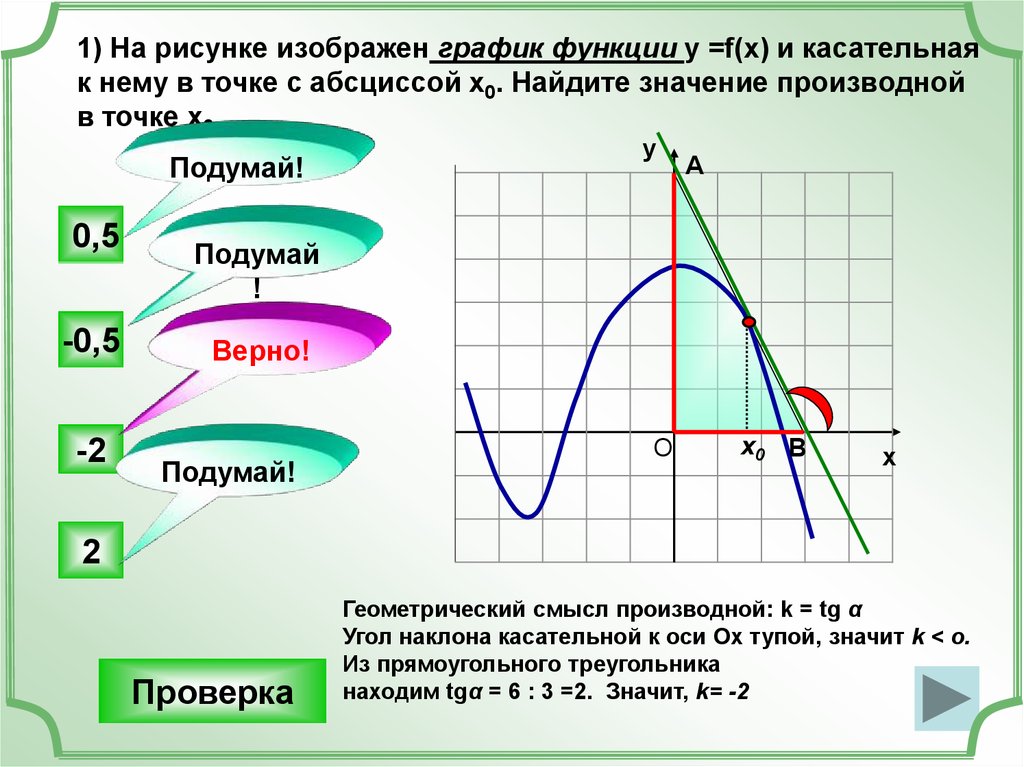
 Для последних четырех используйте определение предела. Обратите особое внимание на имена функций и независимых переменных. Важно уметь использовать буквы, отличные от \(f\) и \(x\text{.}\). Например, для данной функции \(p(z)\text{,}\) мы называем ее производной \(p'(z)\text{.}\) 93\)
Для последних четырех используйте определение предела. Обратите особое внимание на имена функций и независимых переменных. Важно уметь использовать буквы, отличные от \(f\) и \(x\text{.}\). Например, для данной функции \(p(z)\text{,}\) мы называем ее производной \(p'(z)\text{.}\) 93\)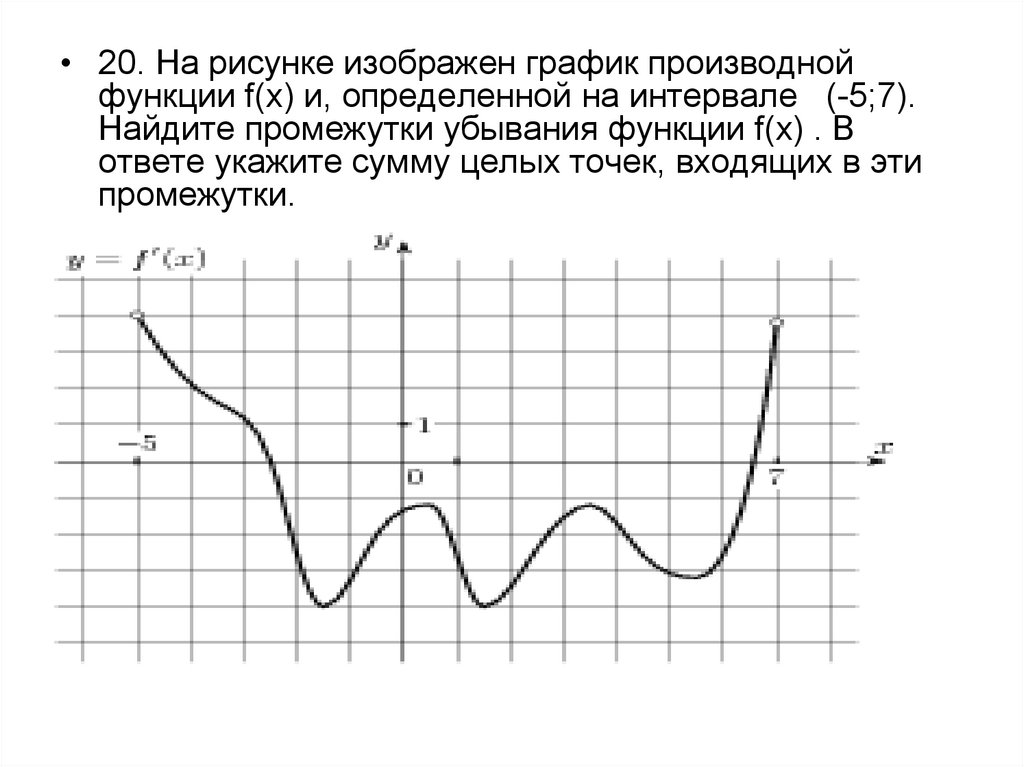
 Нарисуйте график этого и обозначьте каждую часть графика как «возрастающую» или «убывающую».
Нарисуйте график этого и обозначьте каждую часть графика как «возрастающую» или «убывающую».