Графы примеры: Граф Онлайн: Примеры графов

Основные виды графов

• Ориентированные и неориентированные графы
• Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
• Двудольный граф
• Эйлеров граф
• Регулярный граф
• Гамильтонов граф
• Взвешеный граф
• Графы-деревья

Виды графов могут определяться общими принципами их построения (таковы, например, двудольный граф и эйлеров граф), а могут зависеть от тех или иных свойств вершин или рёбер (например, ориентированный и неориентированный граф, обыкновенный граф).

Графы, в которых все рёбра являются звеньями (порядок двух концов ребра графа не существенен), называются неориентированными.

Графы, в которых все рёбра являются дугами (порядок двух концов ребра графа существенен), называются ориентированными графами или орграфами.

Неориентированный граф может быть представлен в виде ориентированного графа, если каждое его звено заменить на две дуги, имеющие противоположные направления.

Если граф содержит петли, то это обстоятельство специально оговаривают, добавляя к основной харатеристике графа слова «с петлями», например, «орграф с петлями». Если граф не содержит петель, то добавляют слова «без петель».

Смешанным называют граф, в котором имеются рёбра хотя бы двух из упомянутых трёх разновидностей (звенья, дуги, петли).

Граф, состоящий только из голых вершин, называется пустым.

Мультиграфом называется граф, в котором пары вершин могут быть соединены более чем одним ребром, то есть содершащий кратные рёбра, но не содержащий петель.

Граф без дуг (то есть неориентированный), без петель и кратных рёбер называется обыкновенным. Обыкновенный граф изображён на рисунке ниже.

Граф заданного типа называют полным, если он содержит все возможные для этого типа рёбра (при неизменном множестве вершин). Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном (рисунок ниже).

Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.

Пример 1. Построить полный двудольный граф.

Полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, соединяющих вершины одного множества с вершинами другого множества (рисунок ниже).

Мы уже касались задачи о кёнигсбергских мостах. Отрицательное решение Эйлером этой задачи привело к первой опубликованной работе по теории графов. Задачу об обходе мостов можно обобщить и получить следующую задачу теории графов: можно ли найти в данной графе цикл, содержащий все вершины и все рёбра? Граф, в котором это возможно, называется эйлеровым графом.

Итак, эйлеровым графом называется граф, в котором можно обойти все вершины и при этом пройти одно ребро только один раз.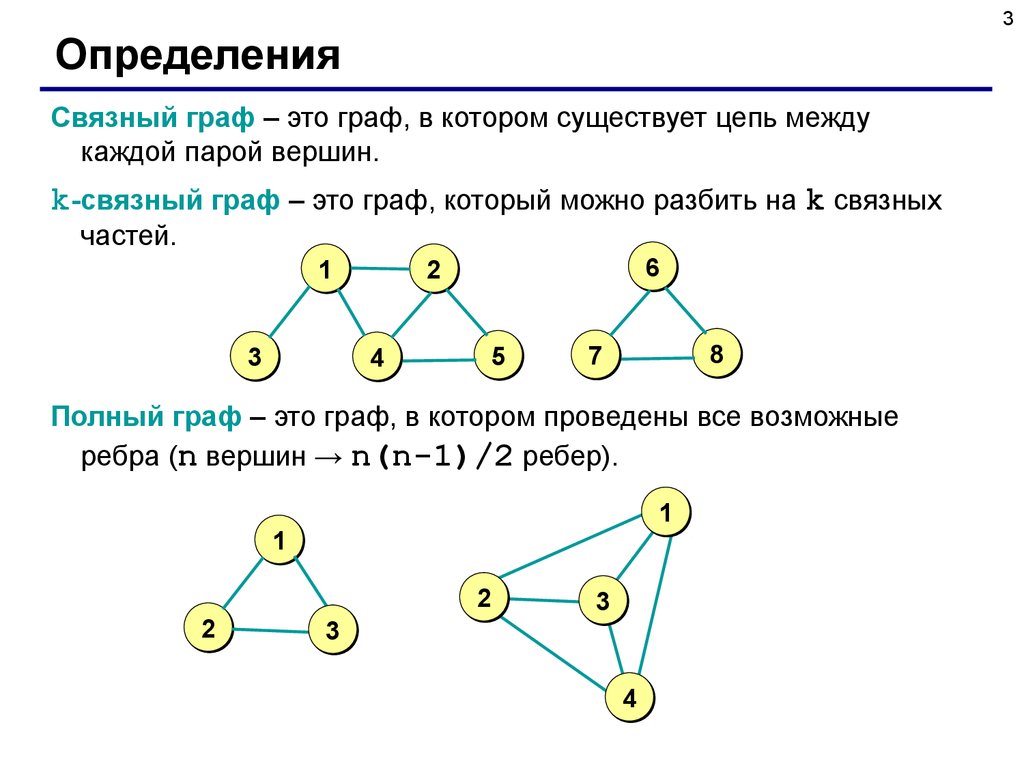 В нём каждая вершина должна иметь только чётное число рёбер.

Пример 2. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом? Объяснить ответ. Привести примеры.

Ответ. Если n — нечётное число, то каждая вершина инцидентна n-1 рёбрам. В таком случае данный граф является эйлеровым графом. Примеры таких графов на рисунке ниже.

Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k. Таким образом, на рисунке к примеру 2 изображены примеры регулярных графов, называемых по степени его вершин 4-регулярными и 2-регулярными графами или регулярными графами 4-й степени и 2-й степени.

Число вершин регулярного графа k-й степени не может быть меньше k+1. У регулярного графа нечётной степени может быть лишь чётное число вершин.

Пример 3. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.

Решение. Рассуждаем так: для того, чтобы длина цикла удовлетворяла заданному условию, требуется, чтобы число вершин графа было кратно четырём. Если число вершин равно четырём, то получится граф, изображённый на рисунке ниже. Он является регулярным, но в нём самый короткий цикл имеет длину 3.

Увеличиваем число вершин до восьми (следующее число, кратное четырём). Соединяем вершины рёбрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи.

Нет времени вникать в решение? Можно заказать работу!

Гамильтоновым графом называется граф, содержащий гамильтонов цикл. Гамильтоновым циклом называется простой цикл, проходящий через все вершины рассматриваемого графа. Таким образом, говоря проще, гамильтонов граф — это такой граф, в котором можно обойти все вершины и каждая вершина при обходе повторяется лишь один раз.

Пример гамильтонова графа — на рисунке ниже.

Пример 4. Задан двудольный граф, в котором n — число вершин из множества A, а m — число вершин из множества B. В каком случае граф будет эйлеровым графом, а в каком случае — гамильтоновым графом?

Ответ. Если n и n — чётные, то граф будет эйлеровым. Если n = n, то граф будет гамильтоновым.

Взвешенным графом называется граф, вершинам и (или) рёбрам которого присвоены «весы» — обычно некоторые числа. Пример взвешенного графа — транспортная сеть, в которой рёбрам присвоены весы, означающие стоимость перевозки груза по ребру и пропускные способности дуг. Пример взвешенного графа на рисунке ниже.

Деревом называется связный граф без циклов (рисунок ниже). Любые две вершины дерева соединены лишь одним маршрутом.

Число q рёбер графа находится из соотношения

q = n — 1,

где n — число вершин дерева.

Приведённое соотношение выражает критическое значение числа рёбер дерева, так как, если мы присоединим к дереву ещё одно ребро, то будет создан цикл, а если уберём одно ребро, то граф-дерево разделится на две компоненты. Граф, состоящий из компонент дерева, называется лесом.

В виде графов, особенно в виде деревьев, строятся многие математические модели, о которых также можно узнать на нашем сайте.

Назад

Листать

Вперёд>>>

Весь блок «Теория графов»

Теория графов: основные понятия и задачи

Инцидентность и смежность в графах. Матрицы смежности, матрицы инцидентности

Математические модели в виде графов. Дерево решений. Дерево игры

Виды вершин и рёбер графа. Маршруты, цепи, циклы в графах

К началу страницы

Теория графов — Типы графов

Существуют различные типы графиков в зависимости от количества вершин, количества ребер, взаимосвязанности и их общей структуры. Мы обсудим только несколько важных типов графиков в этой главе.

Нулевой график

Граф, не имеющий ребер , называется нулевым графом .

пример

На приведенном выше графике есть три вершины с именами «a», «b» и «c», но среди них нет ребер. Следовательно, это нулевой граф.

Тривиальный график

Граф с единственной вершиной называется тривиальным графом .

пример

На приведенном выше графике есть только одна вершина «а» без других ребер. Следовательно, это тривиальный граф.

Ненаправленный граф

Ненаправленный граф содержит ребра, но ребра не являются ориентированными.

пример

В этом графе «a», «b», «c», «d», «e», «f», «g» – вершины, а «ab», «bc», «cd», «da». ‘,’ ag ‘,’ gf ‘,’ ef ‘- ребра графа. Поскольку это ненаправленный граф, ребра «ab» и «ba» совпадают. Точно так же другие ребра также рассматриваются аналогичным образом.

Направленный граф

В ориентированном графе каждое ребро имеет направление.

пример

На приведенном выше графике у нас есть семь вершин «a», «b», «c», «d», «e», «f» и «g», и восемь ребер «ab», «cb», « dc ‘,’ ad ‘,’ ec ‘,’ fe ‘,’ gf ‘и’ ga ‘. Поскольку это ориентированный граф, на каждом ребре есть метка стрелки, показывающая его направление. Обратите внимание, что в ориентированном графе «ab» отличается от «ba».

Простой график

Граф без петель и параллельных ребер называется простым графом.

• Максимально возможное число ребер в одном графе с n вершинами равно ⁿ C _2, где ⁿ C ₂ = n (n – 1) / 2.

• Число простых графов возможно с n вершинами = 2 ^{n c ₂} = 2 ^{n (n-1) / 2} .

Максимально возможное число ребер в одном графе с n вершинами равно ⁿ C _2, где ⁿ C ₂ = n (n – 1) / 2.

Число простых графов возможно с n вершинами = 2 ⁿ

c ₂ = 2 ^{n (n-1) / 2} .

пример

На следующем графике есть 3 вершины с 3 ребрами, которые являются максимальными, исключая параллельные ребра и петли. Это можно доказать с помощью приведенных выше формул.

Максимальное количество ребер с n = 3 вершинами –

n C 2 = n(n–1)/2
   = 3(3–1)/2
   = 6/2
   = 3 edges

Максимальное количество простых графов с n = 3 вершинами –

2 n C 2 = 2 n(n-1)/2
   = 2 3(3-1)/2
   = 2 3
   = 8

Эти 8 графиков, как показано ниже –

Связанный график

Граф G называется связным, если между каждой парой вершин существует путь . Для каждой вершины графа должно быть хотя бы одно ребро. Так что мы можем сказать, что он связан с какой-то другой вершиной на другой стороне ребра.

пример

На следующем графике каждая вершина имеет свое ребро, соединенное с другим ребром. Следовательно, это связный граф.

Отключенный график

Граф G несвязен, если он не содержит хотя бы двух связанных вершин.

Пример 1

Следующий график является примером отключенного графа, где есть два компонента, один с вершинами «a», «b», «c», «d», а другой с «e», «f», «g», ‘h’ вершины.

Два компонента независимы и не связаны друг с другом. Следовательно, он называется несвязным графом.

Пример 2

В этом примере есть два независимых компонента, abfe и cd, которые не связаны друг с другом. Следовательно, это несвязный граф.

Обычный график

Граф G называется регулярным, если все его вершины имеют одинаковую степень . В графе, если степень каждой вершины равна «k», то этот граф называется «k-регулярным графом».

пример

На следующих графиках все вершины имеют одинаковую степень. Поэтому эти графы называются регулярными графами.

В обоих графах все вершины имеют степень 2. Они называются 2-регулярными графами.

Полный график

Простой граф с «n» взаимными вершинами называется полным графом и обозначается «K _n » . В графе вершина должна иметь ребра со всеми остальными вершинами, тогда она называется полным графом.

Другими словами, если вершина связана со всеми остальными вершинами графа, то она называется полным графом.

пример

В следующих графах каждая вершина графа связана со всеми остальными вершинами графа, кроме самой себя.

На графике я

		б	с
	Нет соединения	Связано	Связано
б	Связано	Нет соединения	Связано
с	Связано	Связано	Нет соединения

На графике II

	п	Q	р	s
п	Нет соединения	Связано	Связано	Связано
Q	Связано	Нет соединения	Связано	Связано
р	Связано	Связано	Нет соединения	Связано
s	Связано	Связано	Связано	Нет соединения

Цикл графика

Простой граф с n вершинами (n> = 3) и ребрами n называется графом циклов, если все его ребра образуют цикл длины n.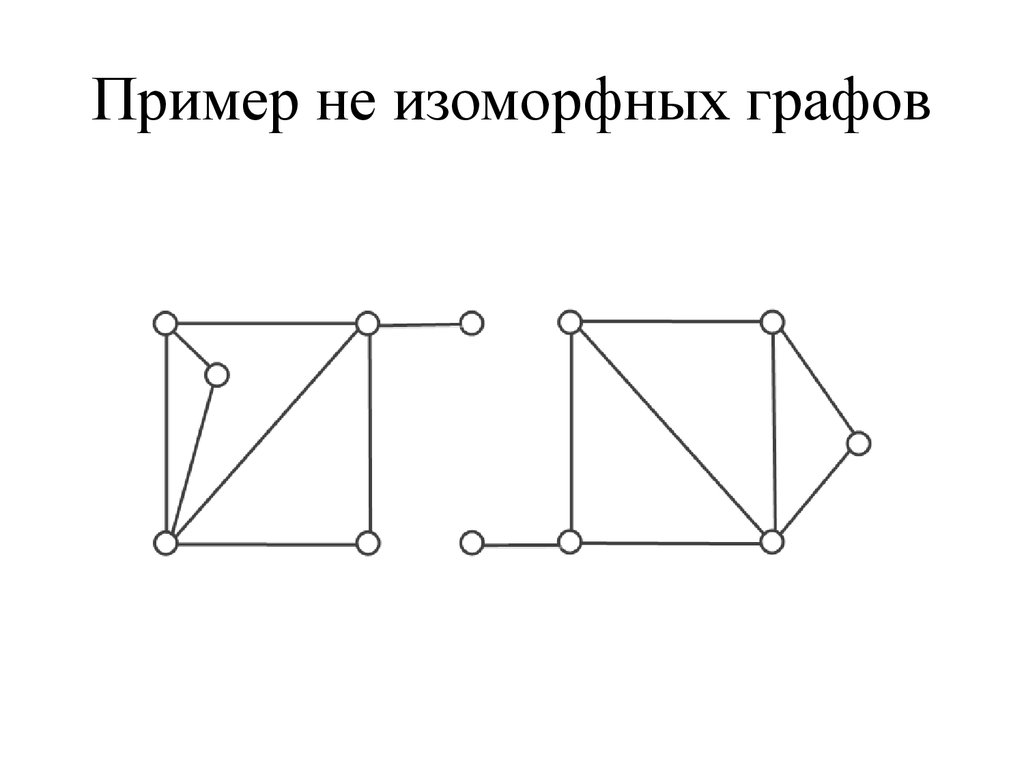

Если степень каждой вершины в графе равна двум, то она называется циклическим графом .

Обозначение – C _n

пример

Посмотрите на следующие графики –

• Граф I имеет 3 вершины с 3 ребрами, которые образуют цикл ‘ab-bc-ca’.

• Граф II имеет 4 вершины с 4 ребрами, которые образуют цикл ‘pq-qs-sr-rp’.

• Граф III имеет 5 вершин с 5 ребрами, которые образуют цикл ‘ik-km-ml-lj-ji’.

Граф I имеет 3 вершины с 3 ребрами, которые образуют цикл ‘ab-bc-ca’.

Граф II имеет 4 вершины с 4 ребрами, которые образуют цикл ‘pq-qs-sr-rp’.

Граф III имеет 5 вершин с 5 ребрами, которые образуют цикл ‘ik-km-ml-lj-ji’.

Следовательно, все данные графы являются графами циклов.

Колесо График

Граф колеса получается из графа циклов C _n-1 путем добавления новой вершины. Эта новая вершина называется Hub, которая связана со всеми вершинами C _n .

Обозначение – W _n

No. of edges in W n = No. of edges from hub to all other vertices +
                     No. of edges from all other nodes in cycle graph without a hub.
                     = (n–1) + (n–1)
                     = 2(n–1)

пример

Посмотрите на следующие графики. Они все колесные графики.

На графике I он получен из C ₃ путем добавления вершины в середине, названной ‘d’. Обозначается как W ₄ .

Number of edges in W 4 = 2(n-1) = 2(3) = 6

На графике II он получен из C ₄ путем добавления вершины в середине, названной ‘t’. Обозначается как W ₅ .

Number of edges in W 5 = 2(n-1) = 2(4) = 8

На графике III он получен из C ₆ путем добавления вершины в середине, названной ‘o’. Обозначается как W ₇ .

Number of edges in W 4 = 2(n-1) = 2(6) = 12

Циклический график

Граф с хотя бы одним циклом называется циклическим графом.

пример

В приведенном выше примере графа у нас есть два цикла abcda и cfgec. Следовательно, он называется циклическим графом.

Ациклический Граф

Граф без циклов называется ациклическим графом.

пример

В приведенном выше примере графа у нас нет циклов. Следовательно, это нециклический граф.

Двудольный график

Простой граф G = (V, E) с разбиением вершин V = {V ₁ , V ₂ } называется двудольным графом, если каждое ребро E соединяет вершину в V ₁ с вершиной в V ₂ .

В общем случае бипертитовый граф имеет два набора вершин, скажем, V ₁ и V ₂ , и если ребро нарисовано, он должен соединить любую вершину в наборе V ₁ с любой вершиной в наборе V ₂ .

пример

На этом графике вы можете наблюдать два набора вершин – V ₁ и V ₂ . Здесь два ребра с именами «ae» и «bd» соединяют вершины двух множеств V ₁ и V _2.

Полный двудольный график

Двудольный граф ‘G’, G = (V, E) с разбиением V = {V ₁ , V ₂ } называется полным двудольным графом, если каждая вершина в V ₁ соединена с каждой вершиной V ₂ .

В общем, полный двудольный граф соединяет каждую вершину из множества V ₁ с каждой вершиной из множества V ₂ .

пример

Следующий граф является полным двудольным графом, потому что у него есть ребра, соединяющие каждую вершину из множества V ₁ с каждой вершиной из множества V ₂ .

Если | V ₁ | = m и | V ₂ | = n, то полный двудольный граф обозначается через K _{m, n} .

• K _{m, n} имеет (m + n) вершин и (mn) ребер.

• K _{m, n} регулярный граф, если m = n.

K _{m, n} имеет (m + n) вершин и (mn) ребер.

K _{m, n} регулярный граф, если m = n.

В общем случае полный двудольный граф не является полным графом .

K _{m, n} полный граф, если m = n = 1.

Максимальное число ребер в двудольном графе с n вершинами

[

п 2/4

]

Если n = 10, k5, 5 = ⌊ n 2/4 ⌋ = ⌊ 10 2/4 ⌋ = 25

Аналогично К6, 4 = 24

К7, 3 = 21

К8, 2 = 16

К9, 1 = 9

Если n = 9, k5, 4 = ⌊ n 2/4 ⌋ = ⌊ 9 2/4 ⌋ = 20

Аналогично К6, 3 = 18

К7, 2 = 14

К8, 1 = 8

«G» является двудольным графом, если в «G» нет циклов нечетной длины. Частным случаем двудольного графа является звездный граф .

Звездный График

Полный двудольный граф вида K _{1, n-1} является графом звезд с n-вершинами. Звездный граф является полным двудольным графом, если одна вершина принадлежит одному набору, а все остальные вершины принадлежат другому набору.

пример

На приведенных выше графиках из n вершин все n – 1 вершины связаны с одной вершиной. Следовательно, оно имеет вид K _{1, n-1,} которые являются графами звезд.

Дополнение графика

Пусть ‘ G – ‘ – простой граф с некоторыми вершинами, такими как у G, и ребро {U, V} присутствует в ‘ G – ‘ , если ребро отсутствует в G. Это означает, что две вершины смежны в « G – », если две вершины не смежны в G.

Если ребра, которые существуют в графе I, отсутствуют в другом графе II, и если граф I и граф II объединены вместе, чтобы сформировать полный граф, то граф I и граф II называются дополнениями друг друга.

пример

В следующем примере graph-I имеет два ребра: «cd» и «bd». Его граф дополнения II имеет четыре ребра.

Обратите внимание, что ребра в графе-I отсутствуют в графе-II и наоборот. Следовательно, комбинация обоих графов дает полный граф из n вершин.

Примечание . Сочетание двух дополнительных графов дает полный граф.

Если «G» – простой граф, то

| E (G) | + | E ( ‘ G – ‘ ) | = | E (K _n ) |, где n = количество вершин в графе.

пример

Пусть ‘G’ – простой граф с девятью вершинами и двенадцатью ребрами, найдите число ребер в ‘ G – ‘ .

У вас есть, | E (G) | + | E ( ‘ G – ‘ ) | = | E (K _n ) |

12 + | E ( ‘ G – ‘ ) | знак равно

9 (9-1) / 2 = ⁹ C ₂

12 + | E ( ‘ G – ‘ ) | = 36

| E ( ‘ G – ‘ ) | = 24

«G» – простой граф с 40 ребрами, а его дополнение « G – » имеет 38 ребер. Найдите количество вершин в графе G или ‘ G – ‘ .

Пусть количество вершин в графе равно n.

Имеем, | E (G) | + | E ( ‘ G – ‘ ) | = | E (K _n ) |

40 + 38 = n (n-1) / 2

156 = n (n-1)

13 (12) = n (n-1)

n = 13

типов графиков и диаграмм и их использование: с примерами и изображениями

Если вам интересно, каковы различные типов графиков и диаграмм ,   их использование и названия, эта страница суммирует их с примерами и изображениями.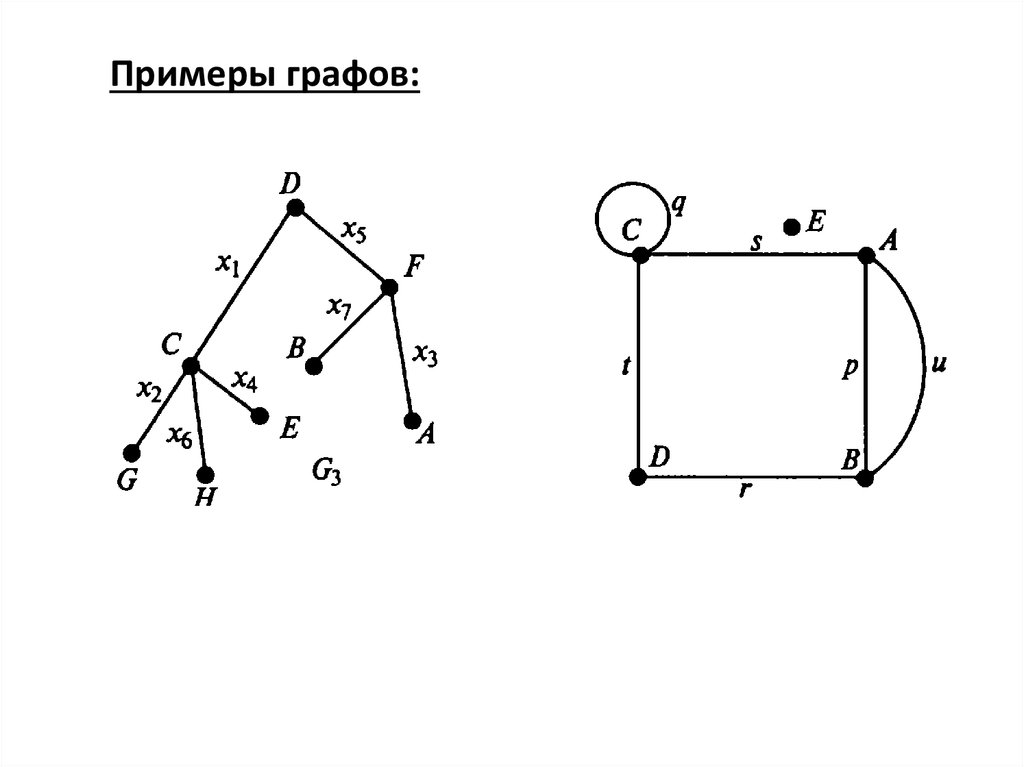

Поскольку различные виды графиков предназначены для представления данных, они используются во многих областях, таких как: статистика, наука о данных, математика, экономика, бизнес и т. д.

Каждый тип графика представляет собой визуальное представление данных на диаграммах (например, гистограмма, круговая диаграмма, линейная диаграмма), которые показывают различные типы тенденций графика и отношения между переменными.

Хотя трудно сказать все типы графиков, эта страница содержит все распространенные типы статистических графиков и диаграмм (и их значения), широко используемые в любой науке.

1. Линейные графики

Линейная диаграмма графически отображает данные, которые непрерывно изменяются во времени. Каждый линейный график состоит из точек, которые соединяют данные, чтобы показать тенденцию (непрерывное изменение). Линейные графики имеют ось X и ось Y. В большинстве случаев время распределяется по горизонтальной оси.

Использование линейных графиков:

• Когда вы хотите показать тренды . Например, как цены на жилье выросли с течением времени.
• Когда вы хотите, чтобы делал прогнозы на основе истории данных с течением времени.
• При сравнении двух или более различных переменных, ситуаций и информации за определенный период времени.

Пример: 

На следующем линейном графике показаны годовые продажи конкретной компании за шесть лет подряд:

Примечание: приведенный выше пример имеет 1 строку. Однако на одном линейном графике можно сравнивать несколько трендов по нескольким линиям распределения.

2. Гистограммы

Гистограммы представляют категориальные данные с прямоугольными столбцами (чтобы понять, что такое категориальные данные, см. примеры категориальных данных). Гистограммы являются одними из самых популярных типов графиков и диаграмм в экономике, статистике, маркетинге и визуализации в цифровом клиентском опыте. Они обычно используются для сравнения нескольких категорий данных.

Длина и высота каждой прямоугольной полосы пропорциональны значениям, которые они представляют.

На одной оси гистограммы представлены сравниваемые категории. Другая ось показывает измеренное значение.

Гистограммы Использование:

• Когда вы хотите отобразить данные, сгруппированные в номинальные или порядковые категории (см. номинальные и порядковые данные).
• Для сравнения данных по разным категориям.
• Гистограммы также могут отображать большое   изменение данных с течением времени.
• Гистограммы идеально подходят для визуализации распределения данных при наличии более трех категорий.

Пример:

На приведенной ниже гистограмме представлена ​​общая сумма продаж продукта А и продукта Б за три года.

Стержни бывают 2-х типов: вертикальные или горизонтальные. Неважно, какой вид вы будете использовать. Вышеупомянутый является вертикальным типом.

3. Круговые диаграммы

Когда дело доходит до статистических типов графиков и диаграмм, круговая диаграмма (или круговая диаграмма) имеет решающее значение и значение. Он отображает данные и статистику в простом для понимания формате «срезов пирога» и иллюстрирует числовую пропорцию.

Размер каждой части круговой диаграммы зависит от размера конкретной категории в данной группе в целом. Другими словами, круговая диаграмма разбивает группу на более мелкие части. Он показывает отношения часть-целое.

Чтобы построить круговую диаграмму, вам понадобится список категориальных переменных и числовых переменных.

Круговая диаграмма Использование:

• Когда вы хотите создать и представить композицию чего-либо.
• Это очень полезно для отображения номинальных или порядковых категорий данных.
• К показать процент или пропорциональные данные.
• Когда сравнения областей роста в рамках бизнеса, таких как прибыль.
• Круговые диаграммы лучше всего подходят для отображения данных для 3–7 категорий.

Пример:

На приведенной ниже круговой диаграмме представлена ​​пропорция видов транспорта, используемых 1000 учащимися для поездки в школу.

Круговые диаграммы широко используются маркетологами, работающими с данными, для отображения маркетинговых данных.

4. Гистограмма

Гистограмма показывает непрерывные данные в упорядоченных прямоугольных столбцах (чтобы понять, что такое непрерывные данные, см. нашу публикацию о дискретных и непрерывных данных). Обычно между столбцами нет пробелов .

Гистограмма отображает частотное распределение (форму) набора данных. На первый взгляд гистограммы похожи на гистограммы. Однако между ними есть ключевое различие. Гистограмма представляет собой категориальные данные, а гистограмма представляет непрерывные данные.

Гистограмма Использование:

• Когда данные непрерывны .
• Если вы хотите представить форму распределения данных .
• Если вы хотите увидеть, отличаются ли выходные данные двух или более процессов.
• Чтобы суммировать больших набора данных графически.
• Для быстрой передачи данных о распределении другим.

Пример:

На приведенной ниже гистограмме представлен доход на душу населения для пяти возрастных групп.

Гистограммы очень широко используются в статистике, бизнесе и экономике.

5. Точечная диаграмма

Точечная диаграмма представляет собой диаграмму X-Y, которая показывает взаимосвязь между двумя переменными. Он используется для построения точек данных по вертикальной и горизонтальной осям. Цель состоит в том, чтобы показать, насколько одна переменная влияет на другую.

Обычно при наличии связи между двумя переменными первая называется независимой. Вторая переменная называется зависимой, потому что ее значения зависят от первой переменной.

Диаграммы рассеяния также помогают прогнозировать поведение одной переменной (зависимой) на основе измерения другой переменной (независимой).

Точечная диаграмма использует:

• При попытке выяснить, существует ли связь между двумя переменными .
• Предсказать поведение зависимой переменной на основе меры независимой переменной.
• При наличии парных числовых данных.
• При работе с инструментами анализа первопричин для выявления потенциальных проблем.
• Когда вы просто хотите визуализировать корреляцию между двумя большими наборами данных без учета времени .

Пример:

На приведенном ниже точечном графике представлены данные по 7 интернет-магазинам, их ежемесячным продажам электронной коммерции и затратам на интернет-рекламу за последний год.

Оранжевая линия, которую вы видите на графике, называется «линия наилучшего соответствия» или «линия тренда». Эта линия используется, чтобы помочь нам делать прогнозы, основанные на прошлых данных.

Точечные диаграммы широко используются в науке о данных и статистике. Они являются отличным инструментом для визуализации моделей линейной регрессии.

Дополнительные примеры и объяснения для точечных диаграмм вы можете увидеть в нашем посте, что показывает точечная диаграмма, и простые примеры линейной регрессии.

6. Диаграмма Венна

Диаграмма Венна (также называемая первичной диаграммой, диаграммой множества или логической диаграммой) использует перекрывающиеся круги для визуализации логических отношений между двумя или более группами элементов.

Диаграмма Венна — это один из типов графиков и диаграмм, используемых в научных и инженерных презентациях, в компьютерных приложениях, в математике и статистике.

Базовая структура диаграммы Венна обычно представляет собой перекрывающиеся круги. Элементы в перекрывающемся разделе имеют определенные общие характеристики. Предметы во внешних частях кругов не имеют общих черт.

Диаграмма Венна Использование:

• Когда вы хотите, чтобы сравнила и сопоставила группы вещей.
• Для классификации или группировки предметов.
• Для иллюстрации логических отношений из различных наборов данных.
• Чтобы определить все возможные отношения между коллекциями наборов данных.

Пример:

В следующем научном примере диаграммы Венна сравниваются особенности птиц и летучих мышей.

7. Диаграммы с областями 

Диаграммы с областями показывают изменение одной или нескольких величин во времени. Они очень похожи на линейный график. Однако область между осью и линией обычно заполняется цветом.

Несмотря на то, что линейные диаграммы и диаграммы с областями поддерживают один и тот же тип анализа, их не всегда можно использовать взаимозаменяемо. Линейные диаграммы часто используются для представления нескольких наборов данных. Диаграммы с областями не могут четко отображать несколько наборов данных, поскольку диаграммы с областями показывают заштрихованную область под линией.

Диаграмма с областями Использование:

• Если вы хотите, чтобы отображал тренды , а не выражал конкретные значения.
• Чтобы показать простое сравнение тенденции наборов данных за определенный период времени.
• Для отображения величины изменения.
• Для сравнения небольшого количества категорий.

Диаграмма с областями имеет 2 варианта: вариант с наложением графиков данных друг на друга и вариант с графиками данных, наложенными друг на друга (известный как диаграмма с накоплением областей — как показано в следующем примере).

Пример:

На приведенной ниже диаграмме с областями показаны квартальные продажи продуктов категорий A и B за последний год.

На этой диаграмме с областями показано быстрое сравнение тенденции квартальных продаж продукта А и продукта В за период прошлого года.

8. Сплайн-диаграмма

Сплайн-диаграмма — один из наиболее распространенных типов графиков и диаграмм, используемых в статистике. Это форма линейной диаграммы, которая представляет плавные кривые через различные точки данных.

Сплайн-диаграммы обладают всеми характеристиками линейных диаграмм, за исключением того, что сплайн-диаграммы имеют подогнанную изогнутую линию для соединения точек данных. Для сравнения, линейные диаграммы соединяют точки данных прямыми линиями.

Сплайн-диаграмма. Используется:

• .
• Сплайн-диаграммы часто используются при разработке диаграмм Парето .
• Сплайн-диаграмма также часто используется для моделирования данных при ограниченном количестве точек данных и оценке промежуточных значений.

Пример:

В следующем примере сплайн-диаграммы показаны продажи компании за несколько месяцев года:

числовых данных через их квартили. Он отображает частотное распределение данных.

Диаграмма с ячейками и усами помогает отображать разброс и асимметрию для заданного набора данных, используя принцип сводки из пяти чисел: минимум, максимум, медиана, нижняя и верхняя квартили. Принцип «сводки по пяти числам» позволяет предоставить статистическую сводку для определенного набора чисел. Он показывает диапазон (минимальное и максимальное число), разброс (верхний и нижний квартили) и центр (медиану) для набора чисел данных.

Очень простое изображение графика с прямоугольниками и усами, которое вы можете увидеть ниже:

Диаграмма с прямоугольниками и усами Использование:

• Когда вы хотите, чтобы наблюдал верхние и нижние квартили, среднее значение, медиану, отклонения и т. д. , для большого набора данных.
• Если вы хотите быстро просмотреть распределение набора данных .
• Когда у вас есть несколько наборов данных , которые поступают из независимых источников и каким-то образом связаны друг с другом.
• Когда вам нужно для сравнения данных из разных категорий.

Пример:

В приведенной ниже таблице и диаграммах в виде прямоугольников и усов показаны результаты тестов по математике и литературе для одного и того же класса.

Maths	35	77	92	43	55	66	73	70
Literature	35	43	40	43	50	60	70	92

Ящик и анализ «Анализ», «Анализ», «Анализ», «Анализ», «Аналитические анализы», «Анализ», «Анализ», «Анализ», «Анализ», «Анализ», «Анализ», «Анализ», «Анализ», «Анализ», «Анализ», «Анализ», «Анализ», «Анализ», «Анализ». анализ и т. д.

10. Пузырьковая диаграмма

Пузырьковые диаграммы — очень полезные типы графиков для сравнения взаимосвязей между данными в трех числовых измерениях: данные по оси Y, данные по оси X. и данные, отражающие размер пузырьков.

Пузырьковая диаграмма очень похожа на точечную диаграмму по осям XY, но пузырьковая диаграмма обладает большей функциональностью — третье измерение данных, которое может быть чрезвычайно ценным.

Обе оси (X и Y) пузырьковой диаграммы являются числовыми.

Пузырьковая диаграмма Использование:

• Когда вам нужно отобразить три или четыре измерения данных.
• Если вы хотите сравнить и отобразить отношения между категоризированными кругами, используя пропорции.

Пример:

На приведенной ниже пузырьковой диаграмме показано соотношение между стоимостью (ось X), прибылью (ось Y) и вероятностью успеха (%) (размер кружка).

11. Пиктограммы

Пиктограмма или пиктограмма — это один из наиболее визуально привлекательных типов графиков и диаграмм, которые отображают числовую информацию с использованием значков или графических символов для представления наборов данных.

Очень удобный для чтения статистический способ визуализации данных. Пиктограмма показывает частоту данных в виде изображений или символов. Каждое изображение/символ может представлять одну или несколько единиц данного набора данных.

Пиктограмма Использование:

• Когда ваша аудитория предпочитает и лучше понимает дисплеи со значками и иллюстрациями. Веселье может способствовать обучению.
• Для инфографики привычно использование пиктограммы.
• Когда вы хотите, чтобы сравнил две точки эмоционально сильным способом.

Пример: 

Следующая пиктограмма представляет количество компьютеров, проданных коммерческой компанией за период с января по март.

Пиктографический пример выше показывает, что в январе было продано 20 компьютеров (4×5 = 20), в феврале было продано 30 компьютеров (6×5 = 30), а в марте было продано 15 компьютеров.

12. Точечный график

Точечный график или точечный график — это лишь один из многих типов графиков и диаграмм для организации статистических данных. Он использует точки для представления данных. Точечный график используется для относительно небольших наборов данных, а значения попадают в ряд дискретных категорий.

Если значение появляется более одного раза, точки располагаются одна над другой. Таким образом, высота столбца точек показывает частоту этого значения.

Точечный график Использование:

• Для построения графика подсчета частоты, когда у вас есть небольшое количество категорий .
• Точечные графики очень полезны, когда переменная является количественной или категориальной .
• Точечные графики также используются для одномерных данных (данные только с одной переменной, которую можно измерить).

Пример:

Предположим, у вас есть класс из 26 учеников. Их просят назвать свой любимый цвет. Точечный график ниже представляет их выбор:

Очевидно, что ученики этого класса предпочитают синий цвет.

13. Радарная диаграмма

Радарная диаграмма — один из самых современных видов графиков и диаграмм — идеально подходит для множественных сравнений. Радарные диаграммы используют круговой дисплей с несколькими различными количественными осями, похожими на спицы на колесе. Каждая ось показывает количество для различных категориальных значений.

Радиолокационные карты также известны как паутинные карты, паутинные карты, звездные графики, неправильные многоугольники, полярные карты, паутинные карты или диаграммы Кивиата.

Радарная диаграмма в настоящее время имеет множество применений в статистике, математике, бизнесе, спортивном анализе, анализе данных и т. д.

Радарная диаграмма Использование:

• каждой переменной.
• Для представления множественных сравнений .
• Когда вы хотите увидеть, какие переменные имеют низкие или высокие оценки в наборе данных. Это делает радарную диаграмму идеальной для отображения производительности .

Пример:

Например, мы можем сравнить производительность сотрудника по шкале от 1 до 8 по таким предметам, как пунктуальность, решение проблем, соблюдение сроков, маркетинговые знания, коммуникации. Точка, расположенная ближе к центру оси, показывает более низкое значение и худшую производительность.

Label	Punctuality	Problem-solving	Meeting Deadlines	Marketing Knowledge	Communications
Jane	6	5	8	7	8
Саманта	7	5	5	4	8

производительность лучше, чем у Джейнтаман.

14. Пирамидальная диаграмма

Когда дело доходит до понятных и красивых типов графиков и диаграмм, пирамидальная диаграмма занимает первое место.

Пирамидальная диаграмма представляет собой диаграмму в форме пирамиды или треугольника. Эти типы диаграмм лучше всего подходят для данных, организованных в какой-либо иерархии. Уровни показывают прогрессивный порядок.

Пирамидальная диаграмма Использование:

• Когда вы хотите, чтобы указывал уровень иерархии среди тем или других типов данных.
• Пирамидальный график часто используется для представления прогрессивных порядков, таких как: «от более старых к более новым», «от более важных к менее важным», «от конкретных к менее конкретным» и т. д.
• Когда у вас есть пропорциональные или взаимосвязанные отношения между данными наборы.

Пример:

Классическим примером диаграммы пирамиды является пирамида здорового питания, которая показывает, что жиры, масла и сахар (вверху) следует есть меньше, чем многие другие продукты, такие как овощи и фрукты (внизу пирамиды). ).

Вывод:

Вы, наверное, знаете, что выбор правильного типа диаграммы — дело непростое.

На практике выбор зависит от двух основных факторов: от типа анализа, который вы хотите выполнить, и от типа имеющихся у вас данных.

Обычно, когда мы стремимся облегчить сравнение, мы используем гистограмму или лепестковую диаграмму. Когда мы хотим показать тенденции во времени, мы используем линейную диаграмму или диаграмму с областями и т. д.

В любом случае, у вас есть широкий выбор типов графиков и диаграмм. При правильном использовании они являются мощным оружием, которое поможет вам сделать ваши отчеты и презентации профессиональными и четкими.

Какие ваши любимые типы графиков и диаграмм? Поделитесь своими мыслями в поле ниже.

11 основных типов графиков (с примерами)

Что может быть лучше, чем страница, полная чисел? Страница, полная чисел, помещенных в график! Графики помогают увидеть, как числа соотносятся друг с другом, и сделать различные предположения или выводы. Однако в математике используется не один тип графика. Взгляните на несколько основных типов графиков, которые вы найдете.

школьный график с линейкой

Реклама

Что такое график?

Математика и числа могут быть трудны для понимания, особенно если у вас много данных, которые вы сравниваете. Однако график может упростить задачу. Почему? Потому что график — это данные или числа, помещенные в удобную для понимания картинку. И в зависимости от типа чисел, над которыми вы работаете; вам может понадобиться другой тип графика для каждого. Например, если вы сравнивали рубашки разных цветов в своем классе, вы можете использовать гистограмму или круговую диаграмму. Однако, если вы хотите соединить числа в линию, вы можете использовать линейный график.

Графики и диаграммы

Хотя вы можете слышать, что диаграмма и диаграмма взаимозаменяемы, эти два термина не совсем одно и то же. Графики — это типы диаграмм. Диаграммы — это способ графического представления информации, включая графики, диаграммы, таблицы и другие визуальные представления данных. Таким образом, хотя все графики являются диаграммами, не все диаграммы являются диаграммами. Поскольку это сбивает с толку, может быть проще запомнить, что визуальные представления математических отношений можно найти на графиках.

Различные типы графиков в математике

Теперь, когда у вас есть представление о том, что такое графики, пришло время погрузиться прямо в мясо и картошку, изучив типы графиков.

1. Гистограмма

Гистограмма показывает числа и статистику с помощью столбцов. Это могут быть бары, которые идут вверх или бары, которые идут вправо. Этот тип графика идеально подходит для отображения соотношения размеров, частот и измерений. Например, вы можете использовать гистограмму, чтобы узнать, сколько людей в вашем классе владеют определенным типом автомобиля.

Реклама

2. Гистограмма

Гистограмма очень похожа на гистограмму; однако этот график предназначен для статистической информации, попадающей в определенные диапазоны. Например, вы можете использовать его для построения графика диапазонов роста людей в классе или доме. Таким образом, у вас может быть 5 человек ростом от 5 футов до 5 футов 5 дюймов. Вы можете увидеть разницу между гистограммой и гистограммой, потому что гистограмма не имеет пробелов между столбцами.

Реклама

3. Распределение частот

Когда дело доходит до графика распределения частот, также называемого набором данных распределения частот, он показывает, сколько раз что-то произошло. Например, он может сказать вам, какой процент людей в вашей школе любит шоколадный торт, пирог или печенье.

Реклама

4. Линейные графики

Когда дело доходит до линейного графика, подумайте о слове линия. Линейные графики — это точки данных, которые помещаются на график и соединяются для создания линии. В качестве примера можно посмотреть на изменение стоимости обедов с 1980 до 2020 на линейном графике.

Реклама

5. График времени

Время всегда можно измерить. И когда это так, вы можете назвать это временным графиком. Этот тип математического графика имеет время на оси X. Затем ось Y будет измерять что-то еще. Таким образом, вы можете создать график зависимости расстояния от времени на графике временного графика.

Реклама

6. Точечная диаграмма

Возможно, вы уже начали замечать, что имена графиков обычно исходят из того, как они выглядят. Это верно для диаграммы рассеяния. Этот тип графика имеет точки, разбросанные по графику. Однако, если вы посмотрите на эти точки, вы сможете увидеть тенденции и отношения между двумя измеряемыми единицами.

Реклама

7. Круговая диаграмма

Какой график выглядит как круг и имеет срезы? Ну и круговая диаграмма, конечно. Круговые диаграммы — это универсальные диаграммы, которые могут отображать отношения между несколькими различными переменными. С помощью круговой диаграммы вы можете показать, какой процент членов вашей семьи любит комедии, научную фантастику, драмы или боевики. Круговая диаграмма показывает, какой процент им нравится больше всего, а какой меньше всего.

Реклама

8. Экспоненциальные графики

В алгебре вы начинаете использовать множество различных показателей и выражений. Эти выражения можно изобразить с помощью оси x и оси y на экспоненциальном графике. Например, y = 2 ^x создает кривую линию на графике, которая движется вверх вправо.

Реклама

9. Логарифмические графики

Если вы знаете, как построить экспоненциальный график, важно также знать, как построить логарифмический график. Почему? Потому что логарифмическая функция в основном является зеркальным отражением экспоненциальной функции. Люди типа Мати называют это обратной функцией. Таким образом, обратная экспоненциальная функция будет y = log2 _х .

Реклама

10. Диаграммы «ящик и ус»

Возможно, вы слышали о медиане в математике. Если у вас есть, вы знаете, что у него есть верхние и нижние крайние значения данных.