Задание 1 — ГДЗ по алгебре 7 класс рабочая тетрадь Миндюк Шлыкова
Авторы: Миндюк, Шлыкова
Издательство: Просвещение
Тип книги: Рабочая тетрадь
1 Часть
1. Числовые выражения
123456789101112131415162. Выражения с переменными
12345678910111213141516173. Сравнение значений выражений
123456789101112131415164. Свойства действий над числами
123456789101112135. Тождества. Тождественное преобразование выражений
1234567891011121314151617186. Уравнение и его корни
123456789101112137. Линейное уравнение с одной переменной
1234567891011121314151617188. Решение задач с помощью уравнений
12345678910111213149. Среднее арифметическое, размах и мода
123456789101112131410. Медиана как статистическая характеристика
123456789101111. Что такое функция
12345678910111212. Вычисление значений функции по формуле
1234567891011121314151613.
График функции 1234567891011121314151614. Прямая пропорциональность и её график
1234567891011121314151617181915. Линейная функция и её график
123456789101112131415161718192016. Определение степени с натуральным показателем
1234567891011121314151617181917. Умножение и деление степеней
12345678910111213141518. Возведение в степень произведения
1234567891011121314151619. Одночлен и его стандартный вид
123456789101112131420. Умножение одночленов. Возведение одночлена в степень
123456789101112131415161721. Функции игрек равно икс в квадрате и игрек равно икс в кубе и их графики
12345678910111213141516172 Часть
22. Многочлен и его стандартный вид
12345678910111213141516171823. Сложение и вычитание многочленов
12345678910111213141516171824. Умножение многочлена на одночлен
123456789101112131415161725. Вынесение общего множителя за скобки
123456789101112131415161726.
Умножение многочлена на многочлен 12345678910111213141516171827. Разложение многочлена на множители способом группировки
12345678910111213141528. Возведение в квадрат и в куб суммы и разности двух выражений
123456789101112131415161729. Разложение на множители с помощью формул квадрата суммы и квадрата разности
1234567891011121330. Умножение разности двух выражений на их сумму
123456789101112131431. Разложение разности квадратов на множители
1234567891011121314151632. Разложение на множители сумммы и разности кубов
123456789101112131433. Преобразование целого выражения в многочлен
12345678910111213141534. Применение различных способов для разложения на множители
123456789101112131435. Линейное уравнение с двумя переменными
12345678910111213141536. График линейного уравнения с двумя переменными
123456789101112131437. Системы линейных уравнений с двумя переменными
1234567891011121338.
Способ подстановки 12345678910111213141539. Способ сложения
1234567891011121340. Решение задач с помощью систем уравнений
1234567891011121314Средняя оценка 0 / 5. Количество оценок: 0
Оценок пока нет. Поставьте оценку первым.
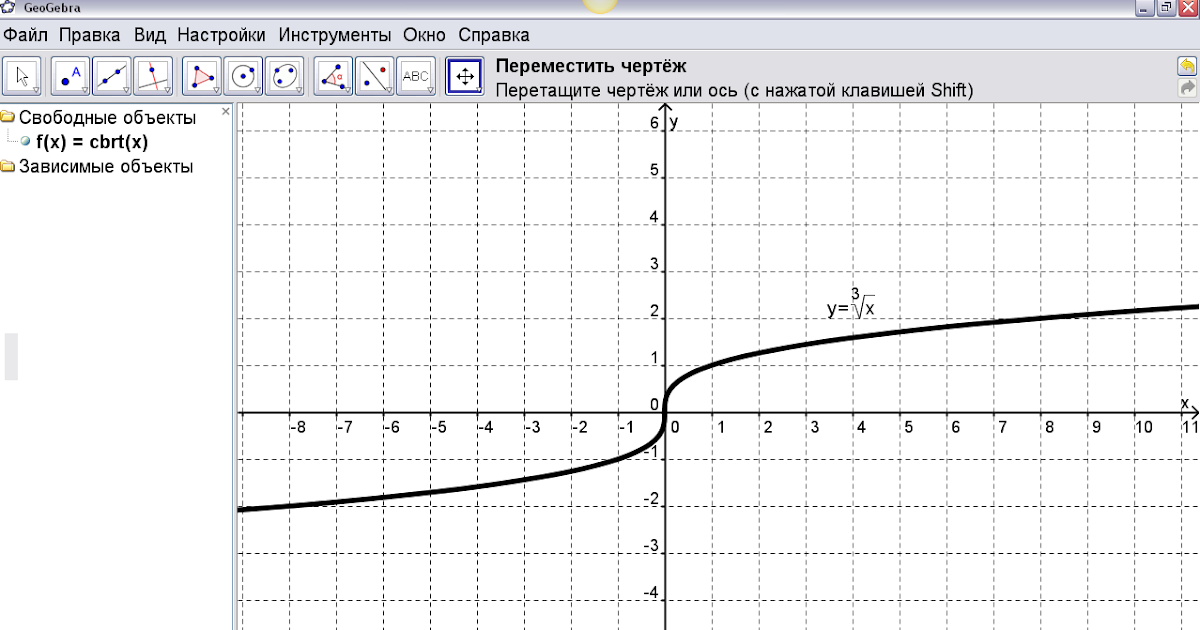
Видео-урок: Кубические функции и их графики
Стенограмма видео
В этом видео мы научимся изображать кубические функции, записывать их правила по их графикам и определять их Особенности. Итак, начнем с рассмотрения стандартная кубическая функция, которая 𝑓 из 𝑥 равна 𝑥 в кубе.
Всегда приятно помнить об этом
мы можем изобразить любую функцию, найдя некоторые координаты, лежащие на этой функции. Мы можем выбрать диапазон ввода или
𝑥-значения и вычислить их соответствующие выходные данные или 𝑓 из 𝑥 значений. Как только мы найдем эти координаты или
упорядоченные пары, мы можем построить их и соединить их кривой.
Итак, давайте посмотрим на характеристики стандартной кубической функции. Во-первых, можно сказать, что значение функции положительна, когда 𝑥 положительна, отрицательна, когда 𝑥 отрицательна, и ноль, когда 𝑥 равно нулю. Во-вторых, как многочлен с нечетная степень три, он имеет противоположное поведение. Это конечное поведение таково, что 𝑥 увеличивается до ∞, то 𝑓 из 𝑥 также увеличивается до ∞. А когда 𝑥 уменьшается, то 𝑓 из 𝑥 также убывает до отрицательных значений ∞. Наконец, мы также можем сказать, что это нечетная функция, поэтому 𝑓 отрицательного 𝑥 равно отрицательному 𝑓 𝑥 для всех значений 𝑥 в домене 𝑓. Заметим также, что при преобразовании этой функции определение кривой сохраняется.
Итак, давайте взглянем на некоторые из
различные преобразования. Мы можем классифицировать различные
преобразования на два основных типа: либо изменение входа, либо изменение
вывод.
Начнем с того, как дополнение изменяет внешний вид функции, начиная с изменений вывода.
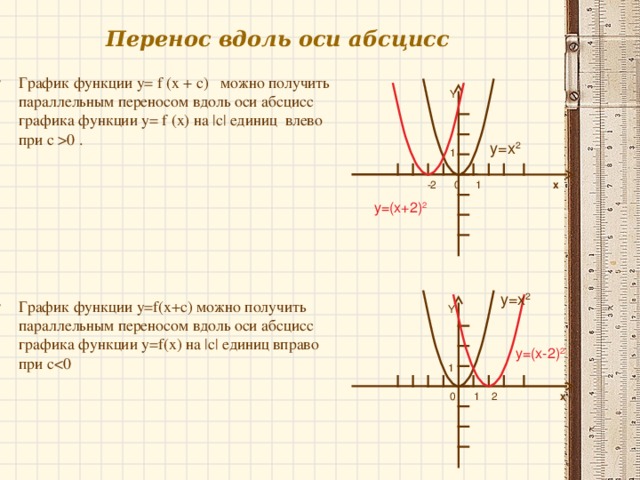
Возьмем стандартную кубическую функция 𝑓 от 𝑥 равна 𝑥 в кубе, и добавьте две другие функции для рассмотрения: 𝑔 из 𝑥 равно 𝑥 в кубе плюс два, а ℎ из 𝑥 равно 𝑥 в кубе минус один. Обратите внимание, как изменился результат в этих двух функциях. Это не просто 𝑥 в кубе; это 𝑥 в кубе плюс два и 𝑥 в кубе минус один. Мы могли бы использовать таблицу значений для помогите нам, а затем отобразите эти три функции вместе на одном графике.
Мы видим, что стандарт
кубическая функция проходит через нуль, нуль, но 𝑔 от 𝑥 равно 𝑥 в кубе плюс два
проходит через точку ноль, два. Точно так же ℎ из 𝑥 равно 𝑥
в кубе минус единица проходит через координату ноль, отрицательную единицу.
Мы можем видеть это в функции 𝑔 из 𝑥. Значение 𝑘 здесь будет плюсом два, и график переместился на две единицы вверх. А если 𝑘 меньше нуля, то его график представляет собой перевод абсолютного значения на 𝑘 единиц вниз график 𝑓 of 𝑥 равен 𝑥 в кубе. Если мы посмотрим на функцию ℎ от 𝑥, значение 𝑘 здесь отрицательно; это отрицательный. Таким образом, его абсолютное значение равно один. И мы видим, что ℎ из 𝑥 является перевод 𝑓 из 𝑥 равен 𝑥 в кубе на одну единицу меньше.
Далее мы посмотрим, как
добавление или вычитание значений из ввода изменяет функцию.
Мы сохраним стандартную кубическую
функция 𝑓 от 𝑥 равна 𝑥 в кубе, но мы можем ввести две новые функции 𝑔 от 𝑥
и ℎ из 𝑥. Поскольку мы меняем ввод, это
раз уже не просто 𝑥 в кубе, а 𝑥 плюс два в кубе и 𝑥 минус один
в кубе.
Мы можем построить все три графика на
одинаковые оси. На этот раз у нас горизонтальная
перевод. 𝑓 из 𝑥 равно 𝑥 в кубе
действительно проходят через ноль на оси 𝑥. Однако 𝑔 из 𝑥 равно 𝑥 плюс
два в кубе проходят через минус два на оси 𝑥. ℎ из 𝑥 равно 𝑥 минус один
куб проходит через положительную единицу на оси 𝑥. Это может быть довольно трудным
трансформация в память. Например, когда мы добавляем два к
функции, заманчиво думать, что это идет в положительном направлении или, в
в этом случае два вправо. Однако 𝑔 слова 𝑥 — это перевод
из 𝑓 из 𝑥 равно 𝑥 в кубе на две единицы влево.
Точно так же, когда мы вычитаем единицу, мы думаю, что перевод должен идти влево. Но на самом деле он идет к правильно. Чтобы помочь нам вспомнить об этом, мы можем сказать, что если мы изменим ввод 𝑥 на 𝑥 минус ℎ, то будет перевод ℎ единиц вправо. Например, в функции ℎ от 𝑥 равно 𝑥 минус единица в кубе, значение ℎ будет равно единице, а перевод произошел на одну единицу вправо. Когда значение ℎ отрицательное, мы ищем перевод абсолютного значения оставшихся ℎ единиц. Это то, что мы имеем в функция 𝑔 от 𝑥, где значение ℎ здесь было бы отрицательным значением два, что является осталось две единицы перевода.
Теперь давайте посмотрим, как
умножение меняет функцию. На этот раз у нас есть 𝑓 из 𝑥
равно 𝑥 в кубе, 𝑔 из 𝑥 равно трем 𝑥 в кубе, а ℎ из 𝑥 равно
половина 𝑥 в кубе. Вот три функции
построены вместе.
Итак, что мы замечаем на этот раз? Ну это не перевод, т.к.
все три функции проходят через одну и ту же координату ноль, ноль. Что мы можем сказать, так это то, что
функция 𝑓 от 𝑥 равна 𝑥 в кубе была расширена по вертикали. 𝑔 из 𝑥 было вертикально
увеличена в три раза, а ℎ из 𝑥 была расширена по вертикали на
коэффициент масштабирования половинный. Таким образом, мы можем сказать, что для любого
положительное значение 𝑎, когда 𝑓 из 𝑥 отображается в 𝑎, умноженное на 𝑓 из 𝑥, существует вертикальная
расширение масштабного коэффициента 𝑎.
А теперь посмотрим, как умножение ввода изменяет функцию.
На этот раз мы можем сравнить друг друга
функция ℎ от 𝑥 равна двум 𝑥 в кубе вместе со стандартной кубической функцией. Для полного понимания того, что
происходит здесь, давайте рассмотрим некоторые координаты в каждой из функций. Возьмем координату два,
восемь в функции 𝑓 от 𝑥.
Мы можем даже рассматривать это с точки зрения
функциональной машины. Ввод двух даст
выход восемь. Затем мы можем посмотреть на функцию ℎ
из 𝑥 и подумайте, какое значение нужно ввести, чтобы получить такой же результат
восемь.
Хорошо, мы знаем, что когда мы вводим значение два, мы получаем восемь. Но на этот раз мы не просто ввод два; мы вводим два 𝑥. И так, чтобы входное значение было два, это означает, что 𝑥 должно быть равно единице. И так координата один, восемь лежит на функции ℎ от 𝑥. В общем то можно сказать что для любого положительного 𝑏 в действительных числах, когда вход 𝑥 меняется на 𝑏 из 𝑥, есть горизонтальное расширение 𝑓 из 𝑥 равно 𝑥 в кубе с коэффициентом один больше 𝑏.
Наконец, давайте посмотрим, как отрицание
изменяет стандартную кубическую функцию. Рассмотрим графики
функций 𝑓 от 𝑥 равно 𝑥 в кубе, а 𝑔 от 𝑥 равно отрицательному 𝑥
в кубе.
Вы можете удивиться, почему это отражение по горизонтальной оси, а не по вертикальной оси. Что ж, давайте рассмотрим, что происходит когда мы меняем ввод. Итак, мы возьмем эту новую функцию ℎ 𝑥 равно отрицательному 𝑥 в кубе. Мы можем упростить эту функцию, написав его без скобок, так как ℎ от 𝑥 равно отрицательному 𝑥 в кубе. Это создает идентичную функцию к тому из 𝑔 из 𝑥. Это особенность того, что кубический граф является нечетной функцией.
В целом можно сказать, что если мы
изменить вывод 𝑓 из 𝑥 функции на отрицательный 𝑓 из 𝑥, что дает
отражение по горизонтальной оси.
До сих пор мы видели, как меняется разные вещи о входе или выходе изменяют функцию. Но, конечно, мы можем изменить кубический функционировать более чем одним способом одновременно. Мы можем объединить все преобразования в одну кубическую функциональную форму. Можно сказать, что если 𝑎, ℎ и 𝑘 находятся в множестве действительных чисел с 𝑎 не равным нулю, то график 𝑓 из 𝑥 равно 𝑎 умноженное на 𝑥 минус ℎ в кубе плюс 𝑘 является преобразованием 𝑦 равно 𝑥 в кубе.
Мы можем обобщить, как различные
значения 𝑎, ℎ и 𝑘 изменяют форму функции. Вы можете приостановить экран
и запишите их.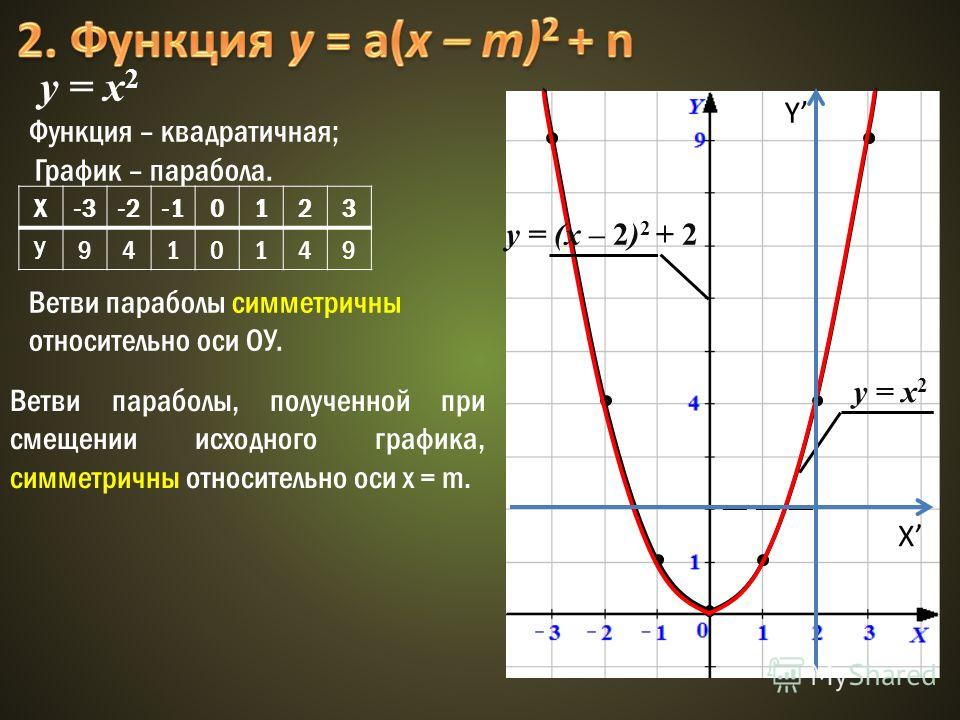
Последнее замечание, порядок, в котором
мы выполняем эти преобразования важно, даже если иногда мы получаем то же самое
график независимо. Сначала проводим вертикаль
расширение, это 𝑎-значение; во-вторых, любой горизонтальный перевод, это
ℎ-значение; и, наконец, любой вертикальный перевод, который является 𝑘-значением. Сейчас мы рассмотрим несколько примеров,
начиная с того, где мы идентифицируем правильное уравнение данного графика.
Какое уравнение соответствует график? Вариант (А) 𝑦 равно 𝑥 минус два в кубе минус один. Вариант (Б) 𝑦 равно 𝑥 плюс два в кубе минус один. Вариант (C) 𝑦 равно 𝑥 плюс два в кубе плюс один. Или вариант (D) 𝑦 равно 𝑥 минус два в кубе плюс один.
Начнем с того, что заметим, что
эта функция очень похожа на стандартную кубическую функцию 𝑓 от 𝑥 равна
𝑥 в кубе, иногда известное как 𝑦 равно 𝑥 в кубе.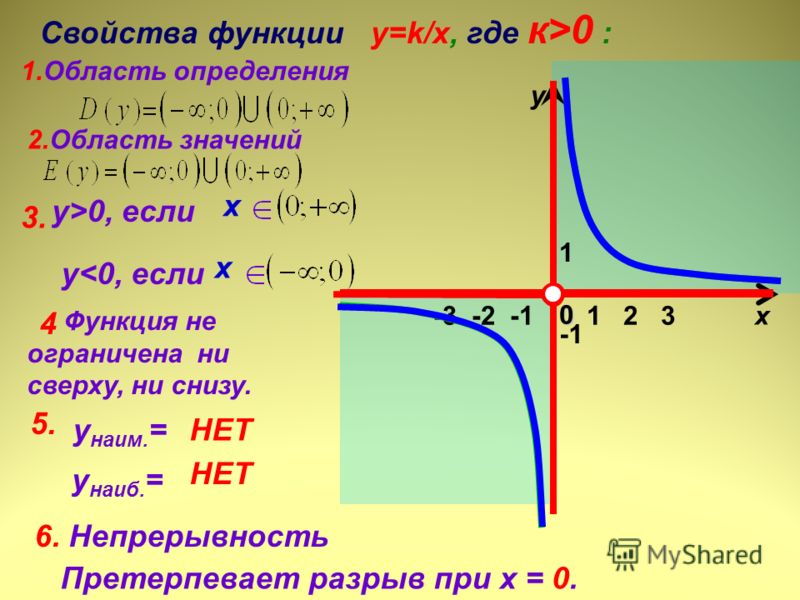
Мы можем нарисовать 𝑦 равным 𝑥 в кубе.
рядом с заданной функцией. График 𝑦 равен 𝑥 в кубе имеет
точка перегиба в нуле, ноль. Точка перегиба данного
функция находится на отрицательном два, отрицательный один. Таким образом, мы могли бы сказать, что
функция 𝑦 равна 𝑥 в кубе должна быть переведена на две единицы влево и на одну единицу
вниз. Обе эти функции имеют
такая же крутизна, и они не нашли отражения, так что дальше нет
преобразования.
Мы можем вспомнить, что кубическая функция
в форме 𝑦 равно 𝑎 умноженному на 𝑥 минус ℎ в кубе плюс 𝑘 является преобразованием
𝑦 равно 𝑥 в кубе для 𝑎, ℎ и 𝑘 в действительных числах, а 𝑎 не равно
нуль. В этой форме значение 𝑎
указывает масштабный коэффициент расширения и отражение, если 𝑎 меньше нуля;
есть горизонтальный перевод ℎ единиц вправо и вертикальный перевод 𝑘
единиц вверх.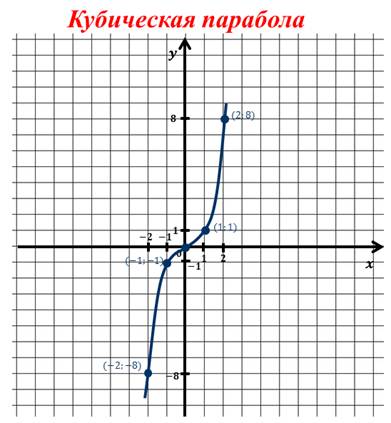
Выполняем эти преобразования
сначала с вертикальным растяжением, затем с горизонтальным перемещением и с вертикальным
перевод третий.
В этом вопросе на графике нет были отражены или расширены, поэтому 𝑎 равно единице. Далее мы определили, что этот граф остался перевод двух единиц. Поскольку эта кубическая форма функции имеет горизонтальный сдвиг единиц ℎ вправо, то это означает, что наше значение ℎ должен быть отрицательным. Итак, ℎ равно отрицательному два. Наконец, мы определили, что существует должен быть вертикальным переводом на одну единицу вниз. Так как эта форма дает нам вертикаль перевод в единицах вверх, то наше значение 𝑘 должно быть отрицательным. Так что это минус.
Теперь все, что нам нужно сделать, это заполнить
значения 𝑎, ℎ и 𝑘 в эту форму кубической функции. Упрощая, мы получаем
уравнение 𝑦 равно 𝑥 плюс два в кубе минус один.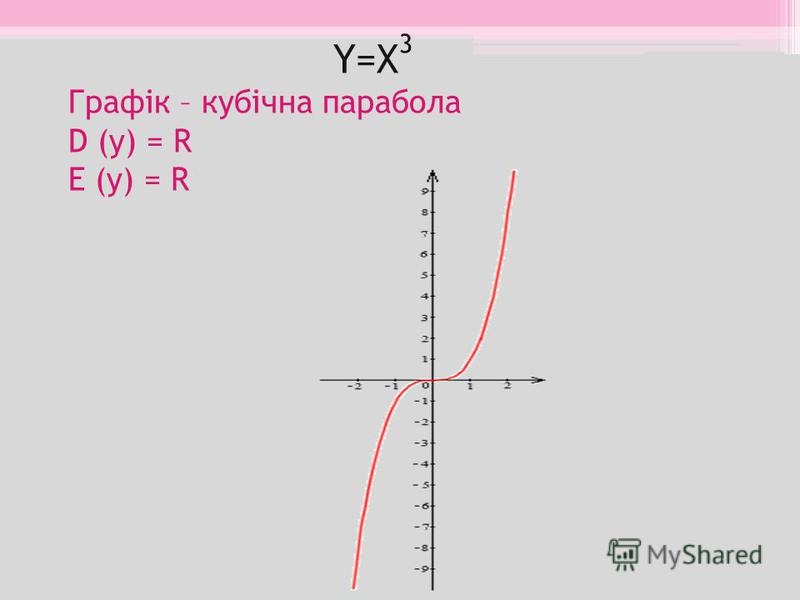
Это уравнение, приведенное в
вариант ответа (Б).
Теперь рассмотрим пример, где мы определяем правильную форму графика кубической функции.
Что из следующего является графом из 𝑓 из 𝑥 равно отрицательному 𝑥 минус два в кубе?
В этом вопросе нам дается кубическая функция. Итак, давайте сравним это с стандартная кубическая функция 𝑓 от 𝑥 равна 𝑥 в кубе. Мы можем сделать быстрый набросок этого функция. Напомним, что кубическая функция в виде 𝑓 из 𝑥 равно 𝑎 умноженному на 𝑥 минус ℎ в кубе плюс 𝑘 преобразование 𝑓 из 𝑥 равно 𝑥 в кубе для 𝑎, ℎ и 𝑘 в действительных числах и 𝑎 не равно нулю.
Здесь 𝑎 представляет расширение или
отражения, ℎ показывает количество единиц, на которые график был переведен в
горизонтальном направлении, а 𝑘 — количество единиц, на которое график переводится в
вертикальное направление.
Выполняем эти преобразования
сначала с вертикальным расширением, затем с горизонтальным перемещением и вертикальным
перевод третий.
Итак, давайте рассмотрим функцию, которую мы были даны. Поскольку 𝑓 из 𝑥 равно отрицательному 𝑥 минус два в кубе, то это означает, что 𝑎 равно отрицательной единице. Это свидетельствует о том, что нет дилатацию, вернее, дилатацию с масштабным коэффициентом один. Однако, поскольку 𝑎 отрицательно, это означает, что есть отражение графика на оси 𝑥. Если мы выполним только отражение, тогда график будет выглядеть розовым цветом.
Далее, в данной функции ℎ
равен двум. Таким образом, это означает, что существует
перевод на две единицы вправо. Это смещает точку перегиба
от нуля, нуля до двух, нуля. Следовательно, функция будет выглядеть
что-то вроде этого. Всегда полезно отметить
любую важную информацию на эскизе.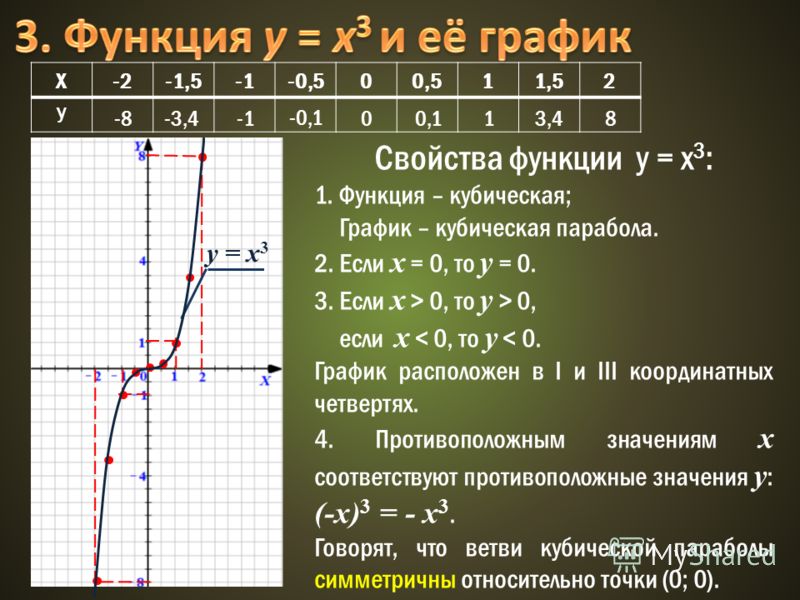
И, конечно же, мы знаем, что это
график пересекает ось 𝑥 в точке два, ноль.
Тогда мы можем дать ответ, что график, который показывает 𝑓 из 𝑥, равен отрицательному 𝑥 минус два в кубе, является заданным в варианте (Е).
Теперь мы можем суммировать ключевые моменты
этого видео. Мы начали со стандартной кубической
функция 𝑓 от 𝑥 равна 𝑥 в кубе. Затем мы определили ряд
важные свойства. Далее мы рассмотрели, как изменить
входы и выходы функции влияют на то, как она выглядит. Далее мы увидели, как форма функции
𝑓 из 𝑥 равно 𝑎 умножить на 𝑥 минус ℎ в кубе плюс 𝑘 позволит нам идентифицировать все
различные преобразования 𝑦 равны 𝑥 в кубе. Наконец, мы увидели, как порядок в
которые мы проводим преобразования этой кубической функции имеет важное значение. Во-первых, это вертикальное расширение,
𝑎-значение; во-вторых, любые горизонтальные переводы, ℎ-значение; и, наконец, любой
вертикальные переводы, 𝑘-значение.
Симметрия и графики | Purplemath
AxialPoint
Purplemath
Симметрия является скорее геометрической, чем алгебраической концепцией, но, как упоминалось на двух предыдущих страницах, тема симметрии возникает в нескольких алгебраических контекстах. Когда вы рисуете квадратичные уравнения, вас могут попросить указать ось симметрии параболы. Обычно это просто вертикальная линия x = h , где « h » — координата вершины x , ( ч , к ). То есть осью симметрии параболы обычно является вертикальная линия, проходящая через ее вершину. Другим обычным контекстом для симметрии является определение по графику, является ли функция четной или нечетной.
Примечание. По определению никакая функция не может быть симметричной относительно оси x (или любой другой горизонтальной линии), поскольку все, что зеркально отражается вокруг горизонтальной линии, нарушает тест вертикальной линии.
Содержание продолжается ниже
MathHelp.
comСимметрия
С другой стороны, функция может быть симметричной относительно вертикальной линии или точки. В частности, функция, симметричная относительно оси y , также является «четной» функцией, а функция, симметричная относительно начала координат, также является «нечетной» функцией. Из-за этого соответствия между симметрией графа и четностью или нечетностью функции «симметрия» в алгебре обычно применяется к y -ось и в начало координат.
Далее перечислите любые симметрии, если таковые имеются, для отображаемого графика и укажите, показывает ли график функцию.
График A: Этот график симметричен относительно своей оси; то есть он симметричен относительно линии x = 3. Другой симметрии нет. На этом графике показана функция.
График B: Этот график симметричен относительно осей; то есть он симметричен относительно прямых x = 0 (ось y ) и y = 0 (ось x ).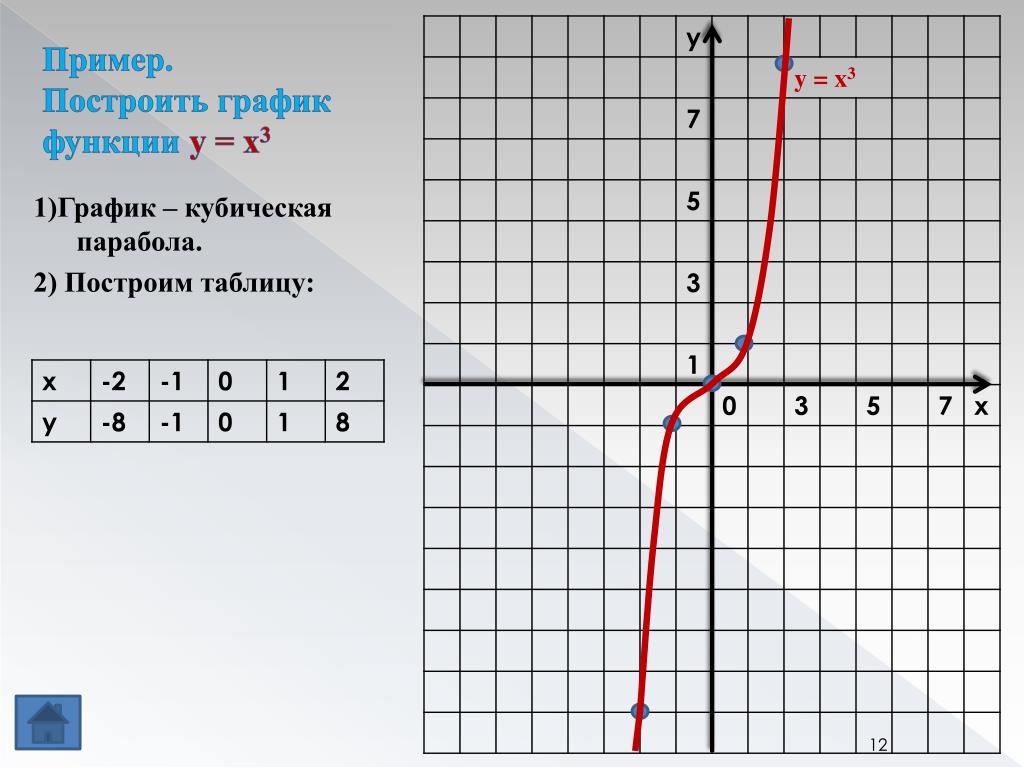
Он также симметричен относительно происхождения. Поскольку существуют вертикальные линии (например, линия x = 2), которые пересекают этот график дважды, то, что он показывает, не является функцией.
График C: Этот график симметричен относительно линий x = 1 и y = −2 и симметричен относительно точки (1, −2). Поскольку можно провести вертикальную линию, дважды пересекающую эллипс, это не функция.
График D: Этот график симметричен относительно наклонных линий: y = x и y = − x . Он также симметричен относительно происхождения. Поскольку эта гипербола имеет правильный угол (так что ни одна вертикальная линия не может пересекать график более одного раза), на графике показана функция.
График E: Этот график (функции квадратного корня) не демонстрирует никакой симметрии, но это функция.
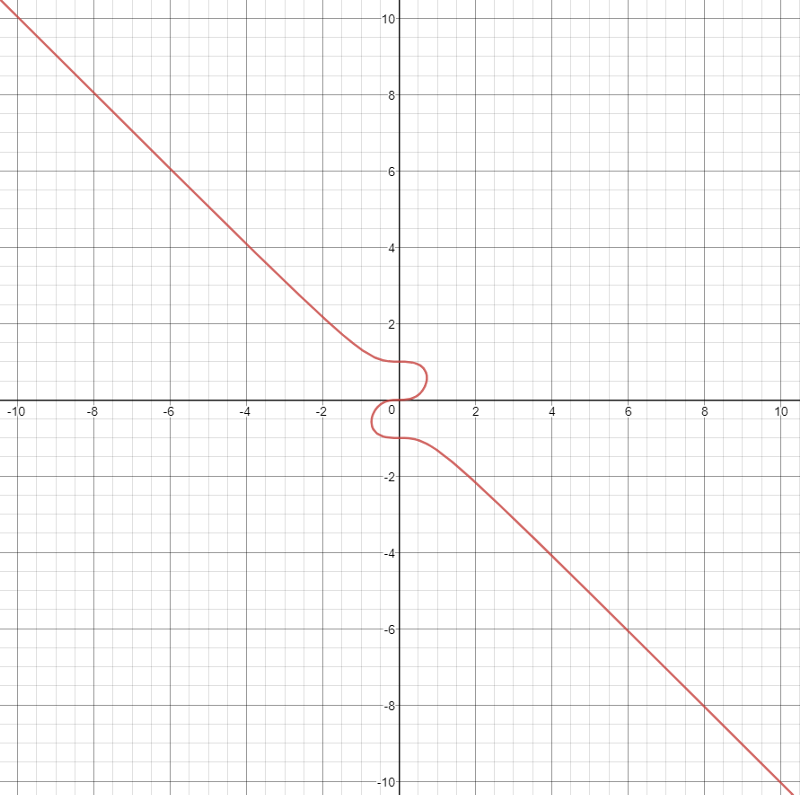
График F: Этот график (кубической функции) симметричен относительно точки (−4, −1), но не относительно каких-либо линий.
Этот график действительно показывает функцию.
График G: Эта парабола лежит на боку. Он симметричен относительно линии y = 2. Это не функция.
График H: Эта парабола вертикальна и симметрична относительно оси y . Это функция; на самом деле это четная функция.
Далее по графикам определите, являются ли отображаемые функции четными, нечетными или ни тем, ни другим.
График A: Этот линейный график проходит через начало координат. Если я поверну график на 180° вокруг начала координат, я получу ту же картину. Так что этот график нечетный. (Функция не была бы нечетной, если бы эта линия не проходила через начало координат.)
График B: Вершина этой параболы находится на оси y , поэтому осью симметрии является ось y . Это означает, что функция четная.
График C: центр куба находится в начале координат. Если я поверну график на 180° вокруг начала координат, я получу ту же картину.
Так что этот график нечетный.
График D: этот кубик с центром в точке (0, −3). Этот график симметричен, но не относительно начала координат или оси y . Таким образом, эта функция не является ни четной, ни нечетной.
График E: Этот кубический корень центрирован в начале координат, поэтому эта функция нечетная.
График F: Этот квадратный корень не имеет симметрии. Функция не является ни четной, ни нечетной.
График G: Этот график выглядит как колоколообразная кривая. Поскольку он зеркально отражается вокруг оси y , функция четная.
График H: Эта гипербола симметрична относительно линий y = x и y = − x , но это ничего не говорит мне о четности или нечетности. Однако график также симметричен относительно начала координат, поэтому эта функция нечетна.
При поиске симметрии вам не нужно просто сидеть и пытаться разгадать эту вещь в своей голове. Вместо этого возьмите бумагу и карандаш и посмотрите, есть ли место, куда вы можете положить ластик карандаша, а затем покрутите бумагу на столе.