Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Будим ли мы в месте придёте ли он назад
Решено
Электрон находится в однородном электрическом поле с напряженностью 0,5 В/м. Найдите скорость, если от начала движения он прошел 45 см вдоль линий поля. Решите задачу двумя способами: с использованием
Найдите скорость, если от начала движения он прошел 45 см вдоль линий поля. Решите задачу двумя способами: с использованием
Решено
Здравствуйте.Скажите, пожалуйста, если сейчас прекратить общение с этим мужчиной, будет ли у меня другой мужчина для поддержки, или просто общаться с ним дальше? Юлия 17.01.1998 Дмитрий 07.06.1974
Купил автомобиль, есть доровор купли продажи, на автомобиле стоит запрет на рег действия по задолжности штрафа, запрет наложен судебным приставом в карачаево черкесии , если я захочу его оформить на
Здравствуйте, мое позывное Андрей 06.13.1933. Я служил в военно-морском флоте целых 34 с половиной года. У меня уже давно есть проблема
Пользуйтесь нашим приложением
Основные методы интегрирования — презентация онлайн
Похожие презентации:
Методы интегрирования
Основные методы интегрирования
Основные методы интегрирования
Неопределенный интеграл. Основные свойства. Методы интегрирования. Первообразная функция. (Лекция 7)
Основные свойства. Методы интегрирования. Первообразная функция. (Лекция 7)
Методы интегрирования
Неопределенный интеграл. Методы интегрирования. Лекция 2
Неопределённый интеграл, его свойства . Непосредственное интегрирование. Метод замены переменной в неопределенном интеграле
Основные методы интегрирования. Интегрирование по частям
Методы интегрирования. (Семинар 14)
Первообразная функция и неопределенный интеграл. Методы интегрирования
1. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
Замена переменной( подведение под знак дифференциала )
ПОВТОРЕНИЕ
Правило дифференцирования сложной функции
Сложная функция (или функция от функции) y f g x дифференцируется
по правилу
y’ f ‘ g x g ‘ x
Восстановление сложной первообразной функции
Проблема состоит в том, что изначально все интегралы задаются в виде
f x dx
Вы сами должны представить подынтегральную функцию в виде
произведения двух сомножителей.
 Один сомножитель – это новая
Один сомножитель – это новая(отличная от f x ) сложная функция h от внутренней функции g x , а
второй сомножитель – это производная внутренней функции g’ x .
f x h g x g ‘ x
Если такое представление сделать удалось, то процесс интегрирования можно
оформить цепочкой равенств.
Предполагается, что новый интеграл
него преобразуется.
h t d t — либо табличный, либо легко в
Главный вопрос – какую часть подынтегральной функции обозначить за
новую переменную? Однозначного ответа нет. Но следует помнить, что внутренняя
функция g x может стоять где угодно – в знаменателе, под корнем, под знаком
логарифма, в степени показательной функции, в аргументе тригонометрической
функции, а её производная может быть только сомножителем.
Пример 1. Найти интеграл
Решение.
x dx
1 x2
x dx
1 x2
Самое главное и одновременно самое сложное в начале решения – увидеть
дифференциальную связь между двумя частями подынтегральной функции.
В данном примере такими частями являются числитель х и сумма в знаменателе
(1 + х2). Важно вспомнить, что производная этой суммы (1 + х2) = 2х, т.е. почти
равна числителю х. Можно сказать и иначе : выражение (1 + х2) – это почти
функции есть ещё операция деления. На этапе замены переменной она роли не
играет. Не старайтесь сразу учесть все действия, которые есть в подынтегральной
функции
За новую переменную t нужно обозначить ту часть
подынтегральной функции, производная которой равна (или
очень близка ) к другой части подынтегральной функции.
Замена
x dx
t 1 x2
1 x2
dt 1 x 2 dx 2 x dx
Замечание. Если Вы ввели новую переменную t, то все подынтегральное
выражение должно содержать только переменную t , в том числе и
дифференциал должен быть dt. Но нельзя просто механически заменить dх
на dt. Выражение, которое Вы замените на dt, находится в заготовке
замены.

В примере 1 в подынтегральном выражении есть только хdx, а нужно 2хdx. Здесь
у Вас два способа.
Способ1: выразить произведение xdx из равенства dt = 2xdx как x dx dt .
2
Замена
t 1 x2
x dx x dx
2
dt
1
x
dx 2 x dx
2
2
1 x
1 x
x dx dt
2
dt
2 dt 1 dt 1 ln t C 1 ln 1 x 2 C
t
2t 2 t 2
2
Способ2: искусственно сделать в числителе подынтегральной дроби 2xdx,
умножив числитель на 2, а весь интеграл на 1 .
2
x dx 1 2 x dx
2 1 x2
1 x2
Замена
t 1 x2
1 dt 1 ln t C 1 ln 1 x 2 C
2 t 2
2
2
dt 1 x dx 2 x dx
ЗАМЕНА ПЕРЕМЕННОЙ
как подведение под знак дифференциала
Замену переменной интегрирования можно сделать и без переобозначения
внутренней функции g x новой буквой t. Последовательность действий в этом
случае задается цепочкой равенств.
f x dx h g x g’ x dx h g x dg x H g x C
Использовали понятие дифференциала функции
d g x g ‘ x dx
Этот метод ещё называется подведением под знак дифференциала (ППЗД).
Образно говоря, производная g ‘ x перемещается за букву d вправо,
превращаясь при этом в свою первообразную g x и становясь новой переменной
интегрирования вместо х.
x dx
1 x2
1
2
x 1 dx 1
2
1 x2
1
1
2
2 x
dx
1 x 1 dx
2
1 x2
1 x2
1 1 x 2 dx 1
2
2
1 x
1
2
1 d 1 x2
1 x2
d 1 x2 1
ln 1 x 2 C
2
1 x2
Можно было бы ……
x dx x 1 dx x arctg x dx x d arctg x
1 x2
1 x2
Верно. Но! Бесполезно, т.к. оставшаяся после подведения под знак дифференциала
функция сократилась до х и выражение её через arctg x возможно, но не рационально.
Пример 2. Найти интеграл
x
dx
2
x 3
Решение.
x
dx
2
x 3
dt
2
t
Замена
t x2 3
dt ( x 2 3) ‘ dx 2 xdx
xdx dt
2
dt
2 t
t C
x2 3 C
ЗАМЕНА ПЕРЕМЕННОЙ
методом определения независимой переменной х как новой функции
новой переменной t.
f x dx .
x t
Пусть требуется найти интеграл
новой переменной t, а именно,
. Предположим, что функция
дифференцируема, т.е. существует производная
dx d t t ‘ dt
Определим х как функцию
x ‘ ‘ t
x t
и её дифференциал
. Тогда переход к новой переменной интегрирования в
искомом интеграле задается цепочкой равенств.
f x dx f t d t f t t ‘ dt y t dt Y t C
Разумеется, последним шагом в решении будет возврат к старой переменной х
по формуле t -1 x . Например, x t 6 t 6 x .
x
Или x 2 sin t t arcsin
2
Внимание! -1
Символом x здесь обозначается функция, обратная функции t ,
как на калькуляторах.
Но!!
Именно с помощью такой замены находятся интегралы от функций, содержащих
корни разных степеней (или иначе от иррациональностей).
Интегрирование простейших иррациональностей
Пример . Найти интеграл
Решение.
dx
x 4 x
x t4
dx
3
dx
4
t
dt
4
x x
t 4 x
2
t
dt 4
4
t 1
Цель замены –
чтобы все корни извлеклись!
4 t 3dt
t4 4 t4
t 2 1 1 dt 4 t 2 1 dt 4
t 1
t 1
3
3
t
dt
t
dt
4 2
4
t t 1
t t
dt 4
t 1
4 x 2
t2
4 t 4 ln t 1 C 4
4 x 4 ln
2
2
4 x 4 x 4 ln
2
4
x 1 C
4
t 1 dt 4 ln t 1
x 1 C
Пример .
 Найти интеграл
Найти интеграл5 x 2 dx
Решение.
5 x
2
Замена
dx x 5 sin t
dx 5 costdt
5 1 sin t 2
5 5 sin t
2
5 cost dt
5 cost dt 5 cost cost dt 5 cos2 t dt
5 1 cos 2t dt 5 dt cos 2t dt 5 t 1 sin 2t C
2
2
2 2
5 arcsin x 1 sin 2 arcsin x C
2
5 2
5
x
5 sin t
t arcsin x
5
English Русский Правила
Интеграл арктангенса – Примеры, интегрирование обратного тангенса x
Интеграл арктангенса представляет собой интегрирование тангенса обратного х, которое также называется первообразной арктангенса и определяется как ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C, где C — постоянная интегрирования. Интеграл от арктангенса можно вычислить методом интегрирования по частям. Интегрирование – это процесс обратного дифференцирования, т. е. определения первообразной.
Изучим интегрирование тангенса обратного x, докажем, что интеграл арктангенса равен ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C и определите определенный интеграл арктангенса вместе с некоторыми решенными примерами для лучшего понимания.
| 1. | Что такое интеграл арктангенса? |
| 2. | Интеграл доказательства арктангенса с использованием интегрирования по частям |
| 3. | Определенный интеграл обратного коэффициента загара x От 0 до 1 |
| 4. | Часто задаваемые вопросы по Integral of Arctan |
Что такое интеграл арктангенса?
Интеграл арктангенса, также называемый интегралом тангенса, обратному х, равен x tan -1 x — ½ ln |1+x 2 | + C. Математически это записывается как ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C. Здесь C — константа интегрирования, dx обозначает, что интегрирование тангенса, обратное x, производится по отношению к x, а ∫ обозначает символ интегрирования. Интеграл от arctan можно вычислить методом ILATE, то есть интегрированием по частям.
Интеграл формулы арктангенса
Формула интеграла арктангенса дана,
Интеграл доказательства арктангенса с использованием интегрирования по частям
Теперь, когда мы знаем, что интеграл от arctan равен x tan -1 x — ½ ln |1+x 2 | + C, докажем это методом интегрирования по частям. Мы будем использовать следующие формулы и факты, чтобы доказать интеграл от arctan.
- Формула интегрирования по частям: ∫f(x)g(x)dx = f(x) ∫g(x)dx — ∫[d(f(x))/dx × ∫g(x) dx ] дх.
- Обратите внимание, что tan -1 x может быть записан как tan -1 x = tan -1 x.1
- Имеем f(x) = tan -1 x, g(x) = 1
- д (загар -1 х)/дх = 1/(1 + х 2 )
Используя эти формулы и факты, мы имеем
∫tan -1 x dx = ∫tan -1 x,1 dx
= tan -1 x ∫1dx — ∫0[d 1 x)/dx × ∫1 dx] dx
= x tan -1 x — ∫[1/(1 + x 2 ) × x] dx
= x tan -1 x — ∫x/(1 + x 2 ) dx
= x tan -1 x — (1/2) ∫2x/(1 + x 2 ) dx [Умножение и деление на 2]
= x tan -1 x — (1/2) ln |1 + x 2 | + C {Используя формулу ∫f'(x)/f(x) dx = ln |f(x)| + C}
Следовательно, мы доказали, что интеграл от tan, обратный x, равен x tan -1 x — (1/2) ln |1 + x 2 | + C, где C — постоянная интегрирования.
Определенный интеграл обратного коэффициента загара x От 0 до 1
Теперь определим определенный интеграл арктангенса в пределах от 0 до 1. Мы будем использовать интеграл тангенса, обратный формуле х, то есть ∫тангенс 92|+C)\\&=\dfrac{\pi}{4}-\ln2+C-0+0-C\\&=\dfrac{\pi}{4}-\ln2 \end{align} \)
Следовательно, определенный интеграл арктангенса от 0 до 1 равен π/4 — ln 2.
Важные замечания относительно интеграла арктангенса
- ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + С
- Определенный интеграл арктангенса от 0 до 1 равен π/4 — ln 2
- Интеграл арктангенса (x/a) определяется как ∫tan -1 (x/a) dx = x tan -1 (x/a) — (a 2 /2) ln |a 2 + x 2 | + С
Связанные темы по интегралу арктангенса
- Интегральное исчисление
- Формулы интегрирования
- Формула арктангенса
Часто задаваемые вопросы по Integral of Arctan
Что такое интеграл арктангенса в исчислении?
Интеграл от арктангенса представляет собой интегрирование тангенса, обратное х, которое определяется как ∫тангенс -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C, где C — постоянная интегрирования.
Какова формула интеграла арктангенса?
Формула интеграла арктангенса задается как ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C.
Как найти интеграл от арктангенса?
Интеграл арктангенса можно вычислить методом ILATE, то есть интегрированием по частям.
Что такое интеграл обратного тангенса х от 0 до 1?
Определенный интеграл арктангенса от 0 до 1 равен π/4 — ln 2.
Является ли интеграл арктангенса тем же самым, что и интеграл тангенса, обратный x?
Арктан также называют инверсным загаром. Следовательно, интеграл от арктангенса такой же, как и интеграл от обратного тангенса.
Является ли интеграл от Arctan равным интегралу от Arccot?
Теперь интеграл от arctan не равен интегралу от arccot, поскольку интеграл от arctan равен x tan -1 x — ½ ln |1+x 2 | + C, а интеграл от arccot равен x cot -1 x + ½ ln |1+x 2 | + К.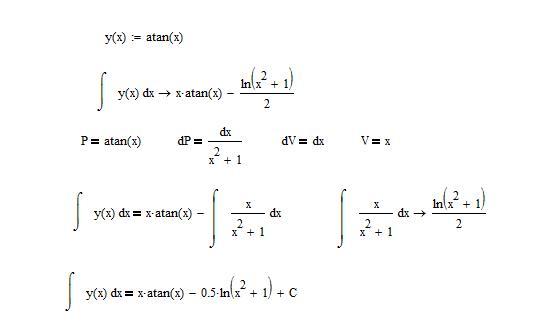

 01.15
01.15