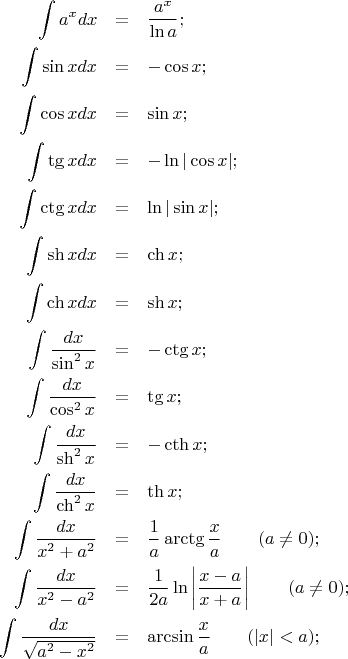Интеграл синуса
Согласно формулам интегрирования интеграл от синуса sin (x) равен косинусу, причем со знаком минус. Многие часто допускает ошибки потому что не может запомнить, что производная от синуса равна минус косинусу, а от косинуса — синусу со знаком плюс.
Те кто изучает первоначальную должны помнить что к правой стороне следует добавить постоянную
Ету постоянную определяют с дополнительной условия.
График синуса имеет вид
Синус нечетная, а косинус — четная функция, поэтому при интегрировании появляется знак минус. В начале всем кажется все простым и понятным. Но рано или поздно наступает время усложнять интеграл, то есть интегрировать синус двойного угла, тройного аргумента и т.д. И во многих возникают трудности с интегрированием. Для вывода формулы интеграла для sin (k*x) проведем все выкладки сначала. Для того чтобы свести интеграл к табличной формулы надо внести коэффициент под дифференциал, но это изменит сам интеграл.
Поэтому одновременно делим на коэффициент
Зная эту формулу, интеграл от синуса двойного угла записываем одной строкой
Далее можем проинтегрировать синус тройного угла
и т.д.
int(sin(k*x)=-1/k*cos(k*x).
По такой же формуле выводят интеграл от синуса половины угла, который равен минус 2 косинус половины угла.
Интеграл от синуса одной третьей х равен
Пример 1. Найти интеграл от sin(4*x).
Решение: По формуле интегрирования находим
Пример 2. Вычислить интеграл от sin(5*x).
Решение: Выполняем интегрирования
Пример 3. Проинтегрировать выражение sin(7*x).
Решение: Находим неопределенный интеграл
Пример 4. Найти интеграл функции y=sin(x/5).
Решение: Находим неопределенный интеграл
Как только Вы научитесь вычислять простые интегралы от синуса можете переходить к определенному интегралу
Пример 5. Найти первоначальную от sin(x) которая в нуле равна 2.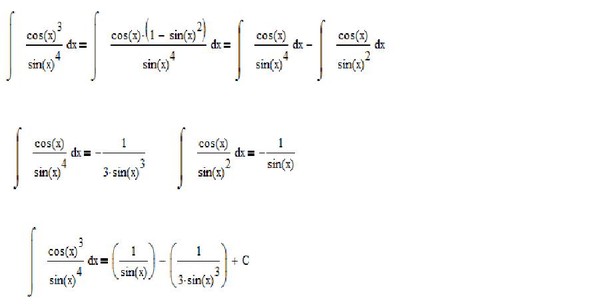
Решение: Вычисляем первоначальную
Из условия на первоначальную находим постоянную
-cos(0)+C=2;
C=2+cos(0)=3.
Возвращаемся к первоначальной и подставляем найденную постоянную
Это и есть ответ к задаче.
Пример 7. Проинтегрировать синус двойного угла y=sin(2*x) от 0 до 45 градусов.
Решение: Записываем интеграл от синуса и подставляем пределы интегрирования
По физическому содержанию определенный интеграл равен площади фигуры ограниченной функцией sin (x) и осью абсцисс.
Но определенный интеграл и площадь, это не одно и то же. Интеграл может быть отрицательным, а площадь нет. Если функция большую площадь имеет под осью абсцисс, то ее определенный интеграл отрицательный.
Площадь криволинейной трапеции равна интегралу от разницы уравнения верхней кривой и нижней.
В данном случае верхняя кривая это ось абсцисс или y = 0. Нижняя — это график синуса. Поэтому формула площади синус функции равна 1, или определенному интегралу по модулю.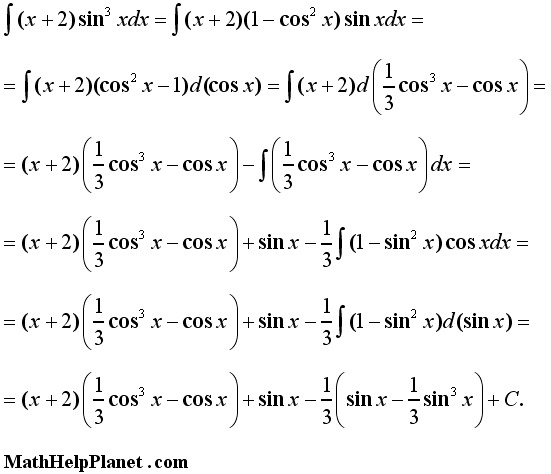
Если функция антисимметрична относительно оси абсцисс то ее интеграл равен нулю, а площадь равна двойному интегралу графика над осью абсцисс. Например, интеграл синуса двойного угла от -45 до 45 градусов равен нулю
В то же время площадь заштрихованной фигуры равна единице.
На графике это будет выглядеть.
Из следующих материалов Вы узнаете, как найти интеграл от функции вида
какие формулы свертки и замены переменных при этом следует использовать. Также Вы овладеете методикой вычисления интегралов вида полином умноженый на синус функцию
где — полином от переменной. В таких случаях применяют интегрирования по частям, но об этом пойдет речь позже.
На этом знакомство с интегрированием синуса завершается. Интегралы от других тригонометрических и обратных к ним функций Вы найдете на страницах категории «Интегрирование функций».
Интеграл от x sin x — Формула, доказательство, примеры
Интеграл от x sin x равен −x cos x + sin x + C, где C — постоянная интегрирования.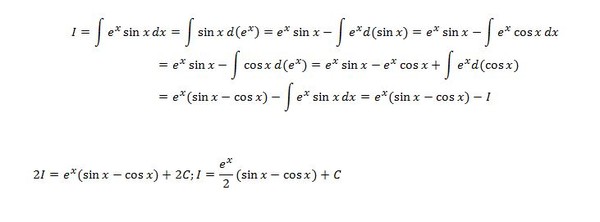
Этот интеграл можно вычислить методом интегрирования по частям. Интеграл функции дает площадь под кривой функции. sin x — одна из важных тригонометрических функций в тригонометрии. Интегрирование x sin x — это процесс нахождения интеграла от x sin x, который также называется первообразной x sin x, поскольку интегрирование — это процесс, обратный дифференцированию.
Далее в этой статье мы вычислим интеграл от x sin методом интегрирования по частям и выведем его формулу. Мы также определим определенную интеграцию x sin x с различными пределами и рассмотрим несколько решенных примеров для лучшего понимания концепции.
| 1. | |
| 2. | Интегрирование x sin x Формула |
| 3. | Интеграл x sin x Доказательство |
| 4. | Определенный интеграл от x sin x |
| 5. | Часто задаваемые вопросы по интегралу x sin x |
Чему равен интеграл от x sin x?
Интеграл x sin x дает функцию для определения площади под кривой функции f(x) = x sin x.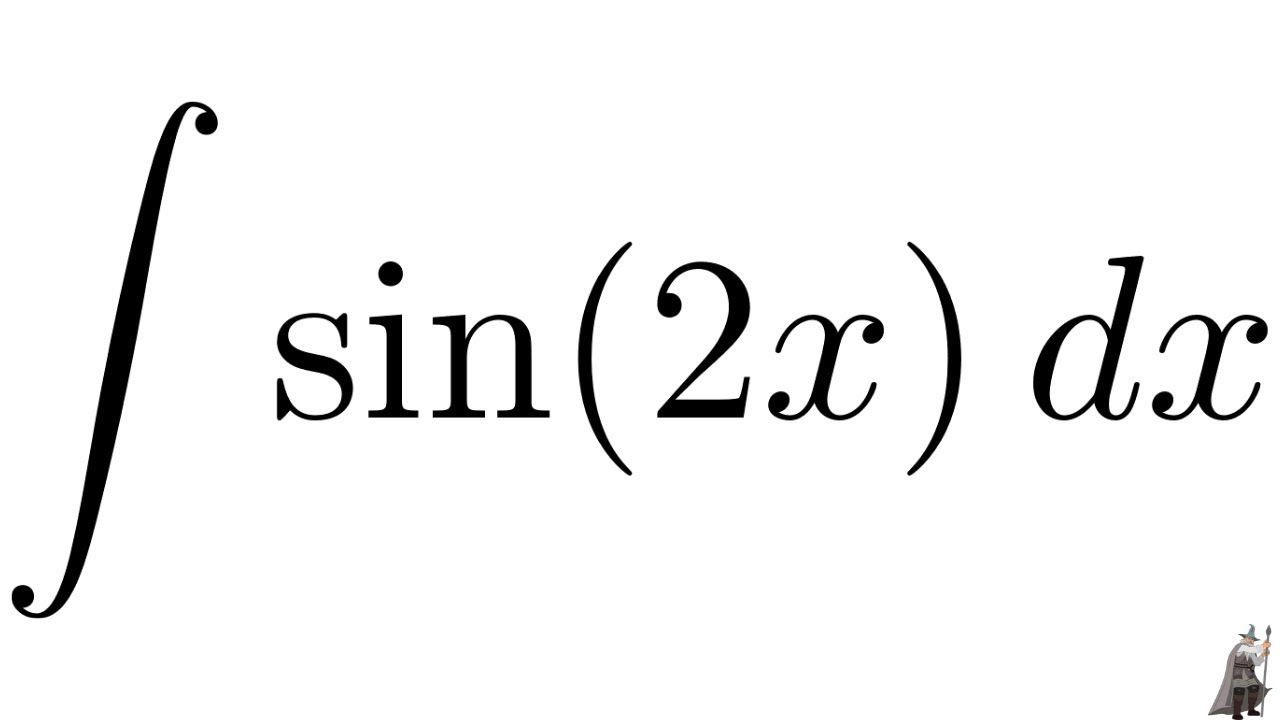
Интеграция x sin x равна −x cos x + sin x + C, и ее можно оценить с помощью метода интегрирования по частям (также известного как правило ILATE ИЛИ правило интегрирования произведения). Математически мы можем записать интеграл от x sin x как ∫xsinx dx = −x cos x + sin x + C, где
- ∫ — символ интегрирования
- dx показывает, что интеграл от x sin x относится к переменной x
- C — постоянная интегрирования
Давайте рассмотрим формулу интегрирования x sin x в следующем разделе.
Интегрирование x sin x Формула
Формула для интеграла от x sin x имеет следующий вид: ∫xsinx dx = −x cos x + sin x + C, где C — постоянная интегрирования. Мы можем вычислить этот интеграл, используя правило интегрирования произведения, где x — первая функция, а sin x — вторая функция, а x sin x записывается как произведение этих двух функций. На изображении ниже показана формула интегрирования x sin x.
Интеграл x sin x Доказательство
Теперь, когда мы знаем, что интеграл от x sin x равен −x cos x + sin x + C, мы выведем эту формулу, используя метод интегрирования по частям.
Мы используем этот метод, чтобы найти интеграл функции, которая задана как произведение двух функций. Поэтому интегрирование по частям также известно как правило интегрирования продукта. Теперь формула для интегрирования по частям имеет вид . Здесь мы выбрали функции f(x) и g(x), используя правило ILATE: I — обратная тригонометрическая функция, L — логарифмическая функция, A — алгебраическая функция, T — тригонометрическая функция, E — экспоненциальная функция.
Используя эту последовательность функций предпочтения, мы получаем f(x) = x (поскольку x — алгебраическая функция) и g(x) = sin x (sin x — тригонометрическая функция). Мы также будем использовать следующую формулу, чтобы найти интеграл x sin x:
- Производная x: dx/dx = 1
- Интеграл sinx: ∫sin x dx = -cos x + C
- Интеграл от cosx: ∫cosx dx = sinx + C
Итак, используя формулу интегрирования по частям и приведенные выше формулы, имеем
∫x sinx dx = x ∫sin x dx — ∫[dx/dx × ∫sin x dx] dx
= x (-cosx) — ∫(1 × -cos x) dx
= — x cosx + ∫(1 × cos x) dx
= -x cosx + ∫cosx dx
= -x cosx + sin x + C
Следовательно, мы получили формулу интегрирования x sin x, которая равна — х cos х + sin х + C.
Определенный интеграл от x sin x
Далее в этом разделе мы вычислим определенный интеграл от x sin x от 0 до π, используя формулу интеграла от x sin x. Для определения определенного интеграла подставим верхний предел и нижний предел в формулу интеграла от x sin x и вычтем их. У нас есть,
0 π ∫x sin x dx = [-x cosx + sin x + C] 0 π
= (-π cosπ + sin π + C) — (-0 cos 0 + грех 0 + C)
= -π (-1) + 0 + C — 0 — 0 — C
= π
Следовательно, определенный интеграл от x sin x от 0 до π равен π.
Важные замечания по интегралу от x sin x
- Интеграл от x sin x равен -x cosx + sin x + C, где C — постоянная интегрирования.
- Мы можем вычислить интеграл от x sin x, используя метод интегрирования по частям.
☛ Похожие темы:
- Производная x sin x
- Производная sin x
- Интегрирование sin x cos x
Часто задаваемые вопросы по интегралу от x sin x
Что такое интеграл от x sin x в исчислении?
9Интеграл 0003 от x sin x равен −x cos x + sin x + C, где C — постоянная интегрирования.