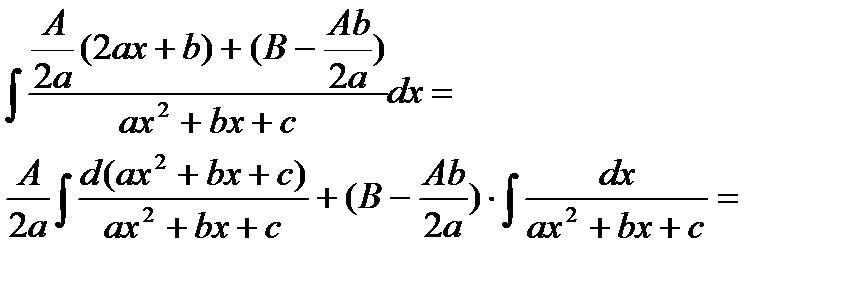Интеграл тангенса и котангенса
Среди простых формул интегрирования отсутствуют готовые зависимости, позволяющих найти интеграл от тангенса (tg (x)) и котангенса (ctg (x)). Но такие примеры в задачах встречаются и нужно знать: «Как вычислить интеграл от тангенса и котангенса?«.
Начнем с тангенса, распишем его в виде частки синуса на косинус
tg(x)=sin(x)/cos(x)
и подставим в интеграл.
Сейчас Вам понятно. Далее нужно внести синус под дифференциал, чтобы свести интеграции в логарифма
В результате получимТаким образом вывели простую и нужную на практике формулу — интеграл от тангенса равен логарифму косинуса со знаком минус.
Int(tan(x),x)=-log(cos(x)).
По приведенной схеме выведем формулу для интеграла от котангенса. Записываем частку косинуса на синус в интеграл и после внесения косинуса под дифференциал сводим интеграл к логарифму
Интеграл от котангенса равный логарифму от синуса.
Int(cot(x),x)=log(sin(x)).
Простые на вид формулы интегралов от тангенса и котангенса позволяют решить немало сложных примеров, например интегрирования тангенса двойного угла или котангенса половины угла.
Пример 1. Найти интеграл от тангенса tan(4*x).
Вычисления: Применяем приведенную выше методику для интегрирования тангенса
Здесь в скобках мы сначала вычисляем дифференциал от косинуса, а дальше выделяем значение, которое нам нужно достать. Далее интегрирования сводим к логарифму.
Таким образом можем записать обобщенную формулу для интегралаtan(k*x)
Int(tan(k*x),x)=-1/k*(log(cos(x)).
По этой формуле интеграл от тангенса двойного угла равен логарифму косинуса двойного угла умноженному на -0,5.
Для тангенса половины угла tan (phi / 2) интеграл равен -2 умножить на логарифм косинуса половины угла
По индукции получим формулу интеграла для тангенса одной третьей угла tan(phi/3)
Пример 2. Проинтегрировать котангенс двойного угла
Вычисления: По аналогии с формулами для тангенса мы могли бы выписать готовую формулу, но лучше выполнить промежуточные переходы чтобы Вы лучше поняли и заучили методику внесения под дифференциал
Таким образом, если имеем котангенс тройного угла то перед интегралом получим множителем 1/3
Интегралы от котангенса половины и трети угла будут иметь множителями перед логарифмом соответственно двойку и тройку
При нахождении первоначальной от тангенса и котангенса следует справа добавить постоянную
Зная данную методику, Вы знаете как найти интеграл от тангенса, аргумент которого содержит множителем произвольное число.
Вычисления определенных интегралов от тангенса и котангенса в данной статье рассматривать не будем. Если Вы вычисляли такие интегралы от простых функций то, зная синусы и косинусы углов найти определенный интеграл от тангенса или котангенса сможете без проблем.
С методикой интегрирования обратных тригонометрических функций, иррациональных и показательных Вы можете ознакомиться на страницах категории «Интегрирование функции» в левом меню сайта.
- Назад
- Вперёд
5.1.3.Интегралы от тригонометрических функций. Примеры решений
На данном уроке мы рассмотрим интегралы от тригонометрических функций, то есть начинкой интегралов у нас будут синусы, косинусы, тангенсы и котангенсы в различных комбинациях. Все примеры будут разобраны подробно, доступно и понятно даже для чайника.
Для
успешного изучения интегралов от
тригонометрических функций Вы должны
хорошо ориентироваться в простейших
интегралах, а также владеть некоторыми
приемами интегрирования.
Ознакомиться
с этими материалами можно на
лекциях Неопределенный
интеграл. Примеры решений и Метод
замены переменной в неопределенном
интеграле.
А
сейчас нам потребуются: Таблица
интегралов, Таблица
производных и Справочник
тригонометрических формул.
Все методические пособия можно найти
на страницеМатематические
формулы и таблицы.
Рекомендую всё распечатать. Особо
заостряю внимание на тригонометрических
формулах,
Но
сначала о том, каких интегралов в данной
статье нет.
Здесь не найдется интегралов вида
,
–
косинус, синус, умноженный на какой-нибудь
многочлен (реже что-нибудь с тангенсом
или котангенсом). Такие интегралы
интегрируются по частям, и для изучения
метода посетите урок Интегрирование
по частям. Примеры решений.Также
здесь не найдется интегралов с
«арками» – арктангенсом, арксинусом и
др.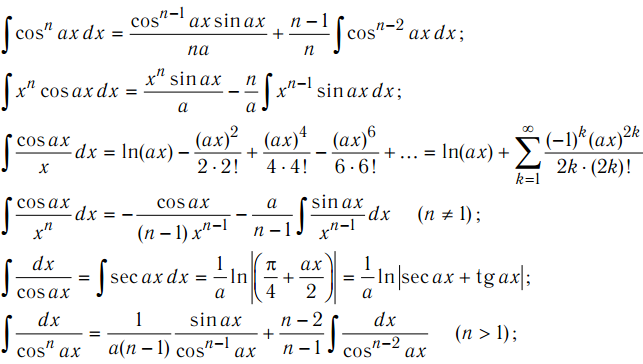
, они тоже чаще всего интегрируются
по частям.
При нахождении интегралов от тригонометрических функций используется ряд методов:
Использование тригонометрических формул
Понижение степени подынтегральной функции
(частный случай п.1)Метод замены переменной
Универсальная тригонометрическая подстановка (частный случай п.3)
В рамках урока я постараюсь подробно разобрать все перечисленные методы и привести примеры решения типовых интегралов. Следует отметить, что данное разделение по параграфам весьма условно, поскольку очень часто вышеперечисленные правила используются одновременно.
Пример 1
Найти неопределенный интеграл.
Сначала полное решение, потом комментарии.
Используем формулу:
(1) Мы
видим, что в подынтегральном выражении
находится произведение двух функций.
К сожалению, в интегральном исчислении
нет удобной формулы для интегрирования
произведения:
,
поэтому приходится прибегать к различным
ухищрениям. В данном случае мы прерываем
решение значком
и
поясняем, что используется тригонометрическая
формула. Данная формула превращает
произведение в сумму.
(2) Используем свойства линейности неопределенного интеграла – интеграл от суммы равен сумме интегралов; константу можно (и нужно) вынести за знак интеграла.
! Справка: При работе с тригонометрическими функциями следует помнить, что:
Косинус – это четная функция, то есть , минус исчезает без всяких последствий. В рассматриваемом примере:
Синус – функция нечетная: – здесь минус, наоборот – не пропадает, а выносится.
(3) Под
интегралами у нас сложные функции
(косинусы не просто от
,
а от сложного аргумента).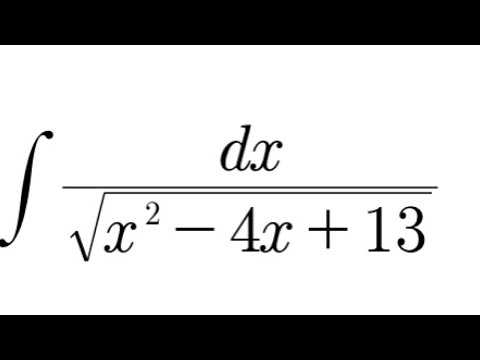
Готово.
Пример 2
Найти неопределенный интеграл.
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Пример 3
Найти неопределенный интеграл.
Классика жанра для тех, кто тонет на зачёте. Как Вы, наверное, заметили, в таблице интегралов нет интеграла от тангенса и котангенса, но, тем не менее, такие интегралы найти можно.
(1) Используем тригонометрическую формулу
(2) Подводим функцию под знак дифференциала.
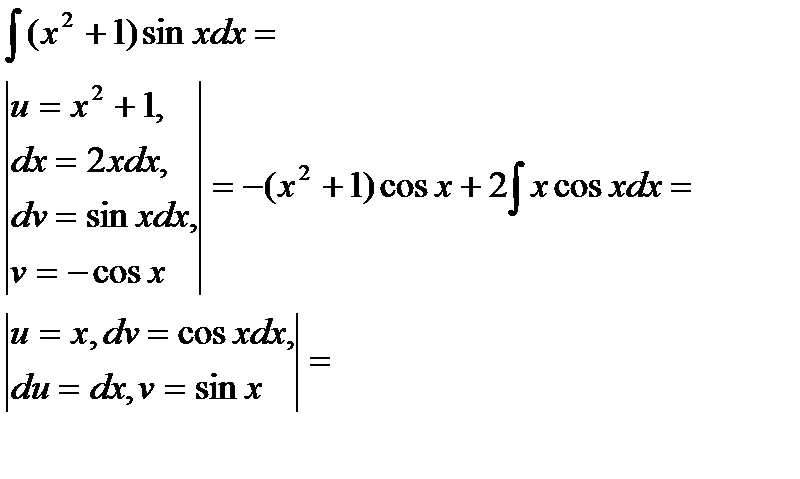
Пример 4
Найти неопределенный интеграл.
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Пример 5
Найти неопределенный интеграл.
Степени у нас будут потихоньку повышаться =). Сначала решение:
(1) Используем формулу
(2) Используем основное тригонометрическое тождество , из которого следует, что .
(3) Почленно делим числитель на знаменатель.
(4) Используем свойство линейности неопределенного интеграла.
(5) Интегрируем с помощью таблицы.
Пример 6
Найти неопределенный интеграл.
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Также
существуют интегралы от тангенсов и
котангенсов, которые находятся в более
высоких степенях.
Интеграл от тангенса
в кубе рассмотрен на уроке Как
вычислить площадь плоской фигуры? Интегралы
от тангенса (котангенса) в четвертой и
пятой степенях можно раздобыть на
странице Сложные
интегралы.
Интегрирование тангенса x
Стандартный результат интегрирования тангенса x: ln|sec x| + C. Тригонометрическая функция tan x интегрируема, и этот стандартный результат интегрирования tan x запоминается как формула. Давайте узнаем, как решить интеграцию tan x в следующем разделе.
| 1. | Что такое интеграция Tan X? |
| 2. | Как решить интеграцию Tan X? |
| 3. | Определенная интеграция Tan X |
| 4. | График интеграции Tan X |
| 5. | Часто задаваемые вопросы по интеграции Tan X |
Что такое интеграция Tan X?
Интегрирование tan x равно -ln|cos x| + C (или) ln|sec x| + C.
Функция f(x) = tan x непрерывна во всех действительных числах, кроме x = (2n + 1)π/2. Область определения функции = область значений функции tan(x), за исключением нечетных кратных π/2. Следовательно, tan x интегрируем, за исключением этого интервала по x. Мы делаем интегрирование тангенса x интегрированием подстановкой.
Как решить интеграцию Tan X?
Чтобы найти интегрирование тангенса х по х, мы выражаем тангенс х через синус и косинус так, чтобы он стал интегрируемой функцией. В соответствии с определением тангенса x мы имеем тангенс x = sin x / cos x
∫ tan x =∫ (sin x /cos x) .dx
Это можно переписать как \(\int \dfrac{1} {\ соз х} \). грех х. dx
Найдем неопределенный интеграл от tan x, используя метод подстановки интегрирования.
∫ f(g(x)) g'(x) dx = ∫ f(u) du = F(u) + C
Пусть u = cos x. Тогда du = — sin x . dx
⇒ dx = — du/ sin x
∫(sin x /cos x). dx = — ∫ du/ u
По стандартной формуле интегрирования мы знаем, что ∫ dx/x = ln x+ C
Таким образом, ∫ (sin x /cos x) .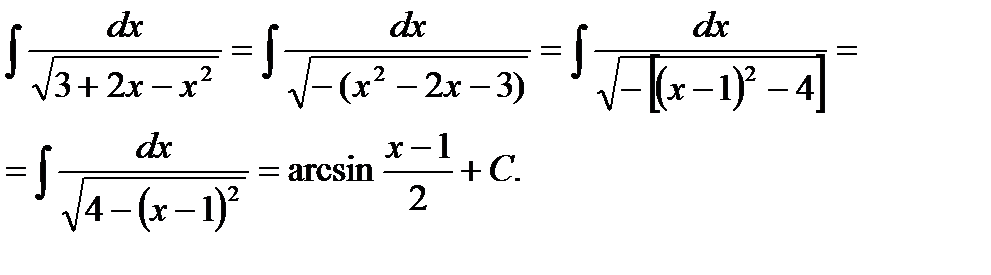
dx = — ∫ du/ u = — ln|u | + c
= -ln |(cos x)+C
= ln |(cos x) -1 +C
= ln (sec x) + C
∫ (sin x /cos x) . dx = ln (сек x) + C
∫ tan x = ln (сек x) + C 9{\pi/2}_0\)
= ln|sec π/2| — ln|сек 0|
=ln(∞)- ln(1)
= ∞
Таким образом, график интеграла от tan x расходится к бесконечности в интервале [0,π/2].
- Формулы интегрирования
- Производное tan x
Часто задаваемые вопросы по интеграции Tan X
Что такое интеграция Tan X?
Интегрирование тангенса x равно ln|sec x| + C (или) -ln|cos x| + С.
Является ли Tan x интегрируемым?
Да, Tan x интегрируем. Tan x — непрерывная функция в своей области определения. Интегрирование тангенса x равно -ln|cos x| + C.
Как сделать интеграцию Tan X?
Интегрирование тангенса х производится методом интегрирования подстановкой.
Tan x = sin x / cos x. Принимая cos x за u, мы получаем du = -sin x dx. ∫ tan x = ∫ (sin x /cos x) .dx
=-∫ du/ u = -ln u + C
= -ln|cos x| + C.
Таким образом, ∫ tan x = = -ln|cos x| + С.
Что такое интеграция 2Tan X?
Интегрирование tan x равно -ln|cos x| + C. Таким образом, \(\int\) 2 tan x = 2 \(\int\) tan x
∫ 2 tan x = -2 ln|cos x| + C.
= — ln|cos 2 x| + C.
Является ли дифференциация и интеграция Tan x одним и тем же?
Нет. дифференцирование и интегрирование тангенса х не одно и то же. Дифференциация тангенса х есть сек 2 х, а интегрирование тангенса х есть ln|сек х| + C.
Какую технику мы используем, чтобы найти интеграцию Tan X?
интегрирование тангенса x производится методом интегрирования u-подстановкой. Запишем tan x в интегрируемой форме sin x / cos x, а затем возьмем u(x) как cos(x).
Методом подстановки мы знаем, что ∫ f(g(x)) g'(x) dx =∫ f(u) du = F(u) + C, где g(x) = f(u) .
Мы применяем этот метод u-подстановки для интегрирования tan x и приходим к стандартному результату: ∫ tan x = log |sec x|
Интегральный тангенс(х)
Интегральный тангенс(х)| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
1. Доказательство
u = СО x. то находим du = — sin x dx заменить du=-sin x, u=COs x
= — пер |у| + С замена назад u=COs x = — ln |СО x| + C |
