Интегральная показательная функция
|
|
|
|||||||||||||||||||||||||||||||||
Что значит интегральный логарифм — Значения слов
Раздел очень прост в использовании. В предложенное поле достаточно ввести нужное слово, и мы вам выдадим список его значений. Хочется отметить, что наш сайт предоставляет данные из разных источников – энциклопедического, толкового, словообразовательного словарей. Также здесь можно познакомиться с примерами употребления введенного вами слова.
Большая Советская Энциклопедия
Интегральный логарифм
специальная функция, определяемая интегралом
Этот интеграл не выражается в конечной форме через элементарные функции.
Эти две функции связаны соотношением:
li (x) − Li (x) = li (2) ≈ 1, 045 163 780 117 492…
Интегральный логарифм введён Леонардом Эйлером в 1768 году.
Интегральный логарифм и интегральная показательная функция связаны соотношением:
li (x) = Ei (lnx).
Интегральный логарифм имеет единственный положительный ноль в точке μ ≈ 1, 451 369 234 883 381 050 283 968 485 892 027 449 493… ( число Рамануджана — Солднера ).
Список интегралов экспоненциальных функций
Из HandWiki
Namespaces
- Page
- Discussion
Page actions
- Read
- View source
- History
- ZWI Export
Short description : List Of Integrals Of Exponential Functions
The following представляет собой список интегралов экспоненциальных функций.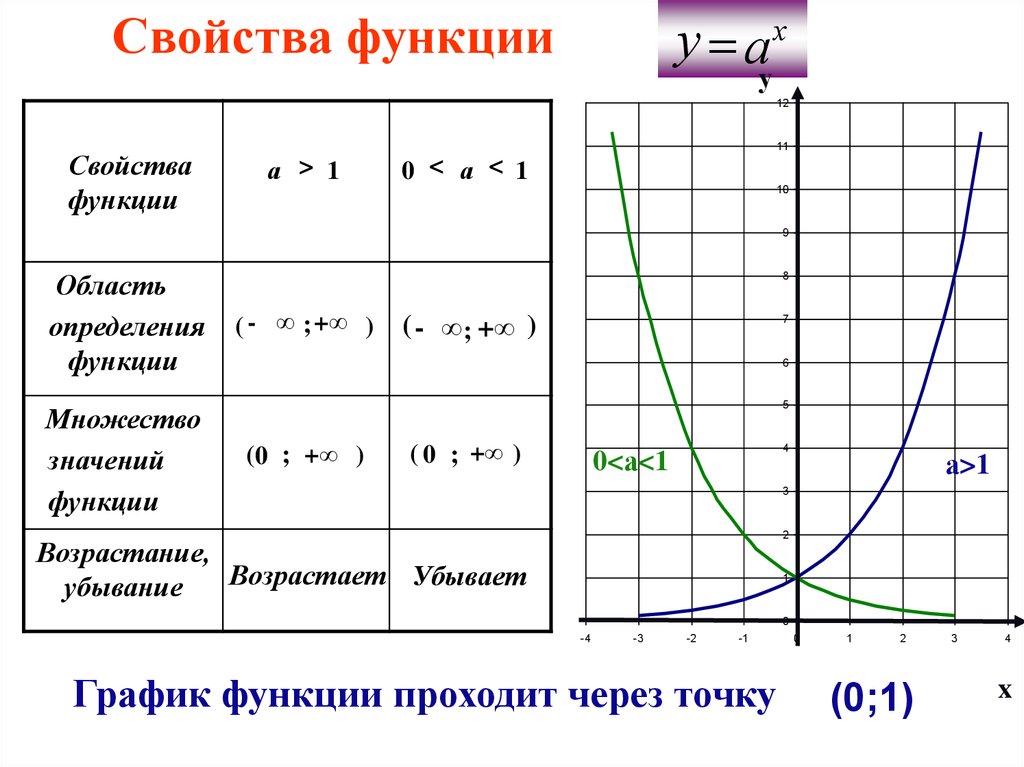 Полный список интегральных функций см. в списке интегралов.
Полный список интегральных функций см. в списке интегралов.
Содержание
- 1 Неопределенный интеграл
- 1.1 Интегралы многочленов
- 1.2 Интегралы, включающие только экспоненциальные функции
- 1.3 Интегралы с функцией ошибок
- 1.4 Прочие интегралы
- 2 Определенные интегралы
- 3 См. также
- 4 Дополнительная литература
- 5 Внешние ссылки
Неопределенный интеграл
Неопределенный интеграл является первообразной функцией. Константа (константа интегрирования) может быть добавлена в правую часть любой из этих формул, но здесь она опущена для краткости. 9{i(m-n)\phi} d\phi = 2 \pi \delta_{m,n} }[/math] (для целых m, n)
, где [math]\displaystyle{ \delta_{m,n } }[/math] — это дельта Кронекера.
См. также
- Градштейн и Рыжик
Дополнительная литература
- Молл, Виктор Гюго (12 ноября 2014 г.
 ). Специальные интегралы Градштейна и Рыжика: Доказательства – Том I . I (1-е изд.). Чепмен и Холл/CRC Press. ISBN 978-1-48225-651-2. http://www.crcpress.com/Special-Integrals-of-Gradshteyn-and-Ryzhik-the-Proofs—Volume-I/Moll/9781482256512 . Проверено 12 февраля 2016 г.
). Специальные интегралы Градштейна и Рыжика: Доказательства – Том I . I (1-е изд.). Чепмен и Холл/CRC Press. ISBN 978-1-48225-651-2. http://www.crcpress.com/Special-Integrals-of-Gradshteyn-and-Ryzhik-the-Proofs—Volume-I/Moll/9781482256512 . Проверено 12 февраля 2016 г. - Молл, Виктор Гюго (27 октября 2015 г.). Специальные интегралы Градштейна и Рыжика: Доказательства – Том II . II (1-е изд.). Чепмен и Холл/CRC Press. ISBN 978-1-48225-653-6. http://www.crcpress.com/Special-Integrals-of-Gradshteyn-and-Ryzhik-the-Proofs—Volume-II/Moll/9781482256536. Проверено 12 февраля 2016 г. .
- Тоеш Пракаш Шарма, https://www.isroset.org/pdf_paper_view.php?paper_id=2214&7-ISROSET-IJSRMSS-05130.pdf
Внешние ссылки
- Wolfram Mathematica Online Integrator
- Молл, Виктор Гюго. «Список с формулами и доказательствами в ОТО». http://www.math.tulane.edu/~vhm/Table.html.
6.7 Интегралы, экспоненциальные функции и логарифмы.
 Расчет, том 1
Расчет, том 1Цели обучения
- 6.7.1 Запишите определение натурального логарифма в виде интеграла.
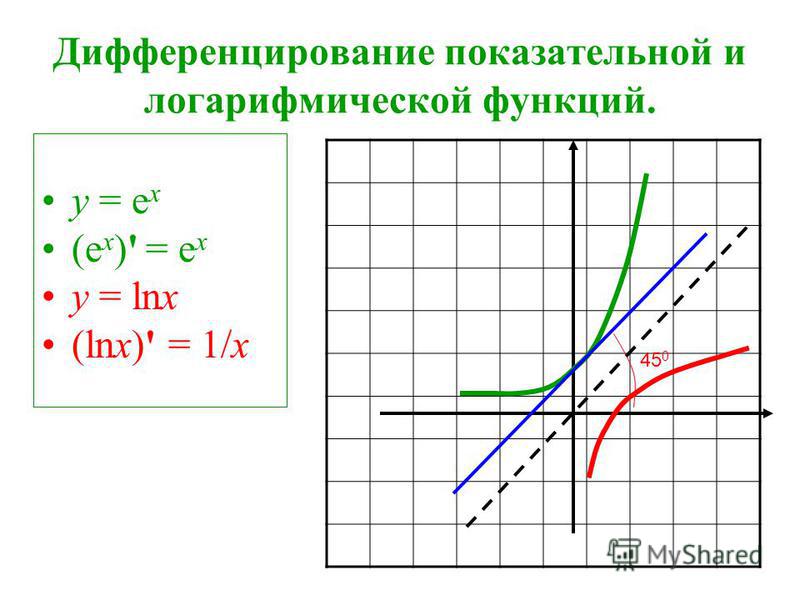
- 6.7.2 Знать производную натурального логарифма.
- 6.7.3 Интегрируйте функции, включающие натуральный логарифм.
- 6.7.4 Определим число ee через интеграл.
- 6.7.5 Знать производную и интеграл экспоненциальной функции.
- 6.7.6 Докажите свойства логарифмов и показательных функций, используя интегралы.
- 6.7.7 Выразите общие логарифмические и экспоненциальные функции в терминах натуральных логарифмов и экспонент.
Мы уже рассматривали экспоненциальные функции и логарифмы в предыдущих главах. Тем не менее, мы упустили некоторые ключевые детали в предыдущих обсуждениях. Например, мы не изучали, как обращаться с экспоненциальными функциями с иррациональными показателями. Определение числа e — еще одна область, где предыдущая разработка была несколько неполной. Теперь у нас есть инструменты для более строгой математической обработки этих концепций, и мы делаем это в этом разделе.
Теперь у нас есть инструменты для более строгой математической обработки этих концепций, и мы делаем это в этом разделе.
Для целей этого раздела предположим, что мы еще не определили натуральный логарифм, число e или какие-либо формулы интегрирования и дифференцирования, связанные с этими функциями. К концу раздела мы изучим эти понятия математически строгим образом (и мы увидим, что они согласуются с понятиями, которые мы изучили ранее).
Мы начинаем этот раздел с определения натурального логарифма через интеграл. Это определение составляет основу раздела. Из этого определения мы выводим формулы дифференцирования, определяем числа e,e и расширяем эти понятия до логарифмов и показательных функций любого основания.
Натуральный логарифм как интеграл
Вспомним правило степени для интегралов:
∫xndx=xn+1n+1+C,n≠−1.∫xndx=xn+1n+1+C,n≠−1.
Ясно, что это не работает, когда n=−1,n=−1, так как это заставит нас делить на ноль. Итак, что нам делать с ∫1xdx?∫1xdx? Напомним из основной теоремы исчисления, что ∫1x1tdt∫1x1tdt является первообразной 1/x.1/x. Поэтому мы можем дать следующее определение.
Итак, что нам делать с ∫1xdx?∫1xdx? Напомним из основной теоремы исчисления, что ∫1x1tdt∫1x1tdt является первообразной 1/x.1/x. Поэтому мы можем дать следующее определение.
Определение
Для x>0,x>0 определите функцию натурального логарифма как
lnx=∫1x1tdt.lnx=∫1x1tdt.
(6.24)
Для x>1,x>1 это просто площадь под кривой y=1/ty=1/t от 11 до x.x. Для x<1,x<1 имеем ∫1x1tdt=−∫x11tdt,∫1x1tdt=−∫x11tdt, так что в данном случае это отрицательная площадь под кривой от xto1xto1 (см. следующий рисунок).
Рисунок 6,75 (a) Когда x>1,x>1, натуральный логарифм представляет собой площадь под кривой y=1/ty=1/t от 1tox.1tox. (b) Когда x<1,x<1, натуральный логарифм равен отрицательному значению площади под кривой от xx до 1,1.
Обратите внимание, что ln1=0.ln1=0. Кроме того, функция y=1/t>0, y=1/t>0 при x>0.x>0. Поэтому по свойствам интегралов видно, что lnxlnx возрастает при x>0.x>0.
Свойства натурального логарифма
Из-за того, как мы определили натуральный логарифм, следующая формула дифференцирования сразу выпадает из основной теоремы исчисления.
Теорема 6.15
Производная натурального логарифма
Для x>0,x>0 производная натурального логарифма определяется как
ddxlnx=1x.ddxlnx=1x.
Теорема 6.16
Следствие из производной натурального логарифма
Функция lnxlnx дифференцируема; следовательно, он непрерывен.
График lnxlnx показан на рис. 6.76. Заметим, что он непрерывен во всей своей области определения (0,∞).(0,∞).
Рисунок 6,76 График f(x)=lnxf(x)=lnx показывает, что это непрерывная функция.
Пример 6,35
Вычисление производных натуральных логарифмов
Вычисление следующих производных:
- ddxln(5×3−2)ddxln(5×3−2)
- ддх(лн(3х))2ддх(лн(3х))2
Решение
Нам нужно применить цепное правило в обоих случаях.
- ddxln(5×3−2)=15x25x3−2ddxln(5×3−2)=15x25x3−2
- ddx(ln(3x))2=2(ln(3x))·33x=2(ln(3x))xddx(ln(3x))2=2(ln(3x))·33x=2(ln( 3x))x
Контрольно-пропускной пункт 6,35
Вычислите следующие производные:
- ddxln(2×2+x)ddxln(2×2+x)
- ddx(ln(x3))2ddx(ln(x3))2
Обратите внимание: если мы используем функцию абсолютного значения и создаем новую функцию ln|x|,ln|x|, мы можем расширить область значений натурального логарифма, включив в нее x<0.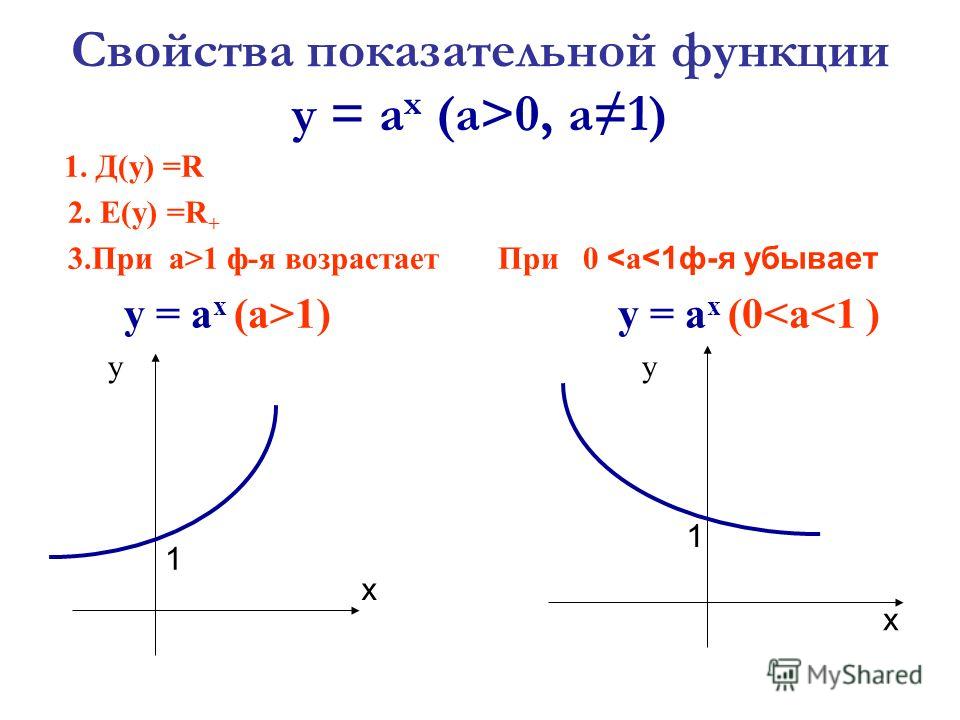 x<0. Тогда (d/(dx))ln|x|=1/x.(d/(dx))ln|x|=1/x. Это приводит к известной формуле интегрирования.
x<0. Тогда (d/(dx))ln|x|=1/x.(d/(dx))ln|x|=1/x. Это приводит к известной формуле интегрирования.
Теорема 6.17
Интеграл от (1/
и ) дюНатуральный логарифм является первообразной функции f(u)=1/u:f(u)=1/u:
∫1udu=ln|u|+C.∫1udu=ln|u|+C .
Пример 6,36
Вычисление интегралов с натуральными логарифмами
Вычисление интеграла ∫xx2+4dx.∫xx2+4dx.
Решение
Используя uu-подстановку, пусть u=x2+4.u=x2+4. Тогда du=2xdxdu=2xdx и имеем
∫xx2+4dx=12∫1udu=12ln|u|+C=12ln|x2+4|+C=12ln(x2+4)+C.∫xx2+4dx= 12∫1udu=12ln|u|+C=12ln|x2+4|+C=12ln(x2+4)+C.
Контрольно-пропускной пункт 6,36
Вычислить интеграл ∫x2x3+6dx.∫x2x3+6dx.
Хотя мы назвали нашу функцию «логарифмом», мы на самом деле не доказали, что для этой функции выполняются какие-либо свойства логарифмов. Мы делаем так здесь.
Мы делаем так здесь.
Теорема 6.18
Свойства натурального логарифма
Если a,b>0a,b>0 и rr — рациональное число, то
- ln1=0ln1=0
- пер(аб)=лна+лнблн(аб)=лна+лнб
- ln(ab)=lna-lnbln(ab)=lna-lnb
- лн(ар)=рлналн(ар)=рлна
Доказательство
я. По определению, ln1=∫111tdt=0.ln1=∫111tdt=0.
II. У нас есть
ln(ab)=∫1ab1tdt=∫1a1tdt+∫aab1tdt.ln(ab)=∫1ab1tdt=∫1a1tdt+∫aab1tdt.
Используйте u-подстановку u-подстановку в последнем интеграле в этом выражении. Пусть u=t/a.u=t/a. Тогда du=(1/a)dt.du=(1/a)dt. Кроме того, когда t=a,u=1,t=a,u=1, и когда t=ab,u=b.t=ab,u=b. Получаем
ln (ab) = ∫1a1tdt+∫aab1tdt = ∫1a1tdt+∫aabat · 1adt = ∫1a1tdt+∫1b1udu = lna+lnb.ln (ab) = ∫1a1tdt+∫aab1tdt = ∫1t.1tdtdtdt+∫aab1t1t. лна+лнб.
IV. Обратите внимание, что
ddxln(xr)=rxr−1xr=rx.ddxln(xr)=rxr−1xr=rx.
Кроме того,
ddx(rlnx)=rx.ddx(rlnx)=rx.
Поскольку производные этих двух функций одинаковы, по основной теореме исчисления они должны отличаться на константу. Итак, мы имеем
ln(xr)=rlnx+Cln(xr)=rlnx+C
для некоторой константы C.C. Принимая x=1,x=1, получаем
ln(1r)=rln(1)+C0=r(0)+CC=0.ln(1r)=rln(1)+C0=r(0 )+СС=0.
Таким образом, ln(xr)=rlnxln(xr)=rlnx и доказательство завершено. Обратите внимание, что мы можем распространить это свойство на иррациональные значения rr позже в этом разделе.
Часть III. следует из части II. и IV. и доказательство остается за вами.
□
Пример 6,37
Использование свойств логарифмов
Использование свойств логарифмов для упрощения следующего выражения до простого логарифма:
ln9−2ln3+ln(13).ln9−2ln3+ln(13).
Решение
Имеем
ln9-2ln3+ln(13)=ln(32)-2ln3+ln(3-1)=2ln3-2ln3-ln3=-ln3. ln9-2ln3+ln(13)=ln(32) −2ln3+ln(3−1)=2ln3−2ln3−ln3=−ln3.
ln9-2ln3+ln(13)=ln(32) −2ln3+ln(3−1)=2ln3−2ln3−ln3=−ln3.
Контрольно-пропускной пункт 6,37
Используйте свойства логарифмов, чтобы упростить следующее выражение до простого логарифма:
ln8-ln2-ln(14).ln8-ln2-ln(14).
Определение номера
eТеперь, когда мы определили натуральный логарифм, мы можем использовать эту функцию для определения числа e.e.
Определение
Число ee определяется как действительное число, такое что
lne=1.lne=1.
Иными словами, площадь под кривой y=1/ty=1/t между t=1t=1 и t=et=e равна 11 (рис. 6.77). Доказательство того, что такое число существует и уникально, остается за вами. ( Подсказка : используйте теорему о промежуточном значении, чтобы доказать существование, и тот факт, что lnxlnx увеличивается, чтобы доказать уникальность.)
Рисунок
6,77
Площадь под кривой от 11 до ee равна единице.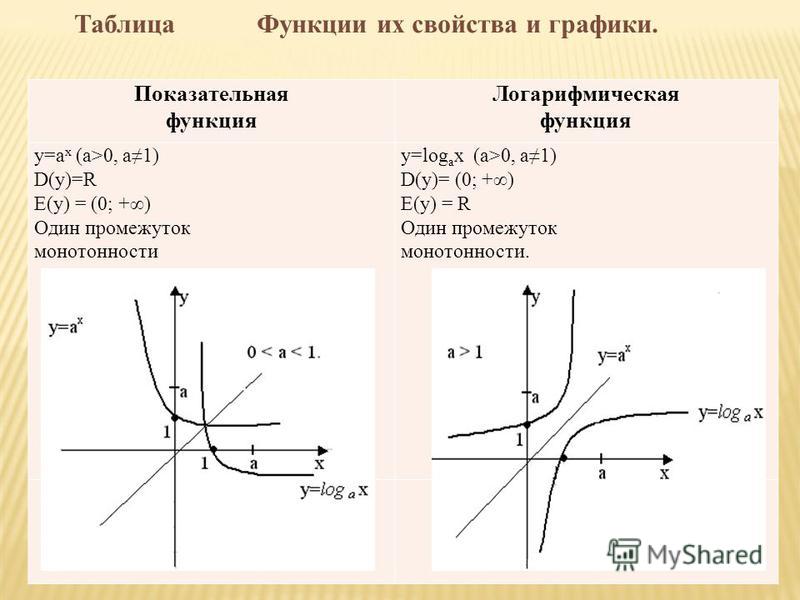
Можно показать, что число ee иррационально, хотя мы не будем этого делать здесь (см. Студенческий проект в сериях Тейлора и Маклорена). Его приблизительное значение равно
.e≈2,71828182846.e≈2,71828182846.
Экспоненциальная функция
Обратимся теперь к функции ex.ex. Обратите внимание, что натуральный логарифм один к одному и, следовательно, имеет обратную функцию. Сейчас мы обозначаем эту обратную функцию как expx.expx. Тогда
exp(lnx)=xforx>0andln(expx)=xfor allx.exp(lnx)=xforx>0andln(expx)=xfor allx.
На следующем рисунке показаны графики expxexpx и lnx.lnx.
Рисунок 6,78 Графики lnxlnx и expx.expx.
Мы предполагаем, что expx=ex.expx=ex. Для рациональных значений x,x это легко показать. Если xx рационально, то имеем ln(ex)=xlne=x.ln(ex)=xlne=x. Таким образом, когда xx рационально, ex=expx.ex=expx. Для иррациональных значений x,x мы просто определяем exex как обратную функцию lnx.lnx.
Определение
Для любого действительного числа x,x определите y=exy=ex как число, для которого
lny=ln(ex)=x. lny=ln(ex)=x.
lny=ln(ex)=x.
(6.25)
Тогда мы имеем ex=exp(x)ex=exp(x) для всех x,x, и, таким образом,
elnx=xforx>0andln(ex)=xelnx=xforx>0andln(ex)=x
(6.26)
для всех х.х.
Свойства показательной функции
Так как экспоненциальная функция была определена через обратную функцию, а не через степень e,e, мы должны проверить, что обычные законы показателей выполняются для функции ex.ex.
Теорема 6.19
Свойства экспоненциальной функции
Если pp и qq — любые действительные числа, а rr — рациональное число, то
- epeq=ep+qepeq=ep+q
- epeq=ep-qepeq=ep-q
- (эп)r=эпр(эп)r=эпр
Доказательство
Обратите внимание, что если pp и qq рациональны, то свойства сохраняются. Однако, если pp или qq иррациональны, мы должны применить определение обратной функции exex и проверить свойства. Здесь проверяется только первое свойство; два других оставлены вам. У нас есть
Здесь проверяется только первое свойство; два других оставлены вам. У нас есть
ln(epeq)=ln(ep)+ln(eq)=p+q=ln(ep+q).ln(epeq)=ln(ep)+ln(eq)=p+q=ln(ep+ р).
Так как lnxlnx один к одному, то
epeq=ep+q.epeq=ep+q.
□
Как и в части iv. свойства логарифма, мы можем расширить свойство iii. к иррациональным значениям r,r, и мы делаем это к концу раздела.
Мы также хотим проверить формулу дифференцирования для функции y=ex.y=ex. Для этого нам нужно использовать неявное дифференцирование. Пусть y=ex.y=ex. Затем
lny=xddxlny=ddxx1ydydx=1dydx=y.lny=xddxlny=ddxx1ydydx=1dydx=y.
Таким образом, мы видим
ddxex=exddxex=ex
по желанию, что сразу приводит к формуле интегрирования
∫exdx=ex+C.∫exdx=ex+C.
Применим эти формулы в следующих примерах.
Пример 6,38
Использование свойств показательных функций
Вычислите следующие производные:
- ddte3tet2ddte3tet2
- ddxe3x2ddxe3x2
Решение
При необходимости применяем цепное правило.
- ddte3tet2=ddte3t+t2=e3t+t2(3+2t)ddte3tet2=ddte3t+t2=e3t+t2(3+2t)
- ddxe3x2=e3x26xddxe3x2=e3x26x
Контрольно-пропускной пункт 6,38
Оценить следующие производные:
- ddx(ex2e5x)ddx(ex2e5x)
- ддт(е2т)3ддт(е2т)3
Пример 6,39
Использование свойств экспоненциальных функций
Вычислите следующий интеграл: ∫2xe-x2dx.∫2xe-x2dx.
Решение
Используя uu-подстановку, пусть u=−x2.u=−x2. Тогда du=-2xdx,du=-2xdx, и мы имеем
∫2xe-x2dx=-∫eudu=-eu+C=-e-x2+C.∫2xe-x2dx=-∫eudu=-eu+C =-e-x2+C.
Контрольно-пропускной пункт 6,39
Вычислите следующий интеграл: ∫4e3xdx.∫4e3xdx.
Общие логарифмические и экспоненциальные функции
Мы завершаем этот раздел рассмотрением экспоненциальных функций и логарифмов с основанием, отличным от e. e. Экспоненциальные функции — это функции вида f(x)=ax.f(x)=ax. Обратите внимание, что если a=e,a=e, у нас все еще нет математически строгого определения этих функций для иррациональных показателей. Давайте исправим это здесь, определив функцию f(x)=axf(x)=ax в терминах экспоненциальной функции ex.ex. Затем мы исследуем логарифмы с основанием, отличным от ee, как функции, обратные экспоненциальным функциям.
e. Экспоненциальные функции — это функции вида f(x)=ax.f(x)=ax. Обратите внимание, что если a=e,a=e, у нас все еще нет математически строгого определения этих функций для иррациональных показателей. Давайте исправим это здесь, определив функцию f(x)=axf(x)=ax в терминах экспоненциальной функции ex.ex. Затем мы исследуем логарифмы с основанием, отличным от ee, как функции, обратные экспоненциальным функциям.
Определение
Для любого a>0,a>0 и любого действительного числа x,x определите y=axy=ax следующим образом:
y=ax=exlna.y=ax=exlna.
Теперь axax строго определен для всех значений x . Это определение также позволяет нам обобщить свойство iv. логарифмов и свойства iii. экспоненциальных функций, применимых как к рациональным, так и к иррациональным значениям r.r. Несложно показать, что свойства экспонент сохраняются для общих экспоненциальных функций, определенных таким образом.
Давайте теперь применим это определение для вычисления формулы дифференцирования для ax. ax. У нас есть
ax. У нас есть
ddxax=ddxexlna=exlnalna=axlna.ddxax=ddxexlna=exlnalna=axlna.
Сразу следует соответствующая формула интегрирования.
Теорема 6.20
Производные и интегралы, включающие общие экспоненциальные функции
Пусть а>0.а>0. Затем
ddxax=axlnaddxax=axlna
и
∫axdx=1lnaax+C.∫axdx=1lnaax+C.
Если a≠1,a≠1, то функция axax является взаимно однозначной и имеет четко определенную обратную. Его инверсия обозначается как logax.logax. Тогда
y=logaxif и только еслиx=ay.y=logaxif и только еслиx=ay.
Обратите внимание, что функции общего логарифма можно записать в виде натурального логарифма. Пусть y=logax.y=logax. Тогда х=ау.х=ау. Возьмем натуральный логарифм обеих частей этого второго уравнения и получим
.lnx=ln(ay)lnx=ylnay=lnxlnalogax=lnxlna.lnx=ln(ay)lnx=ylnay=lnxlnalogax=lnxlna.
Итак, мы видим, что все логарифмические функции постоянно кратны друг другу. Далее мы используем эту формулу, чтобы найти формулу дифференцирования для логарифма с основанием а.о. Снова пусть y=logax.y=logax. Тогда
Далее мы используем эту формулу, чтобы найти формулу дифференцирования для логарифма с основанием а.о. Снова пусть y=logax.y=logax. Тогда
dydx=ddx(logax)=ddx(lnxlna)=(1lna)ddx(lnx)=1lna·1x=1xlna.dydx=ddx(logax)=ddx(lnxlna)=(1lna)ddx(lnx)=1lna·1x =1xlna.
Теорема 6.21
Производные функций общего логарифма
Пусть а>0.а>0. Затем
ddxlogax=1xlna.ddxlogax=1xlna.
Пример 6.40
Вычисление производных общих экспоненциальных и логарифмических функций
Вычисление следующих производных:
- ddt(4t·2t2)ddt(4t·2t2)
- ddxlog8(7×2+4)ddxlog8(7×2+4)
Решение
При необходимости нужно применить цепное правило.
- ddt(4t·2t2)=ddt(22t·2t2)=ddt(22t+t2)=22t+t2ln(2)(2+2t)ddt(4t·2t2)=ddt(22t·2t2)=ddt (22t+t2)=22t+t2ln(2)(2+2t)
- ddxlog8(7×2+4)=1(7×2+4)(ln8)(14x)ddxlog8(7×2+4)=1(7×2+4)(ln8)(14x)
Контрольно-пропускной пункт 6.
 40
40Оценить следующие производные:
- ddt4t4ddt4t4
- ddxlog3(x2+1)ddxlog3(x2+1)
Пример 6.41
Интегрирование общих экспоненциальных функций
Вычислите следующий интеграл: ∫323xdx.∫323xdx.
Решение
Используйте u-подстановкуu-подстановку и пусть u=−3x.u=−3x. Тогда du=−3dxdu=−3dx и имеем
∫323xdx=∫3·2−3xdx=−∫2udu=−1ln22u+C=−1ln22−3x+C.∫323xdx=∫3·2−3xdx=− ∫2udu=-1ln22u+C=-1ln22-3x+C.
Контрольно-пропускной пункт 6.41
Вычислите следующий интеграл: ∫x22x3dx.∫x22x3dx.
Раздел 6.7 Упражнения
Для следующих упражнений найдите производную dydx.dydx.
295.
у=пер(2х)у=пер(2х)
296.
у=пер(2х+1)у=пер(2х+1)
297.
у=1lnxy=1lnx
Для следующих упражнений найдите неопределенный интеграл.
298.
∫dt3t∫dt3t
299.
∫dx1+x∫dx1+x
Для следующих упражнений найдите производную dy/dx.dy/dx. (Вы можете использовать калькулятор, чтобы построить функцию и производную, чтобы убедиться, что она верна.)
300.
[Т] y=ln(x)xy=ln(x)x
301.
[Т] y=xln(x)y=xln(x)
302.
[Т] у=log10xy=log10x
303.
[T] y=ln(sinx)y=ln(sinx)
304.
[Т] y=ln(lnx)y=ln(lnx)
305.
[Т] y=7ln(4x)y=7ln(4x)
306.
[Т] y=ln((4x)7)y=ln((4x)7)
307.
[T] y=ln(tanx)y=ln(tanx)
308.
[T] y=ln(tan(3x))y=ln(tan(3x))
309.
[Т] y=ln(cos2x)y=ln(cos2x)
Для следующих упражнений найдите определенный или неопределенный интеграл.
310.
∫01dx3+x∫01dx3+x
311.
∫01dt3+2t∫01dt3+2t
312.
∫02xdxx2+1∫02xdxx2+1
313.
∫02x3dxx2+1∫02x3dxx2+1
314.
∫2edxxlnx∫2edxxlnx
315.
∫2edxx(lnx)2∫2edxx(lnx)2
316.
∫cosxdxsinx∫cosxdxsinx
317.
∫0π/4tanxdx∫0π/4tanxdx
318.
∫раскладушка(3x)dx∫раскладушка(3x)dx
319.
∫(lnx)2dxx∫(lnx)2dxx
В следующих упражнениях вычислите dy/dxdy/dx путем дифференцирования lny.lny.
320.
у=х2+1у=х2+1
321.
у=х2+1х2-1у=х2+1х2-1
322.
y=esinxy=esinx
323.
у=х-1/ху=х-1/х
324.
у=е(ех)у=е(ех)
325.
у=хей=хе
326.
у=х(ех)у=х(ех)
327.
у=хх3х6у=хх3х6
328.
y=x−1/lnxy=x−1/lnx
329.
у=е-lnxy=е-lnx
Для следующих упражнений оцените любым методом.
330.
∫510dtt-∫5x10xdtt∫510dtt-∫5x10xdtt
331.
∫1eπdxx+∫−2−1dxx∫1eπdxx+∫−2−1dxx
332.
ддкс∫x1dttddx∫x1dtt
333.
ддкс∫xx2dttddx∫xx2dtt
334.
ddxln(secx+tanx)ddxln(secx+tanx)
В следующих упражнениях используйте функцию lnx.lnx. Если вы не можете найти точки пересечения аналитически, воспользуйтесь калькулятором.
335.
Найдите площадь области, ограниченной x=1x=1 и y=5y=5 выше y=lnx.y=lnx.
336.
[T] Найдите длину дуги lnxlnx от x=1x=1 до x=2.x=2.
337.
Найдите площадь между lnxlnx и осью x от x=1tox=2. x=1tox=2.
x=1tox=2.
338.
Найдите объем фигуры, созданной при вращении этой кривой от x=1tox=2x=1tox=2 вокруг оси x , как показано здесь.
339.
[T] Найдите площадь поверхности фигуры, созданной при вращении кривой в предыдущем упражнении от x=1x=1 до x=2x=2 вокруг оси x .
Если вы не можете аналитически найти точки пересечения в следующих упражнениях, используйте калькулятор.
340.
Найдите площадь гиперболической четверти окружности, заключенной в x=2andy=2x=2andy=2 выше y=1/x.y=1/x.
341.
[T] Найдите длину дуги y=1/xy=1/x из x=1tox=4.x=1tox=4.
342.
Найдите площадь под y=1/xy=1/x и над осью x от x=1tox=4.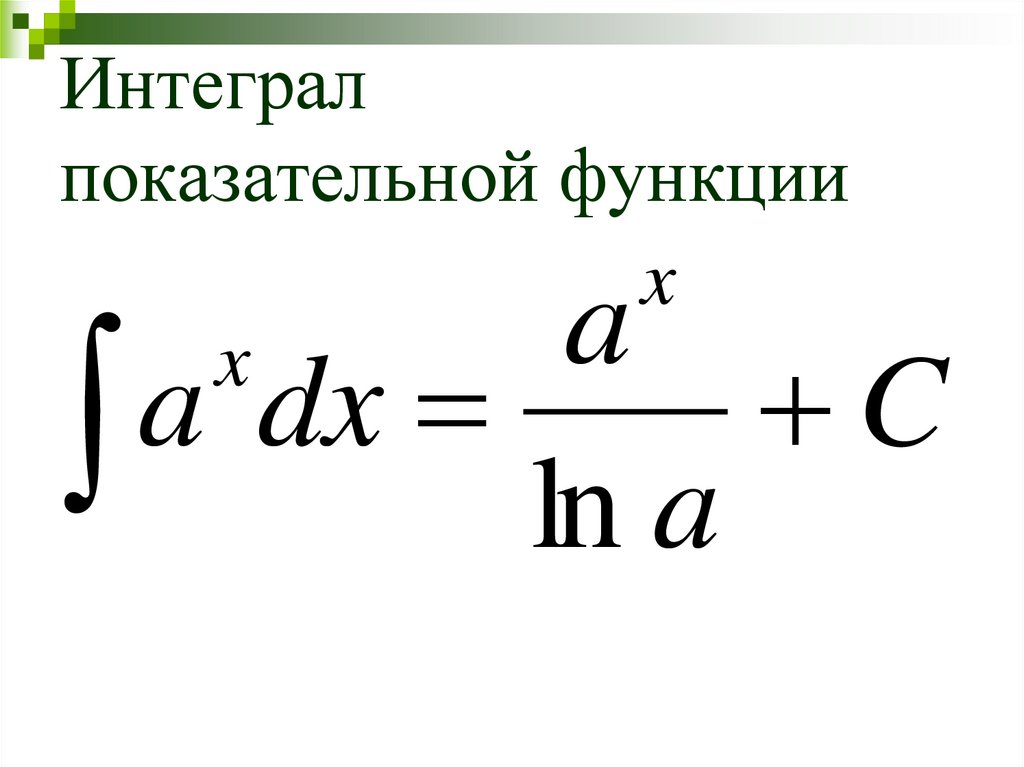



 В этом случае, результат не будет верным, и хотя порядок цифр совпадет, все таки погрешность достаточно велика, что бы использовать результат в дальнейших вычислениях.
В этом случае, результат не будет верным, и хотя порядок цифр совпадет, все таки погрешность достаточно велика, что бы использовать результат в дальнейших вычислениях.
 Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн ). Специальные интегралы Градштейна и Рыжика: Доказательства – Том I . I (1-е изд.). Чепмен и Холл/CRC Press. ISBN 978-1-48225-651-2. http://www.crcpress.com/Special-Integrals-of-Gradshteyn-and-Ryzhik-the-Proofs—Volume-I/Moll/9781482256512 . Проверено 12 февраля 2016 г.
). Специальные интегралы Градштейна и Рыжика: Доказательства – Том I . I (1-е изд.). Чепмен и Холл/CRC Press. ISBN 978-1-48225-651-2. http://www.crcpress.com/Special-Integrals-of-Gradshteyn-and-Ryzhik-the-Proofs—Volume-I/Moll/9781482256512 . Проверено 12 февраля 2016 г.