Интегральные формулы: Недопустимое название — ALL

alexxlab / / Разное

Содержание

Математический анализ. Часть II. (Зорич В.А.)

  

Зорич В. А. Математический анализ: Учебник. Ч. II. — М.: Наука Главная редакция физико-математической литературы, 1984. — 640 с.

В книге отражена ставшая более тесной связь курса классического анализа с современными математическими курсами (алгебры, дифференциальной геометрии, дифференциальных уравнений, комплексного и функционального анализа).

Во вторую часть учебника включены следующие разделы: Многомерный интеграл. Дифференциальные формы и их интегрирование. Ряды и интегралы, зависящие от параметра (в том числе ряды и преобразования Фурье, а также асимптотические разложения).

Текст снабжен вопросами и задачами, дополняющими материал книги и существующих задачников по анализу.

Органической частью текста являются примеры приложений развиваемой теории, которыми часто служат содержательные задачи механики и физики.

Для студентов университетов, обучающихся по специальности «Математика» и «Механика». Может быть полезна студентам факультетов и вузов с расширенной программой по математике, а так же специалистам в области математики и ее приложений.



Оглавление

ПРЕДИСЛОВИЕ
ГЛАВА IX. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ (ОБЩАЯ ТЕОРИЯ)
2. Открытые и замкнутые подмножества метрического пространства.
3. Подпространство метрического пространства.
4. Прямое произведение метрических пространств.
§ 2. Топологическое пространство
2. Подпространство топологического пространства.
3. Прямое произведение топологических пространств.
§ 3. Компакты
2. Метрические компакты.
§ 4. Связные топологические пространства
§ 5. Полные метрические пространства
2. Пополнение метрического пространства.
§ 6. Непрерывные отображения топологических пространств
2. Непрерывные отображения.
§ 7. Принцип сжимающих отображений
ГЛАВА X. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ С БОЛЕЕ ОБЩЕЙ ТОЧКИ ЗРЕНИЯ
2. Норма в линейном пространстве.
3. Скалярное произведение в векторном пространстве.
§ 2. Линейные и полилинейные операторы
2. Норма оператора.
3. Пространство непрерывных операторов.
§ 3. Дифференциал отображения
2. Общие законы дифференцирования.
3. Некоторые примеры.
4. Частные производные отображения.
§ 4. Теорема о конечном приращении и некоторые примеры ее использования
2. Некоторые примеры применения теоремы о конечном приращении.
§ 5. Производные отображения высших порядков
2. Производная по вектору и вычисление значений n-го дифференциала.
3. Симметричность дифференциалов высшего порядка.
4. Некоторые замечания.
§ 3. Формула Тейлора и исследование экстремумов
2. Исследование внутренних экстремумов.
3. Некоторые примеры.
§ 7. Общая теорема о неявной функции
ГЛАВА XI. КРАТНЫЕ ИНТЕГРАЛЫ
§ 1. Интеграл Римана на n-мерном промежутке
2. Критерий Лебега интегрируемости функции по Риману. 3.
3. Дифференциальные операторы rad, rot, div и V.
5. Векторные операции в криволинейных координатах.
§ 2. Интегральные формулы теории поля
2. Физическая интерпретация div, rot, grad.
3. Некоторые дальнейшие интегральные формулы.
§ 3. Потенциальные поля
2. Необходимое условие потенциальности.
3. Критерий потенциальности векторного поля.
4. Топологическая структура области и потенциал.
5. Векторный потенциал. Точные и замкнутые формы.
§ 4. Примеры приложений
2. Уравнение неразрывности.
3. Основные уравнения динамики сплошной среды.
4. Волновое уравнение.
ГЛАВА XV. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ НА МНОГООБРАЗИЯХ
2. Алгебра кососимметрических форм.
3. Линейные отображения линейных пространств и сопряженные отображения сопряженных пространств.
§ 2. Многообразие
2. Гладкие многообразия и гладкие отображения.
3. Ориентация многообразия и его края.
4. Разбиение единицы и реализация многообразий в виде поверхностей в R^n.
§ 3. Дифференциальные формы и их интегрирование на многообразиях
2. Дифференциальная форма на многообразии.
3. Внешний дифференциал.
4. Интеграл от формы по многообразию.
§ 4. Замкнутые и точные формы на многообразии
2. Гомологии и когомологии.
ГЛАВА XVI. РАВНОМЕРНАЯ СХОДИМОСТЬ И ОСНОВНЫЕ ОПЕРАЦИИ АНАЛИЗА НАД РЯДАМИ И СЕМЕЙСТВАМИ ФУНКЦИЙ
§ 1. Поточечная и равномерная сходимость
2. Постановка основных вопросов.
3. Сходимость и равномерная сходимость семейства функций, зависящих от параметра.
4. Критерий Коши равномерной сходимости.
§ 2. Равномерная сходимость рядов функций
2. Признак Вейерштрасса равномерной сходимости ряда.
§ 3. Функциональные свойства предельной функции
2. Условия коммутирования двух предельных переходов.
3. Непрерывность и предельный переход.
4. Интегрирование и предельный переход.
5. Дифференцирование и предельный переход.
§ 4. Компактные и плотные подмножества пространства непрерывных функций
2. Метрическое пространство C(K,Y).
3. Теорема Стоуна.
ГЛАВА XVII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
§ 1. Собственные интегралы, зависящие от параметра
2. Непрерывность интеграла, зависящего от параметра.
3. Дифференцирование интеграла, зависящего от параметра.
4. Интегрирование интеграла, зависящего от параметра.
§ 2. Несобственные интегралы, зависящие от параметра
2. Предельный переход под знаком несобственного интеграла и непрерывность несобственного интеграла, зависящего от параметра.
3. Дифференцирование несобственного интеграла по параметру.
4. Интегрирование несобственного интеграла по параметру.
§ 3. Эйлеровы интегралы
2. Гамма-функция.
3. Связь между функциями В и Г.
4. Некоторые примеры.
§ 4. Свертка функций и начальные сведения об обобщенных функциях
2. Некоторые общие свойства свертки.
3. Дельтаобразные семейства функций и аппроксимационная теорема Вейерштрасса.
4. Начальные представления о распределениях
§ 5. Кратные интегралы, зависящие от параметра
2. Несобственные кратные интегралы, зависящие от параметра.
3. Несобственные интегралы с переменной особенностью.
4. Свертка, фундаментальное решение и обобщенные функции в многомерном случае.
ГЛАВА XVIII. РЯД ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
§ 1. Основные общие представления, связанные с понятием ряда Фурье
2. Коэффициенты Фурье.
3. Ряд Фурье.
4. Об одном важном источнике ортогональных систем функций в анализе.
§ 2. Тригонометрический ряд Фурье
2. Исследование поточечной сходимости тригонометрического ряда Фурье.
3. Гладкость функции и скорость убывания коэффициентов Фурье.
4. Полнота тригонометрической системы
§ 3. Преобразование Фурье
2. Регулярность функции и скорость убывания ее преобразования Фурье.
3. Важнейшие аппаратные свойства преобразования Фурье.
4. Примеры приложений.
ГЛАВА XIX. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ
§ 1. Асимптотическая формула и асимптотический ряд
2. Общие сведения об асимптотических рядах.
3. Степенные асимптотические ряды.
§ 2. Асимптотика интегралов (метод Лапласа)
2. Принцип локализации для интеграла Лапласа.
3. Канонические интегралы и их асимптотика.
4. Главный член асимптотики интеграла Лапласа.
5. Асимптотические разложения интегралов Лапласа.
ЛИТЕРАТУРА
УКАЗАТЕЛЬ ОСНОВНЫХ ОБОЗНАЧЕНИЙ

ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ РЕШЕНИЙ ОСНОВНЫХ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ | Горбачёв

1. Ломакин В. А. Теория упругости неоднородных тел. М.: Изд-во МГУ, 1976. 367 с.

2. Чепмен С., Каулинг Т. Математическая теория неоднородных газов.Перевод с английского Е.В. Малиновской под редакцией академика H.H. Боголюбова. М.: Иностранная литература, 1960. 511 с.

3. Боголюбов Н. Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1963. 412 с.

4. Марченко В. А., Хруслов Е. Я. Краевые задачи в областях с мелкозернистой границей. Киев: Наукова думка, 1974. 416 с.

5. Бердичевский В. Л. Вариационные принципы механики сплошной среды. М.: Наука. 1983. 448 с.

6. Бахвалов Н.С., Панасенко Г. П. Осредненние процессов в периодических средах. М.: Наука, 1984. 352 с.

7. Победря Б. Е. Механика композиционных материалов. М.: Изд-во МГУ, 1984. 336 с.

8. Санчес-Паленсия Э. Неоднородные среды и теория колебаний. М.: Мир, 1984. 472 с.

9. Шкиль Н. И., Вороной А. Н, Лейфура В. Н. Асимптотические методы в дифференциальных и интегро-дифференциальных уравнениях. Киев: Вища школа, 1985. 248 с.

10. Андрианов И. В., Лесничая В. А., Маневич Л. И. Метод усреднения в статике и динамике ребристых оболочек. М.: Наука, 1985. 221 с.

11. Олейник О. А., Иосифьян Г. А., Шамаев А. С. Математические задачи теории сильно неоднородных сред. М.: Изд-во МГУ, 1990. 311 с.

12. Kalamkarov A. L. Composite and reinforced elements of construction. Baffins Lane, Chechester,West Sussex PO19, England.: John wiley & Sons Ltd. 1992.286 c.

13. Жиков В. В., Козлов С. М., Олейник О. А. Усреднение дифференциальных операторов. М.: ФИЗМАТЛИТ, 1993. 462 с.

14. Levinski T., Telega J. J. Plates, Laminates and shells. Asymptotic Analysis and Homogenization. N.J.: World Scientific Publishing Co, 2000. 739 c.

15. Бардзокас Д. И., Зобнин А. И. Математическое моделирование физических процессов в композиционных материалах периодической структуры. М.: Едиториал УРСС. 2003. 376 c.

16. Колпаков А. Г. Композиционные материалы и элементы конструкций с начальными напряжениями. Новосибирск: Издательство СО РАН, 2007. 254 с.

17. Большаков В. И., Андрианов И. В., Данишевский В. В. Асимптотические методы расчета композитных материалов с учетом внутренней структуры. Днепропетровск: Пороги. 2008. 197 с.

18. Левин В. А., Лохин В. В., Зингерман К. М. Об одном способе оценки эффективных характеристик пористых тел при конечных деформациях // Известия РАН. Механика твердого тела, 1997. № 4. С. 45–50.

19. Левин В. А., Лохин В. В., Зингерман К. М. О построении эффективных определяющих соотношений для пористых упругих материалов при конечных деформациях и их наложении // Доклады РАН. 2002.Т. 382. № 4. С. 482–487.

20. Победря Б. Е. Численные методы в теории упругости и пластичности. М.: Изд-во МГУ. 1995. 366 с.

21. Зубчанинов В. Г. Основы теории упругости и пластичности. М.: Высшая школа. 1990. 368 с.

22. Морозов Е. М., Левин В. А., Вершинин А. В. Прочностной анализ. ФИДЕСИС в руках инженера. М.: ЛЕНАНД, 2015.

23. Архипов Г. И., Садовничий В. А., Чубариков В. Н. Лекции по математическому анализу. М.: Высшая школа. 1999. 695 с.

24. Гельфанд И. М., Шилов Г. Е. Обобщенные функции и действия над ними. Изд.2. М.: Физматгиз, 1959. 470 с.

25. Кеч В., Теодореску П. Введение в теорию обобщенных функций с приложениями в технике. М.: Мир, 1978. 518 с.

26. Соболев С. Л. Уравнения математической физики. М.: Наука, 1966. 443 с.

27. Владимиров В. С. Обобщенные функции в математической физике. М.: Наука, 1976. 280 с.

28. Новацкий В. Теория упругости. М.: Мир, 1975. 872 с.

29. Горбачев В. И. О распространении тепла в неоднородном стержне с переменным поперечным сечением // Вестник Московского университета. Математика. Механика. 2017. №2. С. 48–54.

30. Gorbachev V. I. Integral formulas in electromagnetic elasticity of heterogeneous bodies. application in the mechanics of composite materials // Composites: Mechanics, Computations, Applications. An International J. // 2017. V. 8. № 2. С. 147–170.

31. Горбачев В. И. О собственных частотах продольных колебаний неоднородного стержня с переменным поперечным сечением // Вестник Московского университета. Математика. Механика. 2016. №1. С. 31–39.

32. Горбачев В. И. Интегральные формулы в связанной задаче термоупругости. Применение в механике композитов // Прикладная математика и механика. 2014. Т.78. № 2. С. 277–299.

33. Горбачев В. И., Москаленко О. Б. Устойчивость стержней с переменной жесткостью при сжатии распределенной нагрузкой // Вестник Московского университета.

Математика. Механика. 2012. №2. С. 41–47.

34. Горбачев В. И. Динамические задачи механики композитов // Известия РАН. Серия физическая. 2011. Т. 75. № 1. С. 117–122.

35. Горбачев В. И. О колебаниях в неоднородном упругом теле. Упругость и неупругость. Материалы Международного научного симпозиума по проблемам механики деформируемых тел, посвященного 100-летию со дня рождения А.А. Ильюшина. Москва, 20-21 января 2011 г. М.: Изд-во МГУ. 2011. С. 319–326.

36. Горбачев В. И. Интегральные формулы в симметричной и несимметричной упругости // Вестник Московского университета. Математика. Механика. 2009. №6. C. 52–56.

37. Архангельский А. Ф., Горбачев В. И. Эффективные характеристики гофрированных пластин // Изв. РАН МТТ. 2007. № 3. С. 137–155

38. Горбачев В. И. Метод тензоров Грина для решения краевых задач теории упругости неоднородных сред // Вычислительная механика деформируемого твердого тела. 1991. № 2. 61–76.

39. Бреббия К., Теллес Ж., Вроубел Л. Методы граничных элементов. М.: Мир, 1987.

40. Олехова Л. В. Кручение неоднородного анизотропного стержня. Диссертация кандидата физико-математических наук. Master’s thesis, МГУ им. М.В. Ломоносова, Механико-математический факультет, 2009.

41. Емельянов А. Н. Эффективные характеристики в моментной теории упругости. Диссертация кандидата физико-математических наук. Master’s thesis, МГУ им. М.В. Ломоносова, Механико-математический факультет, 2016.

Основные формулы интегрирования — Math Insight версия суммирования

. Но, как это ни парадоксально, часто интегралы вычисляются , рассматривая интегрирование как операцию, обратную по отношению к дифференцированию . (Этот факт представляет собой так называемую Фундаментальную теорему исчисления
.)

Обозначение, на котором мы остановились по историческим причинам, столь же своеобразна, как и обозначение производных: интеграл от функция $f(x)$ относительно $x$ записывается как $$\int f(x)\;dx$$

Замечание о том, что интегрирование является (почти) обратной операцией дифференциация означает, что если $${d\over dx}f(x)=g(x)$$ затем $$\int g(x)\;dx=f(x)+C$$ Дополнительный $C$, называемый константой интегрирования , на самом деле необходимо, так как после всякого дифференцирования уничтожаются константы, которые вот почему интеграция и дифференциация не 92} \; dx&=\arctan x+C \end{align*}

А поскольку производная суммы есть сумма производных, то интеграл от суммы есть сумма интегралов: $$ \int f(x)+g(x)\;dx=\int f(x)\;dx+\int g(x)\;dx$$ И точно так же константы «проходят» знак интеграла: $$\int c\cdot f(x)\;dx=c\cdot \int f(x)\;dx$$

Например, многочлены легко интегрировать даже включая такие термины, как $\sqrt{x}$ и более общие степенные функции. {3/2} \более 3/2}+3\ln x+C$$ Обратите внимание, что нам нужно включить только одну «константу интегрирования». 92 }}\; дх=?$

Формулы интегрирования — список интегральных формул, примеры и часто задаваемые вопросы

Формулы интегрирования — это основные формулы, которые используются для решения различных интегральных задач. Они используются для нахождения интегрирования алгебраических выражений, тригонометрических отношений, обратных тригонометрических функций, а также логарифмических и экспоненциальных функций. Интегрирование — это процесс, обратный дифференцированию, т. е. если d/dx (y) = z, то ∫z×dx = y. Эти формулы интегрирования очень полезны для нахождения интегрирования различных функций.

Давайте подробно узнаем об этих интегральных формулах в этой статье.

Интегральное исчисление

Интегральное исчисление — это раздел исчисления, который занимается теорией и приложениями интегралов. Процесс нахождения интегралов называется интегрированием. Интегральное исчисление помогает найти первообразные функции. Антипроизводные также называют интегралами функции. Обозначается ∫ f(x)dx. Интегральное исчисление имеет дело с общей величиной, такой как длины, площади и объемы. Интеграл можно использовать для нахождения приближенных решений некоторых уравнений по заданным данным. Интегральное исчисление включает два типа интегрирования: 

  • Неопределенный Интеграл
  • Определенный интеграл

Что такое формулы интегрирования?

Формулы интегрирования представлены в виде следующих наборов формул. Формулы включают базовые формулы интегрирования, интегрирование тригонометрических отношений, обратные тригонометрические функции, произведение функций и некоторые расширенные наборы формул интегрирования. По сути, интеграция — это способ объединения частей для получения целого. Это обратная операция дифференцирования. Таким образом, основная формула интегрирования равна 

∫ f'(x) dx = f(x) + C.  

Используя это, выводятся следующие формулы интегрирования.

Различные формулы интегрального исчисления:

  1. d/dx {φ(x)} = f(x)  <=> ∫f(x) dx = φ(x) + C + C, n ≠ -1
  2. ∫(1/x) dx = log e |x| + C
  3. ∫e x dx = e x + C
  4. ∫a x dx = (a x / log e a) + C

    8 в статье

    Примечание

    • d/dx [∫f(x) dx] = f(x)
    • ∫k . f(x) dx = k ∫f(x) dx , где k — константа
    • ∫{f(x) ± g(x)} dx = ∫f(x) dx  ± ∫g(x) dx

    Основные формулы интегрирования

    Некоторые из основных формул интегрирования, которые используются для решения задач интегрирования, обсуждаются ниже. Они выводятся из основной теоремы интегрирования.

    • ∫ 1 dx = x + C
    • ∫ x n dx = x (n + 1) /(n + 1)+ C
    • ∫ 1/x dx = log |x| + C
    • ∫ e ​​ x dx = e x + C
    • ∫ a x dx = a x /log a+ C
    • ∫ 9 x 9009 [f(f 9 x 9009) x)] dx = e x f(x) + C   {где f'(x) = d/dx[f(x)]}

    Формулы интегрирования тригонометрических функций

    Формулы интегрирования тригонометрических функций используется для решения интегральных уравнений с участием тригонометрических функций. Список интегральных формул с участием тригонометрических и обратных тригонометрических функций приведен ниже,

    • ∫ cos x dx = sin x + C
    • ∫ sin x dx = -cos x + C
    • ∫ sec 2 x dx = tan x + C
    • ∫ dx cot = cosec 2 x + C
    • ∫ sec x tan x dx = sec x + C
    • ∫ cosec x cot x dx = -cosec x + C
    • ∫ tan x dx = log |sec x| + C
    • ∫ кроватка x dx = log |sin x| + C
    • ∫ сек х dx = log | сек х + тангенс х | + C
    • ∫ cosec x dx = log |cosec x – cot x| + C

    Формулы интегрирования обратных тригонометрических функций

    Различные формулы интегрирования обратных тригонометрических функций, которые используются для решения интегральных задач, приведены ниже: /√(1 – x 2 ) dx = cos -1 x + C

  5. ∫1/(1 + x 2 ) dx = tan -1 x + C
  6. ∫ -1/( 1 + x 2 ) dx = кроватка -1 x + C
  7. ∫ 1/x√(x 2 – 1) dx = sec -1 x + C
  8. ∫ -1/x√(x 2 – 1) dx = cosec -1 x + C

    9. Расширенные формулы интегрирования

    Некоторые другие расширенные формулы интегрирования, которые имеют большое значение для решения интегралов, обсуждаются ниже.

    • ∫1/(x 2 – a 2 ) dx = 1/2a log|(x – a)(x + a| + C
    • ∫ 1/(a 2 – x 2 ) dx = 1/2a log|(a + x)(a – x)| + C
    • ∫1/(x 2 + a 2 ) dx = 1/a tan -1 x/a + C
    • ∫1/√(x 2 – a 2 )dx = log |x +√(x 2 – a 2 )| + C
    • ∫ √(x 2 – a 2 ) dx = x/2 √(x 2 – a 2 ) -a 2

      /2 log |x + 0 √ 9 – а 2 )| + C

    • ∫1/√(a 2 – x 2 ) dx = sin -1 x/a + C
    • ∫√(a 2 – x 2 ) 2 √(a 2 – x 2 ) dx + a 2 /2 sin -1 x/a + C
    • ∫1/√(x 2 + a 2 ) dx = log |x + √(x 2 + a 2 )| + C
    • ∫ √(x 2 + a 2 ) dx = x/2 √(x 2 + a 2 )+ a 2

      /2 log(x + 0 √ 9 + 2 )| + C

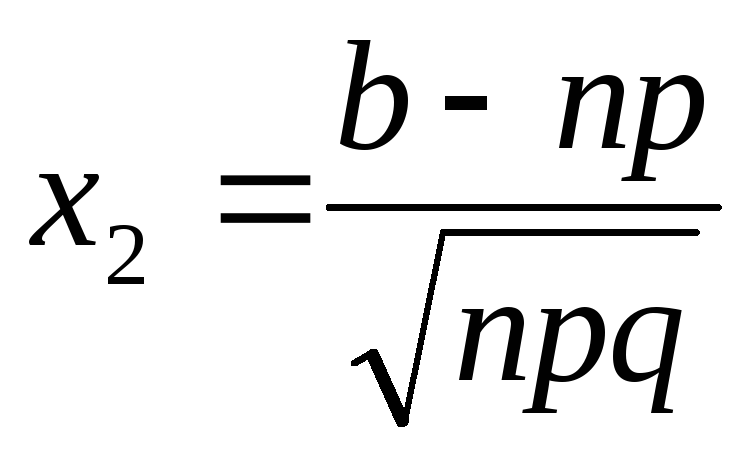
    Различные формулы интегрирования

    Различные методы интегрирования используются для решения различных типов интегральных вопросов. Каждый метод является стандартным результатом и может рассматриваться как формула. Некоторые из важных методов обсуждаются ниже в этой статье. Давайте проверим три важных метода интеграции.

    • Интегрирование по формуле частей
    • Интегрирование по формуле подстановки
    • Интегрирование по формуле частных дробей

    Интегрирование по формуле частей

    Интегрирование по частям Формула применяется, когда данная функция легко описывается как произведение двух функций. Формула интегрирования по Частям, используемая в математике, приведена ниже:

    ∫ f(x) g(x) dx = f(x) ∫g(x) dx – ∫ (∫f'(x) g(x) дх) дх + С

    Пример: вычислить ∫ xe x dx

    Решение:

    ∫ xe x dx имеет вид ∫ xe x dx = 5 f2 x 9x 0 g(x)0 и g(x) = e x

    мы знаем, что ∫ f(x) g(x) dx = f(x) ∫g(x) dx – ∫ (∫f'(x) g(x) DX) DX + C

    ∫ XE x DX = x ∫e x DX — ∫ (1 ∫E x DX) DX + C

    = XE x — E X + C x — E x + C

    x — E x + C

    x — E x + C

    x — E x + C

    x — E

    Для получения дополнительной информации проверьте эту интеграцию по частям

    Интегрирование по формуле подстановки

    Интегрирование по формуле подстановки применяется, когда функция является функцией другой функции. т. е. пусть I = ∫ f(x) dx, где x = g(t) такое, что dx/dt = g'(t), тогда dx = g'(t)dt

    Теперь I = ∫ f( x) dx = ∫ f(g(t)) g'(t) dt

    Пример: вычислить ∫ (4x +3) 3 dx

    Решение: 4x+3) ⇒ du = 4 dx

    ∫ (4x +3) 3 dx

    = 1/4 ∫(u) 3 du

    = 1/4. U 4 /5

    = U 4 /20

    = 4x +3) 4 /20

    Для более подробной информации проверьте эту интеграцию с помощью Formula

    . Формула частных дробей используется, когда требуется интеграл от P(x)/Q(x), а P(x)/Q(x) является неправильной дробью, так что степень P(x)

    < степени Q( x), то дробь P(x)/Q(x) записывается как

    P(x)/Q(x) = R(x) + P 1 (x)/ Q(x), 

    , где R(x) — полином от x и P 1 (x) / Q(x) — правильная рациональная функция.

    Теперь интегрирование R(x) + P 1 (x)/Q(x) легко вычисляется.

    Подробнее см. Интегрирование дробей

    Также см.

    • Неопределенные интегралы
    • Интегрирование тригонометрических функций
    9006 Примеры интегрирования формул0067

    Example 1: Evaluate

    • ∫ x 6 dx  
    • ∫1/x 4 dx  
    • ∫ 3 √x dx  
    • ∫3 x dx  
    • ∫4e x dx  
    • ∫(sin x/cos 2 x) dx  
    • ∫(1/sin 2 x) dx 
    • ∫[1/ √(4 – x 2 )] dx  
    • ∫ [1 /3√ (x 2 — 9)] DX
    • ∫ (1 /cos x tan x) DX

    Решение:

    (I) ∫x 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 68 6. ​​

    :

    . dx  

    = (x 6+1 )/(6 + 1) + C        [∫x n dx = {x n+1 /(n+1)} + C    n 1]

    = (x 7 /7) + C

    (II) ∫1 /x 4 DX

    = ∫x -4 DX [∫X

    = ∫X -4 DX 0098 n dx = {x n+1 /(n+1)} + C    n ≠ -1]

    = (x -4+1 )/(-4 + 1) + C

    = -(x -3 /3) + C

    = -(1 / 3x 3 ) + C

    (III) ∫ 3 √x DX

    = ∫x 1199 a /3 dx                    [∫x n dx = {x n+1 /(n+1)}+ C    n ≠ -1]

    +1 (x +1) ((1/3)+ 1) + С

    = х 4/3 / (4/3) + С

    = (3/4) (x 4/3 ) + C

    (IV) ∫3 x DX

    = C (3 x /log E 3) + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C. [ ∫a x dx = (a x / log e a) + C]                                            

    (v) ∫4e x dx  

    = 4∫e x dx [∫к. f(x) dx = k f(x) dx , где k — константа]

    = 4 E x + C [∫E x DX = E x + C]

    (VI) ∫ (SIN X/COS 2 X) DX

    = ∫ ∫ ∫ ∫ ∫ x 2 x) DX

    = ∫ x. (sin x/cos x) .(1/cos x)] dx

    = ∫tan x . Sec X DX [∫TAN X .SEC X DX = SEC X + C]

    = SEC X + C

    (VII) ∫ (1/SIN 2 X) DX

    = ∫COSEC 2 x dx               [∫cosec 2 x dx  = -cot x + C ]

    = -cot x  + C

    (viii) ∫[1/√(4 – x 2 )] dx  

    = ∫[1/√(2 9 0 9 9 9 9 8 2 9 909) ] dx      [мы знаем, что dx = sin -1 (x/a) + C]

    = sin -1 (x/2) + C

    (ix) ∫[1/{ 3√(x 2 – 9)}] dx

    = ∫[1/{3√(x 2 – 3 2 )}] dx   [мы знаем, что dx = (1/a) сек -1 (x/a) + C]

    = (1/3)сек -1 (x/3) + C

    (x) ∫(1 /cos x tan x) dx  

    = ∫[cos x /(cos x sin x)] dx

    = ∫(1/ sin x ) dx

    = ∫cosec x dx                 [мы знаем, что ∫cosec x dx =  log |cosec x – cot x| + C]

    = log |cosec x – cot x| + C

    Example 2: Evaluate ∫{e 9log e x + e 8log e x }/{e 6log e x + e 5log e x } dx

    Solution:

      Since, e alog e x = x a

    ∫{e 9log e x + e 8log e x }/{e 6log e x + E 5log E x } DX

    = ∫ {x 9 + X 8 }/{x 6 + X 5 }/{x 6 + X 5 }/{x 6 + X 5 }/{x 6 + 5 }/{x 6 + 5 }. x 8 (x + 1)] /[x 5 (x + 1)] DX

    = ∫ x 8 /x 5 DX

    = ∫x 3 DX [Мы знаете что ∫x n dx = {x n+1 /(n+1)} + C    n ≠ -1]

    = (x 4 /4) + C

    Пример 3: Оценка ∫ sin x + cos x dx

    Решение:

    ∫ (sin x + cos x) dx

    = ∫sin x dx + ∫cos x dx [We Know что ∫{f(x) ± g(x)} dx = ∫f(x) dx ± ∫g(x) dx]         

    = -cos x + sin x + C                   [мы знаем, что ∫sin x dx = -cos x + C, ∫cos x dx = sin x + C ]

    0069 Решение:

    ∫4 x+2 dx = ∫4 x . 4 2 дх

    = ∫16. 4 x DX [Мы знали, что ∫K.f (x) dx = k∫f (x) dx, где k постоянна]

    = 16∫ 4 x DX [∫A x DX = (a x / log e a) + C]

    = 16 (4 x /log 4) + C

    дх

    Решение:

    ∫ (x 2 + 3x + 1) DX

    = ∫X 2 DX + 3∫x DX + 1∫ x 0 DX DX DX DX DX DX DX . , ∫x n dx = {x n+1 /(n+1)}+ C n ≠ -1]

    = [x 2+1 /2+1] + 3[[x 1+1 /1+1]] + [х 0+1 /0+1] + С

    = [х 3 /3] + 3[х 2 /2] + х + C

    Пример 6. Вычисление ∫[4/(1 + cos 2x)] dx

    Решение:

    1 + cos 2x = 2cos 2 x

    ∫ [4/(1 + cos 2x)] DX

    = ∫ (4/(2Cos 999999999999999999999 гг. x)] DX

    = ∫ (2/cos 2 x) DX

    = ∫2 с 2 XDX

    = 2∫SEC 2 X DX [мы знаем, что, ∫SEC 2 x dx = tan x + C ]

    = 2 tan x + C 

    Пример 7. Вычисление ∫(3cos x – 4sin x + 5 sec 2 x) DX

    Решение:

    ∫ (3COS x — 4SIN x + 5 Sec 2 X) DX

    = ∫3COS x DX — ∫4SIN xsin xsin xsin xsin xsin xsin xsin x. 2 x dx    [∫k.f(x) dx = k ∫f(x) dx, где k – константа]

    =  3∫cos x dx – 4∫sin x dx + 5∫sec 2 x dx

    = 3sin x – 4(-cos x) + 5 tan x + C

    = 3sin x + 4cos x + 5 tan x + C

    Часто задаваемые вопросы по формулам интегрирования

    Вопрос 1: Что означает интеграция в математике?

    Ответ:

    Если производная функции g(x) равна f(x), то интегрирование f(x) равно g(x), т. е. ∫f(x)dx = g(x)

    Интегрирование представлено символом « ∫ »

    Вопрос 2: Как мы интегрируем, используя формулы интегрирования?

    Ответ:

    Интеграция может быть достигнута с помощью формул,

    • Определить небольшую часть объекта в определенных измерениях, которые путем бесконечного сложения образуют полный объект.
    • Используя формулы интегрирования для этой небольшой части по разным измерениям, мы получим полный объект.

      No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *