Метод непосредственного интегрирования, формулы и примеры решений
Определение
Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
Таким образом, алгоритм действий следующий:
- тождественное преобразование подынтегральной функции;
- применение свойств неопределенного интеграла: вынесение константы за знак интеграла, представление интеграла от суммы функций в вид суммы интегралов;
- использование таблицы интегралов.
В простейших примерах для применения непосредственного интегрирования достаточно разложить подынтегральную функцию на слагаемые и постоянные величины вынести за знак интеграла.
При определенной практике интегрирования обычно эти действия проводят устно, записывая лишь результат интегрирования.
Пример
Задание. {2} x d x=\operatorname{tg} x-x+C$
{2} x d x=\operatorname{tg} x-x+C$
Читать дальше: интегрирование внесением под дифференциал.
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | |||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Поделиться:
 | ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||
6.3 Площадь и определенный интеграл – методы исчисления 1
Перейти к содержимому
Цели обучения
- Дать определение определенного интеграла.

- Объясните термины подынтегральная функция, пределы интегрирования и переменная интегрирования.
- Объясните, когда функция интегрируема.
- Опишите связь между определенным интегралом и чистой площадью.
- Используйте геометрию и свойства определенных интегралов для их вычисления. 9{*})\text{Δ}x.$$
Однако это определение имело ограничения. Мы требовали, чтобы [latex]f(x)[/latex] был непрерывным и неотрицательным. К сожалению, реальные проблемы не всегда соответствуют этим ограничениям. В этом разделе мы рассмотрим, как применить понятие площади под кривой к более широкому набору функций посредством использования определенного интеграла.
Определение и обозначения
Определенный интеграл l обобщает понятие площади под кривой. Мы отменяем требования непрерывности и неотрицательности [latex]f(x)[/latex] и определяем определенный интеграл следующим образом. 9{*})\text{Δ}x,$$
при условии существования предела.
 Если этот предел существует, то функция [latex]f(x)[/latex] называется интегрируемой на [latex]\left[a,b\right],[/latex] или является интегрируемой функцией.
Если этот предел существует, то функция [latex]f(x)[/latex] называется интегрируемой на [latex]\left[a,b\right],[/latex] или является интегрируемой функцией.Символ интеграла в предыдущем определении должен показаться вам знакомым. Мы встречали похожие обозначения в главе о применении производных, где мы использовали символ неопределенного целого числа (без [латекс]а[/латекс] и [латекс]b[/латекс] выше и ниже) для обозначения первообразной. Хотя обозначения неопределенных интегралов могут выглядеть аналогично обозначениям определенных интегралов, они не совпадают. Определенный интеграл – это число. Неопределенный интеграл — это семейство функций. Позже в этой главе мы рассмотрим, как связаны эти понятия. Однако всегда следует уделять пристальное внимание обозначениям, чтобы мы знали, работаем ли мы с определенным интегралом или с неопределенным интегралом.
Интегральное представление восходит к концу семнадцатого века и является одним из вкладов Готфрида Вильгельма Лейбница, которого часто считают одним из первооткрывателей исчисления наряду с Исааком Ньютоном.
 Символ интегрирования ∫ представляет собой удлиненную букву S, что указывает на сигму или суммирование. В определенном интеграле выше и ниже символа суммы находятся границы интервала [латекс]\слева[а,б\справа].[/латекс] Числа [латекс]а[/латекс] и [латекс]b [/latex] являются [latex]x[/latex]-значениями и называются пределами интегрирования; в частности, [латекс]а[/латекс] — нижний предел, а [латекс]b[/латекс] — верхний предел. Чтобы уточнить, мы используем слово ограничивают двумя разными способами в контексте определенного интеграла. Во-первых, мы говорим о пределе суммы как [latex]n\to \infty .[/latex] Во-вторых, границы области называются пределами интегрирования .
Символ интегрирования ∫ представляет собой удлиненную букву S, что указывает на сигму или суммирование. В определенном интеграле выше и ниже символа суммы находятся границы интервала [латекс]\слева[а,б\справа].[/латекс] Числа [латекс]а[/латекс] и [латекс]b [/latex] являются [latex]x[/latex]-значениями и называются пределами интегрирования; в частности, [латекс]а[/латекс] — нижний предел, а [латекс]b[/латекс] — верхний предел. Чтобы уточнить, мы используем слово ограничивают двумя разными способами в контексте определенного интеграла. Во-первых, мы говорим о пределе суммы как [latex]n\to \infty .[/latex] Во-вторых, границы области называются пределами интегрирования .Мы называем функцию [latex]f(x)[/latex] подынтегральной функцией , а dx указывает, что [latex]f(x)[/latex] является функцией относительно [latex]x [/latex], называемая переменной интегрирования . Обратите внимание, что, как и индекс в сумме, переменная интегрирования является фиктивной переменной и не влияет на вычисление интеграла.
 Мы можем использовать любую переменную, которая нам нравится, в качестве переменной интегрирования: 9{*})\text{Δ}x[/latex] существует и является уникальным. Это приводит к следующей теореме, которую мы сформулируем без доказательства.
Мы можем использовать любую переменную, которая нам нравится, в качестве переменной интегрирования: 9{*})\text{Δ}x[/latex] существует и является уникальным. Это приводит к следующей теореме, которую мы сформулируем без доказательства.Непрерывные функции интегрируемы
Если [latex]f(x)[/latex] непрерывен на [latex]\left[a,b\right],[/latex], то [latex]f[/latex] ] интегрируема на [латексе]\слева[а,б\справа].[/латекс]
в зависимости от характера разрывов. Например, интегрируемы функции с конечным числом скачков на отрезке.
Здесь также стоит отметить, что мы сохранили использование регулярного разбиения в суммах Римана. Это ограничение не является строго необходимым. Любое разбиение можно использовать для формирования суммы Римана. Однако, если для определения определенного интеграла используется нерегулярное разбиение, недостаточно принять предел, поскольку количество подынтервалов стремится к бесконечности. Вместо этого мы должны принять предел, поскольку ширина наибольшего подынтервала стремится к нулю.
 Это вводит немного более сложные обозначения в наши пределы и усложняет вычисления, не получая при этом особого дополнительного понимания, поэтому мы придерживаемся регулярных разбиений для сумм Римана.
Это вводит немного более сложные обозначения в наши пределы и усложняет вычисления, не получая при этом особого дополнительного понимания, поэтому мы придерживаемся регулярных разбиений для сумм Римана.Вычисление определенных интегралов
Вычисление определенных интегралов таким способом может быть довольно утомительным из-за сложности вычислений. Далее в этой главе мы разработаем методы вычисления определенных интегралов без ограничения сумм Римана. Однако пока мы можем полагаться на тот факт, что определенные интегралы представляют площадь под кривой, и мы можем вычислить определенные интегралы, используя геометрические формулы для вычисления этой площади. Мы делаем это, чтобы подтвердить, что определенные интегралы действительно представляют площади, поэтому мы можем затем обсудить, что делать в случае, когда кривая функции опускается ниже оси [латекс]х[/латекс]. 9{*})\text{Δ}x=(\text{Площадь прямоугольников над осью}\;x\text{-})-(\text{Площадь прямоугольников под осью}\;x\text{- })$$
Рисунок 6. 11 Для частично отрицательной функции сумма Римана равна площади прямоугольников над осью x за вычетом площади прямоугольников под осью x.
11 Для частично отрицательной функции сумма Римана равна площади прямоугольников над осью x за вычетом площади прямоугольников под осью x.Подробное описание: восемь прямоугольников нарисованы равномерно на [0,2] с высотой, определяемой значением функции в левых конечных точках каждого.
Принимая предел как [latex]n\to \infty ,[/latex] сумма Римана приближается к площади между кривой над осью [latex]x[/latex] и [latex]x[/latex] -ось за вычетом площади между кривой под осью [latex]x[/latex] и осью [latex]x[/latex], как показано на (рис. 6.12). Затем 9{2}f(x)dx\hfill & =\underset{n\to \infty }{\text{lim}}\underset{i=1}{\overset{n}{\text{∑}}}f ({c}_{i})\text{Δ}x\hfill \\ & ={A}_{1}-{A}_{2}.\hfill \end{array}$$
Количество [latex]{A}_{1}-{A}_{2}[/latex] называется чистой подписанной областью .
Рисунок 6.12 В пределе определенный интеграл равен площади [латекс]А1[/латекс] минус площадь [латекс]А2[/латекс] или чистой площади со знаком.
Подробное описание: Область в первом квадранте под кривой выделена синим цветом и помечена A1. Область в четвертом квадранте над кривой и слева от x=2 заштрихована синим цветом и помечена как A2.
Обратите внимание, что чистая область со знаком может быть положительной, отрицательной или нулевой. Если площадь над осью [latex]x[/latex] больше, чистая область со знаком положительна. Если площадь под осью [latex]x[/latex] больше, чистая область со знаком будет отрицательной. Если области выше и ниже оси [latex]x[/latex] равны, чистая область со знаком равна нулю.
Общая площадь
Одним из применений определенного интеграла является нахождение смещения по заданной функции скорости. Если [latex]v(t)[/latex] представляет скорость объекта как функцию времени, то площадь под кривой говорит нам, насколько далеко объект находится от своего исходного положения. Это очень важное применение определенного интеграла, и мы рассмотрим его более подробно далее в этой главе.
Рисунок 6.13 Площадь под кривой [latex]v(t)=75[/latex] показывает, насколько далеко автомобиль находится от начальной точки в данный момент времени. А пока мы просто рассмотрим некоторые основы, чтобы понять, как это работает, изучая постоянные скорости. 9{2}75dt=150.$$
А пока мы просто рассмотрим некоторые основы, чтобы понять, как это работает, изучая постоянные скорости. 9{2}75dt=150.$$Подробное описание: Область под линией v(t) = 75 закрашена синим цветом над [0,2].
В контексте смещения чистая площадь со знаком позволяет учитывать направление. Если автомобиль движется прямо на север со скоростью 60 миль в час в течение 2 часов, он находится на 120 миль к северу от своего начального положения. Если затем автомобиль развернется и поедет на юг со скоростью 40 миль в час в течение 3 часов, он вернется в исходное положение ((Рисунок 6.14)). Опять же, используя интегральное обозначение, мы имеем 9{5}-40dt\hfill & =120-120\hfill \\ & =0.\hfill \end{array}$$
В этом случае смещение равно нулю.
Рисунок 6.14 Площадь над осью и площадь под осью равны, поэтому чистая площадь со знаком равна нулю.
Подробное описание: Первая часть графика — это линия v(t) = 60 на [0,2], а область под линией в первом квадранте заштрихована. Вторая часть графика представляет собой линию v(t) = -40 над [2,5], а область над линией в четвертом квадранте заштрихована.
Предположим, мы хотим узнать, как далеко проезжает машина в целом, независимо от направления. В этом случае мы хотим знать площадь между кривой и осью [latex]x[/latex] независимо от того, находится ли эта область выше или ниже оси. Это называется общей площадью .
Графически проще всего представить общую площадь путем сложения площадей над осью и площадей под осью (вместо вычитания площадей под осью, как мы сделали с чистой площадью со знаком). Чтобы выполнить это математически, мы используем функцию абсолютного значения. Таким образом, общий путь, пройденный автомобилем, равен 9{5}40dt\hfill \\ & =120+120\hfill \\ & =240.\hfill \end{array}$$
Формально объединяя эти идеи, мы формулируем следующие определения.

Определение
Пусть [latex]f(x)[/latex] будет интегрируемой функцией , определенной на интервале [latex]\left[a,b\right].[/latex] Пусть A 1 представляют собой область между [latex]f(x)[/latex] и осью [latex]x[/latex], лежащей на выше оси , и пусть A 9{b}|f(x)|dx={A}_{1}+{A}_{2}.$$
Свойства определенного интеграла
Свойства неопределенных интегралов относятся к определенным интегралам как хорошо. Определенные интегралы также обладают свойствами, относящимися к пределам интегрирования. Эти свойства вместе с правилами интегрирования, которые мы рассмотрим позже в этой главе, помогают нам манипулировать выражениями для вычисления определенных интегралов.
Правило: свойства определенного интеграла
- 9{b}f(x)dx$$
Хотя эта формула обычно применяется, когда [латекс]с[/латекс] находится между [латекс]а[/латекс] и [латекс]b[/латекс], формула верна для всех значения [latex]a[/latex], [latex]b[/latex] и [latex]c[/latex] при условии, что [latex]f(x)[/latex] интегрируем на наибольшем интервале.
Сравнительные свойства интегралов
Иногда изображение может рассказать о функции больше, чем результаты вычислений. Сравнение функций по их графикам, а также по их алгебраическим выражениям часто может дать новое представление о процессе интегрирования. Интуитивно можно сказать, что если функция [latex]f(x)[/latex] находится выше другой функции [latex]g(x),[/latex], то площадь между [latex]f(x)[/latex] ] и ось [latex]x[/latex] больше площади между [latex]g(x)[/latex] и осью [latex]x[/latex]. Это верно в зависимости от интервала, по которому производится сравнение. Свойства определенных интегралов справедливы, если [латекс]а Ь.[/латекс] Следующие свойства, однако, относятся только к случаю [латекс]а\ле Ь,[/латекс] и используются, когда мы хотим сравнить размеры интегралов. 9{b}f(x)dx\hfill \\ & \le M(b-a).\hfill \end{array}$$
Среднее значение функции
Нам часто нужно найти среднее значение набора чисел, например, средней оценки за тест. Предположим, вы получили следующие результаты тестов на уроке алгебры: 89, 90, 56, 78, 100 и 69. Ваша оценка за семестр — это среднее значение результатов тестов, и вы хотите знать, какую оценку ожидать. Мы можем найти среднее значение, сложив все баллы и разделив их на количество баллов. В этом случае имеется шесть тестовых баллов. Таким образом,
Предположим, вы получили следующие результаты тестов на уроке алгебры: 89, 90, 56, 78, 100 и 69. Ваша оценка за семестр — это среднее значение результатов тестов, и вы хотите знать, какую оценку ожидать. Мы можем найти среднее значение, сложив все баллы и разделив их на количество баллов. В этом случае имеется шесть тестовых баллов. Таким образом,
$$\frac{89+90+56+78+100+69}{6}=\frac{482}{6}\примерно 80,33.$$
Таким образом, ваш средний балл за тест составляет приблизительно 80,33, что переводится как B− в большинстве школ.
Предположим, однако, что у нас есть функция [latex]v(t)[/latex], которая дает нам скорость объекта в любое время [latex]t[/latex], и мы хотим найти среднюю скорость объекта скорость. Функция [latex]v(t)[/latex] принимает бесконечное число значений, поэтому мы не можем использовать только что описанный процесс. К счастью, мы можем использовать определенный интеграл, чтобы найти 9{b}f(x)dx.$$
License
Techniques of Calculus 1 Ларри Мусолино находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.

 Шпаргалки. Детский сад, Школа. / / Интегрирование функций. Понятие и основное свойство первообразной. Неопределенный интеграл. Правила интегрирования. Определенный интеграл. Формула Ньютона-Лейбница. Свойства геометрический и физический смысл определенного интеграла
Шпаргалки. Детский сад, Школа. / / Интегрирование функций. Понятие и основное свойство первообразной. Неопределенный интеграл. Правила интегрирования. Определенный интеграл. Формула Ньютона-Лейбница. Свойства геометрический и физический смысл определенного интеграла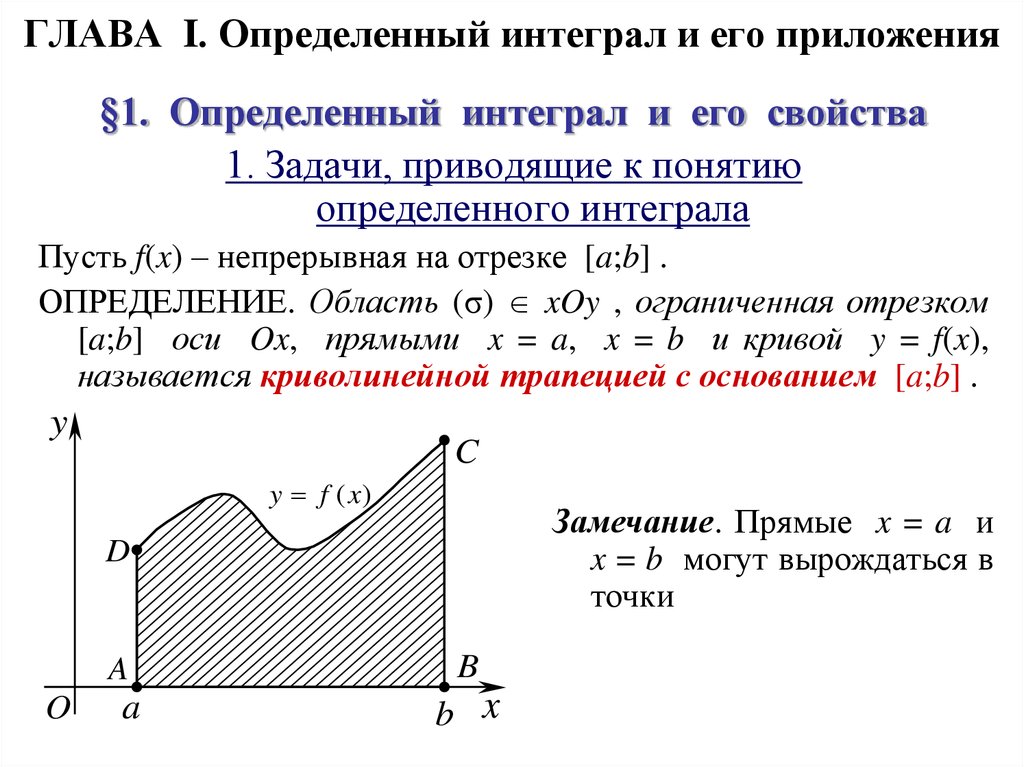
 Если этот предел существует, то функция [latex]f(x)[/latex] называется интегрируемой на [latex]\left[a,b\right],[/latex] или является интегрируемой функцией.
Если этот предел существует, то функция [latex]f(x)[/latex] называется интегрируемой на [latex]\left[a,b\right],[/latex] или является интегрируемой функцией.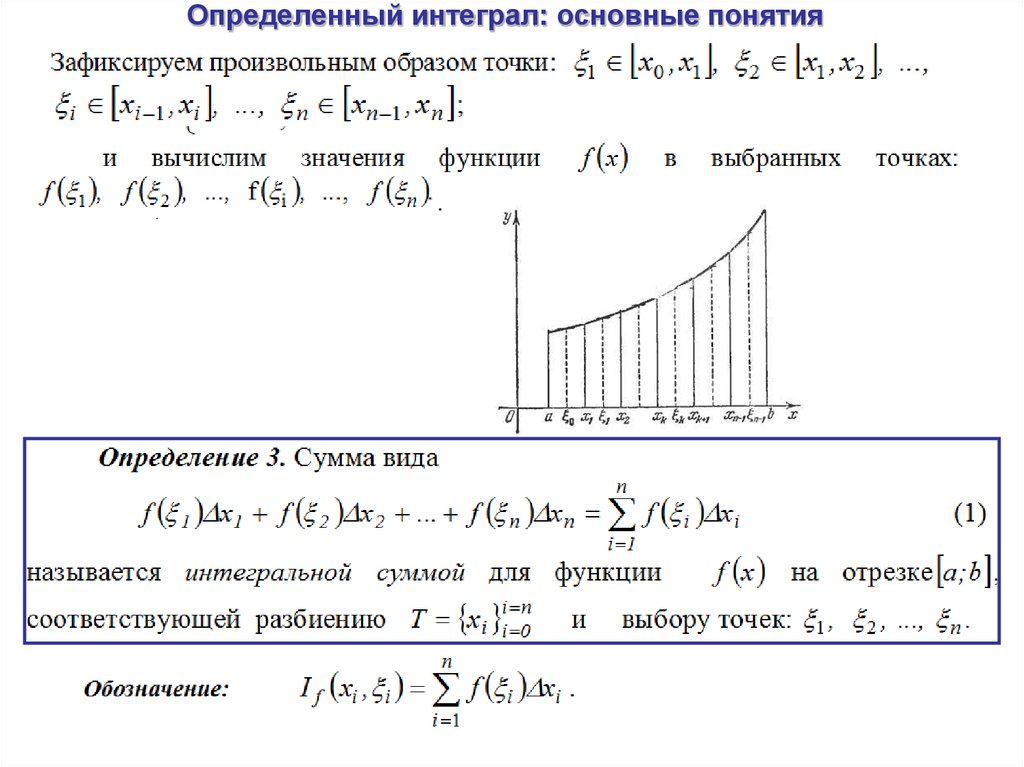 Символ интегрирования ∫ представляет собой удлиненную букву S, что указывает на сигму или суммирование. В определенном интеграле выше и ниже символа суммы находятся границы интервала [латекс]\слева[а,б\справа].[/латекс] Числа [латекс]а[/латекс] и [латекс]b [/latex] являются [latex]x[/latex]-значениями и называются пределами интегрирования; в частности, [латекс]а[/латекс] — нижний предел, а [латекс]b[/латекс] — верхний предел. Чтобы уточнить, мы используем слово ограничивают двумя разными способами в контексте определенного интеграла. Во-первых, мы говорим о пределе суммы как [latex]n\to \infty .[/latex] Во-вторых, границы области называются пределами интегрирования .
Символ интегрирования ∫ представляет собой удлиненную букву S, что указывает на сигму или суммирование. В определенном интеграле выше и ниже символа суммы находятся границы интервала [латекс]\слева[а,б\справа].[/латекс] Числа [латекс]а[/латекс] и [латекс]b [/latex] являются [latex]x[/latex]-значениями и называются пределами интегрирования; в частности, [латекс]а[/латекс] — нижний предел, а [латекс]b[/латекс] — верхний предел. Чтобы уточнить, мы используем слово ограничивают двумя разными способами в контексте определенного интеграла. Во-первых, мы говорим о пределе суммы как [latex]n\to \infty .[/latex] Во-вторых, границы области называются пределами интегрирования . Мы можем использовать любую переменную, которая нам нравится, в качестве переменной интегрирования: 9{*})\text{Δ}x[/latex] существует и является уникальным. Это приводит к следующей теореме, которую мы сформулируем без доказательства.
Мы можем использовать любую переменную, которая нам нравится, в качестве переменной интегрирования: 9{*})\text{Δ}x[/latex] существует и является уникальным. Это приводит к следующей теореме, которую мы сформулируем без доказательства. Это вводит немного более сложные обозначения в наши пределы и усложняет вычисления, не получая при этом особого дополнительного понимания, поэтому мы придерживаемся регулярных разбиений для сумм Римана.
Это вводит немного более сложные обозначения в наши пределы и усложняет вычисления, не получая при этом особого дополнительного понимания, поэтому мы придерживаемся регулярных разбиений для сумм Римана. 11 Для частично отрицательной функции сумма Римана равна площади прямоугольников над осью x за вычетом площади прямоугольников под осью x.
11 Для частично отрицательной функции сумма Римана равна площади прямоугольников над осью x за вычетом площади прямоугольников под осью x.
 А пока мы просто рассмотрим некоторые основы, чтобы понять, как это работает, изучая постоянные скорости. 9{2}75dt=150.$$
А пока мы просто рассмотрим некоторые основы, чтобы понять, как это работает, изучая постоянные скорости. 9{2}75dt=150.$$