Как интерполировать на листе Microsoft Excel? Пошаговое руководство
Le Область применения Excel изучать известные отношения и работать с функциями — это довольно широкий . Поэтому многие люди не знают всей силы этого инструмент расчета .
Несколько сложная задача — оценить значения на основе известных интервалов. Другими словами, чтобы установить с максимально возможной точностью что такое число, взяв за основу определенные значения.
По этой причине существует методика интерполяции данные , которые мы обсудим в следующих параграфах. Мы научим вас, как быстро и безопасно оценить стоимость. Не пропустите ничего.
Что такое анимация данных и для чего она используется в моей электронной таблице?
Интерполяция данных математический инструмент используется для оценки данных в пределах известного диапазона. Зная крайние значения, вы можете интерпретировать те, которые существуют в этом наборе. Противоположно интерполяция известен как экстраполяция и соответствует данным в вне чума известен.
Противоположно интерполяция известен как экстраполяция и соответствует данным в вне чума известен.
Есть разные методы знать внутренние моменты. Следовательно результаты будут приблизительными оценками который будет варьироваться в зависимости от типа метода. Среди наиболее известных мы находим линейная, квадратичная или параболическая интерполяция и полиномы .
Эти методы полезны на практике для оценить значения из известных данных . Например, количество туристов, посетивших Барселону в 2019 году можно оценить в на основании конкретных данных, полученных в 2017 году.
Пар Последовательные, его можно применить к любому типу информации . Будь то температура Автора окружающая среда в определенном регионе нашей страны или Европы плотность застройки , то студентов, обучающихся в образовательном учреждении и даже количество средние годы жизни с разбивкой по полу люди.
Это означает, что Microsoft Excel — отличный инструмент. использовать и получать оценки интерполяция данных .
Типы интерполяции Какие существуют и могут быть выполнены в Excel?
Типы интерполяции, которые вы можете использовать в Excel для оценки значений в известном наборе, следующие:
Линейный
Среди различных существующих типов интерполяции самый простой метод — линейный. . Действительно, возможные решения переменной X только один . Кроме того, объединив две точки на график , линию уже можно провести, таким образом найдя пары X 0 ; ETet X 1 ; Et 1 имеет меньше шагов.
Это не значит, что этот метод не неэффективен или что он намного лучше, чем другие , потому что невозможно точно определить, что лучше, если не учитывать поведение кривой.
Для этой функции используется формула:
- ET+ {[(ХХ)] / (ИКС 1 -X)]} * (Г 1 -Y) .

Вы также можете узнать уравнение линии благодаря следующей функции:
- AXIS ( известный_y ; known_x) для определить постоянную a .
- SLOPE ( известный_y ; known_x) для определить наклон , то есть b.
Параболический
La параболическая функция, также называемая квадратичной полиномом или полиномом уровня 2 , представляет собой график с минимумом или максимумом и имеет формулу уравнения у = а + bx + cx2 . Функция является многочлен который используется для оценки значений у = а + Ь (хх) + с (хх) (хх 1 ).
Для работы в Excel вы можете заменить значения уравнения или используйте такие формулы, как МАТЧ et ИНДЕКС .
Уровень полинома 3
функция у = тревога +… + а1х + ао используется; с n = 3 . (1, 2, 3, 4))
(1, 2, 3, 4))
Уровень полинома 4
как полином уровня 3, le «Число n» многочленов можно запустить , поэтому лечение такое же, как и от уровень 3 до числа n .
Таким образом, можно сделать вывод, что метод степени 4 имеет те же шаги и идентичные характеристики для решения значения в интервале, известном как степень 3 .
Действия по интерполяции данных или диапазонов на листе Microsoft Excel
«ОБНОВЛЕНИЕ ✅ Вы хотите знать, как интерполировать данные или диапазоны в Excel, как эксперт? ⭐ ВОЙДИТЕ ЗДЕСЬ ⭐ и узнайте больше »
Ниже вы можете найти шаги что вам нужно будет выполнить для интерполировать данные в известном диапазоне с помощью Microsoft Excel . Мы покажем вам руководство для линейной функции, параболической функции и для многочленов уровня 3 и 4.
Посмотрим на них:Линейный
Чтобы использовать линейная интерполяция в Excel, вам нужно будет разделить задачу на два этапа.
Первое, что нужно сделать, это следующие шаги:
- Перейти на вкладку «Формула» , затем выполните поиск в меню «Библиотека функций «The инструмент «Исследование и направление» .
- Когда вы нажимаете на нее, окно откроется , вам нужно будет выбрать функцию «СООТВЕТСТВИЕ» . Так как таким образом вы найдете относительное положение в матрице .
- Выбрать как искомая стоимость ячейки где вы хотите получить данные.
- Затем выберите le X- топор матрица .
Полученное значение равно 1 . Cela signifie que значения Y соответствовать оценке, которую вы ищете.
Ты должен сейчас используйте формулу ИНДЕКС определить ценности X;А ТАКЖЕу X 1 ; А ТАКЖЕ 1 .
Для этого выполните следующие действия:
- Используйте формулу ИНДЕКС (массив; значение Y, когда это первый член ) .
- Таким образом, вы можете получить те ценности, которые вы ищете .
- Когда у вас есть четыре значения, вам придется заменить их в формуле Y+ (((ХХ)) / (ИКС 1 -X))) * (У 1 -Y) .
- Вы получаете значение Y . Это означает, что это расчетная стоимость когда X находится между 2 значениями.
Параболический
При нахождении типа уравнения y = a + bx + cx2 Мы сделаем это графически найти параболический метод . Вы также можете сделать это так же, как и мы, с помощью функций МАТЧ и ИНДЕКС , но мы хотим показать вам более простой метод для простых случаев.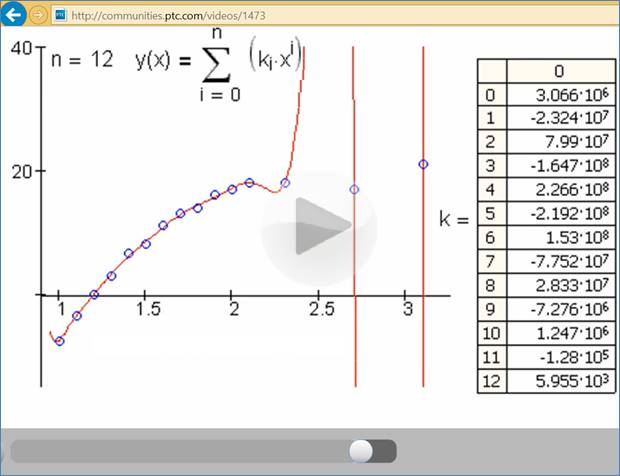
Следующие шаги следующие:
- Когда у вас есть введенные значения X et Y , выберите матрица .
- идти «Вставлять» затем нажмите «Рекомендуемая графика»
- Ищите вариант «Дисперсия (XY)» и нажмите на него.
- Choisissez le графический что подходит вам лучше всего.
- Щелкните правой кнопкой мыши на линия, которая была проведена .
- Нажмите на опцию «Добавить линию тренда …» .
- Выберите функцию «Полином» затем написать «2» в Поле «Степень:» .
- Прокрутите вниз и установите флажки «Точка на перекрестке» , «Показать уравнение на графике» et «Показать квадрат R-значения на графике» . Это будет в Мера’ получить все данные вам нужно найти ценности, которые ты хочешь от Y .

Уровень полинома 3
Следующие шаги такие же, как и для параболической функции. Один раз все данные загружены в таблице вы вставить рисунок , затем установите линию тренда.
Наконец, вы должны активируйте те же поля, и вы получите нужную формулу чтобы получить любое значение Y.
Уровень полинома 4
То же самое происходит с уровнем 2, или параболическим, полиномиальным, и уровнем 3, вам нужно будет проделать те же шаги для
функция уровня 4 .Если у вас есть какие-либо вопросы, оставляйте их в комментариях, мы свяжемся с вами как можно скорее, и это будет большим подспорьем для большего числа участников сообщества. Je Vous remercie!
report this ad
Применение экстраполяции в Microsoft Excel. Применение интерполяции в Microsoft Excel
Бывает ситуация, когда в массиве известных значений нужно найти промежуточные результаты.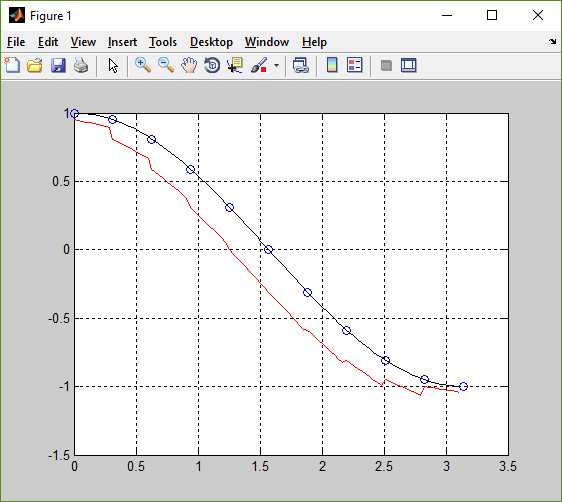 В математике это называется интерполяцией. В Excel данный метод можно применять как для табличных данных, так и для построения графиков. Разберем каждый из этих способов.
В математике это называется интерполяцией. В Excel данный метод можно применять как для табличных данных, так и для построения графиков. Разберем каждый из этих способов.
Главное условие, при котором можно применять интерполяцию – это то, что искомое значение должно быть внутри массива данных, а не выходить за его предел. Например, если мы имеем набор аргументов 15, 21 и 29, то при нахождении функции для аргумента 25 мы можем использовать интерполяцию. А для поиска соответствующего значения для аргумента 30 – уже нет. В этом и является главное отличие этой процедуры от экстраполяции.
Способ 1: интерполяция для табличных данных
Прежде всего, рассмотрим применения интерполяции для данных, которые расположены в таблице. Для примера возьмем массив аргументов и соответствующих им значений функции, соотношение которых можно описать линейным уравнением. Эти данные размещены в таблице ниже. Нам нужно найти соответствующую функцию для аргумента 28 . Сделать это проще всего с помощью оператора ПРЕДСКАЗ .
Способ 2: интерполяция графика с помощью его настроек
Процедуру интерполяции можно применять и при построении графиков функции. Актуальна она в том случае, если в таблице, на основе которой построен график, к одному из аргументов не указано соответствующее значение функции, как на изображении ниже.
Как видим, график скорректирован, а разрыв с помощью интерполяции удален.
Способ 3: интерполяция графика с помощью функции
Произвести интерполяцию графика можно также с помощью специальной функции НД. Она возвращает неопределенные значения в указанную ячейку.
Можно сделать даже проще, не запуская Мастер функций , а просто с клавиатуры вбить в пустую ячейку значение «#Н/Д» без кавычек. Но это уже зависит от того, как какому пользователю удобнее.
Как видим, в программе Эксель можно выполнить интерполяцию, как табличных данных, используя функцию ПРЕДСКАЗ , так и графика.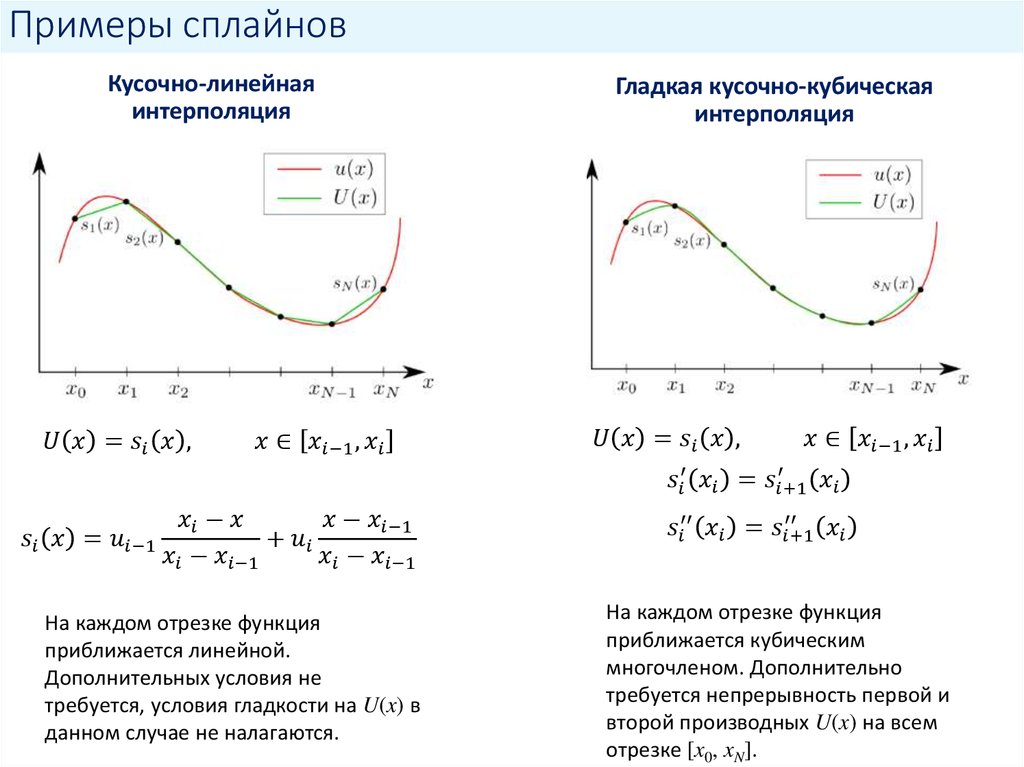 В последнем случае это осуществимо с помощью настроек графика или применения функции НД , вызывающей ошибку «#Н/Д» . Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.
В последнем случае это осуществимо с помощью настроек графика или применения функции НД , вызывающей ошибку «#Н/Д» . Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.
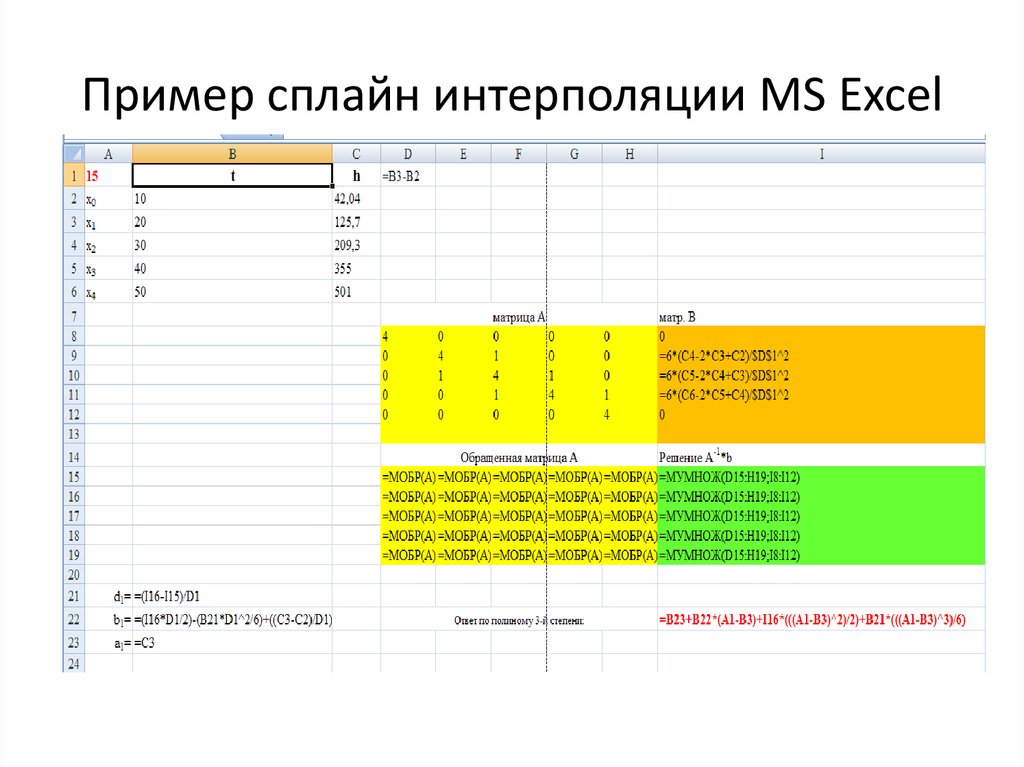
Это глава из книги Билла Джелена .
Задача: некоторые инженерные проблемы проектирования требуют использования таблиц для вычисления значений параметров. Поскольку таблицы являются дискретными, дизайнер использует линейную интерполяцию для получения промежуточного значения параметра. Таблица (рис. 1) включает высоту над землей (управляющий параметр) и скорость ветра (рассчитываемый параметр). Например, если надо найти скорость ветра, соответствующую высоте 47 метров, то следует применить формулу: 130 + (180 – 130) * 7 / (50 – 40) = 165 м/сек.
Скачать заметку в формате или , примеры в формате
Как быть, если существует два управляющих параметра? Можно ли выполнить вычисления с помощью одной формулы? В таблице (рис. 2) показаны значения давления ветра для различных высот и величин пролета конструкций.
Решение: проблему решаем путем расширения метода, используемого для случая с одним управляющим параметром. Выполните следующие действия.
Начните с таблицы, изображенной на рис. 2. Добавьте исходные ячейки для высоты и пролета в J1 и J2 соответственно (рис. 3).
Рис. 3. Формулы в ячейках J3:J17 объясняют работу мегаформулы
Для удобства использования формул определите имена (рис. 4).
Проследите за работой формулы последовательно переходя от ячейки J3 к ячейке J17.
Путем обратной последовательной подстановки соберите мегаформулу. Скопируйте текст формулы из ячейки J17 в J19. Замените в формуле ссылку на J15 на значение в ячейке J15: J7+(J8-J7)*J11/J13. И так далее. Получится формула, состоящая из 984 символов, которую невозможно воспринять в таком виде. Вы можете посмотреть на нее в приложенном Excel-файле. Не уверен, что такого рода мегаформулы полезны в использовании.
Резюме: линейная интерполяция используется для получения промежуточного значения параметра, если табличные значения заданы только для границ диапазонов; предложен метод расчета по двум управляющим параметрам.
Существуют случаи, когда требуется узнать результаты вычисления функции за пределами известной области. Особенно актуален данный вопрос для процедуры прогнозирования. В Экселе есть несколько способов, с помощью которых можно совершить данную операцию. Давайте рассмотрим их на конкретных примерах.
Способ 2: экстраполяция для графика
Выполнить процедуру экстраполяции для графика можно путем построения линии тренда.
- Прежде всего, строим сам график. Для этого курсором при зажатой левой кнопке мыши выделяем всю область таблицы, включая аргументы и соответствующие значения функции. Затем, переместившись во вкладку «Вставка» , кликаем по кнопке «График» . Этот значок расположен в блоке «Диаграммы» на ленте инструментов. Появляется перечень доступных вариантов графиков.
 Выбираем наиболее подходящий из них на свое усмотрение.
Выбираем наиболее подходящий из них на свое усмотрение. - После того, как график построен, удаляем из него дополнительную линию аргумента, выделив её и нажав на кнопку Delete на клавиатуре компьютера.
- Далее нам нужно поменять деления горизонтальной шкалы, так как в ней отображаются не значения аргументов, как нам того нужно. Для этого, кликаем правой кнопкой мыши по диаграмме и в появившемся списке останавливаемся на значении «Выбрать данные» .
- В запустившемся окне выбора источника данных кликаем по кнопке «Изменить» в блоке редактирования подписи горизонтальной оси.
- Открывается окно установки подписи оси. Ставим курсор в поле данного окна, а затем выделяем все данные столбца «X» без его наименования. Затем жмем на кнопку «OK» .
- После возврата к окну выбора источника данных повторяем ту же процедуру, то есть, жмем на кнопку «OK» .
- Теперь наш график подготовлен и можно, непосредственно, приступать к построению линии тренда.
 Кликаем по графику, после чего на ленте активируется дополнительный набор вкладок – «Работа с диаграммами» . Перемещаемся во вкладку «Макет» и жмем на кнопку «Линия тренда» в блоке «Анализ» . Кликаем по пункту «Линейное приближение» или «Экспоненциальное приближение» .
Кликаем по графику, после чего на ленте активируется дополнительный набор вкладок – «Работа с диаграммами» . Перемещаемся во вкладку «Макет» и жмем на кнопку «Линия тренда» в блоке «Анализ» . Кликаем по пункту «Линейное приближение» или «Экспоненциальное приближение» . - Линия тренда добавлена, но она полностью находится под линией самого графика, так как мы не указали значение аргумента, к которому она должна стремиться. Чтобы это сделать опять последовательно кликаем по кнопке «Линия тренда» , но теперь выбираем пункт «Дополнительные параметры линии тренда» .
- Запускается окно формата линии тренда. В разделе «Параметры линии тренда» есть блок настроек «Прогноз» . Как и в предыдущем способе, давайте для экстраполяции возьмем аргумент 55 . Как видим, пока что график имеет длину до аргумента 50 включительно. Получается, нам нужно будет его продлить ещё на 5 единиц.
 На горизонтальной оси видно, что 5 единиц равно одному делению. Значит это один период. В поле «Вперед на» вписываем значение «1» . Жмем на кнопку «Закрыть» в нижнем правом углу окна.
На горизонтальной оси видно, что 5 единиц равно одному делению. Значит это один период. В поле «Вперед на» вписываем значение «1» . Жмем на кнопку «Закрыть» в нижнем правом углу окна. - Как видим, график был продлен на указанную длину с помощью линии тренда.
Итак, мы рассмотрели простейшие примеры экстраполяции для таблиц и для графиков. В первом случае используется функция ПРЕДСКАЗ , а во втором – линия тренда. Но на основе этих примеров можно решать и гораздо более сложные задачи прогнозирования.
Многие из нас сталкивались с непонятными терминами в разных науках. Но находится очень мало людей, которых не пугают непонятные слова, а наоборот, приободряют и заставляют всё больше углубиться в изучаемый предмет. Сегодня речь пойдёт о такой вещи, как интерполяция. Это способ построения графиков по известным точкам, позволяющий с минимальным количеством информации о функции предсказать её поведение на конкретных участках кривой.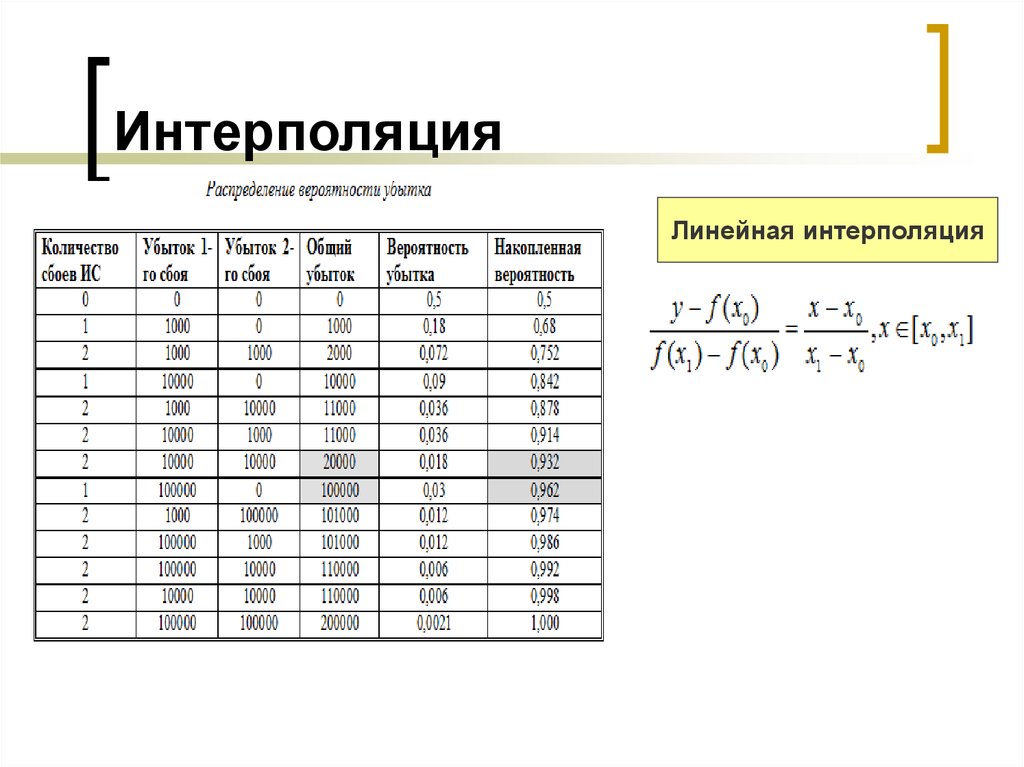
Перед тем как перейти к сути самого определения и рассказать о нём подробнее, немного углубимся в историю.
История
Интерполяция была известна ещё с древнейших времён. Однако своим развитием это явление обязано нескольким самым выдающимся математикам прошлого: Ньютону, Лейбницу и Грегори. Именно они развили это понятие с помощью более продвинутых математических способов, доступных в то время. До этого интерполяцию, конечно, применяли и использовали в вычислениях, но делали это совершенно неточными способами, требующими большого количества данных для построения модели, более-менее близкой к реальности.
Сегодня мы можем даже выбирать, какой из способов интерполяции подходит больше. Всё переведено на компьютерный язык, который с огромной точностью может предсказывать поведение функции на определённом участке, ограниченном известными точками.
Интерполяция представляет собой достаточно узкое понятие, поэтому её история не так богата фактами. В следующем разделе разберёмся, что такое интерполяция на самом деле и чем она отличается от своей противоположности — экстраполяции.
Что такое интерполяция?
Как мы уже говорили, это общее название способов, позволяющих построить график по точкам. В школе в основном это делают с помощью составления таблицы, выявления точек на графике и примерного построения линий, их соединяющих. Последнее действие делается исходя из соображений похожести исследуемой функции на другие, вид графиков которых нам известен.
Однако есть другие, более сложные и точные способы выполнить поставленную задачу построения графика по точкам. Итак, интерполяция — это фактически «предсказание» поведения функции на конкретном участке, ограниченном известными точками.
Существует схожее понятие, связанное с этой же областью, — экстраполяция. Она представляет собой также предсказание графика функции, но за пределами известных точек графика. При таком способе предсказание делается на основе поведения функции на известном промежутке, и потом эта функция применяется и для неизвестного промежутка. Такой способ очень удобен для практического применения и активно используется, например, в экономике для прогнозирования взлётов и падения на рынке и для предсказания демографической ситуации в стране.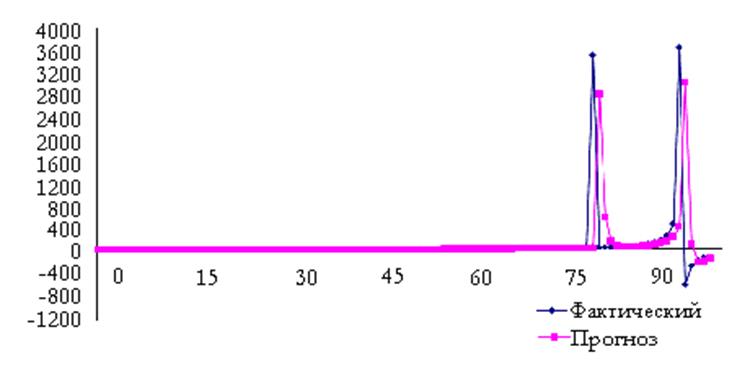
Но мы отошли от основной темы. В следующем разделе разберёмся, какая бывает интерполяция и с помощью каких формул можно произвести эту операцию.
Виды интерполяции
Самым простым видом является интерполяция методом ближайшего соседа. С помощью этого способа мы получаем очень приблизительный график, состоящий из прямоугольников. Если вы видели хоть раз объяснение геометрического смысла интеграла на графике, то поймёте, о каком графическом виде идёт речь.
Кроме этого, существуют и другие методы интерполяции. Самые известные и популярные связаны с многочленами. Они более точны и позволяют предсказывать поведение функции при достаточно скудном наборе значений. Первым методом интерполяции, который мы рассмотрим, будет линейная интерполяция многочленами. Это самый простой способ из данной категории, и им наверняка каждый из вас пользовался в школе. Суть его заключается в построении прямых между известными точками. Как известно, через две точки плоскости проходит единственная прямая, уравнение которой можно найти исходя из координат данных точек.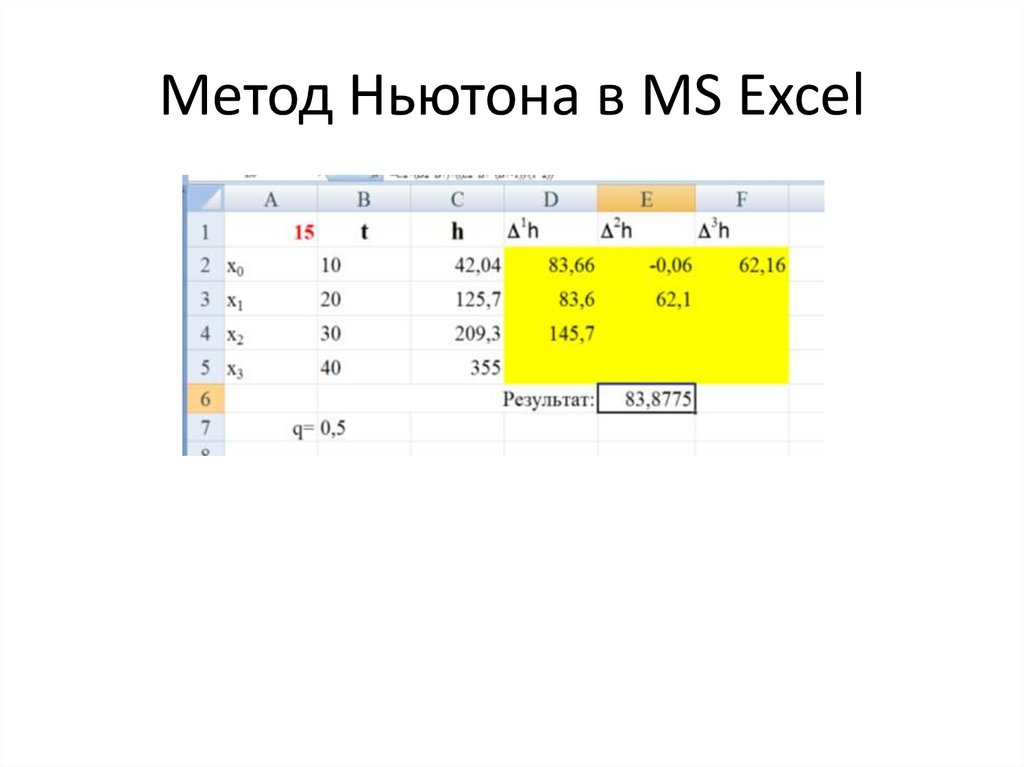 Построив эти прямые, мы получаем ломаный график, который худо-бедно, но отражает примерные значения функций и в общих чертах совпадает с реальностью. Так и осуществляется линейная интерполяция.
Построив эти прямые, мы получаем ломаный график, который худо-бедно, но отражает примерные значения функций и в общих чертах совпадает с реальностью. Так и осуществляется линейная интерполяция.
Усложнённые виды интерполяции
Есть более интересный, но при этом более сложный способ интерполяции. Его придумал французский математик Жозеф Луи Лагранж. Именно поэтому расчет интерполяции по этому методу назван его именем: интерполяция по методу Лагранжа. Фокус тут вот в чём: если способ, изложенный в предыдущем абзаце, использует для расчета только линейную функцию, то разложение методом Лагранжа предполагает также использование многочленов более высоких степеней. Но не так просто найти сами формулы интерполяции для разных функций. И чем больше точек известно, тем точнее получается формула интерполяции. Но есть и масса других методов.
Существует и более совершенный и приближенный к реальности метод расчета. Формула интерполяции, используемая в нём, представляет собой совокупность многочленов, применение каждого из которых зависит от участка функции.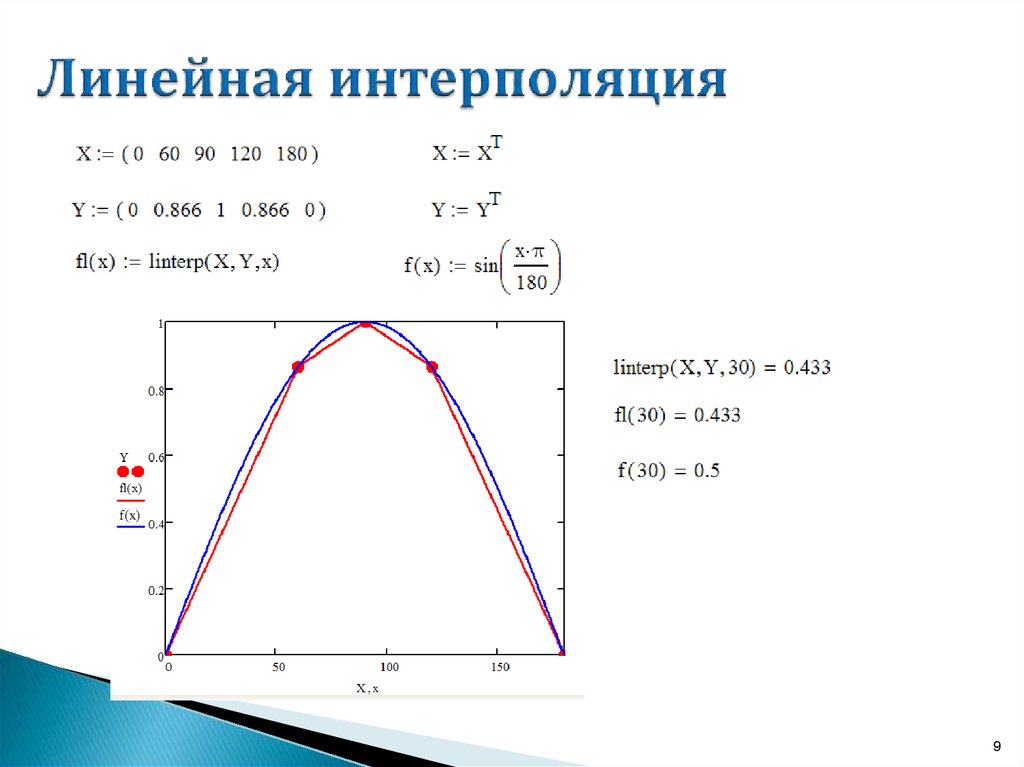 Такой метод называется сплайн-функцией. Кроме того, есть ещё и способы, позволяющие провести такую вещь, как интерполяция функций двух переменных. Тут всего два метода. Среди них билинейная или двойная интерполяция. Этот способ позволяет без труда построить график по точкам в трёхмерном пространстве. Другие методы затрагивать не будем. Вообще, интерполяция — это универсальное называние для всех этих способов построения графиков, но многообразие способов, которыми можно осуществить это действие, заставляет делить их на группы в зависимости от вида функции, которая подлежит этому действию. То есть интерполяция, пример которой мы рассмотрели выше, относится к прямым способам. Есть также обратная интерполяция, которая отличается тем, что позволяет вычислить не прямую, а обратную функцию (то есть x от y). Рассматривать последние варианты мы не будем, так как это достаточно сложно и требует хорошей математической базы знаний.
Такой метод называется сплайн-функцией. Кроме того, есть ещё и способы, позволяющие провести такую вещь, как интерполяция функций двух переменных. Тут всего два метода. Среди них билинейная или двойная интерполяция. Этот способ позволяет без труда построить график по точкам в трёхмерном пространстве. Другие методы затрагивать не будем. Вообще, интерполяция — это универсальное называние для всех этих способов построения графиков, но многообразие способов, которыми можно осуществить это действие, заставляет делить их на группы в зависимости от вида функции, которая подлежит этому действию. То есть интерполяция, пример которой мы рассмотрели выше, относится к прямым способам. Есть также обратная интерполяция, которая отличается тем, что позволяет вычислить не прямую, а обратную функцию (то есть x от y). Рассматривать последние варианты мы не будем, так как это достаточно сложно и требует хорошей математической базы знаний.
Перейдём к, пожалуй, одному из важнейших разделов. Из него мы узнаем, как и где обсуждаемая нами совокупность методов применяется в жизни.
Применение
Математика, как известно, царица наук. Поэтому даже если вы сначала не видите смысла в тех или иных операциях, это не значит, что они бесполезны. Вот, например, кажется, что интерполяция — это бесполезная вещь, с помощью которой только графики строить можно, которые сейчас мало кому нужны. Однако при любых расчётах в технике, физике и многих других науках (например, биологии), крайне важно представлять достаточно полную картину о явлении, имея при этом определённый набор значений. Сами значения, разбросанные по графику, не всегда дают чёткие представления о поведении функции на конкретном участке, значениях её производных и точек пересечения с осями. А это очень важно для многих областей нашей с вами жизни.
А как это пригодится в жизни?
На подобный вопрос бывает очень сложно ответить. Но ответ прост: никак. Именно эти знания вам никак не пригодятся. А вот если вы поймёте этот материал и методы, с помощью которых осуществляются эти действия, вы потренируете свою логику, которая в жизни очень пригодится.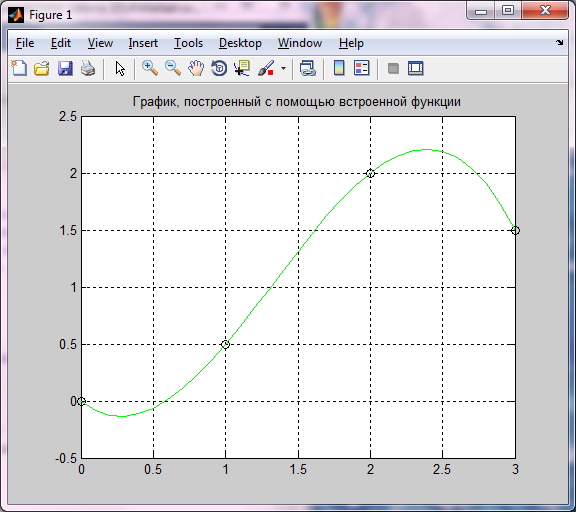 Главное — не сами знания, а те навыки, которые человек приобретает в процессе изучения. Ведь недаром существует поговорка: «Век живи — век учись».
Главное — не сами знания, а те навыки, которые человек приобретает в процессе изучения. Ведь недаром существует поговорка: «Век живи — век учись».
Смежные понятия
Вы можете сами понять, насколько важна была (и до сих пор не теряет свою важность) эта область математики, взглянув на многообразие других концепций, связанных с данной. Мы уже говорили об экстраполяции, но есть ещё и аппроксимация. Может быть, вы уже слышали это слово. В любом случае то, что оно обозначает, мы тоже разбирали в этой статье. Аппроксимация, как и интерполяция, — это понятия, связанные с построением графиков функций. Но отличие первой от второй в том, что она представляет собой приблизительное построение графика на основе сходных известных графиков. Эти два понятия очень похожи между собой, и тем интереснее изучать каждое из них.
Заключение
Математика — не такая сложная наука, как кажется на первый взгляд. Она, скорее, интересная. И в этой статье мы попытались вам это доказать.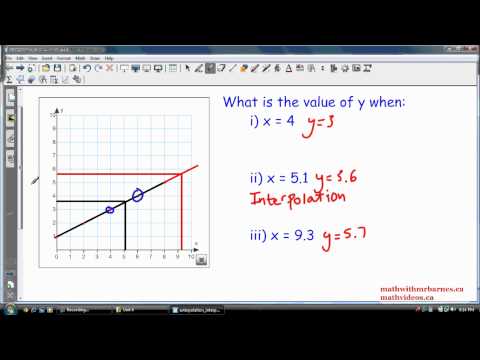 Мы рассмотрели понятия, связанные с построением графиков, узнали, что такое двойная интерполяция, и разобрали на примерах, где она применяется.
Мы рассмотрели понятия, связанные с построением графиков, узнали, что такое двойная интерполяция, и разобрали на примерах, где она применяется.
Практическая работа № 2 Интерполяция в среде excel, Линия тренда. Задача №1
Цель работы– получить аналитическую зависимость функции от аргумента (задано таблично) в средеExcel.
Последовательность выполнения работы
В Excelесть ряд встроенных утилит, которые можно использовать для решения задач по интерполяции и по аппроксимации зависимостей.
Анализ возможностей Excelв данной области начнем с графических утилит. В частности, исследуем вопрос о добавлении линии тренда, которая строится на основе экспериментальных данных и является аппроксимирующей или интерполяционной функцией, в зависимости от выбора типа кривой. Последовательность выполнения:
1. Отображение анализируемых данных в графическом виде.
2. Построение кривой для рассматриваемой зависимости.
3.
Анализ полученной кривой для рассматриваемой
зависимости.
4. Выводы о проделанной работе.
Выполнение работы
Р,МПа | ,кг/м3 |
0,392 | 1,925 |
0,412 | 2,024 |
0,431 | 2,123 |
0,450 | 2,222 |
0,470 | 2,321 |
0,490 | 2,421 |
0,539 | 2,673 |
0,588 | 2,926 |
0,637 | 3,182 |
0,686 | 3,440 |
Из этих данных строим график:
«Мастер
диаграмм – Точечная – Готово».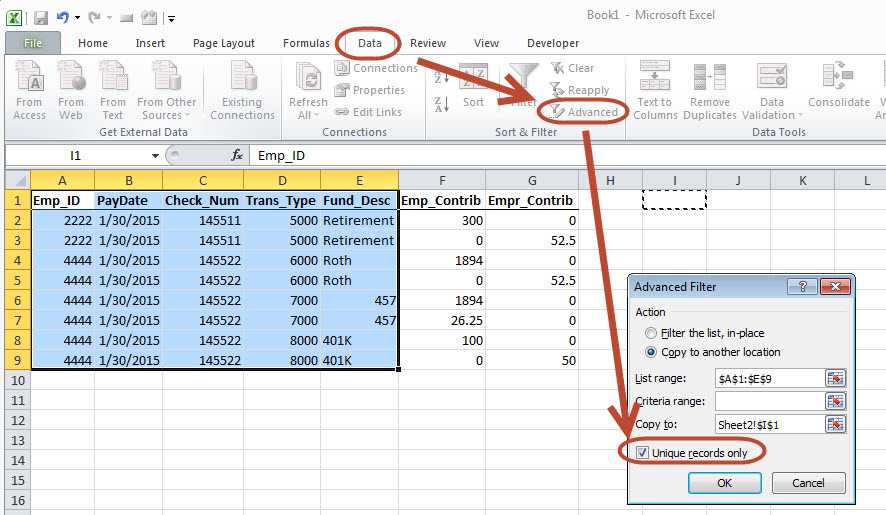 Выбираем
значения «Y» и «X»,
соответственно для «ρ, кг/м3» и
«p, МПа».
Выбираем
значения «Y» и «X»,
соответственно для «ρ, кг/м3» и
«p, МПа».
Вывод: При выполнении работы по интерполяции в средеEXCELмы по заданным значениям зависимости плотности пара, (кг/м3) от давления р, (МПа) получили аналитическое выражение с помощью линии тренда и построили график линии тренда.
Практическая работа № 3 Интерполяция в среде excel, Линия тренда. Задача №2
Цель работы– получить аналитическую зависимость функции от аргумента (задано графически) в средеExcel.
Последовательность выполнения работы
В Excelесть ряд встроенных утилит, которые можно использовать для решения задач по интерполяции и по аппроксимации зависимостей.
Анализ возможностей Excelв данной области начнем с графических
утилит. В частности, исследуем вопрос
о добавлении линии тренда, которая
строится на основе экспериментальных
данных и является аппроксимирующей или
интерполяционной функцией, в зависимости
от выбора типа кривой.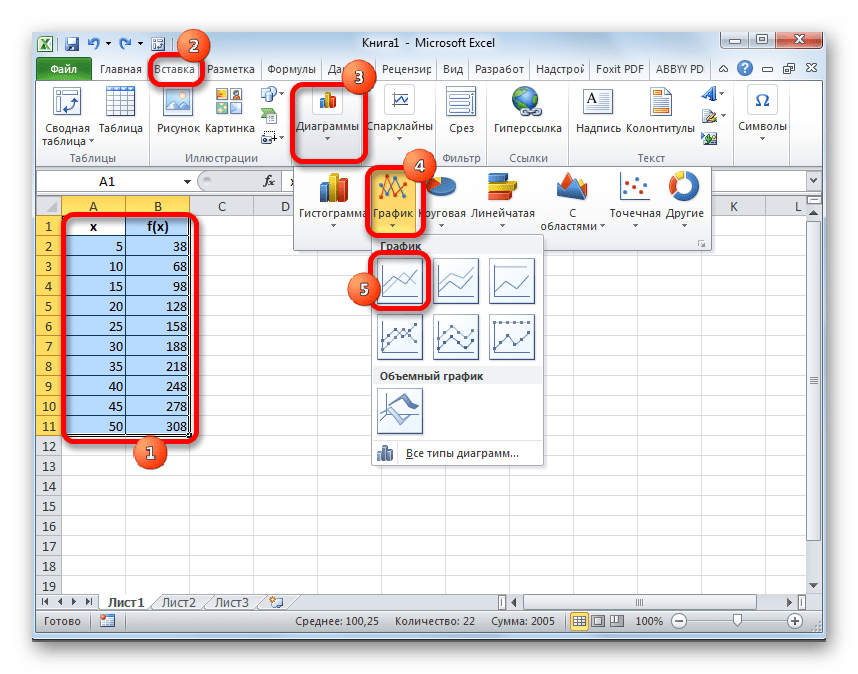 Последовательность
выполнения:
Последовательность
выполнения:
1. Отображение анализируемых данных в графическом виде.
2. Построение кривой для рассматриваемой зависимости.
3. Анализ полученной кривой для рассматриваемой зависимости.
4. Выводы о проделанной работе.
Выполнение работы
Для решения поставленной задачи прежде всего следует отобразить анализируемые данные в виде таблицы.
Данные полученные с графика
t, мин | 0 | 0,97 | 1,8 | 2,63 | 3,29 | 3,65 | 4 | 4,48 | 5,27 | 6,42 | … | 16,21 | |||||||||||||
T,˚C | 25,5 | 29,2 | 36,4 | 46,4 | 54,5 | 66,5 | 75,6 | 80 | 88,2 | 91,5 | … | 103,7 | |||||||||||||
Из этих данных строим график:
«Мастер диаграмм – Точечная – Готово». 2)».
2)».
\
3. После нажатия кнопки ОК получаем результат. На рисунке не видно выпадающих экспериментальных точек на линии тренда и высока степень достоверности.
Для построения интерполяционного полинома, проходящего через все экспериментальные точки, необходимо, чтобы степень полинома была на единицу меньше количества точек. Чем выше степень полинома, тем больше аппроксимирующая кривая приближается к интерполяционному полиному. Однако положительный результат может быть получен и при меньшем количестве точек.
Вывод: При построении линии тренда мы получили аналитическое выражение функции от аргумента. В данном случае степень полинома равна шести, а количество точек – восемнадцати. Достоверность аппроксимацииR2= 0,9987 (величина достоверности вполне удовлетворяет).
Линейная интерполяция в Excel — EngineerExcel
Чтобы выполнить линейную интерполяцию в Excel, используйте функцию ПРОГНОЗ для прямой интерполяции между двумя парами значений x и y.
В приведенном ниже примере формула для интерполяции и нахождения значения y, соответствующего значению x, равному 1,4, выглядит следующим образом: простой метод работает, когда есть только две пары значений x и y. Если пар больше 2, расчет усложняется.
Содержание
- Линейная интерполяция в Excel
- Interpolate в Excel с Xlookup
- Используйте xlookup для поиска значений для интерполяции в Excel
- . ForeCast для InderPolation
- ForeCast для InderPolation
- . Функции ПОИСКПОЗ для интерполяции в Excel
- Как интерполировать в Excel с помощью формулы интерполяции
- Как интерполировать график в Excel?
- Резюме
- x — входное значение
- known_ys — известные значения y
- known_xs — известные значения x
- lookup_value — значение для поиска
- lookup_array — это массив, в котором ищется lookup_value
- return_array — это массив, из которого возвращается результат
- if_not_found — возвращаемое значение, если ничего не найдено (необязательно)
- match_mode сообщает функции, что делать, если точное совпадение не найдено (необязательно)
- search_mode сообщает функции, как искать в массиве (необязательно)
- Введение в интерполяцию в Excel
- Примеры интерполяции в Excel
- x: Это значение или точка данных, соответствующее значение которой мы хотим интерполировать или предсказать.
- known_y’s: это известный диапазон значений y.
- known_x’s: это известный диапазон значений x.
- ссылка: Это начальная точка, с которой начинается подсчет строк и столбцов.
- строк: это количество строк для смещения ниже начальной опорной ячейки.
- столбцов: это количество столбцов для смещения вправо от начальной ячейки ссылки.
- высота: опционально; Из возвращенной ссылки это высота строк. ширина
- : опционально; Из возвращенной ссылки это ширина столбцов.
- искомое_значение: это значение, которое необходимо сопоставить или просмотреть из искомого_массива.
- lookup_array: это массив или диапазон ячеек, в которых нужно искать искомое_значение.
- match_type: необязательно; это может принимать значения 1, 0,-1.
- Процесс получения простой функции из набора данных с дискретными значениями, чтобы функция проходила через все заданные значения, можно использовать для прогнозирования значений между заданными, называемыми интерполяцией.

- Используется для определения того, какие данные могут существовать вне собранных данных.
- Линейная интерполяция не является точным методом в MS Excel; тем не менее, это экономит время и быстро.
- Линейную интерполяцию можно использовать даже для прогнозирования значений осадков, географических точек данных и т. д.
- В случае, если данные нелинейны, то для интерполяции в таких случаях могут использоваться другие методы: полиномиальная интерполяция, сплайн-интерполяция и т. д. Функцию
- ПРОГНОЗ можно использовать даже для экстраполяции или прогнозирования будущих значений.
- Функция ИНДЕКС Excel
- Линейная интерполяция в Excel
- Линейное программирование в Excel
- Формула ПРОГНОЗА в Excel
- Определите, какое значение вы хотите интерполировать и создать новые строк для значения, которое вы хотите интерполировать и интерполировать В этом случае я хочу интерполировать между 8 и выбрал значение 8,5 .
- Теперь введите следующую формулу в ячейку В15 .
- Нажмите кнопку ENTER , и вы увидите с интерполяцией 9Значение 0008 в ячейке C15 .
- В этом случае вы также можете использовать функцию LINEAR . Просто введите в формулу FORECAST.LINEAR вместо FORECAST .
- Нажмите ENTER , и вы увидите то же интерполированное значение , что и раньше.
- Сначала внесите некоторые изменения в набор данных, чтобы разместить координаты .
- Введите следующую формулу в ячейку F7 .
- Нажмите ENTER , чтобы увидеть результат в ячейке F7 .
- Теперь введите следующую формулу в ячейку F8 .
- Нажмите клавишу ENTER , и вы увидите большее значение, чем 6 в ячейке 9.0007 F8 .
- После этого введите следующую формулу в ячейку F9 .
- Нажмите ENTER .
 Эта операция доставит вам значение в ячейке C9 .
Эта операция доставит вам значение в ячейке C9 . - Затем введите формулу в ячейку F10 .
- Нажмите ENTER и вы увидите координату Y ячейки C10 .
- После этого выберите ячейку C15 и введите приведенную ниже формулу.
- Нажмите клавишу ENTER , чтобы увидеть интерполированное значение в ячейке C15 .
- Сначала внесите некоторые изменения в набор данных, чтобы разместить координаты .
- Введите следующую формулу в ячейку F7 .
- Нажмите ENTER , чтобы увидеть результат в ячейке F7 .
- Теперь введите следующую формулу в ячейку F8 .
- Нажмите клавишу ENTER , и вы увидите большее значение, чем 6 в ячейке F8 .
- После этого введите следующую формулу в ячейку F9 .
- Нажмите ENTER .
 Эта операция доставит вам значение в ячейке C9 .
Эта операция доставит вам значение в ячейке C9 . - Затем введите формулу в ячейку F10 .
- Нажмите ENTER и вы увидите координату Y ячейки C10 .
- После этого выберите ячейку C15 и введите приведенную ниже формулу.
- Нажмите клавишу ENTER , чтобы увидеть интерполированное значение в ячейке C15 .
- Внесите некоторые изменения в набор данных для интерполяционного значения и введите следующую формулу в ячейку C15 . Здесь мы хотим найти интерполированное значение , когда координата X равна 75 . И по этой причине мы возьмем X Координаты , которые по соседству меньше или больше, чем 2,75 и соответствующие им 9.0007 Y Координаты в этом наборе данных.
- Теперь просто нажмите ENTER , чтобы увидеть интерполированное значение в ячейке C15 .
- Внесите некоторые изменения в свой набор данных, чтобы сохранить уклон .
- Введите следующую формулу в ячейку E7
- Нажмите ENTER , и вы увидите наклон этих данных в ячейке E7 .
- Теперь введите следующую формулу в ячейку E9 , чтобы найти точку пересечения Y .
- Нажмите ENTER , чтобы увидеть результат в ячейке E9 .
- Вставьте эту формулу в ячейку C15 .
- Нажмите ENTER , чтобы увидеть интерполированное значение в ячейке С15 .
- Внесите некоторые изменения, чтобы сохранить интерполированное Мы хотим интерполировать значение между 5 и 8 . Пусть это будет 6,5 .

- Введите следующую формулу в ячейку C15 .
- Нажмите ENTER и вы увидите интерполированное значение в ячейке C15 .
Линейная интерполяция в Excel
В Excel нет функции линейной интерполяции, но функцию ПРОГНОЗ можно использовать для линейной интерполяции, когда есть только две пары значений x и y.
Он имеет следующий синтаксис:
=ПРОГНОЗ(x,известный_ys,известный_xs)
где:
Функция ПРОГНОЗ использует линейную регрессию для оценки значения y, которое соответствует входному значению x.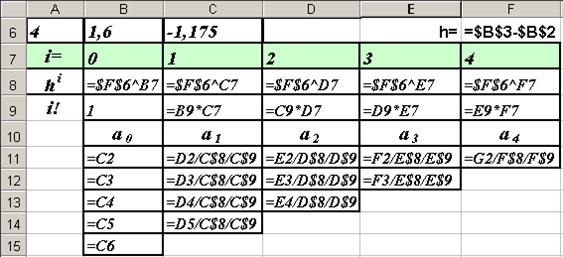 Когда есть только две точки данных, результат линейной регрессии такой же, как и линейная интерполяция.
Когда есть только две точки данных, результат линейной регрессии такой же, как и линейная интерполяция.
Однако, когда количество значений x и значений y больше 2, результатом функции ПРОГНОЗ НЕ будет интерполированное значение y.
Для интерполяции между значениями x и y в большом наборе данных (более 2 пар значений) используйте либо XLOOKUP, либо ИНДЕКС и ПОИСКПОЗ, чтобы извлечь пару значений x и y для интерполяции между ними.
Линейная интерполяция предполагает, что изменение y при заданном изменении x является линейным. В большинстве случаев линейная интерполяция в Excel дает достаточно точные результаты. Однако, если вам нужна еще большая точность, вы можете рассмотреть более продвинутый метод, такой как кубические сплайны.
Интерполяция в Excel с помощью XLOOKUP
Если вы являетесь подписчиком Microsoft 365 или используете Excel 2021, Excel для Интернета или Excel для устройств iOS или Android, вы можете использовать функцию XLOOKUP для извлечения значений. Если вы используете более старую версию Excel, используйте описанный ниже метод ИНДЕКС/ПОИСКПОЗ.
Если вы используете более старую версию Excel, используйте описанный ниже метод ИНДЕКС/ПОИСКПОЗ.
В некоторых других сообщениях о поиске табличных данных в Excel я сосредоточился на том, как извлечь известных значений x и y из таблицы. Но что, если вам нужно интерполировать отсутствующие данные в Excel для большей точности? Что ж, в Excel также можно выполнить линейную интерполяцию, которая позволяет вам оценить значение y для любого значения x, которое не указано явно в данных.
Давайте посмотрим, как интерполировать в Excel некоторые реальные данные.
В таблице ниже приведена зависимость плотности воздуха от температуры с шагом 20 градусов Цельсия. Чтобы получить данные при любой температуре от 0 до 100 °C, нам придется интерполировать.
Чтобы оценить плотность при 53 градусах Цельсия, используйте XLOOKUP, чтобы найти в таблице значения x1=40, y1=1,127, x2=60 и y2=1,067, а затем введите эти значения в функцию ПРОГНОЗ, чтобы выполнить интерполяция.
Использование XLOOKUP для поиска значений для интерполяции в Excel0003
Для интерполяции в Excel используйте функцию XLOOKUP, чтобы найти значения x по обе стороны от входного значения x, а также соответствующие значения y.
Чтобы найти первое значение х из таблицы данных, используйте следующую формулу:
=XLOOKUP(F3,B5:B10,B5:B10,-1,1) искомое_значение, а массив B5:B10 является и искомым_массивом, и возвращаемым_массивом. Установка match_mode в -1 указывает функции возвращать следующий меньший элемент в возвращаемом массиве, а установка search_mode в 1 запускает поиск с вершины массива.
Результирующее значение x1 равно 40, что является максимальной температурой, меньшей 53, значения x.
Очень похожая формула используется для нахождения значения x2:
=XLOOKUP(F3,B5:B10,B5:B10,1,1)
Единственное отличие состоит в том, что match_mode установлен на 1 (а не -1), потому что x2 является следующим по величине значением в возвращаемом массиве.
Результирующее значение x2 равно 60, самая низкая температура выше 53 в массиве поиска.
Затем найдите соответствующие значения y y1 и y2 с помощью XLOOKUP. Для y1 F3 — это искомое_значение, а B5:B10 — это искомый_массив, как и раньше. Чтобы вернуть значение y, которое соответствует значению x, меньшему искомого_значения, C5:C10 является возвращаемым_массивом, а match_mode равен -1.
=XLOOKUP(F3,B5:B10,C5:C10,-1,1)
y1 равно 1,127.
Последнее значение для поиска — y2. Формула лишь немного отличается от формулы для y1. match_mode установлен в 1, чтобы вернуть следующее наибольшее значение y:
match_mode установлен в 1, чтобы вернуть следующее наибольшее значение y:
=XLOOKUP(F3,B5:B10,C5:C10,1,1)
Использовать ПРОГНОЗ для интерполяции Excel
Один раз 2 пары x — и значения y известны, ПРОГНОЗ можно использовать для интерполяции между ними, чтобы оценить значение y для заданного значения x по следующей формуле:
=ПРОГНОЗ(F3,F6:F7,F4:F5)
Оценка для y равна 1,088.
Предотвратить ошибки интерполяции Excel
Ошибка может возникнуть, если значение x равно одному из значений x в массиве поиска. Это приводит к тому, что x1 равен x2, а y1 равен y2. Когда это происходит, ПРОГНОЗ не может рассчитать наклон и возвращает ошибку.
Ошибку можно предотвратить, заключив функцию ПРОГНОЗ в функцию ЕСЛИ, которая проверяет, равны ли значения x и x1.
Если x и x1 равны, y равен y1.
=ЕСЛИ(F3=F4,F6,ПРОГНОЗ(F3,F6:F7,F4:F5))
Эта формула правильно возвращает результат 1,127, когда x равно 40.
Использование функции ИНДЕКС/ПОИСКПОЗ для интерполяции в Excel
Если вы не являетесь подписчиком Microsoft 365 или используете более старую версию Excel, функция XLOOKUP не включена.
Не беспокойтесь!
Вы можете использовать функции ИНДЕКС и ПОИСКПОЗ для получения одинаковых результатов. Синтаксис этих функций объясняется здесь, поэтому, если вам нужно освежить в памяти, обязательно ознакомьтесь с ним.
СВЯЗАННЫЕ: ИСПОЛЬЗОВАНИЕ ФУНКЦИЙ EXCEL ИНДЕКС И ПОИСКПОЗ ДЛЯ ПОИСКА ТЕХНИЧЕСКИХ ДАННЫХ
ПОИСКПОЗ возвращает положение значения (n) в столбце или строке данных.
ИНДЕКС возвращает фактическое значение в позиции n th строки или столбца данных.
Используя эти функции вместе, мы можем извлечь значения x1, y1, x2 и y2, необходимые для интерполяции.
Найдите значение x1 по этой формуле:
=ИНДЕКС(B5:B10,ПОИСКПОЗ(F3,B5:B10,1))
Формула возвращает 40, так как аргумент тип_сопоставления в функции ПОИСКПОЗ имеет значение 1. Это говорит функции ПОИСКПОЗ, что нужно вернуть позицию из массива температур, который меньше искомого_значения, если точное совпадение не найдено.
Это говорит функции ПОИСКПОЗ, что нужно вернуть позицию из массива температур, который меньше искомого_значения, если точное совпадение не найдено.
Найдите значение x2 по этой формуле:
=ИНДЕКС(B5:B10,ПОИСКПОЗ(F3,B5:B10,1)+1)
Формула для x2 возвращает 60, так как результат, возвращаемый функция ПОИСКПОЗ увеличивается на 1, чтобы указать Excel искать следующую строку в массиве.
Для y1 и y2 формулы очень похожи. Единственное отличие состоит в том, что аргументом массива для функции ИНДЕКС является столбец C.
Для y1 формула: y2 формула:
=ИНДЕКС(C5:C10,ПОИСКПОЗ(F3,B5:B10,1)+1)
Наконец, используйте функцию ПРОГНОЗ, как описано выше, чтобы получить оценочное значение y:
=ПРОГНОЗ(F3,F6:F7,F4:F5)
Как выполнить интерполяцию в Excel с помощью формулы интерполяции
Линейную интерполяцию в Excel также можно выполнить без использования функции ПРОГНОЗ. Вместо этого используйте приведенную ниже формулу интерполяции, где y — возвращаемое значение, а x — независимая переменная:
Вместо этого используйте приведенную ниже формулу интерполяции, где y — возвращаемое значение, а x — независимая переменная:
Эту формулу можно использовать в Excel для линейной интерполяции значения y:
=F6+(F3- F4)*(F7-F6)/(F5-F4)
[Подсказка] Используйте именованные ячейки, чтобы упростить понимание формулы:
Как интерполировать график в Excel?
Результаты интерполяции можно отобразить на графике, создав диаграмму Excel с двумя рядами данных. Первая серия состоит из массивов значений x и y. Вторая серия содержит значение x для поиска и результирующую оценку y.
Самое замечательное в настройке формул, как показано выше, заключается в том, что вы можете правильно интерполировать между ЛЮБОЙ парой известных значений x и y.
Вот и все — несколько альтернативных методов выполнения линейной интерполяции в Excel. Надеюсь, вы сможете использовать один из этих методов, чтобы сэкономить время, когда вам нужно интерполировать данные из большого набора данных.
Интерполировать в Excel | Методы интерполяции значений в Excel
Интерполяция Excel (содержание)
Интерполяция — это метод, используемый для оценки или нахождения значения между двумя известными значениями на линии или кривой. Этот вид прогнозирования используется во многих видах анализа, таких как инвестирование в рост, прогнозирование чисел, разработка стратегий, принятие решений о страховании, движение цен, акции и рынки акций и т. д.
Линейная интерполяция означает оценку будущей стоимости определенной переменной на основе текущих данных. В MS-Excel создается прямая линия, которая соединяет два известных значения, и, таким образом, будущее значение рассчитывается с помощью простой математической формулы или с помощью функции ПРОГНОЗ.
Примеры интерполяции в Excel
Давайте разберемся, как интерполировать в Excel, на нескольких примерах.
Вы можете скачать этот шаблон интерполяции Excel здесь — Шаблон интерполяции Excel
Пример № 1 — Использование простой математической формулы
Допустим, у нас есть простой набор данных из двух известных значений x и y, и мы хотим интерполировать значение ( т. е. найти соответствующее значение y для значения x) следующим образом:
Таким образом, простая формула, которая используется для интерполяции этого значения:
y= y 1 + (x – x 1 ) *
Здесь x=22,5
Таким образом, когда мы применяем эту формулу к данному набору данных, мы получаем интерполированное значение y как:
3
9002На приведенном выше снимке экрана видно, что мы интерполировали значение с двумя известными значениями x и y. Бывают моменты, когда становится трудно запомнить формулу. Так что в таких случаях можно использовать функцию ПРОГНОЗ.
Пример 2. Использование функции ПРОГНОЗ
Теперь предположим, что мы хотим интерполировать то же значение в Примере 1, используя функцию ПРОГНОЗ.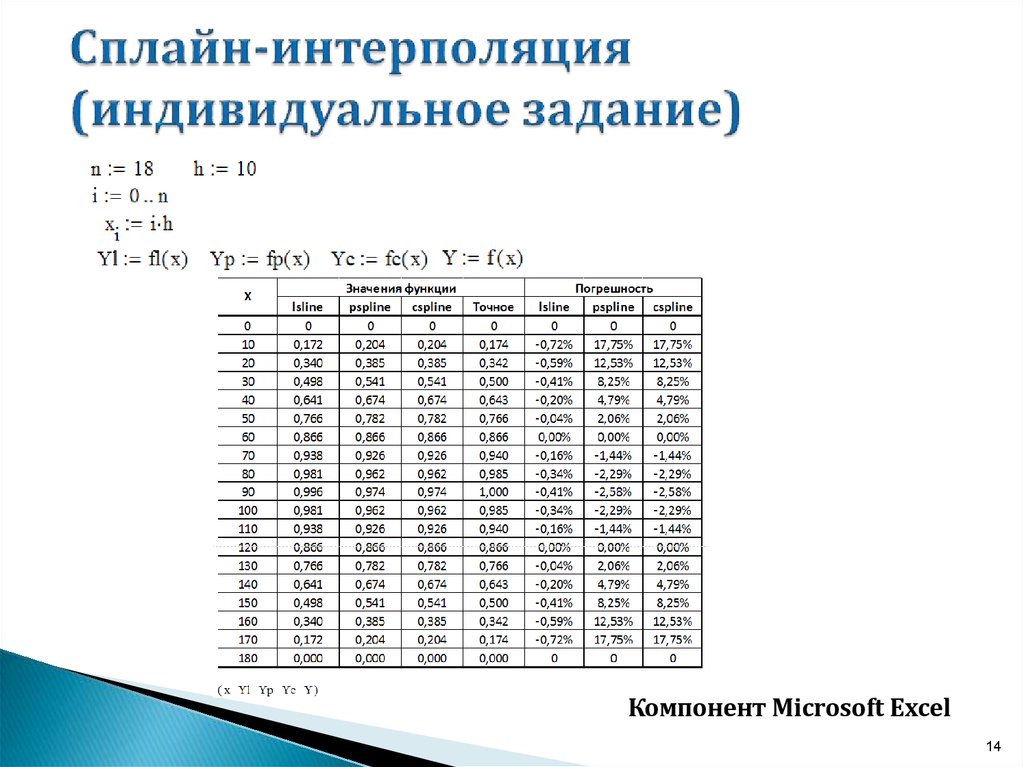
Функция ПРОГНОЗ оценивает значение на основе существующих значений вместе с линейным трендом. Он имеет следующий синтаксис:
ПРОГНОЗ(x, известные_y, известные_x)
Где,
Итак, давайте теперь посмотрим на приведенном ниже снимке экрана, что происходит, когда мы применяем эту функцию ПРОГНОЗ для интерполяции заданного значения x:
Итак, на приведенном выше снимке экрана мы видим, что функция ПРОГНОЗ также хорошо работает для этого.
Пример № 3. Использование функции прогнозирования
Теперь предположим, что у нас есть набор данных розничной фирмы с количеством дней и соответствующими продажами фирмы в эти дни (т. е. количество единиц, проданных в эти дни). ) как показано ниже:
Продажи в этом случае являются линейными (что также можно проверить вручную или с помощью линейного графика).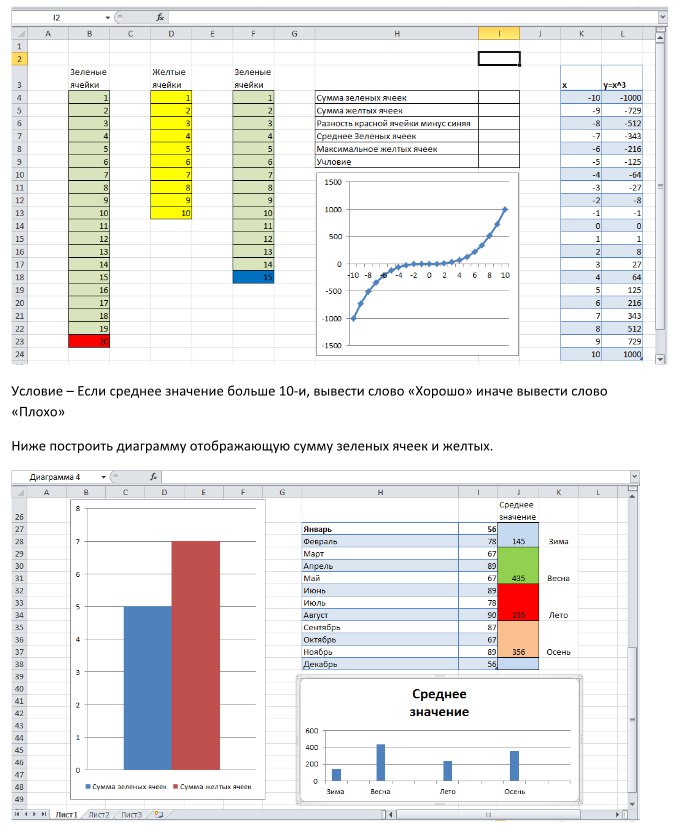 Теперь давайте посмотрим, как мы используем функцию ПРОГНОЗ, когда известные_y и известные_x вычисляются с использованием функции СМЕЩ и ПОИСКПОЗ:
Теперь давайте посмотрим, как мы используем функцию ПРОГНОЗ, когда известные_y и известные_x вычисляются с использованием функции СМЕЩ и ПОИСКПОЗ:
Давайте сначала посмотрим синтаксис функции СМЕЩ и функции ПОИСКПОЗ:
Функция СМЕЩ возвращает ячейку или диапазон ячеек указывается в строках и столбцах, в зависимости от высоты и ширины в указанных строках и столбцах. Он имеет следующий синтаксис:
СМЕЩЕНИЕ (ссылка, строки, столбцы, [высота], [ширина])
Где
Функция ПОИСКПОЗ возвращает относительное положение искомого значения в строке, столбце или таблице, которое соответствует указанному значению в указанном порядке.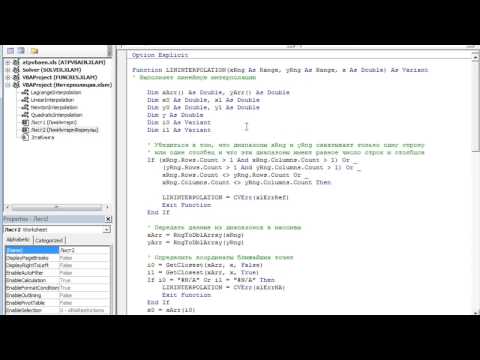 Он имеет следующий синтаксис:
Он имеет следующий синтаксис:
ПОИСКПОЗ (искомое_значение, искомый_массив, [тип_сопоставления])
Где,
Значение по умолчанию для этого match_type равно 1. Для значения 1 функция ПОИСКПОЗ найдет наибольшее значение, которое меньше или равно искомому_значению, и значение должно быть в порядке возрастания. Для значения 0 функция ПОИСКПОЗ находит первое значение, точно равное искомому_значению. Для значения -1 функция найдет наименьшее значение, которое больше или равно искомому_значению, и значение должно быть в порядке убывания.
Теперь, если мы хотим оценить продажи, скажем, за 28 дней, то мы используем эти функции следующим образом: чтобы выбрать known_y (зависимые значения, т. е. продажи).
е. продажи).
Вторая функция OFFSET, используемая в качестве третьего параметра в функции ПРОГНОЗ, используется для выбора известных_x (независимых значений, т. е. количества дней).
Функция ПОИСКПОЗ, используемая в качестве параметра в функции СМЕЩ, используется для создания положения прогнозируемого значения и, таким образом, для расчета количества строк. Столбцы в функции ПОИСКПОЗ, т. е. второй параметр в ней должен быть равен 0, так как требуется зависимое значение в том же выбранном столбце.
Таким образом, за 28 дней мы оценили или спрогнозировали продажи фирмы на уровне 1 120. Точно так же мы можем оценить продажи фирмы за другое количество дней, используя эту функцию ПРОГНОЗА.
Что нужно помнить об интерполяции в Excel
Рекомендуемые статьи
Это руководство по интерполяции в Excel. Здесь мы обсуждаем, как интерполировать в Excel, а также практические примеры и загружаемый шаблон Excel. Вы также можете просмотреть другие наши рекомендуемые статьи —
Как выполнить интерполяцию между двумя значениями в Excel (6 способов)
Интерполяция данных очень важна, когда мы анализируем эксперимент или хотим предсказать или определить результаты события.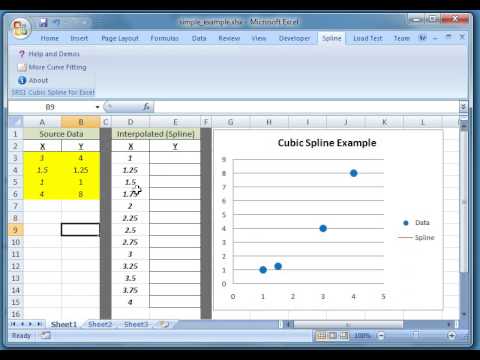 Например, если у нас есть данные по двум разным случаям, мы можем определить данные между этими случаями путем интерполяции. В этой статье кратко описаны методы 6 , как интерполировать между двумя значениями в Excel. В наборе данных у нас есть координат X и координат Y .
Например, если у нас есть данные по двум разным случаям, мы можем определить данные между этими случаями путем интерполяции. В этой статье кратко описаны методы 6 , как интерполировать между двумя значениями в Excel. В наборе данных у нас есть координат X и координат Y .
Скачать практическую рабочую тетрадь
6 способов интерполяции между двумя значениями в Excel
1. Применение функции ПРОГНОЗ/ПРОГНОЗ.ЛИНЕЙНЫЙ для интерполяции между двумя значениями в Excel
2. Использование комбинации функций Excel XLOOKUP и FORECAST для интерполяции между двумя значениями
3. Применение функций ИНДЕКС и ПОИСКПОЗ с функцией ПРОГНОЗ для интерполяции между двумя значениями
4. Интерполяция между двумя значениями с использованием математической формулы
6. Использование функции РОСТА для нелинейной интерполяции
Раздел практики
Вывод
Связанная статья
Загрузить рабочую тетрадь
6 способов интерполяции между двумя значениями в Excel
1. Применение функции ПРОГНОЗ/ПРОГНОЗ.ЛИНЕЙНЫЙ для интерполяции между двумя значениями в Excel
Применение функции ПРОГНОЗ/ПРОГНОЗ.ЛИНЕЙНЫЙ для интерполяции между двумя значениями в Excel Самый простой способ интерполировать между двумя значениями — использовать ПРОГНОЗ/ПРОГНОЗ.ЛИНЕЙНЫЙ 9Функция 0008. Давайте пройдемся по описанию ниже.
Шаги:
=ПРОГНОЗ(C14,C5:C12,B5:B12)
Здесь функция ПРОГНОЗ определяет интерполированное значение в ячейке C15 посредством линейной регрессии . Он работает с диапазонами B5:B12 (как known_Xs ) и C5:C12 (как known_Ys ).
Он работает с диапазонами B5:B12 (как known_Xs ) и C5:C12 (как known_Ys ).
=ПРОГНОЗ.ЛИНЕЙНЫЙ(C14,C5:C12,B5:B12)
Таким образом, вы можете легко интерполировать между двумя значениями, используя функцию ПРОГНОЗ .
Подробнее: Как сделать линейную интерполяцию в Excel (7 удобных методов)
2.
 Использование комбинации функций Excel XLOOKUP и FORECAST для интерполяции между двумя значениями
Использование комбинации функций Excel XLOOKUP и FORECAST для интерполяции между двумя значениями Если вы хотите интерполировать в небольшом диапазоне набора данных, вы можете использовать функцию XLOOKUP для извлечения 0007 координаты в диапазоне и интерполируют значение внутри них. Предположим, мы хотим интерполировать значение 6 в B9:C10 . Давайте обсудим процедуру ниже.
Шаги:
=XLOOKUP(C14, B5:B12,B5:B12,-1,1)
Функция XLOOKUP ищет значение в C14 , ищет это значение в диапазоне B5:B12, и возвращает значение, которое меньше, чем 6,5 , поскольку не может найти это точное значение в этом диапазоне. и мы ставим -1 в связи с этим. Таким образом, мы получаем x1 как 5 .
и мы ставим -1 в связи с этим. Таким образом, мы получаем x1 как 5 .
В этом разделе несколько раз используется аналогичная формула. Когда нам нужно значение, соседнее большее, чем 6.5 , мы использовали « 1 » вместо « -1 » в формуле.
=XLOOKUP(C14, B5:B12,B5:B12,1,1)
=XLOOKUP(C14, B5:B12,C5:C12,-1,1)
=XLOOKUP(C14, B5:B12,C5:C12,1,1)
=ПРОГНОЗ(C14,F9:F10,F7:F8)
Таким образом, вы можете интерполировать между двумя значениями в небольшом диапазоне.
Подробнее: Как выполнять ВПР и интерполировать в Excel (6 способов)
3.
 Применение функций ИНДЕКС и ПОИСКПОЗ с функцией ПРОГНОЗ для интерполяции между двумя значениями
Применение функций ИНДЕКС и ПОИСКПОЗ с функцией ПРОГНОЗ для интерполяции между двумя значениями Мы также можем интерполировать между двумя значениями в небольшом диапазоне набора данных, используя ИНДЕКС и ПОИСКПОЗ функции для извлечения координат в диапазоне и интерполяции значения внутри них. Предположим, мы хотим интерполировать значение 6 в B9:C10 . Давайте обсудим процедуру ниже.
Шаги:
=ИНДЕКС(B5:B12,ПОИСКПОЗ(C14,B5:B12,1))
Здесь функция ПОИСКПОЗ возвращает позицию значения ячейки C14 в диапазоне B5:B12 . И затем функция ИНДЕКС возвращает значение этой позиции в B5:B12 . Таким образом, он вернул x1 .
И затем функция ИНДЕКС возвращает значение этой позиции в B5:B12 . Таким образом, он вернул x1 .
Аналогичная формула используется в этом разделе несколько раз для определения x2 , y1 , и y2 .
=ИНДЕКС(B5:B12,СООТВЕТСТВИЕ(C14,B5:B12,1)+1)
=ИНДЕКС(C5:C12,ПОИСКПОЗ(C14,B5:B12,1))
=ИНДЕКС(C5:C12,ПОИСКПОЗ(C14,B5:B12,1)+1)
=ПРОГНОЗ(C14,F9:F10,F7:F8)
Таким образом, вы можете интерполировать между двумя значениями в небольшом диапазоне.
4. Интерполяция между двумя значениями с использованием математической формулы
Другим эффективным методом интерполяции между двумя значениями является применение математической формулы.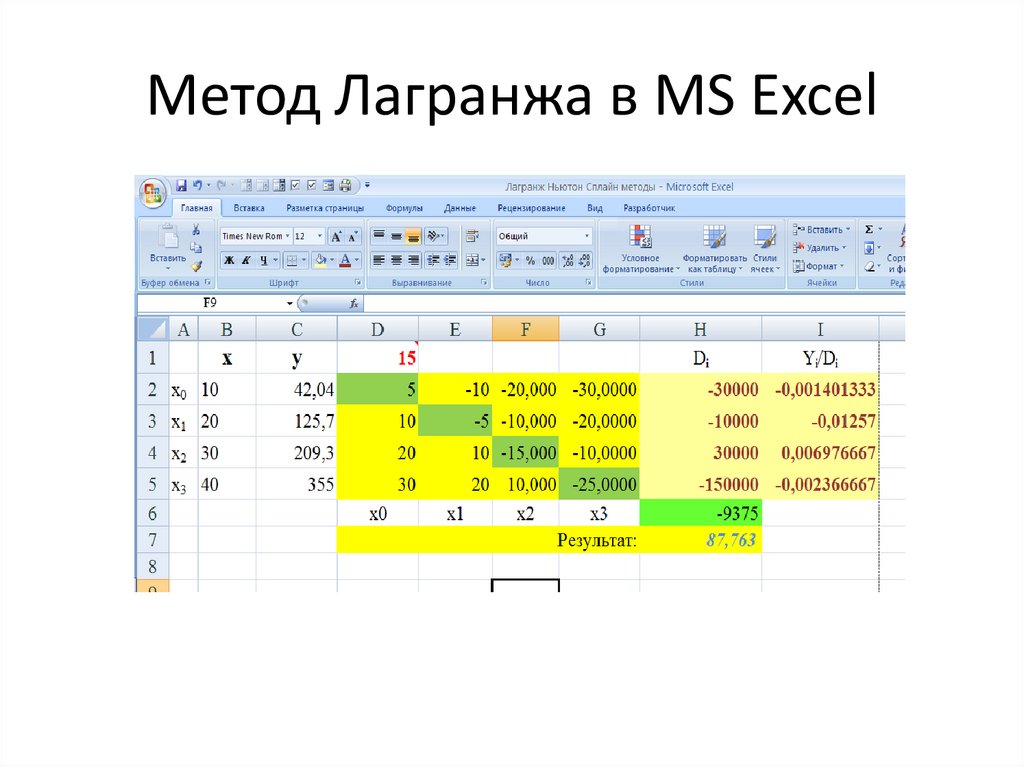 Формула интерполяции приведена ниже.
Формула интерполяции приведена ниже.
Это уравнение прямой линии. Давайте следуем необходимым инструкциям, чтобы применить его к интерполировать между двумя значениями.
Шаги:
=C7+(C14-B7)*(C8-C7)/(B8-B7)
Формула возвращает интерполированное значение путем измерения наклона 2 точек, которые составляют (2,5, 4) и (3, 6) .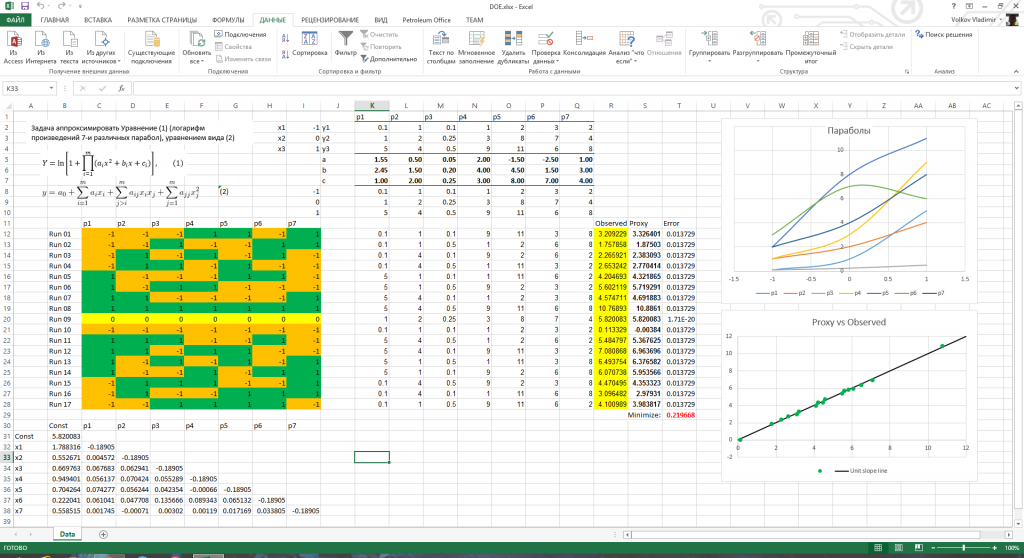
Таким образом, вы можете интерполировать между двумя значениями, просто используя математическое уравнение.
(6 методов) 5. Интерполяция между двумя значениями с помощью функций SLOPE и INTERCEPT
Один из самых простых способов интерполировать между двумя значениями — использовать функции Excel НАКЛОН и ПЕРЕХОД и использовать их результаты в формуле прямой линии . Давайте посмотрим на процедуру ниже. Мы хотим интерполировать Координата X 10.
Шаги:
=УКЛОН(C5:C12,B5:B12)
Функция НАКЛОН возвращает наклон/градиент линии линейной регрессии, состоящей из точек, образованных заданными X и Y Координаты .
=ПЕРЕХОД (C5:C12,B5:B12)
Функция INTERCEPT возвращает Y-пересечение линии линейной регрессии, состоящей из точек, образованных заданными X и Y Координаты .
=E7*C14+E9
Формула представляет собой базовую формулу прямой линии, которая равна y=mx+c .
Таким образом, вы можете определить интерполированное значение между двумя значениями с помощью функций Excel НАКЛОН и ПЕРЕХОД .
6. Использование функции РОСТА для нелинейной интерполяции
Функция РОСТ — это специальная функция для интерполяции нелинейных данных. Наш набор данных в основном состоит из нелинейных отношений между координатами Y и X.0008 . Поэтому лучше всего использовать эту функцию.
Шаги:
=РОСТ(C5:C12,B5:B12,C14)
Здесь Функция РОСТ возвращает интерполированные данные путем прогнозирования экспоненциального роста координат X и Y .
Таким образом, вы можете найти интерполированных значений, используя функцию РОСТ . Поскольку эта функция работает для нелинейных отношений, с ее помощью вы можете получить более точные данные.
Подробнее: Как выполнять интерполяцию с помощью функций РОСТА И ТРЕНДА в Excel
Секция практики
На следующем изображении вы увидите набор данных этой статьи.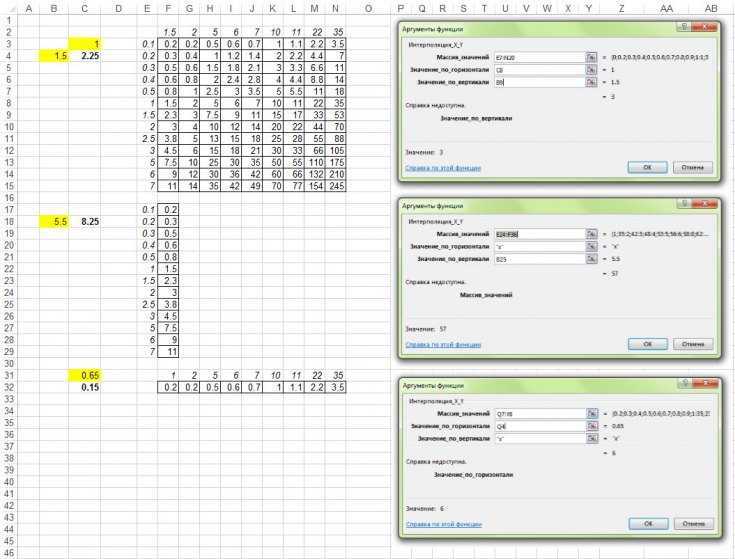


 Выбираем наиболее подходящий из них на свое усмотрение.
Выбираем наиболее подходящий из них на свое усмотрение. Кликаем по графику, после чего на ленте активируется дополнительный набор вкладок – «Работа с диаграммами» . Перемещаемся во вкладку «Макет» и жмем на кнопку «Линия тренда» в блоке «Анализ» . Кликаем по пункту «Линейное приближение» или «Экспоненциальное приближение» .
Кликаем по графику, после чего на ленте активируется дополнительный набор вкладок – «Работа с диаграммами» . Перемещаемся во вкладку «Макет» и жмем на кнопку «Линия тренда» в блоке «Анализ» . Кликаем по пункту «Линейное приближение» или «Экспоненциальное приближение» . На горизонтальной оси видно, что 5 единиц равно одному делению. Значит это один период. В поле «Вперед на» вписываем значение «1» . Жмем на кнопку «Закрыть» в нижнем правом углу окна.
На горизонтальной оси видно, что 5 единиц равно одному делению. Значит это один период. В поле «Вперед на» вписываем значение «1» . Жмем на кнопку «Закрыть» в нижнем правом углу окна.
 Эта операция доставит вам значение в ячейке C9 .
Эта операция доставит вам значение в ячейке C9 . Эта операция доставит вам значение в ячейке C9 .
Эта операция доставит вам значение в ячейке C9 .