Интервальный вариационный ряд – просто и кратко
Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина принимает слишком много различных значений . Зачастую ИВР появляется в результате изучения непрерывной характеристики объектов. Типично – это время, масса, размеры и другие физические величины. Вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.
В таких ситуациях затруднительно либо невозможно применить тот же подход, что для дискретного ряда. Это связано с тем, что ВСЕ варианты различны (во многих случаях). И даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, а фактически значения всё равно отличаются хоть какими-то микрограммами.
Поэтому здесь используется другой подход, а именно определяется интервал,

Если варианта попала на «стык» интервалов, то её относят к старшему интервалу.
Интервальный вариационный ряд (ИВР) статистической совокупности – это упорядоченное множество смежных интервалов и соответствующие им частоты, в сумме равные объёму совокупности. Дабы не плодить лишних букв и индексов, я никак не обозначил эти интервалы. Придирчивый читатель, к слову, наверняка заметил, что через я обозначаю как исходные варианты, так и значения сгруппированного ряда.
Следует отметить, что исследуемая характеристика не обязана быть непрерывной, и мы как раз начнём с такой задачи:
Пример 6
По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в денежных
единицах):
Составить вариационный ряд, построить гистограмму частот, гистограмму и полигон относительных частот + бонус:
эмпирическую функцию распределения.
Решение: очевидно, что перед нами выборочная совокупность объема , и вопрос номер один: какой ряд составлять – дискретный или интервальный? Заметьте, что в вопросе задачи ничего не сказано о характере ряда. Строго говоря, цены дискретны и среди них даже есть одинаковые. Однако они могут быть округлены, да и разброс цен довольно велик. Поэтому здесь целесообразно провести интервальное разбиение.
Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только ручка, карандаш, тетрадь и калькулятор.
Тактика действий похожа на работу с дискретным вариационным рядом. Сначала
окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все
значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае
напрашиваются промежутки единичной длины. Записываем их на черновик:
Записываем их на черновик:
Теперь начинаем вычёркивать числа из исходного списка и записываем их в соответствующие колонки нашей импровизированной
таблицы:
После этого находим самое маленькое число в левой колонке (минимальное значение) и самое большое число – в правой (максимальное значение). Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
ден. ед. – не забываем указывать размерность!
Вычислим размах вариации:
ден. ед. – длина общего
интервала, в пределах которого варьируется цена.
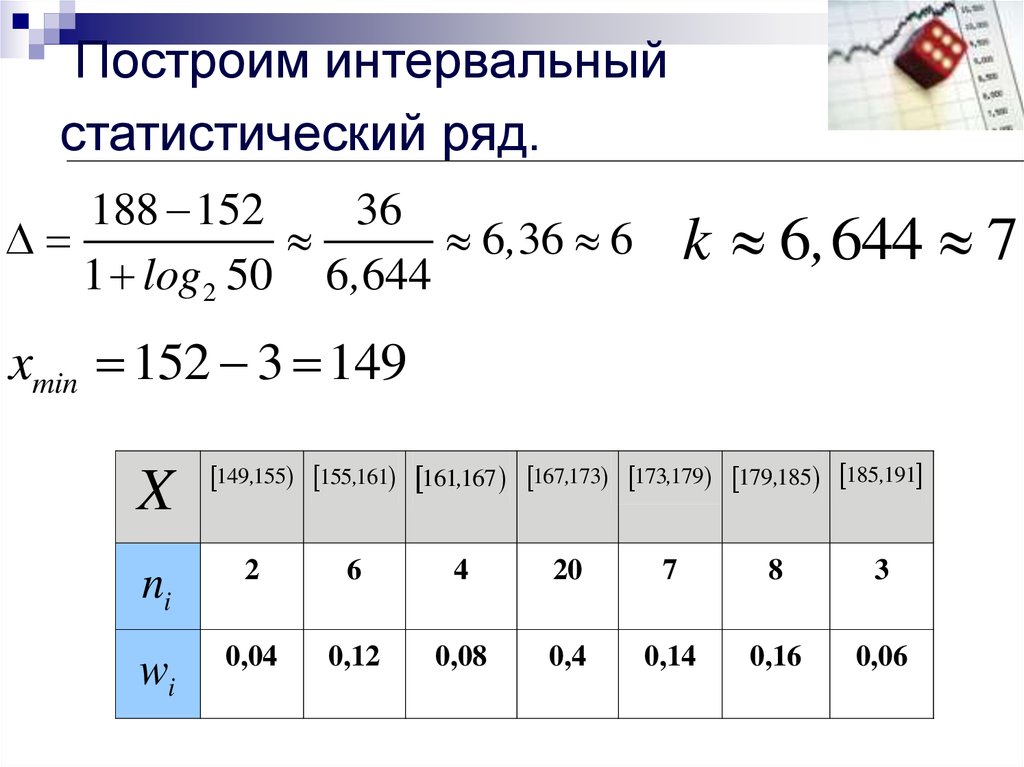
Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса:
, где – десятичный логарифм* от объёма выборки и
– оптимальное количество
интервалов, при этом результат округляют до ближайшего левого целого значения.
* есть на любом более или менее приличном калькуляторе.
В нашем случае получаем: интервалов.
Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов следует проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.
Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную
группировку:
– длина частичного интервала. В
принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.
И коль скоро мы прибавили 0,04, то по пяти частичным интервалам получается «перебор»: . Посему от самой малой варианты отмеряем влево 0,1 влево (половину «перебора») и к
значению 5,7 начинаем прибавлять по ,
получая тем самым частичные интервалы. При этом сразу рассчитываем их середины (например, ) – они требуются почти во всех тематических задачах:
При этом сразу рассчитываем их середины (например, ) – они требуются почти во всех тематических задачах:
– убеждаемся в том, что самая большая варианта вписалась в последний частичный интервал и отстоит от его правого конца на
0,1.
Далее подсчитываем частоты по каждому интервалу. Для этого в черновой таблице обводим значения, попавшие в тот или
иной интервал, подсчитываем их количество и вычёркиваем:
Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее. Варианта попала на «стык» интервалов и, согласно озвученному выше правилу, её следует отнести к последующему интервалу .
В результате получаем интервальный вариационный ряд:
при этом обязательно убеждаемся в том, что ничего не потеряно:
, ОК.
…Да, кстати, все ли представили свой любимый товар, чтобы было интереснее разбирать это длинное решение? J
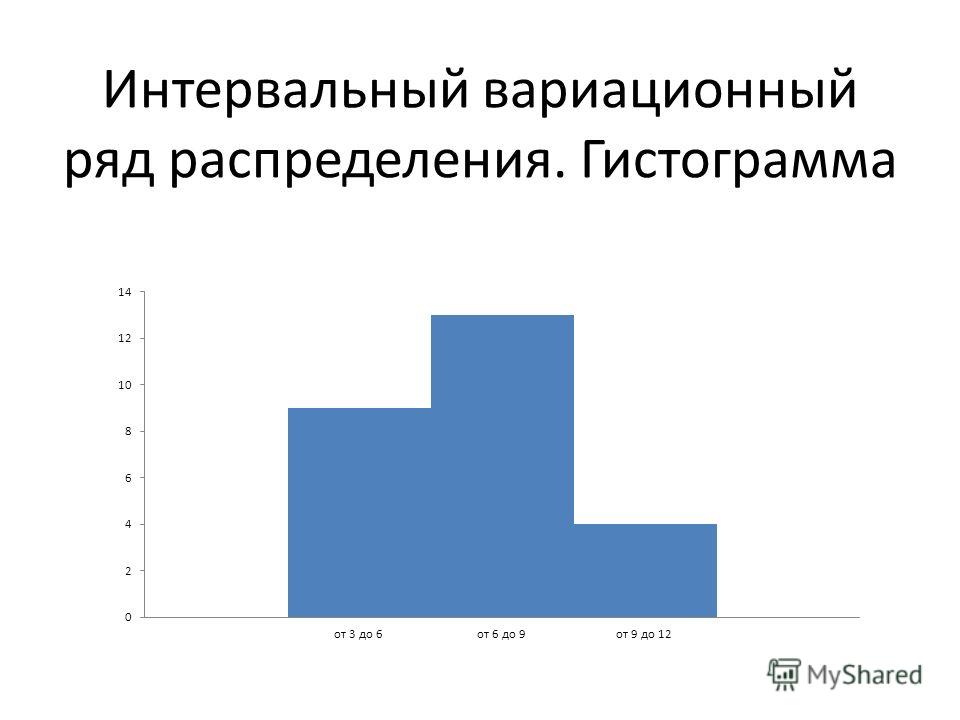
Точно также как и в дискретном случае, интервальный вариационный ряд можно
(и нужно) изобразить графически. И здесь у нас весьма большое разнообразие. Но сначала добавим в таблицу дополнительные
столбцы и продолжим расчёты:
И здесь у нас весьма большое разнообразие. Но сначала добавим в таблицу дополнительные
столбцы и продолжим расчёты:
По каждому интервалу рассчитываем (не тушуемся): плотность частот , относительные частоты (округляем их до 2 знаков после запятой), а также плотность относительных частот . Поскольку длина частичного интервала
, то вычисления заметно упрощаются:Если интервалы имеют разные длины , то при нахождении плотностей каждую частоту нужно разделить на длину своего интервала: . Но у нас группировка равноинтервальная, да не абы какая, а с единичным частичным интервалом. Дело за чертежами. Один за другим:
2.2.1. Гистограммы
2.1.2. Эмпирическая функция распределения
| Оглавление |
|
1.  Вариационный ряд. Вариационный ряд.2.Числовые характеристики вариационного ряда.
|
|||||||||||||||||||||||||||||
| 24 25 26 27 28 29 30 31 32 | |||||||||||||||||||||||||||||
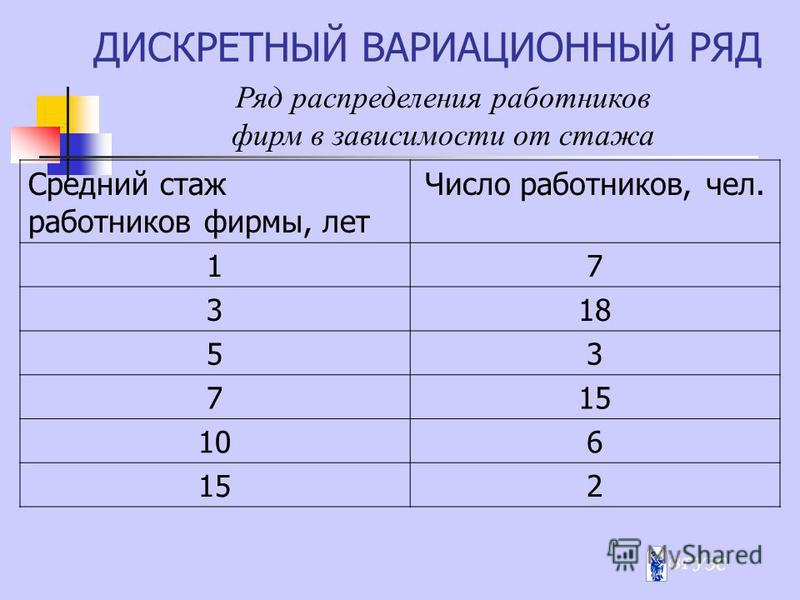
1.Вариационный ряд. Многие явления, в том числе и экономические, имеют большой объем числовой информации. Для того, чтобы обработатать и изучить такой большой объем данных, необходимо сначала каким-то образом его сгруппировать. |
|||||||||||||||||||||||||||||
Таб.1 По данным таблицы построим полигон распределения частот (рис.1) |
Рис.1 |
||||||||||||||||||||||||||||
|
В приведенной выше таблице проданные товары сгруппированы по наименованию бренда товара (например телевизоры разных марок). Т.е. в данном случае признаком является наименование марки (бренда) товара. |
|||||||||||||||||||||||||||||
Таб. 2 По данным таблицы построим гистограмму распределения частот (рис.2) |
Рис.2 |
||||||||||||||||||||||||||||
|
Таблица 2 сгруппирована по ценовым категориям. Каждая группа имеет свой интервал цен. Данный ряд называется интервальный. Из таблицы можно увидеть, что наибольшее значение частоты имеет группа 3 в интервале цен 40-60 соответственно 43шт. Вариационные ряды на порядок меньше всего объема данных и это существенно облегчает их обработку и анализ. Полигон распределения или гистограмма вариационного ряда является аналогом распределения случайной величины. |
|||||||||||||||||||||||||||||
2.Числовые характеристики вариационного ряда. |
|||||||||||||||||||||||||||||
|
Одной из основных числовых характеристик вариационных рядов является средняя арифметическая. Данная величина показывает центральное значение признака, вокруг которого сосредоточенны все наблюдения. Средней арифметической вариационного ряда называется сумма произведений признаков (вариантов) ряда на соответствующие им частости. |
|||||||||||||||||||||||||||||
|
Средним линейным отклонением вариационного ряда называется средняя арифметическая модуля отклонения признаков от их средней арифметической. |
|||||||||||||||||||||||||||||
|
Дисперсией s2 вариационного ряда называется средняя арифметическая квадратов отклонений признаков от их средней арифметической. |
|||||||||||||||||||||||||||||
|
Среднее квадратическое отклонение вариационного ряда равно квадратному корню из дисперсии. |
|||||||||||||||||||||||||||||
|
Важным показателем вариационного ряда является также коэффициент вариации, который показывает однородность исследуемого признака. |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
Пример. |
|||||||||||||||||||||||||||||
В компании по продаже бытовой техники, случайная величина Х (цена за единицу товара (техники) в ден.ед.) сгруппирована по интервалам цен и общий объем продаж составил 400 шт. Необходимо построить полигон распределения случайной величины Х, кумуляту и эмпирическую функцию ряда. Необходимо также найти: среднюю арифметическую, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, начальный (центральный) моменты k-го порядка, коэффициент асиметрии и эксцесс данной случайной величины. |
|||||||||||||||||||||||||||||
|
Решение. Построим таблицу для рассчета средней арифметической и рассчитаем частость для каждого интервала цен. |
|||||||||||||||||||||||||||||
Как видно из таблицы сумма произведений xini = 14610, разделим эту сумму на n и получим среднюю арифметическую вариационного ряда. |
|||||||||||||||||||||||||||||
По данным таблицы построим гистограмму распределения частот.
|
|||||||||||||||||||||||||||||
Построим и эмпирическую функцию распределения случайной величины (кумуляту). |
|||||||||||||||||||||||||||||
|
Далее найдем моду и медиану случайной величины Х. Наиболее вероятное значение случайной величины Х (мода) равно Mo = 34,117. Т.е. Pmax (34,1) = 0,1975. Медиана — Ме = 34,3 (как видно из графика). Теперь рассчитаем начальный и центральный моменты k — го порядка и сведем эти данные в таблицу.
|
|||||||||||||||||||||||||||||
Из данных таблицы найдем дисперсию, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс по следующим формулам:
|
|||||||||||||||||||||||||||||
| 24 25 26 27 28 29 30 31 32 | |||||||||||||||||||||||||||||
Центральная тенденция и изменчивость — Социология 3112 — Факультет социологии
Цели обучения
- Понимание и расчет трех способов определения центра распределения
- Понять и рассчитать четырьмя способами величину дисперсии или изменчивости в распределении можно определить
- Понять, как асимметрия и уровень измерения могут помочь определить, какие меры центральная тенденция и изменчивость наиболее подходят для данного распределения
Ключевые термины
Показатели центральной тенденции: категорий или показателей, которые описывают, что является «средним» или «типичным» для данного распределения. К ним относятся мода, медиана и среднее значение.
К ним относятся мода, медиана и среднее значение.
Процентиль: показатель, ниже которого падает определенный процент данного распределения.
Распределение с положительной асимметрией: распределение с несколькими очень большими значениями.
Распределение с отрицательной асимметрией: — распределение с несколькими чрезвычайно низкими значениями.
Показатели изменчивости: чисел, описывающих разнообразие или дисперсию в распределении данного
переменная.
Блочная диаграмма: графическое представление размаха, межквартильного размаха и медианы заданного
переменная.
Мода
Мода — категория с наибольшей частотой (или процентом). Это не
сама частота. Другими словами, если кто-то спросит вас о режиме раздачи
показано ниже, ответом будет кокосовый орех, а НЕ 22.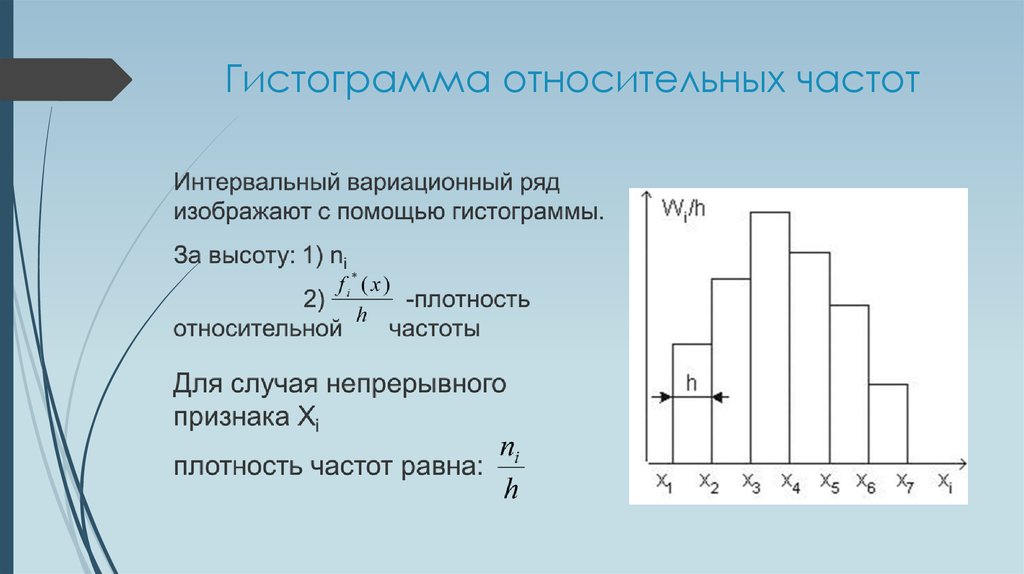 Возможно иметь более
один режим в распределении. Такие распределения считаются бимодальными (если
два режима) или мультимодальный (если режимов больше двух). Дистрибутивы без
четкая мода называется однородной. Режим не особо полезный, но он есть
единственная мера центральной тенденции, которую мы можем использовать с номинальными переменными. Ты найдешь
почему это единственная подходящая мера для номинальных переменных, когда мы узнаем о
медиана и среднее значение рядом.
Возможно иметь более
один режим в распределении. Такие распределения считаются бимодальными (если
два режима) или мультимодальный (если режимов больше двух). Дистрибутивы без
четкая мода называется однородной. Режим не особо полезный, но он есть
единственная мера центральной тенденции, которую мы можем использовать с номинальными переменными. Ты найдешь
почему это единственная подходящая мера для номинальных переменных, когда мы узнаем о
медиана и среднее значение рядом.
Любимые вкусы мороженого:
Кокос = 22
Шоколад = 15
Ваниль = 7
Клубника = 9
Медиана
Медиана — это самое среднее число. Другими словами, это число, которое делит
распределение ровно пополам, так что половина случаев выше медианы, и
половина ниже. Он также известен как 50-й процентиль, и его можно рассчитать для
порядковые переменные и переменные интервала/отношения. Концептуально найти медиану довольно просто.
и влечет за собой только упорядочивание всех ваших наблюдений от наименьшего к наибольшему.
а затем найти любое число, попадающее в середину. Обратите внимание, что нахождение медианы
требует сначала упорядочить все наблюдения от меньшего к большему. Вот почему
медиана не является подходящей мерой центральной тенденции для номинальных переменных,
поскольку номинальные переменные не имеют внутреннего порядка. (На практике нахождение медианы может
быть немного более вовлеченным, особенно если у вас есть большое количество наблюдений — см.
ваш учебник для объяснения того, как найти медиану в таких ситуациях).
Он также известен как 50-й процентиль, и его можно рассчитать для
порядковые переменные и переменные интервала/отношения. Концептуально найти медиану довольно просто.
и влечет за собой только упорядочивание всех ваших наблюдений от наименьшего к наибольшему.
а затем найти любое число, попадающее в середину. Обратите внимание, что нахождение медианы
требует сначала упорядочить все наблюдения от меньшего к большему. Вот почему
медиана не является подходящей мерой центральной тенденции для номинальных переменных,
поскольку номинальные переменные не имеют внутреннего порядка. (На практике нахождение медианы может
быть немного более вовлеченным, особенно если у вас есть большое количество наблюдений — см.
ваш учебник для объяснения того, как найти медиану в таких ситуациях).
Некоторые из вас, вероятно, уже задаются вопросом: «Что произойдет, если у вас будет четное число
случаев? Тогда среднего числа не будет, верно?» Это очень проницательное замечание,
и я рад, что вы спросили. Если в вашем наборе данных четное количество случаев, медиана равна
среднее из двух средних чисел. Например, для чисел 18, 14, 12,
8, 6 и 4 медиана равна 10 (12 + 8 = 20; 20/2 = 10).
Если в вашем наборе данных четное количество случаев, медиана равна
среднее из двух средних чисел. Например, для чисел 18, 14, 12,
8, 6 и 4 медиана равна 10 (12 + 8 = 20; 20/2 = 10).
Одним из преимуществ медианы является то, что она не чувствительна к выбросам. Выброс это наблюдение, которое находится на аномальном расстоянии от других значений в выборке. Наблюдения которые значительно больше или меньше других в выборке, могут повлиять на некоторые статистические показатели таким образом, что они вводят в заблуждение, но медиана невосприимчив к ним. Другими словами, не имеет значения, является ли самое большое число 20 или 20 000; он по-прежнему считается только одним числом. Рассмотрим следующее:
Распределение 1: 1, 3, 5, 7, 20
Распределение 2: 1, 3, 5, 7, 20 000
Эти два распределения имеют одинаковые медианы, хотя распределение 2 имеет очень
большой выброс, что в конечном итоге приведет к довольно значительному искажению среднего значения, как мы
увидеть через мгновение.
Среднее
Среднее — это то, что люди обычно называют «средним». это высшая мера центральной тенденции, под которой я подразумеваю, что он доступен для использования только с интервалом/соотношением переменные. Среднее значение учитывает ценность каждого наблюдения и, таким образом, обеспечивает самая информативная из всех мер центральной тенденции. Однако, в отличие от медианы, среднее значение чувствительно к выбросам. Другими словами, один чрезвычайно высокий (или низкий) значение в вашем наборе данных может значительно повысить (или понизить) среднее значение. Среднее, часто отображается как переменная x или y с линией над ней (произносится как «x-bar» или «y-bar»), это сумма всех баллов, деленная на общее количество баллов. В статистическом обозначение, мы бы записали его следующим образом:
В этом уравнении – среднее значение, X – значение каждого наблюдения, а N – общее
количество дел.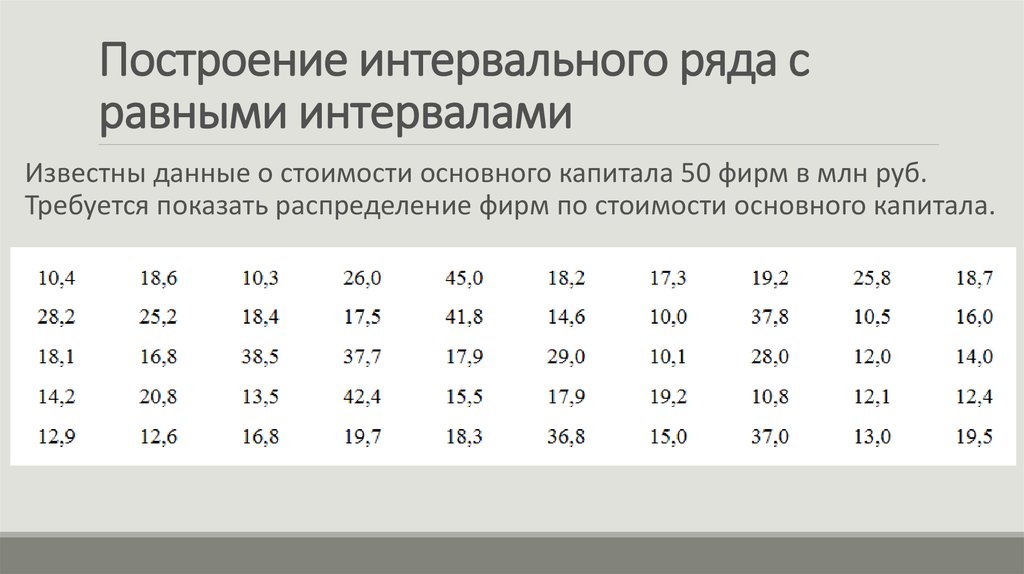 Сигма (Σ) просто говорит нам сложить все оценки вместе.
Тот факт, что вычисление среднего требует сложения и деления, является той самой причиной.
его нельзя использовать ни с номинальными, ни с порядковыми переменными. Мы не можем вычислить среднее
для расы (белый + белый + черный/3 = ?) не больше, чем мы можем вычислить среднее значение за год
в школе (первокурсник + первокурсник + старший/3 = ?)
Сигма (Σ) просто говорит нам сложить все оценки вместе.
Тот факт, что вычисление среднего требует сложения и деления, является той самой причиной.
его нельзя использовать ни с номинальными, ни с порядковыми переменными. Мы не можем вычислить среднее
для расы (белый + белый + черный/3 = ?) не больше, чем мы можем вычислить среднее значение за год
в школе (первокурсник + первокурсник + старший/3 = ?)
Процентили
Процентиль — это число, ниже которого падает определенный процент распределения.
Например, если вы набрали 90-й процентиль на тесте, 90 процентов учащихся
кто прошел тест набрал меньше вас. Если вы набрали 72-й процентиль на тесте,
72 процента учащихся, сдавших тест, набрали меньше, чем вы. Если забит в 5-м
процентиль на тесте, возможно, этот предмет не для вас. Медиана, как вы помните, падает
на 50-м процентиле. Пятьдесят процентов наблюдений попадают ниже него.
Медиана, как вы помните, падает
на 50-м процентиле. Пятьдесят процентов наблюдений попадают ниже него.
Симметричное и асимметричное распределения
Симметричное распределение – это распределение, в котором среднее значение, медиана и мода являются
одно и тоже. С другой стороны, асимметричное распределение — это распределение с экстремальными значениями.
с той или иной стороны, которые заставляют медиану отклоняться от среднего в одном направлении
или другое. Если среднее значение больше медианы, говорят, что распределение
быть положительно перекошены. Другими словами, существует чрезвычайно большое значение, которое «тянет»
среднее к верхнему концу распределения. Если среднее значение меньше, чем
медиану, говорят, что распределение имеет отрицательную асимметрию. Другими словами, существует
чрезвычайно малое значение, которое «тянет» среднее значение к нижнему концу распределения. Распределение доходов обычно имеет положительную асимметрию из-за небольшого количества
люди, которые зарабатывают невероятные суммы денег. Рассмотрим (по общему признанию датированный) случай
Футболисты Высшей лиги как крайний пример. Средняя годовая зарплата MLS
игрок в 2010 году составлял примерно 138 000 долларов, но средняя годовая зарплата составляла всего около
53 000 долларов. Среднее значение было почти в три раза больше, чем медиана, в немалой степени благодаря
часть к тогдашней зарплате Дэвида Бекхэма в размере 12 миллионов долларов.
Распределение доходов обычно имеет положительную асимметрию из-за небольшого количества
люди, которые зарабатывают невероятные суммы денег. Рассмотрим (по общему признанию датированный) случай
Футболисты Высшей лиги как крайний пример. Средняя годовая зарплата MLS
игрок в 2010 году составлял примерно 138 000 долларов, но средняя годовая зарплата составляла всего около
53 000 долларов. Среднее значение было почти в три раза больше, чем медиана, в немалой степени благодаря
часть к тогдашней зарплате Дэвида Бекхэма в размере 12 миллионов долларов.
Пытаясь решить, какую меру центральной тенденции использовать, вы должны учитывать
как уровень измерения, так и перекос. Дело обстоит не так для именных и порядковых
переменные. Если переменная является номинальной, очевидно, что мода является единственной мерой центральной
склонность к употреблению.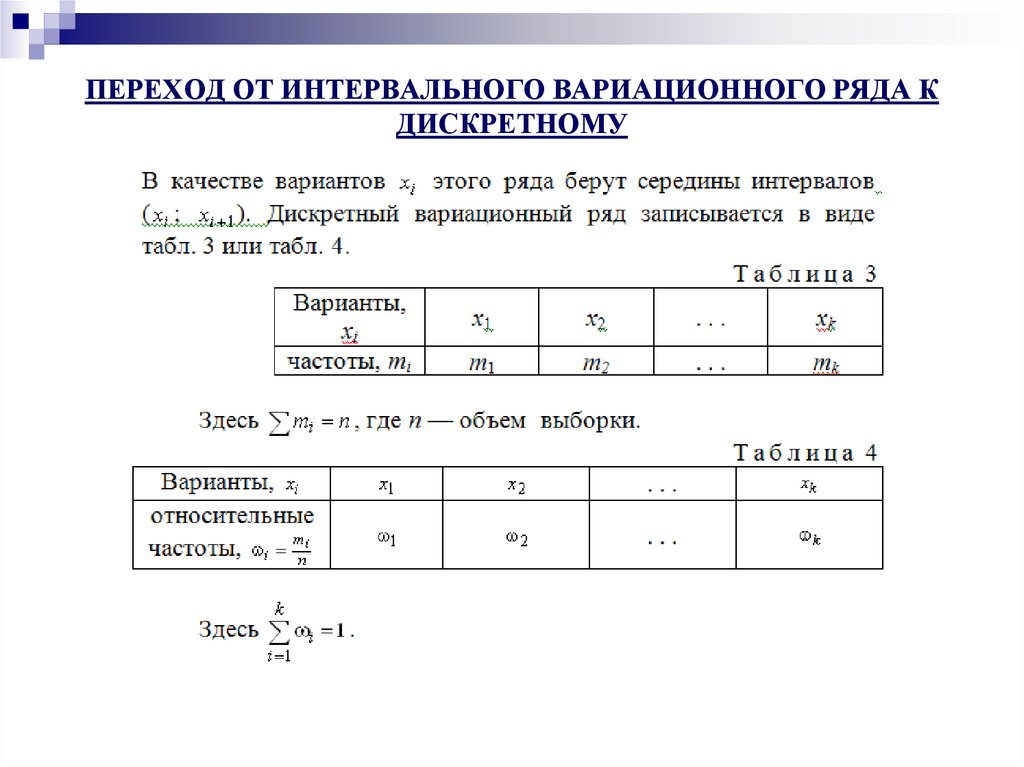 Если переменная порядковая, медиана, вероятно, ваш лучший выбор
потому что он предоставляет больше информации об образце, чем режим. Но если
переменная — интервал/отношение, вам нужно определить, является ли распределение симметричным
или перекошенный. Если распределение симметрично, то среднее является лучшей мерой центральной
тенденция. Если распределение асимметрично как в положительную, так и в отрицательную сторону, медиана
является более точным. В качестве примера того, почему среднее значение может быть не лучшим показателем центрального
тенденцию к асимметричному распределению, рассмотрите следующий отрывок из книги Чарльза Уилана.
Обнаженная статистика: избавление от ужаса данных (2013):
Если переменная порядковая, медиана, вероятно, ваш лучший выбор
потому что он предоставляет больше информации об образце, чем режим. Но если
переменная — интервал/отношение, вам нужно определить, является ли распределение симметричным
или перекошенный. Если распределение симметрично, то среднее является лучшей мерой центральной
тенденция. Если распределение асимметрично как в положительную, так и в отрицательную сторону, медиана
является более точным. В качестве примера того, почему среднее значение может быть не лучшим показателем центрального
тенденцию к асимметричному распределению, рассмотрите следующий отрывок из книги Чарльза Уилана.
Обнаженная статистика: избавление от ужаса данных (2013):
«Среднее, или среднее, оказывается, имеет некоторые проблемы, а именно, что оно склонно к
искажение «выбросами», которые являются наблюдениями, лежащими дальше от центра. Чтобы понять эту концепцию, представьте, что десять парней сидят на барных стульях.
в питейном заведении среднего класса в Сиэтле; каждый из этих парней зарабатывает 35 000 долларов
в год, что составляет средний годовой доход группы 35 000 долларов. Билл Гейтс ходит
в бар с говорящим попугаем на плече. (У попугая нет ничего
как пример, но это как бы оживляет ситуацию.) Давайте предположим, ради
Например, годовой доход Билла Гейтса составляет 1 миллиард долларов. Когда Билл сидит
сидя на одиннадцатом барном стуле, средний годовой доход посетителей бара возрастает до
около 9 долларов1 миллион. Очевидно, что никто из первых десяти пьющих не стал богаче (хотя
было бы разумно ожидать, что Билл Гейтс купит раунд или два). Если бы я описал
посетители этого бара имеют средний годовой доход в размере 91 миллиона долларов, говорится в заявлении.
Чтобы понять эту концепцию, представьте, что десять парней сидят на барных стульях.
в питейном заведении среднего класса в Сиэтле; каждый из этих парней зарабатывает 35 000 долларов
в год, что составляет средний годовой доход группы 35 000 долларов. Билл Гейтс ходит
в бар с говорящим попугаем на плече. (У попугая нет ничего
как пример, но это как бы оживляет ситуацию.) Давайте предположим, ради
Например, годовой доход Билла Гейтса составляет 1 миллиард долларов. Когда Билл сидит
сидя на одиннадцатом барном стуле, средний годовой доход посетителей бара возрастает до
около 9 долларов1 миллион. Очевидно, что никто из первых десяти пьющих не стал богаче (хотя
было бы разумно ожидать, что Билл Гейтс купит раунд или два). Если бы я описал
посетители этого бара имеют средний годовой доход в размере 91 миллиона долларов, говорится в заявлении. будет одновременно статистически правильным и вводит в заблуждение [Примечание: медиана будет
остается неизменным]. Это не бар, где тусуются мультимиллионеры; это бар, где
куча парней с относительно низким доходом сидит рядом с Биллом Гейтсом
и его говорящий попугай».
будет одновременно статистически правильным и вводит в заблуждение [Примечание: медиана будет
остается неизменным]. Это не бар, где тусуются мультимиллионеры; это бар, где
куча парней с относительно низким доходом сидит рядом с Биллом Гейтсом
и его говорящий попугай».
Показатели изменчивости
В дополнение к определению показателей центральной тенденции нам может понадобиться подвести итоги. количество изменчивости, которое мы имеем в нашем распределении. Другими словами, нам необходимо определить, имеют ли наблюдения тенденцию группироваться вместе или они имеют тенденцию к разбросу вне. Рассмотрим следующий пример:
Образец 1: {0, 0, 0, 0, 25}
Образец 2: {5, 5, 5, 5, 5}
Обе эти выборки имеют одинаковые средние значения (5) и одинаковое количество наблюдений
(n = 5), но степень вариации между двумя выборками значительно различается. Образец 2 не имеет изменчивости (все оценки одинаковы), тогда как образец 1 имеет
относительно больше (один случай существенно отличается от четырех других). В этом курсе
мы рассмотрим четыре показателя изменчивости: диапазон, межквартильный
диапазон (IQR), дисперсия и стандартное отклонение.
Образец 2 не имеет изменчивости (все оценки одинаковы), тогда как образец 1 имеет
относительно больше (один случай существенно отличается от четырех других). В этом курсе
мы рассмотрим четыре показателя изменчивости: диапазон, межквартильный
диапазон (IQR), дисперсия и стандартное отклонение.
Диапазон
Диапазон — это разница между самым высоким и самым низким баллами в наборе данных и является простейшей мерой распространения. Мы рассчитываем диапазон, вычитая наименьший значение от наибольшего значения. В качестве примера рассмотрим следующий набор данных:
23 | 56 | 45 | 65 | 69 | 55 | 62 | 54 | 85 | 25 |
Максимальное значение равно 85, а минимальное значение равно 23. Это дает нам диапазон 62 (85
– 23 = 62). Хотя использование диапазона в качестве меры изменчивости мало что нам говорит,
это дает нам некоторую информацию о том, насколько далеко друг от друга самые низкие и самые высокие оценки
находятся.
Это дает нам диапазон 62 (85
– 23 = 62). Хотя использование диапазона в качестве меры изменчивости мало что нам говорит,
это дает нам некоторую информацию о том, насколько далеко друг от друга самые низкие и самые высокие оценки
находятся.
Квартили и межквартильный диапазон
«Квартиль» — еще одно слово, которое знатоки статистики используют, чтобы почувствовать себя важными. В основном это означает «четверть» или «четверть». Футбольный матч имеет четыре квартили, как и Твикс королевского размера. Найти квартили распределения так же просто, как разбить на четверти. Каждая четвертая содержит 25 процентов от общего числа наблюдений.
Квартили делят ранжированный набор данных на четыре равные части. Ценности, которые разделяют
каждая часть называется первой, второй и третьей квартилями; и они обозначаются
на Q1, Q2 и Q3 соответственно.
Q1 — это «среднее» значение в первой половине ранжированного набора данных.
Q2 — среднее значение набора данных
Q3 — «среднее» значение второй половины ранжированного набора данных
Q4 технически было бы самым большим значением в наборе данных, но мы игнорируем его при расчете
IQR (мы уже имели дело с ним, когда рассчитывали диапазон).
Таким образом, межквартильный размах равен Q3 минус Q1 (или 75-й процентиль минус
25-й процентиль, если вы предпочитаете так думать). В качестве примера рассмотрим
следующие числа: 1, 3, 4, 5, 5, 6, 7, 11. Q1 — среднее значение в первой
половина набора данных. Поскольку в первой половине четное количество точек данных
набора данных среднее значение является средним из двух средних значений; то есть,
Q1 = (3 + 4)/2 или Q1 = 3,5. Q3 — среднее значение во второй половине данных.
поставил. Опять же, поскольку вторая половина набора данных имеет четное количество наблюдений,
среднее значение является средним из двух средних значений; то есть Q3 = (6 + 7)/2
или Q3 = 6,5. Межквартильный размах равен Q3 минус Q1, поэтому IQR = 6,5 — 3,5 = 3.
Q3 — среднее значение во второй половине данных.
поставил. Опять же, поскольку вторая половина набора данных имеет четное количество наблюдений,
среднее значение является средним из двух средних значений; то есть Q3 = (6 + 7)/2
или Q3 = 6,5. Межквартильный размах равен Q3 минус Q1, поэтому IQR = 6,5 — 3,5 = 3.
Блочные диаграммы
Блочная диаграмма (также известная как диаграмма с ячейками и усами) разбивает набор данных на квартили.
Тело боксплота состоит из «коробки» (отсюда и название), которая происходит от
от первого квартиля (Q1) до третьего квартиля (Q3). Внутри поля горизонтальная линия
рисуется в Q2, что обозначает медиану набора данных. Две вертикальные линии, известные
как усы, простираются от верхней и нижней части коробки. Нижний ус идет от
Q1 до наименьшего значения в наборе данных, а верхний ус идет от Q3 до
наибольшее значение. Ниже приведен пример коробчатой диаграммы с положительной асимметрией с различными
компоненты промаркированы.
Ниже приведен пример коробчатой диаграммы с положительной асимметрией с различными
компоненты промаркированы.
Выбросы — это экстремальные значения, которые по той или иной причине исключены из набора данных. Если набор данных включает один или несколько выбросов, они отображаются на графике. отдельно как точки на графике. На приведенной выше диаграмме есть несколько выбросов внизу.
Как интерпретировать прямоугольную диаграмму
Горизонтальная линия, проходящая через центр прямоугольника, указывает, где находится медиана
падает. Кроме того, ящичные диаграммы отображают две общие меры изменчивости или разброса.
в наборе данных: диапазон и IQR. Если вас интересует распространение всех
данные, он представлен на диаграмме вертикальным расстоянием между наименьшими
значение и наибольшее значение, включая любые выбросы. Средняя половина набора данных
попадает в межквартильный диапазон. На диаграмме представлен межквартильный диапазон
по ширине коробки (Q3 минус Q1).
Средняя половина набора данных
попадает в межквартильный диапазон. На диаграмме представлен межквартильный диапазон
по ширине коробки (Q3 минус Q1).
Дисперсия
Дисперсия — это мера вариабельности, которая показывает, насколько далеко каждое наблюдение падает из среднего распределения. Для этого примера мы будем использовать следующее пять цифр, которые представляют собой мои ежемесячные покупки комиксов за последний пять месяцев:
2, 3, 5, 6, 9
Формула расчета дисперсии обычно записывается так:
Это уравнение выглядит пугающе, но оно не так уж плохо, если разбить его на
его составные части. S2x — это обозначение, используемое для обозначения дисперсии выборки.
Эта гигантская сигма (Σ) является знаком суммирования; это просто означает, что мы собираемся добавлять вещи
все вместе.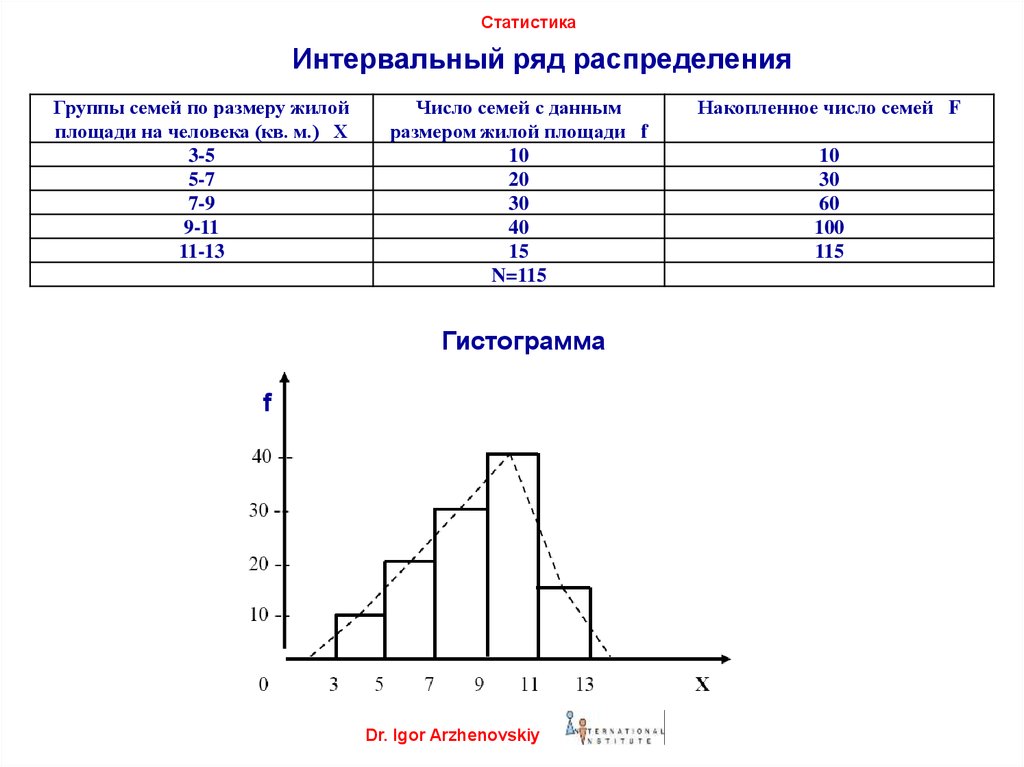 X представляет каждое из наших наблюдений, а x с линией над ним
(часто называемый «x-bar») представляет собой среднее значение нашего распределения. Столица «N» на
внизу общее количество наблюдений. В принципе, эта формула говорит
нам вычесть среднее значение из каждого из наших наблюдений, возвести в квадрат разницу, добавить
их все вместе и разделить на N-1. Давайте сделаем пример, используя приведенные выше числа.
X представляет каждое из наших наблюдений, а x с линией над ним
(часто называемый «x-bar») представляет собой среднее значение нашего распределения. Столица «N» на
внизу общее количество наблюдений. В принципе, эта формула говорит
нам вычесть среднее значение из каждого из наших наблюдений, возвести в квадрат разницу, добавить
их все вместе и разделить на N-1. Давайте сделаем пример, используя приведенные выше числа.
1. Первым шагом в вычислении дисперсии является нахождение среднего значения распределения. В этом случае среднее значение равно 5 (2+3+5+6+9 = 25; 25/5 = 5).
2. Второй шаг – вычесть среднее значение (5) из каждого наблюдения:
2-5 = -3
3-5 = -2
5-5 = 0
6-5 = 1
9 -5 = 4
Обратите внимание: мы можем проверить нашу работу после этого шага, сложив все наши значения вместе. Если их сумма равна нулю, мы знаем, что мы на правильном пути. Если они добавляют к чему-то
помимо нуля, нам, вероятно, следует еще раз проверить нашу математику (-3+-2+0+1+4 = 0, мы золотые).
Если их сумма равна нулю, мы знаем, что мы на правильном пути. Если они добавляют к чему-то
помимо нуля, нам, вероятно, следует еще раз проверить нашу математику (-3+-2+0+1+4 = 0, мы золотые).
3. В-третьих, возводим каждый из этих ответов в квадрат, чтобы избавиться от отрицательных чисел:
(-3)2 = 9
(-2)2 = 4
(0)2 = 0
(1)2 = 1
(4)2 = 16
4. В-четвертых, складываем их все вместе:
9+4+0+1+16=30
5. Наконец, делим на N-1 (общее количество наблюдений равно 5, поэтому 5-1 =4)
30/4 = 7,5
После всех этих довольно утомительных вычислений у нас осталось одно число, которое
быстро и кратко суммирует количество изменчивости в нашем распределении.
чем больше число, тем больше изменчивость в нашем распределении. Пожалуйста, обрати внимание:
дисперсия никогда не может быть отрицательной. Если вы получите дисперсию меньше, чем
ноль, вы сделали что-то не так.
Если вы получите дисперсию меньше, чем
ноль, вы сделали что-то не так.
Стандартное отклонение
Однако существует одно ограничение на использование дисперсии в качестве единственной меры изменчивости. Когда мы возводим числа в квадрат, чтобы избавиться от минусов (шаг 3), мы также непреднамеренно квадрат наша единица измерения. Другими словами, если бы мы говорили о милях, мы случайно превратил нашу единицу измерения в квадратные мили. Если бы мы говорили про комиксы, мы случайно превратили нашу единицу измерения в комиксы в квадрате (что, разумеется, не всегда имеет большой смысл). Чтобы решить эту проблему, мы вычисляем стандартное отклонение. Формула стандарта отклонение выглядит следующим образом:
Другими словами, рассчитать стандартное отклонение так же просто, как взять квадрат
корень из дисперсии, обращая в квадрат квадрат, который мы сделали при вычислении дисперсии. В нашем примере стандартное отклонение равно квадратному корню из 7,5 или 2,74.
Интерпретация не меняется; большое стандартное отклонение свидетельствует о большей
изменчивость, в то время как небольшое стандартное отклонение свидетельствует об относительно небольшой
количество изменчивости. Как и в случае с дисперсией, стандартное отклонение равно
всегда позитивный.
В нашем примере стандартное отклонение равно квадратному корню из 7,5 или 2,74.
Интерпретация не меняется; большое стандартное отклонение свидетельствует о большей
изменчивость, в то время как небольшое стандартное отклонение свидетельствует об относительно небольшой
количество изменчивости. Как и в случае с дисперсией, стандартное отклонение равно
всегда позитивный.
Помните: основное различие между дисперсией и стандартным отклонением заключается в единица измерения. Мы вычисляем стандартное отклонение, чтобы положить нашу переменную обратно в исходную метрику. «Мили в квадрате» возвращаются к просто милям, и «Комиксы в квадрате» снова стали просто комиксами.
Основные моменты
- Показатели центральной тенденции говорят нам, что является общим или типичным в нашей переменной.

- Тремя мерами центральной тенденции являются мода, медиана и среднее значение.
- Режим используется почти исключительно с данными номинального уровня, так как это единственная мера центральной тенденции, доступной для таких переменных. Медиана используется с порядковым номером данных или когда переменная уровня интервала/отношения искажена (вспомните пример Билла Гейтса). Среднее значение можно использовать только с данными уровня интервала/отношения.
- Показатели изменчивости — это числа, описывающие степень изменчивости или разнообразия есть в раздаче.
- Четыре меры изменчивости — диапазон (разница между большим и
наименьшие наблюдения), межквартильный размах (разница между 75-м и
25-й процентиль) дисперсия и стандартное отклонение.

- Дисперсия и стандартное отклонение являются двумя тесно связанными показателями изменчивости. для переменных уровня интервала/отношения, которые увеличиваются или уменьшаются в зависимости от того, насколько близко наблюдения сгруппированы вокруг среднего значения.
- Показатели центральной тенденции и изменчивости в SPSS
Чтобы программа SPSS рассчитала для вас показатели центральной тенденции и изменчивости, щелкните
«Анализ», «Описательная статистика», затем «Частоты». Меры центральной тенденции
и изменчивость также можно рассчитать, нажав «Описание» или «Исследовать»,
но «Частоты» дает вам больше контроля и имеет наиболее полезные параметры для выбора
из. Открывшееся диалоговое окно должно быть вам уже знакомо. Как вы сделали
при расчете частотных таблиц переместите переменные, для которых вы хотите
рассчитать меры центральной тенденции и изменчивости в правой части
коробка. Вы можете снять флажок «Отображать частотные таблицы», если не хотите
видеть любые таблицы и предпочел бы видеть только статистику. Затем нажмите кнопку
справа с надписью «Статистика». В открывшемся диалоговом окне вы можете выбрать
любую статистику по вашему желанию (Примечание: SPSS использует термин «дисперсия», а не
«Изменчивость», но эти два слова являются синонимами). Также имейте в виду, что SPSS
вычислит статистику для любой переменной независимо от уровня измерения. Это
будет, например, вычислять среднее значение для расы или пола, даже если это не имеет смысла
что угодно. Мужчина + мужчина + женщина/3 = 0,66? Совершенно нелогично.
Как вы сделали
при расчете частотных таблиц переместите переменные, для которых вы хотите
рассчитать меры центральной тенденции и изменчивости в правой части
коробка. Вы можете снять флажок «Отображать частотные таблицы», если не хотите
видеть любые таблицы и предпочел бы видеть только статистику. Затем нажмите кнопку
справа с надписью «Статистика». В открывшемся диалоговом окне вы можете выбрать
любую статистику по вашему желанию (Примечание: SPSS использует термин «дисперсия», а не
«Изменчивость», но эти два слова являются синонимами). Также имейте в виду, что SPSS
вычислит статистику для любой переменной независимо от уровня измерения. Это
будет, например, вычислять среднее значение для расы или пола, даже если это не имеет смысла
что угодно. Мужчина + мужчина + женщина/3 = 0,66? Совершенно нелогично. Это один из многих
обстоятельства, в которых вам придется быть умнее, чем пакет анализа данных
ты используешь. То, что SPSS позволяет вам что-то делать, не обязательно означает
это хорошая идея.
Это один из многих
обстоятельства, в которых вам придется быть умнее, чем пакет анализа данных
ты используешь. То, что SPSS позволяет вам что-то делать, не обязательно означает
это хорошая идея.
При расчете показателей изменчивости иногда полезно включить квадрат
участок. Для этого нажмите «Графики», затем «Устаревшие диалоги» и выберите «Коробчатая диаграмма». В качестве
было в случае с графиками, которые вы создали в предыдущей главе, у вас будет несколько
варианты, из которых можно выбрать. Вообще говоря, вам понадобится по одной ящичковой диаграмме для каждого
переменной, поэтому выберите «Сводка отдельных переменных». Переместите переменные, которые вы
хотел бы, чтобы отображались в виде диаграмм в пустом поле справа, и нажмите «ОК».
Если вы хотите отредактировать свои боксплоты, вы можете сделать это почти так же, как вы это делали. графики в главе 2. Вот пошаговое видео:
графики в главе 2. Вот пошаговое видео:
Упражнения
- Выберите три переменные из любого из трех наборов данных (одну номинальную, одну порядковую и один интервал/отношение) и рассчитать все соответствующие меры центральной тенденции для каждый.
- Используя набор данных ADD Health, набор данных NIS и обзор мировых ценностей, рассчитайте
стандартное отклонение, дисперсия и диапазон для переменной «ВОЗРАСТ» в каждом из них. Какой опрос
имеет наибольшую вариацию по возрасту? Какое обследование имеет наименьшую вариацию по возрасту? (Примечание:
для этого вам потребуется открыть набор данных, рассчитать меры изменчивости и
затем откройте следующий набор данных.
 Результаты каждого из них останутся в вашем окне «Вывод».
независимо от того, какой набор данных у вас открыт в данный момент).
Результаты каждого из них останутся в вашем окне «Вывод».
независимо от того, какой набор данных у вас открыт в данный момент). - Выберите любую переменную отношения интервалов и используйте ее для создания коробчатой диаграммы. Теперь интерпретируйте коробочный сюжет. Каков приблизительный диапазон, IQR и медиана этой переменной?
Руководство по статистике GraphPad Prism 9
Доверительный интервал не дает количественной оценки изменчивости
95% доверительный интервал — это диапазон значений, в котором вы можете быть уверены на 95%, он содержит истинное среднее значение генеральной совокупности. Это не то же самое, что диапазон, содержащий 95% от стоимости. График ниже подчеркивает это различие.
На графике показаны три выборки (разного размера), взятые из одной совокупности.
Для небольшой выборки слева доверительный интервал 95% аналогичен диапазону данных. Но только небольшая часть значений в большой выборке справа находится в пределах доверительного интервала. Это имеет смысл. 95-процентный доверительный интервал определяет диапазон значений, в котором вы можете быть уверены на 95 %, что он содержит среднее значение генеральной совокупности. С большими выборками вы знаете это среднее с гораздо большей точностью, чем с маленькой выборкой, поэтому доверительный интервал довольно узок при расчете по большой выборке.
Не просматривайте доверительный интервал и не интерпретируйте его как диапазон, содержащий 95 % значений. |
95% вероятность чего?
Правильно будет сказать, что вероятность того, что рассчитанный вами доверительный интервал содержит истинное среднее значение генеральной совокупности, составляет 95 %. Не совсем корректно говорить, что существует 95% вероятность того, что среднее значение генеральной совокупности находится внутри интервала.
Какая разница?
Среднее значение генеральной совокупности имеет одно значение. Вы не знаете, что это такое (если только вы не занимаетесь моделированием), но у него есть одно значение. Если вы повторите эксперимент, это значение не изменится (и вы все равно не узнаете, что это такое). Поэтому не совсем правильно спрашивать о вероятности того, что среднее значение генеральной совокупности находится в определенном диапазоне.
Напротив, доверительный интервал, который вы вычисляете, зависит от данных, которые вам удалось собрать. Если бы вы повторили эксперимент, ваш доверительный интервал почти наверняка был бы другим. Таким образом, можно спросить о вероятности того, что интервал содержит среднее значение генеральной совокупности.
Не совсем правильно спрашивать о вероятности того, что среднее значение генеральной совокупности находится в интервале. Он либо есть в интервале, либо его нет. В этом нет никаких шансов. Что вы можете сказать, так это то, что если вы проведете такой эксперимент много раз, доверительные интервалы не будут одинаковыми, вы ожидаете, что 95% из них будут содержать среднее значение генеральной совокупности, вы ожидаете, что 5% доверительных интервалов не будут включите среднее значение генеральной совокупности, и вы никогда не узнаете, содержит ли интервал конкретного эксперимента среднее значение генеральной совокупности или нет.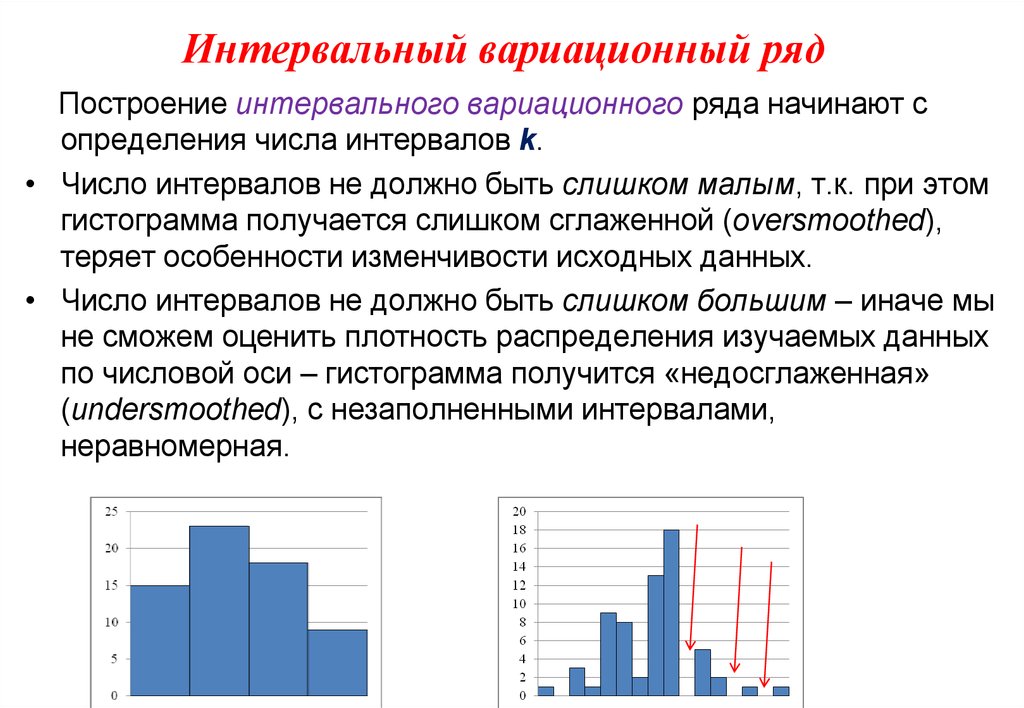

 От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара.
От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара.
 Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.
Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.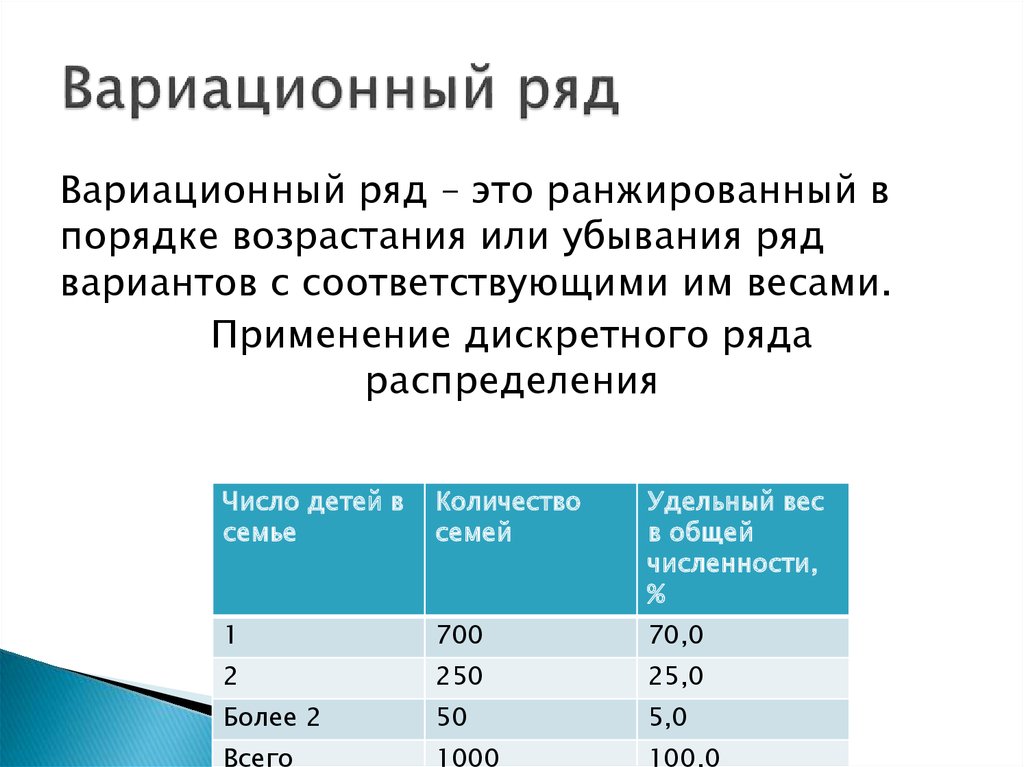



 Результаты каждого из них останутся в вашем окне «Вывод».
независимо от того, какой набор данных у вас открыт в данный момент).
Результаты каждого из них останутся в вашем окне «Вывод».
независимо от того, какой набор данных у вас открыт в данный момент).