Исследование функции без производной 10 класс онлайн-подготовка на Ростелеком Лицей
Центр симметрии кривой
Кривая имеет центр симметрии – точку с координатами .
Доказательство
Рассмотрим функцию . Эта функция нечетная, так как выполнены два условия:
1. Область определения симметрична относительно 0;
2. , для всех
График нечетной функции симметричен относительно точки с координатами . График функции получается из графика функции путем сдвига последнего на 2 единицы вверх по оси . Следовательно, график функции будет симметричен относительно точки (см. Рис. 1).
Рис. 1. Схематическое изображение графиков функции и
Таким образом, мы можем исследовать функцию при , а далее использовать симметрию относительно точки с координатами .
Определение корня функции, преобразование функции
При функция имеет очевидный корень – это :
Следовательно, исследуемую функцию можно представить в следующем виде:
, где – это многочлен четвертой степени.
Доказательство возрастания функции
Докажем, что исследуемая функция монотонно возрастает на множестве .
при
Доказательство
Рассмотрим каждый сомножитель:
Функция возрастает на промежутке (см. Рис. 2). Функция возрастает на промежутке (см. Рис. 2). Функции и возрастающие, поэтому функция также возрастающая. Функция является возрастающей.
Все члены исследуемой функции на промежутке являются положительными.
Рис. 2. Иллюстрация к доказательству
Мы выяснили, что все члены, сомножители возрастают, следовательно, исследуемая функция монотонно возрастает на множестве .
Доказательство убывания функции
Докажем, что функция убывает на промежутке . Для этого сначала рассмотрим промежуток , потом промежуток .
Преобразуем выражение:
Первое слагаемое в правой части убывает при всех х, а второе есть произведение двух сомножителей: и . Из этих сомножителей второй отрицателен и убывает при всех , а первый положителен и возрастает на промежутке , что легко следует из соответствующих свойств параболы . Отсюда вытекает, что второе слагаемое в правой части убывает на промежутке .
Из этих сомножителей второй отрицателен и убывает при всех , а первый положителен и возрастает на промежутке , что легко следует из соответствующих свойств параболы . Отсюда вытекает, что второе слагаемое в правой части убывает на промежутке .
Значит, на этом промежутке убывает и сама функция (сумма убывающих функций – убывающая).
При перепишем функцию в виде:
,
где
Убывание функции ƒ на рассматриваемом промежутке будет доказано, если доказать, что на промежутке убывает каждая из функций , .
Воспользуемся методом выделения полного квадрата и перепишем в виде:
Первая часть – произведение двух сомножителей, из которых первый () возрастает и отрицателен при , а второй – при . Поскольку , отсюда получим: монотонно убывает на требуемом промежутке.
Функцию перепишем в виде:
Она рассматривается аналогично: справа стоит произведение двух сомножителей, из которых первый () возрастает и отрицателен при , а второй при . Поскольку , отсюда получим, что и монотонно убывает на требуемом промежутке.
Поскольку , отсюда получим, что и монотонно убывает на требуемом промежутке.
Таким образом, мы доказали, что исходная функция убывает на всем промежутке .
Построение графика функции
Точка – центр симметрии, поэтому строим график данной функции сначала для . При , .
На промежутке функция убывает. После , то есть на промежутке , функция возрастает (если x стремится к плюс бесконечности, то y тоже стремится к плюс бесконечности) (см. Рис. 3).
Рис. 3. График функции при
Далее отобразим полученный график относительно центра симметрии, то есть точки (см. Рис. 4).
Рис. 4. График функции
Результаты исследования функции
1. Функция возрастает при а также на симметричном множестве .
2. Функция убывает при .
3. – точка максимума.
4. – точка минимума.
Список литературы
- Мордкович А.
 Г., Семенов П.В. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
Г., Семенов П.В. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009. - Мордкович А.Г. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
- Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики). – М.: Просвещение, 1996.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. Алгебра и начала математического анализа: Учебник для 10-11 кл. сред. шк. – М.: Просвещение, 1990.
Дополнительные рекомендованные ссылки на ресурсы Интернет
- Youtube.com (Источник).
- Matematikalegko.ru (Источник).
- Bitclass.ru (Источник).
- Matematiku5.ru (Источник).
Домашнее задание
- Задание 76, 79, 94 (г) (стр.
 274–278) – Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. Алгебра и начала математического анализа (Источник).
274–278) – Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. Алгебра и начала математического анализа (Источник). - Найдите точку минимума функции .
Решение задач без нахождения производной
Здравствуйте! В этой статье речь пойдёт о задачах, которые можно решать без нахождения производной. В данной рубрике мы уже рассмотрели некоторые примеры с логарифмами, числом е, функции с произведениями. Смысл заданий тот же – требуется найти либо точку максимума (минимума) функции, либо определить максимальное (минимальное) значение функции.
В чём суть и каков «стандартный» алгоритм решения — можно посмотреть в этой статье. Но не для всех заданий применение этого алгоритма будет рационально. Если следовать ему в представленных ниже примерах, то процесс решения будет «перегружен» вычислениями. А потеря времени на экзамене вам не нужна. Так какие же задания имеются ввиду?
В условии дана иррациональная, логарифмическая или показательная функция:
при чём под корнем, под знаком логарифма или в показателе находится квадратичная функция вида:
Рассмотрим подход без нахождения производной.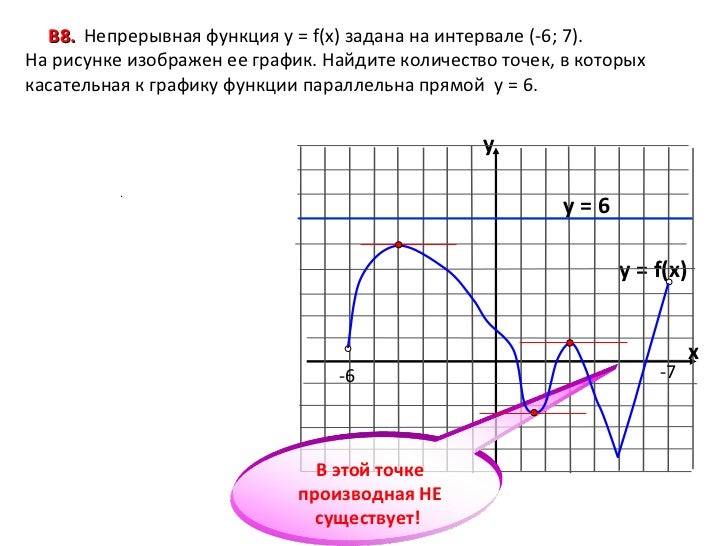 Вы увидите, что такие задачи можно решать устно.
Вы увидите, что такие задачи можно решать устно.
Что необходимо знать? Свойство параболы, напомним его:
Если а > 0, то её ветви направлены вверх.
Если а < 0, то её ветви направлены вниз.
Далее вспомним координату (абсциссу) вершины параболы:
То есть, это точка экстремума квадратичной функции – в ней функция меняет своё поведение с возрастания на убывание или наоборот.
Следующий важный факт (ключевой для этих задач):
Если исходная функция монотонна (непрерывно возрастает или убывает), для нее указанная точка «х» также будет точкой экстремума.
Почему? Давайте рассмотрим отдельно функции подробнее.
Квадратичная функция в показателе степени (при чём n>1):
Смотрите! Представим, что ax2+bx+c=z. Можем записать:
Получается что значение z изменяется следующим образом.
Вариант когда a>0 (ветви параболы направлены вверх) – при х от минус бесконечности до –b/2a z уменьшается, в точке –b/2a значение будет минимальным, далее при х от –b/2a до бесконечности z увеличивается.
Это означает, что и сама функция у=nf(x) будет имет минимальное значение в точке х=–b/2a, так как при минимуме в показателе получится минимум в результате.
Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до –b/2a z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a до бесконечности z уменьшается.
Это означает, что и сама функция у=nf(x) будет иметь максимальное значение в точке х=–b/2a, так как при максимуме в показателе получится максимум в результате.
Квадратичная функция под знаком логарифма (при чём n>1):
Представим, что ax2+bx+c=z. Можем записать:
Получается что значение z изменяется следующим образом:
Вариант когда a>0 (ветви параболы направлены вверх) – при х от минус бесконечности до –b/2a z уменьшается, в точке –b/2a значение будет минимальным, далее при х от–b/2a до бесконечности z увеличивается.
Это означает, что и сама функция lognz будет имет минимальное значение в точке х=–b/2a. Так как логарифмическая функция уменьшается при уменьшении аргумента (видно по графику).
Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до –b/2a z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a до бесконечности z уменьшается.
Это означает, что и сама функция lognz будет имеет максимальное значение в точке х=–b/2a. Так как логарифмическая функция увеличивается при увеличении аргумента (видно по графику).
Квадратичная функция под знаком корня:
Представим, что ax2+bx+c=z. Можем записать:
Получается что:
При a>0 значение z минимально в точке х=–b/2a, а значит и сама функция будет иметь минимальное значение. *Корень из наименьшего значения в результате даст наименьшее число.
При a<0 значение z максимально в точке х=–b/2a, а значит и сама функция будет иметь максимальное значение.
Таким образом, сформулируем ключевое правило:
ВНИМАНИЕ! Конечно, если глубже уйти в тему, то возможны варианты когда сложная функция имеет отрицательный знак, когда логарифм находится в знаменателе дроби, когда основание логарифма или основание степени находится в пределах от 0 до 1. Разумеется, важно понимать как ведёт себя данная в условии функция (возрастает или убывает). Но для решения типовых заданий экзамена указанного вывода вам будет вполне достаточно.
И конечно, не теряйте из виду область допустимых значений заданной функции:
— выражение стоящее под знаком корня, больше или равно нулю (число неотрицательное).
— выражение стоящее под знаком логарифма, есть положительное число.
— выражение стоящее в знаменателе дроби не равно нулю.
В подобных задачах на нахождение наибольшего и наименьшего значения функции, я бы посоветовал находить область определения в любом случае (даже не смотря на то, что в представленных ниже примерах это ничего важного нам не даёт и не влияет на ответ).
Рассмотрим примеры:
Найдите точку максимума функции
Под корнем квадратичная функция 13+6х–х2. Ее график — парабола, ветви направлены вниз, поскольку а=–1<0. Значит максимальное значение функция приобретает в точке:
Проверим чему равно подкоренное выражение при х=3 То есть будет ли оно числом неотрицательным:
13 + 6∙3 – 32 = 13 + 18 – 9 = 22 > 0
Почему необходимо это сделать? Дело в том, что при полученной абсциссе квадратичная функция теоретически может дать отрицательное значение, то есть график такой параболы будет лежать ниже оси ох. Это будет означать что решения (таких вариантов заданий на самом ЕГЭ не будет).
Ответ: 3
Решите самостоятельно:
Найдите точку максимума функции
Посмотреть решение
Найдите наименьшее значение функции
Под корнем квадратичная функция х2 + 8х + 185.
Ее график — парабола, ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины параболы:
Так как ветви параболы направлены вверх, то в точке х = – 4 функция
х2 + 8х + 185 принимает наименьшее значение.
Функция кважратного корня монотонно возрастает, значит х = 4 точка минимума всей функции, вычислим её наименьшее значение:
Ответ: 13
Решите самостоятельно:
Найдите наименьшее значение функции
Посмотреть решение
Найдите точку максимума функции у=log7(–2 – 12х – х2) + 10.
Под знаком логарифма квадратичная функция –2 – 12х – х2.
График — парабола, ветви направлены вниз, так как а = – 1 < 0
Абсцисса вершины параболы:
Проверим, принадлежит ли полученное значение х области определения (выражение под знаком логарифма должно быть число положительное):
– 2 – 12∙(–6) – (–6)2 = – 2 + 72 – 36 = 34 > 0
То есть, в точке х = – 6
функция f (х) = – 2 – 12х – х2 будет иметь максимальное значение.
Значит, и у=log7(–2–12х–х2)+10 в этой точке так же будет иметь максимальное значение.
Ответ: – 6.
Решите самостоятельно:
Найдите точку максимума функции у=log2(2 + 2х – х2) – 2
Посмотреть решение
Найдите наименьшее значение функции у=log9 (х2 – 10х + 754) + 3
Под корнем квадратичная функция х2 – 10х+754.
Ее график — парабола, ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины параболы:
То есть, в точке х = 5 функция f (x) = х2 – 10х + 754 принимает наименьшее значение.
Функция log9х монотонная, значит у =log9 (х2 – 10х + 754) + 3 в точке х = 5 также принимает наименьшее значение, вычислим его:
Ответ: 6
Решите самостоятельно:
Найдите наименьшее значение функции у=log3(х2 – 6х + 10) + 2
Посмотреть решение
Найдите точку максимума функции
В показателе стоит квадратичная функция – 30 + 12х – х2.
График — парабола, ветви направлены вниз, так как а = –1 < 0.
Абсцисса вершины параболы:
То есть, в точке х = 6 функция f (х) = – 30 + 12х – х2 приобретёт максимальное значение. Значит и данная функция в этой точке будет иметь также максимальное значение.
Ответ: 6
Решите самостоятельно:
Найдите точку максимума функции:
Посмотреть решение
Найдите наименьшее значение функции
В показателе стоит квадратичная функция х2 + 16х + 66.
Ее график — парабола, ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины параболы:
То есть, в точке х = – 8 функция х2 + 16х + 66 принимает наименьшее значение.
Показательная функция монотонна, поэтому её наименьшее значение будет также в точке х = – 8, вычислим его
Ответ: 36
Решите самостоятельно:
Найдите наименьшее значение функции
Посмотреть решение
Разумеется, что это краткая схема решения и, конечно же, нужно понимать свойства квадратичной, показательной, логарифмической, дробно-рациональной функции, но эта схема работает.
В данной рубрике мы ещё рассмотрим задания с тригонометрическими функциями, не пропустите! Успеха вам!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.
9.3 Недифференцируемые функции
9.3 Недифференцируемые функцииМожем ли мы дифференцировать любую функцию в любом месте?
Дифференцировать можно только функции, графики которых выглядят как прямые линии вблизи
точку, в которой вы хотите провести различие. В конце концов, дифференциация — это нахождение наклона линии, которая выглядит
как (касательная линия к рассматриваемой нами функции) Отсутствие касательной означает отсутствие производной.
Как и когда возникает недифференцируемость [по аргументу \(x\)]?
Вот несколько способов:
1. Функция прыгает через \(x\) (не является непрерывной), как это происходит на ступеньке лестничного марша.
Функция прыгает через \(x\) (не является непрерывной), как это происходит на ступеньке лестничного марша.
2. График функции имеет излом, как у буквы V. Функция абсолютного значения, которая равна \(x\), когда \(x\) положителен, а \(-x\), когда \(x\) отрицателен, имеет излом в точке \(x = 0\). 9{-2}\) сделать это в \(х = 0\). Обратите внимание, что для конкретного аргумента \(x = 0\) вам нужно разделить на \(0\), чтобы сформировать эту функцию, и деление на \(0\) не является приемлемой операцией, как мы где-то отмечали.
4. Функция совершенно причудливая: рассмотрим функцию, которая равна \(1\) для иррациональных чисел и \(0\) для рациональное число. Это странно.
5. Функция не может быть определена в аргументе \(x\). Когда мы говорим о реальных функциях, квадратный корень
не может быть определено для отрицательных аргументов \(x\). 9{1/3}\) в \(х = 0\).
9{1/3}\) в \(х = 0\).
7. Функция может быть определена и красива, но она может колебаться настолько, что не будет иметь производной. Попробуй дифференцировать \(\sin\left(\frac{1}{x}\right)\) в \(x = 0\). Такое поведение называется an Существенная сингулярность в точке \(x = 0\).
Это единственные виды недифференцируемого поведения, с которыми вы столкнетесь для функций, которые можно описать с помощью формулы, и вы, вероятно, не встретите многих из них.
Теперь вы видели почти все, что можно сказать о дифференцирующих функциях одной переменной. Eсть немного больше; а именно, что происходит, когда вы хотите найти производную функций, определенных с помощью степени ряда или с помощью операции, обратной дифференцированию. Мы доберемся до них позже.
Далее мы хотим изучить, как применить это, а затем как инвертировать операцию дифференцирования.
Недифференцируемая функция — Математическая энциклопедия
Функция, не имеющая
дифференциал. В случае функций одной переменной это функция, не имеющая конечной производной. Например, функция $f(x) = |x|$ не дифференцируема при $x=0$, хотя и дифференцируема в этой точке слева и справа (т.е. имеет конечные левые и правые производные в этой точке). точка). Непрерывная функция $f(x) = x \sin(1/x)$, если $x \ne 0$ и $f(0) = 0$, не только недифференцируема при $x=0$, она не имеет ни левые или правые (и ни конечные, ни бесконечные) производные в этой точке.
9п \пи х),$$
где $0 < a < 1$, $b$ — нечетное натуральное число и $ab > 1 + 3\pi / 2$. Более простой пример, основанный на той же идее, в котором $\cos\omega x$ заменяется более простой периодической функцией — ломаной, — был построен Б.Л. Ван дер Варден. Пусть $u_0(x)$ — функция, определенная для действительного $x$ как абсолютное значение разницы между $x$ и ближайшим целым числом. Эта функция линейна на каждом интервале $[n/2, (n+1)/2]$, где $n$ — целое число; она непрерывна и периодична с периодом 1.
Рисунок: n067010a
Для функций более чем одной переменной дифференцируемость в точке не эквивалентна существованию частных производных в этой точке; есть примеры недифференцируемых функций, имеющих частные производные. Например, функция 92 > 0, \\ 0 & \text{если} x = y = 0, \end{cases}$$ непрерывна во всех точках плоскости и имеет всюду частные производные, но не дифференцируема в $(0, 0)$.
Комментарии
С. Банах доказал, что «большинство» непрерывных функций нигде не дифференцируемы. В частности, он показал, что если через $C$ обозначить пространство всех непрерывных вещественнозначных функций на единичном интервале $[0, 1]$, снабженное равномерной метрикой (супнормой), то множество элементов $C$ которые имеют конечную правую производную в некоторой точке $[0, 1)$, относятся к первой категории Бэра (ср.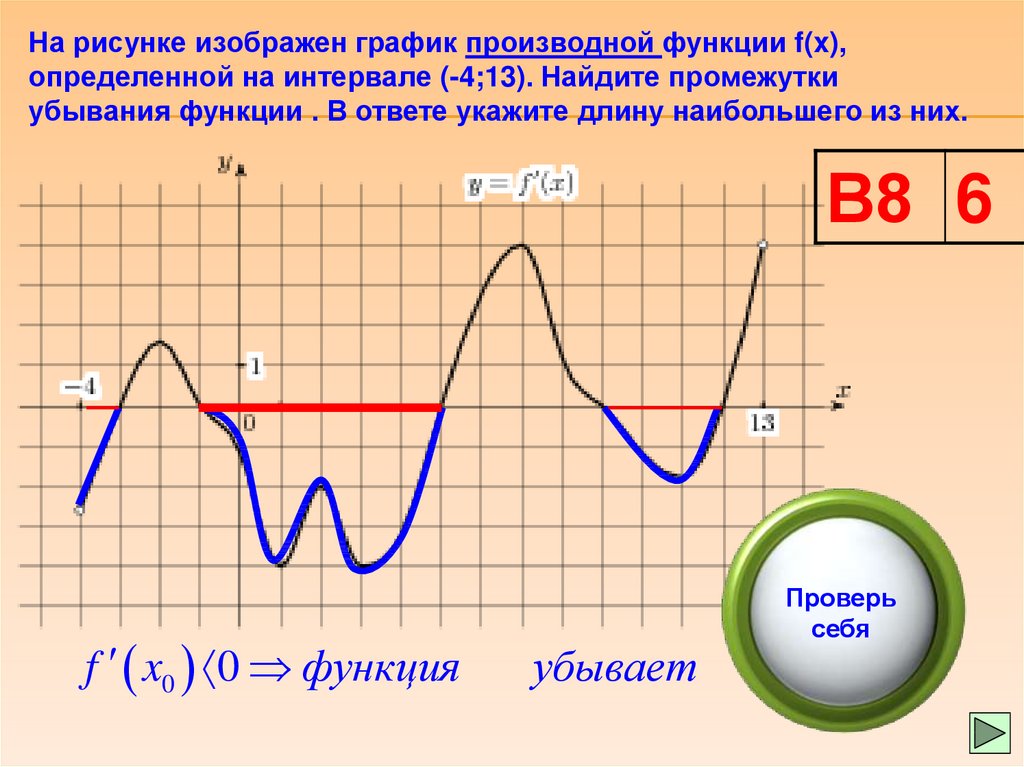

 Г., Семенов П.В. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
Г., Семенов П.В. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009. 274–278) – Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. Алгебра и начала математического анализа (Источник).
274–278) – Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. Алгебра и начала математического анализа (Источник).