Исследование функций с помощью производной: Исследование функций с помощью производных.

Исследование функций с помощью производных

Лекция 26

Лекция 26. Исследование поведения функций с помощью первой и второй производной, асимптоты. Построение графиков функций.

Теорема 1. Если функция возрастает на некотором интервале оси ох (с ростом x растет и y) и дифференцируема на этом интервале, то для любого x из этого интервала (производная имеет знак (+)). А если она убывает на этом интервале (y убывает с ростом x) и дифференцируема на нем, то для любого x из этого интервала (производная имеет знак (–)).

Доказательство.

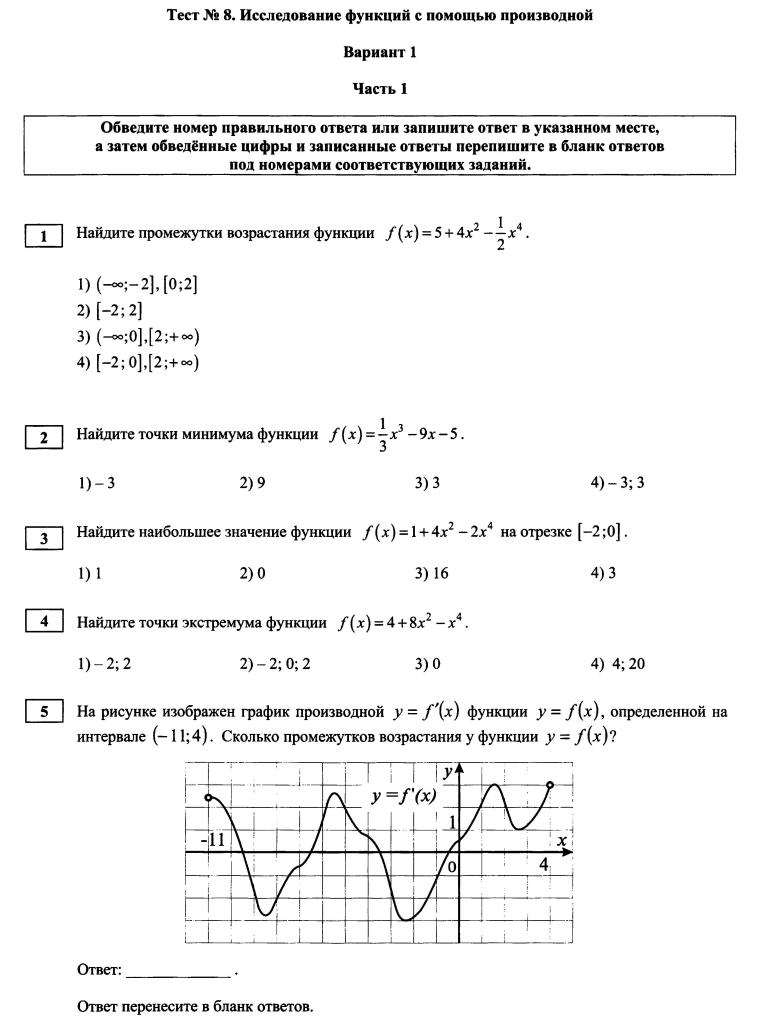
Рассмотрим сначала рис.1. На нем изображен график возрастающей и дифференцируемой на интервале функции . В каждой точке M этого графика касательная составляет с осью ох острый угол (). Но тангенсы острых углов, как известно, положительны.

Значит, согласно геометрического смысла производной, производная положительна для любых x из интервала возрастания функции.

А теперь рассмотрим рис. 2, на котором изображен график убывающей на интервале функции . Здесь для любой точки М графика функции (а значит, для любого x из интервала ) угол наклона касательной, проведенной к графику функции, тупой (). Но тангенсы таких углов отрицательны. А значит и производная отрицательна.

Следствие теоремы 1. Если на некотором интервале оси ох в любой его точке x производная функции положительна, то функция возрастает на этом интервале. А если отрицательна – то убывает. Это следствие играет очень важную роль в исследовании функций. Оно позволяет по знаку производной функции определять, растет или убывает функция, и где именно (для каких x) растет, и где (для каких x) убывает.

Докажем более строгий вариант теоремы 1.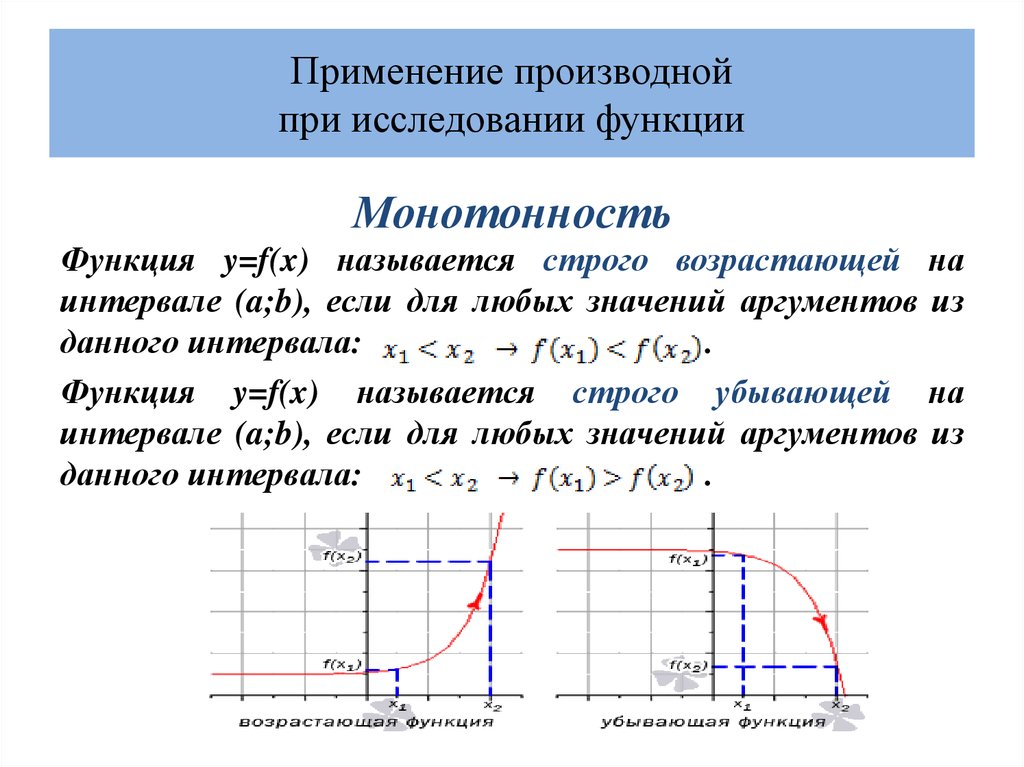

Теорема 2. 1). Если функция , имеющая производную на отрезке , возрастает на этом отрезке, то ее производная на отрезке не отрицательна, т.е. .

2) Если функция непрерывна на отрезке и дифференцируема в промежутке , причем для , то эта функция возрастает на отрезке .

Доказательство. 1) Пусть y=f(x) возрастает на отрезке . Придадим аргументу х приращение и рассмотрим отношение

. (*)

Так как f(x) – функция возрастающая, то

В обоих случаях по свойствам пределов функций. Т.е. , что и требовалось доказать.

2) Пусть при всех значениях

х, принадлежащих промежутку . Рассмотрим два любых значения x₁ и x₂, x₁ < x₂, принадлежащих отрезку . По теореме Лагранжа о конечных приращениях имеем:

По условию , следовательно , а это означает, что f(x) – возрастающая функция.

Аналогичная теорема имеет место и для убывающей дифференцируемой функции.

Теорема 3. 1). Если функция , имеющая производную на отрезке , убывает на этом отрезке, то ее производная на отрезке не положительна, т.е. .

2) Если функция непрерывна на отрезке и дифференцируема в промежутке , причем для , то эта функция убывает на отрезке .

Пример 1. Рассмотрим функцию . Ее производная . Она положительна при и отрицательна при . Значит, при функция возрастает, а при она убывает. График этой функции (парабола) наглядно подтверждает сказанное.

Напомним, что термин «точки экстремума» – это общее название точек максимума и минимума функции. А под ними, в свою очередь, понимаются абсциссы вершин и впадин графика функции (проекции вершин и впадин на ось ох). Или, если не прибегать к геометрической трактовке, точки экстремума функции – это те значения ее аргумента x, при которых функция принимает экстремальные (пиковые) значения – максимальные или минимальные. Точек экстремума у функции столько, сколько вершин и впадин у ее графика.

Определение 1: функция f(x) в точке

х₁ имеет максимум, если значение функции f(x) в точке х₁ больше, чем ее значения во всех точках некоторого интервала, содержащего точку х₁. Другими словами, функция f(x) в точке х=х₁ имеет максимум, если при любых ( положительных и отрицательных ), достаточно малых по абсолютной величине.

Определение 2: функция f(x) в точке х₂ имеет минимум, если значение функции f(x) в точке х₁ меньше, чем ее значения во всех точках некоторого интервала, содержащего точку х₂.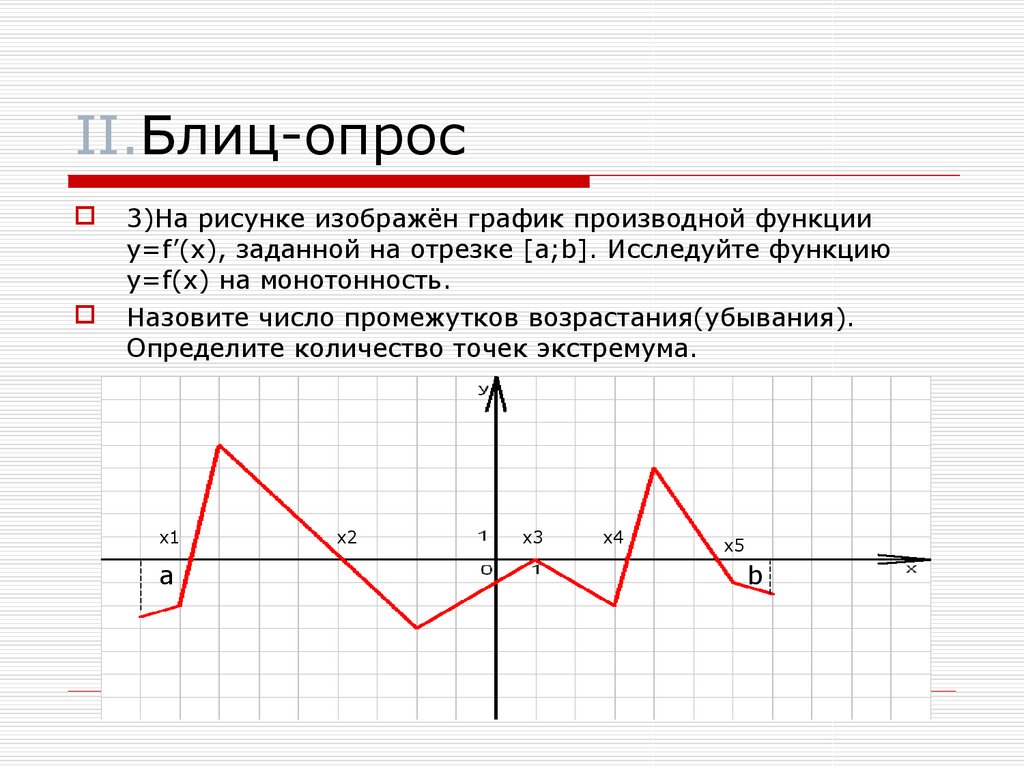 Другими словами, функция f

(x) в точке х=х₂ имеет минимум, если при любых ( положительных и отрицательных ), достаточно малых по абсолютной величине.

Рассмотрим рис.3. На нем изображен график непрерывной функции , имеющей и интервалы возрастания, и интервалы убывания, и точки экстремума:

Интервалы возрастания функции помечены знаком (+), а интервалы убывания – знаком (–). Согласно доказанной выше теореме 1, это заодно и знаки производной функции .

Точками экстремума данной функции являются точки (x₁, x₂, x₃, x₄). Причем точки x₁ и x₃ – точки максимума, а x₂ и x₄ – точки минимума. Точки x₅ и x₆ точками экстремума функции не являются, так как соответствующие им точки графика М

₅ и М₆ – не вершины и не впадины этого графика.

Точки экстремума разделяют интервалы возрастания и убывания функции. В точках максимума совершается переход от возрастания функции (слева от точки максимума) к ее убыванию (справа от точки максимума). То есть в точках максимума знак производной функции меняется с (+) слева на (–) справа. А в точках минимума, наоборот, совершается переход от убывания функции к ее возрастанию. То есть в точках минимума знак производной функции меняется с (–) слева на (+) справа.

Сами же точки экстремума не принадлежат ни к интервалам возрастания, ни к интервалам убывания функции. Потому в точках экстремума производная не может быть ни положительной, ни отрицательной. Значит, в этих точках она или равна нулю, или ее не существует вообще.

Этот вывод понятен и с геометрической точки зрения. Действительно, производная функции, согласно ее геометрического смысла, связана с касательной к графику функции. А именно, представляет собой тангенс угла наклона этой касательной к оси ох. Но точкам экстремума функции соответствуют на ее графике вершины и впадины, в которых касательная к графику или параллельна оси ох (если вершина или впадина графика округлая), или эта касательная отсутствует вообще (если вершина или впадина острая). В первом случае угол наклона касательной к оси ох равен нулю. Значит, и , а значит, и производная . Во втором случае угол не существует вообще, а значит, не существует для данной точки экстремума x и производная . В частности, для рис. 3 имеем:

; – не сущ.; – не сущ.; .

Однако заметим, что не любая точка

x, в которой производная равна нулю или не существует, непременно будет точкой экстремума. В частности, на рис. 3 ; не существует, и тем не менее ни точка x₅, ни точка x₆ не являются точками экстремума функции .

Все сказанное выше о точках экстремума функции можно оформить в виде теоремы.

Теорема 4. Необходимое условие экстремума.

Для того, чтобы некоторая точка x являлась точкой экстремума функции , необходимо, чтобы в этой точке производная этой функции или равнялась нулю, или не существовала. Это условие не является достаточным.

Таким образом, лишь те точки (значения x), в которых производная функции равна нулю или не существует, могут быть точками экстремума этой функции. Но еще не факт, что все такие точки будут точками экстремума. Иначе говоря, точки (значения

x), в которых или не существует, являются лишь подозрительными на экстремум или критическими точками. Чтобы выяснить суть каждой подозрительной точки, нужно посмотреть знак производной слева и справа от неё. Здесь возможны три варианта:

1. Если слева от подозрительной на экстремум точки знак производной (+), а справа (–), то эта подозрительная точка – точка максимума.

2. Если справа от подозрительной на экстремум точки знак производной (–), а справа (+), то эта подозрительная точка – точка минимума.

3. Если слева и справа от подозрительной на экстремум точки знак производной один и тот же, то эта подозрительная точка – не точка экстремума.

Сказанное наглядно иллюстрирует рис. 3. Таким образом, становится понятной и очевидной следующая

Схема исследования функции на возрастание-убывание и точки экстремума.

1. Находим область определения функции. То есть находим все те значения x, для которых существует (можно найти) значение функции . Заодно устанавливаем интервалы непрерывности и точки разрыва функции.

2. Находим производную .

3. Находим точки (значения x), подозрительные на экстремум ( критические точки ). То есть находим те точки (значения x), в которых производная функции или равна нулю, или не существует:

а)

б) не существует

4. Наносим все найденные в пунктах (а) и (б) подозрительные на экстремум точки на область определения функции (на ось ох) и фиксируем (например, дугами) интервалы, на которые разобьется область определения этими точками. Так как внутри каждого такого интервала производная функции существует и не обращается в нуль, то в каждом интервале производная сохраняет свой знак, который может измениться лишь при переходе к другому интервалу. С помощью вычисления производной в пробных внутренних точках определяем знак производной в каждом интервале. По найденным знакам производной устанавливаем интервалы возрастания и убывания функции, а по смене знака производной определяем точки экстремума функции (точки максимума и минимума).

5. В найденных точках максимума и минимума вычисляем значения функции и тем самым определяем вершины и впадины графика функции, отмечая заодно, округлые они или острые.

Пример 2. Исследовать функцию на возрастание-убывание и точки экстремума.

Решение. Действуем по изложенной выше схеме.

1. Функция определена (а следовательно, и непрерывна) для любых x, то есть на всей числовой оси ох (). Значит, её график – сплошная (без разрывов) линия.

2. Найдем производную :

.

3. Найдем точки (значения x), подозрительные на экстремум:

а) .

б) не существует  таких x нет.

4. Нанесем найденные подозрительные на экстремум точки и на область определения функции (на ось ох). Ось ох этими точками разобьется на три интервала:

Определяем знаки производной в этих интервалах (они отмечены на рис. выше). Тем самым устанавливаем интервалы возрастания функции (они помечены стрелкой вверх) и интервал ее убывания (стрелка вниз), а также устанавливаем, что точка – точка максимума функции, а точка – точка ее минимума.

5. Находим (вычисляем) значения функции в точках ее максимума и минимума, устанавливая тем самым вершины и впадины графика функции:

; точка – вершина графика функции (округлая, т. к. ).

; точка – впадина графика функции (округлая, т.к. ).

6. В дополнение к проведенному исследованию найдем еще точки пересечения графика функции с осями координат:

а) С осью ох:

б) С осью оу:

А теперь построим этот график (рис. 4):

Исследование функции с помощью производной и построение графиков функций

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Тема. Исследование функции с помощью
производной и построение графиков
функций.
1.Возрастание и убывание функции.
2. Максимум и минимум функции.
3.Наибольшее и наименьшее значения функции на отрезке.
4. Выпуклость графика функции. Точки перегиба.
5. Асимптоты графика функции и построение графика.
1.Возрастание и убывание функции.
Теорема 1. (достаточное условие возрастания функции)
Если производная дифференцируемой
функции положительна внутри
некоторого промежутка Х, то функция
возрастает на этом промежутке.
Теорема 2. (достаточное условие убывания функции)
Если производная дифференцируемой
функции отрицательна внутри
некоторого промежутка Х, то она
убывает на этом промежутке.
Если касательные к кривой на некотором
промежутке направлены под острыми
углами к оси х, то функция возрастает.
если они направлены под тупыми углами,
то функция убывает.
y
y
x
x
Найти интервалы монотонности
функции
y x 4x 3
2
Найдем производную этой функции:
y ( x 4x 3) 2x 4
2
Исследуем знак этой производной:
y 2 x 4 0 при
x 2
y 2 x 4 0
x 2
при
Следовательно, функция будет возрастать на
промежутке ( 2 ; )
Функция будет убывать на промежутке
( ; 2)
2. Максимум и минимум функции.
Точка х0 называется точкой максимума функции
f(x), если в некоторой окрестности точки х0
выполняется неравенство
f ( x) f ( x0 )
Точка х1 называется точкой минимума функции
f(x), если в некоторой окрестности точки х1
выполняется неравенство
f ( x) f ( x1 )
Значения функции в точках х0 и х1
называются соответственно
максимумом и минимумом функции.
Максимум и минимум функции называется
экстремумом функции.
y
y f (x)
x1 x2
x3
x
На одном промежутке функция может иметь несколько
экстремумов, причем может быть, что минимум в одной
точке больше максимума в другой.
Максимум или минимум функции на некотором
промежутке не являются в общем случае наибольшим и
наименьшим значением функции.
Если в некоторой точке х0 дифференцируемая функция f(x)
имеет экстремум, то в некоторой окрестности этой точки
выполняется теорема Ферма и производная функции в
этой точке равна нулю:
f ( x0 ) 0
Однако, функция может иметь экстремум в точке, в
которой она не дифференцируема.
Например, функция
y x
имеет минимум в точке
x 0
но она в этой точке не дифференцируема.
Для того, чтобы функция y=f(x) имела
экстремум в точке х0 , необходимо, чтобы
ее производная в этой точке равнялась
нулю или не существовала.
Точки, в которых выполняется необходимое
условие экстремума, называются
критическими или стационарными.
Т.об., если в какой-либо точке имеется экстремум, то эта
точка является критической.
Но критическая точка не обязательно является точкой
экстремума.
Найти критические точки и экстремумы
функций:
1
y x
2
Применим необходимое условие экстремума:
y ( x ) 2 x
y 2 x 0 при x 0
2
x 0
y 0
— критическая точка
y
x 0
y x
2
x
2
y x 1
3
Применим необходимое условие экстремума:
y ( x 1) 3x
2
y 3x 0 при x 0
3
x 0
y 1
2
— критическая точка
y
y x 1
3
y 1
x
Если при переходе через точку х0 производная
дифференцируемой функции y=f(x)меняет
знак с плюса на минус, то х0 есть точка
максимума, а если с минуса на плюс, то х0
есть точка минимума.
1
Найти производную функции
y f (x)
2
Найти критические точки функции, в
которых производная равна нулю или не
существует.
3
Исследовать знак производной слева и справа
от каждой критической точки.
4
Найти экстремум функции.
Исследовать функцию на экстремум:
y x( x 1)
3
Применим схему исследования функции на экстремум:
1
Находим производную функции:
y ( x( x 1) ) ( x 1) 3x ( x 1)
3
3
2
( x 1) ( x 1 3x) ( x 1) (4 x 1)
2
2
2
Находим критические точки:
( x 1) (4 x 1) 0
2
x1 1
1
x2
4
3
Исследуем знак производной слева и справа
от каждой критической точки:
y
y
1
4
1
В точке х=1 экстремума нет.
x
4
Находим экстремум функции:
27
1
f min
256
4
3.Наибольшее и наименьшее значения функции на
отрезке.
Согласно теореме Вейерштрасса, если функция
непрерывна на отрезке [a;b], то она достигает
на нем наибольшего и наименьшего значений.
Эти значения могут быть достигнуты на концах
отрезка или в точках экстремума.
1
Найти производную функции.
2
Найти критические точки, в которых
производная равна нулю или не существует.
3
Найти значения функции в критических
точках и на концах отрезка, и выбрать из
них наибольшее и наименьшее значения.
Найти наибольшее и наименьшее
значения функции
y ( x 2) e
2
на отрезке
0 ; 5
x
1
Находим производную функции:
y ( x 2) e
2
x
2( x 2) e
x
x
e ( x 2) ( x 4)
2
Находим критические точки:
x
y e ( x 2) ( x 4) 0
x1 2
x2 4
x
( x 2) e
2
3
Находим
значения
функций
в
критических точках и на концах
отрезка:
f (2) 0
4
f (4) 4
e
f наиб (0) 4
f (0) 4
9
f (5) 5
e
f наим (2) 0
Если функция непрерывна на интервале (а;в),
то она может не принимать на нем наибольшее
и наименьшее значения. В частности, если
дифференцируемая функция y=f(x) на интервале
(а;в) имеет лишь одну точку максимума (или
минимума), то наибольшее (или наименьшее)
значение функции совпадает с максимумом
(минимумом) этой функции.
4. Выпуклость
перегиба.
графика
функции.
Точки
Функция y=f(x) называется выпуклой вниз
(вогнутой) на промежутке Х, если для любых
х1, х2 из этого промежутка выполняется
неравенство:
x1 x2 f ( x1 ) f ( x2 )
f
2
2
y
y f (x)
f ( x1 ) f ( x2 )
2
x1 x2
f
2
x1
x1 x2
2
x2
x
Функция y=f(x) называется выпуклой вверх на
промежутке Х, если для любых х1, х2 из этого
промежутка выполняется неравенство:
x1 x2 f ( x1 ) f ( x2 )
f
2
2
y
x1 x2
f
2
y f (x)
f ( x1 ) f ( x2 )
2
x1
x1 x2
2
x2
x
Функция выпукла вверх (вниз) на
промежутке Х тогда и только тогда,
когда ее первая производная на этом
промежутке монотонно возрастает
(убывает).
Если вторая производная дифференцируемой
функции положительна (отрицательна)
на некотором промежутке Х, то функция
выпукла вниз (вверх) на этом промежутке.
Точкой перегиба графика непрерывной функции
называется точка, разделяющая интервалы,
на которых функция выпукла вверх и вниз.
Точка перегиба – это точка экстремума первой
производной.
Вторая производная дифференцируемой
функции в точке перегиба х0 равна нулю:
f ( x0 ) 0
Если вторая производная
дифференцируемой функции в точке х0
меняет свой знак, то х0 — точка перегиба
ее графика.
1
Найти вторую производную функции.
2
Найти точки, в которых вторая
производная функции равна нулю или
не существует.
3
Исследовать знак второй производной
слева и справа от найденных точек
и сделать вывод об интервалах
выпуклости и точках перегиба.
4
Найти значения функции в точках
перегиба.
Найти интервалы выпуклости и
точки перегиба функции
y x ( x 1)
3
1
Находим вторую производную:
y x ( x 1)
3
( x 1)
3
3x ( x 1)
2
( x 1) ( x 1 3x) ( x 1) (4 x 1)
2
2
y ( x 1) (4x 1) 2( x 1) (4x 1) 4( x 1)
2
2
( x 1) 8x 2 4x 4 ( x 1) 12x 6
2
Находим точки, в которых вторая производная
обращается в нуль: y ( x 1) 12 x 6 0
1
x1
2
3
x2 1
Исследуем знак второй производной слева и
справа от каждой точки:
y
y
1
2
1
x
Точки х1, х2 являются точками перегиба.
Находим значения функции в точках перегиба:
4
1
1
f
16
2
f (1) 0
5. Асимптоты графика функции и построение графика
Асимптотой графика функции y=f(x)
называется прямая, такая что
расстояние от точки (x,f(x)) до этой
прямой стремиться к нулю при
неограниченном удалении точек графика
от начала координат.
y
y f (x)
x
y
y f (x)
x
y
y f (x)
x
Пусть функция y=f(x) определена в
некоторой окрестности точки х0
(исключая, может быть, саму эту
точку) и хотя бы один из пределов
функции при
x x0 0
или
x x0 0
(слева )
(справа )
равен бесконечности, т.е.
lim f ( x)
x x0 0
или
lim f ( x)
x x0 0
Тогда прямая х=х0 является
вертикальной асимптотой графика
функции y=f(x).
Очевидно, что прямая х=х0 не может быть
вертикальной асимптотой, если функция
непрерывна в точке х0, т.к. в этом случае
lim f ( x) f ( x0 )
x x0
Следовательно, вертикальные асимптоты х=х0
следует искать в точках разрыва функции
y=f(x) или на концах ее области определения
(a,b), если a и b – конечные числа.
Пусть функция y=f(x) определена при
достаточно больших х и существует
конечный предел функции
lim f ( x) b
x
Тогда прямая y=b является
горизонтальной асимптотой
графика функции y=f(x).
Пусть функция y=f(x) определена при
достаточно больших х и
существуют конечные пределы
f ( x)
lim
k
x
x
lim f ( x) k x b
x
Тогда прямая y=kx+b является
наклонной асимптотой графика
функции y=f(x).
Найти асимптоты графика функции
3
x
y 2
x 1
1
2
Функция
не
имеет
точек
разрыва,
следовательно вертикальных асимптот у нее
нет.
Найдем горизонтальные асимптоты:
3
x
lim 2
x
x 1
Предел равен бесконечности, следовательно
горизонтальных асимптот нет.
3
Найдем наклонные асимптоты:
f ( x)
x3
x2
lim
lim 2 : x lim 2
1
x
x
x
x
x 1
x 1
k 1
x3
lim f ( x) kx lim 2
x
x
x x 1
x x x
x
lim
lim
0
2
2
x
x
x 1
x 1
3
3
b 0
y x
Следовательно, прямая
является наклонной асимптотой.
Схема исследования функции и построение графика
1
Найти область определения функции.
2
Исследовать функцию на четность и
периодичность.
3
Найти вертикальные асимптоты.
4
Исследовать поведение функции на
бесконечности и найти горизонтальные
или наклонные асимптоты.
5
Найти экстремумы и интервалы
монотонности функции.
6
Найти интервалы выпуклости функции
и точки перегиба.
7
Найти точки пересечения графика с осями
координат и некоторые дополнительные
точки, уточняющие график.
Исследовать функцию и построить
ее график
1 x
y
2
1 x
2
Находим область определения функции.
Функция определена при всех значениях х,
кроме x 1
Следовательно, область определения функции
будет объединение интервалов:
1
( ; 1) ( 1;1) (1; )
2
Исследуем
функцию
периодичность:
на
четность
1 ( x) 1 x
f ( x)
f ( x)
2
2
1 ( x) 1 x
2
2
и
Функция является четной, следовательно ее
график будет симметричен относительно оси
ординат.
Функция не периодична.
3
Находим вертикальные асимптоты.
Вертикальные асимптоты могут быть в точках
разрыва функции х =1 и х = -1.
Сначала рассмотрим точку х =1.
Если хотя бы один из пределов при
x 1
слева и справа равен бесконечности, то прямая
х =1 является вертикальной асимптотой.
При
При
1 x2
lim
2
x 1 0 1 x
x 1
слева
x 1
1 x2
справа lim
2
x 1 0 1 x
Следовательно,
прямая
х=1
является
вертикальной асимптотой.
Аналогично можно проанализировать х=-1, но так
как
график
функции
симметричен
относительно оси ординат, то прямая х=-1
также будет вертикальной асимптотой.
4
Исследуем
поведение
функции
на
бесконечности и найдем горизонтальные и
наклонные асимптоты.
1 x2
1
lim
2
x 1 x
1 x2
1
lim
2
x 1 x
Следовательно, y=-1 — горизонтальная асимптота.
Т.к.
lim
x
f ( x)
1 x2
lim
2
x x (1 x )
x
то наклонных асимптот нет.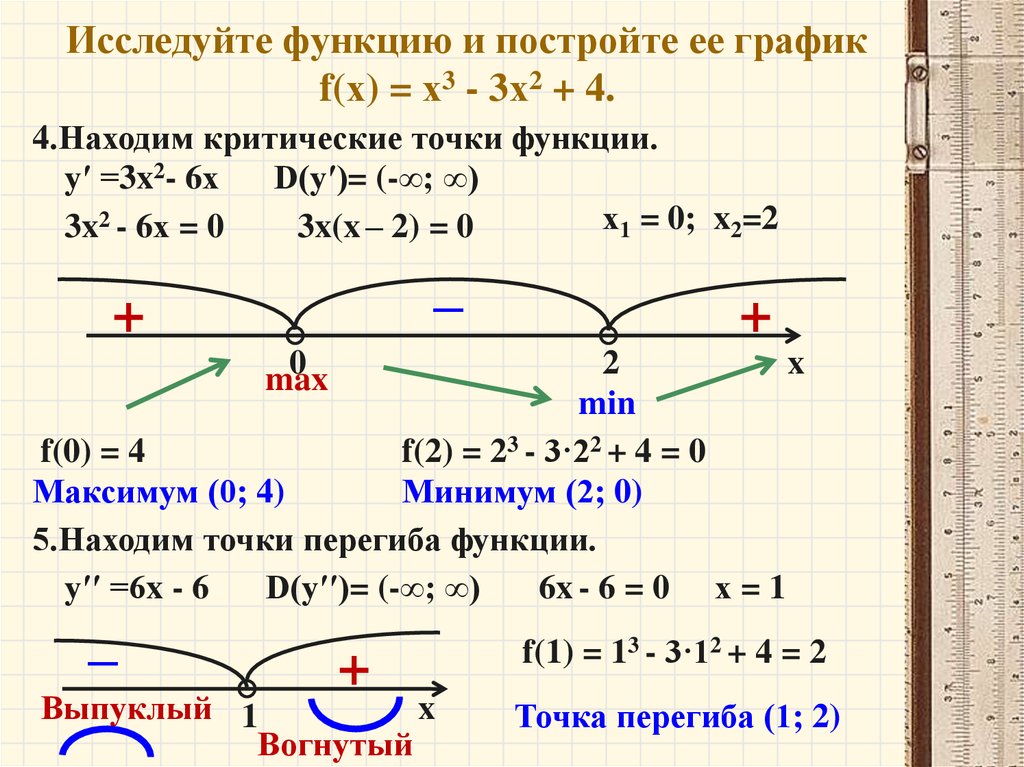
5
Найдем
интервалы
монотонности
и
экстремумы функции.
Для этого вычислим первую производную:
1 x 2 x(1 x 2 ) ( 2 x)(1 x 2 )
y
2
2 2
(1 x )
1 x
2
2 x 2 x3 2 x 2 x3
4x
2 2
(1 x )
(1 x 2 ) 2
Исследуем знак производной при переходе через эту
точку:
y
y
0
f min (0) 1
x
Интервалы монотонности функции:
( ; 1) ( 1;0)
Функция возрастает на: (0;1) (1; )
Функция убывает на:
6
Найдем интервалы выпуклости и точки
перегиба.
Для этого вычислим вторую производную:
2 2
2 2
4 x (4 x) (1 x ) 4 x (1 x )
y
2 2
2 4
(1 x )
(1 x )
4 (1 x 2 ) 2 4 x 2(1 x 2 ) ( 2 x) 4 4 x 2 16 x 2
2 4
2 3
(1 x )
(1 x )
4(1 3x 2 )
(1 x 2 )3
Точек, в которых вторая производная обращается
в ноль, нет. Поэтому точек перегиба у графика
нет.
Числитель всегда положителен, поэтому знак
второй
производной
будет
определяться
знаменателем.
y
y
1
0
x
Интервалы выпуклости функции:
Функция выпукла вниз на:
( 1 ; 1)
Функция выпукла вверх на: ( ; 1) (1; )
Найдем точки пересечения графика функции с
осями координат:
При x 0
1 0
y
1
1 0
(0,1) — точка пересечения с осью ординат.
7
Точек пересечения с осью абсцисс нет.
8 Строим график функции:
y
1 x2
y
2
1 x
1
1
1
1
x

English     Русский Правила

Исчисление I. Применение производных

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

В предыдущей главе мы сосредоточились почти исключительно на вычислении производных. В этой главе основное внимание будет уделено применению производных. Важно всегда помнить, что мы посвятили целую главу вычислению производных не только для того, чтобы говорить о них. Есть много очень важных применений производных.

Два основных приложения, которые мы рассмотрим в этой главе, используют производные для получения информации о графиках функций и задачах оптимизации. Однако это будут не единственные приложения. Мы вернемся к ограничениям и рассмотрим применение производных, которые позволят нам вычислить пределы, которые мы не могли вычислить ранее. Мы также увидим, как можно использовать производные для оценки решений уравнений.

Вот список тем в этом разделе.

Скорость изменения. В этом разделе мы рассмотрим основное применение/интерпретацию производных из предыдущей главы (т. е. скорость изменения), которые мы будем использовать во многих приложениях в этой главе.

Критические точки – В этом разделе мы даем определение критических точек. Критические точки будут показаны в большинстве разделов этой главы, поэтому важно понимать их и то, как их найти. Мы будем работать с рядом примеров, иллюстрирующих, как найти их для самых разных функций.

Минимальные и максимальные значения — в этом разделе мы определяем абсолютные (или глобальные) минимальные и максимальные значения функции и относительные (или локальные) минимальные и максимальные значения функции. Важно понимать разницу между двумя типами минимальных и максимальных (вместе называемых экстремумами) значений для многих приложений в этой главе, поэтому мы используем различные примеры, чтобы помочь с этим. Мы также даем теорему об экстремальных значениях и теорему Ферма, которые очень важны во многих приложениях, которые мы увидим в этой главе.

Поиск абсолютных экстремумов. В этом разделе мы обсудим, как найти абсолютные (или глобальные) минимальные и максимальные значения функции. Другими словами, мы будем находить наибольшее и наименьшее значения, которые будет иметь функция.

Форма графика, часть I. В этом разделе мы обсудим, что первая производная функции может рассказать нам о графике функции. Первая производная позволит нам определить относительные (или локальные) минимальные и максимальные значения функции и где функция будет возрастать и уменьшаться. Мы также дадим критерий первой производной, который позволит нам классифицировать критические точки как относительные минимумы, относительные максимумы или ни минимум, ни максимум.

Форма графика, часть II. В этом разделе мы обсудим, что вторая производная функции может рассказать нам о графике функции. Вторая производная позволит нам определить, где график функции вогнут вверх и вогнут вниз. Вторая производная также позволит нам идентифицировать любые точки перегиба (т. е. места изменения вогнутости), которые может иметь функция. Мы также дадим тест второй производной, который даст альтернативный метод определения некоторых критических точек (но не всех) как относительных минимумов или относительных максимумов.

Теорема о среднем значении – В этом разделе мы приведем теорему Ролля и теорему о среднем значении. С помощью теоремы о среднем значении мы докажем пару очень хороших фактов, один из которых будет очень полезен в следующей главе.

Проблемы оптимизации. В этом разделе мы будем определять абсолютный минимум и/или максимум функции, которая зависит от двух переменных при заданном ограничении или соотношении, которым эти две переменные всегда должны удовлетворять. Мы обсудим несколько способов определения абсолютного минимума или максимума функции. Примеры в этом разделе, как правило, сосредоточены вокруг геометрических объектов, таких как квадраты, прямоугольники, цилиндры и т. д.

Дополнительные задачи оптимизации — В этом разделе мы продолжим работу над задачами оптимизации. Примеры в этом разделе, как правило, немного сложнее и часто включают ситуации, которые легче описать с помощью эскиза, в отличие от «простых» геометрических объектов, которые мы рассматривали в предыдущем разделе.

Правило Лопиталя и неопределенные формы. В этом разделе мы вернемся к неопределенным формам и ограничениям и рассмотрим правило Лопиталя. Правило Лопиталя позволит нам оценить некоторые пределы, которые мы не могли установить ранее.

Линейные аппроксимации. В этом разделе мы обсудим использование производной для вычисления линейной аппроксимации функции. Мы можем использовать линейную аппроксимацию функции для аппроксимации значений функции в определенных точках. Хотя это может показаться бесполезным, когда у нас есть функция, на самом деле есть причины, по которым кто-то может захотеть это сделать. Мы даем два способа, которыми это может быть полезно в примерах.

Дифференциалы – В этом разделе мы вычислим дифференциал для функции. В этом разделе мы дадим применение дифференциалов. Однако одно из наиболее важных применений дифференциалов будет рассмотрено в следующей главе, и, к сожалению, мы не сможем обсуждать его до тех пор.

Метод Ньютона. В этом разделе мы обсудим метод Ньютона. Метод Ньютона — это применение производных, которое позволяет нам аппроксимировать решения уравнения. Есть много уравнений, которые нельзя решить напрямую, и с помощью этого метода мы можем получить приближения к решениям многих из этих уравнений.

Бизнес-приложения. В этом разделе мы дадим беглое обсуждение некоторых основных приложений деривативов в бизнес-сфере. Мы вернемся к поиску максимального и/или минимального значения функции и определим функцию предельных издержек, средние издержки, функцию дохода, функцию предельного дохода и функцию предельной прибыли. Обратите внимание, что этот раздел предназначен только для ознакомления с этими понятиями, а не для того, чтобы рассказать вам о них все.

Производные функции: примеры и формулы

Производные, возможно, являются одним из самых важных понятий, которые мы можем изучать в математике. Почему ты спрашиваешь? Потому что они необходимы во многих приложениях! Вот некоторые из них:

• Производные помогают нам определить взаимосвязь между положением, скоростью и ускорением объекта в физике.

• Они могут сообщить нам скорость изменения таких вещей, как температура, прибыль и численность населения в определенный момент времени.

• Производные являются частью моделей оптимизации для улучшения принятия решений в таких отраслях, как здравоохранение, экономика, бизнес, наука, инженерия и т. д. .

Как мы узнали из нашей статьи о производных, существует метод нахождения производной функции исходной функции. Это означает, что мы можем определить функцию, которая дает нам производную исходной функции в каждой точке области определения исходной функции.

• Производная формулы функции
• Вычисление производной функции
• Обозначения производных
• Производная тригонометрической и обратной тригонометрической функций – примеры
• Производная экспоненциальной и логарифмической функций – примеры

5 Производная функции

Производная функция — это то, что дает нам производную функции в каждой точке области определения функции, в которой определена производная.

• Это означает отсутствие вертикальных касательных, разрыва прыжка, разрыва устранимого разрыва и острых точек.

• Другими словами, предел в приведенном ниже определении должен существовать.

Допустим, у нас есть функция, обозначаемая \(f\). Его производная функция , обозначаемая \(f’\), является функцией, область определения которой состоит из значений \(x\), таких, что предел ниже существует:

\[f'(x) = \lim_{ h \to 0} \frac{f(x+h)-f(x)}{h}\]

Это называется предельным определением производной , а иногда просто определением производной .

Нахождение производной функции с использованием этого предела иногда называют доказательством производной по первому принципу.

• Функция \(f(x)\) считается дифференцируемой в точке \(a\), если ее производная в этой точке \(f'(a)\) существует.
• Таким образом, в общем случае функция считается дифференцируемой на открытом множестве \(S\), если она дифференцируема в каждой точке этого множества.
  • Дифференцируемая функция — это функция, в которой \(f'(x)\) существует в своей области определения.

Вычисление производной функции

В следующих примерах мы используем определение производной функции для нахождения производной функции.

Найдите производную функции квадратного корня:

\[f(x) = \sqrt{x}\]

Решение :

1. Подставьте \(f(x+h) = \sqrt {x+h}\) и \(f(x) = \sqrt{x}\) в \(f'(x) = \lim_{h \to 0} \frac{f(x+h)-f (х)}{ч}\).

\[f'(x) = \lim_{h \to 0} \frac{\sqrt{x+h} — \sqrt{x}}{h}\]

2. Умножить числитель и знаменатель на \(\sqrt{x+h} + \sqrt{x}\).\[f'(x) = \lim_{h \to 0} \frac{\sqrt{x+h} — \sqrt{x} }{h} \cdot \frac{\sqrt{x+h} + \sqrt{x}}{\sqrt{x+h} + \sqrt{x}}\]3. Умножьте числители и упростите, не распределяя знаменатель.\[f'(x) = \lim_{h \to 0} \frac{h}{h\left(\sqrt{x+h} + \sqrt{x} \справа)}\]4. Отмените \(h\).\[f'(x) = \lim_{h \to 0} \frac{1}{\sqrt{x+h} + \sqrt{x}}\]5. Установите \(h = 0\) и оцените предел.\[ \bf{ f'(x) = \frac{1}{2\sqrt{x}} }\] 9{2}}{h}\]

4. Вынесите \(h\) из числителя.

\[f'(x) = \lim_{h \to 0} \frac{h(2x + h)}{h}\]

5. Отменить \(h\).

\[f'(x) = \lim_{h \to 0} (2x + h)\]

6. Установить \(h = 0\) и оценить предел.

\[ \bf{ f'(x) = 2x } \]

Обозначения производных

Существует большое разнообразие обозначений для выражения производной функции. В приведенном выше примере мы доказали, что функция:

\[f(x) = x^{2}\] 9{2}\right) = 2x\]

Подводя итог, можно сказать, что для любой функции \(y = f(x)\) каждое из следующих обозначений представляет производную от \(f(x)\):

\[f'(x), \frac{d}{dx} (f(x)), y’, \frac{dy}{dx} \]

При взятии производной в точке можно также заменить обозначение \(f'(a)\) с обозначением:

\[ \left. \frac{dy}{dx} \right|_{x=a} \]

Чтобы лучше понять обозначения Лейбница, \( \frac{dy}{dx} \), мы должны помнить, что производная функции в точке:

Обычно наклон этих секущих выражается следующим образом:

\[ \frac{\Delta y}{\Delta x} \]

значения, а \(\Delta x \) — разница в значениях x.

Таким образом, производная , или мгновенная скорость изменения y по отношению к x , может быть выражена как:

\[ \frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \]

Графическое представление производной в виде \( \frac{dy}{dx} \) – StudySmarter Originals

Производная триггерной и обратной триггерных функций — примеры

Что такое производная \(sin(x)\)?

Решение :

1. Примените определение производной.

\[ \frac{d}{dx} sin(x) = \lim_{h \to 0} \frac{sin(x+h) — sin(x)}{h} \]

2. Использование сумма углов триггера, чтобы получить:

\[ \frac{d}{dx} sin(x) = \lim_{h \to 0} \frac{ \left[sin(x)cos(h) + cos (x)sin(h)\right] — sin(x)}{h} \]

3. Переставьте члены с \(sin(x)\) рядом друг с другом.

\[ \frac{d}{dx} sin(x) = \lim_{h \to 0} \frac{cos(x)sin(h) — sin(x) + sin(x)cos(h) }{h} \]

4. Вынести за скобки \(sin(x)\).

\[ \frac{d}{dx} sin(x) = \lim_{h \to 0} \frac{cos(x)sin(h) — sin(x)(1 — cos(h))} {h} \]

5. Примените следующие законы пределов: правило постоянного кратного и правило разности.

\[ \frac{d}{dx} sin(x) = cos(x) \left(\lim_{h \to 0} \frac{sin(h)}{h} \right) — sin(x ) \left( \lim_{h \to 0} \frac{1 — cos(h)}{h} \right) \]

6. Если построить график \( \frac{sin(h)}{h} \), мы увидим, что предел при \(h \to 0\) равен \(1\).

Это также можно доказать с помощью теоремы о сжатии.

Предел как \(h \to 0\) для \( \frac{sin(h)}{h} \) равен \(1\) – StudySmarter Originals

7. Если построить график \( \frac{ 1 — cos(h)}{h} \), мы видим, что предел при \(h \to 0\) равен \(0\).

Предел как \(h \to 0\) для \( \frac{1-cos(h)}{h} \) равен \(0\) – StudySmarter Originals

8. Итак, мы можем подключить \(1\) для первого предела и \(0\) для второго предела и упростить. 9{-1}(x) = arcsin(x) \)? ^{1, 2}

Прежде чем мы начнем, знайте, что процесс нахождения этой производной возможен с использованием определения производной (известного как доказательство по первому принципу), однако это сложный и длительный процесс, который также требует сложных алгебраических вычислений. манипуляция. Гораздо проще найти эту производную, используя некоторые производные процессы, которые вы, возможно, еще не знаете:

• Неявное дифференцирование и
• Цепное правило

Пожалуйста, ознакомьтесь с нашими статьями по этим темам, чтобы полностью понять этот процесс. 9{-1}(x) \\ sin(y) & = x \end{align} \]

2. Затем, используя неявное дифференцирование и цепное правило, мы берем производную обеих сторон и находим \( y ‘\).

\[ \begin{align} \frac{dy}{dx} (sin(y)) & = \frac{dy}{dx} (x) \\ \frac{d (sin(y))}{ dy} \cdot \frac{dy}{dx} & = 1 \\ (cos(y)) \cdot y’ & = 1 \\ y’ & = \frac{1}{cos(y)} \end{ align} \]

3. Используя тождество триггера Пифагора, мы можем переписать это уравнение в терминах \( x = sin(y) \). 9{x} \cdot ln (b) } \]

Производные логарифмических функций – примеры

Что такое производная \(L(x) = ln(x)\)?

Решение :

1. Примените определение производной.

\[ L'(x) = \lim_{h \to 0} \frac{ln(x+h)-ln(x)}{h} \]

2. Используйте частное правило логарифмов, \ ( ln(a)-ln(b) = ln\left( \frac{a}{b} \right) \), чтобы переписать предел как:

\[ L'(x) = \lim_{h \to 0} \frac{ ln \left( \frac{x+h}{x} \right)}{h} \] 9{\frac{1}{y}} = \frac{1}{x} ln (e) = \frac{1}{x} \]

9. Следовательно,

\[ \bf{ L'( x) = \frac{1}{x} } \]

Какова производная от \( A(x) = log_{a}(x) \)?

Мы можем найти эту производную, используя две вещи, которые мы уже знаем:

1. Производная от \( ln(x) \) равна \( \frac{1}{x} \).
2. Изменение основного правила логарифмирования: \( log_{a}(x) = \frac{ln(x)}{ln(a)} \)

Решение :

1. Используйте замену базового правила, чтобы переписать функцию как:

\[ A(x) = \frac{ln(x)}{ln(a)} \]

2. Теперь мы можем взять производную.

\[\begin{align}A'(x) & = \frac{d}{dx} \left( \frac{ln (x)}{ln(a)} \right) \\& = \frac {1}{ln(a)} \cdot \frac{d}{dx} (ln(x)) \\& = \frac{1}{ln(a)} \cdot \frac{1}{x} \\\bf{ A'(x) } & = \bf{ \frac{1}{x ln(a)} }\end{align}\]

Производные функции – ключевые выводы

• Мы можем найти производная функция функции с использованием предельного определения производной:

\[ f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]

• Для любой функции \(y = f(x)\), каждое из следующих обозначений представляет собой производную от \(f(x)\):

\[ f'(x), \, \frac{d}{dx}, \, f ‘(f(x)), \, y’, \, \frac{dy}{dx} \]

• Использование предельного определения производной — утомительный процесс! Вот почему математики разработали несколько правил дифференцирования, чтобы упростить задачу.

  No related posts.