исследование линейных систем уравнений
Вы искали исследование линейных систем уравнений? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и исследование матрицы на совместимость, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «исследование линейных систем уравнений».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как исследование линейных систем уравнений,исследование матрицы на совместимость,исследование на совместимость матрицы,исследование на совместность системы линейных уравнений,исследование систем линейных уравнений,исследование системы линейных уравнений на совместность,исследование системы на совместность онлайн,исследовать на совместность систему линейных уравнений онлайн,исследовать на совместность систему на совместность онлайн,исследовать на совместность систему уравнений,исследовать систему линейных уравнений,исследовать систему линейных уравнений на совместность,исследовать систему линейных уравнений на совместность онлайн,исследовать систему на совместность и определенность не решая ее,исследовать систему на совместность и решить ее если она совместна,исследовать систему на совместность онлайн,исследовать систему уравнений на совместимость и определенность не решая ее,исследовать систему уравнений на совместность,как исследовать систему линейных уравнений на совместность,как определить совместность системы линейных уравнений,как проверить на совместность систему,как проверить систему на совместность,как проверить совместность системы линейных уравнений,как проверить совместность системы уравнений,матрицы исследование на совместимость,проверить на совместность систему,проверить систему на совместность,проверить совместность системы уравнений,проверка на совместность системы,совместность системы линейных уравнений как проверить.
Где можно решить любую задачу по математике, а так же исследование линейных систем уравнений Онлайн?
Решить задачу исследование линейных систем уравнений вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Исследование систем линейных уравнений. Теорема Кронекера
Теорема
1(Кронекера-Капелли). Система m – линейных уравнений с n – неизвестными совместна только
тогда, когда ранг матрицы системы равен
рангу расширенной матрицы.
Система m – линейных уравнений с n – неизвестными совместна только
тогда, когда ранг матрицы системы равен
рангу расширенной матрицы.
r (A) = r (Aв)
Пример:
│А│= = 65 0, r (А) = 3;
AB= =r (AB) ≤ 3, так как
= ‒ 8 + 45 + 144 ‒ 40 + 72 ‒ 18 = 195 =r (AB) = 3 =
r(A) = r (AB) => по теореме Кронекера ‒ Капелли система совместна.
Теорема 2. Если ранг матрицы совместной системы равен числу неизвестных, т. е. r(A) = n, то система имеет единственное решение.
Если ранг матрицы системы меньше числа неизвестных, т. е. r (A) < n, то система имеет множество решений.
Тогда
переменные х1,
х2,
…, хr называются базисными,
если минор, составленный из коэффициентов
при этих неизвестных
0, остальные (n – r)
– неизвестных называются свободными.
Пример: найти базисное решение системы уравнений.
Решение:
х1, х2, х3 – базисные, х4 – свободная.
Пусть х4= C = const; х3= 2, тогда
2 х2+ 2 + 2 C= 0 | · 2
х2= – C – 1
х1 – C – 1 + 2 + C= 2;
х1= 1
Ответ:
х1= 1;
х2= – C – 1;
х3 = 2;
х4= C.
Найдем частное решение:
Пусть C = 1, тогда
х1= 1;
х2= – 2;
х3 = 2;
х4= 1.
Проверка:
Подставим значения х1
, х2, х3, и х4 в систему уравнений,
Получим
Системы линейных однородных уравнений.
 Исследование решений. Фундаментальная система решений.
Исследование решений. Фундаментальная система решений.Однородной системой m – линейных уравнений с n – неизвестными называется система уравнений вида:
Теорема. Система (3) всегда имеет хотя бы одно тривиальное решение: х1= х2 = … = хn= 0.
При решении однородной системы линейных уравнений возможны следующие случаи:
1) Если m = n и определитель матрицы системы ∆ 0, то ∆ x1 = ∆ x2 = = … = ∆ xn= 0. Тогда система (3) имеет единственное тривиальное решение х1= х

2) Если m = n, но определитель матрицы системы ∆ = 0, то система (3) имеет множество решений.
3) Если m<n, то система (3) имеет множество решений.
Определение. Система линейно независимых решений el, е2, …, еk называется фундаментальной, если каждое решение системы (3) является линейной комбинацией решений el, е2 , …, еk.
Теорема. Если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений (3) меньше числа переменных n, то всякая фундаментальная система решений системы (3) состоит из n – r решений.
Пример:
m = 3; n = 4.
х1,
х2,
х3 –
базисные, x4 –
свободное.
Пустьх4= C, тогда
х3 = х4=>х3= C
х2– 7C– 14C= 0
х2= 21C
х1– 21C + 2C + 5C = 0
х1= 14C
Ответ:
х1= 14C;
х2= 21C;
х
х4= C.
Модель Леонтьева многоотраслевой экономики. Продуктивные модели Леонтьева.
Модель Леонтьева многоотраслевой экономики (модели межотраслевого баланса)
Макроэкономика
функционирования многоотраслевого
хозяйства требует баланса между
отдельными отраслями. Каждая отрасль,
с одной стороны, является производителем,
а с другой — потребителем продукции,
выпускаемой другими отраслями. Возникает
довольно непростая задача расчета связи
между отраслями через выпуск и потребление
продукции разного вида. Впервые эта
проблема была сформулирована в виде математической
модели в
1936 г. в трудах известного американского
экономиста В. В. Леонтьева, который
попытался проанализировать причины
экономической депрессии США 1929-1932 гг.
Эта модель основана на алгебре матриц
и использует аппарат матричного анализа.
Возникает
довольно непростая задача расчета связи
между отраслями через выпуск и потребление
продукции разного вида. Впервые эта
проблема была сформулирована в виде математической
модели в
1936 г. в трудах известного американского
экономиста В. В. Леонтьева, который
попытался проанализировать причины
экономической депрессии США 1929-1932 гг.
Эта модель основана на алгебре матриц
и использует аппарат матричного анализа.
онлайн-видеолекции по линейной алгебре, МАТЕМАТИКА 3328/2318
онлайн-видеолекции по линейной алгебре, МАТЕМАТИКА 3328/2318 Онлайн-видео-лекции по линейной алгебре, МАТЕМАТИКА 3328/2318 Доступ или своевременное обновление этого веб-сайта не гарантируется. Посещайте все занятия для получения последней информации.
Ежедневные объявления
Перейдите сюда для просмотра видео, совместимых с IPAD/Iphone/Mac . Следующие видеоролики представлены в формате *.wmv для проигрывателя Windows Media.
Перейдите к началу лекций по линейной алгебре, затем прокрутите вниз до текущей лекции.
Общая информация
1) Домашнее задание
2) Информация о курсе, весна 2013 г., возможны изменения
4) Текст: Элементарная линейная алгебра с приложениями, 3-е издание, Ричард Хилл, ISBN 0030103479.
Доступно в книжных магазинах, а также в Интернете, например,
Работа на дому:
Как минимум, повторите задачи, сделанные в классе или тексте, а затем выполните задачи, перечисленные в листе домашних заданий, который выдается в начале семестра.
Следуйте методам, используемым в классе или показанным в учебнике.
Сравните свой окончательный ответ с решением нечетных задач в конце текста.
Формировать учебные группы.
Используйте бесплатное обучение, доступное на L209, M-R 8-6, F 8-2. Поговорите с несколькими репетиторами. Задавайте вопросы коллективно.
Поднимите свои оставшиеся без ответа вопросы в рабочее время.
Или поднимите свои оставшиеся без ответа вопросы в классе.
Как помочь себе подготовиться к тестам:
Устройте себе самопроверку: напишите задачи (решения которых вы видели) на флэш-карте. Укажите, где можно найти решение и выделенное время. Хранить в коробке. Нарисуйте 10 случайных вопросов, устройте себе тест на время. Оцените, используя доступные решения. Повторно изучите проблемы, которые вы пропустили.
В случае, если мы используем гибридный подход, вы хотите убедиться, что ваши конспекты лекций и папки с домашними заданиями полны, доступны для поиска и чтения для вас самих.
Ограничение/политика в отношении ноутбуков и калькуляторов
На контрольные работы допускается только одна тетрадь с собственноручно написанными заданиями.
Печатная бумага не допускается. Копирование бумаги запрещено. Это приведет к оценке F за курс, даже если он не используется!
На испытаниях не допускается использование незакрепленной бумаги любой формы. Запрещается использовать рваную/склеенную/сшитую/сшитую бумагу.
У вас может быть обычный базовый научный калькулятор (около 20 долларов) на тестах.
Использование продвинутых калькуляторов (таких как TI80 и т. д.) приведет к оценке F за тест.
Запрещено использование беспроводных устройств. Калькулятор в стиле мобильного телефона/ipod запрещен.
Если у вас нет собственного калькулятора, вы будете сдавать экзамен без него.
Совместимость:
Перейдите сюда для просмотра видео, совместимых с IPAD/Iphone/Mac . Следующие видеоролики представлены в формате *.wmv для проигрывателя Windows Media.
Видеоконтент этой страницы работает с Windows и имеет формат WMV (Windows Media Video). В частности, у вас не должно возникнуть проблем с проигрывателем Windows Media и различными браузерами (Internet Explorer, Firefox, Chrome) в Windows XP/Vista/Windows 7. Другие операционные системы (например, Apple/Mac или Unix) несовместимы с видео без дополнительного ПО.
Как просматривать видео на MacBook: (предложено Кевином Табиеном, сентябрь 2009 г. ).
).
1. Скачайте MPlayer. Получите версию OS X 1.0.
2. Загрузите DLL-файлы. Получите файл windows-all-20071007.zip (или самую последнюю версию).
3. Перейдите в Finder на вкладке go, нажмите «Перейти к папке» и введите «/usr/lib/»
здесь вы создадите новую папку с именем «win32».
Возможно, вам придется ввести пароль для вашего компьютера и стать администратором, так как папка «usr» скрыта, и запись или изменение файлов здесь может вызвать проблемы, поэтому делайте только то, что необходимо. Если вас это не устраивает, спросите в окне компьютерной помощи в Maes Building.
4. В эту папку вы извлечете все содержимое загруженного zip-файла.
5. Откройте MPlayer, перейдите в «Настройки» и измените модель видеовыхода на Quartz/Quicktime.
6. Теперь откройте видеофайлы с помощью MPlayer.
Дополнительно:
Онлайн-курсы, тексты, интерактивные калькуляторы, симуляторы, игры и демонстрации, связанные с линейной алгеброй:
Linear Algebra Гилберта Стрэнга, полный пакет курсов. Вы также можете использовать 1999 версия.
Вы также можете использовать 1999 версия.
Курс линейной алгебры Алекса Постникова, 2009 г.
Матричный анализ и прикладная линейная алгебра Текст Карл Д. Мейер.
Введение в матричную алгебру Текст Autar K. kaw.
Текст по линейной алгебре Джима Хефферона. Скачать большой PDF. Как ускорить воспроизведение видео.
Интерактивные приложения
Linear Algebra Toolkit Calculator Пшемыслава Богацки, Университет Олд Доминион
Калькулятор базовой матричной алгебры для умножения, определителя, инверсии, исключения Гусса или rref (приведение строк к ступенчатой форме).
Пошаговые операции
3D-графики
Игры
Lights Out 1 , Дэвид Гишар, Whitman College. Игра на линейную алгебру, чем-то похожая на классическую игру Отелло/Реверси, но для одного игрока. Можете ли вы узнать, как решить головоломку Lights Out, применяя линейную алгебру?
Lights Out 2, автор Миша Гайсински, Penn State.
Пятнадцать, Миша Гайсински, Penn State. Этот требует перестановок.
Начало лекций по линейной алгебре:
Прочтите Раздел 1.1 Страницы 1-3
Решайте задачи с 1 по 20.
Лекция 1, Введение
линейные уравнения, решение, решение, множество решений, параметрическое решение, система линейных уравнений, линейные системы, несовместные системы, совместные системы, графическое решение, линейная система может иметь 0 или 1 или бесконечно много решений.
Прочтите Раздел 1.1 Страницы 4-9
Выполняйте задачи с 21 по 32.
Лекция 2, Введение
Мотивация для изучения линейной алгебры, исключения Гаусса, треугольной формы, формы эшелона, обратной замены, матрицы коэффициентов, расширенной матрицы, правого столбца, элементарных операций над линейной системой, элементарных операций над строками над матрицей.
Дополнительно: Чтобы проверить свои элементарные операции со строками, вы можете попробовать этот калькулятор, нажав на первую ссылку инструмента «Калькулятор операций со строками» на странице.
Матрица Инструментарий
Если вы хотите ПОСМОТРЕТЬ, как выглядит определенная формула с тремя переменными, используйте следующую интерактивную страницу/апплет/приложение:
3D-графики
Прочтите раздел 1.2, страницы 10-13.
Решайте задачи с 1 по 14.
Лекция 3, Исключение Гаусса
параметрические уравнения и решение 0, 1 или бесконечного числа решений, ступенчатая форма, начальные нули, опорные элементы, ведущие/зависимые переменные, свободные/независимые переменные, как решить уравнение, заданное в ступенчатой матричной форме.
Прочтите Раздел 1.2 Страницы 13-21.
Решайте задачи с 15 по 29.
Лекция 4, Исключение Гаусса
Элементарные операции со строками, используемые для приведения уравнения к его ступенчатой форме; так что это может быть решено обратной заменой.
Чтобы проверить форму своего эшелона или решить свою систему, вы можете попробовать этот калькулятор (используйте 2-й или 4-й инструмент).
Matrix Toolkit
Прочтите раздел 1. 3, страницы 23-27
3, страницы 23-27
Решайте задачи с 1 по 14.
Лекция 5, Матричная алгебра
Задача 15 из 1.2, матричный элемент или элемент, размер или размер матрицы, двойной индекс, сложение и вычитание матриц, скаляры и матрицы, умножение скаляра на матрицу, скалярное произведение или скалярное произведение, матричное произведение как совокупность скалярных произведений.
Чтобы проверить умножение, попробуйте этот калькулятор
Базовая матричная алгебра
Чтобы увидеть демонстрацию умножения
, найдите «выработать», нажмите «умножить две матрицы», следуйте инструкциям.
Прочтите Раздел 1.3 Страницы 27-29
Решайте задачи с 15 по 16.
Лекция 6, Умножение матриц
подробнее о матричном произведении как наборе точечных произведений, общей формуле с использованием записи суммирования
Чтобы проверить умножение, попробуйте этот калькулятор
Базовая матричная алгебра
Чтобы увидеть демонстрацию умножения
, найдите «выработать», нажмите «умножить две матрицы», следуйте инструкциям.
Прочтите Раздел 1.3 Страницы 30-31
Выполняйте задачи с 21 по 26, попробуйте с 27 по 32, особенно с 31, пропустите 17–20.
Лекция 7, Интерпретация матричного умножения
умножение на диагональную матрицу, линейная система, записанная как произведение матриц, подстановка как произведение матриц, умножение матриц как сумма произведений столбцов на строки.
Прочтите раздел 1.3, страницы 32–34, 1.4, страницы 38–39
Выполните задачи из 1.3, 33-42. По крайней мере, один из каждого типа, даже если он не в списке на синей странице!
Лекция 8, Различные стили умножения матриц
Интерпретации AB в терминах точечных произведений строк A со столбцами B, A со столбцами B, строк A с B, матриц-строк A с матрицами-столбцами B, суммы внешних произведений столбцов A с соответствующими строками из B. AX, X вектор, является линейной комбинацией столбцов A с весами, такими же, как элементы вектора X.
Прочтите Раздел 1.4 Страницы 38-45
Решайте задачи с 1,3,5,8,10,11,14.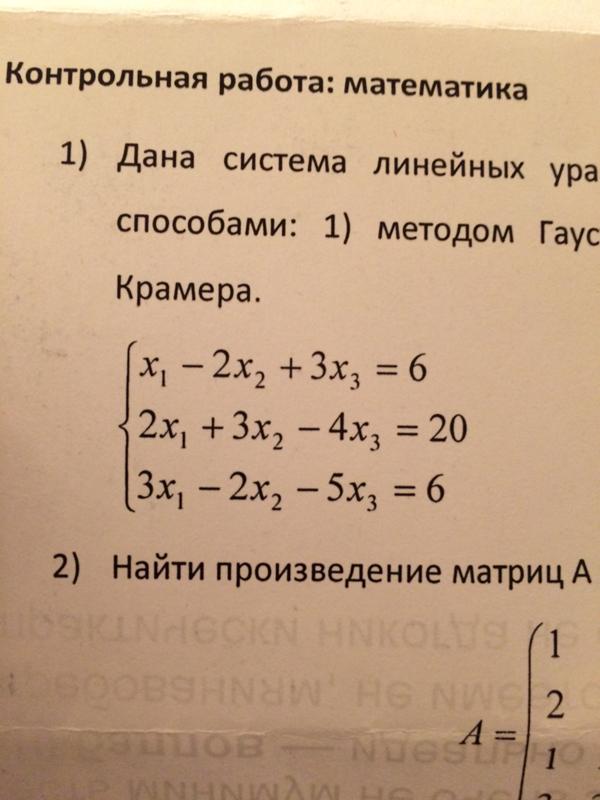
Лекция 9, Обратные и элементарные матрицы
Элементарная матрица, связанная с умножением строки и заменой двух строк.
Прочтите Раздел 1.4 Страницы 38-45
Решите задачи 1-24, 36, 39, 40, 41-43, 45, 49, 50.
Лекция 10, Обратные и элементарные матрицы
Элементарные операции COLUMN (относящиеся к задаче 50).
Задача 37 из 1.3, разные стили (разложение по строкам, разложение по столбцам, разложение по внешнему произведению) для умножения матриц, относящееся к лекции 8.
Элементарная матрица, связанная с добавлением нескольких строк к другой строке.
Общая процедура нахождения обратного.
Прочтите Раздел 1.4 Страницы 48-49
Решайте задачи с 9-20, 25-45.
Лекция 11, Нахождение инверсий с использованием элементарных матриц
Пример инвертированной матрицы 3*3. Краткое обсуждение необратимых матриц.
Прочтите Раздел 1.5 Страницы 57-64
Решайте задачи с 1 по 8.
Лекция 12, LU-факторизация
Факторизация ЛУ для простого случая (без перестановок), описание алгоритма и обоснование процедуры.
Прочтите Раздел 1.5 Страницы 62-64.
Решайте задачи с 9 до 24.
Лекция 13, Решение AX=B с помощью факторизации LU
Преимущества факторизации LU, решение систем с факторизацией, общие матрицы перестановок, PA=LU.
Прочтите раздел 1.5, страницы 64–67, 1.6, страницы 71–72, 3.1, страницы 130–131
Делай задачи с 1.5 33-36, с 1.6 1-7, 13,14,19, 20.
Лекция 14, Решение AX=B с помощью факторизации PA=LU,
пример, симметричные, кососимметричные, определители матриц 2*2 и 3*3, векторы в физике
Читать раздел 3.1 Страницы 132-137, 151
Решайте задачи из 3.1, 1-30 (вопросы на размах отложите)
Лекция 15, Векторы
скаляры, векторы, матрицы, графическое сложение, вычитание и скалярное умножение векторов
Читать Раздел 3.1 Страницы 132-141
Решайте задачи из 3.1, 1-36
Лекция 16, длина и скалярное произведение векторов
диапазон, расстояние, норма (длина, величина, размер) вектора, угол между векторами, скалярное произведение через угол, длина в терминах скалярного произведения, скалярное произведение в терминах компонентов, пример: найти угол между двумя векторами.
Прочтите Раздел 3.1 Страницы 140-144
Решайте задачи из 3.1, 31-42
Лекция 17, Теорема скалярного произведения, Проекции
Пример 5,11,36. Доказательство закона косинусов, Доказательство U.V= u1 v1+ u2 v2 + u3 v3 = |U| |В| cos угла. Формула прогнозов
Прочтите Раздел 3.1 Страницы 144-146
Решайте задачи из 3.1, 43-50
Лекция 18, Процесс Грама-Шмидта
Пример 21. Получение набора взаимно перпендикулярных векторов P_i из произвольно заданных векторов V_i с помощью проекций.
Прочтите Раздел 3.2 и 3.3 Страницы 149-165
Решайте задачи из 3.2, 3.3 все
Лекция 19, Евклидово n-пространство, Общие векторные пространства
Закрытие.
Просмотрите раздел 1.4,1.5,1.6,3.1,3.2
Лекция 20, Обзор обратного, LU, PA=LU
Биреф обзор.
Прочтите Раздел 3.4 Страницы 165-169
Решайте задачи из 3.4, 1-24
Лекция 21, Подпространства
Замыкание относительно сложения векторов и скалярного умножения.
Прочтите Раздел 3.4 Страницы 168-169
Решайте задачи из 3.4, 1-24
Лекция 22, Подпространства
примеры подпространств
Прочтите Раздел 3.4 Страницы 169-173
Решайте задачи из 3.4, 33-40
Лекция 23, Подпространства
Нулевые пространства, NS(A), линейные комбинации
Прочтите Раздел 3.4 Страницы 173-176, 3.5 179-180
Решайте задачи из 3.4, 41-48, 3.5 1-3
Лекция 24, Подпространства
линейные комбинации, интерпретация AX=B, линейная зависимость и независимость
Прочтите Раздел 3.5 Страницы 179-180
Решайте задачи из 3.5 1-6
Лекция 25, Линейная независимость
Задачи 29 и 38 из 3.4, Введение в линейную зависимость и независимость
Прочтите Раздел 3.5 Страницы 180-185
Решайте задачи из 3.5 7-24
Лекция 26, Линейная независимость
линейная зависимость и независимость
Прочтите Раздел 3.6 Страницы 187-192
Решайте задачи из 3.6 1-20
Лекция 27, Базис
Учитывая набор векторов, как определить, являются ли они основой для данного пространства?
Прочтите Раздел 5. 1 Страницы 320-326
1 Страницы 320-326
Решайте задачи из 5.1 1-20
Лекция 28, Детерминанты
Введение в определители, короткие пути, формула расширения/рекурсии
Прочтите Раздел 5.1 Страницы 326-329
Решайте задачи из 5.1 21-39
Лекция 29, Детерминанты
Примеры, три теоремы.
Прочтите Раздел 5.2 Страницы 331-334
Решайте задачи из 5.2 1-9, часть b только из 11-22
Лекция 30, Введение в собственные значения и собственные векторы
Примеры, определения.
Прочтите Раздел 5.2 Страницы 331-335
Решайте задачи из 5.2 1-9, только части a,b из 11-22
Лекция 31, действительные, комплексные, двойные собственные значения, характеристический полином матрицы
несколько примеров.
Прочтите Раздел 5.2 Страницы 331-335
Решайте задачи из 5.2 1-9, только часть a,b,c из 11-22
Лекция 32, Нахождение собственных векторов матрицы, матричная факторизация в матрицу собственных векторов *матрица собственных значений*, обратная матрице собственных векторов
несколько примеров. -1
-1
Прочтите раздел 5.3 342-349
Решите задачи из 5.3 1-26
Лекция 37, Диагонализация
Примеры, недиагонализуемые матрицы.
Прочтите раздел 5.4 352-358
Выполните задачи из 5.4 1-9
Лекция 38, Симметричные матрицы
Свойства, Ортогональные (ортонормированные) матрицы, Теорема: Собственные значения реальной симметричной матрицы 2 * 2 действительны.
Прочтите раздел 5.4 352-358
Решайте задачи из 5.4 1-9
Лекция 39, Обзор симметричных матриц
Решение задачи 1
Лекция 40, Частичный обзор собственных значений, собственных векторов,
диагонализация, решение системы дифференциальных уравнений
Охватывает части 5.2,5.3,5.6 (для 5.6 используйте конспект лекции)
Прочтите вторую часть Раздела 5.5 352-358
Делайте задачи из видео
Лекция 41, Марковские процессы, пример
CUDA Toolkit Documentation 12.1
Разработка, оптимизация и развертывание приложений с ускорением на GPU
Набор инструментов NVIDIA® CUDA® Toolkit предоставляет среду разработки для создания высокопроизводительных приложений с ускорением на GPU. Приложения. С помощью CUDA Toolkit вы можете разрабатывать, оптимизировать и развертывать свои приложения на GPU-ускоренных платформах.
встроенные системы, настольные рабочие станции, корпоративные центры обработки данных, облачные платформы и суперкомпьютеры HPC.
Инструментарий включает в себя библиотеки с ускорением на графическом процессоре, инструменты отладки и оптимизации, компилятор C/C++ и среду выполнения.
библиотека для развертывания вашего приложения.
Приложения. С помощью CUDA Toolkit вы можете разрабатывать, оптимизировать и развертывать свои приложения на GPU-ускоренных платформах.
встроенные системы, настольные рабочие станции, корпоративные центры обработки данных, облачные платформы и суперкомпьютеры HPC.
Инструментарий включает в себя библиотеки с ускорением на графическом процессоре, инструменты отладки и оптимизации, компилятор C/C++ и среду выполнения.
библиотека для развертывания вашего приложения.
Использование встроенных возможностей для распределения вычислений между конфигурациями с несколькими GPU, учеными и исследователями может разрабатывать приложения, которые масштабируются от рабочих станций с одним GPU до облачных установок с тысячами GPU.
- Примечания к выпуску
Примечания к выпуску набора инструментов CUDA.
- Архив функций CUDA
Список функций CUDA по выпускам.
- ЛСКП
Лицензионное соглашение с конечным пользователем набора инструментов CUDA применяется к набору инструментов NVIDIA CUDA, примерам NVIDIA CUDA, драйверу дисплея NVIDIA, инструментам NVIDIA Nsight (Visual Studio Edition) и соответствующей документации по API CUDA, модели программирования и инструментам разработки.
 Если вы не согласны с условиями лицензионного соглашения, не загружайте и не используйте программное обеспечение.
Если вы не согласны с условиями лицензионного соглашения, не загружайте и не используйте программное обеспечение.
Руководства по установке
- Краткое руководство
В этом руководстве представлены минимальные инструкции по установке и проверке CUDA в стандартной системе.
- Руководство по установке Windows
В этом руководстве рассказывается, как установить и проверить правильность работы средств разработки CUDA в системах Microsoft Windows.
- Руководство по установке Linux
В этом руководстве рассказывается, как установить и проверить правильность работы средств разработки CUDA в системах GNU/Linux.
Руководства по программированию
- Руководство по программированию
В этом руководстве подробно рассматривается модель программирования CUDA и интерфейс программирования. Затем описывается аппаратная реализация и даются рекомендации по достижению максимальной производительности.
 Приложения включают в себя список всех устройств с поддержкой CUDA, подробное описание всех расширений языка C++, списки поддерживаемых математических функций, функции C++, поддерживаемые в коде хоста и устройства, сведения о выборке текстур, технические характеристики различных устройств и выводы. путем внедрения API низкоуровневого драйвера.
Приложения включают в себя список всех устройств с поддержкой CUDA, подробное описание всех расширений языка C++, списки поддерживаемых математических функций, функции C++, поддерживаемые в коде хоста и устройства, сведения о выборке текстур, технические характеристики различных устройств и выводы. путем внедрения API низкоуровневого драйвера.- Best Practices Guide
В этом руководстве представлены общепринятые методы распараллеливания и оптимизации, а также поясняются метафоры и идиомы кодирования, которые могут значительно упростить программирование для архитектур GPU с поддержкой CUDA. Цель состоит в том, чтобы предоставить рекомендации по получению максимальной производительности от графических процессоров NVIDIA с помощью набора инструментов CUDA.
- Руководство по совместимости Maxwell
Это примечание по применению призвано помочь разработчикам убедиться, что их приложения NVIDIA CUDA будут правильно работать на графических процессорах на базе архитектуры NVIDIA Maxwell.
 Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с Maxwell.
Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с Maxwell.- Руководство по совместимости с Pascal
Это примечание к применению предназначено для того, чтобы помочь разработчикам убедиться, что их приложения NVIDIA CUDA будут правильно работать на графических процессорах на базе архитектуры NVIDIA Pascal. Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с Pascal.
- Руководство по совместимости Volta
Эти указания по применению предназначены для того, чтобы помочь разработчикам убедиться, что их приложения NVIDIA CUDA будут правильно работать на графических процессорах на базе архитектуры NVIDIA Volta. Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с Volta.
- Руководство по совместимости с Turing
Это примечание к применению предназначено для того, чтобы помочь разработчикам убедиться, что их приложения NVIDIA CUDA будут правильно работать на графических процессорах на основе архитектуры NVIDIA Turing.
 Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с Turing.
Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с Turing.- Руководство по совместимости с архитектурой графического процессора NVIDIA Ampere
Эти указания по применению предназначены для того, чтобы помочь разработчикам убедиться, что их приложения NVIDIA CUDA будут правильно работать на графических процессорах, основанных на архитектуре графических процессоров NVIDIA Ampere. Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с архитектурой графического процессора NVIDIA Ampere.
- Руководство по совместимости Hopper
Это примечание к применению призвано помочь разработчикам убедиться, что их приложения NVIDIA CUDA будут правильно работать на графических процессорах Hopper. Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с архитектурой Hopper.
- Руководство по совместимости с Ada
Это примечание к применению призвано помочь разработчикам убедиться, что их приложения NVIDIA CUDA будут правильно работать на графических процессорах Ada.
 Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с архитектурой Ada.
Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с архитектурой Ada.- Руководство по настройке Maxwell
Maxwell — это архитектура NVIDIA 4-го поколения для вычислительных приложений CUDA. Приложения, которые следуют лучшим практикам для архитектуры Kepler, обычно должны видеть ускорение в архитектуре Maxwell без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложений для получения дополнительных ускорений за счет использования архитектурных возможностей Maxwell.
Руководство по настройке- Pascal
Pascal — это архитектура NVIDIA 5-го поколения для вычислительных приложений CUDA. Приложения, которые следуют лучшим практикам для архитектуры Maxwell, обычно должны видеть ускорение в архитектуре Pascal без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложений для получения дополнительных ускорений за счет использования архитектурных возможностей Pascal.

- Volta Руководство по настройке
Volta — это архитектура NVIDIA 6-го поколения для вычислительных приложений CUDA. Приложения, которые следуют рекомендациям для архитектуры Pascal, обычно должны видеть ускорение в архитектуре Volta без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложений для получения дополнительных ускорений за счет использования архитектурных функций Volta.
- Turing Tuning Guide
Turing — это архитектура NVIDIA 7-го поколения для вычислительных приложений CUDA. Приложения, которые следуют лучшим практикам для архитектуры Pascal, обычно должны видеть ускорение в архитектуре Turing без каких-либо изменений кода. В этом руководстве приведены способы тонкой настройки приложений для получения дополнительных ускорений за счет использования архитектурных функций Turing.
Руководство по настройке архитектуры GPU NVIDIA AmpereАрхитектура NVIDIA Ampere GPU — это архитектура NVIDIA 8-го поколения для вычислительных приложений CUDA.
 Приложения, которые следуют рекомендациям для архитектуры NVIDIA Volta, как правило, должны получать ускорение на архитектуре графического процессора NVIDIA Ampere без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложений для получения дополнительных ускорений за счет использования возможностей архитектуры графических процессоров NVIDIA Ampere.
Приложения, которые следуют рекомендациям для архитектуры NVIDIA Volta, как правило, должны получать ускорение на архитектуре графического процессора NVIDIA Ampere без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложений для получения дополнительных ускорений за счет использования возможностей архитектуры графических процессоров NVIDIA Ampere.- Руководство по настройке бункера
Архитектура Hopper GPU — это архитектура NVIDIA 9-го поколения для вычислительных приложений CUDA. Приложения, которые следуют лучшим практикам для архитектуры NVIDIA Volta, как правило, должны видеть ускорение на архитектуре Hopper GPU без каких-либо изменений кода. В этом руководстве описаны способы точной настройки приложений для получения дополнительных ускорений за счет использования функций архитектуры графического процессора Hopper.
- Руководство по настройке Ada
Архитектура графического процессора NVIDIA® Ada — это новейшая архитектура NVIDIA для вычислительных приложений CUDA®.
 Архитектура графического процессора NVIDIA Ada сохраняет и расширяет ту же модель программирования CUDA, что и предыдущие архитектуры графических процессоров NVIDIA, такие как NVIDIA Ampere и Turing, и приложения, которые следуют лучшим практикам для этих архитектур, обычно должны получать ускорение архитектуры NVIDIA Ada без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложения для получения дополнительных ускорений за счет использования возможностей архитектуры графического процессора NVIDIA Ada.
Архитектура графического процессора NVIDIA Ada сохраняет и расширяет ту же модель программирования CUDA, что и предыдущие архитектуры графических процессоров NVIDIA, такие как NVIDIA Ampere и Turing, и приложения, которые следуют лучшим практикам для этих архитектур, обычно должны получать ускорение архитектуры NVIDIA Ada без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложения для получения дополнительных ускорений за счет использования возможностей архитектуры графического процессора NVIDIA Ada.- PTX ISA
В этом руководстве содержатся подробные инструкции по использованию PTX, низкоуровневой виртуальной машины с параллельным выполнением потоков и архитектуры набора инструкций (ISA). PTX представляет GPU как вычислительное устройство с параллельными данными.
- Руководство разработчика для Optimus
В этом документе объясняется, как API CUDA можно использовать для запроса возможностей графического процессора в системах NVIDIA Optimus.

- Видеодекодер
Видеодекодер NVIDIA (NVCUVID) устарел. Вместо этого используйте SDK NVIDIA Video Codec (https://developer.nvidia.com/nvidia-video-codec-sdk).
- Совместимость PTX
В этом документе показано, как написать PTX, совместимый с ABI и совместимый с другим кодом CUDA.
- Встроенная сборка PTX
В этом документе показано, как встроить операторы языка ассемблера PTX (выполнение параллельных потоков) в код CUDA. В нем описаны доступные параметры и ограничения операторов ассемблера, а также в документе приведен список некоторых ловушек, с которыми вы можете столкнуться.
- Калькулятор занятости CUDA
Калькулятор занятости CUDA позволяет вычислить многопроцессорную занятость графического процессора данным ядром CUDA.
Ссылки на API CUDA
- CUDA Runtime API
Поля в структурах могут отображаться в порядке, отличном от порядка объявления.

- CUDA Driver API
Поля в структурах могут отображаться в порядке, отличном от порядка объявления.
- Математический API CUDA
Математический API CUDA.
- cuBLAS
Библиотека cuBLAS представляет собой реализацию BLAS (базовых подпрограмм линейной алгебры) поверх среды выполнения NVIDIA CUDA. Он позволяет пользователю получить доступ к вычислительным ресурсам графического процессора NVIDIA (GPU), но не выполняет автоматическую распараллеливание между несколькими GPU.
- API cuDLA
API cuDLA.
- NVBLAS
Библиотека NVBLAS — это ускоренная вставка BLAS (подпрограммы базовой линейной алгебры) для нескольких графических процессоров, созданная на основе библиотеки NVIDIA cuBLAS.
- nvJPEG
Библиотека nvJPEG обеспечивает высокопроизводительные функции декодирования JPEG с ускорением на графическом процессоре для форматов изображений, обычно используемых в глубоком обучении и гипермасштабируемых мультимедийных приложениях.

- cuFFT
Руководство пользователя библиотеки cuFFT.
- CUB
Руководство пользователя CUB.
- Стандартная библиотека CUDA C++
Справочник по API для libcu++, стандартной библиотеки CUDA C++.
- Справочное руководство по API cuFile
Справочное руководство по API NVIDIA® GPUDirect® Storage cuFile предоставляет информацию о предварительной версии справочного руководства по API cuFile, которое используется в приложениях и средах для использования технологии GDS, а также описывает назначение, контекст и работу тех API, которые являются частью технологии GDS.
- cuRAND
Руководство пользователя библиотеки cuRAND.
- cuSPARSE
Руководство пользователя библиотеки cuSPARSE.
- NPP
NVIDIA NPP — это библиотека функций для выполнения ускоренной обработки CUDA. Первоначальный набор функций в библиотеке ориентирован на обработку изображений и видео и широко применим для разработчиков в этих областях.
 NPP со временем будет развиваться, чтобы охватывать больше вычислительных задач в различных предметных областях. Библиотека NPP написана для максимальной гибкости при сохранении высокой производительности.
NPP со временем будет развиваться, чтобы охватывать больше вычислительных задач в различных предметных областях. Библиотека NPP написана для максимальной гибкости при сохранении высокой производительности.- nvJitLink
Руководство пользователя библиотеки nvJitLink.
- NVRTC (компиляция среды выполнения)
NVRTC — это библиотека компиляции среды выполнения для CUDA C++. Он принимает исходный код CUDA C++ в виде строки символов и создает дескрипторы, которые можно использовать для получения PTX. Строка PTX, сгенерированная NVRTC, может быть загружена с помощью cuModuleLoadData и cuModuleLoadDataEx и связана с другими модулями с помощью cuLinkAddData API драйвера CUDA. Это средство часто может обеспечить оптимизацию и производительность, невозможные при чисто автономной статической компиляции.
- Thrust
Руководство по началу работы с Thrust.
- cuSOLVER
Руководство пользователя библиотеки cuSOLVER.

Ссылки на API компилятора PTX
- API-интерфейсы компилятора PTX
В этом руководстве показано, как скомпилировать программу PTX в ассемблерный код графического процессора с помощью API-интерфейсов, предоставляемых статической библиотекой компилятора PTX.
- Образцы CUDA
- CUDA Demo Suite
В этом документе описаны демонстрационные приложения, поставляемые с CUDA Demo Suite.
- CUDA в WSL
Это руководство поможет пользователям начать работу с NVIDIA CUDA в подсистеме Windows для Linux (WSL 2). Руководство охватывает установку и запуск приложений и контейнеров CUDA в этой среде.
- Многоэкземплярный графический процессор (MIG)
В этом выпуске руководства пользователя описывается функция Multi-Instance GPU графического процессора NVIDIA® A100.
- Совместимость с CUDA
В этом документе описывается совместимость с CUDA, включая расширенную совместимость с CUDA и обновление с прямой совместимостью с CUDA.

- CUPTI
CUPTI-API. Интерфейс инструментов профилирования CUDA (CUPTI) позволяет создавать инструменты профилирования и отслеживания, предназначенные для приложений CUDA.
- API отладчика
API отладчика CUDA.
- GPUDirect RDMA
Технология, представленная в графических процессорах класса Kepler и CUDA 5.0, обеспечивающая прямой путь для связи между графическим процессором и сторонним одноранговым устройством на шине PCI Express, когда устройства совместно используют один и тот же корневой комплекс восходящего потока с использованием стандартного особенности PCI Express. В этом документе представлена технология и описаны шаги, необходимые для включения подключения GPUDirect RDMA к графическим процессорам NVIDIA в рамках модели драйвера устройства Linux.
- GPUDirect Storage
Документация по GPUDirect Storage.
- vGPU
vGPU с поддержкой CUDA.

Разное
Инструменты
- NVCC
Это справочный документ для nvcc, драйвера компилятора CUDA. nvcc принимает ряд стандартных опций компилятора, например, для определения макросов и путей включения/библиотеки, а также для управления процессом компиляции.
- CUDA-GDB
Инструмент NVIDIA для отладки приложений CUDA, работающих в Linux и QNX, предоставляющий разработчикам механизм отладки приложений CUDA, работающих на реальном оборудовании. CUDA-GDB — это расширение порта x86-64 GDB, отладчика проекта GNU.
- Compute Sanitizer
Руководство пользователя Compute Sanitizer.
- Руководство по установке подключаемых модулей Nsight Eclipse
Руководство по установке подключаемых модулей Nsight Eclipse
- Nsight Eclipse Plugins Edition
Nsight Eclipse Plugins Edition руководство по началу работы
- Nsight Systems
Документация для Nsight Systems.

- Nsight Compute
NVIDIA Nsight Compute — это интерактивный профилировщик ядра нового поколения для приложений CUDA. Он предоставляет подробные показатели производительности и отладку API с помощью пользовательского интерфейса и инструмента командной строки.
- Nsight Visual Studio Edition
Документация для Nsight Visual Studio Edition.
- Profiler
Это руководство по Profiler.
- Двоичные утилиты CUDA
Замечания по применению для cuobjdump, nvdisasm и nvprune.
Белые книги
- Плавающая запятая и IEEE 754
Ряд проблем, связанных с точностью и совместимостью с плавающей запятой, часто является источником путаницы как для ЦП, так и для ГП. Цель этого технического документа — обсудить наиболее распространенные проблемы, связанные с графическими процессорами NVIDIA, и дополнить документацию в Руководстве по программированию CUDA C++.

- Неполный LU и итерационные методы с предварительной обработкой по Холески
В этом техническом документе мы показываем, как использовать библиотеки cuSPARSE и cuBLAS для достижения двукратного ускорения по сравнению с ЦП в итерационных методах с неполной LU и предварительной обработкой по Холески. Мы сосредоточимся на итерационных методах Bi-Conjugate Gradient Stabilized и Conjugate Gradient, которые можно использовать для решения больших разреженных несимметричных и симметричных положительно определенных линейных систем соответственно. Кроме того, мы комментируем параллельное разреженное треугольное решение, которое является важным строительным блоком в этих алгоритмах.
Указания по применению
- CUDA для Tegra
В этом примечании к применению представлен обзор архитектуры памяти NVIDIA® Tegra® и рекомендации по переносу кода с дискретного графического процессора (dGPU), подключенного к системе x86, на интегрированный графический процессор Tegra® (iGPU).


 Если вы не согласны с условиями лицензионного соглашения, не загружайте и не используйте программное обеспечение.
Если вы не согласны с условиями лицензионного соглашения, не загружайте и не используйте программное обеспечение. Приложения включают в себя список всех устройств с поддержкой CUDA, подробное описание всех расширений языка C++, списки поддерживаемых математических функций, функции C++, поддерживаемые в коде хоста и устройства, сведения о выборке текстур, технические характеристики различных устройств и выводы. путем внедрения API низкоуровневого драйвера.
Приложения включают в себя список всех устройств с поддержкой CUDA, подробное описание всех расширений языка C++, списки поддерживаемых математических функций, функции C++, поддерживаемые в коде хоста и устройства, сведения о выборке текстур, технические характеристики различных устройств и выводы. путем внедрения API низкоуровневого драйвера. Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с Maxwell.
Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с Maxwell. Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с Turing.
Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с Turing. Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с архитектурой Ada.
Этот документ содержит рекомендации по обеспечению совместимости ваших программных приложений с архитектурой Ada.
 Приложения, которые следуют рекомендациям для архитектуры NVIDIA Volta, как правило, должны получать ускорение на архитектуре графического процессора NVIDIA Ampere без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложений для получения дополнительных ускорений за счет использования возможностей архитектуры графических процессоров NVIDIA Ampere.
Приложения, которые следуют рекомендациям для архитектуры NVIDIA Volta, как правило, должны получать ускорение на архитектуре графического процессора NVIDIA Ampere без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложений для получения дополнительных ускорений за счет использования возможностей архитектуры графических процессоров NVIDIA Ampere. Архитектура графического процессора NVIDIA Ada сохраняет и расширяет ту же модель программирования CUDA, что и предыдущие архитектуры графических процессоров NVIDIA, такие как NVIDIA Ampere и Turing, и приложения, которые следуют лучшим практикам для этих архитектур, обычно должны получать ускорение архитектуры NVIDIA Ada без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложения для получения дополнительных ускорений за счет использования возможностей архитектуры графического процессора NVIDIA Ada.
Архитектура графического процессора NVIDIA Ada сохраняет и расширяет ту же модель программирования CUDA, что и предыдущие архитектуры графических процессоров NVIDIA, такие как NVIDIA Ampere и Turing, и приложения, которые следуют лучшим практикам для этих архитектур, обычно должны получать ускорение архитектуры NVIDIA Ada без каких-либо изменений кода. В этом руководстве описаны способы тонкой настройки приложения для получения дополнительных ускорений за счет использования возможностей архитектуры графического процессора NVIDIA Ada.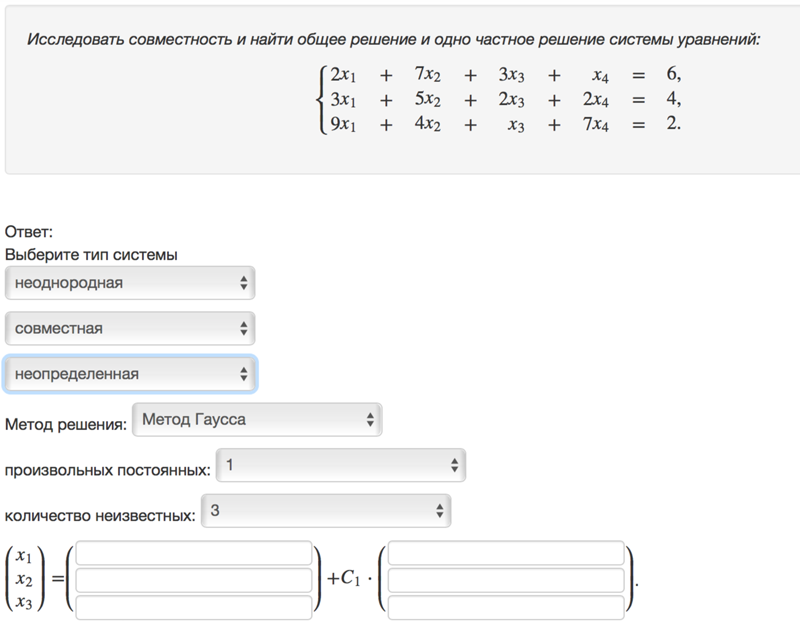


 NPP со временем будет развиваться, чтобы охватывать больше вычислительных задач в различных предметных областях. Библиотека NPP написана для максимальной гибкости при сохранении высокой производительности.
NPP со временем будет развиваться, чтобы охватывать больше вычислительных задач в различных предметных областях. Библиотека NPP написана для максимальной гибкости при сохранении высокой производительности.




