Исследовать функции на экстремум: Исследовать на экстремум функции двух переменных

11. Экстремумы функции нескольких переменных

Локальный экстремум (т.е. максимум или минимум) для ФНП определяется так же, как и для функции одной переменной.

1. Функция , определенная в некоторой области, имеет локальный максимум в точке , если в некоторой окрестности этой точки верно неравенство:

,

и локальный минимум, если выполняется неравенство:

.

Очевидно, что в окрестности точки экстремума приращение функции

сохраняет знак, а именно:

, если — точка максимума

и , если — точка минимума.

Для исследования функции на экстремум применяют следующие теоремы.

Теорема 1. (Необходимые условия экстремума). Функция нескольких переменных может иметь экстремум только в точках, лежащих внутри области определения функции, в которых все частные производные первого порядка одновременно равны нулю или не существуют.

Такие точки будем называть критическими точками. Точки, в которых все частные производные первого порядка одновременно равны нулю, — стационарными.

Не всякая критическая точка является точкой экстремума. Другими словами, необходимый признак существования экстремума не является достаточным.

Например, для функции ее частные производные и одновременно обращаются в нуль в точке О(0, 0), но:

, а ,

поэтому в точке О(0, 0) экстремума нет.

Таким образом, для исследования функции на экстремум нужно:

1) найти критические точки (в которых все частные первого порядка одновременно обращаются в нуль или не существуют)

2) исследовать функцию в критических точках, используя достаточные признаки экстремума или определение экстремума (исследование знака приращения функции в критической точке).

Теорема 2. (Достаточные признаки экстремума для функции двух переменных).

Пусть — критическая точка функции , а сама функция дважды дифференцируема в критической точке.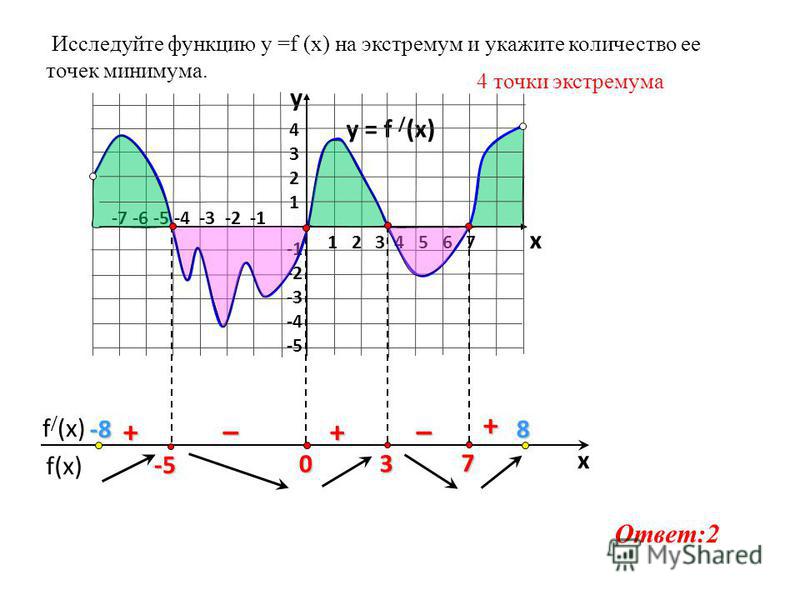

Обозначим:

, , и .

Тогда

1) если определитель , то — точка экстремума, причем если

— то точка минимума

— точка максимума:

2) если определитель , то функция экстремума в данной точке не имеет;

3) если определитель , то для решения вопроса о наличии или отсутствии экстремума в точке требуются дальнейшие исследования, например, по знаку приращения функции вблизи этой точки.

Примеры.

1. Исследовать на экстремумы функции:

а) .

1) Ищем критические точки из условия одновременного обращения в нуль ее частных производных первого порядка в нуль:

система имеет 2 решения, а, значит, 2 критические точки: и .

2) Для исследования этих точек на экстремум найдем производные 2-го порядка и вычислим определитель:

, , , откуда .

В точке : , следовательно, согласно достаточному признаку, экстремума нет.

В точке : , следовательно, согласно достаточному признаку, экстремум есть. Причем , т.е. — точка максимума.

3) .

б) .

1) Ищем критические точки .

Из системы уравнений находим и .

2) Найденные точки принадлежат области определения исследуемой функции:

(которая представляет собой половину плоскости хОу, лежащую выше оси Ох, включая и саму ось Ох).

Но эти точки расположены не внутри области определения, а на ее границе , поэтому не являются критическими.

3) Частные производные первого порядка для данной функции существуют во всей области определения, поэтому и других критических точек функция не имеет. Следовательно, она не имеет экстремумов, согласно необходимому признаку.

Если не учесть, что граничные точки области определения функции не могут быть точками экстремума, то определив знак определителя точки , мы бы пришли к ошибочному заключению, что она есть точка минимума.

в) .

1) Ищем критические точки .

Решая систему уравнений ,

находим единственную точку , которая является единственной критической точкой функции.

2) Для исследования этой точки на экстремум воспользуемся необходимым признаком экстремума: найдем производные 2-го порядка и вычислим определитель:

, , , откуда .

Здесь определитель, как оказалось, не имеет знака, поэтому требуется дополнительное исследование. Чтобы установить, имеется ли экстремум в найденной критической точке , исследуем знак приращения функции вблизи нее:

.

Пусть точка лежит на биссектрисе .

Тогда .

Если точка будет расположена ниже , т.е. если ордината точки : , то . Если точка будет выше , т.е. если ордината точки : , то и приращение функции .

Таким образом, вблизи разность не сохраняет знака и, следовательно, функция не имеет экстремума.

г) .

1) Ищем критические точки: , , .

Очевидно, что эти частные производные не обращаются в нуль ни при каких значениях . Они не существуют в точке , которая лежит внутри области определения функции (т.к. область определения данной функции – совокупность всех точек пространства). Поэтому данная точка – критическая точка.

2) Исследуя знак приращения функции вблизи найденной критической точки:

убеждаемся, что при любых, отличных от нуля значениях , приращение сохраняет положительный знак. Следовательно, точка — точка минимума и .

Теорема 3. (Достаточные признаки экстремума для функции нескольких переменных).

Пусть — критическая точка функции , а сама функция дважды дифференцируема в критической точке. Обозначим:

, , , …

.

Тогда

1) если определители , то — точка минимума;

2) если знаки определителей , чередуются, начиная со знака минус, то — точка максимума.

Условный экстремум.

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение

(х, у) = 0, которое называется уравнением связи.

Тогда из переменных х и у только одна будет независимой, т. к. другая может быть выражена через нее из уравнения связи.

Тогда u = f(x, y(x)).

В точках экстремума:

=0 (1)

Кроме того:

(2)

Умножим равенство (2) на число  и сложим с равенством (1).

Для выполнения этого условия во всех точках найдем неопределенный коэффициент  так, чтобы выполнялась система трех уравнений:

Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.

Выражение u = f(x, y) + (x, y) называется функцией Лагранжа.

Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи:

2x + 3y – 5 = 0

Таким образом, функция имеет экстремум в точке .

Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.

Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.

Исследование функции на экстремум с помощью первой и второй производной

Байланысты:
40.Исследование функции на экстремум с помощью первой и второй производной
40.Исследование функции на экстремум с помощью первой и второй производной, 1- күн — 4.1.-ресурсы Тыңдалым және айтылым дағдыларын меңгерту

---

©melimde.com 2023
әкімшілігінің қараңыз

40. Тема: Исследование функции на экстремум с помощью первой и второй производной  Цель урока: 1. Обеспечение усвоения понятий экстремумов функции и критических точек. 2.Формирование представлений о правилах нахождения экстремумов функции с помощью первой и второй производных. 3.Формирование умений определять экстремумы функции с помощью первой и второй производных. Ход урока: Точки минимума и максимума функции. Точка x0 из области определения функции f(x) называется точкой минимума (точкой максимума) этой функции, если существует такая δ-окрестность (x0–δ, x0+δ) точки x0, что для всех x≠x0 из этой окрестности выполнятся неравенство f(x)≥f(x0) (f(x)≤f(x0)). Точки минимума и максимума функции называются экстремальными точками (или точками экстремума) данной функции, а значения функции в этих точках – минимумом и максимумом (или экстремумами функции). Точками экстремума могут служить только критические точки – это точки из области определения функции, в которых производная функции f′(x)=0 или терпит разрыв. Если при переходе через критическую точку x0 производная f′(x) меняет знак, то функция f(x) имеет в точке x0 экстремум: минимум – если f′(x) меняет знак с «–» на «+», максимум – если f′(x) меняет знак с «+» на «–». Если же при переходе через критическую точку x0 производная f′(x) не меняет знака, то функция f(x) в точке x0 не имеет экстремума. Правило нахождения экстремумов функции y=f(x) с помощью первой производной: Найти производную f′(x). II. Найти критические точки функции y=f(x), т.е. точки, в которых f′(x)=0 или терпит разрыв. III. Исследовать знак производной f′(x) в промежутках, на которые найденные критические точки делят область определения функции f(x). При этом критическая точка x0 – точка минимума, если она отделяет промежуток, в котором f′(x)0, и точка максимума – в противном случае. Если же в соседних промежутках, разделенных критической точкой x0, знак производной не меняется, то в точке x0 функция экстремума не имеет. IV. Вычислить значения функции в точках экстремума. Примеры. Исследовать на экстремум следующие функции: f(x)=x² — 4x f′(x)=2x – 4 f′(x)=0 2x – 4=0 x=2 Составим таблицу: Точка минимума (2;-4) – вершина параболы. x -∞ f(x)= — x² + 5x + 6 f′(x)= — 2x + 5 f′(x)=0 -2x + 5=0 x=5/2 Составим таблицу: График функции – парабола. x -∞ f(x)= x³ — 3x² f′(x)= 3x² — 6x f′(x)=0 3x² — 6x =0 x=0, x=2 Составим таблицу:: x -∞ Вторая производная. Если y′ есть производная от функции y=f(x), то производная от y′ по x (если она существует) называется второй производной (или производной второго порядка): y′′ f′′(x) Правило нахождения экстремумов функции y=f(x) с помощью второй производной: Найти производную f′(x). II. Найти критические точки данной функции, в которых f′(x)=0. III. Найти вторую производную f′′(x). IV. Исследовать знак второй производной в каждой из критических точек. Если при этом f′′(x)0, то – минимум. Если же f′′(x)=0, экстремум функции надо искать с помощью первой производной. V. Вычислить значения функции в точках экстремума. Примеры. Исследовать на экстремум с помощью второй производной следующие функции: 1. f(x)=x² — 2x – 3 f′(x)=2x – 2 f′(x)=0 2x – 2=0 x=1 – критическая точка f′′(x)=2>0, тогда при x=1 fmin=f(1)= — 4 2. f(x)=x³ — 9x² + 24x – 12 f′(x)=3x² — 18x +24 f′(x)=0 3x² — 18x +24=0 x² — 6x +8 =0 x=2, x=4 – критические точки f′′(x)=6x – 18 f′′(2)=6·2 – 180, значит при x=2 fmin=f(4)=42>0>2> жүктеу/скачать 16. 67 Kb. Достарыңызбен бөлісу:

1.4 Методы оптимизации | Блог турбомашин

Предыдущая глава Следующая глава

Ключевые символы
Индексы и другие обозначения
Сокращения

1.4.1 Общие сведения об экстремальных задачах

Для решения задач с единым критерием оптимальности разработаны строгие математические методы.

Прямые методы вариационного исчисления — одного из разделов теории экстремальных задач для функционала — сводят задачу нахождения экстремума функционала к оптимизации функций.

Существуют аналитические и численные методы поиска оптимальных решений. Как правило, реальные задачи решаются численно, и лишь в некоторых случаях удается получить аналитическое решение.

Оптимизация функций с помощью дифференцирования

Нахождение экстремума функции одной или нескольких переменных возможно методами дифференциального исчисления. Говорят, что точка X̂   дает функции f (x) локальный максимум, если существует число Ɛ>0, при котором из неравенства | х-х| < Ɛ после него следует неравенство f (x) ≤ f (x̂).

Функция называется одноэкстремальной (унимодальной), если она имеет один экстремум, и многоэкстремальной (мультимодальной), если имеет более одного экстремума. Точка, в которой функция имеет максимальное или минимальное значение из всех локальных экстремумов, называется точкой глобального экстремума.

Необходимое условие экстремума дифференцируемой функции одной переменной дает знаменитая теорема Ферма: пусть f (x) – функция одной переменной, дифференцируемая в точке x̂. Если x̂ – локальная крайняя точка, то f’ (x̂) = 0,

Точки, в которых выполняется это соотношение, называются стационарными. Стационарные точки не обязательно являются точками экстремума. Достаточные условия максимума и минимума функций одной переменной – соответственно f” (x̂) <0,  f” (x̂) > 0.

Прежде чем перейти к необходимым и достаточным условиям экстремумов функций многих переменных, введем некоторые определения. Градиент функции f (x) представляет собой вектор

Вещественная симметричная матрица H называется положительной (отрицательной), определенной, если X ^T = Hx>0(<0) для каждого набора действительных чисел x _{1 ,} x _{2, ….} x _n, не все из которых равны нулю.

Необходимые условия для этого x̂ – точка локального экстремума n переменных функции f(x), x ƐE ⁿ  следующие:

ⁿ , является достаточным условием унимодальности функции. Для проверки определенности матрицы А применяется критерий Сильвестра, согласно которому необходимым и достаточным условием положительной определенности являются неравенства:

Этот случай связан с определением экстремума в бесконечном диапазоне изменения переменных x _{1 ,} x _{2, ….} х _с.ш. Если на оптимизируемую функцию наложены дополнительные условия (ограничения), говорят о проблеме условного экстремума.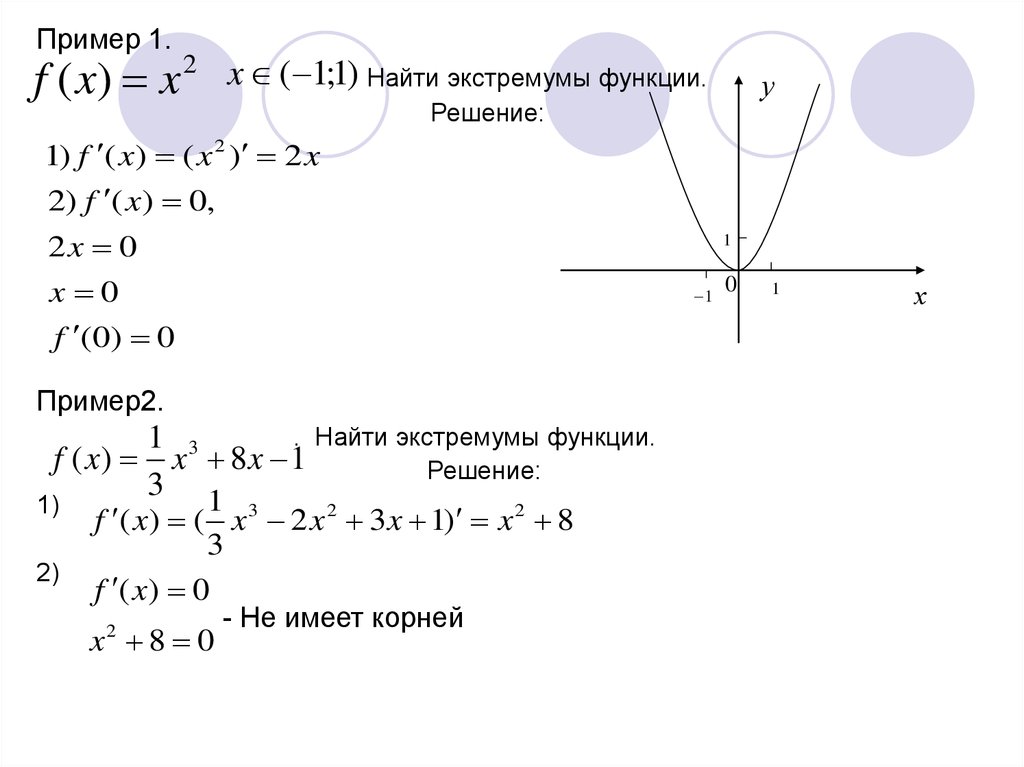 В общем случае требуется найти экстремум f(x), xƐE ⁿ при ограничениях

1,4

Для решения задачи (1.14) только с ограничениями в виде уравнений используется метод множителей Лагранжа, основанный на поведение функции Лагранжа: 

где λ _j  – неопределенные множители Лагранжа. Запишем необходимые условия оптимальности в задаче условного экстремума с ограничениями-равенствами:

Это система n + m уравнений, из которых можно определить x _i , i=1,…,n, λ _j , j=1,…,m. Строгое доказательство условий Лагранжа, изложенных в конкретных руководствах. Объясните смысл метода следующим образом. С одной стороны, для всех x, удовлетворяющих ограничениям h _j (x)=0, j=1,…,m, очевидно, L=(x, λ) = f(x). С другой стороны, крайняя точка функции Лагранжа также удовлетворяет этим условиям (второе уравнение (1.14), и поэтому, находя экстремум L(x, λ), мы одновременно получаем условный f (x) экстремум. вопрос о наличии стационарной точки, являющейся локальным экстремумом в задаче об условном экстремуме, разложим функцию Лагранжа в ряд Тейлора при условии выполнения соотношений h _j (х)=0.

Оптимизация с ограничениями в виде неравенств

Рассмотренные выше классические методы нахождения условных и безусловных экстремумов функций в ряде случаев позволяют решать задачи с ограничениями-неравенствами.

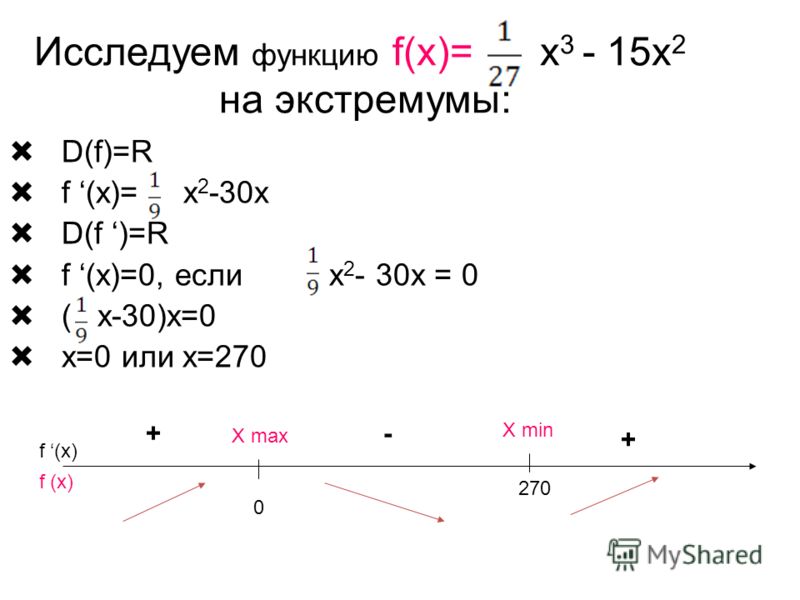
Рис. 1.4 Для определения экстремума функции одной переменной на интервале.

Пусть поставлена ​​задача найти максимум функции одной переменной f(x) на интервале a≤x≤b. Используя необходимые условия оптимальности, находим корни f'(x) = 0, лежащие в интервале [a, b]; Проверяем достаточные условия максимума f”(x̂) <0 и выбираем точки, соответствующие максимуму. Также вычисляем значения функции на границах отрезка, где она может принимать более высокие значения, чем интервал (рис. 1.4). Обратимся теперь к случаю нескольких переменных и рассмотрим задачу оптимизации: найти максимум f(x), xƐE ⁿ  , с учетом ограничений:

На первом этапе решения методом множителей Лагранжа находим все стационарные точки, лежащие в положительном октанте n-мерного пространства, и выделяем максимальные точки на основе достаточные условия экстремума. Затем исследуем положительную границу октанта, по очереди приравнивая к нулю во всевозможных комбинациях 1, 2,…,n-m+1 переменных и каждый раз решая задачу оптимизации с ограничениями-равенствами. В результате вычислительного процесса, сложность которого очевидна, из всех экстремумов должен быть выбран наибольший.

Более общая задача, найти максимум

Для задачи могут быть записаны необходимые условия оптимальности (обобщенное правило множителей Лагранжа), однако оно используется редко из-за сложности решения полученной системы уравнений.

1.4.2 Нелинейное программирование

Предмет нелинейного программирования

Нелинейное программирование – раздел прикладной математики, занимающийся нахождением экстремума функции многих переменных при наличии нелинейных ограничений в виде равенств и неравенств, т.е. решения задачи (1.14), рассмотренной в предыдущем разделе [3].

В нее входят классические методы оптимизации, а также такие дисциплины, как линейное, квадратичное, разделимое программирование. Однако наибольший практический интерес для нас представляют численные или прямые методы нелинейного программирования, особенно интенсивно развивающиеся в последние годы.

Ни один из предложенных алгоритмов не является абсолютно лучшим, поэтому выбор численного метода диктуется содержанием конкретной задачи, которую необходимо решить. Вычислительные методы классифицируются по той или иной особенности задачи (без ограничений, с ограничениями-равенствами, неравенствами и т. д.), характером методов решения (например, с использованием или без использования производных), типом ЭВМ, языком программирования , и так далее.

Поиск экстремума функции одной переменной

Ряд методов поиска экстремума функции многих переменных используют в составе процедуры одномерной оптимизации. В случае, когда функция одной переменной является многоэкстремальной, единственным правильным методом нахождения глобального экстремума является прямой перебор ряда значений с некоторым шагом их изменения.

Очевидно, что функция может резко меняться, тем меньшую сетку следует выбирать. После грубого определения окрестности экстремума приступаем к поиску его точного значения. Для этого используются одномерные алгоритмы поиска экстремумов унимодальных функций на заданном интервале.

Одним из самых эффективных методов является так называемое золотое сечение. Напомним, что если отрезок разделить на две части так, что отношение длин на большей относительной длине равно длине большей части всего отрезка, получится так называемое золотое сечение (составляет примерно 0,38:0,62). Метод золотого сечения как раз и основан на многократном делении интервала неопределенности, т.е. интервала, в котором
экстремумов заключены в соответствующем соотношении.

Для уменьшения диапазона неопределенности в 100 раз требуется 11 расчетов, в 10000 раз – 21 расчет. Для сравнения, метод деления пополам (дихотомия) приводит к соответствующему сужению диапазона оценки 14 и 28 функций.

Преимущество золотого сечения в том, что оно одинаково хорошо работает как для гладких, так и для негладких функций. Выяснилось, что в случае гладких функций полиномиальной аппроксимацией можно быстро определить число экстремумов с той же точностью, что и методом золотого сечения.

Если оптимизируемая функция определена и унимодальна на всей действительной оси, нет необходимости беспокоиться о выборе начального интервала неопределенности. Например, в методе Дэвиса, Свена и Кэмпи (сокращенно DSC) с определенной точки делается нарастающий шаг до прохождения экстремума, а затем производится квадратичная интерполяция на основе информации о функциях в последних трех точках. определяется экстремум интерполяционного полинома.

Алгоритм Пауэлла квадратичной полиномиальной интерполяции проводится в трех произвольных точках, находится приближенный экстремум, отбрасывается одна из четырех точек и процедура повторяется до сходимости. Наиболее эффективным является сочетание описанных алгоритмов или так называемый метод DSC-Powell . В соответствии с этим первым алгоритмом ДСК ищется интервал, в котором экстремум, выбираются три точки и переносятся туда по параболе. Ориентировочное значение в экстремуме рассчитывается как в методе Пауэлла:

Если значения функции в точке x̂ от оптимальных значений f(x ₁ ), f(x ₂ ), f(x ₃ ) отличаются менее чем на заданную точность, завершить расчеты ,
иначе отбросить худшие из точек x ₁ , x ₂ , x ₃ ,x̂ и построить новую параболу. Для функций, достаточно близких к квадратичным, эффективность ДСК-Пауэлла очень высока: как правило, решение с точностью 10 ^-5 …10 ^-6 достигается 6–8 расчетов целевой функции.

Методы безусловной оптимизации

Рассмотрим задачу нахождения максимума функции многих переменных без ограничений. Найдите максимум f(x), xƐE ⁿ Одним из самых известных является градиентный метод решения этой задачи. Они основаны на том, что продвижение целевой функции в экстремум в пространстве E ⁿ производится по правилу:

Вектор s _k задает другое направление поиска, а λ _j – длину шага в этом направлении. Очевидно, что λ _j следует выбирать так, чтобы максимально приблизиться к экстремуму. Используются различные методы выбора направления поиска. Простейший из них состоит в том, что перемещение точки x _k производится в направлении наибольшего увеличения f(x _k ), т. е. в направлении функции градиента в данной точке.

Согласно этому методу, называемому методом наискорейшего спуска ,

Теория показывает, а практика расчетов подтверждает, что метод наискорейшего спуска малоэффективен в тех случаях, когда кривые уровня целевой функции сильно растянуты, т.е. есть глубокие овраги при поиске минимума или хребты при поиске максимума. Направление наискорейшего спуска почти ортогонально наилучшему направлению поиска, как следствие, оптимальный шаг все время уменьшается, и алгоритм «зависает», не доходя до экстремума. Выходом из этой ситуации может стать масштабирование переменных, при котором линии уровня будут как бы близки к окружности.

Для уменьшения объема вычислений целевой функции, связанных с численным определением частных производных, иногда применяют метод покоординатного спуска, который также называют релаксационным или методом Гаусса-Зейделя. Пусть e _i – ось x _i единичный вектор, а x={x ₁ …,x _n – начальная точка поиска. Один интернационал координатного спуска должен сделать шаги: x _k-1 =x _k +λ _k e _k , k = 1,…, n .

Шаг как и в методе наискорейшего спуска определяется условием max f(x _k +λ _k s _k Метод Гаусса-Зейделя страдал тем же недостатком, что и метод наискорейшего спуска, – плохой сходимость при наличии оврагов

Один из способов преодоления вычислительных трудностей, связанных с овражной структурой целевой функции, заключается в использовании информации не только о ее первой производной, но и более высокого порядка, содержащейся во вторых частных производных. произвольную функцию можно представить в виде ее квадратичного разложения в ряд Тейлора в окрестности точки x:

Уравнения (1.26) или (1.27) применяются итеративно до тех пор, пока не будет достигнут критерий конечного процесса расчета, называемый методом Ньютона. Трудности использования алгоритма Ньютона связаны, во-первых, с обращением матрицы Гессе, во-вторых, с вычислением вторых частных производных, что ограничивает его практическое применение.

Методы сопряженных направлений лишены недостатков градиентных методов и имеют скорость сходимости, близкую к методу Ньютона. В то же время они являются методами первого порядка, как и градиентные. Положительно определенная квадратичная форма от n переменных минимизируется методом сопряженных градиентов не более чем за n шагов. Метод сопряженных градиентов подходит для минимизации неквадратичных функций только тогда, когда они являются итерационными.

Существуют различные способы построения сопряженных направлений. В частности, Флетчер и Ривз предложили метод, названный методом сопряженных градиентов, согласно которому последующее направление поиска представляет собой линейную комбинацию направления наискорейшего спуска и предыдущего направления, т. е.:

Некоторые методы не используют производные функций, а направление оптимизации в которых определяется только на основе последовательных вычислений целевой функции. В тех случаях, когда определение производных целевой функции затруднено, предпочтительными могут быть поисковые алгоритмы. В случае одномерного поиска аналогом метода является метод золотого сечения, а методом использования производных – метод ДСК-Пауэлла.

Методы оптимизации с ограничениями

В дополнение к описанному ранее методу множителей Лагранжа для нахождения экстремума функций с ограничениями разработан ряд численных методов. Первый подход к построению алгоритмов условной оптимизации заключается в монотонном движении к оптимуму целевой функции и одновременном стремлении уложиться в точные или приближенные пределы.
Методов этого типа много, но сложность, отсутствие гибкости и большой объем вычислительной работы ограничивают их использование в практических расчетах.

Более изящные, простые в реализации и эффективные методы, основанные на сведении задач с ограничениями к решению последовательности
задач безусловной оптимизации – так называемые методы штрафных функций. Существует несколько вариантов этих методов.

Начнем их рассмотрение с метода внутренних точек для задач с ограничениями-неравенствами:

Организация численного поиска максимума (1.29) должна быть такой, чтобы точка не покидала допустимую область. Этот дефицит лишен метод внешней штрафной функции , который для задачи вида (1.33) предполагает построение ассоциированной целевой функции.

Можно показать, что последовательность точек x̂ _k сходится к решению задачи (1.33), но в отличие от метода внутренних точек к крайнему движению происходит вне допустимого множества, и берется от названия метода внешних штрафных функций. Этот метод применим и к общей задаче нелинейного программирования (1.14), для которой используется присоединенная целевая функция

Алгоритм решения тот же, что и для задачи (1.34).

Решение задач нелинейного программирования с ограничениями методом штрафной функции осложняется тем, что с ростом коэффициента штрафной функции (1.35) выражена овражная структура. Как было показано ранее, не все методы безусловной оптимизации справляются с такими задачами, поэтому выбор метода нахождения экстремума присоединенной целевой функции имеет принципиальное значение.

Важную роль также играет стратегия изменения штрафного коэффициента, так как если выбрать его сразу большим, ограничения задачи выполняются хорошо, но целевая функция не улучшается. Напротив, при слишком малых значениях Λ _k движение происходит в сторону улучшения целевой функции, но практически не учитываются ограничения, которые могут привести к сбою в областях Е ⁿ где целевая функция и ограничения не определены.

Например, при наличии в целевой функции или в ограничениях членов вида х ^и вход в зону х≤0 недопустим. быть введением подходящей замены переменных. В частности, для выполнения условия x>0 подходит замена x=e, которая уже zƐE ¹ . Если такой прием невозможен, то должны быть тщательно подобраны константы методов безусловного поиска, так как длина шага в направлении спуска, изменение этого шага в процессе нахождения одномерного вектора переменных не покидала области где целевая функция и ограничения
проблема определена.

В заключение рассмотрим возможность использования методов нелинейной оптимизации для решения систем нелинейных уравнений. Предположим, что в задаче (1.14) отсутствуют ограничения в виде неравенств, а количество переменных равно количеству ограничений в виде уравнений, т. е. фактически задача решения системы m уравнений с м неизвестные. Формируем функцию

 

и находим ее максимум. Если система уравнений h _j (x)=0, j=1,…m , имеет решение, то, очевидно, одновременно с максимумом I ^* является корнем системы уравнений. В частности, если функции h _j (x) линейны, функция (1.36) получается квадратичной и может быть эффективно решена методом Ньютона и методом сопряженных градиентов.

Замена задачи решения систем линейных уравнений на экстремальные задачи оправдана в тех случаях, когда матрица системы плохо обусловлена ​​(например, в задаче аппроксимации методом наименьших квадратов) и не может быть решена обычными методами, в частности, методом исключения.

Значения h _j (x) в (1.35) называются остатками, а решение нелинейных уравнений заменяется минимизацией суммы квадратов невязок.

1.4.3 Методы оптимизации трудновычислимых функций

В некоторых задачах, когда расчет значения целевой функции может занимать минуты, часы и даже дни работы ЭВМ, круг допустимых методов оптимизации значительно сужается

К таким задачам, в частности, относится аэродинамическая оптимизация лопаток турбины с помощью CFD.

Метод Нелдера-Мида (Nelder A. -Mead R.), также известный как метод гибкого многогранника или симплекс-метод, представляет собой метод безусловной оптимизации функций многих переменных. Не требуя вычисления функции градиента, она применима к негладким, зашумленным функциям и особенно эффективна при небольшом (до 6) числе переменных параметров. Суть его заключается в следующе-последовательном движении и деформации симплекса вокруг точки экстремума. Метод является локальным экстремумом и может «застрять» в одном из них. Если вам все же нужно найти глобальный экстремум, можно попробовать выбрать другой начальный симплекс.

Более развитый подход к исключению локальных экстремумов предложен алгоритмом, основанным на методе Монте-Карло, а также эволюционными алгоритмами.

Генетический алгоритм (ГА) – эвристический метод глобального поиска, используемый для решения задач оптимизации и моделирования путем случайного выбора, сочетания и варьирования требуемых параметров с использованием механизмов, напоминающих биологическую эволюцию. Использование ГА предполагает его тщательную настройку на специальных тестовых функциях, что, однако, не гарантирует эффективности алгоритма и точности решений функции.

Этот алгоритм хорошо подходит для исследования зашумленных функций, но требует большого количества CFD-расчетов и, следовательно, большего времени на оптимизацию. Последнее вынуждает исследователей использовать грубые сетки и не совсем точные, но легко рассчитываемые модели турбулентности, что неизбежно приводит к потере точности численных расчетов.

Методы Монте-Карло (случайный поиск) позволяют находить экстремумы многомодальных и зашумленных функций; использовать различные ограничения при оптимизации; особенно эффективен при большом количестве переменных параметров; требует тщательной настройки для тестовых функций; это один из самых распространенных методов оптимизации и решения различных задач в математике, физике,
экономики и др. Однако метод требует десятков тысяч вычислений целевой функции и практически не применим для прямой оптимизации на основе CFD-расчетов. Для повышения эффективности случайного поиска использовали квазислучайную последовательность чисел (LPτ [4] Соболь), Форе, Халтон и др.). Повышение эффективности достигается за счет устранения кластеризации, возникающей при случайном поиске, т. е. за счет более равномерного распределения точек в исследуемой области поиска экстремума функции.

В последнее время в алгоритмах оптимизации широко используются методы планирования эксперимента. Используя методы теории планирования эксперимента
(Design of the Experiment – ​​DOE), исходную математическую модель можно аппроксимировать квадратичным полиномом. Одна из актуальных схем планирования эксперимента, описанная в разделе 1.3. Эти квадратичные полиномы можно использовать для дальнейшей оптимизации с применением универсального и надежного метода глобального поиска с использованием квазислучайных последовательностей.

Предыдущая глава Следующая глава

Поиск абсолютных экстремальных значений функции — ToronadoSD

21 декабря 2022 г. 20 ноября 2022 г.

Существует несколько способов найти абсолютные экстремальные значения функции. Во-первых, найти критические точки функции, то есть точки, в которых производная функции либо равна 0, либо не определена. Эти точки могут быть локальными экстремальными значениями , но они могут не быть абсолютными экстремальными значениями. Чтобы найти абсолютные экстремальные значения, вы также можете посмотреть на конечные точки области определения функции, поскольку они также будут экстремальными значениями.

Учитывая экстремальное значение в его вершинах, f(x)=ax2+bx+c является квадратичной функцией , поэтому, если a>0 является максимальным, f(*ba) является минимальным, а если a** *0 — минимум,

Как найти абсолютные экстремальные значения?

Источник: numerade.com

Существует несколько способов найти абсолютные экстремальные значения функции. Один из способов — взять производную функции и приравнять ее к нулю. Это даст вам критические точки функции, то есть точки, в которых функция находится либо на максимуме, либо на минимуме. Другой способ найти абсолютные экстремальные значения — посмотреть на график функции и найти точки, в которых функция находится в самой высокой или самой низкой точке.

Абсолютное экстремальное значение — это значение функции, которое больше или меньше или равно значению всей величины. Абсолютный максимум функции можно получить, вычислив ее значение x в абсолютных терминах . Если функция меньше точки вокруг нее, локальный минимум будет равен x. Важно отметить, что относительные экстремумы не возникают в конечных точках домена. Если у вас есть критические точки и вы можете их оценить, вы можете легко найти абсолютные экстремумы. Другими словами, максимальное значение в случае высокой вероятности успеха всегда является абсолютным минимумом, тогда как наименьшее значение всегда имеет низкую вероятность успеха. Другие методы также могут использоваться для определения абсолютного экстремизма, но они зависят от расчета производной.

Как найти экстремальные значения функции?

Источник: cheggcdn.com

Установите значение f равным (x)=0 и найдите экстремальное значение функции f. Вычисляются координаты экстремальных значений/локальных максимумов и минимумов. Например, его можно использовать. Например, если x(x) = x26x+5, это представляет x26x+5 = f(x).

На графике точкой относительного максимума функции является точка. Все остальные координаты больше, чем координата*. Есть точки, в которых это проявляется одинаково. Как правило, точкой относительного минимума является интервал в (alt xlt b). Значение f(z) вычисляется путем сложения всех z этого интервала одновременно. Из-за сильной интуитивной привлекательности теоремы Ферма вы можете принять ее существование и вернуться к ее доказательству позже. Для рассмотренного выше случая существует относительный максимум при (x=ext), который меняется от точки к точке в заданном интервале.

Поскольку в * (слева (c, d * справа) с * (clt a * lt d *) и * (f * слева (x * 1)) есть открытые интервалы), мы можем заключить, что f'(a ) существует. В отсутствие производной вы можете не знать, что могут быть максимум и минимум. В результате вы должны определить, существует ли где-либо в мире производная. Поскольку производная равна нулю или не определена в обоих точки относительного максимума и точки относительного минимума, нам нужен способ определить, какая из них верна, а какая нет.Прямая проверка, чтобы определить, находятся ли точки вблизи интереса на пороге интереса или выше него, является наиболее элементарным подходом. невозможно определить производную функции функции в любом месте на графике, и она равна нулю или отсутствует в любой точке рядом или слева от производной. Если значения по обе стороны от [math](ds x_2*] меньше, должны быть относительным максимумом в этой точке

Когда мы находим два из них, но не другое, в этой точке нет абсолютного максимума или минимума. Найдите максимальную и минимальную точки для *(f(x)=*sin x plus *cos x ext= в [math](f(x)=*sin x plus *cos x ext=]math[/math] Производная Функция состоит в том, чтобы указать точку единичной окружности, когда она является результатом комбинации синуса и косинуса.В тригонометрической функции [pi/4*pm 2kpipi] имеется относительных максимумов (pi/4*pm 2kpipi). Поскольку у не определено для любых точек, в которых оно является критическим, единственная критическая точка находится при *(x = 0,5 ext*: *, и, таким образом, f(x) имеет относительный минимум при * 0,5-0,75. Полином функции y’ = 3×2-18x+24x, что означает, что ее область определения равна ((-*infty, *infty). Каждая точка в ряду действительных чисел соответствует заданному значению ее относительных максимумов и минимумов, а область определения действительного числа есть f(x). Только *(x=0) и *(1/x-1) считаются критическими точками при оценке f'(x), так как это единственные действительные числа в уравнении.

У нас есть бесконечные критические точки, в которых нет решений, когда уравнение f'(x) = -2*sin(1x) – 1, при условии, что все решения заданы. В результате график действительных чисел не определен, потому что он имеет угол при x=2 ext. Поскольку решения для *(x * 5 ext) нет, единственными критическими точками являются точки x=3 и x=5. Другими словами, поскольку f(x) определено для всех действительных чисел, в f(x) есть только одна критическая точка: никакие действительные числа не могут быть записаны в виде многочленов. Многочлены — это полиномиальные производные числа, которые определяются действительными числами, поэтому любой многочлен P(x) имеет точно такую ​​же критическую точку, как и любой многочлен. В следующем разделе выполните упражнение 5.5. Чтобы определить, имеет ли кубический многочлен ноль, одну или две критические точки, вы должны сначала определить, имеет ли он ноль, одну или две критические точки.

Производная обычно обозначается как P’_3(x), а используемые решения известны как P’_3(x). Упражнение 5.5-7 должно быть выполнено. Сколько критических точек имеют многочлены степени f? Согласно основной теореме алгебры степени n имеют не менее n корней как многочлены. Когда одно из этих действительных чисел (математика) переходит от 0 к 1, а затем к следующему, сколько всего баллов можно получить от этого числа? Рекомендуется пробежка 6,6 км. Во второй половине статьи мы более подробно рассмотрим первые два вопроса.

Абсолютный экстремум — это непрерывная функция с абсолютными минимумами и абсолютными максимумами на интервале. Мы можем найти абсолютные экстремумы для функции, которая находится на отрезке, используя разработанный нами метод. Доказательство основано на понятии компактности, которое обсуждается только в Анализе. Согласно теореме об экстремальных значениях, для функции с постоянным интервалом не дается ни абсолютного максимума, ни абсолютного минимума. Если 1 не входит в интервал, мы не достигнем того же результата, как если бы он был. Когда экстремум возникает ближе к концу интервала, его можно только обнаружить. Производная задается как *(f'(x).

критических значений равно 0 (для 3 = =3×2-2x ext) и (2), которые оба находятся в интервале. Чтобы найти абсолютные экстремумы, мы должны сначала рассмотреть все критические значения в пределах интервала (например, -3). В этом уравнении есть два абсолютных максимума и два абсолютных минимума. Упражнение в общей сложности 5,8 раза. Найдите абсолютные экстремумы для каждой функции в заданном интервале. Абсолютный минимум определяется числом (x *in [math][0,3] ext*.]) и должен соблюдаться на всех конечных точках.

То есть, если f(0) = -frac4-4, то 1 равно. В результате делаем вывод, что (0.0, 1) Абсолютный минимум равен трем, а абсолютный максимум четырем. В уравнении f'(x) есть две критические точки, одна из которых является абсолютным максимумом, а другая — абсолютным минимумом: f'(x=1 ext.) и f'(x-1,1) находятся вне пределов интервал. Мы не считаем их конечными точками из-за их относительных экстремумов. Мы будем искать корни f’(x) так же, как и раньше, чтобы увидеть, связаны ли они между собой. В следующем разделе нарисуйте потенциальный график непрерывной функции на отрезке ([0,4) с заданными свойствами. На этой странице описана функция с абсолютным минимумом 0, абсолютным максимумом 2 и относительным максимумом 3.

В исчислении экстремум определяется как любая точка в цепочке создания стоимости, где функция является наибольшей или наименьшей. Грамматики применяют к уравнению два типа экстремума: абсолютный и относительный (или локальный).
Максимальное значение функции определяется абсолютным экстремумом этой функции. Это точка на шкале от нуля до единицы, где значение функции является самым низким, но только для входных данных. Рассмотрим функцию y в следующем примере. Это 2х2. Когда x = 0, значение функции равно 2, но по мере увеличения x ее значение уменьшается. Относительный экстремум равен x = 3 и x = 1 соответственно.
Описывает точку, в которой значение функции изменяется больше всего для определенного набора входных данных. Рассмотрим функцию y в качестве примера. х2. Если x значительно уменьшается, его значение возрастает. Локальный экстремум относится к организмам, обитающим в естественной для них среде.

Почему важно находить экстремальные значения

Определение экстремальных значений функций необходимо по целому ряду причин. Если вы пытаетесь найти наименьшее или наибольшее значение для набора характеристик, экстремальные значения будут наиболее репрезентативной выборкой всех значений в наборе. Также можно найти решения задач, связанных с максимизацией или исключением, путем поиска экстремальных значений.

Что такое абсолютное предельное значение?

Что такое абсолютная крайность? Например, если M = f(c) для некоторого C в D, мы говорим, что M является абсолютным максимумом, когда f(x) равно значениям xrange во всем D, и абсолютным минимумом, когда f(x) равно xrange. значения по всему D.

Мы используем абсолютный максимум и минимум, чтобы определить, что функция «максимизирует» или «минимизирует», что является двумя разными способами ее определения. Это тот случай, когда функция приближается к максимуму или минимуму в этих точках.
Абсолютный максимум и абсолютный минимум уравнения можно определить с помощью системы уравнений. Мы можем найти абсолютный максимум f(c), решив его для ff(c) следующим образом:
Bx равно a.c, а c= bx.
Единственное решение этого уравнения, f(0)=b, может быть найдено при c=0. Абсолютный максимум для f равен нулю.
Вот грубая схема того, как найти абсолютный минимум с помощью f(c).
Если [math]f(c)]bx[/math], то [math]f(c)a].
Это уравнение не имеет решения при c=0. F, с другой стороны, имеет абсолютный минимум.

При наличии экстремального значения

Значение с экстремальным значением определяется как точка на границе интервала, которая является максимальным или минимальным значением для этой характеристики.

Об авторе

Джуэлс Бриггс

Джуэлс Бриггс — талантливый бармен и эксперт по коктейлям с более чем 15-летним опытом. Она создала уникальные и вкусные коктейли для некоторых лучших ресторанов и баров страны.