Исследовать на четность функцию: исследуйте функцию на четность y=корень x-3 +x в квадрате

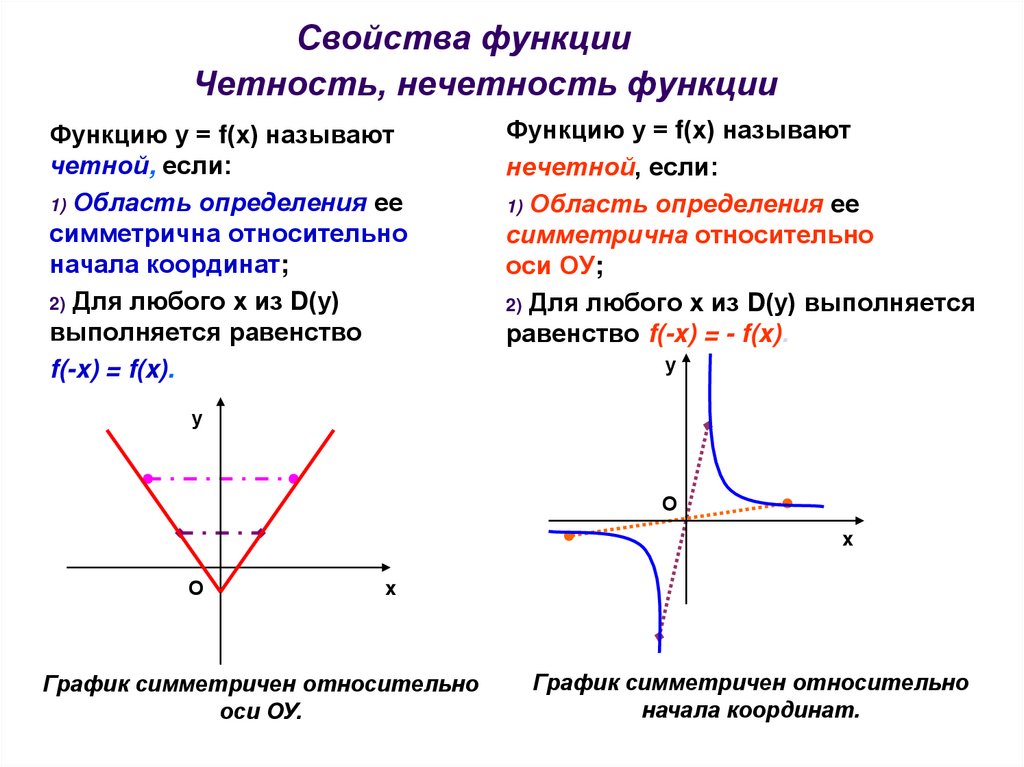
2. Исследование функции на четность и нечетность.

Функция называется четной (нечетной), если для любогои выполняется равенство

.

График четной функции симметричен относительно оси .

График нечетной функции симметричен относительно начала координат.

Пример 6.2. Исследовать на четность или нечетность функции

1) ; 2); 3).

Решение.

1) Функция определена при . Найдем.

, т.е. . Значит, данная функция является четной.

2) Функция определена при

, т.е. . Таким образом, данная функция нечетная.

3) функция определена для , т.е. для

, . Поэтому функция не является ни четной, ни нечетной. Назовем ее функцией общего вида.

3. Исследование функции на монотонность.

Функция называется возрастающей (убывающей) на некотором интервале, если в этом интервале каждому большему значению аргумента соответствует большее (меньшее) значение функции.

Функции возрастающие (убывающие) на некотором интервале называются монотонными.

Если функция дифференцируема на интервалеи имеет положительную (отрицательную) производную, то функциявозрастает (убывает) на этом интервале.

Пример 6.3. Найти интервалы монотонности функций

1) ; 3).

Решение.

1) Данная функция определена на всей числовой оси. Найдем производную .

Производная равна нулю, если и. Область определения – числовая ось, разбивается точками,на интервалы. Определим знак производной в каждом интервале.

В интервале производная отрицательна, функция на этом интервале убывает.

В интервале производная положительна, следовательно, функция на этом интервале возрастает.

2) Данная функция определена, если или

.

Определяем знак квадратного трехчлена в каждом интервале.

Таким образом, область определения функции

.

Найдем производную ,, если, т.е., но. Определим знак производной в интервалах.

В интервале производная отрицательна, следовательно, функция убывает на интервале. В интервалепроизводная положительна, функция возрастает на интервале.

4. Исследование функции на экстремум.

Точка называется точкой максимума (минимума) функции, если существует такая окрестность точки, что для всехиз этой окрестности выполняется неравенство.

Точки максимума и минимума функции называются точками экстремума.

Если функция в точкеимеет экстремум, то производная функции в этой точке равна нулю или не существует (необходимое условие существования экстремума).

Точки, в которых производная равна нулю или не существует называются критическими.

5. Достаточные условия существования экстремума.

Правило 1. Если при переходе (слева направо) через критическую точку производнаяменяет знак с «+» на «–», то в точкефункцияимеет максимум; если с «–» на «+», то минимум; еслине меняет знак, то экстремума нет.

Правило 2. Пусть в точке первая производная функцииравна нулю, а вторая производная существует и отлична от нуля. Если, то– точка максимума, если, то– точка минимума функции.

Пример 6.4. Исследовать на максимум и минимум функции:

1) ; 2); 3);

4) .

Решение.

1) Функция определена и непрерывна на интервале .

Найдем производную и решим уравнение, т.е..Отсюда– критические точки.

Определим знак производной в интервалах ,.

При переходе через точки ипроизводная меняет знак с «–» на «+», поэтому по правилу 1– точки минимума.

При переходе через точку производная меняет знак с «+» на «–», поэтому– точка максимума.

, .

2) Функция определена и непрерывна в интервале . Найдем производную.

Решив уравнение , найдеми– критические точки. Если знаменатель, т.е., то производная не существует. Итак,– третья критическая точка. Определим знак производной в интервалах.

Следовательно, функция имеет минимум в точке , максимум в точкахи.

.

3) Функция определена и непрерывна, если , т.е. при.

Найдем производную

.

Найдем критические точки:

Окрестности точек не принадлежат области определения, поэтому они не являются т. экстремума. Итак, исследуем критические точкии.

.

4) Функция определена и непрерывна на интервале . Используем правило 2. Найдем производную.

Найдем критические точки:

Найдем вторую производную и определим ее знак в точках

.

В точках функция имеет минимум.

.

В точках функция имеет максимум.

9 класс. Алгебра. Четные и нечетные функции. — Исследование функции на четность.

Комментарии преподавателя

На этом уроке мы подробно рассмотрим исследование функции на четность. Вначале вспомним определения четных и нечетных функций и их важное свойство – симметричность. Далее сформулируем алгоритм исследования функции на четность и покажем применение этого алгоритма для решения конкретных задач.

 

Тема: Чис­ло­вые функ­ции

Урок: Ис­сле­до­ва­ние функ­ций на чет­ность

 

В этом уроке мы на­пом­ним опре­де­ле­ния и свой­ства чет­ных и нечет­ных функ­ций, сфор­му­ли­ру­ем ал­го­ритм ис­сле­до­ва­ния функ­ций на чет­ность, и по­ка­жем при­мер ис­поль­зо­ва­ния ал­го­рит­ма для ре­ше­ния кон­крет­ных задач.

На­по­ми­на­ние:

Функ­ция  на­зы­ва­ет­ся чет­ной, если для лю­бо­го   

Гра­фик чет­ной функ­ции сим­мет­ри­чен от­но­си­тель­но оси y. Верно и об­рат­ное – если гра­фик функ­ции сим­мет­ри­чен от­но­си­тель­но оси y, то функ­ция чет­ная.

Функ­ция  на­зы­ва­ет­ся нечет­ной, если для лю­бо­го  

Гра­фик нечет­ной функ­ции сим­мет­ри­чен от­но­си­тель­но на­ча­ла ко­ор­ди­нат. Верно и об­рат­ное – если гра­фик функ­ции сим­мет­ри­чен от­но­си­тель­но на­ча­ла ко­ор­ди­нат, то функ­ция нечет­на.

При­ве­ден­ные факты сфор­му­ли­ру­ем более крат­ко и про­ил­лю­стри­ру­ем на гра­фи­ке.

 

1.(Рис).

2.(Рис. 2).

Этими опор­ны­ми фак­та­ми мы будем поль­зо­вать­ся при опре­де­ле­нии чет­но­сти функ­ции.

Из при­ве­ден­ных опре­де­ле­ний и свойств вы­те­ка­ет

Ал­го­ритм ис­сле­до­ва­ния функ­ции  на чет­ность.

1. Ис­сле­до­вать  на сим­мет­рич­ность от­но­си­тель­но нуля Если  не сим­мет­рич­на от­но­си­тель­но нуля, это функ­ция об­ще­го вида.

2. Найти 

3. Срав­нить 

— если  то функ­ция чет­ная;

— если  то функ­ция нечет­ная;

— если хотя бы для од­но­го 

то это функ­ция об­ще­го вида.

Рас­смот­рим кон­крет­ные при­ме­ры.

Ис­сле­до­вать функ­цию на чет­ность:

1. 

Ре­ше­ние:

(Рис. 3).

Об­ласть опре­де­ле­ния со­сто­ит из всех дей­стви­тель­ных чисел, кроме нуля. Об­ласть опре­де­ле­ния сим­мет­рич­на от­но­си­тель­но нуля.

 

Ответ: Функ­ция чет­ная.

2. .

Ре­ше­ние:

(Рис. 4).

 несим­мет­рич­на от­но­си­тель­но нуля, зна­чит это функ­ция об­ще­го вида.

Ответ: Функ­ция об­ще­го вида.

3. 

Ре­ше­ние:

 об­ласть опре­де­ле­ния сим­мет­рич­на от­но­си­тель­но нуля.

 

Ответ: Функ­ция нечет­ная.

4. 

Ре­ше­ние:  (Рис. 5).

Об­ласть опре­де­ле­ния сим­мет­рич­на от­но­си­тель­но нуля.

 

Ответ: Функ­ция нечет­ная.

5. 

Ре­ше­ние: 

Об­ласть опре­де­ле­ния сим­мет­рич­на от­но­си­тель­но нуля (Рис. 5).

 

Ответ: Функ­ция чет­ная.

6. 

Ре­ше­ние:  Об­ласть опре­де­ле­ния сим­мет­рич­на от­но­си­тель­но нуля.

 

 

Мы видим, что для :

 

 

Функ­ция не яв­ля­ет­ся ни чет­ной, ни нечет­ной, зна­чит, это функ­ция об­ще­го вида

Ответ: Функ­ция об­ще­го вида.

7..

Ре­ше­ние:  (Рис. 6).

Об­ласть опре­де­ле­ния несим­мет­рич­на от­но­си­тель­но нуля.

Ответ: Функ­ция об­ще­го вида.

8. 

Ре­ше­ние:

По­стро­им гра­фик функ­ции (Рис.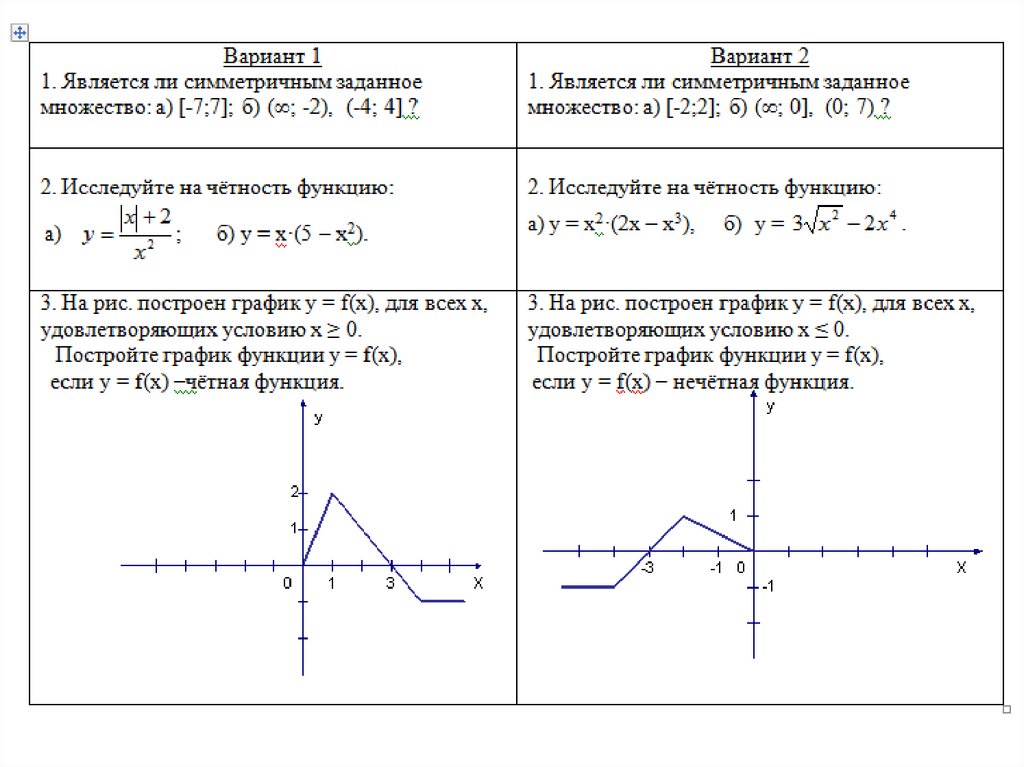 7).

Гра­фик сим­мет­ри­чен от­но­си­тель­но оси y, функ­ция чет­ная.

Эту же функ­цию можно за­дать как 

Ответ: Функ­ция чет­ная.

9. По­строй­те гра­фик функ­ции  и про­чи­тай­те его, если

 

Ре­ше­ние: По­стро­им гра­фик функ­ции (Рис. 8).

Гра­фик сим­мет­ри­чен от­но­си­тель­но оси y, функ­ция чет­ная.

Функ­ция воз­рас­та­ет при 

Функ­ция убы­ва­ет при 

Источник конспекта: http://interneturok.ru/ru/school/algebra/9-klass/chislovye-funktsii/issledovanie-funktsiy-na-chetnost?konspekt&chapter_id=34

Источник видео: http://www.youtube.com/watch?v=fUPLarmiN84

Определение функции четности и интуиция, характеристическая функция множества.

Мы определяем $\tilde x\in\mathbb{Z}$ и $\tilde x_i\in\mathbb{Z_2}$ (это битовое значение),

и $\tilde x_i = 1-2x_i$ ясно представлена ​​следующая функция:

\begin{align*} f(x) = \begin{случаи} 1 &\text{если $x$ = 0}\\ -1 &\text{если $x$ = 1} \end{cases}\end{align*}

Когда $x$ (входной бит) равен $0$, функция возвращает $1$, иначе, если $x$ равно $1$, функция возвращает $-1$ .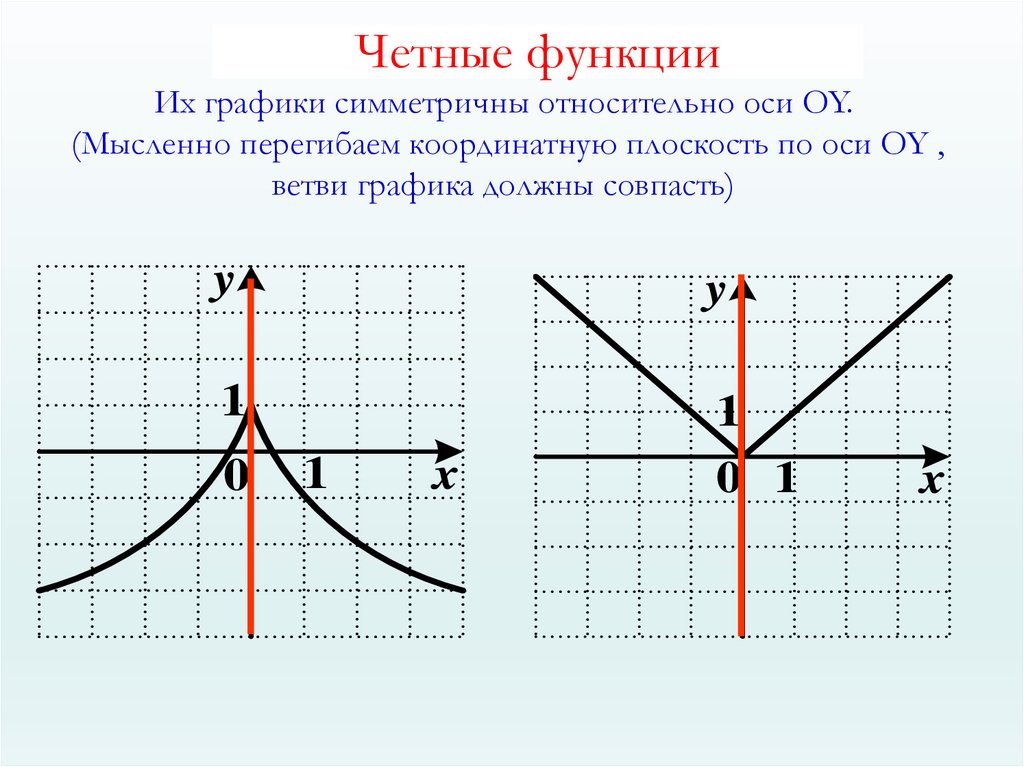 9{N-1} е (\ тильда x_i), \end{align*}

Заглавная буква «пи» обозначает умножение последовательных значений. Следовательно, мы перемножаем вместе все четности. А поскольку $f(x)$ возвращает либо $1$, либо $-1$, то $P(\tilde x)$ возвращает либо значение $-1$, либо значение $1$. Процесс $P$ является итеративным, и значение $-1$ никогда не изменяется, если только последующая четность также не равна $-1$ (тогда она меняет свой знак), эта четность будет переворачиваться столько раз, сколько единиц в таблице. бинарное расширение ($\tilde x$) и сохранение конечного состояния при $i=N-1$. Конечное состояние в основном зависит от количества $1$ в двоичном расширении. Короче говоря, каждый раз, когда $\tilde x_i=1$, произведение будет менять свой знак, но когда $\tilde x_i=0$, произведение никак не повлияет на результат. Эти два ряда действий легко понять, когда $x\cdot -1=-x$ и $x\cdot 1=x$. то есть:

$$+\cdot+ = +$$ $$+\cdot- = -$$ $$-\cdot+ = -$$ $$-\cdot- = +$$

Из приведенных выше рассуждений мы можем вывести некоторые факты:

1. когда $\tilde x$ имеет нечетное количество $1$ в своем двоичном представлении, $P$ вернет $-1$.
2. , когда $\tilde x$ имеет четное число $1$ в своем двоичном представлении, $P$ вернет $1$.

Примеры:

$$P(2_{10}) = P(10_2) = -1$$ $$P(13_{10}) = P(1101_2) = -1$$ $$P(27_{10}) = P(11011_2) = 1$$ $$P(60_{10}) = P(111100_2) = 1$$

Другие факты:

Длина бита сама по себе не влияет на четность.

---

Ответы:

1) Функция, которая возвращает младший (самый правый) бит аргумента.

$$P(00_2) = 1$$ $$P(01_2) = -1$$ $$P(10_2) = -1$$ $$P(11_2) = 1$$

Есть два возможных входа, при которых возвращается $1$: $0$ и $3_{10}$.

2) Функция, возвращающая k-нумерованный бит аргумента, где k меньше n.

Я не уверен, что вы имеете в виду под k-нумерованным битом аргумента. Предполагая, что вы имеете в виду битовую длину аргумента, это не влияет на выходную четность.

3) const f(x) = 1

Функция является четной только тогда, когда $\tilde x = 0$ или в двоичном представлении $\tilde x$ есть четное число $1$.

4) const f(x) = 0

$0=$ паритет $1$

5) «Характеристическая функция множества мощности 5»

Предположим, вы имеете в виду, что паритет $1$ четный, тогда $5$ четный.

6) f(x)=1, только если x имеет нечетное количество единиц при записи в двоичном формате

False, $P(\tilde x)=-1$, если число единиц нечетное.

7) f(x)=1, только если x имеет четное число единиц при записи в двоичном формате

Верно, $P(\tilde x)=1$, если число единиц четное.

Что такое четность? — Определение из WhatIs.com

По

• Эд Ханнан

В компьютерах четность (от латинского

paritas , что означает равный или эквивалентный) — это метод, который проверяет, были ли данные потеряны или перезаписаны, когда они перемещаются из одного места в хранилище в другое или когда они передаются между компьютерами.

Как работает контроль четности

Поскольку передача данных не является полностью безошибочным процессом, данные не всегда принимаются тем же способом, которым они были переданы. Бит четности добавляет к данным контрольные суммы, которые позволяют целевому устройству определить, правильно ли были получены данные.

Дополнительная двоичная цифра, бит четности , , добавляется к группе битов, которые перемещаются вместе. Этот бит, иногда называемый проверочным битом , используется только для определения того, успешно ли прибыли перемещенные биты.

Бит четности против нечетного бита

Существует два типа битов четности:

• При четности подсчитывается количество битов со значением 1. Если это число нечетное, значение бита четности устанавливается равным единице, чтобы общее количество единиц в наборе (включая бит четности) было четным. Если количество битов со значением 1 четное, значение бита четности устанавливается равным нулю, так что общее количество единиц в наборе (включая бит четности) остается четным числом.
• При нечетной четности , если количество битов со значением 1 является четным числом, значение бита четности устанавливается равным единице, чтобы общее количество единиц в наборе (включая бит четности) было нечетным. Если количество битов со значением 1 нечетное, значение бита четности устанавливается равным нулю, так что общее количество единиц в наборе (включая бит четности) остается нечетным числом.

На принимающей стороне каждая группа входящих битов проверяется, чтобы определить, является ли группа в сумме четным или нечетным числом. Если возникает ошибка передачи, передача повторяется или система останавливается, и пользователю отправляется сообщение об ошибке.

Обнаружение ошибки четности

Приведенное выше описание объясняет, как проверка четности работает на компьютере. В частности, шина межсоединений периферийных компонентов и контроллер шины ввода-вывода используют метод контроля ошибок с проверкой на нечетность.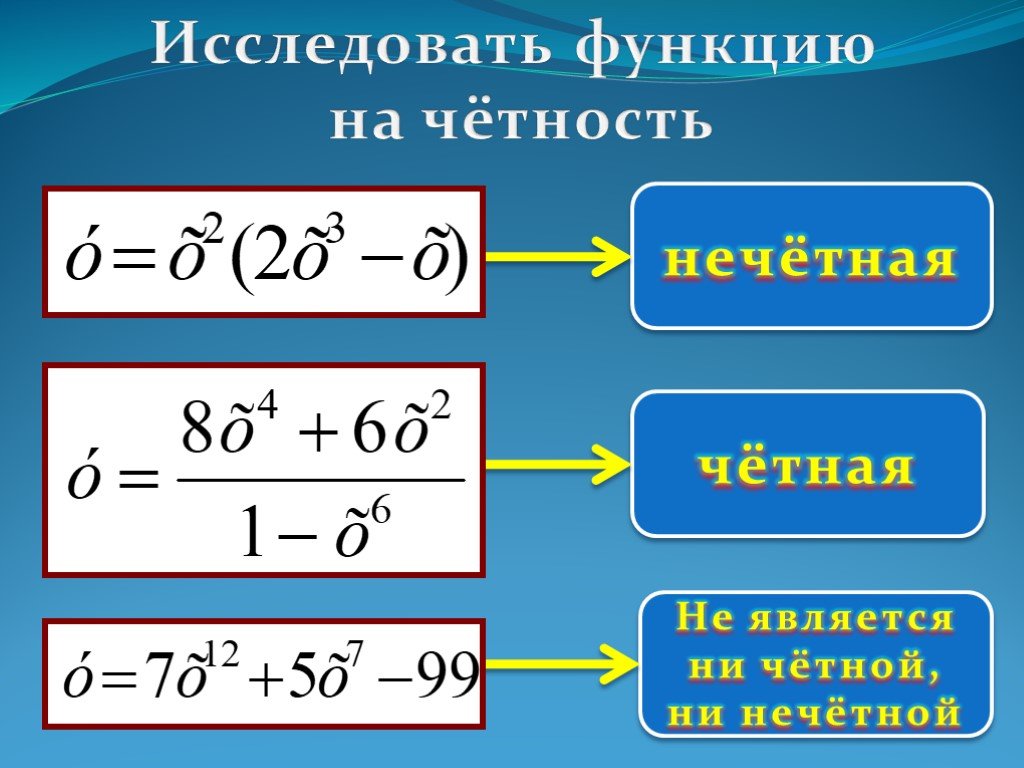 Проверка битов четности не является безошибочным методом проверки ошибок, поскольку возможно, что два бита могут быть ошибочными при передаче, смещая друг друга. Для передач внутри персонального компьютера такая возможность считается крайне маловероятной. В некоторых больших компьютерных системах, где целостность данных считается чрезвычайно важной, для проверки четности выделяются три бита.

Проверка четности также используется при обмене данными между модемами. Здесь можно выбрать четную проверку четности (успешная передача формирует четное число) или нечетную. Пользователи также могут выбрать отсутствие четности, что означает, что модемы не будут передавать или проверять бит четности. Когда четность не выбрана (или установлена ​​по умолчанию), предполагается, что существуют другие формы проверки, которые обнаружат любые ошибки при передаче. Отсутствие четности также обычно означает, что бит четности может использоваться для данных, что ускоряет передачу. При межмодемной связи тип четности согласовывается передающим и принимающим модемами до того, как произойдет передача.

Проверка четности и код исправления ошибок

На уровне 64-битного слова проверка четности и код исправления ошибок (ECC) требуют одинакового количества дополнительных битов. В то время как проверка четности просто обнаруживает ошибку — она не имеет возможности исправления — технология ECC позволяет не только обнаруживать ошибки, но и исправлять их. Это означает, что система может продолжать работать без повреждения данных. В целом, ECC обеспечивает большую надежность любой вычислительной или телекоммуникационной системы без больших затрат.

Контроль четности и RAID

Концепция контроля четности также используется в защите избыточного массива независимых дисков (RAID). Устройства RAID используют расширенные формы проверки четности, такие как вертикальная и горизонтальная четность. Некоторые группы RAID, такие как RAID 4 или RAID 5, имеют один или несколько дисков, содержащих информацию о четности, которая позволяет им восстанавливать данные в случае отказа диска. Например, RAID с двойной четностью (также известный как RAID 6) распределяет данные по набору не менее четырех дисков на блочном уровне, как в RAID 5, но затем записывает второй набор данных четности на все диски.

Этот подход защищает от потери данных на двух отказавших дисках. Недостатки RAID с двойной четностью включают использование сложного контроллера, стоимость двух дополнительных дисков для реализации и более медленные транзакции записи из-за дополнительного набора четности.

RAID 6, или RAID с двойной четностью, защищает от сбоев нескольких дисков, создавая два набора данных четности на массиве жестких дисков.

Когда данные записываются в группу RAID, они всегда будут иметь правильную четность, так как они прошли через различные алгоритмы проверки ошибок. Таким образом, если диск в группе RAID выходит из строя, система использует информацию об оставшихся дисках вместе с информацией о четности для восстановления данных на неисправном диске на резервный диск.

Как это происходит? Если группа RAID использует четную четность, она может выяснить, что было на неисправном диске, сложив биты на оставшихся дисках. Если данные на оставшихся дисках составляют нечетное число, информация на неисправном диске должна быть равна единице, чтобы поддерживать четность. Если данные на оставшихся дисках составляют четное число, данные на неисправном диске должны быть нулевыми.

Последнее обновление: август 2016 г.

Продолжить чтение О паритете

• Использование четности в RAID 5

• Вычисление четности для групп четности

• Хранилище с контролем четности в конфигурации RAID 5

• Объяснение RAID-5 и чередования четности

• Восстановление потерянных данных с помощью битов четности

• Узнайте о роли бита четности в RAID

Подробно изучите архитектуру и стратегию хранения данных

• Код Хэмминга

  Автор: Гэвин Райт

• RAID 6

  Автор: Ким Хефнер

• CRC-4 (проверка циклическим избыточным кодом 4)

  Автор: Рахул Авати

• Сравнение уровней RAID: 0, 1, 5, 6, 10 и 50 объяснение

  Автор: Эрин Салливан

SearchDisasterRecovery

• Trilio Continuous Restore нацелен на более быстрое восстановление

  Обновление Trilio 3. 0 для своего TrilioVault для Kubernetes включает общедоступное непрерывное восстановление и добавленную поддержку…

• Как планы обеспечения непрерывности бизнеса подходят для атаки программ-вымогателей?

  Восстановление — не единственный приоритет при атаке программ-вымогателей. Тщательное планирование, обучение и координация между ИТ-командами имеют решающее значение для…

• Создайте план обеспечения непрерывности бизнеса при наводнениях, чтобы оставаться на плаву

  В случае наводнения не соглашайтесь на размытые планы действий. Загрузите наш бесплатный шаблон плана обеспечения непрерывности бизнеса при наводнениях, чтобы…

SearchDataBackup

• Commvault Metallic добавляет архив в облачный сервис

  Компания Commvault добавила автономную облачную службу архивирования файлов и объектов в свою SaaS Metallic, чтобы помочь справиться с ростом неструктурированных данных . ..

• Veritas Alta переносит управление корпоративным резервным копированием в облако

  Veritas Alta планирует перенести полный набор продуктов Veritas Technologies для резервного копирования в облако с возможностью приобретения SaaS …

• Плюсы и минусы защиты неструктурированных данных

  Защита неструктурированных данных требует от администраторов резервного копирования некоторых дополнительных соображений. Растущие требования к емкости хранилища и …

SearchDataCenter

• Включите VXLAN в центры обработки данных для повышения скорости сети

  VXLAN добавляют сетевую изоляцию и позволяют организациям более эффективно масштабировать сети центров обработки данных. Рассмотрите VXLAN для расширения…

• HPE обновляет серверы ProLiant в комплекте с лицензией GreenLake

  HPE добавила еще один вариант программного обеспечения и услуг с новыми серверами ProLiant с GreenLake, улучшенным программным обеспечением для обеспечения безопасности и .

  No related posts.