Исследуйте функцию на непрерывность онлайн: Точки разрыва функции онлайн

Непрерывность функций — презентация онлайн

Непрерывность функций
Непрерывность функций
Определение №1
Функция y=f(x) называется непрерывной в
точке х0, если выполнены условия:
Непрерывность функций
Определение №1
Функция y=f(x) называется непрерывной в точке х0, если
выполнены условия:
1. Функция определена в точке х0 , т.е.
определено число f(x0)
Непрерывность функций
Определение №1
Функция y=f(x) называется непрерывной в точке х0, если
выполнены условия:
1. Функция определена в точке х0 , т.е. определено число
f(x0)
2. Существует конечный предел функции f(x)
при х→ х0
Непрерывность функций
Определение №1
Функция y=f(x) называется непрерывной в точке х0, если
выполнены условия:
1. Функция определена в точке х0 , т.е. определено число
f(x0)
2. Существует конечный предел функции f(x) при х→ х0
3. Этот предел равен значению функции в этой
точке:
lim f x f x0 .
x x0
Непрерывность функций
Определение
Функция y=f(x) называется непрерывной в
точке х0 справа (слева), если выполнены
условия:
1. Функция определена в точке х0 , т.е.
определено число f(x0)
Непрерывность функций
Определение
Функция y=f(x) называется непрерывной в точке х0 справа
(слева), если выполнены условия:
1. Функция определена в точке х0 , т.е. определено число
f(x0)
2. Существует конечный предел функции f(x)
при х→ х0 справа (слева)
3. Этот предел равен значению функции в этой
точке:
lim f x f x0
x x0 0
lim f x f x
0
x
x
0
0
Непрерывность функций
Определение №2
Если существуют конечные левый и правый
пределы,
равные
между
собой
и
равные
значению функции в точке х0 , то функция y=f(x)
называется непрерывной в этой точке.
Т.е.
lim f x lim f x f x0
x x0 0
x x0 0
Непрерывность функций
Пусть функция у = f(x) определена в некотором
интервале (a;b).
Возьмем произвольную точку x0 ϵ (a;b).
Непрерывность функций
Пусть функция у = f(x) определена в некотором интервале
(a;b).
Возьмем произвольную точку x0 ϵ (a;b).
Для любого x ϵ (a;b) разность x – x0 называется
приращением аргумента х в точке х0 и
обозначается Δx.
Т.е. Δx = x – x0. Тогда х = х0 + Δх.
Непрерывность функций
Разность
соответствующих
значений функции
f(x) – f(x0) называется
приращением
функции f(х) в точке
х0 и обозначается Δу.
Т.е. Δу = f(x) – f(x0).
Непрерывность функций
Определение №3
Функция y=f(x) называется непрерывной в
точке х0 , если ее приращение в этой точке
является бесконечно малой функцией при х→ х0,
т.е.
lim у 0
x 0
Свойства функций, непрерывных в точке
Теорема
Если функции f(x) и g(x) непрерывны в точке х0 ,
то их сумма, разность, произведение и частное
(при g(x)≠0) непрерывны в этой точке.
Свойства функций, непрерывных в точке
Теорема
Если функции f(x) и g(x) непрерывны в точке х0 ,
то их сумма, разность, произведение и частное
(при g(x)≠0) непрерывны в этой точке.
Доказательство следует непосредственно из
соответствующих теорем о пределах.
Свойства функций, непрерывных в точке
Теорема
Если функция g(x) непрерывна в точке х0, а
функция f(g) непрерывна в точке g0, причем
g0 = g(х0), тогда сложная функция f(g(х))
непрерывна в точке х0.
Свойства функций, непрерывных в точке
Теорема
Если
функция
f(x)
имеет
обратную
функцию f -1(у) и непрерывна в точке х0, то
функция f
-1(у)
причем у0 =f(х0).
непрерывна в точке у0,
Свойства функций, непрерывных в точке
Теорема
Всякая элементарная функция непрерывна
в каждой точке, в которой она определена.
Свойства функций, непрерывных в точке
Теорема
Всякая элементарная функция непрерывна в каждой
точке, в которой она определена.
Доказательство:
Пусть f(x) = 7х-3. Докажем, что функция
непрерывна в любой точке х0.
lim f x lim 7 x 3 7 x0 3 f x0
x x0
x x0
Свойства функций, непрерывных в точке
Пусть f(x) = sinx. Докажем, что функция
непрерывна в любой точке х0.
Свойства функций, непрерывных в точке
Пусть f(x) = sinx. Докажем, что функция непрерывна в
любой точке х0.
lim у lim sin x0 x sin x0
x 0
x 0
Свойства функций, непрерывных в точке
Пусть f(x) = sinx. Докажем, что функция непрерывна в
любой точке х0.
lim у lim sin x0 x sin x0
x 0
x 0
2 x0 x
x
lim 2 sin
cos
x 0
2
2
Свойства функций, непрерывных в точке
Пусть f(x) = sinx. Докажем, что функция непрерывна в
любой точке х0.
lim у lim sin x0 x sin x0
x 0
x 0
2 x0 x
x
cos
lim 2 sin
x 0
2
2
2 x0 x
lim x cos
0
x 0
2
Свойства функций, непрерывных в точке
Пусть f(x) = еx. Докажем, что функция
непрерывна в любой точке х0.
Свойства функций, непрерывных в точке
Пусть f(x) = еx. Докажем, что функция
непрерывна в любой точке х0.
lim у lim е
x 0
x 0
x0 x
е
x0
Свойства функций, непрерывных в точке
Пусть f(x) = еx. Докажем, что функция непрерывна в
любой точке х0.
x0 x
х
1
lim у lim е
x 0
x 0
х0
lim е е
x 0
е
x0
Свойства функций, непрерывных в точке
x 0 x
х
lim у lim е
x 0
x 0
е
lim е е 1
х0
x 0
lim е х 0
x 0
х0
x0
Точки разрыва функции и их
классификация
Точки разрыва функции и их классификация
Определение
Точки, в которых нарушается условие
непрерывности функции называются точками
разрыва этой функции.
Точки разрыва функции и их классификация
Определение
Точка разрыва х0 называется точкой разрыва
первого рода функции y=f(x), если в этой точке
существуют конечные пределы функции слева
и справа, т. е.
lim f x А1 и
x x0 0
lim f x А2
x x0 0
Точки разрыва функции и их классификация
Определение
Точка разрыва х0 называется точкой разрыва первого
рода функции y=f(x), если в этой точке существуют
конечные пределы функции слева и справа, т. е.
lim f x А1 и
x x0 0
lim f x А2
x x0 0
При этом:
1.Если А1= А2, то точка х0 называется точкой
устранимого разрыва.
Точки разрыва функции и их классификация
Определение
Точка разрыва х0 называется точкой разрыва первого рода
функции y=f(x), если в этой точке существуют конечные пределы
функции слева и справа, т. е.
lim f x А1 и
x x0 0
lim f x А2
x x0 0
При этом:
2.Если А1 ≠ А2, точка х0 называется точкой
неустранимого разрыва.
Величина |А1 ̶ А2| называется
скачком
функции.
Точки разрыва функции и их классификация
Определение
Точка разрыва х0 называется точкой разрыва
второго рода функции y=f(x), если в этой
точке хотя бы один из односторонних
пределов равен бесконечности или не
существует.
Пример 1
Исследовать на непрерывность функцию
х 1, 1 х 2,
у
2 х, 2 х 5.
Пример 1
Исследовать на непрерывность функцию
х 1, 1 х 2,
у
2 х, 2 х 5.
Найдем односторонние пределы в точке х = 2:
Пример 1
Исследовать на непрерывность функцию
х 1, 1 х 2,
у
2 х, 2 х 5.
Найдем односторонние пределы в точке х=2:
lim f x lim х 1 1
x 2 0
x 2 0
Пример 1
Исследовать на непрерывность функцию
х 1, 1 х 2,
у
2 х, 2 х 5.
Найдем односторонние пределы в точке х=2:
lim f x lim х 1 1
x 2 0
x 2 0
lim f x lim 2 х 0
x 2 0
x 2 0
Пример 1
lim f x lim х 1 1
x 2 0
x 2 0
lim f x lim 2 х 0
x 2 0
x 2 0
Пределы конечны, значит в точке х = 2 разрыв первого рода.
Т.к. 1≠0 х = 2 — точка неустранимого
разрыва.
|1 — 0|=1 – скачок функции.
Пример 2
Исследовать на непрерывность функцию
1
у
х 2
Пример 2
Исследовать на непрерывность функцию
1
у
х 2
Найдем односторонние пределы в точке х=2:
1
1
lim f x lim
x 2 0
x 2 0 х 2
2 0 2
Пример 2
Исследовать на непрерывность функцию
1
у
х 2
Найдем односторонние пределы в точке х=2:
1
1
lim f x lim
x 2 0
x 2 0 х 2
2 0 2
1
1
lim f x lim
x 2 0
x 2 0 х 2
2 0 2
Пример 2
1
1
lim f x lim
x 2 0
x 2 0 х 2
2 0 2
1
1
lim f x lim
x 2 0
x 2 0 х 2
2 0 2
Пределы равны бесконечности, значит х = 2 – точка
разрыва второго рода.
Свойства функций, непрерывных
на отрезке
Свойства функций, непрерывных на отрезке
Определение
Функция у = f(x) называется непрерывной на
интервале (a;b), если она непрерывна в каждой
точке этого интервала.
Свойства функций, непрерывных на отрезке
Определение
Функция у = f(x) называется непрерывной на
отрезке [a;b], если она непрерывна на
интервале (a;b) и непрерывна справа в точке a
и слева в точке b.
Свойства функций, непрерывных на отрезке
Теорема Вейерштрасса
Всякая непрерывная на отрезке [a;b] функция
ограничена на нем и достигает на этом отрезке
своего наибольшего и наименьшего значений.
Свойства функций, непрерывных на отрезке
Теорема Вейерштрасса
Всякая непрерывная на отрезке [a;b] функция
ограничена на нем и достигает на этом отрезке
своего наибольшего и наименьшего значений.
Свойства функций, непрерывных на отрезке
Теорема Больцано-Коши
Если функция у = f(x) определена и непрерывна
на отрезке [a;b] и принимает на его концах
неравные значения А и В, тогда для любого числа
С, находящегося между А и В, найдется такое
число с, принадлежащее интервалу (a;b), что
f(с)=С.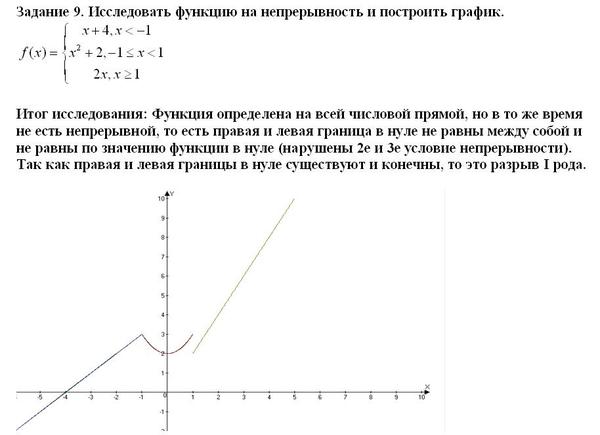
Свойства функций, непрерывных на отрезке
Теорема Больцано-Коши
Если функция у = f(x) определена и непрерывна на отрезке
[a;b] и принимает на его концах неравные значения А и В,
тогда для любого числа С, находящегося между А и В,
найдется такое число с, принадлежащее интервалу (a;b),
что у = f(с)=С.
Свойства функций, непрерывных на отрезке
Следствие
Если функция у = f(x) непрерывна на отрезке
[a;b] и принимает на его концах значения
разных знаков, то внутри этого отрезка
найдется хотя бы одна точка с, в которой
данная функция обращается в нуль: f(с)=0.
Свойства функций, непрерывных на отрезке
Следствие
Если функция у = f(x) непрерывна на отрезке [a;b] и
принимает на его концах значения разных знаков, то внутри
этого отрезка найдется хотя бы одна точка с, в которой данная
функция обращается
в нуль: f(с)=0.

Математический анализ: задачи, примеры, решения

• Вычислительная математика.
• Вычислить несобственные интегралы или доказать их расходимость.
• Вычислить полный дифференциал.
• Вычислить предел числовой последовательности.
• Вычислить пределы при заданных значениях параметров пpи q, не используя правило Лопиталя.
• Вычислить пределы.
• Вычислить приближенно значение функции.
• Вычислить приближенно число a с заданной точностью ε.
• Вычислить производную.
• Вычислить производные и дифференциалы первых двух порядков от следующих функций.
• Данную функцию исследовать на экстремум.
• Даны множества А и С. Найти объединение,пересечение,разность и декартово произведение.
• Для функции u = u(x, y, z) найти значение в точке А.
• Для функции найти градиент и производную по направлению вектора.
• Доказать неравенство/тождество.
• Задана функция f(x) и два значения аргумента x1 и x2.
• Записать формулу Тейлора с остаточным членом в форме Лагранжа и Пеано.
• Исследовать на непрерывность функцию.
• Исследовать на экстремум функцию.
• Исследовать функцию и построить её график
• Исследовать функцию и построить график. 3 ).
• Найти вторую производную
• Найти главную часть бесконечно малой функции при х → х0.
• Найти значение предела последовательности.
• Найти значения x, при которых значение производной функции f(x) равно нулю.
• Найти коэффициент эластичности E. Является ли в этой точке функция эластичной.
• Найти множество значений функции.
• Найти наибольшее и наименьшее значение функции на отрезке.
• Найти наибольшее и наименьшее значения функции в области D.
• Найти области определения функций одной переменной:
• Найти область аналитичности функции.
• Найти область определения функции двух переменных (дать геометрическое истолкование).
• Найти область определения функции.
• Найти предел с помощью правила Лопиталя.
• Найти предел функций.
• Найти предел.
• Найти пределы функций (не используя правило Лопиталя).
• Найти пределы, не применяя дифференциальное исчисление (правило Лопиталя)
• Найти производную 3-го порядка.
• Найти производную функции заданной неявно x/(y+1)+arctg(y/x)=0.
• Найти производную функции.
• Найти производные первого порядка функций.
• Найти производные указанных функций, используя правила дифференцирования
• Найти производные указанных функций.
• Найти скорость и ускорение в момент времени t.
• Найти точки разрыва и исследовать их характер. Построить графики функций.
• Найти точки разрыва функции, доопределить функцию по непрерывности в точках устранимого разрыва.
• Найти функцию, обратную данной.
• Найти экстремумы функции.
• Определить четность/нечетность функции.
• Построить график функции с помощью дифференциального исчисления.
• Построить график функции.
• Построить эскиз графика основной элементарной функции.
• Провести полное исследование данной функции и построить ее график.
• Провести полное исследование функции и построить ее график.
• Продифференцировать функцию.
• Сложное движение.
• Составить уравнение касательной к графику функции.
• Сравнить функции f(x) и g(x) при х → х0
• Теория множеств.
• Является ли в точке функция эластичной.

Равномерная непрерывность — Mathonline

Равномерная непрерывность

Эта страница предназначена для использования в разделе реального анализа Math Online. Подобные темы также можно найти в разделе сайта «Исчисление».

Сгиб Содержание Равномерная непрерывность

Определение: Пусть $f : A \to \mathbb{R}$ — функция. Мы говорим, что $f$ является равномерно непрерывным в области $A$, если $\forall \epsilon > 0$, $\существует \delta > 0$ такое, что если $x, y \in A$ и мы имеем $\mid x — y \mid < \ delta$, то $\mid f(x) - f(y) \mid < \epsilon$.

По определению равномерной непрерывности функция $f$ равномерно непрерывна, если задано любое $\epsilon > 0$, то можно найти такое $\delta > 0$, что для любого $x y \in A$, если мы имеем, что расстояние между $x$ и $y$ меньше, чем $\delta$, то мы будем иметь, что расстояние между $f(x)$ и $f(y)$ будет меньше, чем $\epsilon$.

Следует отметить, что это должно работать для всех $x$ и $y$, которые находятся в пределах $\delta$ друг от друга. Это должно быть довольно очевидно, но если функция $f : A \to \mathbb{R}$ равномерно непрерывна на $A$, то $f$ также должна быть непрерывной на $A$. Следующая теорема хорошо резюмирует это.

Теорема 1: Если функция $f : A \to \mathbb{R}$ равномерно непрерывна на $A$, то $f$ также непрерывна на $A$.

• Доказательство: Предположим, что $f$ равномерно непрерывна. Тогда $\forall \epsilon > 0$ $\существует \delta > 0$ такое, что если $x, y \in A$ удовлетворяют $\mid x — y \mid < \delta$, то $\mid f(x) - f(y) \mid < \epsilon$. Мы хотим показать, что $f$ непрерывна на $A$.

• Пусть $c \in A$. Так как $f$ равномерно непрерывна, то $\forall \epsilon >
  0$ $\существует \delta > 0$ такое, что если $x \in A$ удовлетворяет условию $\mid x -c \mid < \delta$, то $\ mid f(x) - f(c) \mid < \epsilon$. Следовательно, $f$ непрерывна в $c \in A$, а поскольку $c$ произвольно, мы заключаем, что $f$ непрерывна на всем $A$. $\черный квадрат$

Теперь мы рассмотрим несколько примеров функций, которые являются равномерно непрерывными.

Сначала рассмотрим функцию $f : \mathbb{R} \to \mathbb{R}$, определенную как $f(x) = c$, где $c \in \mathbb{R}$. Ясно, что $f$ — непрерывная функция, и нетрудно видеть, что $f$ также равномерно непрерывна. Для $\epsilon > 0$ будет работать любое $\delta > 0$, так как если $x, y \in \mathbb{R}$, то $\mid f(x) — f(y) \mid = \mid c — c \mid = 0 < \epsilon$ независимо от $\delta$. На следующем графике представлена ​​функция $f(x) = \frac{5}{2}$.

Другим примером равномерно непрерывной функции является $f : [0, \infty ) \to \mathbb{R}$, определяемый равенством $f(x) = x$. Чтобы доказать это, пусть задано $\epsilon > 0$. Мы хотим найти $\delta > 0$ такое, что если $x, y \in [0, \infty)$ удовлетворяют $\mid x — y \mid < \delta$, то $\mid f(x) - f( у) \mid < \epsilon$. Сначала посмотрите на $\mid f(x) — f(y) \mid = \mid x — y \mid$. Если положить $\delta (\epsilon ) = \epsilon$, то если $\mid x — y \mid < \delta$, то $\mid x - y \mid = \mid f(x) - f( у) \mid < \delta = \epsilon$. Следующий график представляет график $f$:

Лучшее объяснение того, что такое равномерная непрерывность, может быть описано с помощью контрпримера функции, которая НЕ является равномерно непрерывной. Рассмотрим функцию $f :(0, \infty) \to \mathbb{R}$, определенную как $f(x) = \frac{1}{x}$, и пусть $\epsilon > 0$. Предположим, мы утверждаем, что $\delta >

0$ существует. Для некоторых значений $x$ и $y$, находящихся в пределах $\delta$ друг от друга, $f(x)$ и $f(y)$ находятся в пределах $\epsilon$ друг от друга:

Однако теперь рассмотрим следующие $x$ и $y$. Они находятся в пределах $\delta$ друг от друга, но $f(x)$ и $f(y)$ не находятся в пределах $\epsilon$ друг от друга. Поэтому эта $\delta$ не работает.

Нетрудно заметить, что для этого $\epsilon > 0$ не существует такого $\delta > 0$, что если $\mid x — y \mid < \delta$, то $\mid f(x) - f(y) \mid < \epsilon$. Например, если мы возьмем значения $x$ и $y$, сколь угодно близкие к нулю, то нам придется делать $\delta$ все меньше и меньше, поскольку $f(x)$ и $f(y)$ будет очень большим, и нам нужно, чтобы $f(x)$ и $f(y)$ находились в пределах $\epsilon$ друг от друга. Следовательно, $f(x) = \frac{1}{x}$ не является равномерно непрерывным.

Если не указано иное, содержимое этой страницы находится под лицензией Creative Commons Attribution-ShareAlike 3.0 License

Дифференцируемость и преемственность | MIT OpenCourseWare

Дифференцируемость и непрерывность | MIT OpenCourseWare | Бесплатные материалы онлайн-курса

Расширенный Поиск

Выберите тему —выберите тему—Анализ графиковПределы функцийАсимптотическое и неограниченное поведениеНепрерывность: свойство функцийПараметрические, полярные и векторные функцииПонятие о производнойПроизводная в точкеПроизводная как функцияВторые производныеПрименения производныхВычисление производныхИнтерпретации и свойства определенных интеграловПрименения интеграловФундаментальная теорема исчисленияАнтидифференциация АнтидифференцированиеЧисленные приближения к определенным интеграламПонятие о рядахРяды константРяд Тейлора

Выберите подтему —выберите подтему—Производная, представленная графически, численно и аналитически. Производная, интерпретированная как мгновенная скорость изменения.

• Дифференцируемость стандартных функций
• Примеры недифференцируемого поведения
• Пределы и непрерывность

• Кусочно-определенные функции
• Дифференцируемость кусочно-определенных функций

 

Дифференцируемость стандартных функций

Примеры, когда стандартные функции являются или не являются дифференцируемыми.

Учебный материал, относящийся к этой теме:

• Прочитайте главу 6 онлайн-учебника

Наверх

Примеры недифференцируемого поведения

Графики типов разрывов, включая точки возврата, скачкообразный разрыв, устранимый разрыв, бесконечный разрыв и существенный разрыв.

Учебный материал, относящийся к этой теме:

• Прочитайте главу 6 онлайн-учебника

Наверх

Пределы и непрерывность

Десять вопросов, которые включают вычисление одно- и двусторонних пределов, идентификацию точек разрыва и приведение кусочно определенных функций к непрерывности и дифференцируемости.

• 18.01 Исчисление одной переменной, Осень 2006 г.
  Проф. Дэвид Джерисон

Учебный материал, относящийся к этой теме:

• Завершите экзаменационные задачи с 1D–1 на стр. 3 до задач 1D–10 на стр. 4.
• Проверьте решение экзаменационных задач на стр. 7–8

Наверх

Кусочно-определенные функции

• 18.01 Исчисление одной переменной, Осень 2006 г.
  Проф. Дэвид Джерисон

Материалы курса, относящиеся к этой теме:

Нахождение значений, при которых кусочно-определенная функция будет непрерывной и дифференцируемой.

• Завершить экзаменационную задачу 5 на стр. 1
• Проверьте решение экзаменационной задачи 5 на страницах 3–4.

Поиск значений, при которых кусочно-определенная функция будет дифференцируемой.

• Завершить экзаменационную задачу 5 на стр.

  No related posts.