метод Якоби, Зейделя, простой итерации
В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.
Общие сведения об итерационных методах или методе простой итерации
Определение 1Метод итерации — это численный и приближенный метод решения СЛАУ.
Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x0.
Пример 1Рассмотрим систему Ax=b.
Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x=Bx+d. Затем выбираем начальное приближение к решению СЛАУ x(0)=(x10, x20,. ..xm0) и находим последовательность приближений к корню.
..xm0) и находим последовательность приближений к корню.
Для сходимости итерационного процесса является достаточным заданное условие В<1. Окончание итерации зависит от того, какой итерационный метод применили.
Метод Якоби
Определение 2Результатом служит матрица В, в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:
bij=-aij/aii, i,j=1, 2…, n
Элементы (компоненты) вектора d вычисляются по следующей формуле:
di=bi/aii, i=1, 2,…, n
Расчетная формула метода простой итерации:
x(n+1)=Bx(x)+d
Матричная запись (координатная):
xi(n+1)=bi1xn1+bi2x(n)2+…+b
Критерий окончания в методе Якоби:
x(n+1)-x(n)<ε1, где ε1=1-BBε
В случае если B<1/2, то можно применить более простой критерий окончания итераций:
x(n+1)-x(n)<ε
Пример 2Решить СЛАУ методом Якоби:
10×1+x2-x3=11×1+10×2-x3=10-x1+x2+10×3=10
Как решить?
Необходимо решить систему с показателем точности ε=10-3.
Приводим СЛАУ к удобному виду для итерации:
x1=-0,1×2+0,1×3+1,1×2=-0,1×1+0,1×3+1×3=0,1×1-0,1×2+1
Выбираем начальное приближение, например: x(0)=1,111 — вектор правой части.
В таком случае, первая итерация имеет следующий внешний вид:
x1(1)=-0,1×1+0,1×1+1,1=1,1×2(1)=-0,1×1,1+0,1+1=0,99×3(1)=0,1×1,1-0,1×1+1=1,01
Аналогичным способом вычисляются приближения к решению:
x(2)=1,1020,9911,011, x(3)=1,1020,99091,0111, x(4)=1,102020,990911,01111
Находим норму матрицы В, для этого используем норму B∞.
Поскольку сумма модулей элементов в каждой строке равна 0,2, то B∞=0,2<1/2, поэтому можно вычислить критерий окончания итерации:
x(n+1)-x(n)<ε
Далее вычисляем нормы разности векторов:
x(3)-x(2)∞=0,002, x(4)-x(3)∞=0,00002.
Поскольку x(4)-x(3)∞<ε, то можно считать, что мы достигли заданной точности на 4-ой итерации.
Ответ:
x1=1,102; x2=0,991; x3=1,011.
Метод Зейделя
Определение 2Метод Зейделя — метод является модификацией метода Якоби.
Суть: при вычислении очередного (n+1)-го приближения к неизвестному xi при i >1 используют уже найденные (n+1)-е приближения к неизвестным x1, x2, …, xi —1, а не n-ое приближение, как в методе Якоби.
Матричная запись:
xi(n+1)=bi1x1(n+1)+bi2x2(n+1)+…+bi,i-1xi-2(n+1)+bi,i+1xi+1(n)+
+…+bimxm(n)+di
i=1, 2,…m…
За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.
Пример 2Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.
Как решать?
Решим 3 системы уравнений:
2×1+x2=3×1-2×2=1, x1+2×2=32×1-x2=1, 2×1-0,5×2=32×1+0,5×2=1
Приведем системы к удобному для итерации виду:
x1(n+1)=-0,5×2(n)+1,5×2(n+1)=0,5×1(n+1)+0,5, x1(n+1)=-2×2(n)+3×2(n+1)=2×1(n+1)-1, 2×1-0,5×2=32×1+0,5×2=1.
Отличительная особенность, условие сходимости выполнено только для первой системы:
B<1
Вычисляем 3 первых приближения к каждому решению:
1-ая система: x(0)=1,5-0,5, x(1)=1,750,375, x(2)=1,31250,1563, x(3)=1,42190,2109
Решение: x1=1,4, x2=0,2. Итерационный процесс сходится.
2-ая система: x(0)=3-1, x(1)=59, x(2)=-15-31, x(3)=65129
Итерационный процесс разошелся.
Решение: x1=1, x2=2
3-я система: x(0)=1,52, x(1)=2-6, x(2)=02, x(3)=02
Итерационный процесс зациклился.
Решение: x1=1, x1=2
Метод простой итерации
Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:
x=x-τ(Ax-b), τ — итерационный параметр.
Расчетная формула имеет следующий внешний вид:
x(n+1)=x(n)-τ(Axn-b).
Здесь B=E-τA и параметр τ>0 выбирают таким образом, чтобы по возможности сделать максимальной величину B2.
Пусть λmin и λmax — максимальные и минимальные собственные значения матрицы А.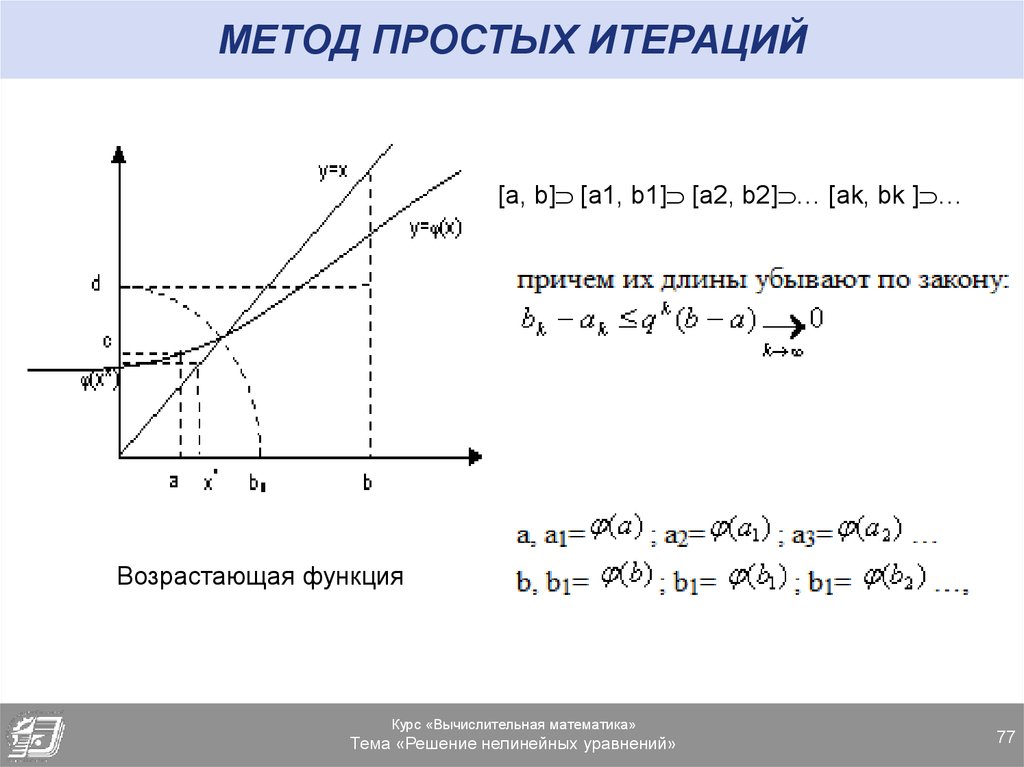
τ=2/(λmin+λmax) — оптимальный выбор параметра. В этом случае B2 принимает минимальное значение, которое равняется (λmin+λmax)/(λmin-λmax).
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Навигация по статьям
Предыдущая статья
Исследование СЛАУ
Следующая статья
Исследование СЛАУ. Общие сведения
- Исследование СЛАУ.
 Общие сведения
Общие сведения - Матричный метод решения СЛАУ
- Метод Гаусса
- Метод Жордана-Гаусса
- Метод Крамера
- Все темы по математике
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Узнать подробнее
Обратная матрицаРанг матрицы
Вид работы:
Реферат
Выполнена:

Стоимость:
1 200 руб
Заказать такую же работу
Общие требования к автомобильным топливам и смазочным материалам Понятие о химмотологии Влияние качества автомобильных бензинов на отказы современных двигателей Свойства тормозных жидкостей гигроскопичность вязкость смазочные
Заказать такую же работу
Дизельный отопитель вебасто
Заказать такую же работу
Расчт эл и магнитных цепей постоянного и переменного тока
Вид работы:
Курсовая работа
Выполнена:
19 июня 2022 г.

Стоимость:
9 600 руб
Заказать такую же работу
тема примерная Интегралы
Вид работы:
Онлайн-помощь
Выполнена:
22 мая 2022 г.

Стоимость:
2 400 руб
Заказать такую же работу
Отправляю вам шаблон презентации и задание преддипломной практики Компания на основе которой выполняется работа все та же Маркетплейс Ozon
Заказать такую же работу
Смотреть все работы по высшей математике
Решение систем линейных алгебраических уравнений итерационными методами
Тема 3. Решение систем линейных алгебраических уравнений итерационными методами.
Решение систем линейных алгебраических уравнений итерационными методами.
Описанные выше прямые методы решения СЛАУ не очень эффективны при решении систем большой размерности (т.е. когдо значение n достаточно велико). Для решения СЛАУ в таких случаях больше подходят итерационные методы
Итерационные методы решения СЛАУ (их второе название — методы последовательного приближения к решению) не дают точного решения СЛАУ, а дают только приближение к решению, причем каждое следующее приближение получается из предыдущего и является более точным, чем предыдущее (при условии, что обеспечена сходимость итераций). Начальное (или, так называемое, нулевое) приближение выбирается вблизи предполагаемого решения или произвольно (в качестве его можно взять вектор правой части системы). Точное решение находится как предел таких приближений при стремлении их количества к бесконечности. Как правило, за конечное число шагов (т.е. итераций) этот предел не достигается. Поэтому, на практике, вводится понятие точности решения, а именно задается некоторое положительное и достаточно малое число e и процесс вычислений (итераций) проводят до тех пор, пока не будет выполнено соотношение .
Как правило, за конечное число шагов (т.е. итераций) этот предел не достигается. Поэтому, на практике, вводится понятие точности решения, а именно задается некоторое положительное и достаточно малое число e и процесс вычислений (итераций) проводят до тех пор, пока не будет выполнено соотношение .
Здесь — приближение к решению, полученное после итерации номер n, а — точное решение СЛАУ (которое заранее неизвестно). Число итераций n=n(e), необходимое для достижения заданной точности для конкретных методов можно получить из теоретических рассмотрений (т. е. для этого имеются расчетные формулы). Качество различных итерационных методов можно сравнить по необходимому числу итераций для достижения одной и той же точности.
Для исследования итерационных методов на сходимость необходимо уметь вычислять нормы матриц. Норма матрицы — это некая числовая величина, характеризующая величину элементов матрицы по абсолютной величине. В высшей математике имеется несколько различных видов норм матриц, которые, как правило, являются эквивалентными. В нашем курсе мы будем пользоваться только одной из них. А именно, под нормой матрицы мы будем понимать максимальную величину среди сумм абсолютных величин элементов отдельных строк матрицы. Для обозначения нормы матрицы — ее название заключается в две пары вертикальных черточек. Так, для матрицы A под ее нормой будем понимать величину
Норма матрицы — это некая числовая величина, характеризующая величину элементов матрицы по абсолютной величине. В высшей математике имеется несколько различных видов норм матриц, которые, как правило, являются эквивалентными. В нашем курсе мы будем пользоваться только одной из них. А именно, под нормой матрицы мы будем понимать максимальную величину среди сумм абсолютных величин элементов отдельных строк матрицы. Для обозначения нормы матрицы — ее название заключается в две пары вертикальных черточек. Так, для матрицы A под ее нормой будем понимать величину
. (3.1)
Так, к примеру, норма матрицы А из примера 1 находится следующим образом :
.
Наиболее широкое применение для решения СЛАУ получили три итерационных метода
— метод простой итерации
— метод Якоби
— метод Гуасса-Зейделя.
Метод простой итерации предполагает переход от записи СЛАУ в исходном виде (2.1) к записи ее в виде
(3.2)
или, что тоже, в матричном виде,
x = С×x + D, (3.3)
где :
C — матрица коэффициентов преобразованной системы размерности n´n
x — вектор неизвестных, состоящий из n компонент
D — вектор правых частей преобразованной системы, состоящий из n компонент.
Система в виде (3.2) может быть представлена в сокращенном виде
Исходя из этого представления формула простой итерации будет иметь вид
(3. 4)
4)
где m — номер итерации, а — значение xj на m-ом шаге итерации. Тогда, если процесс итераций сходится, с увеличением количества итераций будет наблюдаться
Доказано, что процесс итераций сходится, если норма матрицы D будет меньше единицы.
Если за начальное (нулевое) приближение взять вектор свободных членов, т.е. x(0) = D, то величина погрешности имеет вид
(3.5)
здесь под x* понимается точное решение системы. Следовательно,
если , то по заданной точности e можно заранее расчитать необходимое количество итераций. А именно, из соотношения
А именно, из соотношения
после небольших преобразований получим
. (3.6)
При выполнении такого количества итераций гарантировано будет обеспечена заданная точность нахождения решения системы. Эта теоретическая оценка необходимого количества шагов итерации несколько завышена. На практике необходимая точность может быть достигнута за меньшее количество итераций.
Поиск решений заданной СЛАУ методом простой итерации удобно производить с занесением полученных результатов в таблицу следующего вида :
Следует особо отметить, что в решении СЛАУ этим методом наиболее сложным и трудоемким является выполнение преобразования системы из вида (2.1) к виду (3.2). Эти преобразования должны быть эквивалентными, т.е. не меняющими решения исходной системы, и обеспечивающие величину нормы матрицы C (после выполнения их) меньшей единицы. Единого рецепта для выполнения таких преобразований не существует. Здесь в каждом конкретном случае необходимо проявлять творчество. Рассмотрим примеры, в которых будут приведены некоторые способы преобразования системы к необходимому виду.
Единого рецепта для выполнения таких преобразований не существует. Здесь в каждом конкретном случае необходимо проявлять творчество. Рассмотрим примеры, в которых будут приведены некоторые способы преобразования системы к необходимому виду.
Пример 1. Найдем решение системы линейных алгебраических уравнений методом простой итерации (с точностью e=0.001)
Эта система приводится к необходимому виду простейшим способом. Перенесем все слагаемые из левой части в правую, а затем к обоим частям каждого уравнения прибавим по xi (i=1, 2, 3, 4). Получим преобразованную систему следующего вида
.
Матрица C и вектор D в этом случае будут следующими
C = , D = .
Вычислим норму матрицы C. Получим
Так как норма оказалась меньшей единицы — сходимость метода простой итерации обеспечена. В качестве начального (нулевого) приближения примем компоненты вектора D. Получим
, , , .
По формуле (3.6) вычислим необходимое число шагов итерации. Определим сначала норму вектора D. Получим
Тогда
.
Следовательно, для достижения заданной точности необходимо выполнить не менее 17 итераций. Выполним первую итерацию. Получим
или
Выполнив все арифметические операции, получим
.
Продолжая аналогично, выполним дальнейшие шаги итераций. Результаты их сведем в следующую таблицу (D — наибольшая величина изменения компонент решения между текущим и предыдущим шагами)
Результаты их сведем в следующую таблицу (D — наибольшая величина изменения компонент решения между текущим и предыдущим шагами)
Так как уже после десятого шага разность между значениями на двух последних итерациях стала меньше заданной точности — процесс итераций прекратим. В качестве найденного решения примем значения, полученные на последнем шаге.
Пример 2. Преобразуем систему уравнений
к виду, который позволил бы использовать при ее решении метод простой итерации.
Поступим сначала аналогично предыдущему примеру. Получим
Матрица C такой системы будет
C =.
Вычислим ее норму. Получим
Очевидно, что итерационный процесс для такой матрицы сходящимся не будет.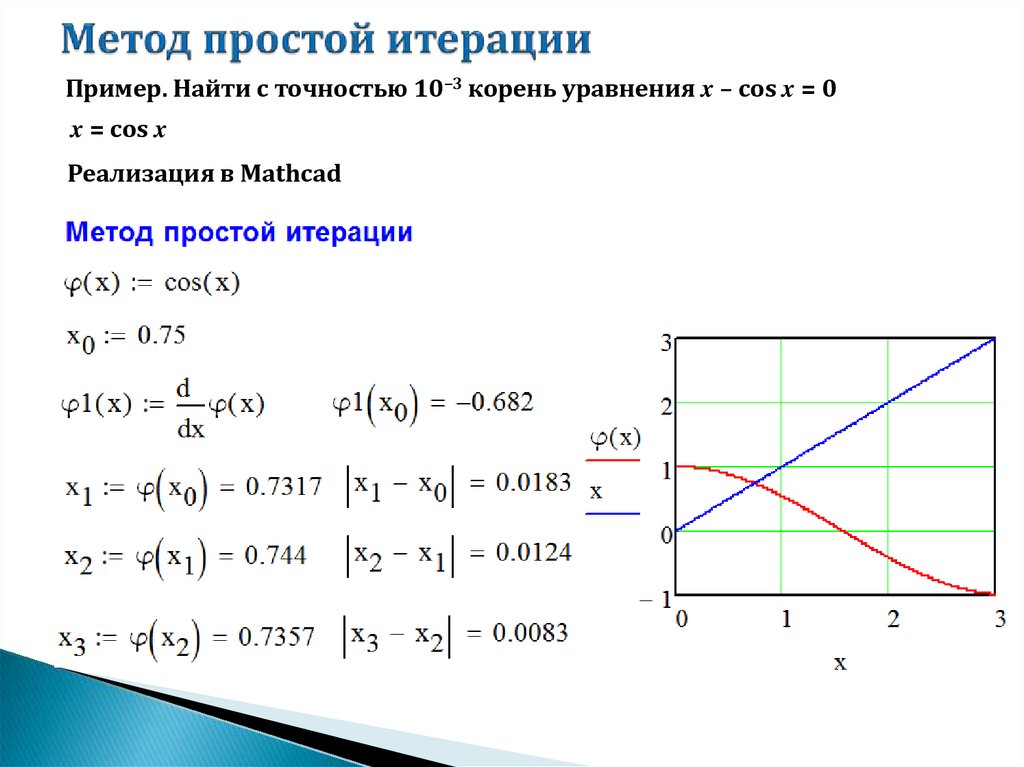 Необходимо найти иной способ преобразования заданной системы уравнений.
Необходимо найти иной способ преобразования заданной системы уравнений.
Переставим в исходной системе уравнений отдельные ее уравнения так, чтобы третья строка стала первой, первая — второй, вторая — третьей. Тогда, преобразуя ее тем же способом, получим
Матрица C такой системы будет
C =.
Вычислим ее норму. Получим
Так как норма матрицы C оказалась меньшей единицы, преобразованная таким образом система пригодна для решения методом простой итерации.
Пример 3. Преобразуем систему уравнений
к виду, который позволил бы использовать при ее решении метод простой итерации.
Поступим сначала аналогично примеру 1. Получим
Матрица C такой системы будет
C =.
Вычислим ее норму. Получим
Очевидно, что итерационный процесс для такой матрицы сходящимся не будет.
Для преобразования исходной матрицы к виду, удобному для применения метода простой итерации поступим следующим образом. Сначала образуем “промежуточную” систему уравнений, в которой
— первое уравнение является суммой первого и второго уравнений исходной системы
— второе уравнение — суммой удвоенного третьего уравнения со вторым за вычетом первого
— третье уравнение — разность третьего и второго уравнений исходной системы.
В результате получим эквивалентную исходной “промежуточную” систему уравнений
Из нее несложно получить еще одну систему “промежуточную” систему
,
а из нее преобразованную
.
Матрица C такой системы будет
C =.
Вычислим ее норму. Получим
Итерационный процесс для такой матрицы будет сходящимся.
Метод Якоби предполагает, что все диагональные элементы матрицы A исходной системы (2.2) не равны нулю. Тогда исходную систему можно переписать в виде
(3.7)
Из такой записи системы образована итерационная формула метода Якоби
. (3.8)
Условием сходимости итерационного процесса метода Якоби является так называемое условие доминирования диагонали в исходной системе (вида (2,1)). Аналитически это условие записывается в виде
. (3.9)
Следует отметить, что если в заданной системе уравнений условие сходимости метода Якоби (т. е. условие доминирования диагонали) не выполняется, во многих случаях можно путем эквивалентных преобразований исходной СЛАУ привести ее решение к решению эквивалентной СЛАУ, в которой это условие выполняется.
е. условие доминирования диагонали) не выполняется, во многих случаях можно путем эквивалентных преобразований исходной СЛАУ привести ее решение к решению эквивалентной СЛАУ, в которой это условие выполняется.
Пример 4. Преобразуем систему уравнений
к виду, который позволил бы использовать при ее решении метод Якоби.
Эту систему мы уже рассматривали в примере 3, поэтому перейдем от нее к полученной там “промежуточной” системе уравнений. Легко установить, что у нее условие доминирования диагонали выполняется, поэтому преобразуем ее к виду, необходимому для применения метода Якоби. Получим
Из нее получаем формулу для выполнения вычислений по методу Якоби для заданной СЛАУ
Взяв за начальное, т.е. нулевое, приближение вектор свободных членов выполним все необходимые вычисления. Результаты сведем в таблицу
Довольно высокая точность полученного решения достигнута за шесть итераций.
Метод Гаусса-Зейделя является усовершенствованием метода Якоби и также предполагает, что все диагональные элементы матрицы A исходной системы (2.2) не равны нулю. Тогда исходную систему можно переписать в виде аналогичном методу Якоби, но несколько отличном от него
.
Здесь важно помнить, что если в знаке суммирования верхний индекс меньше нижнего, то никакого суммирования не производится.
Идея метода Гаусса-Зейделя заключается в том, что авторы метода усмотрели возможность ускорить процесс вычислений по отношению к методу Якоби за счет того, что в процессе очередной итерации найдя новое значение x1 можно сразу же использовать это новое значение в этой же итерации для вычисления остальных переменных. Аналогично этому, дальше, найдя новое значение x2 можно его также сразу использовать в этой же итерации и т. д.
д.
Исходя из этого, формула итераций для метода Гаусса-Зейделя имеет следующий вид
. (3.10)
Достаточным условием сходимости итерационного процесса метода Гаусса-Зейделя является все то же условие доминирования диагонали (3.9). Скорость сходимости этого метода несколько выше, чем в метода Якоби.
Пример 5. Решим методом Гаусса-Зейделя систему уравнений
Эту систему мы уже рассматривали в примерах 3 и 4, поэтому сразу перейдем от нее к преобразованой системе уравнений (см. пример 4), в которой условие доминирования диагонали выполняется. Из нее получаем формулу для выполнения вычислений по методу Гаусса-Зейделя
Взяв за начальное (т.е. нулевое) приближение вектор свободных членов, выполним все необходимые вычисления. Результаты сведем в таблицу
Довольно высокая точность полученного решения достигнута за пять итераций.
4.3 Итерационные методы решения линейных систем
4.3 Итерационные методы решения линейных системДалее: 4.4 Собственные значения и собственные векторы Up: 4. Численная линейная алгебра Предыдущий: 4.2 Прямые методы для
Подразделы
- 4.3.1 Общий принцип итерационных методов для линейных систем
- 4.3.2 Метод Якоби
- 4.3.3 Метод Гаусса-Зейделя
- 4.3.4 Метод последовательной чрезмерной релаксации
- 4.3.5 Градиентные методы
- 4.3.5.1 Метод Гаусса-Зейделя как градиентный метод
- 4.3.5.2 Метод наибольшего спуска
- 4.3.5.3 Метод сопряженных градиентов
Прямые методы решения линейных систем теоретически дают точные
решение за конечное число шагов, см.
Разд. 4.2. К сожалению, это редко верно в
приложений из-за ошибок округления: ошибка сделана за один шаг
распространяется дальше на всех последующих шагах! В отличие от прямых методов,
итерационные методы строят серию приближений решения, таких
что оно сходится к точному решению системы. Их главная
преимущество в том, что они самокорректируются, см. разд. 4.3.1.
Их главная
преимущество в том, что они самокорректируются, см. разд. 4.3.1.
В этом разделе мы сначала обсудим общие принципы итеративного методы, решающие линейную систему (4.6), , при этом мы предполагаем, что и система имеет ровно одно решение (дополнительную информацию см. в разделе 4.2. подробности о других случаях). Позже мы опишем наиболее распространенные итерационные Методы Якоби, Гаусса-Зейделя, последовательная чрезмерная релаксация и градиентные методы (разделы 4.3.2-4.3.5). Монографии, содержащие подробное обсуждение этих методов, включают [7,24] и [27]. Хотя мы рассматривать эти методы отдельно от прямых методов, упомянем здесь итерационные методы обычно выигрывают от комбинации с исключением Гаусса, см. [46] и [1], например.
Чтобы унифицировать представление всех методов, пусть , , и обозначают диагональную, нижнюю треугольную и верхнюю треугольную части матрица по всему этому разделу:
4.
 3.1 Общий принцип
3.1 Общий принцип итерационных методов для линейных систем
Итерационный метод решения линейной системы строит серию итераций , , что под при некоторых условиях сходится к точному решению системы ( ). Таким образом, необходимо выбрать начальную точка и многократно применяйте правило, которое вычисляет из уже известного .
Начальный вектор обычно выбирается как некоторое приближение из . (К счастью, его выбор не может привести к расхождению сходящийся метод.) Далее, учитывая , последующие элемент ряда вычисляется с помощью правила формы
| (4.8) |
где , матричные ряд. Различные варианты и определить разные итерационные методы.
Обсудим теперь минимальный набор условий на и в (4.8), гарантирующие сходимость итерационный метод. Прежде всего, он должен держать это для всех , или эквивалентно,
(4. 9) 9) |
Другими словами, как только итерационный процесс достигает точного решения , все последовательные итерации должны оставаться равными и метод не может отойти от этого решения. Во-вторых, начиная с точка , мы должны убедиться, что аппроксимации будет сходиться к по мере увеличения.
Теорема 6 Серия итераций (4.8) сходится к решение системы (4.6) для любого выбранного если
На практике используются стационарные итерационные методы, т. е. методы с постоянным и , . Следовательно, итерационный ряд затем строится с использованием
| (4.10) |
и условие сходимости в теореме 6 имеет более простая форма.
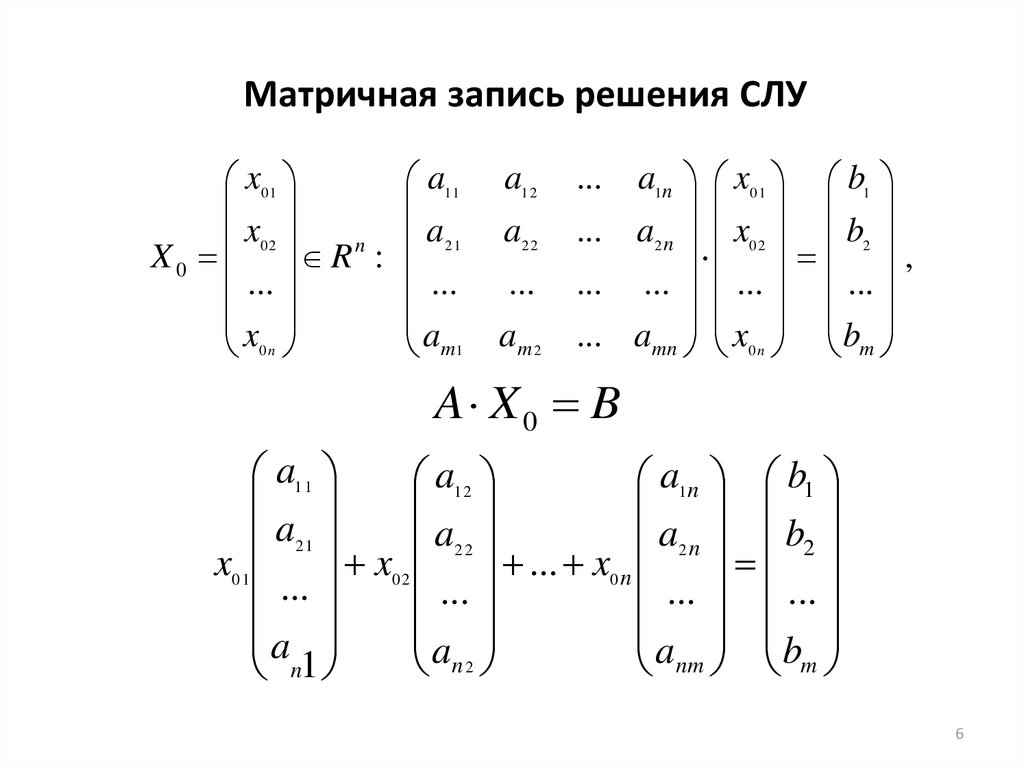
Теорема 7 Серия итераций (4.10) сходится к решение системы (4.6) для любого выбранного если спектральный радиус , куда и представлять собственные значения .
Отметим, что условие сходимости держит, для пример, если в любой матричной норме. Более того, Теорема 7 гарантирует свойство самокорректировки итерационных методов, так как сходимость происходит независимо от начальное значение . Таким образом, если вычислительные ошибки отрицательно сказываются на во время й итерации, можно рассматривать как новый начальный вектор, а итерационный метод сходятся. Следовательно, итерационные методы в целом более прочнее, чем прямые.
По-видимому, такой итерационный процесс может продолжаться сколь угодно долго.
пока не
в какой-то момент. Это непрактично и обычно
ненужный. Поэтому используются критерии остановки (или сходимости)
которые останавливают итеративный процесс, когда предварительно заданное условие
встретились. Обычно используемые критерии остановки основаны на изменении
решения или остаточного вектора, достигнутого за один
итерация. В частности, учитывая небольшой
,
итерационный процесс останавливается после й итерации, когда
,
, или же
, куда
остаточный вектор. Кроме того, максимально допустимый
обычно указывается количество итераций.
Обычно используемые критерии остановки основаны на изменении
решения или остаточного вектора, достигнутого за один
итерация. В частности, учитывая небольшой
,
итерационный процесс останавливается после й итерации, когда
,
, или же
, куда
остаточный вектор. Кроме того, максимально допустимый
обычно указывается количество итераций.
4.3.2 Метод Якоби
Метод Якоби мотивирован следующим наблюдением. Позволять имеют ненулевые диагональные элементы (строки любых неособых матрица может быть реорганизована для достижения этой цели). Затем диагональная часть из невырождена и система (4.6) может быть переписан как . Следовательно,
Замена с левой стороны по и на с правой стороны приводит к итерационной формуле Метод Якоби:
Интуиция метода Якоби очень проста: если приближение решения, выразим компонент как функция других компонентов из уравнения и вычислить заданное :
| (4.11) |
(см. рис. 4.4).
Метод Якоби сходится для любого начального вектора так долго как , видеть Теорема 7. Это условие выполняется для относительно большой класс матриц, включая диагонально доминирующие матрицы (матрицы такой, что за ) и симметричные матрицы такой, что , , и все положительные определенный. Хотя есть много улучшений основного принципа метода Якоби с точки зрения сходимости к , видеть Секты. 4.3.3 и 4.3.4, его преимущество простая и быстрая реализация (элементы новой итерации может рассчитываются независимо друг от друга).
4.3.3 Метод Гаусса-Зейделя
Аналогично методу Якоби можно переписать
система (4. 6) как
, который
далее подразумевает
. Это ведет к
итерационная формула метода Гаусса-Зейделя:
6) как
, который
далее подразумевает
. Это ведет к
итерационная формула метода Гаусса-Зейделя:
| (4.12) |
Основное отличие от методов Якоби заключается в более эффективном использовании из (4.11). При вычислении элемента , первые элементы уже известны (и предположительно точнее, чем ). Таким образом, возможно использовать эти новые значения вместо старых и ускорить конвергенция (схему см. на рис. 4.5). Более того, используя этой стратегии вновь вычисленные элементы может напрямую перезаписать соответствующие элементы и сохранить память таким образом.
Следуя теореме 7, метод Гаусса-Зейделя
сходится для любого начального вектора
если
. Это условие выполняется, например, для диагонально доминирующих
матриц, так и для положительно определенных.
4.3.4 Метод последовательной чрезмерной релаксации
Метод последовательной чрезмерной релаксации (SOR) направлен на дальнейшее уточнение Метод Гаусса-Зейделя. Формула Гаусса-Зейделя (4.12) может быть переписан как
который описывает разницу между и выраженный для th элемента от уравнение, . Вопрос, который ставит SOR, заключается в том, метод может сходиться быстрее, если мы «чрезмерно» исправим в каждый шаг; то есть, если корректируется несколькими в каждой итерации. Эта идея приводит к SOR формула:
или в виде (4.10),
(4.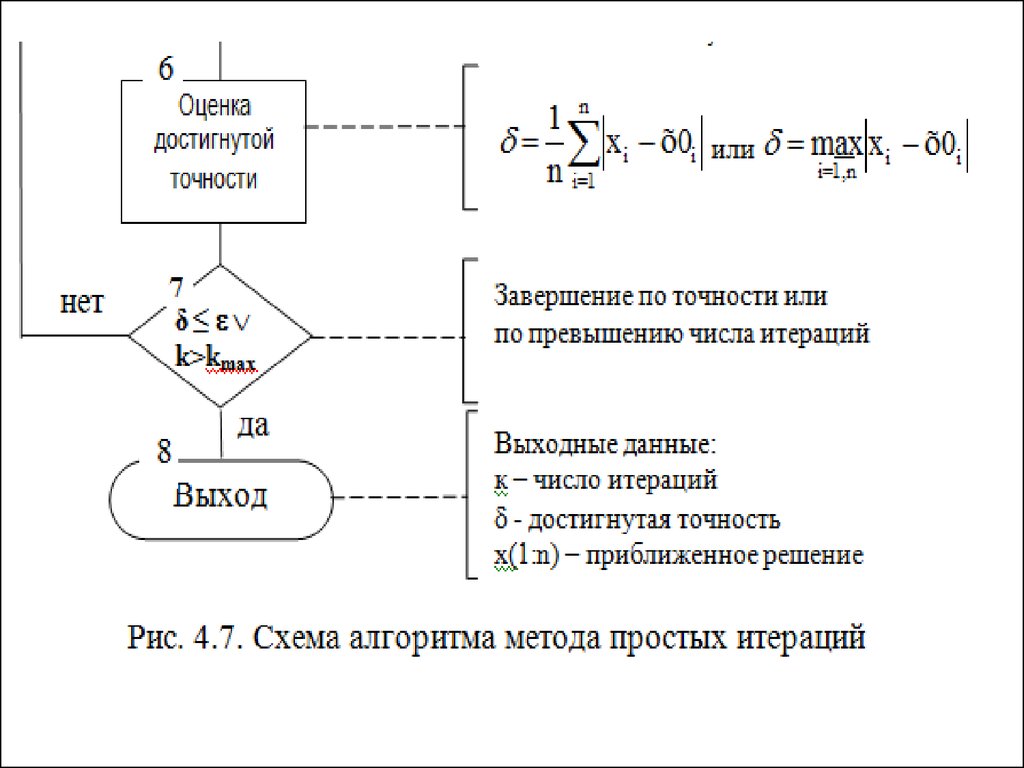 13) 13) |
Параметр называется параметром (сверх)релаксации, и он можно показать, что SOR сходится только для , результат получено по [41].
Правильный выбор параметра может ускорить сходимость, поскольку измеряется спектральным радиусом соответствующей итерационной матрицы (см. теорему 7; нижний спектральный радиус означает более быструю сходимость). Есть выбор литературы посвящена оптимальной настройке параметра релаксации: см. [28] для недавнего обзора основных результатов, касающихся СОР. Мы приведем лишь один важный результат, связанный с [66].
Определение 1 Матрица называется двуциклическим последовательно упорядоченным, если собственные значения матрицы , , не зависят от .
Теорема 8 Пусть матрица
быть двуциклически последовательно упорядоченной. Пусть
соответствующая матрица итераций Гаусса-Зейделя имеют спектральный радиус
. Тогда оптимальное расслабление
параметр в SOR определяется как
Тогда оптимальное расслабление
параметр в SOR определяется как
и для этого оптимального значения выполняется .
Использование SOR с оптимальным параметром релаксации существенно увеличивает скорость сходимости. Заметим, однако, что сходимость ускорение получается только для очень близких к . Если не может быть вычислено точно, лучше взять чуть крупнее, чем меньше. [24] описывают алгоритм аппроксимации за .
С другой стороны, если предположения теоремы 8 не выполняются
удовлетворены, можно использовать симметричный SOR (SSOR), который выполняет
Итерация SOR дважды: один раз, как обычно, см. (4.13), и один раз
с взаимозаменяемыми
и
. SSOR требует больше вычислений
за итерацию и обычно сходится медленнее, но работает для любых
положительно определенная матрица и может комбинироваться с различными ускорениями
методы. Подробнее см. [7] и [28].
Подробнее см. [7] и [28].
4.3.5 Градиентные методы
Градиентные итерационные методы основаны на предположении, что является симметричная положительно определенная матрица . Они используют это предположение переформулировать (4.6) как задачу минимизации: является единственный минимум квадратичной формы
Учитывая эту проблему минимизации, градиентные методы строят итерационный ряд векторов, сходящийся к используя следующие принцип. Имея th приближение , выберите направление и найдите такое число, что новый вектор
– минимум на линии , . Различные варианты направлений затем визуализировать различные градиентные методы, в общем случае нестационарные ( изменения в каждой итерации).
 Здесь мы обсудим три метода:
метод Гаусса-Зейделя (как градиентный метод), метод наискорейшего спуска и
методы сопряженных градиентов.
Здесь мы обсудим три метода:
метод Гаусса-Зейделя (как градиентный метод), метод наискорейшего спуска и
методы сопряженных градиентов.4.3.5.1 Метод Гаусса-Зейделя как градиентный метод
Интересно, что метод Гаусса-Зейделя можно рассматривать как градиентный метод выбора
куда обозначает й единичный вектор. Гаусса-Зейделя итерация соответствует подитерациям с за .
4.3.5.2 Метод наибольшего спуска
Метод наискорейшего спуска основан на направлении данный градиент в . Обозначая остаток приближение , формула итерации
где представляет направление и его коэффициент в — сведение к минимуму выбора .
 По определению это
метод уменьшает
на каждом шагу, но это не очень
эффективный. Метод сопряженных градиентов, обсуждаемый в следующем
subsection обычно работает лучше.
По определению это
метод уменьшает
на каждом шагу, но это не очень
эффективный. Метод сопряженных градиентов, обсуждаемый в следующем
subsection обычно работает лучше.4.3.5.3 Метод сопряженных градиентов
В методе сопряженных градиентов (СГ), предложенном в [33], направления генерируются -ортогонализация остаточные векторы. Учитывая симметричную положительно определенную матрицу , -ортогонализация — это процедура, которая строит ряд линейно независимые векторы такой, что для (сопряжения или -условие ортогональности). Это можно использовать для решения системы (4.6) следующим образом ( представляет остатки).
Алгоритм 8
до
Интересное теоретическое свойство CG состоит в том, что он достигает точного
решение не более чем за шаги, потому что их не более
(
-)ортогональные векторы. Принцип CG имеет множество расширений, применимых также для
несимметричные невырожденные матрицы: например, обобщенные минимальные
остаток, [55]; (стабилизированные) бисопряженные градиенты,
[64]; или квазиминимальная невязка, [13]. Главная » Публикации MAA » Периодика » Loci/JOMA » Итерационные методы решения Ax = b Итерационные методы решения \(Ax = b\) - Введение в модуль › Автор(ы): David M. Strong Информация для инструкторов Этот модуль состоит из двух учебных пособий с соответствующими упражнениями и апплета Java для выполнения необходимых вычислений и графического отображения результатов. Мы исследуем три различных итерационных метода, то есть методы, предназначенные для создания последовательных приближений к точному решению линейной системы уравнений. Дэвид Стронг — доцент кафедры математики Университета Пеппердайн. Итерационные методы играют важную роль в решении многих современных проблем реального мира, поэтому важно, чтобы ваше первое знакомство с этими методами было как можно более позитивным и простым, а также информативным и образовательным. Более подробно, вот основные функции апплета: Вы увидите, что апплет работает только с системами 2 x 2, то есть с двумя линейными уравнениями с двумя неизвестными. В реальном мире мы бы никогда не использовали итерационный метод для решения такой маленькой системы или даже для решения значительно больших (например, 64 x 64 512 x 512 и т. д.) систем. В моих собственных исследованиях по обработке изображений я обычно имею дело с (разреженными) системами 65536(256 2 ) или 262144 (512 2 ) уравнений с тем же числом переменных. Обычно мы не используем ни один из трех методов (Якоби, Гаусса-Зейделя, SOR), обсуждаемых в модуле, хотя некоторые из их основных идей можно найти в любом итерационном методе. до выполнения критерия остановки Таким образом, CG не является действительно итеративным
метод. (Этого не должно быть, если
единственное число или
неквадратная матрица, см. [42].) С другой стороны,
обычно используется как итерационный метод, потому что он может дать решение
с заданной точностью гораздо раньше, чем после
итерации. Более того, если приближенное решение
после
итераций недостаточно точна (из-за ошибок вычислений),
алгоритм можно перезапустить с помощью
установлен в
. Наконец, пусть
Отметим, что CG привлекательна для использования с большими разреженными матрицами.
потому что он обращается
только путем умножения на
вектор. Эта операция может быть выполнена очень эффективно для правильного
сохраненная разреженная матрица, см. разд. 4.5.
Таким образом, CG не является действительно итеративным
метод. (Этого не должно быть, если
единственное число или
неквадратная матрица, см. [42].) С другой стороны,
обычно используется как итерационный метод, потому что он может дать решение
с заданной точностью гораздо раньше, чем после
итерации. Более того, если приближенное решение
после
итераций недостаточно точна (из-за ошибок вычислений),
алгоритм можно перезапустить с помощью
установлен в
. Наконец, пусть
Отметим, что CG привлекательна для использования с большими разреженными матрицами.
потому что он обращается
только путем умножения на
вектор. Эта операция может быть выполнена очень эффективно для правильного
сохраненная разреженная матрица, см. разд. 4.5.
Далее: 4. 4 Собственные значения и собственные векторы Up: 4. Численная линейная алгебра Предыдущий: 4.2 Прямые методы для
4 Собственные значения и собственные векторы Up: 4. Численная линейная алгебра Предыдущий: 4.2 Прямые методы для Итерационные методы решения Ax = b
Вы здесь
 Имея это в виду, основная цель учебных пособий и апплета состоит в том, чтобы обеспечить легкую визуализацию и экспериментирование.
Имея это в виду, основная цель учебных пособий и апплета состоит в том, чтобы обеспечить легкую визуализацию и экспериментирование.


 Общие сведения
Общие сведения


 4: Схема метода Якоби
4: Схема метода Якоби