Калькулятор извлечения корня n-ой степени. Простые и не очень способы того, как вычислить кубический корень
До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
Шаги
Разложение на простые множители
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
- Записать это можно следующим образом: √400 = √(25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
- В нашем примере извлеките корень из 25 и из 16.
- √(25 х 16)
- √25 х √16
- 5 х 4 = 20
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа.
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
- = √(49 х 3)
- = √49 х √3
- = 7√3
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3.
 Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ – разложите подкоренное число на простые множители . Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.
- = √(2 х 44)
- = √ (2 х 4 х 11)
- = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
- = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Вычисление квадратного корня вручную
При помощи деления в столбик
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой.
 Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа).
 Результат вычисления запишите под вычитаемым (квадратом числа n).
Результат вычисления запишите под вычитаемым (квадратом числа n).- В нашем примере вычтите 4 из 7 и получите 3.
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере второй парой чисел является «80». Запишите «80» после 3. Затем, удвоенное число сверху справа дает 4. Запишите «4_×_=» снизу справа.
Заполните прочерки справа.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.

- В нашем примере, вычтите 329 из 380, что равно 51.
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114).
 Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114).
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).
Понимание процесса
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
Мысленно представьте квадрат, площадь которого вам нужно вычислить.
 A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.
Задайте букву для каждой пары первых цифр. Обозначим через S a первую пару цифр в значении S, через S b — вторую пару цифр и так далее.
Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.
Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.
Что нужно знать о корне произвольной степени?
Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».
Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.
Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.
Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.
Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.
Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ».
В-третьих, для них справедливы все действия со степенями.
- Их можно перемножать. Тогда показатели степеней складываются.

- Корни можно разделить. Степени нужно будет вычесть.
- И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.
В чем сходства и различия квадратного и кубического корней?
Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.
А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.
Извлечение кубического корня на калькуляторе
Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?
На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».
Извлечение кубического корня вручную
Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?
- Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой.
 Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать. - Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
- Выполнить вычитание.
- К остатку приписать первую группу цифр после запятой.
- В черновике записать выражение: а 2 * 300 * х + а * 30 * х 2 + х 3 . Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
- Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
- Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.
Наглядный пример вычисления кубического корня
Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.
Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.
- 15> 2 3 , значит под целой частью записана 8, а над корнем 2.
- После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
- а = 2. Поэтому: 2 2 * 300 * х +2 * 30 * х 2 + х 3
- Методом подбора получается, что х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
- Вычитание дает 1176, а над корнем появилось число 4.
- Приписать к остатку три нуля.
- а = 24. Тогда 172800 х + 720 х 2 + х 3
- х = 6. Вычисление выражения дает результат 1062936. Остаток: 113064, над корнем 6.
- Снова приписать нули.
- а = 246. Неравенство получается таким: 18154800х + 7380х 2 + х 3
- х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.
Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.
Необычный способ извлечения кубического корня
Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. Причем таких слагаемых должно быть минимально возможное число.
К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.
Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем.
Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.
Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.
Ниже мы по очереди рассмотрим основные способы извлечения корней.
Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т. п.
п.
Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.
Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.
Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.
Приступим.
Использование таблицы квадратов, таблицы кубов и т.д.
В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.д. Что же представляют собой эти таблицы?
Таблица квадратов целых чисел от 0
до 99
включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0
до 99
. Для примера выберем строку 8
десятков и столбец 3
единицы, этим мы зафиксировали число 83
. Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0
до 99
. На пересечении выбранной нами строки 8
десятков и столбца 3
единицы находится ячейка с числом 6 889
, которое является квадратом числа 83
.
На пересечении выбранной нами строки 8
десятков и столбца 3
единицы находится ячейка с числом 6 889
, которое является квадратом числа 83
.
Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.
Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
Допустим, нам нужно извлечь корень n -ой степени из числа a , при этом число a содержится в таблице n -ых степеней. По этой таблице находим число b такое, что a=b n . Тогда , следовательно, число b будет искомым корнем n -ой степени.
В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683
. Находим число 19 683
в таблице кубов, из нее находим, что это число является кубом числа 27
, следовательно, .
Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.
Разложение подкоренного числа на простые множители
Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Пусть из натурального числа a
извлекается корень n
-ой степени, и его значение равно b
. В этом случае верно равенство a=b n
. Число b
как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m
в виде p 1 ·p 2 ·…·p m
, а подкоренное число a
в этом случае представляется как (p 1 ·p 2 ·…·p m) n
. Так как разложение числа на простые множители единственно, то разложение подкоренного числа a
на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n
, что дает возможность вычислить значение корня как .
Так как разложение числа на простые множители единственно, то разложение подкоренного числа a
на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n
, что дает возможность вычислить значение корня как .
Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.
Разберемся с этим при решении примеров.
Пример.
Извлеките квадратный корень из 144 .
Решение.
Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .
Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.
Разложим 144
на простые множители:
То есть, 144=2·2·2·2·3·3
. На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2
. Следовательно, .
Следовательно, .
Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .
Ответ:
Для закрепления материала рассмотрим решения еще двух примеров.
Пример.
Вычислите значение корня .
Решение.
Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .
Ответ:
Пример.
Является ли значение корня целым числом?
Решение.
Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.
Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.
Ответ:
Нет.
Извлечение корней из дробных чисел
Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q
. Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Разберем пример извлечения корня из дроби.
Пример.
Чему равен квадратный корень из обыкновенной дроби 25/169 .
Решение.
По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5 , а квадратный корень из знаменателя равен 13 . Тогда . На этом извлечение корня из обыкновенной дроби 25/169 завершено.
Ответ:
Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.
Пример.
Извлеките кубический корень из десятичной дроби 474,552 .
Решение.
Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000
. Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13=
(2·3·13) 3 =78 3
и 1 000=10 3
, то и . Осталось лишь завершить вычисления .
Так как 474 552=2·2·2·3·3·3·13·13·13=
(2·3·13) 3 =78 3
и 1 000=10 3
, то и . Осталось лишь завершить вычисления .
Ответ:
.
Извлечение корня из отрицательного числа
Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a и нечетного показателя корня 2·n−1 справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Рассмотрим решение примера.
Пример.
Найдите значение корня .
Решение.
Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .
Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .
Приведем краткую запись решения: .
Ответ:
.
Порязрядное нахождение значения корня
В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n -ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n
числа 0, 10, 100, …
до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n
на предыдущем этапе, укажет соответствующий старший разряд.
Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =05 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.
Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2 , на втором – 2,2 , на третьем – 2,23 , и так далее 2,236067977… . Опишем, как происходит нахождение значений разрядов.
Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9
. При этом параллельно вычисляются n
-ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9
.
Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.
Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9
, вычисляя соответственно 0 2 , 1 2 , …, 9 2
до того момента, пока не получим значение, большее подкоренного числа 5
. Все эти вычисления удобно представлять в виде таблицы:
Так значение разряда единиц равно 2
(так как 2 2 5
). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Так как 2,2 2 5
, то значение разряда десятых равно 2
. Можно переходить к нахождению значения разряда сотых:
Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .
Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.
Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100
и т.д. пока не получим число, превосходящее 2 151,186
. Имеем 0 3 =02 151,186
, таким образом, старшим разрядом является разряд десятков.
Для этого возводим в куб числа 0, 10, 100
и т.д. пока не получим число, превосходящее 2 151,186
. Имеем 0 3 =02 151,186
, таким образом, старшим разрядом является разряд десятков.
Определим его значение.
Так как 10 3 2 151,186
, то значение разряда десятков равно 1
. Переходим к единицам.
Таким образом, значение разряда единиц равно 2
. Переходим к десятым.
Так как даже 12,9 3
меньше подкоренного числа 2 151,186
, то значение разряда десятых равно 9
. Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
На этом этапе найдено значение корня с точностью до сотых: .
В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.
Список литературы.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
- Колмогоров А.
 Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений. - Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:
Совсем немного, а если потренируетесь два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.
*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.
Мы знаем, что:
Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):
Вы без труда сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать?
Что нужно знать?
1. Это кубы чисел кратных десяти:
Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно.
2. Это свойство чисел при произведении.
Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?
Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.
1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 …
То есть, при возведении в куб числа с единицей на конце в результате у нас всегда получится число с единицей в конце.
При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.
Покажем соответствие в табличке для всех чисел:
Знания представленных двух моментов вполне достаточно.
Рассмотрим примеры:
Извлечь кубический корень из 21952.
Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.
Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.
Извлечь кубический корень из 54852.
Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.
Извлечь кубический корень из 571787.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.
Извлечь кубический корень из 614125.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.
Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.
Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.
Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.
После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉
На самом ЕГЭ задач с такими «страшненькими» корнями нет. Например, в требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема.
Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Инструкция
Чтобы возвести число в степень 1/3, введите это число, затем нажмите на кнопку возведения в степень и наберите приблизительное значение числа 1/3 — 0,333. y».
y».
Корень третьей степени можно вычислить и в программе MS Excel. Для этого введите в любую клетку «=» и выберите значок «вставка » (fx). Выберите в появившемся окошке функцию «СТЕПЕНЬ» и нажмите кнопку «Ок». В появившемся окошке введите значение числа, для которого необходимо вычислить корень третьей степени. В «Степень» введите число «1/3». Число 1/3 набирайте именно в таком виде – как обыкновенную . После этого нажмите кнопку «Ок». В той клетке таблицы, где создавалась , появится кубический корень из заданного числа.
Если корень третьей степени приходится вычислять постоянно, то немного усовершенствуйте описанный выше метод. В качестве числа, из которого требуется извлечь корень, укажите не само число, а клетку таблицы. После этого, просто каждый раз вводите в эту клетку исходное число – в клетке с формулой будет появляться его кубический корень.
Видео по теме
Обратите внимание
Заключение. В данной работе были рассмотрены различные методы вычисления значений кубического корня. Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках.
Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках.
Полезный совет
Корни второй и третьей степени употребляются особенно часто и поэтому имеют специальные названия. Квадратный корень: В этом случае показатель степени обычно опускается, а термин «корень» без указания степени чаще всего подразумевает квадратный корень. Практическое вычисление корней Алгоритм нахождения корня n-ной степени. Квадратные и кубические корни обычно предусмотрены во всех калькуляторах.
Источники:
- корень третий степени
- Как извлечь квадратный корень в N степени в Excel
Операцию нахождения корня третьей степени обычно называют извлечением «кубического» корня, а заключается она в нахождении такого вещественного числа, возведение которого в куб даст значение равное подкоренному числу. Операция извлечения арифметического корня любой степени n эквивалентна операции возведения в степень 1/n. Для практического вычисления кубического корня можно использовать несколько способов.
Операция извлечения арифметического корня любой степени n эквивалентна операции возведения в степень 1/n. Для практического вычисления кубического корня можно использовать несколько способов.
Извлечение квадратных корней без калькулятора
Городская научно-практическая конференция школьников
«Интеллектуал»
Секция МАТЕМАТИКИ
«Извлечение квадратных корней без калькулятора»
Автор работы:
Каширина Елизавета Сергеевна
8 Б класс
МАОУ «СОШ № 93»
Руководитель:
Мартынюк Татьяна Владимировна,
учитель математики МАОУ «СОШ № 93»
г. Кемерово
2018 г.
Оглавление
Введение ……………………………………………………………………………… 2
Глава 1. Способ разложения на простые множители …………………………….….4
Глава 2. Способ использования таблицы квадратов двузначных чисел ……… ….5
Глава 3. Формула Древнего Вавилона ……………………………………………… ..6
Глава 4. Через решение уравнения ……………………………………………………7
Глава 5. Деление на пары через составление ребуса …………………….……………8
Глава 6. Геометрический метод ……………………………………………….…….12
Глава 7. Графический метод ………………………………………….………..……..13
Глава 8. Канадский метод ………………………………………………..…..………14
Глава 9.Метод вычетов нечетного числа ……………………………………………14
Глава 10.Другие методы …………………………………………………………………………………..15
Заключение …………………………………………………………………………….16
Список литературы ……………………………………….…………….…..…………17
Приложение 1…………………………………………………………………………..18
Введение
При изучении темы квадратных корней на уроках алгебры часто приходилось использовать таблицу квадратов и калькулятор. Извлекать квадратные корни приходилось и на уроках геометрии при изучении теоремы Пифагора, и при решении текстовых задач, в которых нужно было найти корни квадратного уравнения с большим дискриминантом. Но не всегда под рукой был калькулятор и таблица квадратов. Уже тогда возникал вопрос, как же быть в тех случаях, когда на экзаменах ГИА и ЕГЭ использовать калькулятор запрещено. Кроме того таблица квадратов целых чисел не даёт ответ на такие вопросы, как, например, чему равен , , и др. даже приблизительно.
Извлекать квадратные корни приходилось и на уроках геометрии при изучении теоремы Пифагора, и при решении текстовых задач, в которых нужно было найти корни квадратного уравнения с большим дискриминантом. Но не всегда под рукой был калькулятор и таблица квадратов. Уже тогда возникал вопрос, как же быть в тех случаях, когда на экзаменах ГИА и ЕГЭ использовать калькулятор запрещено. Кроме того таблица квадратов целых чисел не даёт ответ на такие вопросы, как, например, чему равен , , и др. даже приблизительно.
Все знают, что извлечь квадратный корень без калькулятора — это непосильная задача. В лучшем случае, в ситуации, когда решение задач требует извлечения корня, а калькулятора нет под рукой, прибегают к методу подбора и пытаются вспомнить данные из таблицы квадратов целых чисел, но это не всегда спасает. Сколько раз все попадали в подобные ситуации?
Как-то на уроке при изучении темы квадратных корней учительница математики показала, как в столбик можно извлекать квадратные корни. Вычислить корень можно с произвольной точностью, найти сколько угодно цифр в его десятичной записи, даже если он получается иррациональным. Алгоритм плохо запомнился, остались вопросы. Я решила разобраться в этом приеме извлечения квадратного корня, стала работать над этим вопросом. Также я узнала, что извлекать корни люди научились задолго до изобретения «умной» техники, что существуют и другие способы извлечения квадратного корня. Мои вопросы и легли в основу исследования, которое для меня стало маленьким открытием. Исследуя эту тему, я нашла не один, а несколько способов решения данной проблемы.
Вычислить корень можно с произвольной точностью, найти сколько угодно цифр в его десятичной записи, даже если он получается иррациональным. Алгоритм плохо запомнился, остались вопросы. Я решила разобраться в этом приеме извлечения квадратного корня, стала работать над этим вопросом. Также я узнала, что извлекать корни люди научились задолго до изобретения «умной» техники, что существуют и другие способы извлечения квадратного корня. Мои вопросы и легли в основу исследования, которое для меня стало маленьким открытием. Исследуя эту тему, я нашла не один, а несколько способов решения данной проблемы.
Актуальность исследования обусловлена желанием углублить математические знания путем изучения простейших способов извлечения квадратных корней без калькулятора, распространить алгоритмы извлечения корней среди учащихся, что особенно актуально при сдаче экзаменов, где запрещено пользоваться калькулятором, а также использовать эти знания при работе с вычислениями корней на уроках математики в ситуациях отсутствия калькулятора.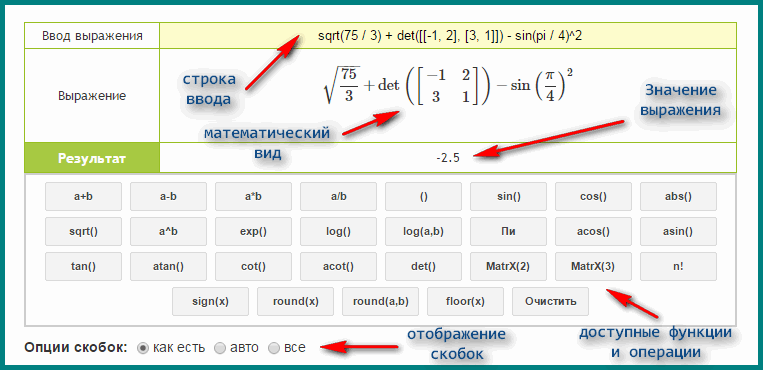
Цель работы: изучить способы извлечения квадратных корней без калькулятора и отобрать самые рациональные для практического применения.
Задачи:
- Изучить всю найденную литературу по данному вопросу, научные статьи, исторические справки и работы современных учёных и исследователей.
- Рассмотреть найденные способы и описать их алгоритм.
- Познакомить с результатами полученных исследований одноклассников и друзей.
Гипотеза: Существует не менее двух-трёх способов извлечения квадратных корней без калькулятора.
Предмет исследования: извлечение квадратных корней без калькулятора.
Объект исследования: способы извлечения квадратных корней без калькулятора.
Глава 1. Способ разложения на простые множители
Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения.
Этим способ принято использовать при решении заданий, связанных с извлечением квадратных корней, в школе.
Пример 1:
11025│5
2205│5
441│3
147│3
49│7
7│7
= = 3∙5∙7 = 105
Пример 2:
213444│2
106722│2
53361│3
17787│3
5929│11
539│11
49│7
7│7
= = 2∙3∙7∙11 = 462;
Многие применяют его успешно и считают единственным. Извлечение корня разложением на множители довольно трудоёмкая задача, которая тоже не всегда приводит к желаемому результату. Попробуйте извлечь квадратный корень из числа 820836. Разложение на простые множители дает произведение 2∙2∙3∙3∙22801. А как быть дальше? С этой задачей сталкиваются все, и спокойно в ответе записывают остаток от разложения под знак корня. Методом проб и ошибок, подбором разложение, конечно, можно выполнить, если быть уверенным в том, что получится красивый ответ, но практика показывает, что очень редко предлагаются задания с полным разложением. Чаще бывает так, что корень до конца не извлечь.
Методом проб и ошибок, подбором разложение, конечно, можно выполнить, если быть уверенным в том, что получится красивый ответ, но практика показывает, что очень редко предлагаются задания с полным разложением. Чаще бывает так, что корень до конца не извлечь.
Поэтому, этот способ лишь частично решает проблему извлечения квадратного корня без калькулятора.
Глава 2. Способ с применением таблицы квадратов
двузначных чисел
С этим способом мы познакомились на уроках математики. Способ очень прост в применении и даёт мгновенное извлечение квадратного корня из любых целых чисел от 1 до 100 с точностью до десятых без калькулятора. Но для этого метода требуется наличие таблицы квадратов натуральных чисел от 10 до 99. (Она есть во всех учебниках алгебры 8 класса, и на экзамене ГИА предлагается в качестве справочного материала).
Откройте таблицу и проверьте скорость нахождения ответа. Но при использовании таблицы квадратов для извлечения квадратного корня нужно не перепутать, что крайний левый столбик определяет цифру, стоящую в разряде целых, а самая верхняя строчка – это десятые в ответе. А дальше всё просто: закройте две последние цифры числа в таблице и найдите нужное вам, не превосходящее 100 подкоренное число, и далее действуйте по правилам этой таблицы.
А дальше всё просто: закройте две последние цифры числа в таблице и найдите нужное вам, не превосходящее 100 подкоренное число, и далее действуйте по правилам этой таблицы.
Пример 1: Найдём значение .
Решение: Мысленно отбрасываем две последние цифры у всех чисел в таблице и находим 57 или близкие к 57-ти – такое число одно 5776. Левый столбик даёт ответ 7 (это целые), а верхняя строчка 6 (это десятые). Значит ≈ 7,6. Проверим на микрокалькуляторе ≈ 7,549834.
Пример 2: Найдём значение .
Решение: Мысленно поставим запятые, отсчитав две последние цифры, у всех чисел в таблице и находим близкие для 89 – таких только два 88,36 и 90,25. Но 90,25 – это много, 88,36 ближе к 89. Значит, выбираем 8836.
Левый столбик даёт ответ 9 (это целые), а верхняя строчка 4 (это десятые). Значит ≈ 9,4. Проверим на микрокалькуляторе ≈ 9,43398113.
Быстро, просто, доступно на экзамене. Но сразу понятно, что корни, большие 100 мы уже этим способом извлечь не сможем. Способ удобен для заданий с маленькими корнями и при наличии таблицы.
Способ удобен для заданий с маленькими корнями и при наличии таблицы.
Глава 3. Формула Древнего Вавилона
Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня из числа n.
Число n они представляли в виде суммы а2 + b, где а2 ближайший к числу n точный квадрат натурального числа а и пользовались формулой:
Извлечём с помощью этой древней формулы корень квадратный из числа 40:
Глава 4. Через решение уравнения
На самом деле существует удобный способ нахождения квадратного корня «вручную» через решение уравнения, ведь математика — наука с многовековой историей, а калькуляторы были не всегда. Способ этот дает возможность вычислить значение корня с точностью до одного — двух знаков после запятой, а, при желании, достичь и большей точности. Звучит невероятно, но попробуйте испытать этот способ при вычислении квадратного корня.
Звучит невероятно, но попробуйте испытать этот способ при вычислении квадратного корня.
Суть этого способа рассмотрим на примере и попробуем вычислить значение .
Сначала определим границы искомого корня в целых числах. Легко догадаться, что это числа 16 = 4² и 25 = 5²,
поэтому и .
Пусть х – это та разница, на которую отличны друг от друга и ,
следовательно = 4 + х.
Возведем в квадрат обе части полученного уравнения и раскроем скобки при помощи формулы суммы квадрата:
( ) ² = (4 + х)² ; 20 = (4 + х)² ; 20 = 16 + 8х + х².
Так как мы рассчитываем получить результат с точностью до десятых или до сотых, а х² явно достаточно малая дробь, то ей вполне можно пренебречь.
В результате приходим к простому линейному уравнению
20 = 16 + 8х.
Решив его, получаем значение х = 0,5.
Значит ≈ 4 + 0,5 ≈ 4,5 .
На самом деле, при расчете на калькуляторе, значение этого корня равно 4,47213595, то есть погрешность при нашем расчете составила 0,02786405. Не правда ли, вполне приличная точность!
Но если все же решение задач по математике требует еще большей точности, то можно достичь ее тем же способом, просто продолжив вычисления с уже полученным значением корня. Так что подобный способ вычисления квадратного корня необычайно точен и удобен, а погрешность вычисления зависит исключительно от вашего терпения и упорства.
Но и этот способ требует терпения и умения решать уравнения с использованием формул сокращённого умножения.
Глава 5. Извлечение квадратного корня в столбик
(деление на пары через составление ребуса)
Пример 1: Найдём значение .
1. Разбиваем число на пары справа налево:
5`54`13`16
2. Извлекаем квадратный корень из первой группы цифр слева — в нашем случае это 5 (ясно, что точно корень может не извлекаться, берем число, квадрат которого максимально близок к нашему числу, образованному первой группой цифр, но не превосходит его). В нашем случае это будет число 2. Записываем 2 в ответ — это старшая цифра корня.Так мы получаем первую цифру числа, которое является значением квадратного корня.
В нашем случае это будет число 2. Записываем 2 в ответ — это старшая цифра корня.Так мы получаем первую цифру числа, которое является значением квадратного корня.
3. Возводим число, которое стоит уже в ответе ( это 2 ) в квадрат и вычитаем из первой слева группы цифр, т. е. из числа 5.
4. Находим разность первой группы и квадрата первой цифры (5 4 = 1).
4
1
5.Сносим следующие две цифры, т.е. приписываем справа следующую группу из двух цифр (54), получили число 154:
4
154
6. Удваиваем первую, найденную нами цифру (т. е. 2), записываем слева от
4 (2∙2 = 4):
4 4
154
7.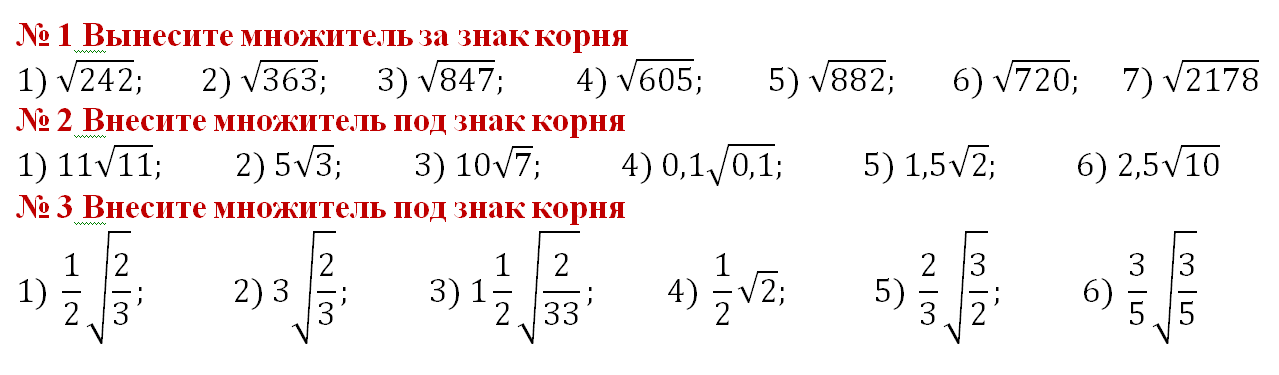 Далее необходимо найти вторую цифру. Нам нужно к числу 4 справа приписать одну цифру (обозначим a), и число 4a умножить на a ( удвоенная первая цифра, найденная нами, становится цифрой десятков числа), то есть на ту же самую приписанную цифру. Результат должен быть как можно ближе к 154, но опять-таки не больше этого числа.
Далее необходимо найти вторую цифру. Нам нужно к числу 4 справа приписать одну цифру (обозначим a), и число 4a умножить на a ( удвоенная первая цифра, найденная нами, становится цифрой десятков числа), то есть на ту же самую приписанную цифру. Результат должен быть как можно ближе к 154, но опять-таки не больше этого числа.
4a 4
a 154
В нашем случае это будет цифра 3 (так как 43∙ 3 = 129)., ее записываем в ответ после 2. Это следующая цифра в десятичной записи нашего числа, которое является значением квадратного корня.
Число 129 подписываем под числом 154:
43 4
3 154
129 129
8. Находим разность (154 – 129 = 25).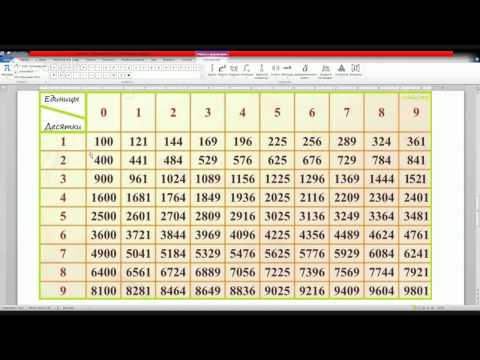
9. Сносим следующую группу (получаем число 2513):
43 4
3 154
129 129
2513
10. Удваиваем число 23, получаем 46, записываем слева от 129:
43 4
3 154
129 46 129
2513
11. Теперь необходимо найти третью цифру: 46 десятков в числе, при умножении которого на число единиц(обозначено буквой a), мы должны получить число меньшее 2513
43 4
3 154
129 46a 129
a 2513
(это цифра 5, так как 465∙5=2325).
5 третья цифра числа, которое является значением квадратного корня. Далее процесс повторяется. 12.Число 2325 подписываем под числом 2513:
43 4
3 154
129 465 129
5 2513
2325 2325
13.Находим разность (2513 – 2325 = 188).
14. Сносим следующую группу (получаем число 18816):
43 4
3 154
129 465 129
5 2513
2325 2325
18816
15. Удваиваем число 235, получаем 470, записываем слева от 2325:
Удваиваем число 235, получаем 470, записываем слева от 2325:
43 4
3 154
129 465 129
5 2513
2325 470 2325
18816
16. Теперь необходимо найти четвёртую цифру: 470 десятков в числе, при умножении которого на число единиц(обозначено буквой a), мы должны получить число меньшее 18816 (или равное ему в случае, если –целое число, так как мы снесли последнюю группу чисел):
43 4
3 154
129 465 129
5 2513
2325 470a 2325
a 18816
(это цифра 4, так как 4704∙4 = 18816).
4 четвёртая цифра числа, которое является значением квадратного корня. 17.Число 18816 подписываем под числом 18816 и вычитаем:
43 4
3 154
129 465 129
5 2513
2325 4704 2325
4 18816
18816 18816
Этим же способом можно извлечь квадратный корень и из десятичной дроби. В случае десятичной дроби разбиваем его цифры на пары следующим образом: те, что стоят слева от десятичной запятой, группируем по две справа налево, а те, что правее – по две слева направо. Далее применяем этот же алгоритм, поставив в соответствующем месте запятую.
Способ почти универсальный, так как применим к любым числам, но составление ребуса (угадывание цифры на конце числа) требует логики и хороших вычислительных навыков столбиком.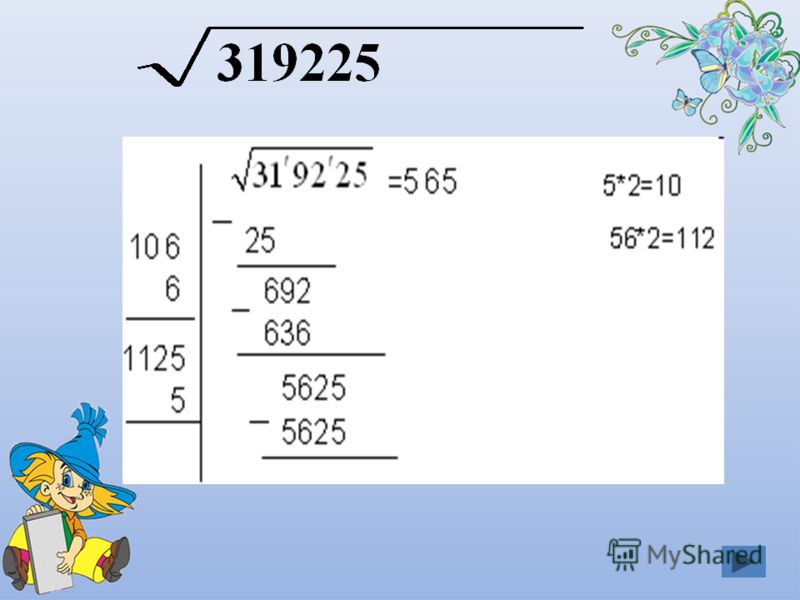 Он трудоёмкий, но очень точный.
Он трудоёмкий, но очень точный.
Глава 6. Геометрический метод
(с использованием циркуля и измерительной линейки с прямым углом или угольника)
Прежде всего стоит заметить, что использование этого метода обещает значительные погрешности, которые могут зависеть и от чистоты построения чертежей, и от точности измерительных инструментов.
Этот метод предполагает знание двух теорем геометрии :
а) Нахождение высоты прямоугольного треугольника, опущенной из прямого угла ( h =)
б) Свойство вписанного угла, опирающегося на диаметр окружности ∠АВС= 90º
А подробнее это можно описать так: Положите перед собой чистый лист, циркуль и карандаш с линейкой. Попробуем геометрическим способом извлечь квадратный корень числа 7. Работаем в сантиметрах.
Начертим отрезок АС = АН + НС, то есть АС = 1+ 7 = 8(см)
Найдём середину АС – точку О (АО = ОС) и при помощи циркуля построим окружность с центром О и радиусом ОС и отметим точку Н на отрезке АС так, что АН = 1 см , построим перпендикуляр НВ в точке Н к отрезку АС.
Измерим длину полученного отрезка ВН. Получили 2 см и 6 мм.
Этот результат и будет примерно равен .
Вывод: геометрическим способом нашли результат ≈ 2,6
Минусы этого способа сразу понятны: неточность в измерениях и построении, однако его можно применять в ситуациях недоступности калькулятора и отсутствия клеточной бумаги, что тоже иногда может спасти ситуацию.
Глава 7. Графический метод.
Графический метод извлечения квадратных корней наш учитель математики предлагает использовать для маленьких чисел, когда под рукой нет таблицы квадратов. Он полностью основан на графическом решении уравнения b= х², полученном из = х путём возведения в квадрат первого. С алгоритмом решения этого уравнения знаком каждый школьник: Построим на клеточной бумаге в одной системе координат два графика функций у = b и у = х². Найдём точку пересечения в первой четверти системы координат. Абсцисса этой точки и будет соответствовать значению квадратного корня из числа b.
Какие же неудобства и трудности испытывают при применении такого способа решения данной проблемы:
1)предварительная подготовка – построение графика параболы;
2) ограничение размером тетрадного листа (о чём сразу предупреждали), поэтому невозможно извлечение чисел, больших 40, так как длина тетрадного листа 40 клеток;
3) неточность в построении кривых линий и получение больших погрешностей, в отличие от других методов.
Глава 8. Канадский метод
Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность : не более двух – трёх знаков после запятой. Вот их формула:
= + , где X — число, из которого необходимо извлечь квадратный корень, а S — число ближайшего точного квадрата.
Давайте попробуем извлечь квадратный корень из 75
X = 75, S = 81. Это означает, что = 9.
Просчитаем по этой формуле :
= 9 + = 9 – = 9 – 0,333 = 8,667
При детальном изучении этого метода легко можно доказать его сходство с вавилонским и поспорить за авторские права изобретения этой формулы, если такие есть в действительности. Метод несложный и удобный.
Метод несложный и удобный.
Глава 9. Метод вычетов нечётного числа
Этот способ предлагает преподаватель математики одной из школ Вашингтона миссис Бруксбанк своим ученикам. Он заключается в том, чтобы последовательно вычитать нечётные числа 1,3,5,7 и т.д. пока не дойдете до нуля, а затем подсчитать число вычитаний. Это и будет ответ.
Например, чтобы получить квадратный корень из 36 и 121 это:
36 – 1 = 35 – 3 = 32 – 5 = 27 – 7 = 20 – 9 = 11 – 11 = 0
Общее количество вычитаний = 6, поэтому = 6.
121 – 1 = 120 – 3 = 117 – 5 = 112 – 7 = 105 – 9 = 96 – 11 = 85 – 13 =
=72 – 15 = 57 – 17 = 40 – 19 = 21 – 21 = 0
Общее количество вычитаний = 11, поэтому = 11.
Российские учёные называют этот метод арифметическим извлечением квадратного корня, а за глаза «методом черепахи» из-за его медлительности.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня. Попробуйте извлечь квадратный корень из числа, например, 5963364 этим способом и вы поймёте, что он «работает», безусловно, без погрешностей для точных корней, но очень длинный в решении.
В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня. Попробуйте извлечь квадратный корень из числа, например, 5963364 этим способом и вы поймёте, что он «работает», безусловно, без погрешностей для точных корней, но очень длинный в решении.
Глава 10. Другие методы
В ходе моего исследования я отыскала ещё несколько способов решения моей проблемы. Это метод степенных рядов высших степеней и метод определения путём составления таблицы. Изучив эти алгоритмы, я оценила их сложность и в некоторых местах непонимание, поэтому не стала глубоко изучать эти методы, понимая, что это уровень высшей математики или даже научной диссертации.
Если метод степенных рядов сложен в вычислении и запоминании огромной формулы, то метод таблицы так запутан, что его сложно даже пересказать, а тем более овладеть для практики.
Заключение
Во время работы я нашла не один, а нескольких способов извлечения квадратных корней. В ходе исследования было выявлено, что современной науке известно много таких способов, начиная со способа математиков Древнего Вавилона и заканчивая способом степенных рядов сложных степеней из разделов высшей математики. Мною были изучены, описаны и отработаны на практике 9 способов. Работа по данной теме меня так увлекла, что я решила продолжить свои исследования уже за рамками своего проекта. В учебнике алгебры автор знакомит восьмиклассников с корнями третьей степени и других степеней, предлагая подождать с их изучением до 11 класса. Но мне стало очень интересно узнать и про эту новую для меня тему в математике. И в продолжение моего исследования я хочу разобрать те способы, которые пока мне сложно разобрать, и выяснить, существуют ли способы извлечения корня третьей степени без калькулятора.
В ходе исследования было выявлено, что современной науке известно много таких способов, начиная со способа математиков Древнего Вавилона и заканчивая способом степенных рядов сложных степеней из разделов высшей математики. Мною были изучены, описаны и отработаны на практике 9 способов. Работа по данной теме меня так увлекла, что я решила продолжить свои исследования уже за рамками своего проекта. В учебнике алгебры автор знакомит восьмиклассников с корнями третьей степени и других степеней, предлагая подождать с их изучением до 11 класса. Но мне стало очень интересно узнать и про эту новую для меня тему в математике. И в продолжение моего исследования я хочу разобрать те способы, которые пока мне сложно разобрать, и выяснить, существуют ли способы извлечения корня третьей степени без калькулятора.
Таким образом, хочу подвести итог проделанной работы и сделать вывод. На основании результатов данного исследования доказано, что науке известно много способов извлечения квадратного корня без калькулятора. У всех способов различные алгоритмы и степень сложности вычислений, но не один из них не входит в школьный курс, так как относится к разделу высшей или прикладной математики. В ходе исследования были отработаны 9 способов, а их практическое применение доказало все недостатки и преимущества каждого из методов.
У всех способов различные алгоритмы и степень сложности вычислений, но не один из них не входит в школьный курс, так как относится к разделу высшей или прикладной математики. В ходе исследования были отработаны 9 способов, а их практическое применение доказало все недостатки и преимущества каждого из методов.
В ходе работы было доказано на практике, что умение извлекать корни без калькулятора не только полезно и актуально, но и очень увлекательно.
Список использованной литературы и сайты Интернета:
- Мордкович А.Г. Алгебра, 8 класс, учебник — Москва, Мнемозина, 2005г
- Пичугин Л.Ф. За страницами учебника алгебры. Книга для учащихся 7- 9 классов средней школы. – Москва, Просвещение, 1990 г.
- Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса учебных заведений. – Москва, Просвещение, 1994г.
- http://festival.1september.ru
- http://ru.wikipedia.ord /wiki /teorema/
Приложение 1
Этот способ нахождения хорошо известен как российским учёным, так и зарубежной общественности. Убедиться в этом легко, зайдя на любой научный или образовательный форум. Ссылки на этот способ почти во всех комментариях студентов и школьников. О нём пишут учёные и исследователи СНГ, Канады, Великобритании и Америки. Я разобрала несколько десятков примеров по этому способу, поэтому недостатка материала в изучении не испытывала. Предлагаю несколько примеров:
Убедиться в этом легко, зайдя на любой научный или образовательный форум. Ссылки на этот способ почти во всех комментариях студентов и школьников. О нём пишут учёные и исследователи СНГ, Канады, Великобритании и Америки. Я разобрала несколько десятков примеров по этому способу, поэтому недостатка материала в изучении не испытывала. Предлагаю несколько примеров:
ЕГЭ по математике — без ошибок и без калькулятора
Вы хотите хорошо сдать ЕГЭ по математике? Тогда вам необходимо уметь считать быстро, правильно и без калькулятора. Ведь главная причина потери баллов на ЕГЭ по математике – вычислительные ошибки.
По правилам проведения ЕГЭ, пользоваться калькулятором на экзамене по математике запрещается. Цена может быть слишком высокой — удаление с экзамена.
На самом деле калькулятор на ЕГЭ по математике не нужен. Все задачи решаются без него. Главное – внимание, аккуратность и некоторые секретные приемы, о которых мы расскажем.
. Начнем с главного правила. Если какое-то вычисление можно упростить – упростите его.
Если какое-то вычисление можно упростить – упростите его.
Вот, например, такое «дьявольское уравнение»:
Семьдесят процентов выпускников решают его «в лоб». Считают дискриминант по формуле , после чего говорят, что корень невозможно извлечь без калькулятора. Но ведь можно разделить левую и правую части уравнения на . Получится
Какой способ проще? 🙂
. Многие школьники не любят умножение в «столбик». Никому не нравилось в четвертом классе решать скучные «примеры». Однако перемножить числа во многих случаях можно и без «столбика», в строчку. Это намного быстрее.
Обратите внимание, что мы начинаем не с меньших разрядов, а с бoльших. Это удобно.
. Теперь – деление. Нелегко «в столбик» разделить на . Но вспомним, что знак деления : и дробная черта – одно и то же. Запишем в виде дроби и сократим дробь:
Другой пример.
. Как быстро и без всяких столбиков возвести в квадрат двузначное число? Применяем формулы сокращенного умножения:
Иногда удобно использовать и другую формулу:
. Числа, оканчивающиеся на , в квадрат возводятся моментально.
Числа, оканчивающиеся на , в квадрат возводятся моментально.
Допустим, надо найти квадрат числа ( — не обязательно цифра, любое натуральное число). Умножаем на и к результату приписываем . Всё!
Например: ( и приписали ).
( и приписали ).
( и приписали ).
Этот способ полезен не только для возведения в квадрат, но для извлечения квадратного корня из чисел, оканчивающихся на .
. А как вообще извлечь квадратный корень без калькулятора? Покажем два способа.
Первый способ – разложение подкоренного выражения на множители.
Например, найдем
Число делится на (так как сумма его цифр делится на ). Разложим на множители:
Найдем . Это число делится на . На оно тоже делится. Раскладываем на множители:
Еще пример.
Есть и второй способ. Он удобен, если число, из которого надо извлечь корень, никак не получается разложить на множители.
Например, надо найти . Число под корнем – нечетное, оно не делится на , не делится на , не делится на . .. Можно и дальше искать, на что же оно все-таки делится, а можно поступить проще – найти этот корень подбором.
.. Можно и дальше искать, на что же оно все-таки делится, а можно поступить проще – найти этот корень подбором.
Очевидно, что в квадрат возводили двузначное число, которое находится между числами и , поскольку , , а число находится между ними. Первую цифру в ответе мы уже знаем, это .
Последняя цифра в числе равна . Поскольку , , последняя цифра в ответе – либо , либо . Проверим:
. Получилось!
Найдем .
, . Значит, первая цифра в ответе – пятерка.
В числе последняя цифра – девятка. , . Значит, последняя цифра в ответе – либо , либо .
Проверим:
Если число, из которого надо извлечь квадратный корень, заканчивается на или – значит, квадратный корень из него будет числом иррациональным. Потому что ни один квадрат целого числа не заканчивается на или . Помните, что в задачах части 1 вариантов ЕГЭ по математике ответ должен быть записан в виде целого числа или конечной десятичной дроби, то есть должен являться рациональным числом.
. Квадратные уравнения встречаются нам в самых разнообразных задачах ЕГЭ. В них нужно считать дискриминант, а затем извлекать из него корень. И совсем не обязательно искать корни из пятизначных чисел. Во многих случаях дискриминант удается разложить на множители.
Например, в уравнении
. Иногда дискриминант удается посчитать по известной формуле сокращенного умножения: . Вот, например, такое уравнение вполне может получиться при решении текстовой задачи:
. Еще одна ситуация, в которой выражение под корнем можно разложить на множители, взята из задачи по планиметрии.
Гипотенуза прямоугольного треугольника равна , один из катетов равен , найти второй катет.
По теореме Пифагора, он равен . Можно долго считать в столбик, но проще применить формулу сокращенного умножения:
А теперь расскажем самое интересное — из-за чего все-таки выпускники теряют на ЕГЭ драгоценные баллы. Ведь ошибки в вычислениях возникают не просто так.
1. Верный путь к потере баллов — неаккуратные вычисления, в которых что-то исправлено, зачеркнуто, одна цифра написана поверх другой. Посмотрите на свои черновики. Возможно, они выглядят так же? 🙂
Пишите разборчиво! Не экономьте бумагу. Если что-то неправильно – не исправляйте одну цифру на другую, лучше напишите заново.
2. Почему-то многие школьники, считая в столбик, стараются сделать это 1) очень-очень быстро, 2) очень мелкими цифрами, в уголке тетради и 3) карандашом. В результате получается вот что:
Разобрать что-либо невозможно. Что ж тогда удивляться, что оценка за ЕГЭ ниже, чем ожидали?
3. Многие школьники привыкли игнорировать скобки в выражениях. Иногда встречается и такое:
Помните, что знак равенства ставится не где попало, а только между равными величинами. Пишите грамотно, даже на черновике.
4. Огромное количество вычислительных ошибок связано с дробями. Если вы делите дробь на дробь – пользуйтесь тем, что
Здесь нарисован «гамбургер», то есть многоэтажная дробь. Крайне сложно при таком способе получить правильный ответ.
Крайне сложно при таком способе получить правильный ответ.
Подведем итоги.
Проверка заданий первой части профильного ЕГЭ по математике — автоматическая. Здесь не бывает «почти правильного» ответа. Либо он правилен, либо нет. Одна вычислительная ошибка – и привет, задача не засчитывается. Поэтому в ваших интересах научиться считать быстро, правильно и без калькулятора.
Задания второй части профильного ЕГЭ по математике проверяет эксперт. Позаботьтесь о нем! Пусть ему будет понятен и ваш почерк, и логика решения.
Самое главное – ваши вычисления должны быть максимально простыми. Есть известный принцип, применяемый в программировании и дизайне. По-английски он звучит так: «Keep it simple, stupid!» и легко запоминается как KISS 🙂
9.1: Извлечение квадратных корней — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 18382
- Анонимный
- LibreTexts 9{2}+b x+c=0\]
- Ответ
\(15\pm 6\sqrt{3}\)
- Извлечение корней включает выделение квадрата и последующее применение свойства квадратного корня. После применения свойства квадратного корня у вас есть два линейных уравнения, каждое из которых можно решить. Обязательно упростите все подкоренные выражения и при необходимости рационализируйте знаменатель.
, где a , b и c — действительные числа и \(a\neq 0\). Решение такого уравнения называется корнем . Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь действительного решения. Если квадратное выражение на левых факторах, то мы можем решить его факторингом. Ниже приводится обзор шагов, используемых для решения факторингом:
Решение такого уравнения называется корнем . Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь действительного решения. Если квадратное выражение на левых факторах, то мы можем решить его факторингом. Ниже приводится обзор шагов, используемых для решения факторингом:
Шаг 1: Выразите квадратное уравнение в стандартной форме. 9{2}\).
После применения свойства квадратного корня у нас остается квадратный корень из отрицательного числа. Следовательно, реального решения этого уравнения нет.
Ответ :
Нет действительного решения
Обратный процесс, чтобы найти уравнения с заданными решениями вида ±k .
Пример \(\PageIndex{5}\)
Найдите уравнение с решениями \(-2 \sqrt{3}\) и \(2 \sqrt{3}\).
Решение 9{2}} & {=25} & {\color{Cerulean}{Применить\: the\:square \:root \:property.}} \\ {x+2} & {=\pm \sqrt{25} } & {\color{Cerulean}{Упрощение. }} \\ {x+2}& {=\pm5} \\ {x}&{=-2\pm5}\end{массив}\)
}} \\ {x+2}& {=\pm5} \\ {x}&{=-2\pm5}\end{массив}\)
На этом этапе разделите «плюс или минус» на два уравнения и упростить каждое в отдельности.
\(\ begin {массив} {ll} {x = -2-5} & {\ text {или} x = -2 + 5} \\ {x = -7} & {\ quad \: \: x=3}\end{массив}\)
Ответ :
Решения: -7 и 3. 9{2}-2=0\)
Пример \(\PageIndex{9}\)
Длина прямоугольника в два раза больше его ширины. Если диагональ равна 2 футам, найдите размеры прямоугольника.
Рисунок \(\PageIndex{1}\)Решение
Пусть w представляет ширину.
Пусть 2w представляет длину.
Диагональ любого прямоугольника образует два прямоугольных треугольника. Таким образом, применима теорема Пифагора. Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы: 9{2}&=\frac{4}{5}\quad\:\:\quad\color{Cerulean}{Extract\:the\:roots. } \\ w&=\pm\sqrt{\frac{4} {5}}\\w&=\pm\frac{2}{\sqrt{5}} \end{aligned}\)
} \\ w&=\pm\sqrt{\frac{4} {5}}\\w&=\pm\frac{2}{\sqrt{5}} \end{aligned}\)
Здесь мы получаем два решения, \(w=-\frac{2}{\sqrt {5}}\) и \(w=\frac{2}{\sqrt{5}}\). Поскольку задача требовала длины прямоугольника, мы не учитываем отрицательный ответ. Кроме того, мы рационализируем знаменатель и представим наши решения без каких-либо радикалов в знаменателе.
\(\begin{aligned} w &=\frac{2}{\sqrt{5}} \quad\quad\quad\quad\color{Cerulean}{Rationalize\:the\:знаменатель.} \\ & =\frac{2}{\sqrt{5}} \cdot \color{Cerulean}{\frac{\sqrt{5}}{\sqrt{5}}} \\ &=\frac{2 \sqrt{5 }}{\sqrt{25}} \\ &=\frac{2 \sqrt{5}}{5} \end{выровнено}\) 9{2}+c=0\) путем извлечения корней.
Упражнение \(\PageIndex{3}\) извлечение квадратных корней
Решите с помощью факторизации, а затем решите с помощью извлечения корней. {2}-36=0\) 9{2}−52=0\)
{2}-36=0\) 9{2}−52=0\)
- Ответить
1. ±4
3. ±3
5. ±\(\frac{1}{2}\)
7. ±0,5
9. ±\(2\sqrt{3}\)
11. ±\(\frac{3}{4}\)
13. ±\(\sqrt{\frac{1}{2}}\)
15. ±10
17. Нет реального решения
19. ±\(\frac{2}{3}\)
21. ±0,3
23. ±\(\sqrt{7}\)
25. ±\(2\sqrt{2}\)
27. Нет реального решения
29. ±\(\frac{3 \sqrt{3}}{4}\)
31. ±\(6\sqrt{2}\)
33. ±\(3\sqrt{3}\)
35. \(−9, −5\)
37. \(−3, 6\)
39. \(5\)±\(2\sqrt{5}\)
41. ±\(\frac{\sqrt{6}-2}{3}\)
43. ±\(\frac{\sqrt{3}}{2}-2\)
45. ±\(\frac{3 \sqrt{3}-2}{6}\)
47. Нет реального решения
49. ±\(\frac{4 \sqrt{6}}{3}+23\)
Упражнение \(\PageIndex{5}\) извлечение квадратных корней
Найдите квадратное уравнение в стандартной форме со следующими решениями. {2}−49{2}\)
{2}−49{2}\)
- Ответить
1. ±0,33
3. ±5,66
5. ±7,94
7. ±3,61
Упражнение \(\PageIndex{7}\) извлечение квадратных корней
Составьте алгебраическое уравнение и используйте его для решения следующего.
- Если из 4-кратного квадрата числа вычесть 9, то получится 3. Найдите число.
- Если из квадрата числа вычесть 20, то получится 4. Найдите число.
- Если к 3-кратному квадрату числа прибавить 1, то получится 2. Найдите число.
- Если к удвоенному квадрату числа прибавить 3, то получится 12. Найдите число.
- Если площадь квадрата 8 квадратных сантиметров, то найдите длину каждой стороны.
- Если площадь круга 32\(\pi\) квадратных сантиметров, то найдите длину радиуса. 9{2}\).)
- Длина прямоугольника в 6 раз больше его ширины.
 Если площадь равна 96 квадратных дюймов, то найдите размеры прямоугольника.
Если площадь равна 96 квадратных дюймов, то найдите размеры прямоугольника. - Основание треугольника вдвое больше его высоты. Если площадь 16 квадратных сантиметров, то найдите длину его основания.
- Квадрат имеет площадь 36 квадратных единиц. На какую величину нужно увеличить стороны, чтобы получился квадрат с удвоенной площадью?
- Круг имеет площадь 25\(\pi\) квадратных единиц. На сколько надо увеличить радиус, чтобы получился круг с удвоенной площадью?
- Если сторона квадрата равна 1 единице, то найдите длину диагонали.
- Если сторона квадрата равна 2 единицам, то найдите длину диагонали.
- Диагональ квадрата равна 5 дюймов. Найдите длину каждой стороны.
- Диагональ квадрата равна 3 дюймам. Найдите длину каждой стороны.
- Длина прямоугольника в два раза больше его ширины. Если диагональ равна 10 см, найдите размеры прямоугольника.
- Длина прямоугольника в два раза больше его ширины.
 {2}+9{2}+1600\), где t в секундах.
{2}+9{2}+1600\), где t в секундах.- Сколько времени потребуется, чтобы преодолеть половину расстояния до земли?
- Сколько времени потребуется, чтобы преодолеть оставшееся расстояние до земли? Округлите до сотых долей секунды.
- Создайте собственное уравнение, которое можно решить, извлекая корень. Поделитесь им вместе с решением на доске обсуждений.
- Объясните, почему метод извлечения корней значительно расширяет наши возможности решения квадратных уравнений.
- Объясните своими словами, как решить путем извлечения корней. 106. Выведите формулу диагонали квадрата через его стороны.
- Ответить
1. \(−\sqrt{3}\) или \(\sqrt{3}\)
3. \(−3\sqrt{3}\) или \(3\sqrt{3}\)
5. \(2\sqrt{2}\) см
7. \(3\sqrt{2}\) см
9. Длина: 24 дюйма; ширина: 4 дюйма
11. \(−6+6\sqrt{2}\ок.
 2,49\) ед.
2,49\) ед.13. \(\sqrt{2}\) единиц
15. \(52\sqrt{2}\) дюймов
17. Длина: \(4\sqrt{5}\) футов; ширина: \(2\sqrt{5}\) футов
19. Длина: \(310−−\sqrt{2}\) метров; ширина: \(10−−\sqrt{2}\) метров
21. \(\frac{3}{4}\) секунды
23. а. 2,12 секунды б. 0,88 секунды
25. Ответы могут отличаться
Эта страница под заголовком 9.1: Извлечение квадратных корней распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Anonymous.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Аноним
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Программа OER или Publisher
- Издатель, имя которого нельзя называть
- Показать страницу TOC
- нет
- Теги
- корни
- квадратный корень
6.
 1: Извлечение квадратных корней и завершение квадрата
1: Извлечение квадратных корней и завершение квадрата- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 6268
- Анонимный
- LibreTexts
Цели обучения
- Решение некоторых квадратных уравнений путем извлечения квадратных корней. 9{ 2 } — 9 & = 0 \\ ( 2 x + 3 ) ( 2 x — 3 ) & = 0 \end{aligned}\)
\(\begin{array} { c } { 2 x + 3 = 0 \quad \text { или }\quad 2 x — 3 = 0 } \\ { 2 x = — 3 \quad \quad\:\:\:2 x = 3 } \\ { x = — \frac { 3 } { 2 } \quad\quad\:\:\:\: x = \frac { 3 } { 2 } } \end{array}\)
Два решения: \(± \frac{3}{2 }\). Здесь мы используем \(±\) для записи двух решений в более компактной форме.
 Целью этого раздела является разработка альтернативного метода, который можно использовать для простого решения уравнений, где \(b = 0\), что дает форму 9{ 2 } & = \frac { 8 } { 9 } \end{aligned}\)
Целью этого раздела является разработка альтернативного метода, который можно использовать для простого решения уравнений, где \(b = 0\), что дает форму 9{ 2 } & = \frac { 8 } { 9 } \end{aligned}\)Затем примените свойство квадратного корня. Не забудьте включить \(±\) и упростить.
\(\begin{align} x & = \pm \sqrt { \frac { 8 } { 9 } } \\ & = \pm \frac { 2 \sqrt { 2 } } { 3 } \end{align} \)
Для полноты проверьте, что эти два действительных решения решают исходное квадратное уравнение.
Проверка \(x = — \frac { 2 \sqrt { 2 } } { 3 }\) Проверка \(x = \frac { 2 \sqrt { 2 } } { 3 }\) 9{ \color{black}{2} } — 8 & = 0 \\ 9 \left( \frac { 4.2 } { 9 } \right) — 8 & = 0 \\ 8 — 8 & = 0 \\ 0 & = 0\:\:\color{Cerulean}{✓} \end{выровнено}\) Таблица \(\PageIndex{1}\) Ответ :
Два действительных решения, \(\pm \frac { 2 \sqrt { 2 } } { 3 }\)
Иногда квадратные уравнения не имеют реального решения.
 В этом случае решения будут комплексными числами.
В этом случае решения будут комплексными числами.Пример \(\PageIndex{2}\):
9{ 2 } & = — 25 \\ x & = \pm \sqrt { — 25 } \end{aligned}\)После применения свойства квадратного корня у нас остается квадратный корень из отрицательного числа. Следовательно, у этого уравнения нет реального решения; решения сложные. Мы можем записать эти решения в терминах мнимой единицы \(i = \sqrt {- 1 }\).
\(\begin{align} x & = \pm \sqrt { — 25 } \\ & = \pm \sqrt { — 1 \cdot 25 } \\ & = \pm i \cdot 5 \\ & = \ pm 5 я \end{выровнено}\) 9{ 2 } & = 9 \quad\quad\quad\color{Cerulean}{}Применить\:the\:square\:root\:property. \\ x + 5 & = \pm \sqrt { 9 } \quad\:\:\color{Cerulean}{Simplify.}\\ x + 5 & = \pm \sqrt { 9 } \\ x & = — 5 \pm 3 \end{aligned}\)
Теперь разделите «плюс-минус» на два уравнения и решите каждое по отдельности.
\(\begin{array} {l} { x = — 5 + 3 \quad\text { or } \quad x = — 5 — 3 } \\ { x = — 2 \quad\quad\quad \quad \quad x = — 8 } \end{массив}\)
Ответ 9{ 2 } & = \frac { 5 } { 2 } \end{aligned}\)
Затем извлеките корни, найдите \(x\) и затем упростите.

\(\begin{align} x — 2 & = \pm \sqrt { \frac { 5 } { 2 } }\quad\quad\quad\quad\color{Cerulean}{Рационализировать\:the\:знаменатель. } \\ x & = 2 \pm \frac { \sqrt { 5 } } { \sqrt { 2 } } \cdot \color{Cerulean}{ \frac { \sqrt { 2 } } { \sqrt { 2 } } } \\ x & = 2 \pm \frac { \sqrt { 10 } } { 2 } \\ x & = \frac { 4 \pm \sqrt { 10 } } { 2 } \end{aligned}\) 9{ 2 } &= 49 \quad\quad\quad\color{Cerulean}{Extract\:the\:roots.} \\ x + 1 &= \pm \sqrt { 49 } \\ x + 1 &= \pm 7 \\ x &= — 1 \pm 7 \end{aligned}\)
Теперь разделите «плюс-минус» на два уравнения и решите каждое по отдельности.
\(\begin{array} { l } { x = — 1 — 7 \text { or } x = — 1 + 7 } \\ { x = — 8 \quad\quad\quad x = 6 } \end {массив}\)
Ответ :
Решения: \(-8\) и \(6\).
Примечание 9{ 2 } & = — \ frac { 7 } { 4 } \\ x + \ frac { 3 } { 2 } & = \ pm \ sqrt { \ frac { — 1 \ cdot 7 } { 4 } } \\ x + \ frac { 3 } { 2 } & = \ pm \ frac { i \ sqrt { 7 } } { 2 } \\ x & = — \ frac { 3 } { 2 } \ pm \ frac { \ sqrt { 7 } } { 2 } i \end{aligned}\)
Ответ :
Решения: \(- \frac { 3 } { 2 } \pm \frac { \sqrt { 7 } } { 2 } i\) .
 {2} = q\). 9{2} — q = 0, p, q > 0\)
{2} = q\). 9{2} — q = 0, p, q > 0\) - Диагональ квадрата равна \(3\) сантиметрам. Найдите длину каждой стороны.
- Длина прямоугольника в два раза больше его ширины. Если диагональ прямоугольника равна \(10\) метров, то найдите размеры прямоугольника.
- Если площадь круга равна \(50π\) квадратных сантиметров, найдите его радиус.
- Если площадь квадрата равна \(27\) квадратных сантиметров, найдите длину каждой стороны. 9{2} + 50\), где \(t\) представляет время в секундах после падения объекта. Через какое время объект упадет на землю? (Округлить до сотых долей секунды.)
- Какой высоты достигает \(22\)-футовая лестница, если ее основание находится в \(6\) футах от здания, на которое она опирается? Округлите до ближайшей десятой доли фута.
- Высота треугольника равна \(\frac{1}{2}\) длине его основания. Если площадь треугольника равна \(72\) квадратных метров, найдите точную длину основания треугольника.

- Ответить
1. \(\pm 9\)
3. \(\pm \frac{1}{3}\)
5. \(\pm 2 \sqrt { 3 }\)
7. \(\pm \frac { 3 } { 4 }\)
9. \(\pm \frac {\sqrt { 2 } } { 2 }\)
11. \(\pm 2 \sqrt { 10 }\)
13. \(\pm i\)
15. \(\pm \frac { \sqrt { 5 } } { 5 }\)
17. \(\pm \frac { \sqrt { 2 } } { 4 } i\)
19. \(\pm 2 i\)
21. \(\pm \frac { 2 } { 3 }\)
23. \(\pm 2 \sqrt { 2 }\)
25. \(\pm 2 i \sqrt { 2 }\)
27. \(\pm \frac { \sqrt { 10 } } { 5 }\)
29. \(-9,-5\)
31. \(5 \pm 2 \sqrt { 5 }\)
33. \(- \frac { 2 } { 3 } \pm \frac { \sqrt { 6 } } { 3 } i\)
35. \(\frac { — 2 \pm 3 \sqrt { 3 } } { 6 }\)
37. \(\frac { 1 } { 3 } \pm \frac { \sqrt { 6 } } { 6 } i\)
9{2}=3(3 т+1)\)- \((3 т+2)(т-4)-(т-8)=1-10 т\)
- Ответить
1.
 \(-3 \pm \sqrt{10}\)
\(-3 \pm \sqrt{10}\)3. 1\(\pm 2 \sqrt{2}\)
5. 1\(\pm i \sqrt{3}\)
7. \(-15,5\)
9. \(-\frac{1}{3}, 1\)
11. \(\frac{-1 \pm \sqrt{5}}{2}\)
13. \(\frac{-3 \pm \sqrt{17}}{2}\)
15. \(-\frac{3}{2} \pm \frac{\sqrt{11}}{2} i\)
17. \(\frac{7 \pm 3 \sqrt{3}}{2}\)
19. \(\frac{1 \pm \sqrt{17}}{4}\)
21. \(\frac{2 \pm \sqrt{5}}{2}\)
23. \(\frac{-3 \pm \sqrt{6}}{3}\)
25. \(\frac{-1 \pm \sqrt{10}}{3}\)
27. \(\frac{3 \pm 2 \sqrt{6}}{2}\)
29. 1\(\pm 2 i\)
31. \(\frac{1 \pm \sqrt{17}}{4}\)
33. \(\frac{-1 \pm \sqrt{7}}{3}\)
35. 2\(\pm 2 \sqrt{5}\)
37. 5\(\pm \sqrt{3}\) 9{2}-6(6 х+1)=0\)
- Ответить
1. \(0,19,1,31\)
3. \(-0,45,1,12\)
5. \(0,33,0,67\)
Упражнение \(\PageIndex{11}\)
- Создайте собственное уравнение, которое можно решить путем извлечения корней.
 Поделитесь им вместе с решением на доске обсуждений.
Поделитесь им вместе с решением на доске обсуждений. - Объясните, почему метод извлечения корней значительно расширяет наши возможности решения квадратных уравнений. 9{2} = q\).
Эта страница под названием 6.1: Извлечение квадратных корней и завершение квадрата распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Anonymous с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Аноним
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Программа OER или Publisher
- Издатель, имя которого нельзя называть
- Показать страницу TOC
- нет
- Теги
- заполнение квадрата
- источник@https://2012books.
 lardbucket.org/books/advanced-алгебра/index.html
lardbucket.org/books/advanced-алгебра/index.html
Алгоритм извлечения квадратного корня
Квадратный корень легко извлекается с помощью калькулятора. Для этого достаточно набрать на нем исходный номер и нажать корневую клавишу
Если у вас нет под рукой калькулятора, извлеките квадратный корень, используя алгоритм для извлечения квадратного корня .
Применение алгоритма может быть очень полезным для тестов и экзаменов. Ведь чаще всего на таких мероприятиях запрещено пользоваться калькулятором.
Как пользоваться алгоритмом
Рассмотрим применение алгоритма извлечения квадратного корня на конкретных примерах. Позже мы поговорим о том, почему алгоритм следует применять таким образом.
Пример 1. Извлеките квадратный корень из 4096, используя алгоритм извлечения квадратного корня.
Прежде всего, сгруппируем число 4096 по двум цифрам.
 Двигаясь от конца влево, сделайте небольшой маркер:
Двигаясь от конца влево, сделайте небольшой маркер:Сгруппированные цифры исходного числа называются гранями , а сама группировка по двум цифрам называется делением граней . Количество граней предполагает, сколько цифр будет содержать извлеченный корень. В нашем примере извлеченный корень будет содержать две цифры, так как исходное число содержит две грани.
Теперь нам нужно извлечь квадратный корень из числа 40 в целые числа, таким образом, мы получим 6. Запишем 6 после знака равенства:
Затем возведем число 6 в квадрат и запишем результат под числом 40
Затем из числа 40 вычитаем число 36 и получаем 4. Записываем это число под 36
Убираем оставшиеся цифры из-под корня, а именно 96. Остаток 496
Теперь нужно найти следующая цифра корня. Это находится следующим образом. Первую найденную цифру корня, а именно 6 умножаем на 2, получаем 12. К числу 12 в конце нужно добавить еще одну цифру (эта цифра позже и будет следующей цифрой корня) и полученное умножить числа той же добавленной цифрой.
 Полученное произведение должно быть равно остатку 496 или, по крайней мере, максимально близко к нему, но не превышая его.
Полученное произведение должно быть равно остатку 496 или, по крайней мере, максимально близко к нему, но не превышая его.Итак, например, давайте проверим число 5. Прибавим его к числу 12 и умножим полученное число 125 на 5. не подходит в качестве следующей цифры корня. Затем проверим число 4. Прибавим его к числу 12 и умножим полученное число 124 на 4
Получится 496, что и есть наш остаток. Таким образом, цифра 4, добавленная к числу 12, является следующей цифрой корня. Вернитесь к исходному примеру и напишите в ответе цифру 4 после цифры 6
А число 496, являющееся результатом умножения 124 на 4, запишем под остатком 496
Вычтем 496 — 496 = 0. Ноль в остатке означает, что решение завершено:
Для удобства нахождения второй цифры слева от остатка проводится вертикальная черта и за этой чертой пишется умножение. В нашем случае умножение 124 на 4. Результат умножения сразу записывается под остатком:
Таким образом, квадратный корень из 4096 равен 64
Пример 2.
 Извлеките квадратный корень из числа 441, используя алгоритм извлечения квадратного корня.
Извлеките квадратный корень из числа 441, используя алгоритм извлечения квадратного корня.Прежде всего, сгруппируем число 441 по двум цифрам. Двигаясь от конца влево, сделайте небольшую отметку. В этом случае число 441 состоит всего из трех цифр. Поэтому сгруппируем цифры 4 и 1. Последние четыре слева будут сами по себе:
Теперь нам нужно извлечь квадратный корень из числа 4 в целые числа, таким образом, мы получим 2. Запишем 2 после равенства знак:
Затем возводим в квадрат число 2 и записываем результат под числом 4
Из числа 4 вычитаем 4, чтобы получить 0. Ноль принято не писать. Удалите остальные цифры корня, а именно 41
Теперь найдите следующую цифру корня. Первую цифру корня, 2, умножаем на 2, чтобы получить 4. К числу 4 в конце нужно добавить еще одну цифру (эта цифра впоследствии станет следующей цифрой корня) и полученное число умножить на такая же добавленная цифра. Полученное произведение должно быть равно остатку 41 или, по крайней мере, максимально близко к нему, но не превышая его.

Так, например, проверим число 2. Прибавим его к числу 4 и умножим полученное число 42 на ту же прибавленную цифру 2. Результат умножения запишем прямо под остатком 41
Полученное число равно 84, что больше остатка от 41. Таким образом, число 2 не подходит в качестве следующей цифры корня. Затем проверим число 1. Прибавим его к числу 4 и умножим полученное число 41 на ту же лишнюю цифру 1
Мы получили число 41, это и есть наш остаток. Таким образом, цифра 1, добавленная к числу 4, является следующей цифрой корня. Запишем цифру 1 после цифры 2
А число 41, являющееся результатом умножения 41 на 1, запишем под остатком 41
Вычтем 41 — 41 = 0. Ноль в остатке означает, что решение завершено:
Пример 3: Извлеките квадратный корень из числа 101761, используя алгоритм извлечения квадратного корня.
Разбиваем число 101761 на грани:
В результате получается три грани.
 Таким образом, корень будет состоять из трех цифр.
Таким образом, корень будет состоять из трех цифр.Извлекаем квадратный корень из первой грани (из числа 10) в целые числа, получаем 3. Записываем 3 после знака равенства:
Далее возводим в квадрат число 3 и записываем результат под первой гранью (под число 10)
Вычтем 9 из 10 и получим 1. Отбросим следующую грань, а именно число 17. Остаток равен 117
Теперь найдите вторую цифру корня. Первую найденную цифру корня, а именно 3 умножаем на 2, получаем 6. К числу 6 добавляем в конце еще одну цифру (эта цифра впоследствии станет второй цифрой корня) и полученное число умножаем на такое же прибавленное цифра. Полученное произведение должно быть равно остатку 117 или хотя бы максимально близко к нему, но не превышая его.
Так, например, проверим число 2. Прибавим его к числу 6 и умножим полученное число 62 на ту же добавленную цифру 2. Результат умножения будет записан непосредственно под остатком 117
Результат 124, что больше остатка от 117.
 Таким образом, число 2 не подходит в качестве второй цифры корня. Затем проверим число 1. Прибавим его к числу 6 и умножим полученное число 61 на эту же цифру 1
Таким образом, число 2 не подходит в качестве второй цифры корня. Затем проверим число 1. Прибавим его к числу 6 и умножим полученное число 61 на эту же цифру 1Получится 61, что не превосходит остатка 117. Значит цифра 1 прибавляется к числу 6 это вторая цифра корня. Запишите это в ответ после числа 3
Теперь вычтите 117 — 61 = 56.
Отбрасываем следующую грань, а именно число 61. Получаем новый остаток 5661
Теперь найдем третью цифру корня. Первые две найденные цифры корня, а именно число 31 умножаем на 2, получаем 62. К числу 62 в конце добавляем еще одну цифру (эта цифра впоследствии станет третьей цифрой корня) и полученное число умножаем на такая же добавленная цифра. Полученное произведение должно быть равно остатку 5661 или хотя бы максимально близко к нему, но не превышая его.
Так, например, проверим число 9. Прибавим его к числу 62 и умножим полученное число 629 на ту же добавленную цифру 9. Результат умножения запишем прямо под остатком 5661
Получили число 5661, которое является нашим остатком.
 Таким образом, цифра 9, добавленная к числу 62, является третьей цифрой корня. Напишите в ответе цифру 9 после цифры 1
Таким образом, цифра 9, добавленная к числу 62, является третьей цифрой корня. Напишите в ответе цифру 9 после цифры 1Вычтите 5661 — 5661 = 0. Ноль в остатке означает, что решение завершено:
Пример 4. Извлечение квадратного корня из 30,25 с использованием алгоритма извлечения квадратного корня.
Это десятичное число. В этом случае грань должна делить целую часть и дробную часть. Целую часть на грани нужно делить, перемещаясь влево от точки. И дробная часть перемещается вправо от точки:
У вас есть одна грань в каждой части. Это означает, что корень будет состоять из двух цифр: одна цифра в целой части корня и одна цифра в дробной части.
Извлекаем квадратный корень из первой грани (из числа 30) в целые числа, получаем 5. Записываем 5 после знака равенства:
Далее возводим в квадрат число 5 и записываем результат под первой гранью (под число 30)
Вычтем из числа 30 число 25, чтобы получить 5.

Извлечение корня из целой части базового выражения завершено. На данный момент мы извлекли корень из 30,25 до ближайшего целого числа и получили ответ 5. Последний остаток 5 показывает, что целая часть 30 превышает квадрат 52 на 5 квадратных единиц.
Для дальнейшего извлечения корня (с точностью до десятой) сносим следующую грань, а именно число 25, получаем остаток 525. А в ответе после числа 5 нужно поставить точку, потому что сейчас мы собираемся Найдите дробную часть корня.
Затем снимаем следующую грань, это число 25. Остаток 525
Далее работаем по тому же принципу, что и раньше. Найдите следующую цифру корня. Для этого умножаем уже найденный корень, а именно число 5 на 2, чтобы получить 10. К числу 10 в конце добавляем еще одну цифру (эта цифра впоследствии станет следующей цифрой корня) и полученное число умножаем на такая же добавленная цифра. Полученное произведение должно быть равно остатку 525 или, по крайней мере, максимально близко к нему, но не превышая его.

Так, например, проверим число 5. Прибавим его к числу 10 и умножим полученное число 105 на ту же прибавленную цифру 5
Получилось число 525, которое и есть наш остаток. Таким образом, цифра 5, добавленная к числу 10, является следующей цифрой корня. Вернитесь к исходному примеру и напишите в ответе цифру 5 после точки:
Вычтите 525 — 525 = 0. Ноль в остатке означает, что решение завершено:
В подкоренном выражении можно использовать следующую технику: умножить подкоренное число на 100 и получить под корнем число 3025. Затем извлеките из него квадратный корень, как из обычного целого числа. Тогда ответ будет 55
Тогда вы можете разделить 3025 обратно на 100 (или переместить точку влево на две цифры). В результате получится то же число 30,25 под корнем, а правая часть будет уменьшена в десять раз, чтобы получить квадратный корень из 30,25.
Пример 5. Извлеките квадратный корень из числа 632,5225, используя алгоритм извлечения квадратного корня.

Это десятичное число. Разделите число на грани. Целая часть и дробная часть должны быть разделены на грани. Целая часть на грани должна быть разделена путем перемещения влево от точки. И дробную часть, переместив вправо от точки:
Получится четыре грани. В целой части две грани, а в дробной части две грани. Это значит, что корень будет состоять из четырех цифр: две цифры будут в целой части корня, и две цифры после запятой.
Извлеките квадратный корень из первой грани (из числа 6) в целые числа, получим 2. Запишите 2 после знака равенства:
Далее возведите в квадрат число 2 и запишите результат под первой гранью (под число 6)
Из числа 6 вычтем число 4, чтобы получить 2. Затем сносим следующую грань, а именно число 32. Остаток равен 232.
Теперь найдем вторую цифру корня. Первая цифра корня 2 умножается на 2, получается 4. К числу 4 в конце нужно прибавить еще одну цифру (эта цифра впоследствии станет второй цифрой корня) и умножить полученное число той же добавленной цифрой.
 Полученное произведение должно быть равно остатку 232 или хотя бы максимально близко к нему, но не превышая его.
Полученное произведение должно быть равно остатку 232 или хотя бы максимально близко к нему, но не превышая его.Так, например, проверим число 6. Прибавим его к числу 4 и умножим полученное число 46 на ту же добавленную цифру 6. Результат умножения будет записан сразу под остатком 232
Полученное число равно 276, что больше остатка от 232. Таким образом, число 6 не подходит в качестве второй цифры корня. Проверим число 5. Прибавим его к числу 4 и умножим полученное число 45 на ту же добавленную цифру 5
Полученное число равно 225, что не превышает остатка 232. Таким образом, цифра 5, добавленная к числу 4, является второй цифрой корня. Запишите его в ответ после числа 2
Теперь вычтите 232 — 225 = 7.
Извлечение корня из целой части базового выражения завершено. На данный момент мы извлекли корень из 632,5225 до ближайшего целого числа, что дало ответ 25. Последний остаток 7 показывает, что целая часть 632 превышает квадрат 25 2 на 7 кв.

Для дальнейшего извлечения корня (с точностью до десятых и сотых) сносим следующую грань, а именно число 52, получаем остаток 752. А в ответе после числа 25 ставим точку, т.к. ищем дробные части корня:
Далее работаем по тому же принципу что и раньше. Найдите первую цифру корня после точки. Для этого умножьте уже найденные цифры, а именно 25 на 2, чтобы получить 50. К числу 50 в конце нужно добавить еще одну цифру (эта цифра впоследствии будет первой цифрой корня после точки) и умножить полученное число той же добавленной цифрой. Полученное произведение должно быть равно остатку 752 или, по крайней мере, максимально близко к нему, но не превышая его.
Так, например, проверим число 2. Прибавим его к числу 50 и умножим полученное число 502 на ту же добавленную цифру 2. Интуитивно видно, что число 2 большое, потому что 502 × 2 = 1004. И число 1004 больше остатка 752. Тогда очевидно, что первой цифрой после точки будет цифра 1
Теперь вычитаем 752 — 501 = 251.
 Сразу сносим следующую грань 25. Остаток равно 25125.
Сразу сносим следующую грань 25. Остаток равно 25125.Теперь найдите вторую цифру корня после точки. Не обращая внимания на точку, умножаем найденные цифры корня на 2. Получаем 502.
К числу 502 в конце нужно добавить еще одну цифру (эта цифра впоследствии станет второй цифрой корня после точки) и умножить полученное число на эту же добавленную цифру. Полученное произведение должно быть равно остатку 25125 или хотя бы максимально близко к нему, но не превышая его.
Так, например, проверим число 6. Прибавим его к числу 502 и умножим полученное число 5026 на ту же добавленную цифру 6. Результат умножения будет записан сразу под остатком 25125
Получившееся число равно 30156, что больше остатка от 25125. Так что число 6 не годится в качестве второй цифры корня после точки. Затем проверим число 5. Прибавим его к числу 502 и умножим полученное число 5025 на ту же добавленную цифру 5
Получили число 25125, которое и есть наш остаток.
 Таким образом, цифра 5, добавленная к числу 502, является второй цифрой корня после точки. Напишите в ответе цифру 5 после цифры 1
Таким образом, цифра 5, добавленная к числу 502, является второй цифрой корня после точки. Напишите в ответе цифру 5 после цифры 1Теперь вычтите 25125 — 25125 = 0. Ноль в остатке означает, что решение завершено:
В этом примере мы могли бы использовать метод умножения подкорневого выражения на 10000. Тогда подпрограмма число с корнем будет 6325225. Его можно разделить на грани, двигаясь справа налево. Результатом будет корень из 2515.
Подкорневое число 6325225 затем делится на 10000, чтобы вернуться к исходному числу 632,5225. В результате этого деления ответ уменьшится в 100 раз и станет 25,15.
Пример 6. Используя алгоритм извлечения квадратного корня, извлеките квадратный корень из 11 с точностью до тысячных:
Это число имеет только одну грань 11. Извлеките из него корень из целых чисел, получим 3
Теперь возведите число 3 в квадрат и запишите результат под первой гранью (под номером 11)
Вычтите 11 — 9 = 2
Извлечение корня из целой части базового выражения завершено.
 На данный момент мы извлекли корень числа 11 до ближайшего целого числа, получив ответ 3. Последний остаток 2 показывает, что целая часть 11 превышает квадрат 3 2 на две квадратные единицы.
На данный момент мы извлекли корень числа 11 до ближайшего целого числа, получив ответ 3. Последний остаток 2 показывает, что целая часть 11 превышает квадрат 3 2 на две квадратные единицы.Нашей задачей было извлечь корень числа 11 с точностью до тысячных. Итак, нам нужно снять следующую грань, но в данном случае ее нет.
Если вы поставите точку после целого числа и напишете столько нулей, сколько хотите, значение этого числа не изменится. Таким образом, после 11 можно поставить точку и написать несколько нулей (несколько граней), которые потом можно снести до остатка.
Если корень извлечен до тысячных, то в ответе должно быть три цифры после точки. Поэтому в подкоренном выражении ставим точку и пишем три грани, состоящие из нулей:
Теперь вы можете снять следующую грань, а именно два нуля. Получаем остаток 200. И в ответе после цифры 3 ставим точку, потому что сейчас будем искать дробные части корня:
Теперь найдем первую цифру после точки в ответе.
 Первую цифру корня, а именно 3, умножаем на 2, чтобы получить 6. К числу 6 нужно прибавить еще одну цифру (эта цифра впоследствии станет первой цифрой после точки) и полученное число умножить на такое же прибавленное цифра. Полученное произведение должно быть равно остатку 200 или хотя бы максимально близко к нему, но не превышая его.
Первую цифру корня, а именно 3, умножаем на 2, чтобы получить 6. К числу 6 нужно прибавить еще одну цифру (эта цифра впоследствии станет первой цифрой после точки) и полученное число умножить на такое же прибавленное цифра. Полученное произведение должно быть равно остатку 200 или хотя бы максимально близко к нему, но не превышая его.В этом случае подойдет цифра 3.
Вычесть 200 — 189, а затем снять следующую грань 00
Найдите вторую цифру корня после точки. Не обращая внимания на точку, умножаем найденные цифры корня на 2. Получаем 66.
К числу 66 в конце нужно добавить еще одну цифру (эта цифра впоследствии станет второй цифрой корня после точки) и умножьте полученное число на ту же добавленную цифру. Полученное произведение должно быть равно остатку 1100 или хотя бы максимально близко к нему, но не превышая его.
В этом случае подойдет цифра 1.
Вычтем 1100-661 и снесем следующую грань 00
Найдите третью цифру корня после точки.
 Не обращая внимания на точку, умножаем найденные цифры корня на 2. Получаем 662.
Не обращая внимания на точку, умножаем найденные цифры корня на 2. Получаем 662.К числу 662 добавляем еще одну цифру (эта цифра в дальнейшем становится третьей цифрой корня после точки) и полученное число умножаем на такое же добавленная цифра. Полученное произведение должно быть равно остатку 43900 или, по крайней мере, максимально близко к нему, но не превышая его.
Проверим цифру 7
Получившееся число равно 46389, что больше остатка от 43900. Значит, число 7 не годится в качестве третьей цифры корня после точки. Затем проверим число 6. Прибавим его к числу 662 и умножим полученное число 6626 на ту же добавленную цифру 6
Получившееся число 39756, которое не превосходит остаток от 43900. Таким образом, цифра 6, добавленная к числу 662, является третьей цифрой корня после точки. Напишите в ответе число 6 после числа 1
Вычтите 43900 — 39756 = 4144
Дальнейшие вычисления не требуются, так как корень нужно было извлечь с точностью до тысячных.

Но в примерах, подобных этому, вы можете найти десятичную точку бесконечно. Например, вы можете продолжить этот пример, найдя значение корня с точностью до десятитысячных:
Принцип работы алгоритма
Алгоритм извлечения квадратного корня основан на формуле возведения в квадрат суммы двух выражений:
( a + b ) 2 06 907 = + 2 ab + b 2
Геометрически эту формулу можно представить так:
Это делает исходный квадрат больше. Чтобы вычислить площадь такого квадрата, нужно отдельно вычислить площади квадратов и прямоугольников, составляющих этот квадрат, и сложить полученные результаты. Вы должны иметь хорошее представление об этой фигуре. Без понимания этого невозможно понять, как работает алгоритм извлечения квадратного корня.
Обратите внимание, что формула возведения в квадрат суммы двух выражений позволяет возводить в квадрат любое число.
 Используя цифры, исходное число представляется в виде суммы чисел, а затем эта сумма возводится в квадрат.
Используя цифры, исходное число представляется в виде суммы чисел, а затем эта сумма возводится в квадрат.Например, вот как можно возвести в квадрат число 21: представить это число как сумму двух десятков и одной единицы, а затем возвести эту сумму в квадрат:
21 2 = (20 + 1) 2 = 20 2 + 2×20×1 + 1 2 = 400 + 40 + 1 = 441
Геометрически это будет выглядеть так: сторона квадрата, равная 21, делится на две составляющие: 20 и 1.
Затем отдельно рассчитайте площади квадратов и прямоугольников, входящих в большой квадрат. А именно: один квадрат со стороной 20 (с площадью 400), два прямоугольника со сторонами 20 и 1 (с площадью 20), один квадрат со стороной 1 (с площадью 1). Результаты вычисления площадей складываются, и окончательное значение равно 441.
Обратите внимание, что возведение десятков в квадрат приводит к сотням. В этом случае возведение 20 в квадрат дает 400. Это говорит о том, что если корень представляет собой двузначное число, то десятки этого корня должны быть найдены в сотнях подкоренного числа.
 Действительно,
Действительно,. Корень десятков это число 2, это корень числа 4, который отвечает за сотни числа 441.
И возведение сотен в квадрат дает десятки тысяч. Например, возведем в квадрат число 123, используя формулу возведения в квадрат суммы двух выражений. Число 123 — это сто, два десятка и три единицы:
123 2 = (100 + 20 + 3) 2
При изучении многочленов мы выяснили, что если многочлен содержит более двух членов и становится необходимым применить формулу суммы-квадрата, тогда некоторые члены могут быть заключены в скобки, чтобы получилось выражение вида ( a + b ) 2
Давайте рассмотрим подробное извлечение квадратного корня из 4096. В то же время давайте пройдемся по основным шагам алгоритма извлечения квадратного корня, рассмотренного в предыдущем разделе.
Предположим, что число 4096 есть площадь следующего квадрата:
Извлечь корень из 4096 означает найти длину стороны данного квадрата:
Сначала узнаем, сколько цифр в корень будет состоять из.
 Ближайшие известные квадраты к 4096 — это 3600 и 4900. Между ними находится квадрат 4096. Запишем это в виде неравенства:
Ближайшие известные квадраты к 4096 — это 3600 и 4900. Между ними находится квадрат 4096. Запишем это в виде неравенства:Запишем каждое число под знаком корня:
Мы знаем квадратные корни из 3600 и 4900. Это корни из 60 и 70 соответственно:
Корни 60 и 70 — двузначные числа. Если квадратный корень из 4096 находится между 60 и 70, этот корень также является двузначным числом.
Двузначное число состоит из десятков и единиц. Это означает, что квадратный корень из 4096 можно представить в виде суммы a + b, где a — это десятки корня, b — единицы корня. Сумма a + b во второй степени будет 4096
( a + b ) 2 = 4096
Тогда сторона квадрата будет разделена на две составляющие: a и b
Пусть перепишем левую часть равенства (a + b) 2 = 4096 как a 2 + 2 ab + b 2
A 2 +2 AB + B 2 = 4096
.
 Затем рисунок иллюстрирует площадь из 4096. значения переменных a и b, мы знаем длину стороны квадрата. Проще говоря, мы знаем сам корень.
Затем рисунок иллюстрирует площадь из 4096. значения переменных a и b, мы знаем длину стороны квадрата. Проще говоря, мы знаем сам корень.Вернемся к извлечению рута. Мы выяснили, что корень — это двузначное число. Двузначное число состоит из десятков и единиц. Если возвести десятки в квадрат, то получатся сотни. Десятки корня можно найти в сотнях подкоренного числа. В подкорневом числе 40 сотен. Разделите их небольшим обозначением:
Извлечь корень из числа 40. Корень из числа 40 извлечь нельзя. Поэтому извлечение следует округлить до целых чисел.
Ближайший меньший квадрат к числу 40 равен 36. Извлеките корень из этого квадрата и вы получите 6. Таким образом, мы получим первую цифру корня:
На самом деле из числа 40 корень не извлекается, а от сорока сотен. Метка, стоящая после 40, разделяет цифры числа под корневым знаком. Следует понимать, что в данном случае 40 — это 4000.
Корень не может быть извлечен из 4000, а также из 40, поэтому он также должен быть извлечен методом приближения.
 Для этого найдите ближайший к числу 4000 метод наименьших квадратов. Но следует учитывать следующее. Десятки — это числа с одним нулем на конце. Примеры:
Для этого найдите ближайший к числу 4000 метод наименьших квадратов. Но следует учитывать следующее. Десятки — это числа с одним нулем на конце. Примеры:10 — один десяток
30 — три десятка
120 — двенадцать десятков
Возведение этих чисел в квадрат дает числа с двумя нулями в конце:0907 = 900
120 2 = 14400
Ищем десятки корня в сотнях 4096, то есть в числе 4000. Но нет числа с нулем на конце, вторая степень которого равна 4000. Значит ищем ближайший меньший квадрат, но опять же с двумя нулями в конце. Это квадрат 3600. Из этого квадрата нужно извлечь корень.
Вернемся к нашему рисунку. Большой квадрат со стороной а и площадью 2 это тот же квадрат 3600. Вместо 2 давайте укажем значение 3600
Теперь извлечем квадратный корень из квадрата 3600. Ранее мы говорили, что если число содержит квадрат и четное количество нулей, мы можем извлечь корень из этого числа. Для этого сначала извлечем корень из уже известного нам квадрата, а затем запишем половину количества нулей исходного числа:
Итак, мы нашли сторону квадрата площадью 3600.
 Пусть подпишем сторону a как 60
Пусть подпишем сторону a как 60Но раньше в ответе мы писали 6, а не 60. Это сокращенный вариант. Число 6 в данном случае означает шесть десятков:
Итак, десятки корня найдены. Их шесть. Теперь нам нужно найти единицы корня. Единицами корня являются длина оставшейся малой стороны квадрата, то есть значение переменной b.
Чтобы найти b, вычтите квадрат с площадью 4096 из суммы квадратов с площадью 3600. В результате получится фигура, площадь которой равна 4096 — 3600 = 496
На рисунке показано, как квадрат площадью 4096 отделяется от квадрата площадью 3600. Остается фигура площадью 496.
Вот почему в В процессе применения алгоритма первая цифра найденного корня возводится в квадрат, чтобы вычесть результат возведения в квадрат из сотен подкоренного выражения.
Таким образом, из 40 сотен вычитается 36 сотен, остается четыре сотни плюс девяносто шесть единиц. Эти четыреста девяносто шесть единиц вместе составляют 49.
 6 единиц:
6 единиц:Оставшаяся цифра есть не что иное, как удвоенное произведение первого выражения a плюс квадрат второго выражения b
Сумма площадей 2ab + b 2 должна соответствовать числу 496 Запишем это в виде следующего равенства:
2 ab + b 2 = 496
Значение a уже известно. Оно равно 60. Тогда уравнение примет вид:
2 × 60 × B + B 2 = 496
120 B + B 2 = 496
Теперь наша задача-это значение B , таким образом, стойкое равновесие, что левое в руках, так, что левое в руках. или хотя бы близко к этому числу. Поскольку b — это единицы искомого корня, значение b — однозначное число. То есть значение b — это число от 1 до 9. Это число можно найти подгонкой. В этом случае очевидно, что число b равно 4.
120 × 4 + 4 2 = 496
480 + 16 = 496
496 = 496
Но для удобства нахождения этого числа переменная b.
 Вернемся к выражению 120b + b 2 = 496 и вынесем b за скобки:
Вернемся к выражению 120b + b 2 = 496 и вынесем b за скобки:b (120 + b ) = 496
. Теперь правую часть можно понять так: до 120 следует добавьте некоторое число b, которое при умножении на то же b даст 496.
Именно поэтому при использовании алгоритма уже найденное число умножается на 2. Итак, мы умножили 6 на 2 и получили 12, а затем добавили цифру к 12 и умножили полученное число на такое же добавленное цифра, пытаясь получить остаток 496.
Но опять же, это упрощенный вариант. На самом деле не просто 6 умножается на 2, а найденные десятки (в нашем случае число 60), в результате чего получается число 120. Далее следует нахождение числа вида b(120 + b). То есть число b добавляется к 120, что при умножении на b дает остаток 49.6.
Итак, b = 4. Тогда:
4(120 + 4) = 496
4 × 124 = 496
496 = 496
Подстановка числа 4 вместо b дает остаток 496. означает, что единицы корня найдены.
 Квадрат площадью 4096 имеет сторону, равную 60 + 4, т.е. 64.
Квадрат площадью 4096 имеет сторону, равную 60 + 4, т.е. 64.Если из общей площади вычесть 3600, то 496, получится 0. Остаток, равный нулю, показывает, что решение готово:
4096 − 3600 − 496 = 0
Пример 2. Извлечь квадратный корень из 54756
Пусть число 54756 будет площадью следующего квадрата:
Извлечь корень из числа значит найти 54756 длина стороны данного квадрата:
Пока неизвестно, является ли квадратный корень из 54756 целым или дробным числом. Для начала выясним, из скольких цифр состоит весь корень.
Число 54756 больше 10000, но меньше числа
0
10000 < 54756 <
Корни 10000 и
— трехзначные числа.
Тогда корень 54756 также будет трехзначным числом. Трехзначное число состоит из сотен, десятков и единиц.
Квадратный корень из 54756 можно представить в виде суммы a + b + c, где a — это сотни корня, b — десятки корня, а c — единицы корня.
 Сумма a + b + c во второй степени будет 54756
Сумма a + b + c во второй степени будет 54756( a + b + c ) 2 = 54756
Тогда сторона квадрата будет разделена на три составляющие: a, b и c
Возведение в квадрат левой части равенства (a + б + в) 2 = 54756:
Тогда фигуру, изображающую квадрат с площадью 54756, можно представить следующим образом: два прямоугольника площадью (a + b)c заменены на 2ac + 2bc , потому что (a + b)c = ac + bc . Если мы дважды повторим выражение ac + bc , то получим 2ac + 2bc
2( ac + bc ) = 2 ac + 2 bc
2 90 Если мы знаем значения переменных a , b и c, мы знаем длину стороны квадрата. Проще говоря, мы знаем сам корень.
Вернемся к извлечению рута. Мы выяснили, что корень – это трехзначное число. Трехзначное число состоит из сотен, десятков и единиц.
Возведение сотен в квадрат дает десятки тысяч. Сотни можно найти в десятках тысяч подкорневого числа.
 Подкорневое число имеет пять десятков тысяч. Разделите их маркером:
Подкорневое число имеет пять десятков тысяч. Разделите их маркером:Извлеките корень из числа 5. Из числа 5 корень извлечь нельзя. Поэтому извлечение следует округлить до целых чисел. Ближайший наименьший квадрат к 5 равен 4. Извлекаем корень из этого квадрата и получаем 2. Это дает нам первую цифру корня:
На самом деле корень извлекается не из числа 5, а из пяти десятков тысяч. Метка, которая следует за цифрой 5, разделяет цифры числа под корневым знаком. Следует понимать, что в данном случае 5 — это 50 000.
Из 50 000 рут не извлечь так же как и из 5, так что тоже примерно надо извлекать. Для этого найдите ближайший к числу 50 000 метод наименьших квадратов. Но учтите, что сотни — это числа с двумя нулями на конце. Примеры:
100 — сто
500 — пятьсот
900 — девятьсот
Возведение таких чисел в квадрат дает четыре нуля на конце:
100 2 3 = 100300 900 = 250000
900 2 = 810000
Ищем сотни корней в десятках тысяч числа 54756, то есть в числе 50000.
 Но нет такого числа с двумя нулями на конце, у которого второй степень равна 50000. Значит, ищем ближайший меньший квадрат, но опять же с четырьмя нулями в конце. Это квадрат 40000.
Но нет такого числа с двумя нулями на конце, у которого второй степень равна 50000. Значит, ищем ближайший меньший квадрат, но опять же с четырьмя нулями в конце. Это квадрат 40000.Вернемся к нашему рисунку. Большой квадрат со стороной а и площадью 2 это тот же квадрат 40000. Укажем значение 40000 вместо 2
Теперь извлекаем квадратный корень из 40000
Итак, мы нашли сторону квадрата площадью 40000. Обозначим сторону a как 200
Но раньше в ответе мы писали 2, а не 200. Это сокращенный вариант. Число 2 в данном случае означает двести: 9.0032
Теперь вытаскиваем остаток. Из пяти десятков тысяч только четыре десятка тысяч имеют рут. Так что в остатке остается один десяток тысяч. Вычитаем:
Опять же, надо понимать, что 4 равно 40000, а 1 равно 10000. Используя цифру, это можно объяснить так: квадрат, площадь которого равна 40000, вычитается из общего квадрата, площадь которого равна 54756.
 , Это оставляет фигуру, площадь которой 54756 — 40000 = 14756.
, Это оставляет фигуру, площадь которой 54756 — 40000 = 14756.Теперь нам нужно найти десятки в корне. Рассмотрим на рисунке сумму площадей ab + ab + b 2 (или 2ab + b 2 ). В эту сумму войдут одна десятка тысяч, оставшаяся от нахождения сотен корня, удвоенное произведение сотен и десятков корня 2ab и десятки корня, возведенные в квадрат на b 2 .
Десятки в квадрате дают сотни. Поэтому десятки корня надо искать в сотнях подкоренного числа. Сейчас под корнем 47 сотен. Отведите их к остатку 1, предварительно отделив под корень маркером:
Одна десятая тысячи — это сто сотен плюс 47 сотен сбитых. Всего 100 + 47 = 147 сотен. Эти 147 сотен должны включать сумму 2ab + b 2
2 ab + b 2 = 14700
Переменная a уже известна; оно равно 200. Подставим это значение в это уравнение:
2 × 200 × b + b 2 = 14700
400 b + b 2 = 14700Теперь наша задача — найти такое значение b, что левая часть равна 14700 или хотя бы близка к этому числу, но не превосходит его.
 Поскольку b — это корень десятков, значение b — двузначное число с одним нулем в конце. Такое число можно найти путем сопоставления. Для удобства поместим в скобки слева
Поскольку b — это корень десятков, значение b — двузначное число с одним нулем в конце. Такое число можно найти путем сопоставления. Для удобства поместим в скобки слеваb (400 + b ) = 14700
. Теперь левую часть можно понять так: к 400 нужно прибавить какое-то число 9.0047 b , что при умножении на те же b даст 14700 или число близкое к 14700 и не превышающее его. Подставим, например, 40
40(400 + 40) = 14700
17600 ≠ 14700
. Получается 17600, что превышает число десятков. Значит, число 40 в качестве корня не годится. Проверим тогда число 30
30(400 + 30) = 14700
12900 ≤ 14700
. Получится число 12900, которое не превосходит 14700. Значит, число 30 подходит как корень десятков. Числа от 30 до 40 проверять не нужно, так как нас сейчас интересуют только двузначные числа с одним нулем на конце:
Вернемся к нашему рисунку. Сторона b — это десятки корня.
 Укажем вместо b найденные десятки 30. А квадрат, площадь которого b 2 есть найденные десятки во второй степени, то есть число 900. Укажем также площади прямоугольников аб . Они равны произведению сотен корня на десятки корня, т.е. 200×30 = 6000
Укажем вместо b найденные десятки 30. А квадрат, площадь которого b 2 есть найденные десятки во второй степени, то есть число 900. Укажем также площади прямоугольников аб . Они равны произведению сотен корня на десятки корня, т.е. 200×30 = 6000Ранее в ответе мы писали 3 вместо 30. Это сокращенный вариант. Число 3 в данном случае означает три десятка.
Теперь вытаскиваем остаток. На 147 соток подходят только 129 соток. Таким образом, остаток равен 147 — 129 = 18 сотен плюс мы убираем число 56 из подкоренного выражения. В результате получается новый остаток 1856
Это можно объяснить с помощью фигуры следующим образом: Из фигуры, площадь которой равна 14756, вычесть площадь 12900. Получится фигура, площадь которой равна 14756 — 12900 = 1856.
Теперь нам нужно найти единицы корня. Рассмотрим на рисунке сумму площадей 2(a + b)c + c 2 . В эту сумму должен входить последний остаток 1856
2( a + b ) c + c 2 = 1856
Переменные a и уже известны; они равны 200 и 30 соответственно.
 Замените эти значения в это уравнение:
Замените эти значения в это уравнение:2 (200+30) C+C 2 = 1856
2 × 230 C+C 2 = 1856
46047 C+C+C 8
46047 C+C+C+C 8
46047 C+C+C . = 1856
Теперь наша задача найти такое значение c , чтобы левая часть стала равной 1856 или хотя бы близкой к этому числу, но не превышающей его. Поскольку c — это единицы требуемого корня, значение c — однозначное число. То есть значение c представляет собой число от 1 до 9. Это число можно найти с помощью метода подгонки. Для удобства поместим в скобки слева
с (460 + c ) = 1856
Теперь левую часть можно понимать так: некоторое число c нужно прибавить к 460, что при умножении на те же c даст 1856 или число близкое к 1856 и не превышающее его. Например, подставим число 4
4(460 + 4) = 1856
4 × 464 = 1856
1856 = 1856
Поэтому при использовании алгоритма первые найденные цифры умножаются на 2.
 Итак, , мы умножили 23 на 2, получили 46, а затем добавили цифру к 46 и умножили полученное число на ту же добавленную цифру, пытаясь получить остаток 1856
Итак, , мы умножили 23 на 2, получили 46, а затем добавили цифру к 46 и умножили полученное число на ту же добавленную цифру, пытаясь получить остаток 1856Итак, c = 4. Подстановка числа 4 вместо c дает остаток 1856. Это означает, что единицы корня найдены.
Квадрат площадью 54756 имеет сторону, равную 200 + 30 + 4, т.е. 234.
вы получаете 0. Остаток, равный нулю, означает, что решение завершено:
54756 — 40000 — 6000 — 6000 — 900 — 920 — 920 — 16 = 0
Пример 3: Извлечение квадратного корня из 3
Извлечение квадратного корня из числа 3 невозможно. Ранее мы говорили, что квадратные корни из таких чисел можно извлечь лишь приблизительно с определенной точностью.
Пусть 3 будет площадью следующего квадрата:
Чтобы извлечь корень из 3, нужно найти длину стороны данного квадрата:
Корень из 3 больше, чем корень из 1 , но меньше корня из 4
√1 < √3 < √4
Корни 1 и 4 являются целыми числами.

√1 < √3 < √4
1 < √3 < 2
Между числами 1 и 2 нет целых чисел. Значит, корень числа 3 — десятичная дробь. Найдите этот корень с точностью до десятых.
Квадратный корень из числа 3 можно представить как a + b , где a — целая часть корня, а b — дробная часть. Тогда сторону квадрата можно разделить на две составляющие: a и b
The sum of a + b in the second power must approximate 3.
( a + b ) 2 ≈ 3
Squared the left side of this equality:
a 2 + 2 ab + b 2 ≈ 3
Тогда фигуру, изображающую квадрат площади 3, можно представить следующим образом:
Найти a. Извлекая корень из числа 3 в целые числа, мы получаем 1
Если 2 равно 1, а площадь всего квадрата равна 3, тогда в остатке должно быть 2. В этом остатке должна быть площадь оставшейся фигуры:
Найдем b.
 Для этого рассмотрим сумму площадей 2ab + b 2 . Эта сумма должна примерно равняться остатку 2, но не превышать его +б 2 ≈ 2
Для этого рассмотрим сумму площадей 2ab + b 2 . Эта сумма должна примерно равняться остатку 2, но не превышать его +б 2 ≈ 2Возьмем b за скобки
b (2 + b ) ≈ 2
Теперь прибавим некоторое число b к 2 при умножении 90 на 2 слева. b будет приблизительно равно 2.
Значение b является дробным числом, а именно десятой частью. Оно равно любому числу из интервала [0,1; 0,9]. Возьмите любое число из этого интервала и подставьте его в уравнение. Например, подставим 0,8
0,8(2 + 0,8) ≈ 2
2,24 ≈ 2
Результат равен 2,24, что превышает 2. Таким образом, 0,8 не подходит в качестве значения b . Тогда проверим 0.7.
0,7(2 + 0,7) ≈ 2
1,89 ≈ 2
Результат равен 1,89, что примерно равно 2 и не превосходит его. Таким образом, 0,7 — это значение b
Таким образом, квадратный корень из 3 равен примерно 1 + 0,7 с точностью до десятых.

К сожалению, понять механизм алгоритма извлечения квадратного корня намного сложнее, чем использовать сам алгоритм. Решите несколько примеров, как пользоваться алгоритмом, и понять механизм его работы вам будет намного легче.
Задания для самостоятельного решения
Задача 1. Извлечь квадратный корень из числа 169 с помощью алгоритма извлечения квадратного корня
Решение:
Показать решение
Задание 2. Извлечь квадратный корень из числа 289 с помощью алгоритма извлечения квадратного корня алгоритм
Решение:
Показать решение
Задача 3. Извлечь квадратный корень из числа 1089 с помощью алгоритма извлечения квадратного корня
Решение:
Показать решение
Задача 4. Извлечь квадратный корень из числа 1764 с помощью алгоритма извлечения квадратного корня
Решение:
Показать решение
Задача 5. Извлечь квадратный корень из числа 4761 с помощью алгоритма извлечения квадратного корня
Решение:
Показать решение
Задача 6.


 Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70». Результат вычисления запишите под вычитаемым (квадратом числа n).
Результат вычисления запишите под вычитаемым (квадратом числа n).
 Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173. A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
 Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать. Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений. Если площадь равна 96 квадратных дюймов, то найдите размеры прямоугольника.
Если площадь равна 96 квадратных дюймов, то найдите размеры прямоугольника. {2}+9{2}+1600\), где t в секундах.
{2}+9{2}+1600\), где t в секундах. 2,49\) ед.
2,49\) ед. Целью этого раздела является разработка альтернативного метода, который можно использовать для простого решения уравнений, где \(b = 0\), что дает форму 9{ 2 } & = \frac { 8 } { 9 } \end{aligned}\)
Целью этого раздела является разработка альтернативного метода, который можно использовать для простого решения уравнений, где \(b = 0\), что дает форму 9{ 2 } & = \frac { 8 } { 9 } \end{aligned}\) В этом случае решения будут комплексными числами.
В этом случае решения будут комплексными числами.
 {2} = q\). 9{2} — q = 0, p, q > 0\)
{2} = q\). 9{2} — q = 0, p, q > 0\)
 \(-3 \pm \sqrt{10}\)
\(-3 \pm \sqrt{10}\) Поделитесь им вместе с решением на доске обсуждений.
Поделитесь им вместе с решением на доске обсуждений. lardbucket.org/books/advanced-алгебра/index.html
lardbucket.org/books/advanced-алгебра/index.html Двигаясь от конца влево, сделайте небольшой маркер:
Двигаясь от конца влево, сделайте небольшой маркер: Полученное произведение должно быть равно остатку 496 или, по крайней мере, максимально близко к нему, но не превышая его.
Полученное произведение должно быть равно остатку 496 или, по крайней мере, максимально близко к нему, но не превышая его. Извлеките квадратный корень из числа 441, используя алгоритм извлечения квадратного корня.
Извлеките квадратный корень из числа 441, используя алгоритм извлечения квадратного корня.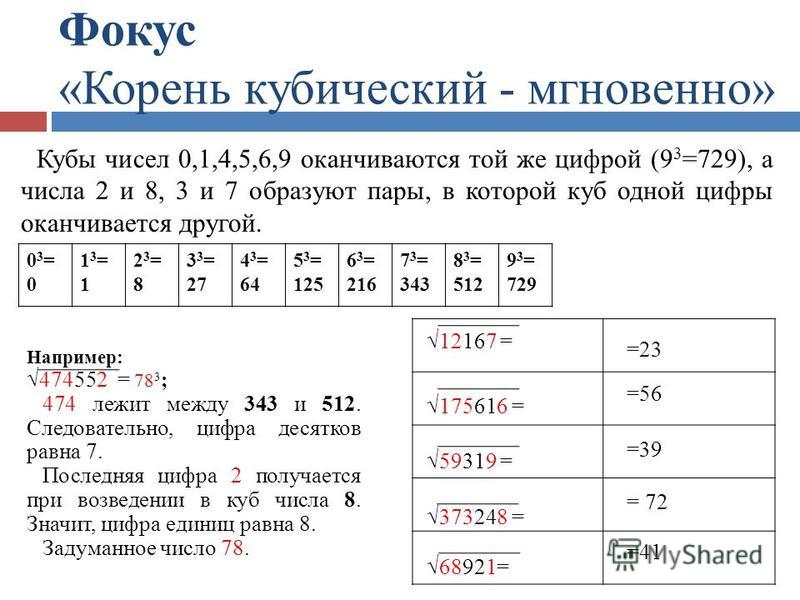
 Таким образом, корень будет состоять из трех цифр.
Таким образом, корень будет состоять из трех цифр. Таким образом, число 2 не подходит в качестве второй цифры корня. Затем проверим число 1. Прибавим его к числу 6 и умножим полученное число 61 на эту же цифру 1
Таким образом, число 2 не подходит в качестве второй цифры корня. Затем проверим число 1. Прибавим его к числу 6 и умножим полученное число 61 на эту же цифру 1 Таким образом, цифра 9, добавленная к числу 62, является третьей цифрой корня. Напишите в ответе цифру 9 после цифры 1
Таким образом, цифра 9, добавленная к числу 62, является третьей цифрой корня. Напишите в ответе цифру 9 после цифры 1


 Полученное произведение должно быть равно остатку 232 или хотя бы максимально близко к нему, но не превышая его.
Полученное произведение должно быть равно остатку 232 или хотя бы максимально близко к нему, но не превышая его.
 Сразу сносим следующую грань 25. Остаток равно 25125.
Сразу сносим следующую грань 25. Остаток равно 25125. Таким образом, цифра 5, добавленная к числу 502, является второй цифрой корня после точки. Напишите в ответе цифру 5 после цифры 1
Таким образом, цифра 5, добавленная к числу 502, является второй цифрой корня после точки. Напишите в ответе цифру 5 после цифры 1 На данный момент мы извлекли корень числа 11 до ближайшего целого числа, получив ответ 3. Последний остаток 2 показывает, что целая часть 11 превышает квадрат 3 2 на две квадратные единицы.
На данный момент мы извлекли корень числа 11 до ближайшего целого числа, получив ответ 3. Последний остаток 2 показывает, что целая часть 11 превышает квадрат 3 2 на две квадратные единицы. Первую цифру корня, а именно 3, умножаем на 2, чтобы получить 6. К числу 6 нужно прибавить еще одну цифру (эта цифра впоследствии станет первой цифрой после точки) и полученное число умножить на такое же прибавленное цифра. Полученное произведение должно быть равно остатку 200 или хотя бы максимально близко к нему, но не превышая его.
Первую цифру корня, а именно 3, умножаем на 2, чтобы получить 6. К числу 6 нужно прибавить еще одну цифру (эта цифра впоследствии станет первой цифрой после точки) и полученное число умножить на такое же прибавленное цифра. Полученное произведение должно быть равно остатку 200 или хотя бы максимально близко к нему, но не превышая его. Не обращая внимания на точку, умножаем найденные цифры корня на 2. Получаем 662.
Не обращая внимания на точку, умножаем найденные цифры корня на 2. Получаем 662.
 Используя цифры, исходное число представляется в виде суммы чисел, а затем эта сумма возводится в квадрат.
Используя цифры, исходное число представляется в виде суммы чисел, а затем эта сумма возводится в квадрат. Действительно,
Действительно, Ближайшие известные квадраты к 4096 — это 3600 и 4900. Между ними находится квадрат 4096. Запишем это в виде неравенства:
Ближайшие известные квадраты к 4096 — это 3600 и 4900. Между ними находится квадрат 4096. Запишем это в виде неравенства: Затем рисунок иллюстрирует площадь из 4096. значения переменных a и b, мы знаем длину стороны квадрата. Проще говоря, мы знаем сам корень.
Затем рисунок иллюстрирует площадь из 4096. значения переменных a и b, мы знаем длину стороны квадрата. Проще говоря, мы знаем сам корень. Для этого найдите ближайший к числу 4000 метод наименьших квадратов. Но следует учитывать следующее. Десятки — это числа с одним нулем на конце. Примеры:
Для этого найдите ближайший к числу 4000 метод наименьших квадратов. Но следует учитывать следующее. Десятки — это числа с одним нулем на конце. Примеры: Пусть подпишем сторону a как 60
Пусть подпишем сторону a как 60 6 единиц:
6 единиц: Вернемся к выражению 120b + b 2 = 496 и вынесем b за скобки:
Вернемся к выражению 120b + b 2 = 496 и вынесем b за скобки: Квадрат площадью 4096 имеет сторону, равную 60 + 4, т.е. 64.
Квадрат площадью 4096 имеет сторону, равную 60 + 4, т.е. 64.