К боковой поверхности цилиндра вращающегося вокруг своей оси прижимают: К боковой поверхности цилиндра, вращающегося вокруг своей оси, прижимают второй цилиндр с осью, параллельной оси первого, и радиусом,

alexxlab / / Разное

Содержание

Тестирование

Тестирование
  1. Человек обошел круглое озеро диаметром 1 км. О пути, пройденном человеком, и модуле его перемещения можно утверждать, что
    путь равен 3,14 км, модуль перемещения равен 1 км
    путь равен 3,14 км, модуль перемещения равен нулю
    путь равен нулю, модуль перемещения равен нулю
    путь равен нулю, модуль перемещения равен 3,14 км
     
  2. Четыре тела двигались по оси Ох. В таблице представлена зависимость их координат от времени.

    t, c

    1

    2

    3

    4

    5

    x1, м

    2

    4

    6

    8

    10

    x2, м

    x3, м

    1

    4

    9

    16

    25

    x4, м

    2

    -2

    2

    У какого из тел скорость могла быть постоянна и отлична от нуля?
    1
    2
    3
    4

  3. Тело движется по оси х.
    По графику зависимости проекции скорости тела vx от времени t установите, какой путь прошло тело за время от t1 = 0 до t2 = 6 с.
    10 м
    15 м
    25 м
    45 м

  4. Автомобиль движется по шоссе с постоянной скоростью и начинает тормозить. Проекция ускорения на ось, направленную по вектору начальной скорости автомобиля:
    отрицательна
    положительна
    равна нулю
    может быть любой по знак

  5. Мальчик съезжает с горки на санках, двигаясь прямолинейно и равноускоренно. За время спуска скорость мальчика увеличилась на 10 м/с, его ускорение равно 0,5 м/с
    2. Сколько времени длится спуск?
    0,05 c
    2 c
    5 c
    20 c

  6. На соревнованиях по бегу спортсмен в течение первых двух секунд после старта двигался равноускоренно и разогнался из состояния покоя до скорости 10 м/с, после чего в течение еще 9 секунд бежал с этой постоянной скоростью. Какой путь прошел спортсмен за 11 секунд?
    110 м
    100 м
    90 м
    130 м

  7. Камень свободно падает с некоторой высоты Н с начальной скоростью, равной нулю. Сопротивление воздуха пренебрежимо мало. Скорость, которую приобретает камень, пропорциональна
    H2
    1/H
    H1/2
    H

  8. Тело свободно падает из состояния покоя с высоты 50 м.
    На какой высоте окажется тело через 3 с падения? Сопротивлением воздуха пренебречь.
    0 м
    5 м
    10 м
    45 м

  9. Вектор ускорения при равномерном движении по окружности
    постоянен по модулю и направлению
    равен нулю
    постоянен по модулю, но непрерывно меняется по направлению
    постоянен по направлению, но непрерывно изменяется по модулю

  10. К боковой поверхности цилиндра вращающегося вокруг своей оси, прижимают второй цилиндр с осью, параллельной оси первого, и радиусом, вдвое превосходящим радиус первого. При совместном вращении двух цилиндров без проскальзывания у них совпадают:

    Периоды вращения
    Частоты вращения
    Линейные скорости точек на поверхности
    Центростремительные ускорения точек на поверхности


    
     

Дистанционное обучение | Образовательная социальная сеть

Опубликовано 09. 10.2013 — 22:13 — Лисовская Ирина Александровна

Видеоуроки физика    https://infourok.ru/videouroki/fizika    

 

10 класс. Он-лайн тест — контрольная работа «Кинематика». https://goo.gl/forms/Lb2FuHpkKTD80CyR2

 

9 класс: подготовка к ОГЭ по физике:

1) Открытый банк заданий ОГЭ http://oge.fipi.ru/os/xmodules/qprint/index.php?pr…

2) он-лайн курсы (платные) http://ege.yandex.ru/physics-gia/?from=kold

3) Презентации для повторения материала   http://www.uchportal.ru/load/251-1-2

4) Сборники для подготовки к ГИА и ЕГЭ, рекомендуемые АППО  http://www.eduspb.com/node/1868

Интерактивные задания для учащихся: 

Материалы моих коллег с сайта:

 

Скачать:


Предварительный просмотр:

Кинематика                                                                                 часть А                                                                 Стр.  из

Кинематика 1 вар

ГРАФИКИ

Определение  вида движения по графику

  1. Равноускоренному движению соответствует график зависимости модуля ускорения от времени, обозначенный на рисунке буквой
  1.  А        
  2.  Б        
  3.  В        
  4.  Г
  1. Парашютист движется вертикально вниз с постоянной по значению скоростью. Какой график — 1, 2, 3 или 4 — правильно отражает зависимость его координаты Y от времени движения t относительно поверхности земли? Сопротивлением воздуха пренебречь.

1) 1                  2) 2                              3) 3                        4) 4

Определение  и  сравнение  характеристик  движения  по  графику

  1. На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении. Определите проекцию  ускорения тела.
  1. – 10 м/с2
  2.  – 8 м/с2
  3. 8 м/с2
  4. 10 м/с2

4. По графику зависимости проекции скорости от времени, представленному па рисунке, определите модуль ускорения прямолинейно движущегося тела в момент времени t = 2 с.

  1. 2 м/с2     
  2. 3  м/с2     
  3. 10 м/с2    
  4. 27 м/с2

5. Четыре тела движутся вдоль оси Оx.На рисунке изображены графики зависимости проекций скоростей υx от времени t для этих тел. Какое из тел движется с наименьшим по модулю ускорением?

1) 1                      2) 2            3) 3                           4) 4

6.На рисунке приведен график зависимости проекции скорости тела от времени.

Проекция ускорения тела в интервале времени от 5 до 10 с представлена графиком

1) 1                    2) 2                                       3) 3                                 4) 4

7.Материальная точка движется прямолинейно с ускорением, зависимость от времени которого приведена на рисунке. Начальная скорость точки равна 0. Какая точка на графике соответствует максимальной скорости материальной точки:

  1. 2                    
  2. 3                
  3. 4                        
  4. 5

Составление кинематических зависимостей (функций зависимости кинематических величин от времени) по графику

8. На рис. изображен график зависимости координаты тела от времени. Определите кинематический закон движения этого тела

  1. x(t) = 2 + 2t                       
  2. x(t) =  – 2 – 2t                       
  3. x(t) =  2 – 2t
  4. x(t) = – 2 + 2t

Определение  перемещения и пути по графику

9.По графику зависимости скорости тела от времени определите путь, пройденный прямолинейно движущимся телом за 3 с.

  1.  2 м
  2.  4 м
  3.  18 м
  4.  36 м

10.Камень брошен вертикально вверх. Проекция его скорости на вертикальное направление изменяется со временем согласно графику на рисунке. Чему равно перемещение камня за первые 3 с?

  1.  0 м
  2. 30 м
  3.  45 м
  4.  60 м

11.Камень брошен вертикально вверх. Проекция его скорости на вертикальное направление изменяется со временем согласно графику на рисунке к заданию 10. Чему равно перемещение камня за  все время полета?

  1.  0 м
  2. 30 м
  3. 60 м
  4. 90 м

УРАВНЕНИЯ

12.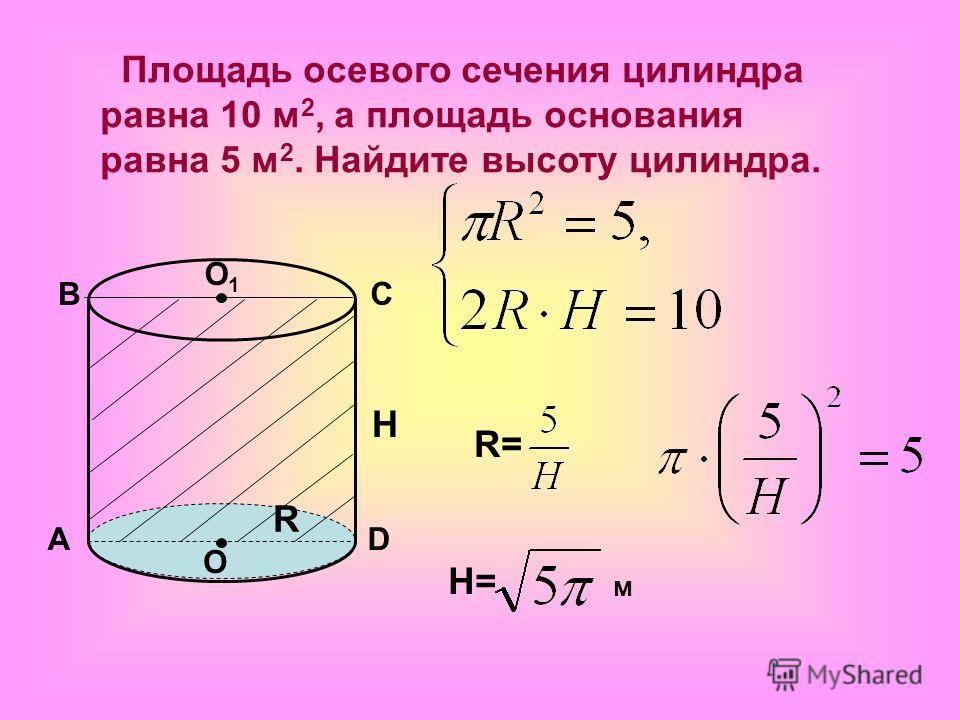 Движение троллейбуса при аварийном торможении задано уравнением: x = – 2,5 t2 +15t +30 , м           Чему равна начальная координата троллейбуса?

  1.  2,5 м
  2.  5 м
  3.  15 м
  4.  30 м

13.Уравнение зависимости проекции скорости движущегося тела от времени: vx = 2 +3t (м/с). Каково соответствующее уравнение проекции перемещения тела?

1) Sx = 2t + 3t2            2) Sx = 4t + 3t2             3) Sx =  t + 6t2                   4) Sx = 2t + 1,5t2

14.Зависимость координаты от времени для некоторого тела описывается уравнением х = 8t – t2 .  В какой момент времени скорость тела равна нулю?

  1. 8 с
  2. 4 с
  3. 3 с
  4. 0 c

ТАБЛИЦЫ

15.В таблице представлена зависимость координаты х равномерного движения тела от времени t:

t, с

0

1

2

3

4

х, м

0

2

4

6

8

С какой скоростью двигалось тело от момента времени 0 с до момента времени 4 с?

  1. 0,5 м/с
  2. 1,5 м/с
  1. 2 м/с
  2. 3 м/с

Движение по окружности

  1. При равномерном движении точки по окружности со скоростьюv.  Модуль изменения скорости |∆v|за половину периода равен

       l) v/2       2) v     3) v                4) 2v

2.Вектор ускорения при равномерном движении точки по окружности

  1. постоянен по модулю и по направлению; 2) равен нулю

3)постоянен по модулю, но непрерывно изменяется по направлению

4)постоянен по направлению, но непрерывно изменяется по модулю

3.Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории его центростремительное ускорение максимально?

  1. 1
  2. 2
  3. 3
  4. Во всех точках одинаково
  1. Период обращения Земли вокруг Солнца равен одному году, радиус орбиты Земли равен 150 млн.км. Скорость движения Земли по орбите равна примерно
  1. 30 м/с
  2. 30 км/с
  3. 150 км/с
  4. 1800 км/с
  1. Диск радиусом 20 см равномерно вращается вокруг своей оси. Скорость точки, находящейся на расстоянии 15 см от центра диска, равна 1,5 м/с. Скорость крайних точек диска равна

1) 4 м/с        2) 0,2 м/с                           3) 2 м/с                               4) 1,5 м/с

  1. Точка движется по окружности радиуса R со скоростью v. Как изменится центростремительное ускорение точки, если скорость уменьшить в 2 раза, а радиус окружности в 2 раза увеличить?
  1. уменьшится в 2 раза
  2. увеличится в 2 раза
  3. уменьшится в 8 раз
  4. не изменится
  1. Два спутника движутся по разным круговым орбитам   вокруг   Земли.   Скорость   первого   из   них   в 2 раза больше, а радиус орбиты в 4 раза меньше, чем второго. Центростремительное ускорение первого спутника а1, второго — а2? Чему равно отношение a1 / a2?

1) 1

2) 2

3) 4

4) 16

  1. Две материальные точки движутся по окружностям радиусами R1 и R2 = 2R1 с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением
  1. Т1=0,5Т2
  2. Т1=Т2
  3. Т1=2Т2
  4. Т1=4Т

Задания части В

  1. Материальная точка движется по окружности радиуса R. Что произойдет с периодом, частотой обращения и центростремительным (нормальным) ускорением точки при увеличении линейной скорости движения?

Установите соответствие между физическими величинами и их изменением: к каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

ИХ ИЗМЕНЕНИЕ

А)

Период обращения материальной точки

1)

Увеличится

Б)

Частота обращения материальной точки

2)

Уменьшится

В)

Центростремительное (нормальное) ускорение
материальной точки

3)

Не изменится

Получившуюся последовательность цифр перенесите в бланк ответов (без пробелов и каких-либо   символов).

Предварительный просмотр:

Кинематика                           Движение по окружности                                                                    Страница  из

Кинематика 2 вариант

ГРАФИКИ

Определение  вида движения по графику

  1. На рисунках изображены графики зависимости модуля ускорения от времени для разных видов движения. Какой график соответствует равномерному движению?

1) 1                  2) 2                              3) 3                        4) 4

  1. Какой из графиков зависимости проекции скорости от времени (рис.) соответствует движению тела, брошенного вертикально вверх с некоторой скоростью (ось Y направлена вертикально вверх)?

1) 1                       2) 2                                   3) 3                                        4) 4

Определение  и  сравнение  характеристик  движения  по  графику

  1. На рисунке изображен график зависимости скорости движения тел от времени. Чему равно ускорение тела?
  1.  1 м/с2
  2.  2 м/с2
  3.  3 м/с2
  4.  18 м/с2
  1. На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке х =  0, а пункт Б  в точке х = 30 км. Чему равна скорость автобуса на пути из А в Б?
  1.  40 км/ч
  2.  50 км/ч
  1.     60 км/ч
  2.     75 км/ч

  1. Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени. Модуль ускорения максимален в интервале времени
  1.  от 0 с до 10 с

2)         от 10 с до 20 с

3)         от 20 с до 30 с

4)         от 30 с до 40 с

  1. На рисунке представлен график зависимости пути S велосипедиста от времени t. Определите интервал времени, когда велосипедист двигался со скоростью 2,5 м/с.
  1. от 5 с до 7 с
  2. от 3 с до 5 с
  3. от 1 с до 3 с
  4. от 0 до 1 с

7. Материальная точка движется прямолинейно с ускорением, зависимость от времени которого приведена на рисунке. Начальная скорость точки равна 0. Какая точка на графике соответствует максимальной скорости материальной точки:

  1. 2                    
  2. 3                
  3. 4                        
  4. 5

Составление кинематических зависимостей (функций зависимости кинематических величин от времени) по графику

8.На рис. изображен график зависимости координаты тела от времени. Определите кинематический закон движения этого тела

  1. x(t) =  — 2 + 2t                      
  2. x(t) =  – 2 – 2t                      
  3. x(t) =  2 – 2t
  4. x(t) =  2 + 2t

Определение  перемещения и пути по графику

9.Камень брошен вертикально вверх. Проекция его скорости на вертикальное направление изменяется со временем согласно графику на рисунке. Чему равен путь, пройденный камнем за первые 3 с?

  1. 30 м
  2. 45 м
  3. 60 м
  4. 90 м

10. Камень брошен вертикально вверх. Проекция его скорости на вертикальное направление изменяется со временем согласно графику на рисунке к заданию 9. Чему равно перемещение камня за 6 с?

  1.  0 м
  2. 30 м
  3.  45 м
  4.  60 м

  1. На рисунке дан график зависимости   проекции   скорости тела, движущегося вдоль оси Ох,  от времени. Чему равен путь, пройденный телом к моменту времени t = 10 с?
  1. 1м    2) 6м        3) 7м       4) 13м

УРАВНЕНИЯ

  1. Движение самолета при  разбеге  задано уравнением: x = 100 + 0,85t2, м Чему равно ускорение самолета?
  1.  0 м/с2
  2.  0,85 м/с2
  3.  1,7 м/с2
  4.  100 м/с2

13.Уравнение зависимости проекции скорости движущегося тела от времени: vx = 5 — 3t (м/с). Каково соответствующее уравнение проекции перемещения тела?

1) Sx = 5t — 3t2            2) Sx = — 3t + 10t2     

       

3) Sx =  5t — 6t2                   4) Sx = 5t — 1,5t2

14. Зависимость координаты от времени для некоторого тела описывается уравнением х = 8t – t2 .  В какой момент времени скорость тела равна нулю?

  1. 8 с
  2. 4 с
  3. 3 с
  4. 0 c

ТАБЛИЦЫ 

15.Четыре тела двигались по оси  Ох. В таблице представлена зависимость их координат от времени.

t, с

0

1

2

3

4

5

x1 м

6

4

2

0

-2

-4

х2, м

3

3

3

3

3

3

х3, м

0

1

4

9

16

25

х4, м

0

2

0

-2

0

2

У какого из тел скорость могла быть постоянна и отлична от нуля?

1) 1                 2) 2             3) 3                4) 4            

Движение по окружности

1. При равномерном движении по окружности модуль вектора изменения скорости при перемещении из точки А в точку В (см. рис.) равен

       l) 0         2) v            3) v               4) 2v

2.Какая   из   физических   величин   не   изменяется   при  равномерном движении по окружности?

  1. Перемещение
  2. Ускорение
  3. Скорость
  4. Все перечисленные выше величины изменяются

3.Автомобиль движется по закруглению дороги радиусом 20 м с центростремительным ускорением 5 м/с2. Скорость автомобиля равна

  1. 12,5 м/с      
  2. 10 м/с      
  3.  5 м/с
  4. 4 м/с

4.Материальная точка, двигаясь равномерно по окружности против часовой стрелки, через 3 секунды первый раз попала из точки А в точку В (см. рисунок). Частота обращения точки равна

  1. 1/12 с-1
  2. 1/4 с-1
  3. 1/3 с-1
  4. 1/2 с-1

5.На рисунке изображены  положения шарика, равномерно движущегося по окружности радиусом 1 м в горизонтальной плоскости.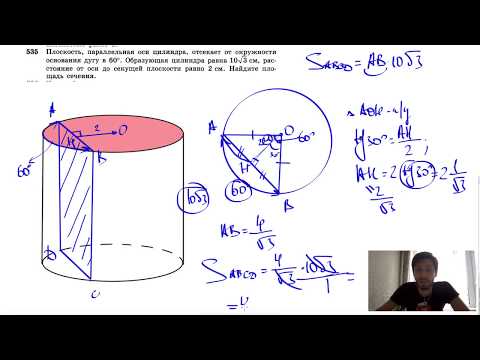 Положения шарика зафиксированы через каждые 0,1 с. Каков модуль скорости шарика?

1) 1,07 м/с           2) 3,14 м/с        3) 6,28 м/с           4) 31,4 м/с

6.Точка движется с постоянной по модулю скоростью v по окружности радиуса R. Как изменится центростремительное ускорение точки, если ее скорость увеличить вдвое, а радиус окружности вдвое уменьшить?

1)уменьшится в 2 раза        

3)увеличится в 4 раза

2)увеличится в 2 раза        

4)увеличится в 8 раз

  1. Две материальные точки движутся по окружностям радиусами R1 и R2 = 3R1 с одинаковой угловой скоростью. Отношение модулей их центростремительных ускорений a2 / a1 равно
  1. 9
  2. 3
  3. 1

Блок В

Тело брошено под углом к горизонту. Как меняются в ходе полета до верхней точки траектории модуль его скорости, проекция скорости на горизонтальную ось и ускорение?

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

ИХ ИЗМЕНЕНИЕ

А)

модуль скорости тела

1)

Не изменяется

Б)

проекция скорости тела на горизонтальную ось

2)

Увеличивается

В)

модуль ускорения тела

3)

Уменьшается

Модуль скорости тела

Проекция скорости тела на горизонтальную ось

Модуль ускорения тела

Предварительный просмотр:

Кинематика                            Движение по окружности                                                                       Страница  из

Кинематика 3 вариант

ГРАФИКИ

Определение  вида движения по графику

  1. Тело, двигаясь вдоль оси Ох прямолинейно и равноускоренно, за некоторое время уменьшило свою скорость в 2 раза. Какой из графиков зависимости проекции ускорения от времени соответствует такому движению?

1) 1                  2) 2                              3) 3                        4) 4

  1. Тело бросили вертикально вверх с некоторой начальной скоростью с поверхности земли. Какой из графиков зависимости высоты тела над поверхностью земли от времени (рис.) соответствует этому движению?

1) 1                       2) 2                                   3) 3                                        4) 4

Определение  и  сравнение  характеристик  движения  по  графику

  1. На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке х =  0, а пункт Б  в точке х = 30 км. Чему равна скорость автобуса на пути из Б в А?
  1.  40 км/ч
  2.  50 км/ч
  3.  60 км/ч
  4.  75 км/ч
  1. На рисунке представлен график зависимости координаты тела, движущегося вдоль оси Oх, от времени. Сравните скорости v1 , v2  и v3 тела в моменты времени t1, t2 , t3
  1. v1  > v2  = v3
  2. v1  > v2  > v3
  3. v1  
  4. v1  = v2  > v3
  1. Четыре тела движутся вдоль оси Оx.На рисунке изображены графики зависимости проекций скоростей υx от времени t для этих тел. Какое из тел движется с наибольшим  по модулю ускорением?

1) 1                      2) 2            3) 3                           4) 4

  1. Материальная точка движется прямолинейно с ускорением, зависимость от времени которого приведена на рисунке. Начальная скорость точки равна 0. Какая точка на графике соответствует максимальной скорости материальной точки:
  1. 2                    
  2. 3                
  3. 4                        
  4. 5
  1. По графику зависимости скорости тела от времени определите функцию зависимости скорости этого тела от времени
  1.  vx=  – 30 + 10t
  2.  vx = 30 + 10t
  3.  vx = 30 – 10t
  4.  vx = – 30 + 10t

Определение  перемещения и пути по графику

  1. Камень брошен вертикально вверх. Проекция его скорости на вертикальное направление изменяется со временем согласно графику на рисунке к заданию 7. Чему равен путь, пройденный камнем  за все время полета?
  1. 30 м
  2. 45 м
  3. 60 м
  4. 90 м

9.Камень брошен вертикально вверх. Проекция его скорости на вертикальное направление изменяется со временем согласно графику на рисунке к заданию 7. Чему равно перемещение камня за первые 3 с?

  1.  0 м
  2. 30 м
  3.  45 м
  4.  60 м

10.Тележка начинает движение из состояния покоя вдоль бумажной ленты. На тележке стоит капельница, которая через равные промежутки времени оставляет на ленте пятна краски.

Выберите график зависимости величины скорости от времени, который правильно описывает движение тележки.

1) 1               2) 2                 3) 3               4) 4            

УРАВНЕНИЯ

11.Движение легкового автомобиля  задано уравнением: x = 30t + 0,7t2 +150 , м. Чему равна начальная скорость автомобиля?

1) 0,7 м/с      2) 1,4 м/с       3) 30 м/с        4) 150 м/с

12.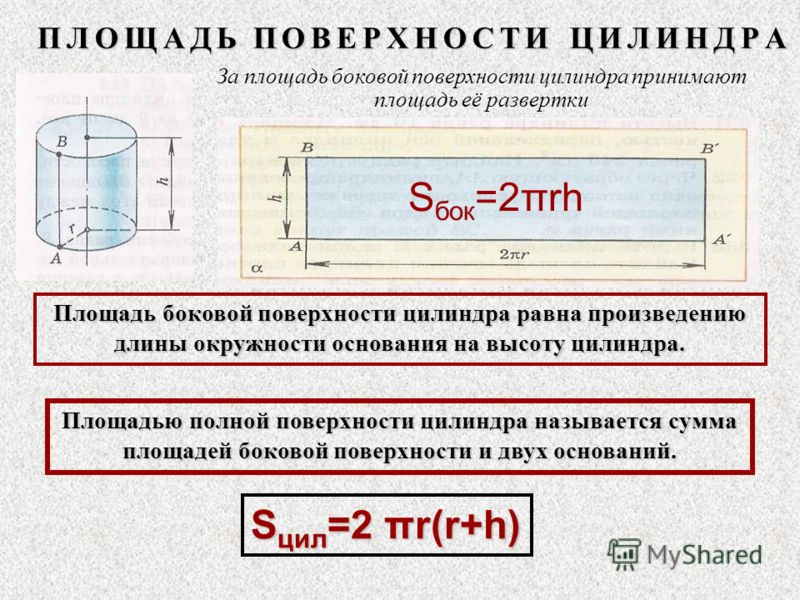 Уравнение зависимости проекции скорости движущегося тела от времени: vx = 3 +2t (м/с). Каково соответствующее уравнение проекции перемещения тела?

1) Sx = 2t + 3t2            2) Sx = 4t + 3t2             3) Sx =  3t + 6t2                   4) Sx = 3t + t2

13.Зависимость координаты от времени для некоторого тела описывается уравнением х = 8t – 2t2 .  В какой момент времени скорость тела равна нулю?

  1. 4 с    2) 3 с       3)  2 с    4) 0 c

ТАБЛИЦЫ

14.В таблице представлена зависимость координаты х движения тела от времени t:

t, с

0

1

3

5

х, м

0

1

1

2

Определите среднюю скорость движения тела в интервале времени от 1с до Зс.

  1.  0 м/с
  2.  ≈0,33 м/с
  3.  0,5 м/с
  4.  1 м/с

15. Четыре тела двигались по оси Ох. В таблице представлена зависимость их координат от времени.

t, с

0

1

2

3

4

5

x1 м

6

4

2

0

-2

-4

х2, м

3

3

3

3

3

3

х3, м

0

1

4

9

16

25

х4, м

0

2

0

-2

0

2

У какого из тел ускорение могло быть постоянно и отлично от нуля?

1) 1              2) 2           3) 3               4) 4

Движение по окружности

  1. Часовая и минутная стрелки различаются размерами и скоростями. Куда направлено центростремительное (нормальное) ускорение конца часовой стрелки (короткая стрелка) в положении, которое изображено на рис. а? На рис. б указаны варианты направлений ускорения часовой стрелки.

1) 1                             2) 2                           3) 3                        4) 4

  1. Кинематическое уравнение движения некоторой точки по окружности имеет вид s = 2t (все величины в системе СИ). Точка находится на расстоянии 0,4 м от центра окружности. Центростремительное ускорение указанной точки равно

1) 12,5 м/с2                       2) 10 м/с2                     3) 5 м/с2                     4) 0,8 м/с2

  1. Период обращения тела, движущегося равномерно по окружности, увеличился в 2 раза. Частота обращения
  1. возросла в 2 раза
  2. уменьшилась в 2 раза
  3. возросла в 4 раза
  4. уменьшилась в 4 раза

4.Период равномерного движения материальной точки по окружности равен T, радиус окружности R. Точка пройдет по окружности путь, равный πR, за время

5. Материальная точка равномерно движется со скоростью v по окружности радиусом r. Если скорость точки будет вдвое больше, то модуль ее центростремительного ускорения

  1. не изменится
  2. уменьшится в 2 раза
  3. увеличится в 2 раза
  4. увеличится в 4 раза
  1. Две материальные точки движутся по окружностям радиусами R1 и R2, причем R2 = 2R1 При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением
  1. a1 =2a2
  2. a1 =a2
  3. a1 =0,5a2
  4. a1 =4a2
  1. К боковой поверхности цилиндра, вращающегося вокруг своей оси, прижимают второй цилиндр с осью, параллельной оси первого, и радиусом, вдвое превосходящим радиус первого. При совместном вращении двух цилиндров без проскальзывания у них совпадают
  1. центростремительные ускорения точек на поверхности
  2. периоды вращения
  3. частоты вращения
  4. линейные скорости точек на поверхности

Часть В

  1. Материальная точка движется с постоянной скоростью по окружности радиуса R, совершая один оборот за время T. Как изменятся перечисленные в первом столбце физические величины, если радиус окружности увеличится, а период обращения останется прежним?

Установите соответствие между физическими величинами и их изменением: к каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами. Цифры могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

ИХ ИЗМЕНЕНИЕ

А)

Скорость

1)

Увеличится

Б)

Угловая скорость

2)

Уменьшится

В)

Центростремительное (нормальное) ускорение
материальной точки

3)

Не изменится

Получившуюся последовательность цифр перенесите в бланк ответов (без пробелов и каких-либо   символов).


Вращающийся цилиндр: научный проект по математике, механике и восприятию

Кусок трубы с отметками на каждом конце приводится во вращение и вращение одновременно. В размытии движущегося цилиндра одна из меток появляется трижды, образуя неподвижный треугольник.

Предмет: 

Данные

Сбор и анализ данных

Математика

Восприятие

Оптические иллюзии

Физика

3 Механика

Ключевые слова:

Вращение

NGSS и EP & CS:

ETS

ETS1

CCCS

Паттерны

. Материалы

  • Около 2 футов (60 см) трубы из ПВХ сортамента 40 с наружным диаметром 3/4 дюйма (2 см).
  • Ножовка или резак для ПВХ
  • Цветные маркеры (не перманентные)
  • Гладкая поверхность, например столешница.
  • Прозрачная поверхность (по желанию)
  • Правитель

Сборка

  1. Отрежьте кусок трубы из ПВХ, длина которой в три раза больше ее диаметра. (Ошибаетесь в длинной стороне, этот эксперимент все еще будет работать с трубками длиной до 3,15 диаметра.)
  2. Сделайте простую отметку рядом с одним концом трубы и другую отметку на другом конце. Например, на изображении ниже труба отмечена X и O ; на фотографиях в верхней части этой страницы он отмечен знаком плюс и минус — неважно, что это за отметки, главное, чтобы они были разными.
  3. Отрежьте еще несколько отрезков трубы, чтобы у вас получился набор труб, длина которых в два, три, четыре и пять раз превышает их диаметр. После первого эксперимента вам понадобятся эти дополнительные куски трубы.

Действия и уведомления

Возьмите кусок трубы, длина которого в три раза больше ее диаметра. Поместите палец на X  и одним быстрым движением нажмите вниз, одновременно потянув трубу на себя, чтобы она закрутилась. (См. анимацию ниже.)

Цилиндр трубы будет вращаться и вращаться, образуя размытый круг, в котором вы должны увидеть X с.

Обратите внимание, что когда вращающийся цилиндр стабилизируется, вы можете увидеть три X s, которые отмечают вершины треугольника. Обратите внимание, что O не отображается.

Затем поместите палец на O и вращайте цилиндр. Обратите внимание, что по мере стабилизации движения появляются три O , каждая из которых находится в вершине треугольника. Обратите внимание, что X не отображается.

Проведите несколько экспериментов, чтобы выяснить, что происходит. Вот несколько предложений:

  • Сделайте несколько отметок на одном конце.
  • Посмотрите на вращающийся цилиндр снизу, через прозрачный стол.
  • Посмотрите на вращающийся цилиндр при солнечном свете (который не включается и не выключается, как это делают флуоресцентные лампы).
  • Посмотрите на вращающийся цилиндр с помощью стробоскопа (самодельный стробоскоп, в котором прорези прорезаны по краям вращающегося диска, отлично работает).
  • Нарисуйте линию вниз по стороне цилиндра. Сделайте одну половину линии красной, а другую половину синей.
  • Попробуйте цилиндры разной длины. Обратите внимание на различные устойчивые шаблоны.
  • Обратите внимание, что цилиндр вращается одним концом, касающимся поверхности стола.
  • Обратите внимание, что центр вращающегося цилиндра находится над столом.

Что происходит?

Примечание. Чтобы получить максимальную отдачу от этого задания, не читайте этот раздел, пока сами не проведете несколько экспериментов!

Когда вы запускаете цилиндр, он вращается вокруг своей длинной оси и вращается вокруг линии, перпендикулярной этой оси. При вращении вокруг своего центра цилиндр образует размытый круг на столешнице. Когда цилиндр вращается, вершина одного конца движется в том же направлении, что и вращающийся конец, а вершина другого конца движется в направлении, противоположном вращению.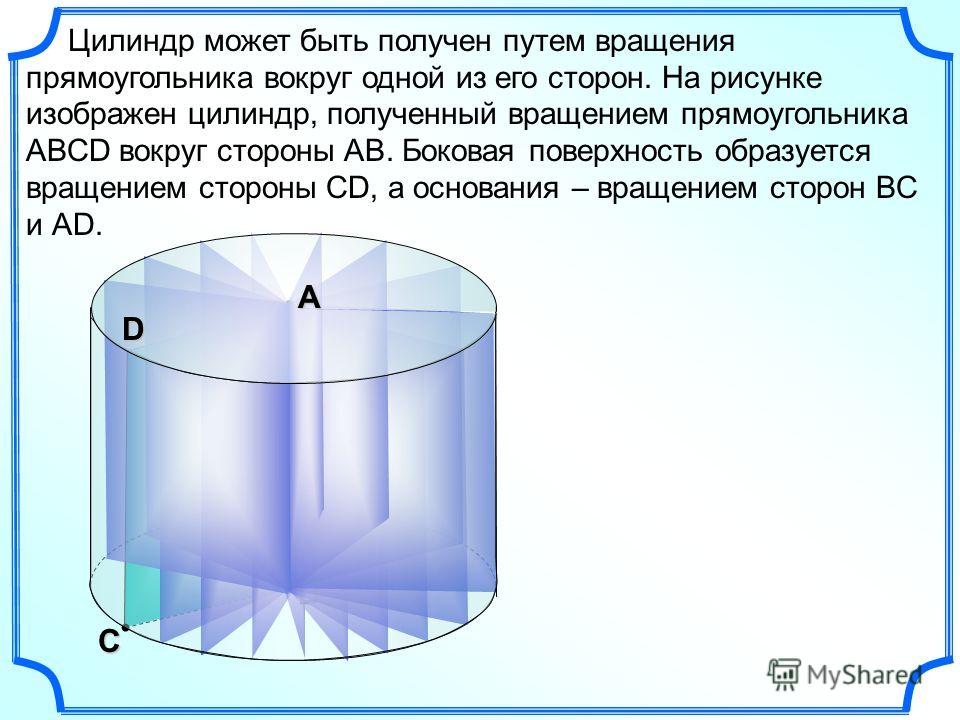

Стрелки на диаграмме ниже, показывающие вид трубы сверху, иллюстрируют эти взаимосвязи.

Две стрелки внутри цилиндра показывают, как он вращается. Две стрелки снаружи цилиндра показывают, как он вращается. На правом конце два движения компенсируют друг друга, и когда отметка на вращающемся цилиндре находится вверху, он фактически останавливается на мгновение (математическое объяснение см. в разделе «Дальше»). На левом конце два движения складываются, и когда отметка на вращающемся цилиндре достигает вершины, он движется в два раза быстрее, чем при одном движении (опять же, математическое объяснение см. в разделе «Дальше» ниже). .

Человеческие глаза могут легко увидеть остановившуюся метку, в то время как сверхбыстро движущаяся метка выглядит размытой. Таким образом, видна только метка на одном конце. Поскольку мы видим три метки вокруг размытого круга, мы знаем, что цилиндр совершает три оборота за каждый оборот (математическое объяснение см. в разделе «Дальше»).

Цилиндры, обрезанные так, чтобы их длина равнялась четырем диаметрам, имеют устойчивый квадрат с четырьмя маркировками. Те, что разрезаны на два диаметра, создают устойчивый узор из двух меток.

Сначала при использовании цилиндра длиной в три диаметра появляются метки на одном конце, но они не образуют устойчивого рисунка. Однако через несколько секунд метки превращаются в устойчивый треугольный узор, который сохраняется до тех пор, пока цилиндр не остановится. Чтобы понять это поведение, заметьте, что цилиндр вращается и вращается одним концом на столе, а другим концом в воздухе. Цилиндр образует устойчивый рисунок, когда конец, касающийся стола, катится без проскальзывания. Обычно цилиндр запускают так, чтобы он крутился быстрее, чем вращался. Это означает, что конец, касающийся стола, трется о стол, рассеивая энергию и замедляясь до тех пор, пока не достигнет скорости, при которой он катится без проскальзывания. Вот почему паттерн сначала нестабилен, а затем стабилизируется.

Дальше

Приведенное ниже обсуждение дает «математический корень» некоторых моделей поведения, отмеченных в предыдущем разделе. Ссылки на левый и правый концы цилиндра относятся к следующей схеме, на которой труба показана сверху:

Окружность вращения цилиндра равна пи, умноженной на его длины:

С = πL

Окружность самого цилиндра равна pi в раз больше его диаметра:

с = πd

Таким образом, число оборотов цилиндра за один оборот равно Кл/с = 3 . Вот почему есть три маркировки!

С= 3πd = 3с

Линейная скорость из-за вращения на любом конце цилиндра:

В вращение = расстояние/время = 3πd/T

где T это время одного полного оборота.

Линейная скорость из-за вращения на обоих концах цилиндра:

В вращение = расстояние/время = πd/t

где t — время одного полного вращения. Но на каждый оборот приходится три вращения, поэтому T = 3t , и, следовательно:

В вращение = 3πd/T = 3πd/3t = πd/t = В спин

Это показывает, что две скорости равны (см. стрелки на диаграмме в начале этого раздела). Это означает, что в тот момент, когда метки обращены вверх, метка на правом конце фактически останавливается, так как скорости противоположны, а метка на левом конце движется вдвойне быстрее, так как скорости находятся в то же направление.


Сопутствующие закуски

Whirling Watcher

Короткие серии движущихся изображений создают интересные эффекты.

Вращающаяся классная доска

Создавайте изящные петли и спирали, рисуя на вращающемся диске.

Чертежная доска

Маятник, движущийся в двух направлениях, создает красивые узоры.



Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4. 0 International License.

Атрибуция: Исследовательский педагогический институт

Rot Динамика и равновесие

Динамика и равновесие Rot

Глава 11; Вращательная динамика и статическое равновесие

| КП, Глава 11 | Календарь курсов |

D11.1 Твердый однородный цилиндр радиусом 12 см и массой 5,0 кг может свободно вращаться вокруг своей симметрии ось. На барабан наматывают шнур и к нему прикрепляют груз массой 1,2 кг. конец шнура. Найдите ускорение подвешенной массы, угловое ускорение цилиндра и натяжение шнура.

Для массы 1,2 кг возьмите уменьшить как положительное и применить секунду Ньютона Закон,

F нетто = m a
F нетто = 12 N — T = (1,2 кг) a
12 N — T = (1,2 кг) a

Для вращающегося цилиндра, применить вращательную форму второго закона Ньютона,

сетка = I
нетто = r F sin
нетто = (0,12 м) (Т) (1)

с = 90°

Для твердых цилиндр,

я = M r 2
I = (0,5) (5,0 кг) (0,12 м) 2
I = 0,036 кг m 2

Следовательно,

сетка = (0,12 м) T = (0,036 кг м 2 ) a

На данный момент у нас есть три неизвестных, Т, а и , в два уравнения . Угловое ускорение цилиндра и линейное ускорение шнура или подвешенного груза связаны через

а = г
а = (0,12 м)
= а / 0,12 м

(0,12 м) T = (0,036 кг м 2 ) а / 0,12 м
T = (0,036 кг м 2 ) а / (0,12 м) 2
T = (2
T = (2
) кг) а

Теперь у нас есть два уравнения в два неизвестные

12 N — T = (1,2 кг) a
12 N — (2,5 кг) a = (1,2 кг) a
12 N — (2,5 кг) a = (1,2 кг) a
12 N = (3,7 кг) а
а =
а = 3,24

Т = 8,1 N

D11.2 Блок массой 10 кг стоит на горизонтальной поверхность с коэффициентом трения 0,2 между блоком и поверхностью. От этого бруска проходит струна по колесу радиусом 10 см и моментом инерции 2,0 кг м 2 и прикреплен к подвесной массе 5 кг. Найдите ускорение масс, угловое ускорение колеса и напряжение в шнур с каждой стороны.


Обратите внимание, что натяжение отличается на две стороны шкива, потому что шкив (очень) массивный.
Для 10-килограммового блока в горизонтальной плоскости можно напишите

F нетто,x = Т Л — Ф f = (10 кг) a

и

F нетто,г = F N — M g = F N — (10 кг) (10 м/с 2 ) = 0

Ж Н = 100 N

Мы можем использовать это информация для определения силы трения,

F f = мк F Н = (0,2) (100 Н) = 20 Н

Затем сеть F ,x уравнение становится

Т Д = 20 Н + (10 кг) а

Для массивного шкива мы есть

сетка = r T R — r T L = (0,10 м) T R — (0,10 м) T L
нетто = я = (10 кг м 2 )
(0,10 м) T R — (0,10 м) T L = (2,0 кг м 2 )

Теперь у нас есть четыре неизвестных — T л , Т Р , а, и — в два уравнения . Угловое ускорение цилиндра и линейное ускорение шнура или подвешенного груза связаны через

а = г
а = (0,10 м)
= a / 0,10 м
(0,10 м) T R — (0,10 м) T L = (2,0 кг м 2 )
(0,10 м) T R — (0,10 м) T L = (2,0 кг м 2 ) а / 0,10 м
Т Р — Т L = (2,0 кг м 2 ) а / (0,10 м) 2

Т Р — Т Л = (200 кг)

Теперь у нас есть три неизвестных —T L , T R , а a — в два уравнения. Мы все еще должны применить ньютоновскую Второй закон висячей массы. Здесь мы также можем принять за минус как положительное,

F нетто = ш — T R = m a
(5 кг)(10 м/с 2 ) — T R = (5 кг) a
50 кг м/с 2 — T R = (5 кг) a

Теперь у нас есть три уравнения для три неизвестных,

T L = 20 N + (10 кг) a
T R — T L = (200 кг) a
50 N — T R = (5 кг) a

T R — [20 N + (10 кг) a] = (200 кг) a
T R = 20 N + (190 кг) a

50 N — [20 N + (190 кг) a] = (5 кг) a
30 N = (195 кг) a
a = = 0,15
а = 0,15
= a / 0,10 м = 1,5
T L = 20 Н + (10 кг) a = 20 Н + 1,5 Н = 21,5 Н

T R = 20 Н + (190 кг) (0,15 ) = 49,2 Н

D11. 3 Допустим игровая карусель быть однородным цилиндром или диском массой 150 кг и радиусом 1,8 м. Каков его момент инерции?

Первоначально находится в состоянии покоя, когда ребенок массой 50 кг, бегущий со скоростью 4 м/с по касательной к краю карусели, запрыгивает. Какова его угловая скорость после того, как ребенок сядет на край?


Для сплошного диска или цилиндра,

I диск = М р 2

Следовательно, момент инерция карусели

я диск = (150 кг)(1,8 м) 2 = 243 кг м 2

Начальный угловой момент ребенок

L = m v r = (50 кг)(4 )(1,8 м) = 360 кг м 2 /с

Начальный угловой момент карусель нулевая.
Таким образом, суммарных начальных угловых моментов всей системы это

L инициал = 360 кг м 2 /с

Если подшипники карусели хорошо смазаны это должно быть итог финал угловой момент,

L окончание = 360 кг м 2 /с
L окончание = I

но теперь момент инерции момент инерции карусели и ребенок

I ребенок = m r 2 = (50 кг)(1,8 м) 2 = 162 кг м 2
I всего = I диск + I детский = 243 кг м 2 + 162 кг м 2
I всего = 405 кг м 2
L окончание = I = (405 кг м 2 ) = L исходный
(405 кг м 2 ) = 360 кг м 2 /с
= 0,89

D11. 4 Корзина томатов массой 20,0 кг поднимается лебедкой. Веревка намотана на ось, сплошной деревянный цилиндр радиусом 0,1 м и массой 10 кг. Масса рукояток пренебрежимо мало. Оператор отпускает ручку, когда корзина находится на высоте 6 м над землей. С какой линейной скоростью ударяет корзина земля?


Момент инерции сплошного цилиндра (или диска) равен

я = ( 1 / 2 ) M R 2
I = ( 1 / 2 ) (10 кг) (0,1 М) 2
I = 0,05 KG M 2 9018 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ).

Скорость груза и угловые скорости брашпиля связаны через

v = r
v = (0,1 м)
= v / 0,1 м

Как всегда, хорошие диаграммы делают жизнь гораздо проще.

Первоначально перед лебедкой и нагрузка отпущена, имеем

КЭ итого, я = 0 так как ничего не движется
PE i = m g h = (20 кг)(9,8 м/с 2 )(6,0 м) = 1,176 кг м 2 /с 2 = 1,176 Дж
E tot,i = 1,176 Дж

В этой задаче, как и в предыдущий, кинетическая энергия колесо или барабан или цилиндр намного больше, чем кинетическая энергия масс и доминирует во всем движении.
Наконец, после того, как лебедка увеличила свою угловую скорость и нагрузка увеличила свою линейную скорость, и как раз перед ударом нагрузки пол, у нас есть

КЭ тр,ф = ( 1 / 2 ) m v 2 = ( 1 / 2 ) (20 кг) v 2 = 10 кг в 2
КЭ гниль,f = ( 1 / 2 ) I 2 = ( 1 / 2 ) (0,05 кг·м 2 ) 2 = ( 1 / 2 ) (0,05 кг·м 2 ) ( v / 0,1 m ) 2 =
KE rot,f = (2.5 kg) v 2
KE tot,f = (12.5 kg) v 2
PE f = 0
E tot ,f = (12,5 кг) v 2 = 1,176 Дж = E TOT, I
(12,5 кг) V 2 = 1176 J
V 2 = 1,176 J / 12,5 KG
V 2 12,5 KG
V 2 12,5 KG
V 2 . v = 9,7 м/с
v = 9,7 м/с

D11.5 Для демонстрации сохранения углового момента профессор физики стоит на вращающемся столе без трения с груз массой 2 кг в каждой вытянутой руке. Помощник дает ей маленький инициал угловая скорость 2 рад/с. Затем она опускает руки по бокам, и ее угловатые скорость резко возрастает. В качестве грубой оценки считайте, что ее руки массой по 5 кг каждая и представлять собой стержни длиной 1 м, шарнирно закрепленные на оси вращения. остальная часть ее тела имеет примерный момент инерции 0,55 кг м 2 . Найдите ее конечную угловую скорость, когда массы находятся на расстоянии 0,25 м от оси вращение. Рассчитать начальное и конечное значения кинетической энергии вращения и объясните причину разницы в этих значениях.

I корпус = 0,55 кг м 2
I стержень = M l 2
I рычаги, внешние = 2 [ (5 кг)(1 м) 2 ] = 3,33 кг м 2
I вес, выход = 2 [ (2 кг) (1 м) 2 ] = 4 кг м 2
I всего, исходное = (0,55 + 3,33 + 4) кг м 2 = 7,88 кг м 2

Начальный угловой момент это

L исходный = I исходный исходный
L исходный = (7,88 кг м 2 ) (2 ) = 15,76
КЭ начальный = я 2 = (7,88 кг м 2 )(2 ) 2
KE исходный = 15,75 Дж

(Это всего лишь совпадение что L и KE случаются так, что имеют одинаковое числовое значение!).
Когда она тянет в руках, общий момент инерции изменения,

I корпус = 0,55 кг м 2
I рычагов, в = 2 [ (5 кг)(0,25 м) 2 ] = 0,21 кг м 2
I вес, в = 2 [ (2 кг) (0,25 м) 2 ] = 0,25 кг м 2 I общая, окончательная =(0,55 + 0,21 + 0,25) кг м 2 = 1,01 кг м 2

Суммарный угловой момент равен законсервированный,

L окончательный = L начальный
L окончательный = I окончательный окончательная = 15,76 = L начальный
(1,01 кг м 2 ) окончательный = 15,76
окончательная = 15,6
КЭ окончательная = я 2 = (1,01 кг м 2 )(15,6 ) 2
KE окончательный = 123 Дж

Работа должна быть выполнена на гирях тянуть их в по направлению к оси вращения. Эта работа, которую выполняет головокружение профессора проявляется как увеличение кинетической энергии.

D11.6 Шт. трубы иногда можно использовать в качестве «мошенника», чтобы эффективно удлинить момент рука гаечного ключа. Если используется труба, как показано на рисунке, чтобы выдержать усилие 150 Н. на расстоянии 30 см от болта, какой крутящий момент действует на болт?


= г F sin
= (0,30 м) (150 Н) (1)
= 45 м-N

D11.7 A облегченный , Единый столб длиной 6 м крепится одним концом к стене с помощью шарнира. шест удерживается горизонтальной растяжкой под углом 30° над горизонтом провод, прикрепленный к столбу в 4,0 м от конца, прикрепленного к стене. Нагрузка 600 N свисает с верхнего конца шеста. Найдите натяжение в растяжке и компоненты силы, действующей на столб со стороны стены.


Как всегда, диаграмма свободного тела или диаграмма силы необходимы .


Из первого условия равновесия имеем

Ф = 0

Но на самом деле это означает

F х = 0
и
Ф у = 0
Ф х = Ф х — Т = 0
F y = F y — 600 N = 0
Ф х = Т
F у = 600 Н

Для решения T и F требуется дополнительная информация x . Мы можем получить эту информацию из второго условия равновесия. До начинаем считать моменты, надо решить по опорной точке , о которых мы будем считать эти крутящие моменты. Если мы выберем нижний, левый конец стержня, две силы, F х и Ф у , у которого будет ноль крутящего момента. Это уменьшит количество терминов во всех наших уравнений. Таким образом, это хороший выбор для источника или ссылки точка или ось вращения.

Перечислите каждую силу и крутящий момент, вызванный этой силой:

F x : = 0 (поскольку r = 0 в = r F sin )
Ф у : = 0 (поскольку r = 0 в = r F sin )
Т: против часовой стрелки = (4 м)(T)(sin 30°) = (4 м) T ( 0,50) = (2 м) T
600 N: cw = (6 м)(600 Н)(sin 60°) = (6 м)(600 Н)(0,866) = 3118 м-Н

против часовой стрелки = по часовой стрелке
(2 м) T = 3118 м-N
T = 1559 N

Следовательно,

Ф х = Т

F x = 1559 №

А мы уже знали

Ф у = 600 Н

D11. 8 Универсальный столб длина 6 м весит 300 Н и крепится шарнир на одном конце к стене. Шест держится под углом 30° выше горизонтальной горизонтальной оттяжкой, прикрепленной к столбу в 4,0 м от конец прикреплен к стене. На верхнем конце стержня висит груз массой 600 Н. Найдите натяжение троса и составляющие силы, действующей на него. столб у стены.

(Сравните с предыдущим вопросом, D11.7).

D не забудьте про груз 300 Н самого столба!!!

Как всегда, хорошая свободная диаграмма тела необходима !


Из первого условия равновесия имеем

Ф = 0

Но это векторное уравнение, так что на самом деле оно означает

F х = 0
и
Ф у = 0
Ф х = Ф х — Т = 0
F y = F y — 600 Н — 300 Н = 0
Ф х = Т
F у = 900 Н

Для решения T и F требуется дополнительная информация x . Мы можем получить эту информацию из второго условия равновесия. До начинаем считать моменты, надо решить по опорной точке о какой мы рассчитаем эти крутящие моменты. Если мы выберем нижний, левый конец полюса, есть две силы, F x и Ф у , у которого будет ноль крутящего момента. Это уменьшит количество терминов во всех наших уравнений. Таким образом, это хороший выбор для источника или ссылки точка или ось вращения.

Перечислите каждую силу и крутящий момент, вызванный этой силой:

F x : = 0 (поскольку r = 0 в = r F sin )
Ф у : = 0 (поскольку r = 0 в = r F sin )
Т: против часовой стрелки = (4 м)(T)(sin 30°) = (4 м) T ( 0,50) = (2 м) T
600 N: cw = (6 м)(600 Н)(sin 60°) = (6 м)(600 Н)(0,866) = 3118 м-Н

300 Н: по часовой стрелке = (3 м)(300 Н)(sin 60°) = (3 м)(300 Н)(0,866) = 779 м-Н

по часовой стрелке = по часовой стрелке
(2 м) T = 31179 м-N m-N
(2 м) T = 3897 N

Т = (3897/2) Н

Т = 1948,5 Н

Следовательно,

Ф х = Т

F x = 1948,5 №

А мы уже знали

Ф у = 900 Н

D11. 9 Плотницкий угольник имеет размеры показано на рисунке. Изготавливается из металла одинаковой толщины. Найдите его центр тяжести или центра масс.

Представьте, что квадрат состоит из двух прямоугольников.

Центр тяжести каждого прямоугольника находится в геометрический центр этого прямоугольника и масса (или вес), расположенная в этом position пропорциональна площади этого прямоугольника.

Обратите внимание, что все положения измеряются от нижнего левый угол столярного угольника. Теперь мы можем использовать определения центра гравитации, уравнения 8.10 и 8.11, чтобы найти центр тяжести весь объект,



D11.10 Задачи с лестницами — это весело. Лестничные задачи являются классическими. Задача с лестницей обязательно появится на часовом экзамене или в финальном экзамене.

Человек массой 800 Н поднимается на вершину 6-метровой лестницы. который опирается на гладкую (т.е. без трения) стену под углом 60° с горизонталью, как показано на рисунке ниже. Неоднородная лестница весит 400 Н, а его центр тяжести находится на расстоянии 2 м от подножия лестницы. Каким должен быть минимальный коэффициент статического трения между грунтом а подножка лестницы если не скользит?


Используя первое условие равновесия, имеем

F x = F стена — Ф Ф = 0

F стена = Ф Ф

и

Ф у = Ф Н — 400 Н — 800 Н = 0

Ж Н = 1200 Н

Решение для F стена и, таким образом, для F f , мы должны использовать второй состояние равновесия. При расчете крутящих моментов рассчитаем крутящие моменты про подножку лестницы. Этот выбор означает две силы, Ф Н и Ф ф , обеспечит нулевой крутящий момент и это уменьшит количество терминов в нашем уравнения. Будьте очень осторожны с углами!

= г F sin
F стена : кв = (6,0 м)(F стена )(sin 60°) = (6,0 м)(F стена )(0,866)
кв = (5,2 м) F стена

800 Н: против часовой стрелки = (6,0 м)(800 Н)(sin 30°) = 2400 м-Н
400 Н: против часовой стрелки = (2,0 м)(400 Н)(sin 30°) = 400 м-Н

F стена : = 0
Ф Ф : = 0

= против часовой стрелки
(5,2 м) F стена = 2400 м-С + 400 м-С
(5,2 м) F стена = 2800 м-N
F стена = 538 Н
Ж Ж = 538 Н

мк = 0,45

| Возврат в Календарь |

(С) 2005; Дуг Дэвис, все права защищены.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *