| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.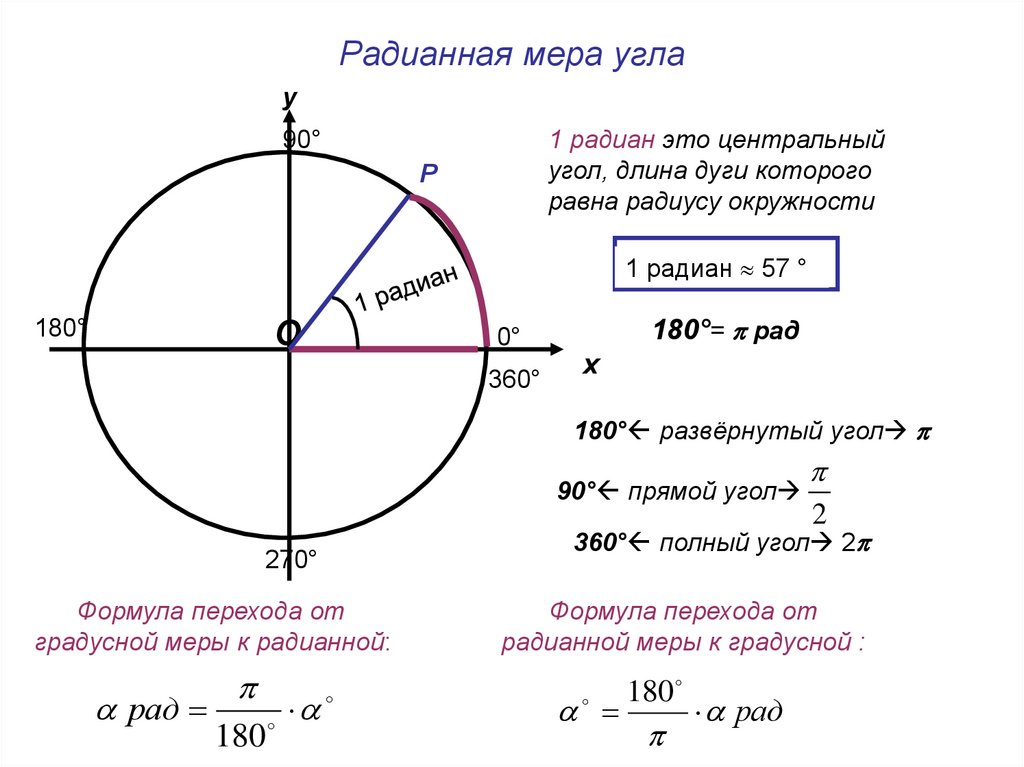 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| Найти точное значение | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | ||
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Перевод градусов в радианы в Excel — TutorExcel.Ru
Перевод градусов в радианы в Excel
Разберем как перевести градусы в радианы (и наоборот) с помощью стандартных функций Excel, а также узнаем как это можно сделать без применения функций.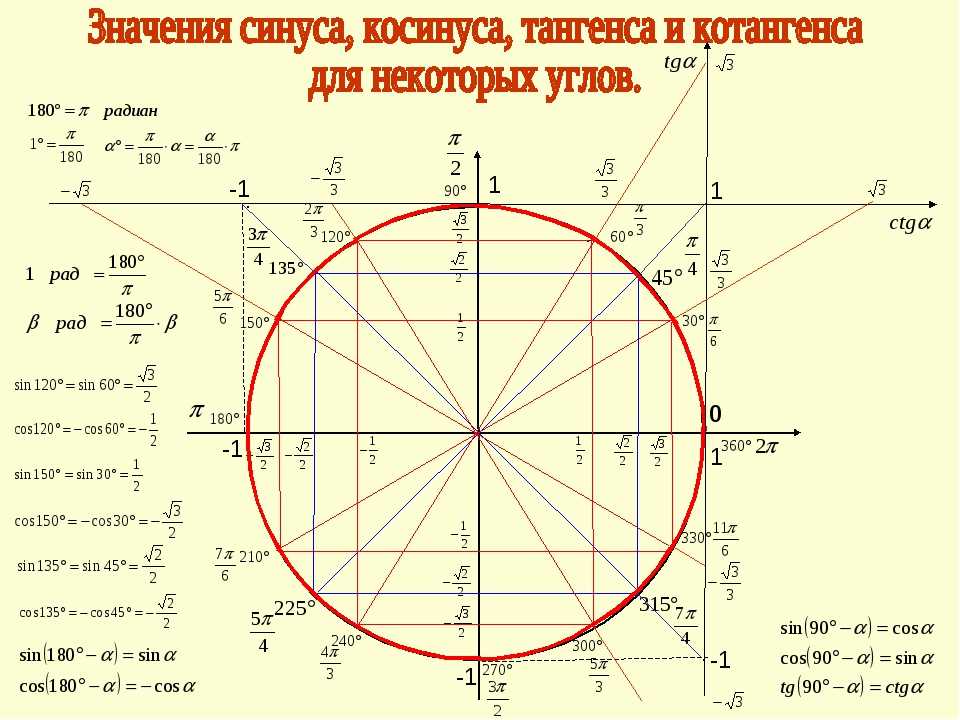
В повседневной жизни мы привыкли оперировать градусами, как основной единицей измерения углов.
Однако не всегда градусы удобно использовать в расчетах, к примеру, в математическом анализе при работе с тригонометрическими функциями аргумент по умолчанию считается выраженным в радианах.
Вдобавок в тригонометрических функциях в Excel, таких как SIN (синус), COS (косинус), TAN (тангенс), в качестве аргумента указывается угол в радианной мере, поэтому для корректной работы с данными формулами необходимо предварительно перевести его в радианы.
Перед тем как перевести угол из градусной меры в радианную вспомним, что радиан — это угол, соответствующий дуге, длина которой равна ее радиусу. Из определения следует, что один полный оборот в 360° составляет 2π радиан, откуда можно получить формулу перевода угла из одной системы измерения в другую:
Из определения следует, что один полный оборот в 360° составляет 2π радиан, откуда можно получить формулу перевода угла из одной системы измерения в другую:
В Excel есть две стандартные функции, которые позволяют перевести градусы в радианы и наоборот.
Давайте подробно остановимся на особенностях применения каждой из них.
Функция РАДИАНЫ в Excel
Синтаксис и описание:
РАДИАНЫ(угол)
Преобразует градусы в радианы.
- Угол (обязательный аргумент) — угол в градусной мере, преобразуемый в радианы.
В качестве аргумента задаем угол в градусной мере, в результате преобразования получаем радианную:
Функция ГРАДУСЫ в Excel
Синтаксис и описание:
ГРАДУСЫ(угол)
Преобразует радианы в градусы.
- Угол (обязательный аргумент) — угол в радианной мере, преобразуемый в градусы.

Функция по сути аналогична описанной выше, но в данном случае на входе мы задаем радианы, а на выходе получаем градусы:
Альтернативный способ перевода
Перевести угол из градусной меры в радианную можно и без использования стандартных формул перевода углов в Excel.
Действительно, мы уже выяснили, что в развернутом угле (180°) содержится π радиан, поэтому умножая угол выраженный в градусах на коэффициент π/180 (с помощью константы Пи) получим радианную меру угла:
Аналогично умножая на обратный коэффициент 180/π можно сделать перевод из радианной меры в градусную:
Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!
Поделиться с друзьями:
Поиск по сайту:
Математика,Формулы,Функции
- ← Точка пересечения графиков в Excel
- Модуль числа в Excel →
Преобразование градусов в радианы с помощью калькулятора TI-84 Plus Для чайников
Графический калькулятор TI-84 Plus CE Для чайников
Посмотреть книгу Купить на Amazon
Функции, расположенные в меню «Угол» калькулятора TI-84 Plus, позволяют выполнять преобразование между градусами и радианами или между прямоугольными и полярными координатами. . Чтобы преобразовать градусы в радианы, выполните следующие действия:
. Чтобы преобразовать градусы в радианы, выполните следующие действия:Переведите калькулятор в режим радиан.
Нажмите [MODE], с помощью клавиш со стрелками выделите RADIAN, а затем нажмите [ENTER].
При необходимости нажмите [2nd][MODE] для доступа к главному экрану.
Введите количество градусов.
Нажмите [2nd][APPS][1], чтобы вставить функцию степени.
Нажмите [ENTER], чтобы преобразовать градусную меру в радианы.
Это показано на первом экране.
Если вы приверженец чистоты и предпочитаете, чтобы радианы выражались как дробное число, кратное числу пи, то выполнение следующих шагов позволит достичь этой цели, если это математически возможно.
Чтобы разделить значение радиана на число пи, нажмите
.Это показано на втором экране.
Нажмите [MATH][ENTER][ENTER], чтобы преобразовать результат в дробь, если это возможно.

Это показано на третьем экране. Если калькулятор не может преобразовать десятичную дробь, полученную на шаге 6, в дробь, он сообщает об этом, возвращая десятичную дробь на шаге 7.
Чтобы преобразовать радианы в градусы:
Переведите калькулятор в режим градусов.
Нажмите [MODE], с помощью клавиш со стрелками выделите DEGREE, а затем нажмите [ENTER].
При необходимости нажмите [2nd][MODE] для доступа к главному экрану.
Введите значение в радианах.
Если мера радиана вводится как арифметическое выражение, заключите это выражение в круглые скобки.
Нажмите [2nd][APPS][3], чтобы вставить функцию r .
Нажмите [ENTER], чтобы перевести радианы в градусы.
Это показано на первом экране.
TI-84 Plus — сложный инструмент, и с ним легко сделать ошибку. Для получения дополнительной помощи ознакомьтесь с 10 распространенными ошибками при использовании калькулятора TI-84 Plus.
Об этой статье
Эта статья из книги:
- Графический калькулятор TI-84 Plus CE для чайников,
Об авторах книги:
Джефф МакКалла — учитель математики в Епископальной школе Святой Марии в Мемфисе, Теннесси. Он стал соучредителем группы суперпользователей TI-Nspire и получил Президентскую премию за выдающиеся достижения в области преподавания естественных наук и математики.
К.К. Эдвардс — преподаватель, который провел множество семинаров по использованию калькуляторов TI.
Джефф МакКалла — учитель математики в Епископальной школе Святой Марии в Мемфисе, Теннесси. Он стал соучредителем группы суперпользователей TI-Nspire и получил Президентскую премию за выдающиеся достижения в области преподавания естественных наук и математики.
К.К. Эдвардс — преподаватель, который провел множество семинаров по использованию калькуляторов TI.
Эту статью можно найти в категории:
- Графические калькуляторы ,
Преобразование радианов в градусы
Сокращение углов Справочные углы
Purplemath
Два типа единиц измерения радианов и градусов. Существует очень много таких единиц (таких как «градианы» и «MRAD»), но градусы и радианы — это те, с которыми вы, скорее всего, столкнетесь в средней школе и колледже.
ГрадусыГрадусы используются для выражения направления и величины угла.
Если вы стоите лицом прямо на север, вы смотрите в направлении ноль градусов, что записывается как 0°. (Верхний индекс «круг» означает «градусы».) Если вы полностью развернетесь и в конечном итоге снова окажетесь лицом на север, вы «повернетесь» на 360 °; то есть один полный оборот (или один круг) составляет 360 °.
Содержание продолжается ниже
MathHelp.com
Почему один оборот делится на 360 частей, называемых «градусами»? Потому что древние вавилоняне, умершие уже четыре или пять тысяч лет назад, придавали числам 6, 12 и 60 особое религиозное значение.
Именно из-за них у нас двенадцать часов ночи и двенадцать часов дня, где каждый час делится на шестьдесят минут, а каждая минута делится на шестьдесят секунд. Также их вина в том, что «один оборот» (то есть один полный оборот) делится на 6×60 = 360 частей, называемых «градусами».
Таким образом, полный оборот составляет 360°, а пол-оборота (или «оборота») — 180°. Если вы начнете, повернувшись лицом на север, а затем повернетесь на юг, вы сделаете пол-оборота, пол-оборота или пройдете половину круга. Вы также «развернетесь» на 180°.
Если вы снова начнете, повернувшись лицом на север, а затем повернетесь на восток, вы сделаете поворот на 90° или четверть поворота и будете смотреть на 90°. Если вы начнете смотреть на север, а затем повернетесь на запад, вы сделаете еще один поворот на 90°, но на этот раз вы будете смотреть на 270°. Это связано с тем, что градусы направления (обычно) начинаются с 0 ° для «севера», а затем идут по часовой стрелке.
Это связано с тем, что градусы направления (обычно) начинаются с 0 ° для «севера», а затем идут по часовой стрелке.
Если при повороте на четверть с «севера» на «запад» вы держите руку прямо перед собой, говорят, что ваша рука «размахнулась» на 9угол 0°. Этот угол был бы образован начальным положением вашей руки («начальная» сторона угла) и конечным положением вашей руки («конечная» сторона угла). Путь кончиков пальцев при движении руки будет «дугой», а угол, на который вы повернетесь, называется «стягивающим» эту дугу.
Примечание. Когда направления задаются в градусах, направление (обычно) определяется, начиная с «севера», равного 0°, и двигаясь по часовой стрелке на заданное количество градусов. Другой способ указать направление с использованием степени — это форма N36 ° W или S27 ° E. Это означает «36 градусов к западу от севера» и «27 градусов к востоку от юга» соответственно. Какие бы соглашения ни использовались в вашей книге, они должны быть конкретно определены в книге; спросите своего инструктора, если это не ясно.
И да, этот способ измерения направления (а именно, начиная с севера и двигаясь по часовой стрелке) отличается от того, как вы будете измерять углы. Когда вы делаете графики и рисунки с измеренными углами, вы начинаете с 0 °, обозначающего «восток» (на самом деле это будет ось x ), и вы будете вращаться против часовой стрелки.
Десятичные градусы и DMSКогда вы работаете со степенями, вы почти всегда будете работать с десятичными степенями; то есть с градусами, выраженными десятичными числами, такими как 43,1025 °. Но точно так же, как «1,75» часа можно выразить как «1 час и 45 минут», так и «градусы» можно выразить в более мелких единицах. Эти единицы, так же как и «часы», называются «минуты» и «секунды». Точно так же, как «часы» могут быть выражены как десятичные часы или как «часы — минуты — секунды», так и «градусы» могут быть выражены как десятичные градусы или иначе как «градусы — минуты — секунды», обозначаемые как «DMS».
Я вижу, что у меня 43°, но что мне делать с дробной частью градуса «0,1025»?
Я буду рассматривать эту дробную часть как процент от шестидесяти минут в одном градусе. Используя это рассуждение, я могу затем узнать, сколько минут составляет этот процент от градуса:
Используя это рассуждение, я могу затем узнать, сколько минут составляет этот процент от градуса:
= 6,15 минут
…или 6 минут и 0,15 другой минуты.
Каждая минута состоит из шестидесяти секунд. Я могу применить те же рассуждения и метод, что и для дробной части градуса, к этой дробной части минуты:
= 9 секунд
Тогда 43,1025° равно 43 градусам, 6 минутам и 9 секундам, или, в нотации DMS:
43° 6′ 9″
Обратите внимание на символы, которые я ответ выше. Вы уже знали, что кружок в верхнем индексе означает «градусы». Теперь вы можете видеть, что одинарная кавычка (апостроф) указывает на «минуты», а двойная кавычка указывает на «секунды».
Это похоже к обозначениям (в британских единицах измерения) для «футов» и «дюймов». Вы можете сохранить обозначения прямыми, помня, что, как и в случае с «футами» и «дюймами», меньшая единица (а именно, «секунды» ) получает больший маркер (а именно, двойную кавычку).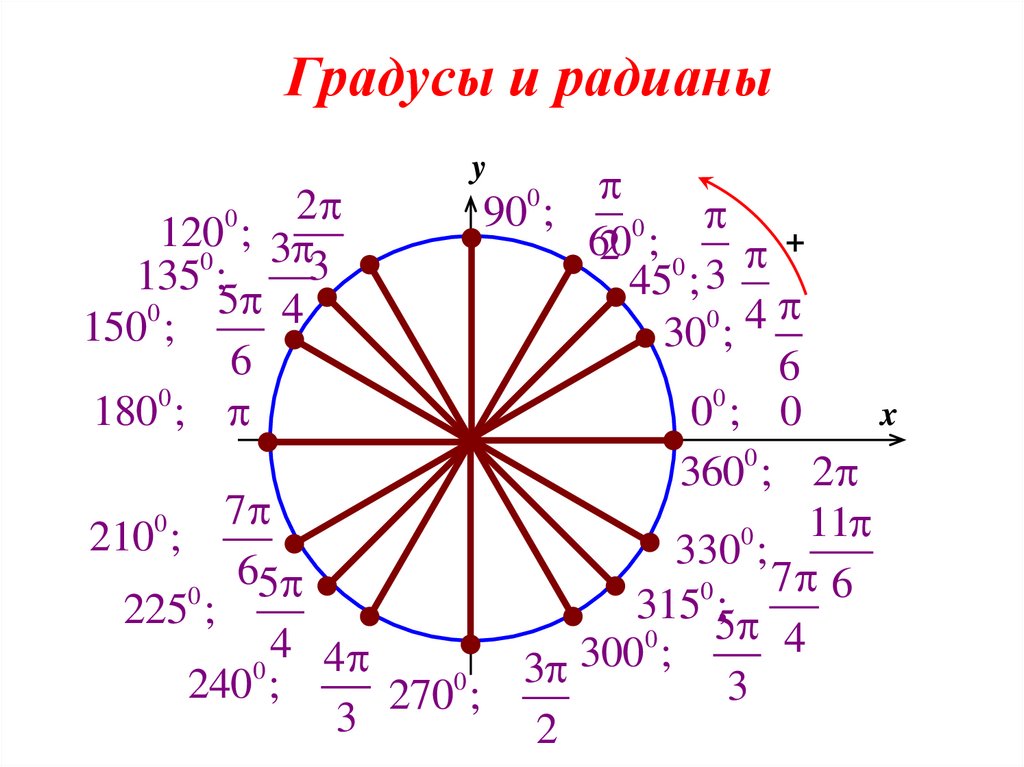 0005
0005
Понятно, что у меня 102°, но как перевести минуты и секунды в десятичную форму?
Я сделаю преобразование, используя определения «градусов», «минут» и «секунд»; и выполнив соответствующие деления.
Каждый градус содержит шестьдесят минут. Тогда 45′ означает, что у меня
45/60 градусов. Упрощение этой дроби, а затем выполнение длинного деления дает мне:
45/60 = 3/4 = 0,75
Таким образом, 45′ составляет 0,75°. (Это похоже на то, что 45 минут времени составляют 0,75 часа.)
Теперь мне нужно разобраться с 54″. Так как каждая минута состоит из шестидесяти секунд, то я получаю:
54/60 = 9/10 = 0,9
Но это число, 0,9, выражено в минутах, оно означает «девять десятых одной угловой минуты». Мне нужно преобразовать 0,9 минуты в значение в градусах. составляют шестьдесят минут в одном градусе, тогда:
= 0,015 градуса
Складывая их, я получаю:
102° 45′ 54″
= 102° + 0,75° + 0,015°
= 102,765°
, в десятичной форме равно 102° 45′. to:
to:
102,765°
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании из DMS в десятичные градусы. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или продолжить урок.)
Пожалуйста, примите «предпочтительные» файлы cookie, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
Радианы
Зачем нам изучать радианы, когда у нас уже есть отличные степени ? Потому что степени, с технической точки зрения, на самом деле не являются числами, и мы можем заниматься математикой только с числами. Это чем-то похоже на разницу между десятичными дробями и процентами. Да, «83%» имеет ясное значение, но для выполнения математических вычислений вы должны сначала преобразовать его в эквивалентную десятичную форму, 0,83. Здесь происходит что-то подобное (что будет иметь больше смысла, когда вы углубитесь в исчисление и т. д.).
Здесь происходит что-то подобное (что будет иметь больше смысла, когда вы углубитесь в исчисление и т. д.).
360° за один оборот («один раз вокруг») достаточно запутанно. Почему значение одного оборота в радианах является иррациональным значением 2π? Потому что это значение делает математику правильной.
Вы знаете, что длина окружности C радиуса r равна C = 2π r . Если r = 1, то C = 2π. По причинам, которые вы узнаете позже, математики любят работать с кругом «единицы», поскольку это круг с r = 1. Чтобы математика имела смысл, «числовое» значение, соответствующее 360°, должно быть определено как (то есть должно быть изобретено со свойством) «2π является числовым значением «один раз вокруг ‘ круг.»
Преобразование радианов в градусы
Каждый радиан и градус имеет свое место. Если вы описываете мне дорогу, я бы предпочел, чтобы вы сказали: «Поверните на шестьдесят градусов вправо, когда будете проходить мимо оранжевого почтового ящика», а не «Поверните на (1/3) π радиан» в этот момент. Но если мне нужно найти площадь сектора круга, я бы предпочел, чтобы вы дали мне числовую меру в радианах, которую я могу подставить непосредственно в формулу, а не градусную меру, которую мне пришлось бы сначала преобразовать.
Но если мне нужно найти площадь сектора круга, я бы предпочел, чтобы вы дали мне числовую меру в радианах, которую я могу подставить непосредственно в формулу, а не градусную меру, которую мне пришлось бы сначала преобразовать.
Но вам не всегда будут давать меры угла в той форме, которую вы предпочитаете, поэтому вам нужно будет иметь возможность конвертировать радианы в градусы. Для этого вы воспользуетесь тем фактом, что 360° — это «один раз», как и 2π. Однако вы будете использовать этот факт эквивалентности в виде несколько упрощенного соответствия 180° π.
Я знаю, что 180° равняется π, поэтому я могу использовать это соотношение для преобразования. У меня есть градусы, и мне нужны радианы, поэтому я хочу, чтобы «градусы» как единица сокращались. Поскольку они дали мне градусы, то «градусы» в настоящее время находятся сверху (от дроби над «1»), поэтому я поставлю «180» для «градуса» внизу при умножении, чтобы получить нужное сокращение.
Тогда эквивалентный угол в радианах:
Мне нужно преобразовать из радианов в градусы, поэтому я буду использовать свой коэффициент преобразования с «радианами» внизу, так что единица, которую я не ‘t хочу отменить:
Тогда эквивалентный угол в градусах будет:
30°
Обратите внимание, что способ, которым я использовал соответствие, варьировался в зависимости от того, что мне дали.