§2. Достаточные признаки сходимости положительных рядов.
1. Признак Даламбера.
Теорема (признак Даламбера сходимости положительных рядов).
Рассмотрим положительный числовой ряд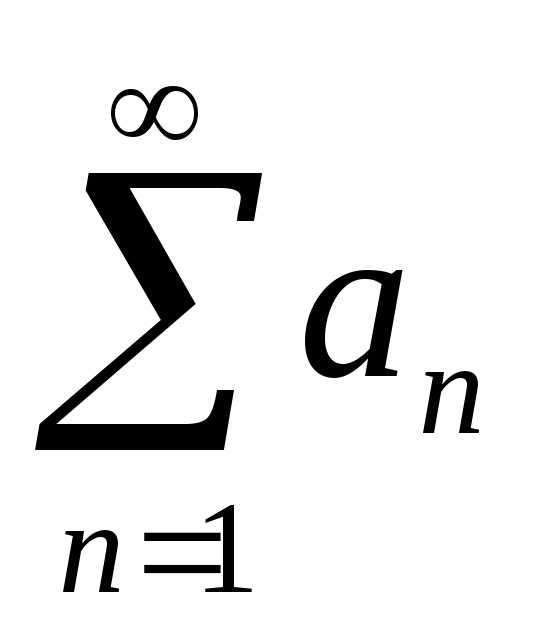 
.
Если существует конечный предел
,
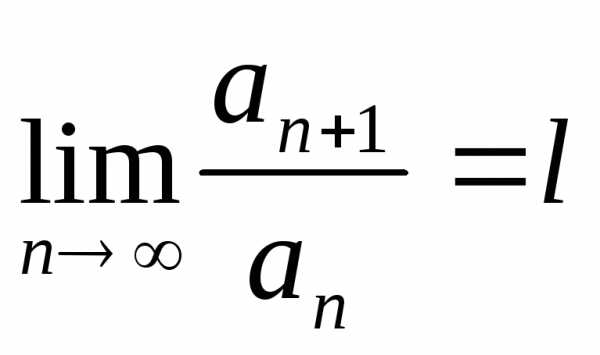то
при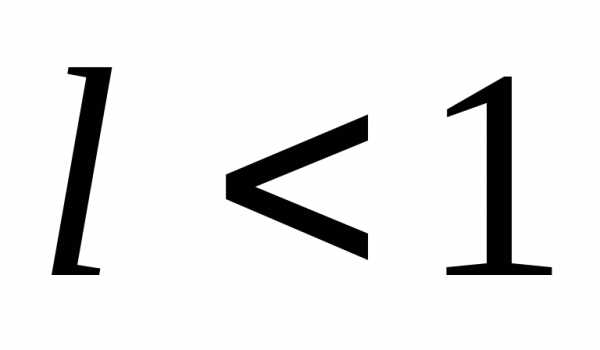 
ряд сходится,
при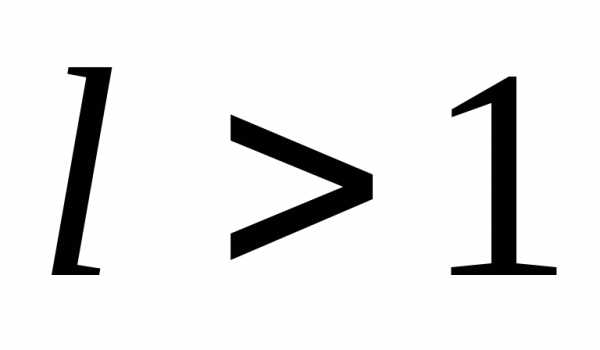 
ряд расходится.
Заметим, при 
вопрос о сходимости ряда остается
нерешенным и нужно подобрать другой
признак для исследования данного ряда.
Задача №1. Исследовать на сходимость
ряд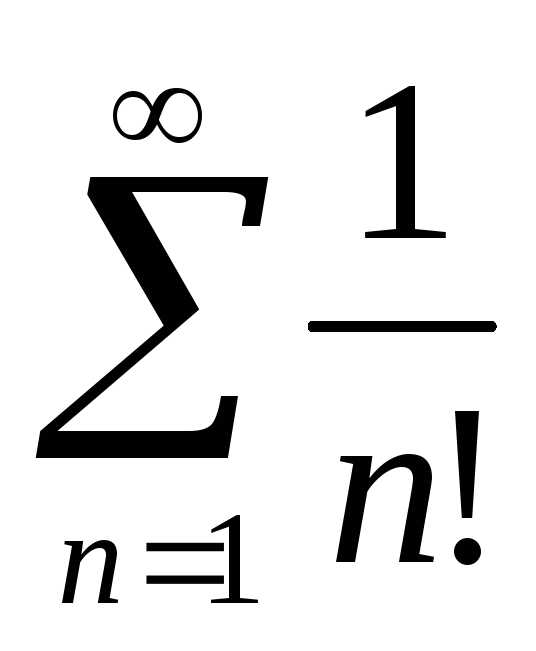
Решение.,
,
следовательно, по признаку Даламбера ряд сходится.
Задача №2.Исследовать на сходимость
ряд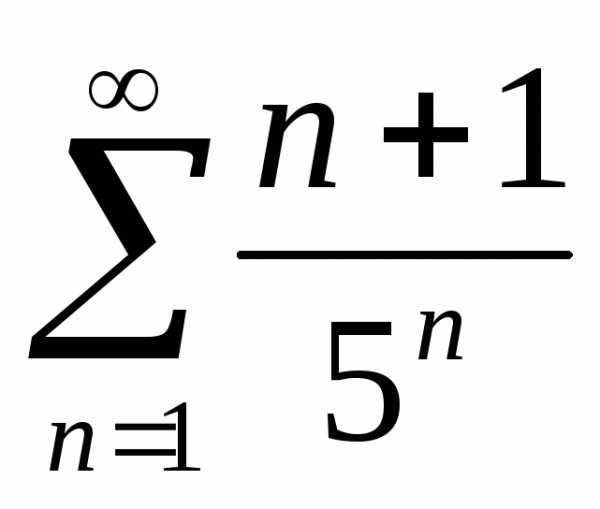
.
Решение.
,поэтому
ряд сходится по признаку Даламбера.
Ответ: ряд расходится.
Задача №3.Исследовать на сходимость
ряд
.
Решение.
, тогда
Ряд сходится по признаку Даламбера.
Ответ: ряд сходится.
Задача №4. Исследовать на сходимость
ряд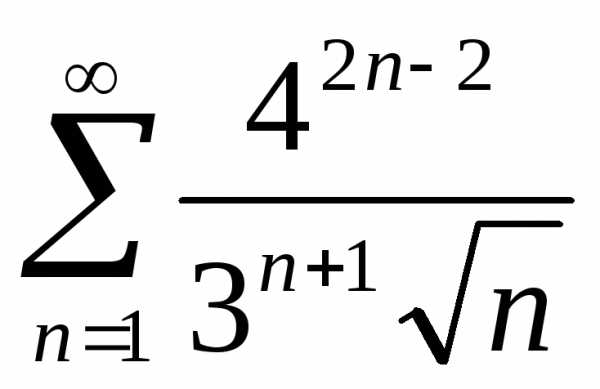
.
Решение.
, тогда
по признаку Даламбера ряд расходится.
Ответ: ряд расходится.
Рассмотренные примеры позволяют
сделать вывод о том, что к большинству
рядов, общий член которых содержит
функции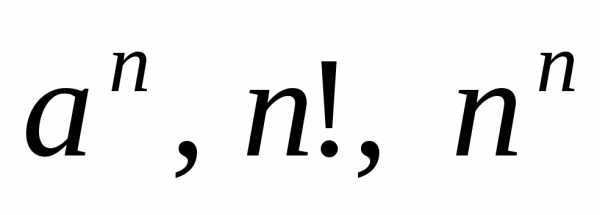 
2. Интегральный признак.
Теорема (интегральный признак сходимости Коши-Маклорена).
Пусть дан ряд
,
члены которого положительны и не возрастают.
Пусть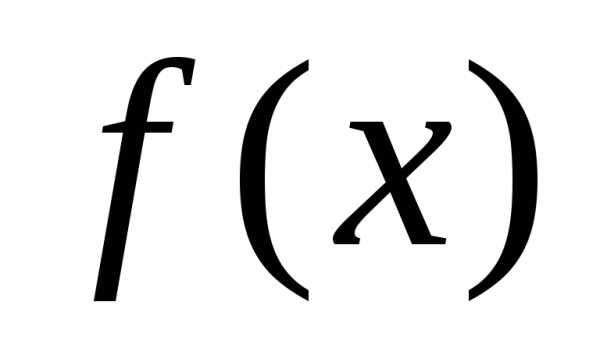
— функция, которая определена для всех
действительных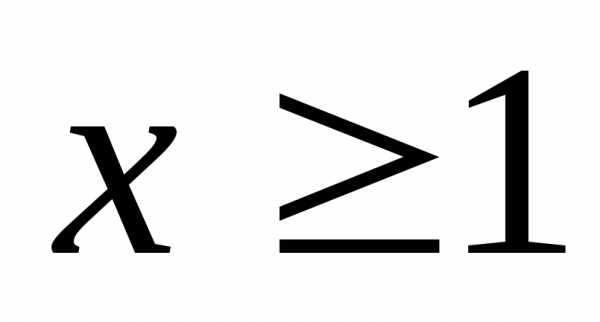
,
непрерывна, не возрастает и такая, что
,
тогда для сходимости ряда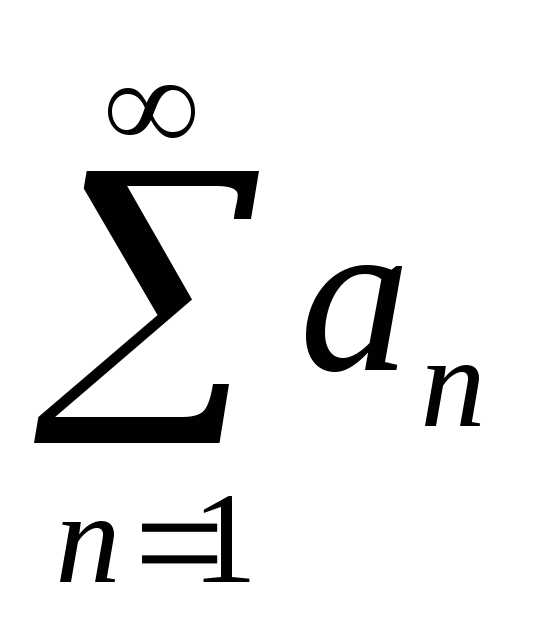 
необходимо
и достаточно, чтобы сходился (существовал)
интеграл
.
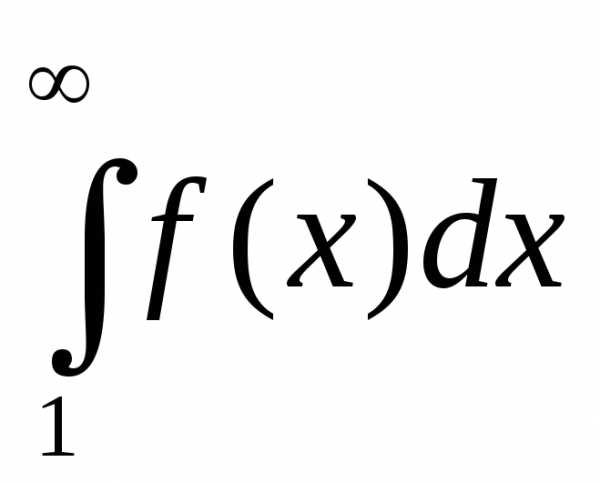Достоинство интегрального признака состоит в его высокой чувствительности: этот признак четко проводит различие между сходящимся и расходящимся рядами, даже если члены одного из них незначительно отличаются от членов другого.
Сформулируем важное следствие интегрального признака: если положительный ряд можно исследовать на сходимость по интегральному признаку, то его остаток оценивается по формуле:
.
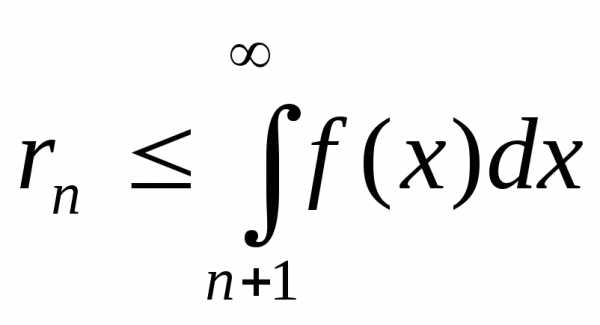Эта оценка используется для приближенного вычисления суммы сходящихся рядов.
Задача №5. Исследовать на сходимость
ряд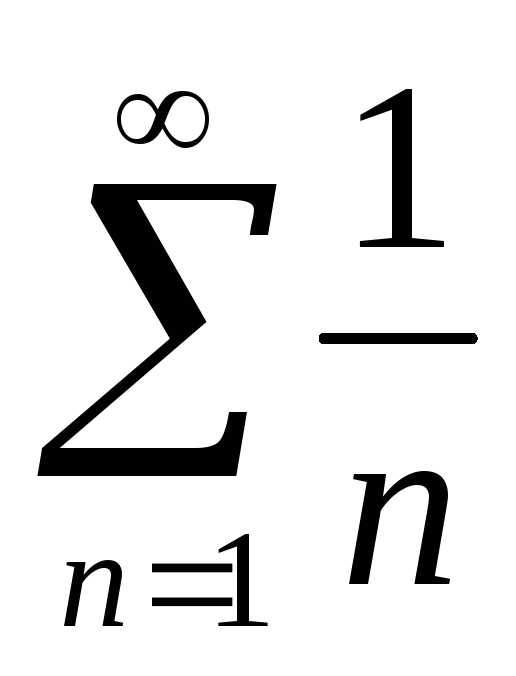
.
Решение.Воспользуемся интегральным
признаком. Введем функцию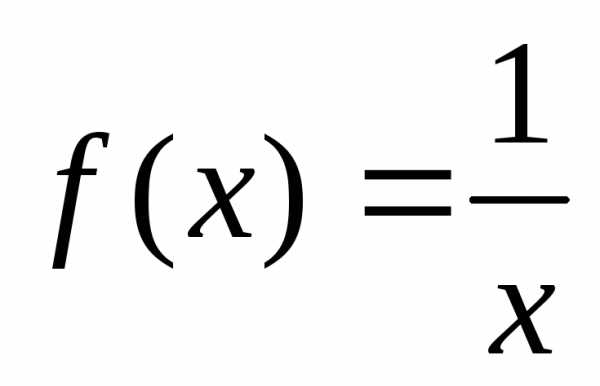
,
такую, что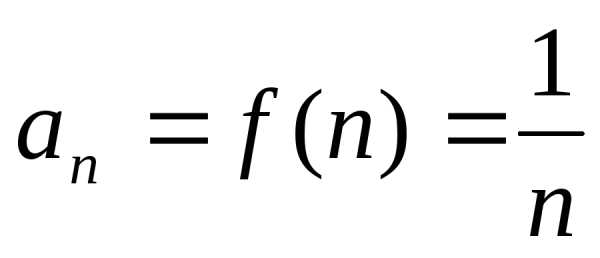
.
Рассмотрим несобственный интеграл
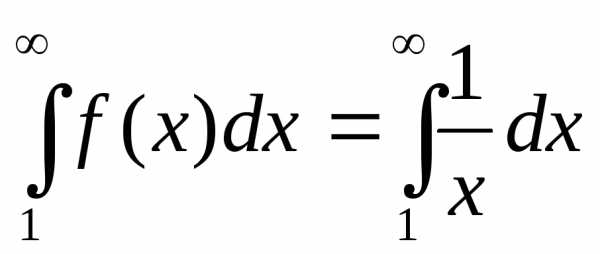
и исследуем его на сходимость:
,
интеграл расходится, поэтому должен расходиться и ряд.
Ответ: ряд расходится.
Задача №6.Исследовать на сходимость
ряд
.
Решение.
, 
,
,
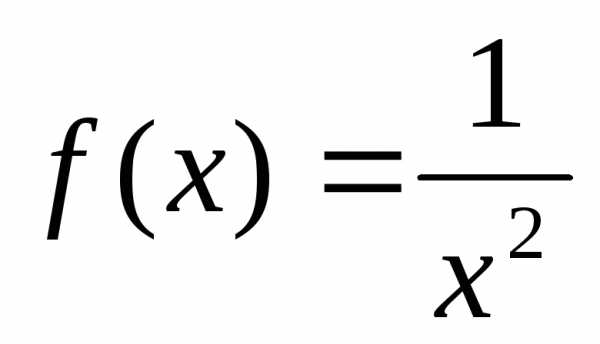несобственный интеграл сходится (равен конечному числу), следовательно, по интегральному признаку ряд сходится.
Ответ: ряд сходится.
Ряд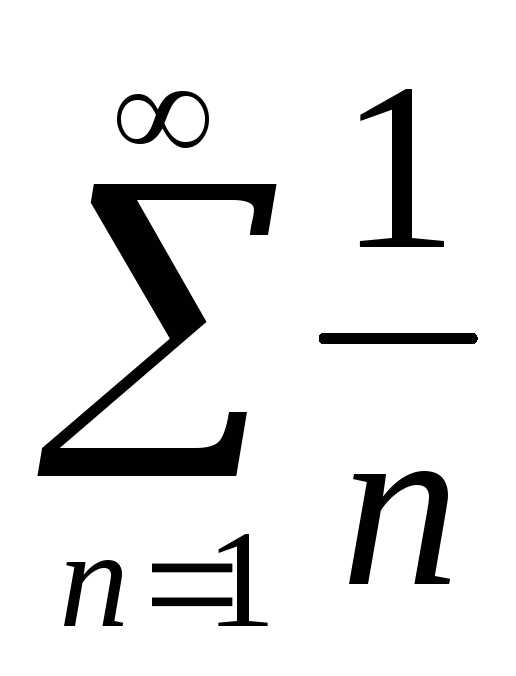 
называетсягармоническим, а ряд
вида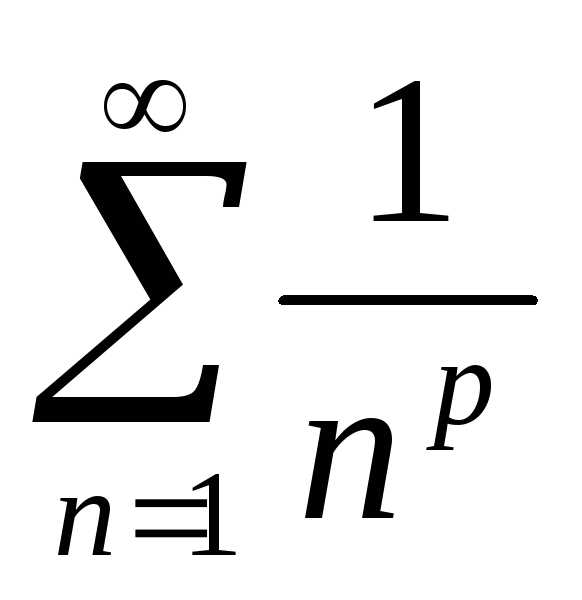
при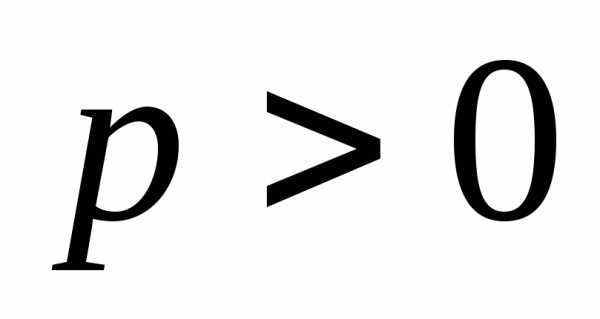
называется рядом Дирихле или
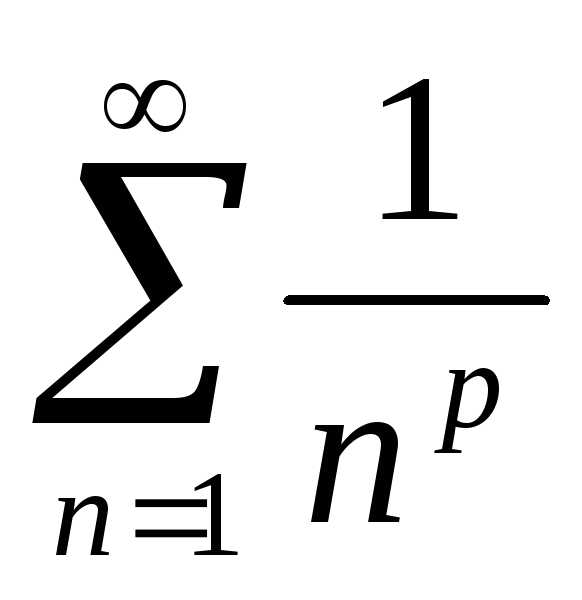—сходится
при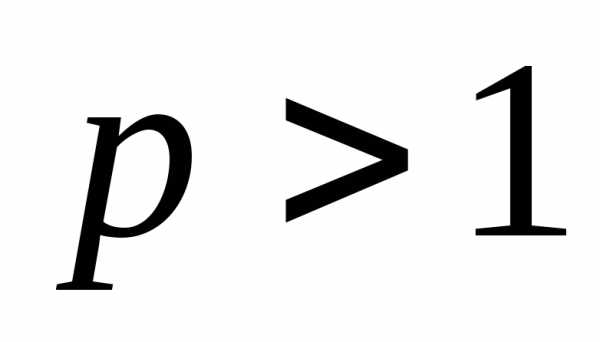
и расходится при
.
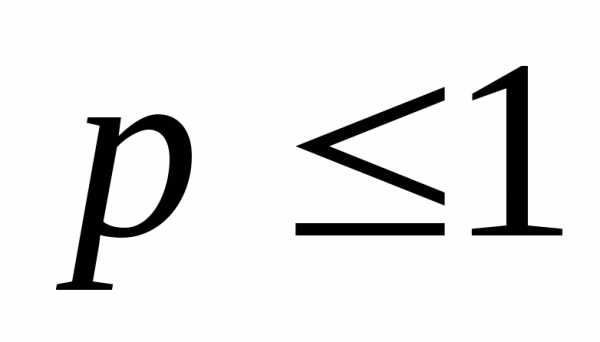Задача №7. Исследовать на сходимость
ряд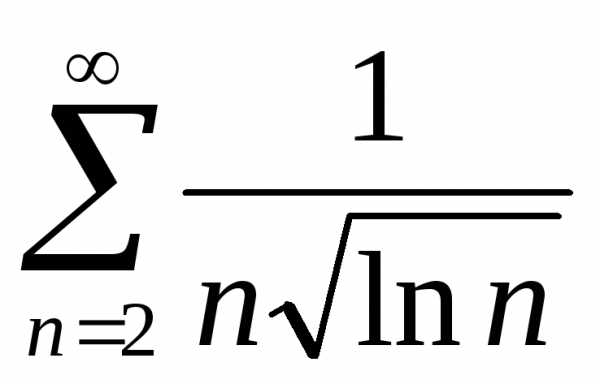
.
Решение.,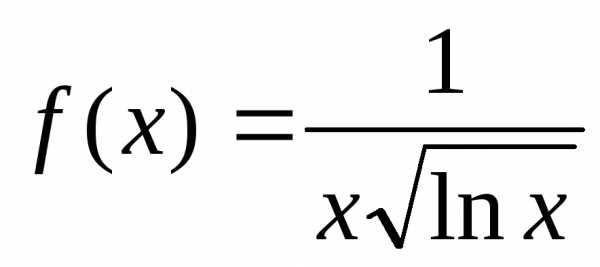
,
вычислим несобственный интеграл, используя метод замены переменной:
Согласно интегральному признаку из расходимости интеграла следует расходимость ряда.
Ответ: ряд расходится.
3. Признаки сравнения положительных рядов.
К числу достаточных признаков сходимости относятся признаки, позволяющие выяснить вопрос о сходимости некоторого ряда с помощью другого ряда, поведение которого в смысле сходимости нам известно. Такие признаки называются признаками сравнения.
Теорема 1.(признак сравнения рядов с положительными членами).
Если ряд с положительными членами
сравнить с другим рядом с положительными членами
сходимость или расходимость которого нам известна, и если начиная с некоторого номера
1). 
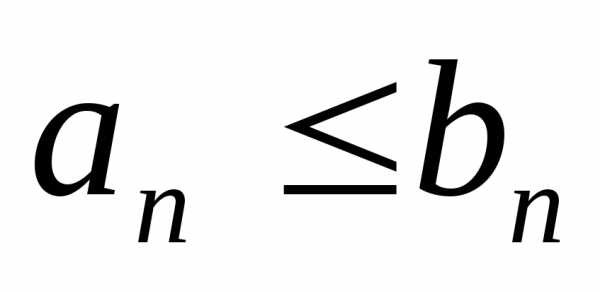и ряд
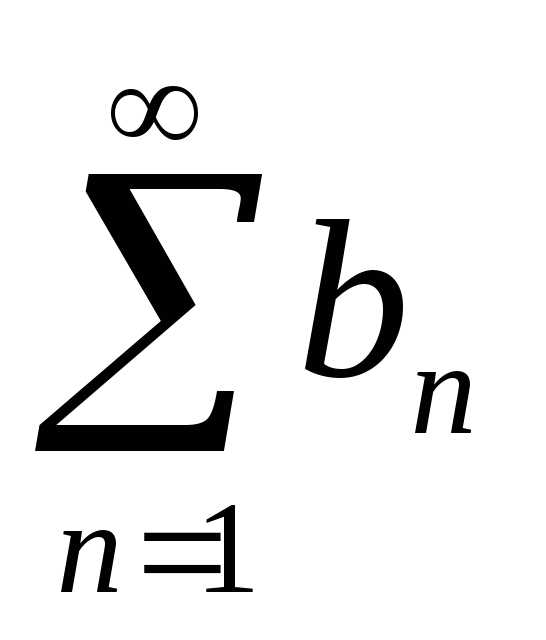сходится,
то ряд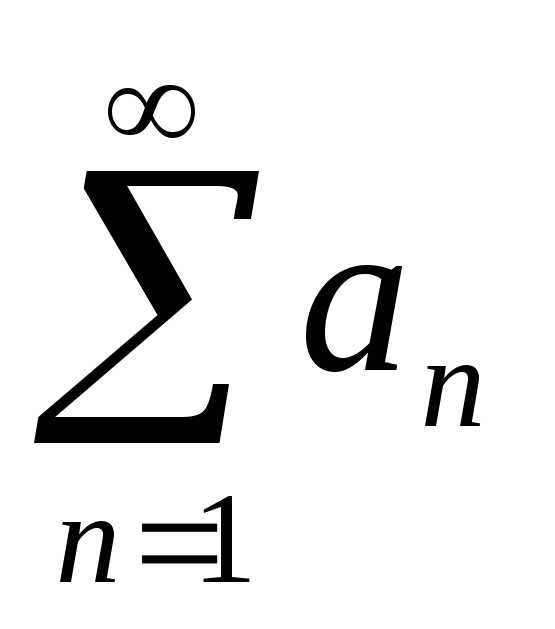
также сходится;
2). 
и ряд
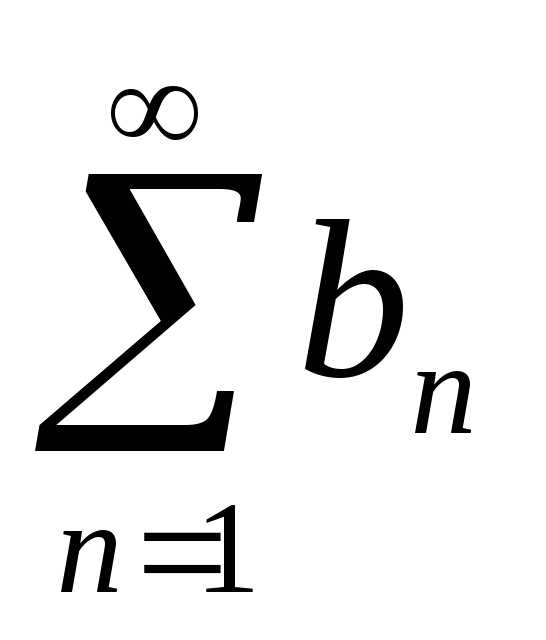расходится,
то ряд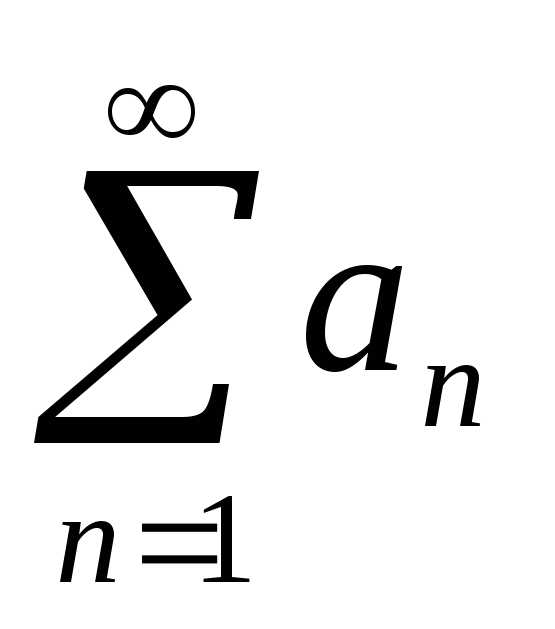
также расходится.
Заметим, что утверждения, обратные утверждениям 1) и 2) в условии теоремы неверны: если сходится ряд с меньшими членами, то о сходимости ряда с большими членами ничего определенного сказать нельзя, и наоборот, если расходится ряд с большими членами, то ряд с меньшими членами может быть как сходящимся так и расходящимся.
При использовании этого признака
исследуемый ряд чаще всего сравнивается
либо с бесконечной геометрической
прогрессией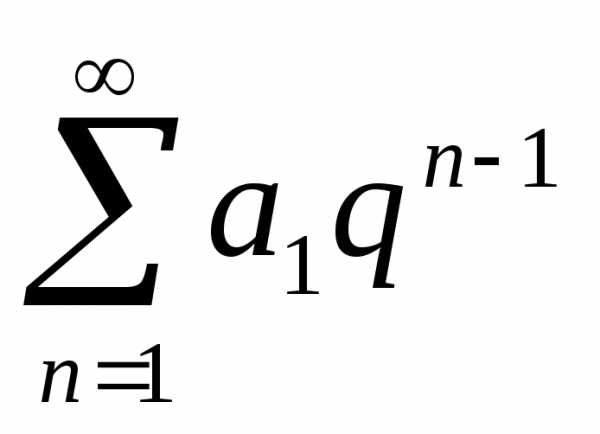 
,
либо с обобщенными гармоническими
рядами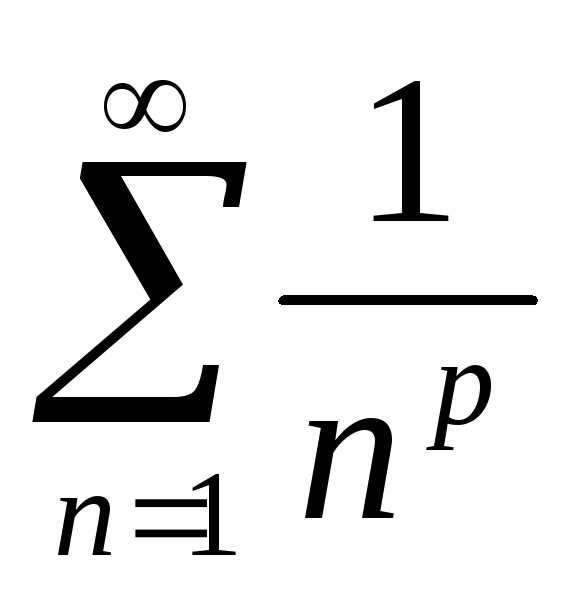
,
поведение которых в смысле сходимости
мы обсудили выше.
Задача №8. Исследовать на сходимость
ряд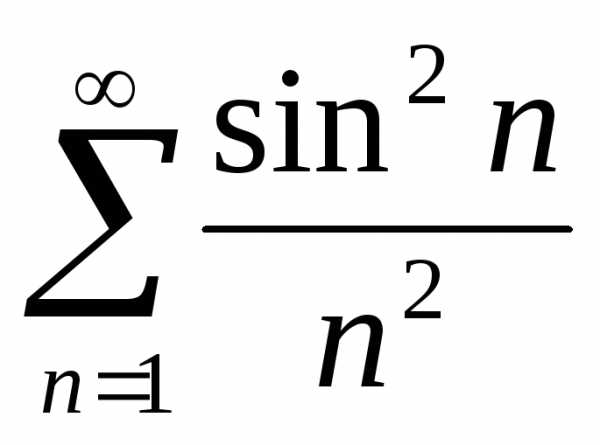
.
Решение.Сравним данный ряд с
обобщенным гармоническим рядом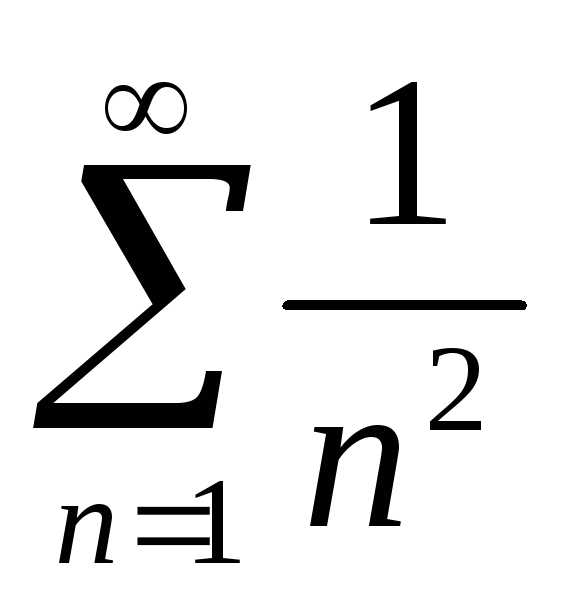
.
Каждый член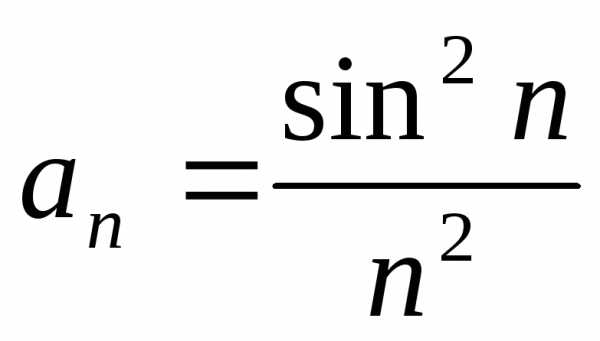 
данного ряда, начиная с
,
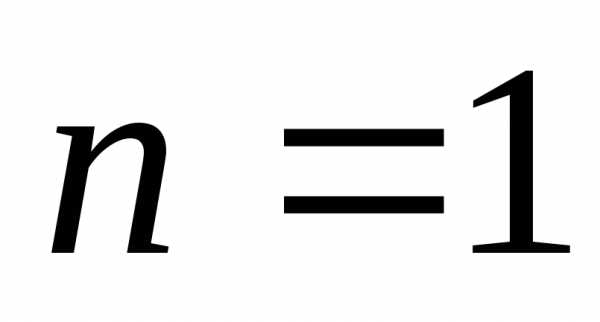меньше соответствующего члена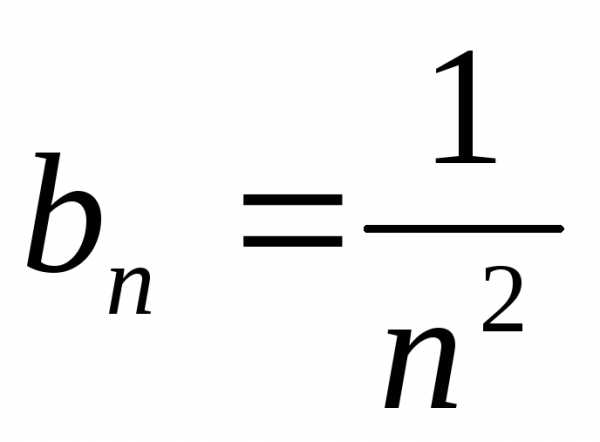
обобщенного
гармонического ряда:
,
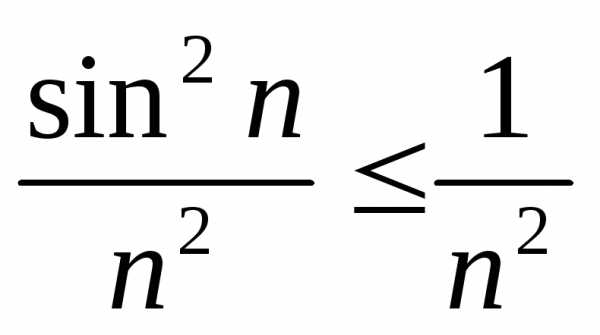и поскольку ряд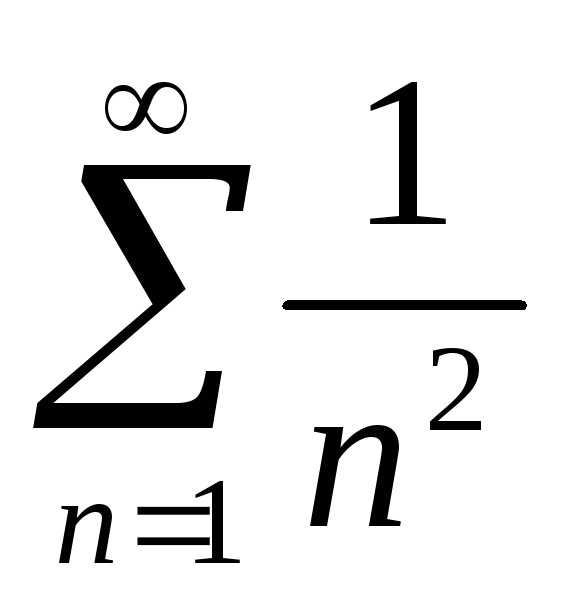 
сходится (
),
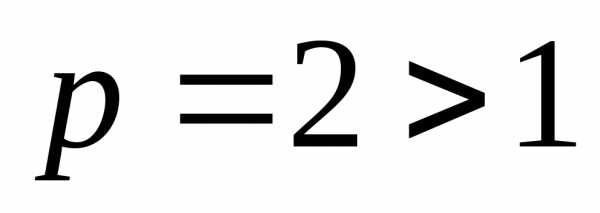то согласно утверждению 1) признака
сравнения исследуемый ряд также сходится.
Ответ: ряд сходится.
Задача №9. Исследовать на сходимость
ряд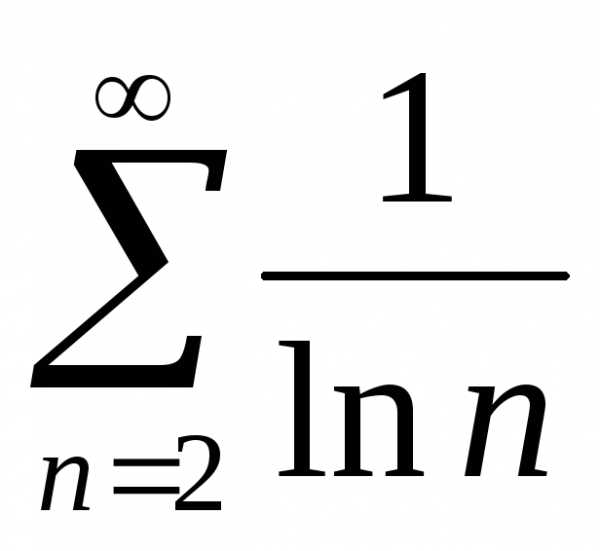
.
Решение.Сделаем предположение о том, что данный ряд расходится. Тогда используем утверждение 2) признака сравнения и подбираем расходящийся ряд с меньшими членами:
,
,
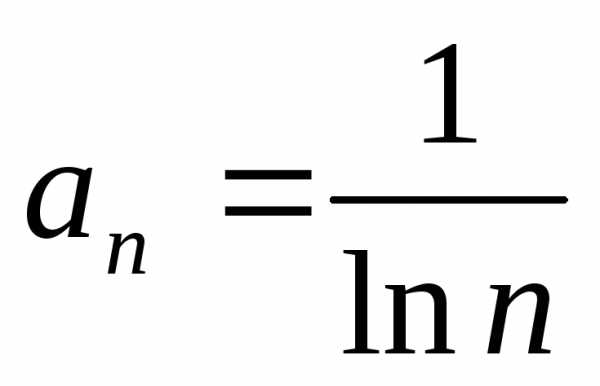Поскольку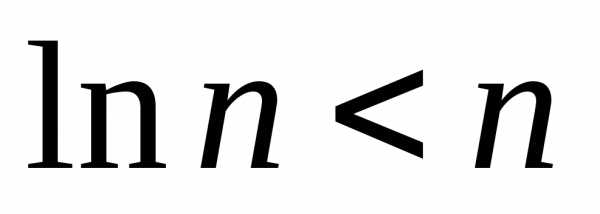 
для всех натуральных
,
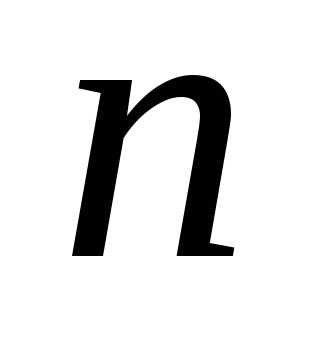то
.
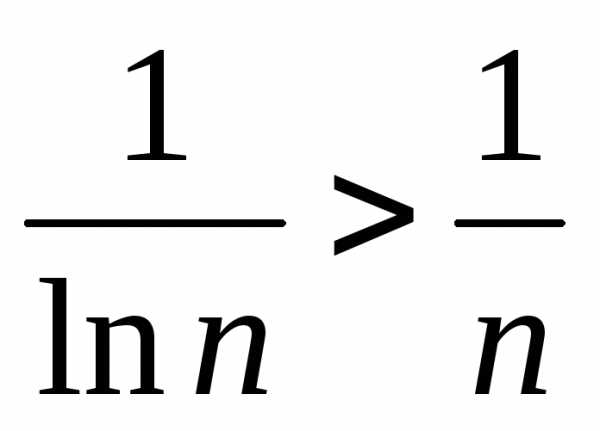Гармонический 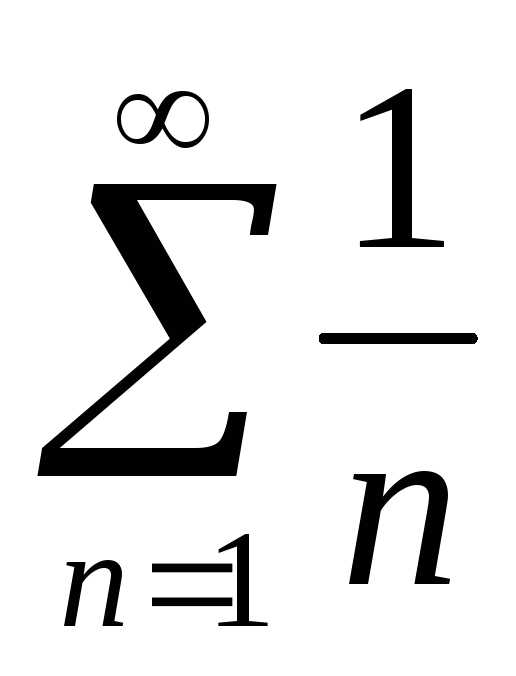ряд 
расходится, следовательно по признаку
сравнения ряд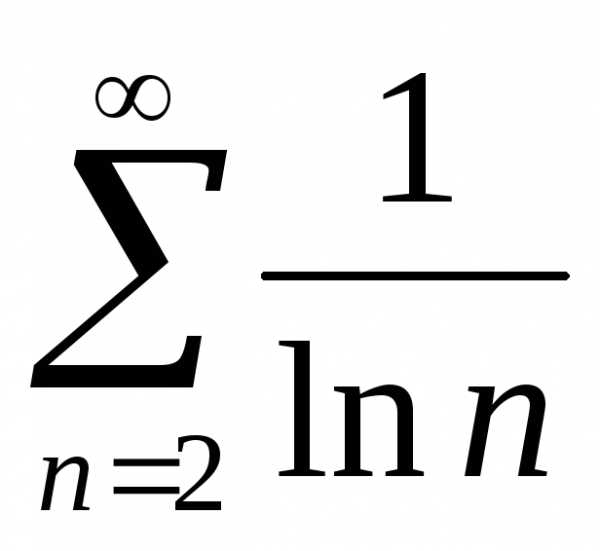
также расходится.
Ответ: ряд расходится.
Задача №10. Исследовать ряд на
сходимость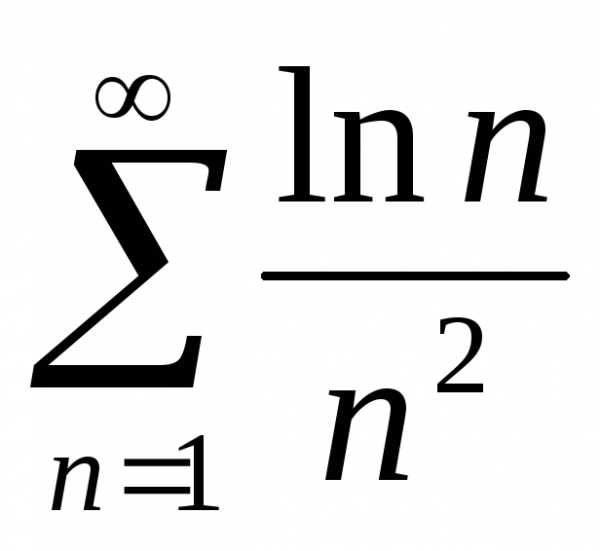
.
Решение.Главная особенность
использования признака сравнения
состоит в том, что здесь, в отличие от
других достаточных признаков сходимости,
необходимо делать предположение о том,
сходится ряд или расходится. Докажем
сходимость данного ряда. Для этого
докажем, что, начиная с некоторого номера
.
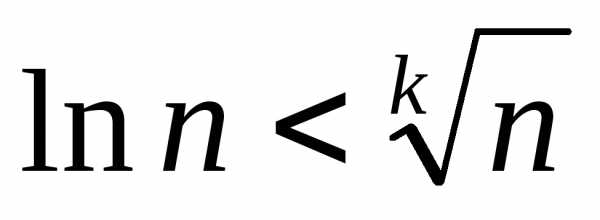Применяя правило Лопиталя (дифференцирование
по 
)
получим
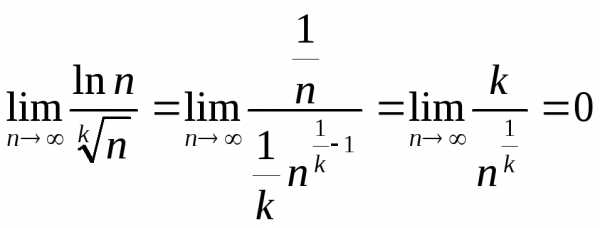
значит, начиная с некоторого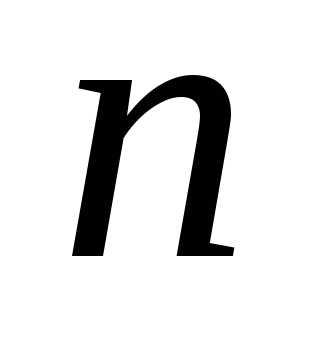 
,
функция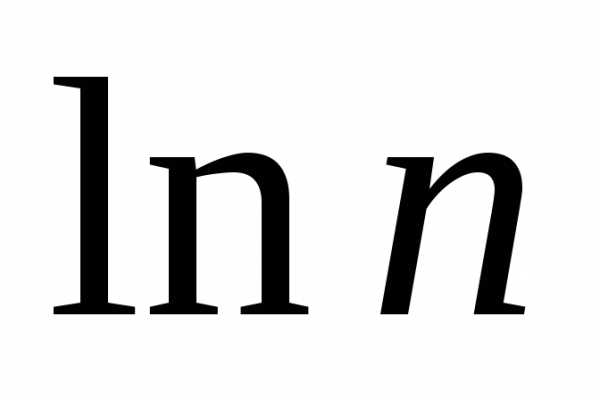
меньше
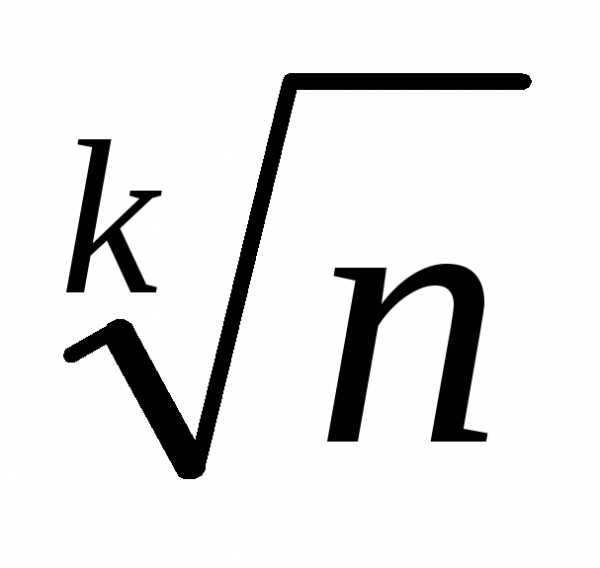для любого
.
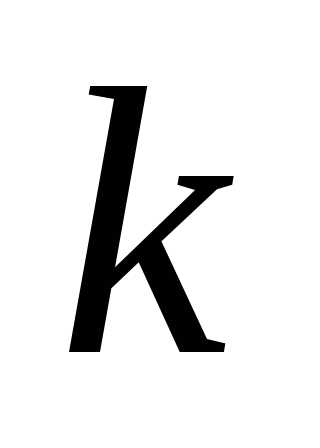Положим , тогда
,
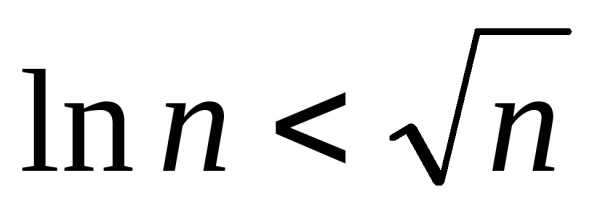откуда имеем
.
,
.
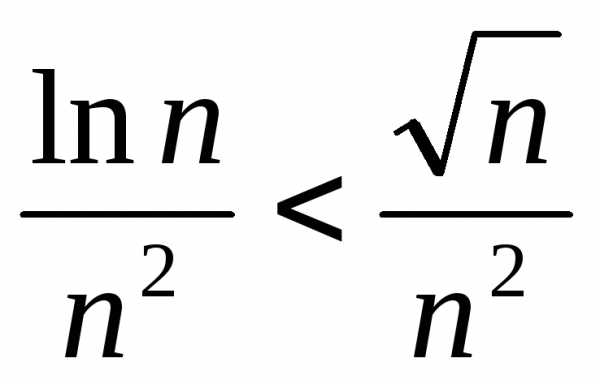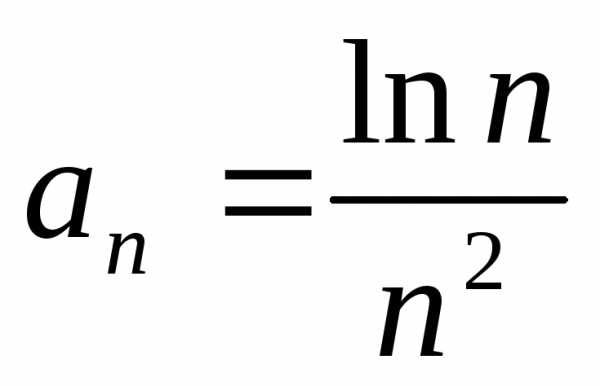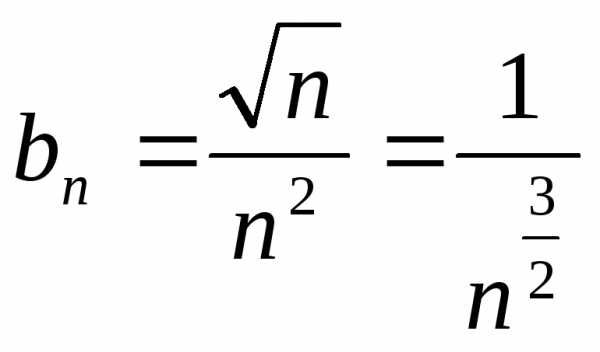Обобщенный гармонический ряд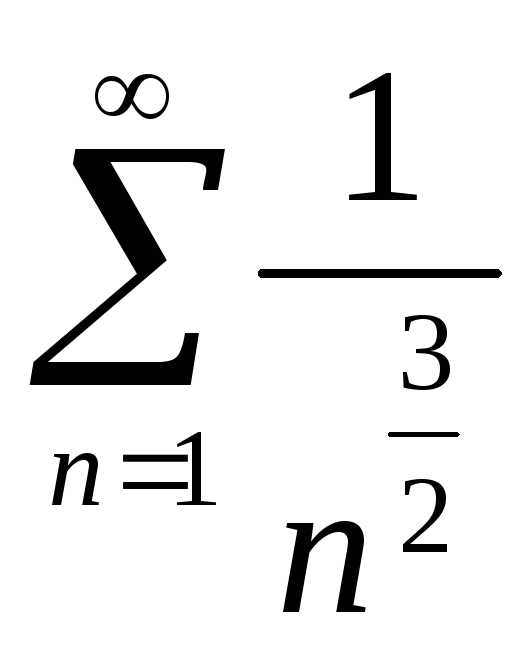 
сходится (
),
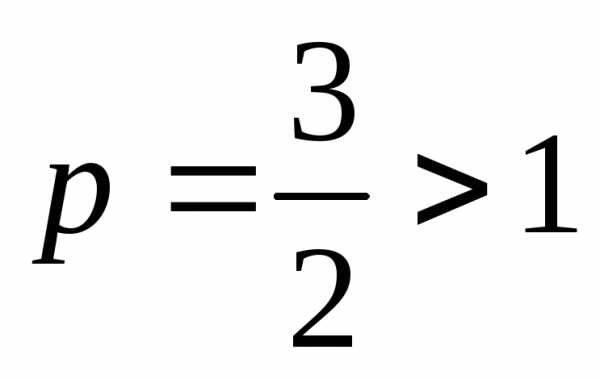следовательно, по признаку сравнения
ряд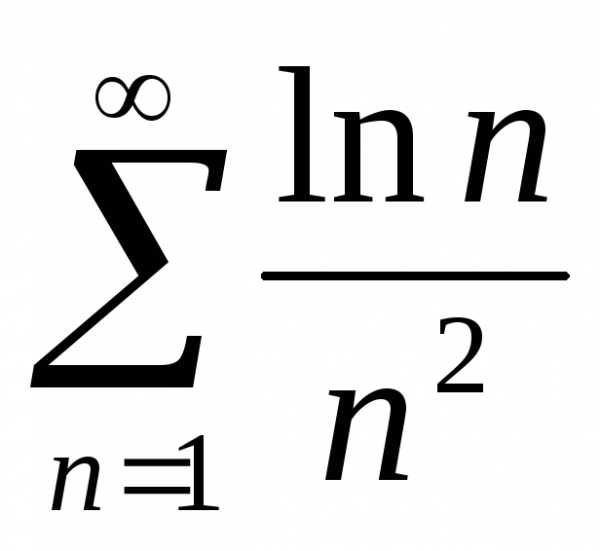
с меньшими членами также сходится.
Ответ: ряд сходится.
Сформулируем еще один признак сравнения.
Теорема 2. (обобщенный признак сравнения рядов с положительными членами).
Пусть даны два ряда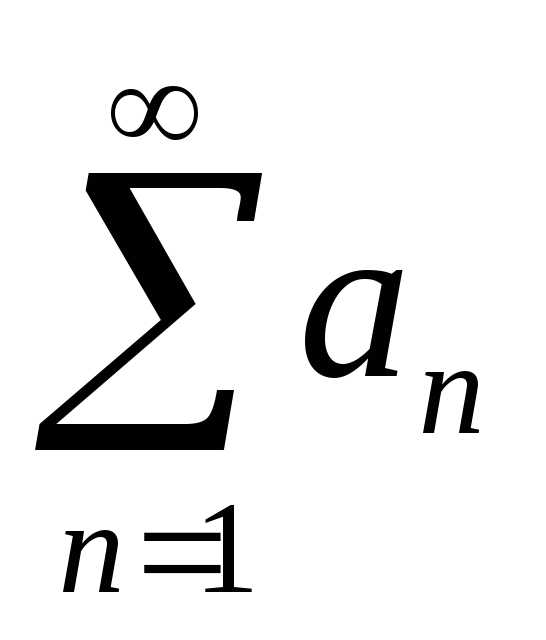 
и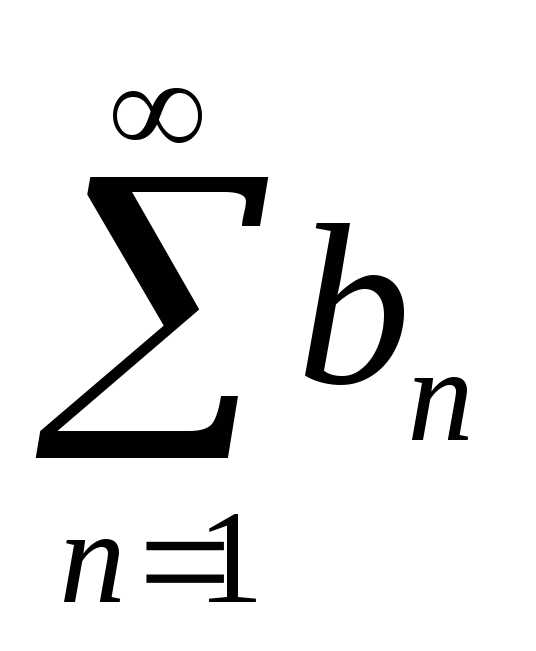
.
Если предел отношения общих членов этих
рядов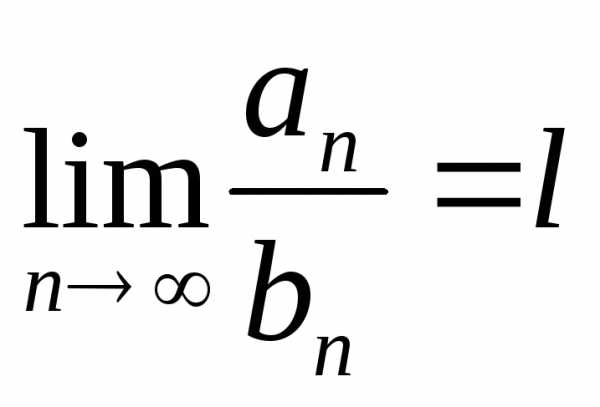
существует, конечен и не равен нулю, то
ряды одновременно сходятся или расходятся.
Задача №11.Исследовать на сходимость
ряд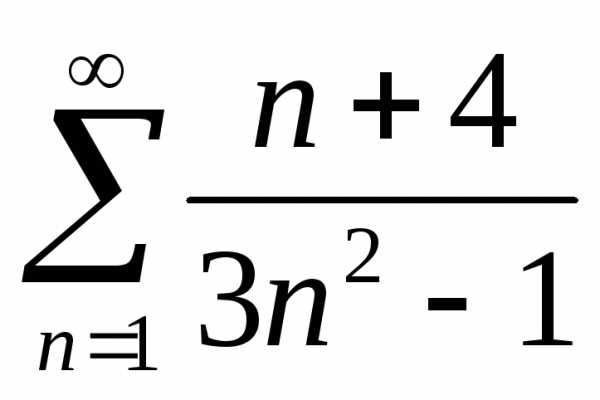
.
Решение.Обсудим сначала, каким
образом в этом случае подобрать
гармонический ряд. Очевидно, что главными
в числителе и в знаменателе являются
слагаемые, содержащие старшие степени
переменной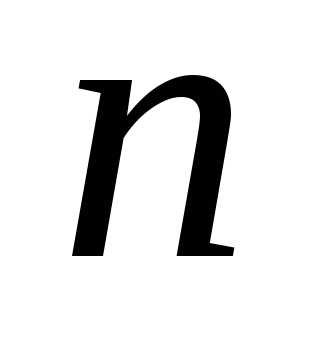
,
именно их и оставим при переходе к
гармоническому ряду:
.
Обозначим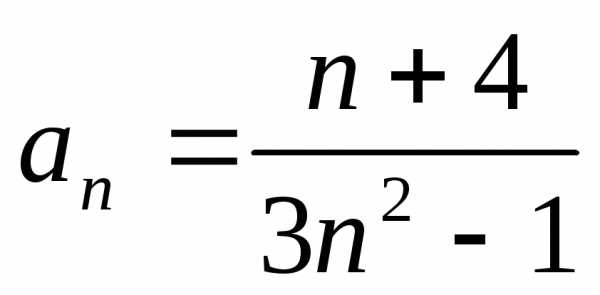 
,
.
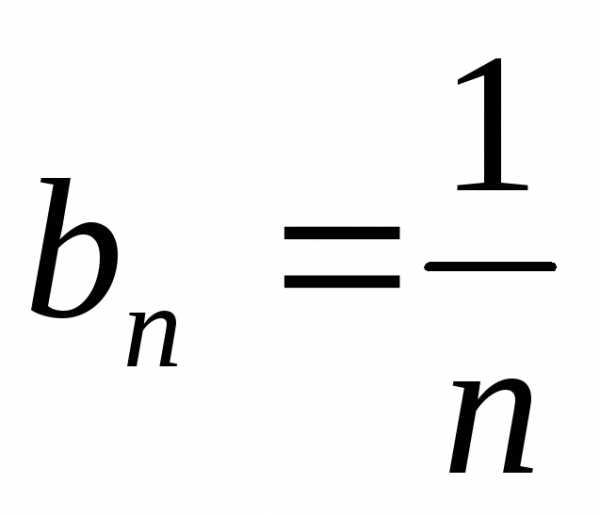Вычислим предел, который подтверждает, что ряды сходятся или расходятся одновременно:
.
Ряд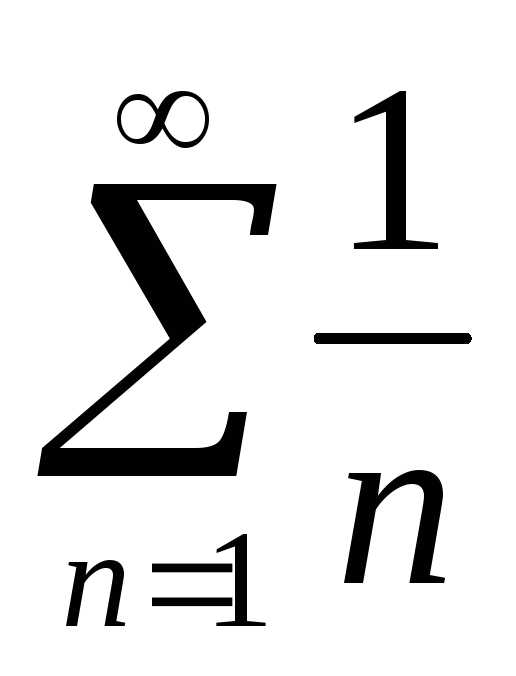 
расходится как гармонический.
Следовательно, по обобщенному признаку сравнения исходный ряд также расходится.
Ответ: ряд расходится.
Задача №12. Исследовать на сходимость
ряд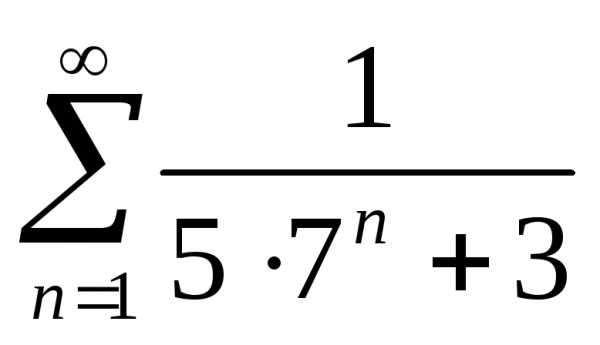
.
Решение.Сравним данный ряд с рядом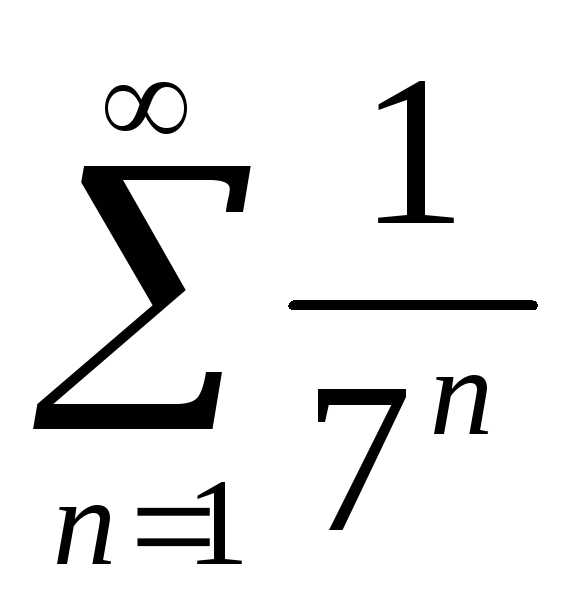
.
Докажем, что ряды ведут себя одинаково. Обозначим
,
,
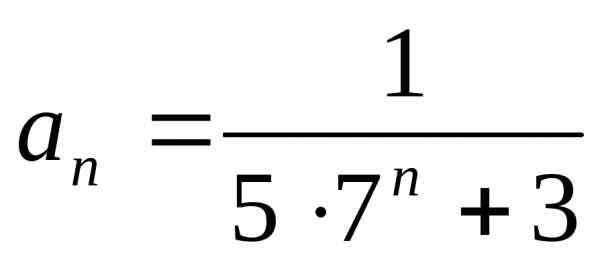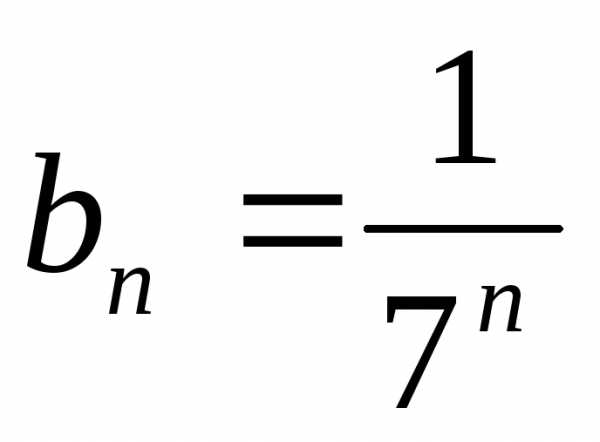тогда
.
Ряд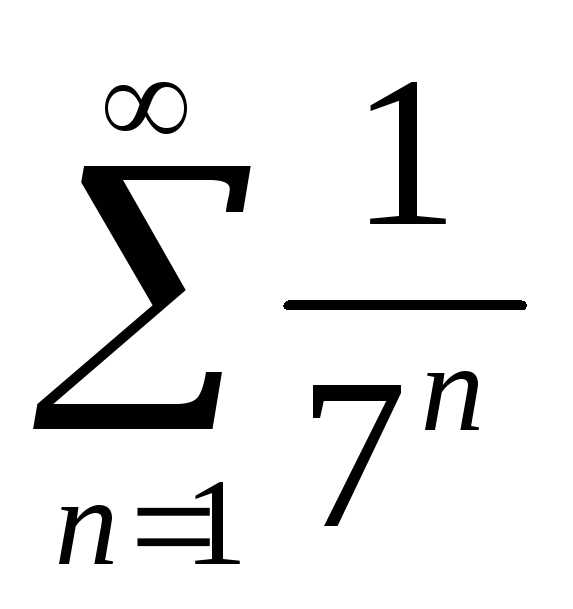 
состоит из членов бесконечно убывающей
геометрической прогрессии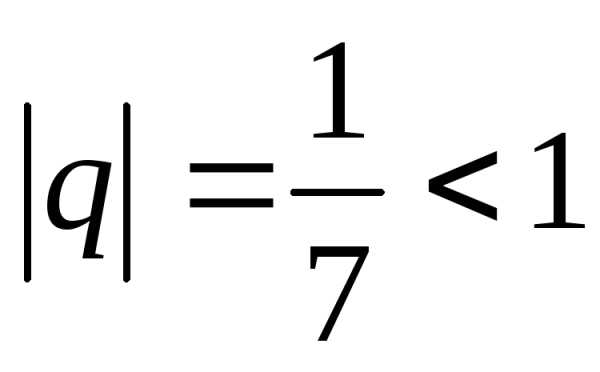
и, следовательно, сходится. По обобщенному
признаку сравнения сходится и исследуемый
ряд.
Ответ: ряд сходится.
Задача №13.Исследовать на сходимость
ряд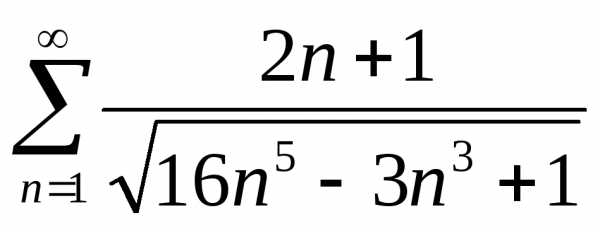
.
Решение. Сравним данный ряд с обобщенным гармоническим рядом:
.
Обозначим
,
.
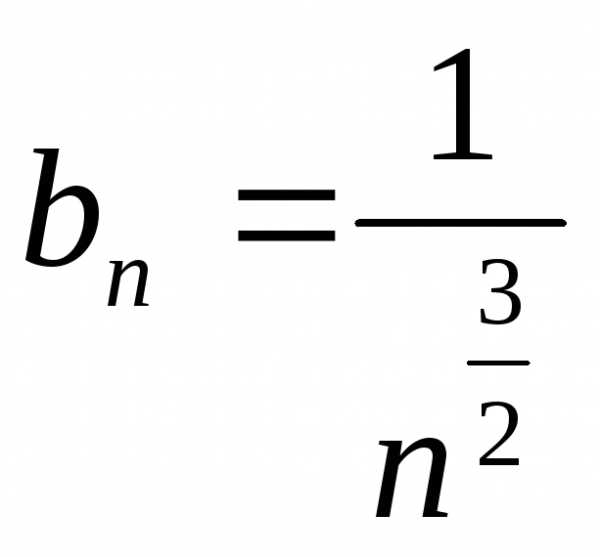Вычислим предел
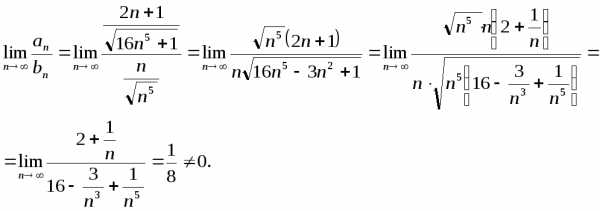
Следовательно, ряды в смысле сходимости ведут себя одинаково.
Ряд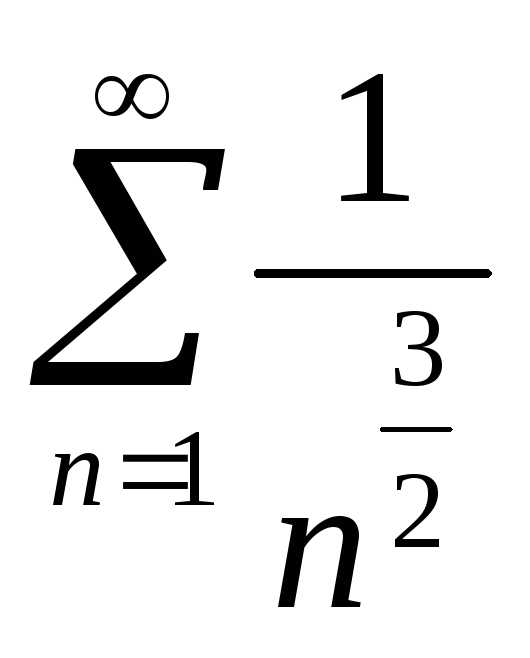 
сходится, поскольку является обобщенным
гармоническим,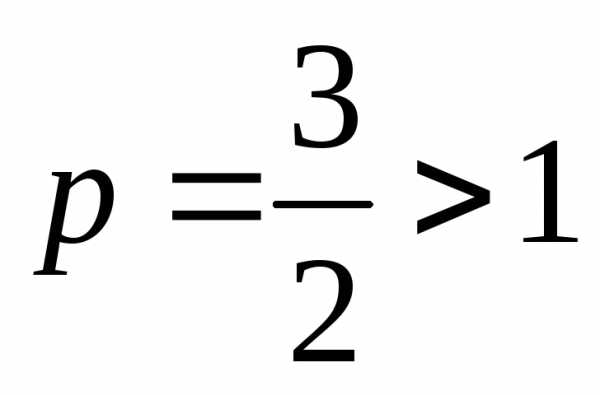
.
Тогда по обобщенному признаку сравнения
исходный ряд также сходится.
Ответ: ряд сходится.
Задача №14. Исследовать на сходимость
ряд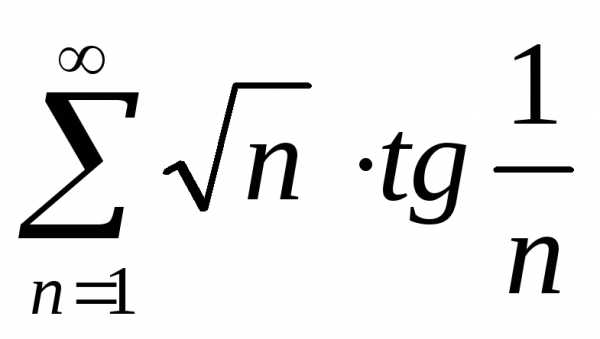
.
Решение.Подберем данному ряду обобщенный гармонический ряд так, чтобы ряды сходились или расходились одновременно:
.
Обозначим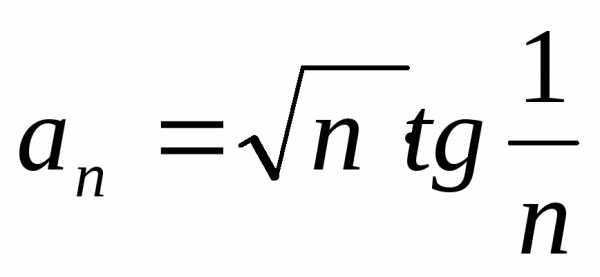 
,
,
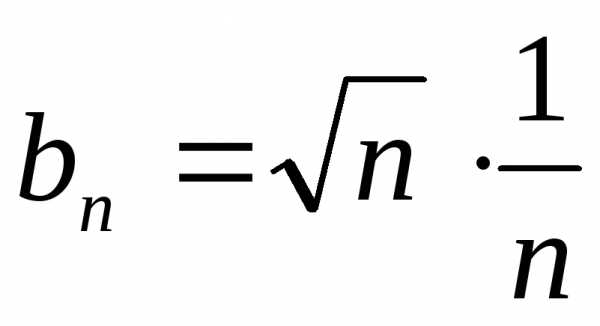тогда
Здесь использовалась формула
.
Обобщенный гармонический ряд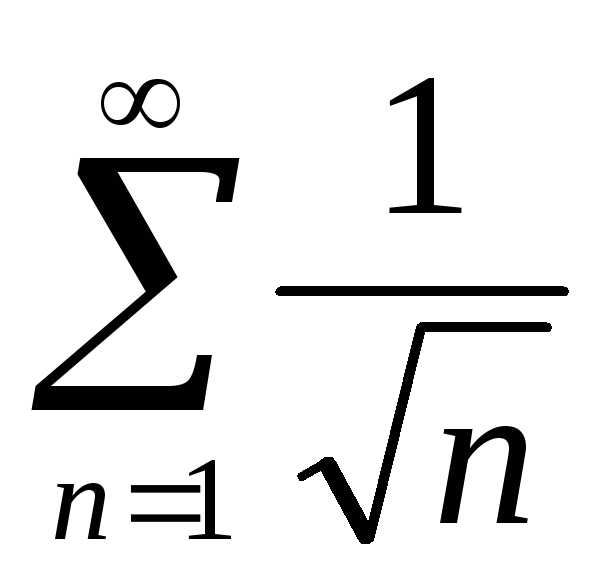 
расходится,
.
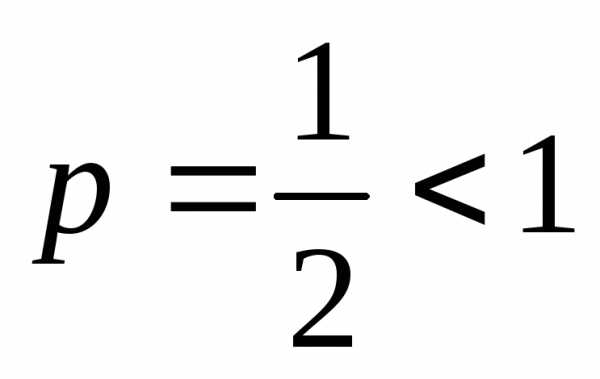Используя обобщенный признак сравнения,
делаем вывод о том, что исходный ряд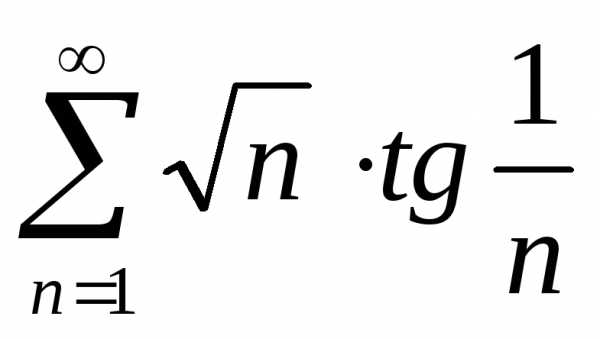
расходится.
Ответ:ряд расходится.
Завершая обсуждение признаков сравнения, добавим, что более простым из них в применении является обобщенный признак сравнения (теорема 2). Признак сравнения (теорема 1) более сложный, но, тем не менее, существуют ряды, которые исследуются на сходимость только с помощью этого признака (именно такие ряды рассмотрены в примерах). Это связано с невозможностью в некоторых случаях вычислить предел, и, следовательно, применить обобщенный признак сравнения.
studfiles.net
Исследовать сходимость рядов — matematiku5.ru
1.2.9. Пользуясь известными признаками сходимости, исследовать сходимость следующих рядов:
Воспользуемся признаком Даламбера:
При решении использовали – второй замечательный предел.
Так как – то данный ряд сходится.
По радикальному признаку Коши:
Так как – то данный ряд расходится.
По интегральному признаку Коши:
Ряд расходится.
1.3.9. Исследовать на сходимость знакочередующийся ряд:
Воспользуемся достаточным признаком сходимости знакопеременных рядов. Для этого определим сходимость ряда составленного из модулей членов данного ряда:
Воспользуемся признаком Даламбера:
Так как , то ряд, составленный из модулей членов данный ряд, сходится.
Таким образом, исходный ряд является абсолютно сходящимся.
Воспользуемся достаточным признаком сходимости знакопеременных рядов. Для этого определим сходимость ряда составленного из модулей членов данного ряда:
По интегральному признаку Коши:
Ряд, составленный из модулей членов данный ряд, расходится.
Исследуем исходный ряд по признаку Лейбница:
1. последовательность абсолютных величин членов ряда монотонно убывает:
2. Общий член ряда стремится к нулю, при этом сумма S ряда удовлетворяет неравенствам :
;
с погрешность вычисления равной .
Таким образом,
Ряд является условно сходящимся, т. к. ряд составленный из модулей членов данного рядя расходится, а данный ряд сходится по признаку Лейбница.
1.4.9. Найти область сходимости степенного ряда:
По признаку Даламбера:
Область сходимости ряда: => =>
При имеем ряд:
По интегральному признаку Коши:
Ряд расходится.
Тогда область сходимости ряда:
1.5.9. Разложить в ряд Маклорена функцию . Указать область сходимости полученного ряда:
Преобразуем функцию:
Разложим подынтегральную функцию в ряд Маклорена:
Тогда:
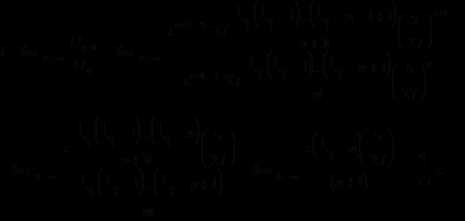
Область сходимости ряда: => =>
Тогда область сходимости ряда:
1.8.9. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.
Разложим подынтегральную функцию в ряд Маклорена:
Тогда:
Найдем значение интеграла:
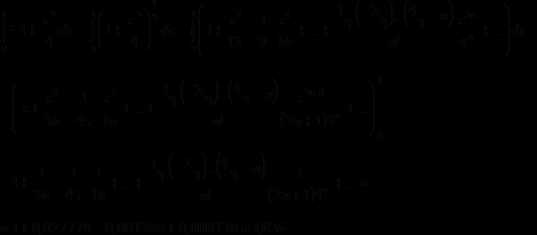
1.9.9. Найти разложение в степенной ряд по степеням х решения дифференциального уравнения (записать три первых, отличных от нуля члена этого разложения).
,
Будем искать решение уравнения в виде:
Здесь:
Будем искать:
при x=0
при x=0
Подставляем найденные значения производных в исходный ряд, получаем:
Окончательно:
4.1.9. Основные понятия и теоремы теории вероятностей:
Вероятность попадания в цель равна 0,003. Сколько нужно произвести выстрелов, чтобы с вероятностью, большей 0,94, можно было утверждать, что цель будет поражена?
По условию:
; ; ;
По формуле Бернулли:
Подставим исходные значения:
Найдем максимальное значение n, решая правую часть неравенства.
Чтобы найти максимум данной функции, найдем ее производную:
Найдем критические точки:
Тогда:
Тогда неравенство никогда не будет выполнено:
С вероятностью, большей 0,94, мы не можем утверждать, что цель будет поражена, если вероятность попадания в цель равна 0,003.
4.3.9. Схема повторных испытаний:
Из каждого десятка деталей 9 удовлетворяют стандарту. Найти вероятность того, что из 50 взятых со склада деталей число стандартных окажется между 42 и 48.
По интегральной теореме Лапласа: Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна (0 при этом , событие наступит не менее k1 раз и не более k2 раз, приближенно равна:
Здесь:
– функция Лапласа
;
Значения функции Лапласа находим по специальной таблице.
Найдем вероятность появления стандартной детали и вероятность появления нестандартной:
;
Подставим все известные значения:
Функция Лапласа (по таблице):
Искомая вероятность:
4.4.9. Случайные величины:
Дискретная случайная величина Х имеет только два возможных значения: и , причем . Вероятность того, что Х примет значения , равна 0,2. Найти закон распределения Х, зная математическое ожидание и среднее квадратичное отклонение .
Запишем закон распределения Х в общем виде:
Впишем все известные значения:
X | ||
P(X) | 0,2 | 0,8 |
Найдем возможные значения Х:
Находим математическое ожидание:
Подставляем все известные значения:
Находим среднее квадратичное отклонение:
Находим дисперсию:
Подставляем все известные значения:
Составим систему уравнения для нахождения возможных значений Х:
Подставляем все известные значения:
=>=>=>
или
Тогда:
или
Принимая во внимание условие выбираем пару: и
Запишем закон распределения Х:
4.5.9. Случайные величины:
Случайная величина Х задана функцией распределения:
Выбрать коэффициенты a, b и c таким образом, чтобы данное распределение соответствовало случайной величине непрерывного типа, написать выражение для плотности р(х).
По условию задачи функция F(x) непрерывна. Выберем коэффициенты a, b и c таким образом, чтобы не было разрыва, для этого составим систему уравнений:
Тогда:
=> => => =>
Выберем: , тогда , .
Подставим найденные значения в функцию распределения:
Плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке и является производной функции распределения.
matematiku5.ru
Как исследовать на сходимость ряд
Вам понадобится
- Учебник по высшей математике, таблица признаков сходимости
Инструкция
По определению ряд называется сходящимся, если существует такое конечное число, которое заведомо больше суммы элементов этого ряда. Другими словами, ряд сходится, если сумма его элементов конечна. Выявить тот факт, является сумма конечной или бесконечной помогут признаки сходимости ряда.Одним из самых простых признаков сходимости является признак сходимости Лейбница. Его мы можем использовать, если рассматриваемый ряд является знакопеременным (то есть каждый последующий член ряда меняет знак с «плюса» на «минус»). По признаку Лейбница, знакопеременный ряд является сходящимся в случае, если последний член ряда по модулю стремится к нулю. Для этого в пределе функции f(n) устремляем n к бесконечности. Если этот предел равен нулю, то ряд сходится, в противном случае — расходится.
Еще один распространенный способ проверить ряд на сходимость (расходимость) — использование предельного признака Даламбера. Для его использования мы делим n-ый член последовательности на предыдущий ((n-1)-ый). Это отношение мы вычисляем, его результат берем по модулю (n снова устремляем к бесконечности). Если мы получаем число меньшее единицы — ряд сходится, иначе — ряд расходится.
Радикальный признак Даламбера чем-то похож на предыдущий: мы извлекаем корень n-ой степени из n-ого ее члена. Если мы получаем в результате число, меньшее единицы, то последовательность сходится, сумма ее членов — конечное число.
В ряде случаев (когда мы не можем применить признак Даламбера) выгодно воспользоваться интегральным признаком Коши. Для этого заносим функцию ряда под интеграл, дифференциал берем по n, расставляем пределы от нуля до бесконечности (такой интеграл называется несобственным). Если численное значение этого несобственного интеграла равно конечному числу, то ряд является сходящимся.
Иногда для того чтобы узнать, к какому типу относится ряд, необязательно пользоваться признаками сходимости. Можно просто сравнить его с другим сходящимся рядом. Если ряд меньше заведомо сходящегося ряда, то он также является сходящимся.
www.kakprosto.ru
Иллюстрированный самоучитель по Maple 9 › Числовые и функциональные ряды › Исследование рядов на сходимость [страница — 80] | Самоучители по математическим пакетам
Исследование рядов на сходимость
Существенным является класс задач, в которых предусматривается исследование рядов на предмет сходимости. В этом случае нет необходимости суммировать ряд – нужно только сделать вывод, сходится ряд или расходится.
Рассмотрим примеры исследования рядов на сходимость.
Задача 3.3
Исследовать на сходимость ряд .
Задаем общую зависимость члена ряда от индекса суммирования.
Проверяем необходимое условие сходимости ряда.
Необходимое условие выполнено, поэтому далее вступают в силу более существенные критерии – в данном случае признак Даламбера.
Проверяем, меньше ли это значение, чем 1.
Таким образом, по признаку Даламбера ряд сходится. В следующих примерах для исследования рядов на сходимость предлагается специальная процедура.
samoychiteli.ru