Как находить объем: «По какой формуле можно найти объем?» — Яндекс Кью

4. Объем фигур — Фигуры В Пространстве

4. Объем фигур     Объем — это величина фигуры в дину, высоту и ширину, измеряемая в кубических единицах.     Свойства объемов: Равные тела имеют равные объемы. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.     1. Объем куба равен кубу длины его граней.     Формула объема куба:   V =  a 3      где V — объем куба,             a — длина грани куба.      2. Объем призмы равен произведению основания призмы на ее высоту.      Формула объема призмы:  V =  So h      где V — объем призмы,             So — площадь основания,            h — длина высоты.      3. Объем параллелепипеда равен произведению площади снования на высоту.     Формула объема параллелепипеда:  V =  So · h     где  V  — объем параллелепипеда,            So  — площадь основания,             h  — длина высоты.     Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.  Формула объема прямоугольного параллелепипеда:  V =  a · b · h          где  V  — объем прямоугольного параллелепипеда,              a  — длина,              b  — ширина,              h  — высота.     4. Объем пирамиды равен трети от произведения площади ее основания на высоту.     Формула объема пирамиды:  V =  1   So · h 3                                                                     где  V  — объем пирамиды,             So  — площадь основания пирамиды,               h  — длина высоты пирамиды.     5. Объем цилиндра равен произведению площади его основания на высоту.     Формулы объема цилиндра: V =  π R 2  h V =  So h     где  V  — объем цилиндра,              So  — площадь основания цилиндра,              R  — радиус цилиндра,              h  — высота цилиндра,              π = 3,141592 .     6. Объем конуса равен трети от произведения площади его основания на высоту.     Формулы объема конуса:  V =  1   π R 2  h 3 V =  1   So h 3     где  V  — объем конуса,            So  — площадь основания конуса,             R  — радиус основания конуса,             h  — высота конуса,             π = 3,141592 .     7. Объем шара равен четырем третьим от его радиуса в кубе помноженного на число.     Фор мула объема шара: V =  4 π R 3 3     где  V  — объем шара,             R  — радиус шара,             π = 3. 141592 .

По какой формуле вычисляется объем прямоугольного параллелепипеда? / Справочник :: Бингоскул

Параллелепипед – многогранник, состоящий из шести четырехугольных поверхностей с попарно параллельными сторонами. Различают несколько видов параллелепипедов в зависимости от вида четырехугольников, лежащих в их основе. Рассмотрим, какими они бывают, чем отличаются. Научимся находить площадь и объем прямоугольного и наклонного параллелепипедов по известным формулам.

Прямоугольный параллелепипед

Кубоидом или прямоугольным называется шестигранный многогранник с прямоугольниками в основании. Его противоположные поверхности взаимно параллельны, а сходящиеся в одной вершине – перпендикулярны. Ребра, выходящие из одной вершины, называются измерениями.

Свойства геометрического тела:

• Диагонали многогранника в месте пересечения делятся на равные отрезки.
• Место пересечения диагоналей – центр симметрии геометрического тела.
• Размеры противоположных граней равны.
• Квадрат диагонали равен сумме квадратов измерений.

Рассмотрим формулы объема прямоугольного параллелепипеда и его площади.

Как найти площадь параллелепипеда

Площадью называется численная характеристика плоской фигуры, показывающая, сколько квадратов со стороной, равной единице, поместятся на её поверхности. Вычисляется как сумма площадей шести поверхностей в виде прямоугольников.

Формула площади:

S = 2 (ab + bc + ac),

где: ab, bc и ac – площади поверхностей.

Так как стороны парные, получившуюся сумму умножают на два.

Для примера, имеем тело с размерами:

a = 3, b = 4 и c = 5 см.

Полная площадь поверхности равна:

S = 2 * (3*4 + 4*5 + 5*3) = 2 * (12 + 20 +15) = 2 * (47) = 94 см.

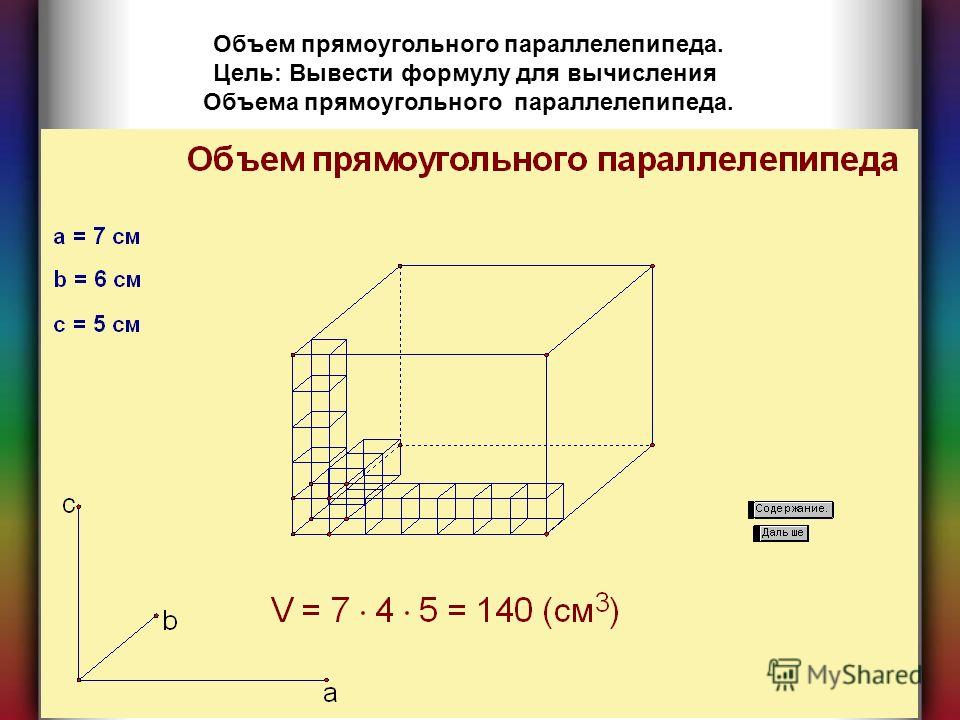
Объем параллелепипеда

Объемом называется численная характеристика тела, отражающая занимаемое им пространство. Определяется как количество кубов со стороной единица, которое поместится в многоугольнике.  

Объем прямоугольного параллелепипеда вычисляется по формуле: V = a * b * c, где

a, b, c – размеры измерений, выходящих из одной точки, или длина, ширина и высота многогранника.

Чтобы найти объем прямоугольного параллелепипеда по приведенной формуле, в нее подставляют размеры граней многоугольника, например:

• высота – 4 см;
• ширина – 3 см;
• глубина – 5 см.

V = 4* 3 * 5 = 60 см³.

Измеряется в кубических единицах – сантиметрах, метрах и т.д. либо литрах: 1 литр равен 1 дециметру кубическому.

Физический смысл объема прост:

• по высоте в параллелепипед поместится 4 куба с гранью 1 см;
• по ширине – 3 штук;
• по длине – 5 кубиков.

Вторая формула понадобится, когда в исходных данных есть площадь одной из поверхностей (S_осн) и длина третьей грани (h) или высота.

V = S_осн* h, здесь:

Смысл вычислений остается прежним – перемножить площадь поверхности на длину третьей стороны тела.

Объем наклонного параллелепипеда

К наклонным параллелепипедам относят четырехугольные призмы с параллелограммом в основании, боковые грани которого относительно него расположены под углом, отличным от 90°.

Площадь и объем наклонного параллелепипеда вычисляются по тем формулам, что и прямоугольного: V = S_осн * h или V = a * b * c.

Площадь определяются иначе, хоть и равна сумме поверхностей боковых граней и оснований.

S = S₁ + S₂ +S_осн. Боковые поверхности – прямоугольники, их площади S₁ b S₂ равны производным ширины на длину прямоугольников, которыми они представлены: a*c и a*b. Размеры оснований – параллелограммов – вычисляются так: S_осн = b * h.

S = 2ac + 2ab + 2 bh.

Мы рассмотрели способы, как найти объем основных параллелепипедов по разным формулам в зависимости от исходных данных. В сложных задачах придется применять иные геометрические и тригонометрические формулы для определения требуемых данных.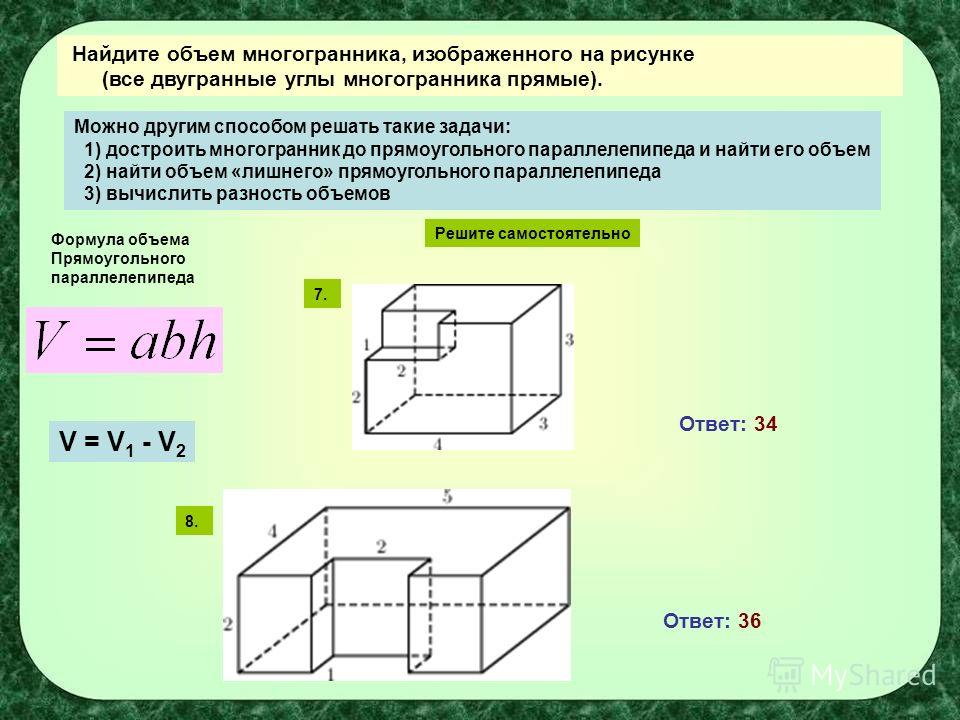

Как рассчитать объем

Примечание: эта страница содержит устаревшие ресурсы, которые больше не поддерживаются. Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.

Что такое объем?

Объем показывает, сколько места занимает объект. Иногда вы можете услышать такие вопросы, как «Какова вместимость коробки?» или «сколько может вместить коробка?» Вы можете предположить, что эти вопросы потребуют расчета объема.
Примечание. Если быть совсем умным, объем и вместимость не всегда совпадают — представьте себе коробку с очень толстыми стенками!

Вычисление объема

Объем измеряется в кубах (или кубических единицах).

Сколько кубиков в этой прямоугольной призме (прямоугольнике)?

Мы можем посчитать кубики, хотя быстрее взять длину, ширину и высоту и использовать умножение. Прямоугольная призма выше имеет объем 48 кубических единиц.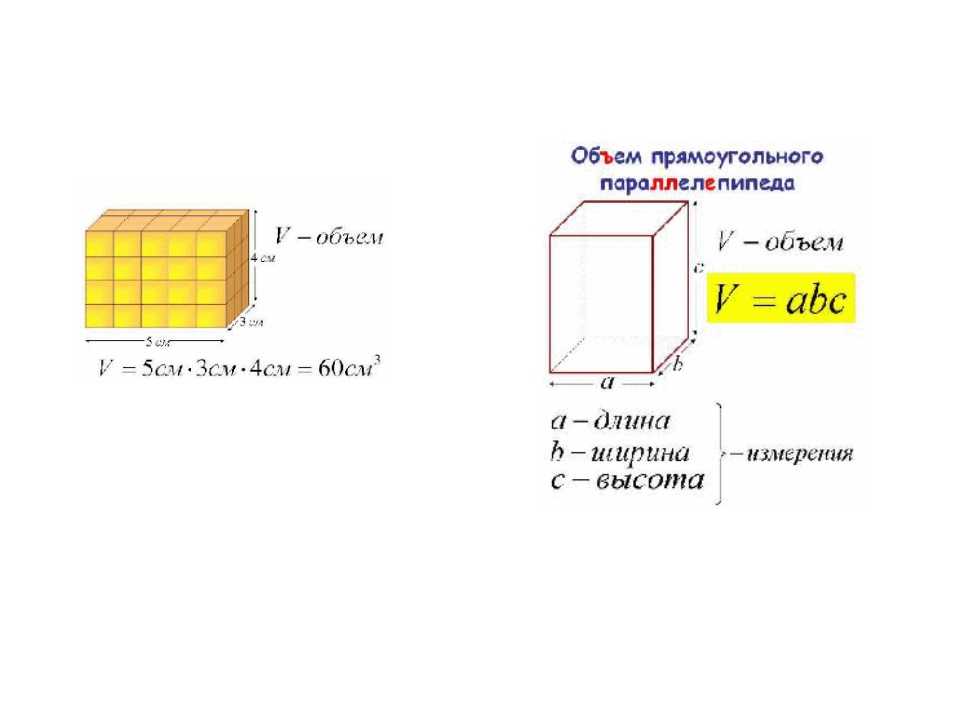

Объем прямоугольной призмы = длина х ширина х высота

Примеры вычисления площади прямоугольника

Нам нужно сделать два умножения, чтобы вычислить объем. Мы вычисляем площадь одной грани (или стороны) и умножаем ее на высоту. В приведенных ниже примерах показано, как это сделать тремя способами.

Обратите внимание, что мы получаем один и тот же ответ независимо от того, с какой стороны мы находим область.

Когда ваш ребенок начинает работать с площадью и периметром, он или она обычно будет работать с двумя измерениями – квадратами, прямоугольниками, треугольниками и т. д., которые отображаются на бумаге как плоские – глубины или третьего измерения нет. Работа с объемом включает в себя 3 измерения. Убедитесь, что ваш ребенок знает об этом и не думает о кубах и других трехмерных фигурах, изображенных на бумаге, как о еще одной «фигуре на странице». Покажите им настоящие коробки и покажите, как их можно нарисовать (или представить) на двухмерном листе бумаги. Другими словами, убедитесь, что установлена ​​связь между тем, что на бумаге, и тем, что это представляет в реальном мире.

Убедитесь, что вашего ребенка не смущает использование громкость , когда речь идет о громкости.

Единицы измерения объема

Существуют очень большие различия между единицами измерения объема. Например, в 1 метре 100 сантиметров, а в кубическом метре 1 000 000 (да, миллион) кубических сантиметров.

Почему такая большая разница? Потому что в объеме у нас есть не только длина; у нас есть длина, ширина и высота. Пример с кубиком сахара ниже показывает это.

Сколько сахара? 1 м ³  или 1 000 000 см ³

Представьте, что вы наполняете очень большую коробку (она должна быть 1 метр в ширину, 1 метр в длину и 1 метр в высоту) кубиками сахара (с каждой стороной 1 сантиметр).

1 000 000 см ³  в 1 м ³  – будьте осторожны, чтобы не было слишком много сахара!

Существуют и другие единицы измерения объема; кубические дюймы, кубические футы, кубические ярды — все это единицы, используемые для измерения объема. Миллилитры, литры, галлоны также используются особенно при измерении жидкостей.

Не забудь пи 3

Мы пишем кубические размеры, используя маленькую 3 рядом с единицей измерения. Пишем мм 3 , см 3 , м 3 , км 3 , см 3 Можно сказать «85 сантиметров в кубе» или «85 кубических сантиметров»

Примеры расчета объема прямоугольных призм

Объем цилиндра

Расчет объема цилиндра включает умножение площади основания на высоту цилиндра. Основание цилиндра круглое, и формула площади круга: площадь круга = πr ²  . Здесь больше о площади круга.

Примечание. В приведенных ниже примерах мы будем использовать 3,14 в качестве приблизительного значения π (Пи).

Пример расчета объема цилиндра

Объем конуса

Объем конуса равен одной трети объема цилиндра с соответствующей высотой и площадью основания. Это дает формулу объема конуса, как показано ниже.

Пример расчета объема конуса

Объем сферы

Формула объема сферы показана ниже.

Пример вычисления объема сферы

Рабочий лист объема для печати Генераторы

Используйте приведенный ниже рабочий лист, чтобы попрактиковаться в вычислении объемов.

• Нахождение объема в кубических единицах – прямоугольные призмы и композиты
• Объемы прямоугольных призм
• Объемы прямоугольных призм
• Объемы объектов «реального мира», например. коробок с хлопьями
• Расчет объемов, например. треугольных призм и цилиндров

Здесь вы получите другие рабочие листы по геометрии по периметру, площади и т. д.

Ссылка/ссылка на нас

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника.

Мы ценим вашу поддержку!

• Как рассчитать объем

• «Как рассчитать объем». Помощь в математике . По состоянию на 22 ноября 2022 г. https://helpingwithmath.com/calculate-the-volume/.

• «Как рассчитать объем». Помощь с математикой , https://helpingwithmath.com/calculate-the-volume/. По состоянию на 22 ноября 2022 г.

• Как рассчитать объем. Помощь с математикой. Получено с https://helpingwithmath.com/calculate-the-volume/.

Калькулятор объема

| Pi Day

Sphere

Radius

Volume

Cylinder

Radius

Height

Volume

Cube

Volume

Cone

Radius

Height

Volume

Rectangular cuboid

Length

Высота

Объем

Вернуться на страницу калькуляторов

Калькулятор объема определит объем наиболее распространенных геометрических тел.

Что такое объем?

Объем — это общее пространство внутри твердого тела. Зная определение объема, мы можем теперь сосредоточиться на формулах объема обычных геометрических тел. Использовать эти формулы вручную не составит труда, но для получения быстрых и точных результатов каждый раз используйте калькулятор объема. 9{3}\), где r — радиус.

Просто введите размеры в калькулятор, чтобы найти объем. Единицы объема всегда будут кубическими, по сравнению с квадратными единицами площади поверхности.

@mometrixНужен калькулятор объема? Ссылка в био. ##pi ##piday ##volume ##sphere ##math ##mathhelp ##mometrix ##fyp

♬ оригинальный звук – Подготовка к тесту Mometrix

Вычисление объема куба Пример

Вот пример для расчет объема куба. 9{2}(4)=12\pi\) кубических сантиметров

Можно задаться вопросом, где этот калькулятор может быть полезен в реальных условиях.