Вычисление длины вектора по его координатам правило. Как найти координаты вектора. Как найти координаты вектора онлайн
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Пример 1
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Решение
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2: a → = 7 2 + e 2 = 49 + e
Ответ: a → = 49 + e .
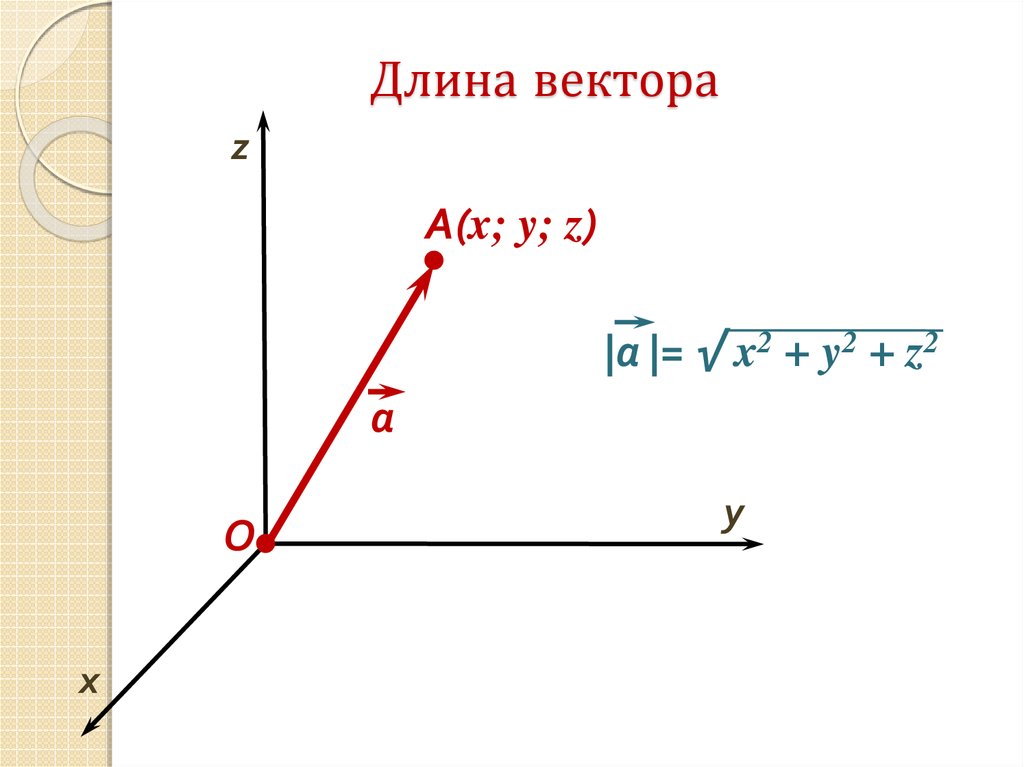
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Пример 2
Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.
Решение
Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2 .
Ответ: a → = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A (a x ; a y) и B (b x ; b y) , отсюда вектор A B → имеет координаты (b x — a x ; b y — a y) значит, его длина может быть определена по формуле: A B → = (b x — a x) 2 + (b y — a y) 2
А если даны точки с заданными координатами A (a x ; a y ; a z) и B (b x ; b y ; b z) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2
Пример 3
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .
Решение
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = (b x — a x) 2 + (b y — a y) 2: A B → = (- 3 — 1) 2 + (1 — 3) 2 = 20 — 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = (- 3 — 1 ; 1 — 3) = (- 4 ; 1 — 3) ; A B → = (- 4) 2 + (1 — 3) 2 = 20 — 2 3 . —
Ответ: A B → = 20 — 2 3 .
Пример 4
Определить, при каких значениях длина вектора A B → равна 30 , если A (0 , 1 , 2) ; B (5 , 2 , λ 2) .
Решение
Для начала распишем длину вектора A B → по формуле: A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2 = (5 — 0) 2 + (2 — 1) 2 + (λ 2 — 2) 2 = 26 + (λ 2 — 2) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ:
26 + (λ 2 — 2) 2 = 30 26 + (λ 2 — 2) 2 = 30 (λ 2 — 2) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Пример 5
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Решение
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ (A B , → A C →) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Ответ: B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = (b x — a x) 2 + (b y — a y) 2 или A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2 , в некоторых случаях следует использовать теорему косинусов.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Угол между прямыми на плоскости (вывод).
Как построить эллипс?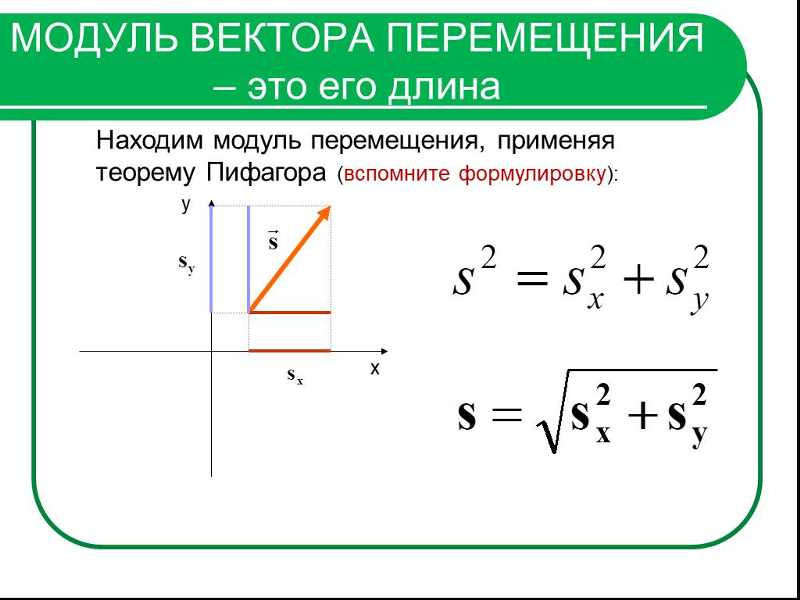
Определение производной. Геометрический смысл, механический смысл производной. Уравнения касательной и нормали к кривой и точке.
Теоремы о необходимом и достаточном условиях существования точек перегиба.
Вектором называется направленный отрезок. Длиной или модулем вектора называется длина соответствующего направленного отрезка.
Модуль вектора a обозначается . Векторa называется единичным, если . Векторы называются коллинеарными, если они параллельны одной прямой. Векторы называются компланарными, если они параллельны одной плоскости.
2. Умножение вектора на число. Свойства операции.
Умножение вектора на число, даёт противоположно направленный вектор в длиной враз больше. Умножение вектора на число в координатной форме производится умножением всех координат на это число:
Исходя из определения получается выражение для модуля вектора, умноженного на число:
Аналогично как и числами, операции сложение вектора с самим с собой можно записать через умножение на число:
А вычитание векторов можно переписать через сложение и умножение:
Исходя из того, что умножение на не меняет длины вектора, а меняет только направление и учитывая определение вектора, получаем:
3.
Сложение векторов, вычитание векторов.В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:
Для геометрического построения вектора суммы используют различные правила (методы), однако они все дают одинаковый результат. Использование того или иного правила обосновывается решаемой задачей.
Правило треугольника
Правило треугольника наиболее естественно следует из понимания вектора как переноса. Ясно, что результат последовательного применения двух переносов инекоторой точки будет тем же, что применение сразу одного переноса, соответствующего этому правилу. Для сложения двух векторовипо правилутреугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.
Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной :
Правило многоугольника
Начало
второго вектора совмещается с концом
первого, начало третьего — с концом
второго и так далее, сумма же
векторов
есть вектор, с началом, совпадающим с
началом первого, и концом, совпадающим
с концом-го
(то есть изображается направленным
отрезком, замыкающим ломаную).
Так же
называется правилом ломаной.
Правило параллелограмма
Для сложения двух векторов ипо правилупараллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала. (Легко видеть, что эта диагональ совпадает с третьей стороной треугольника при использовании правила треугольника).
Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.
Модуль суммы векторов
Модуль суммы двух векторов можно вычислить, использую теорему косинусов :
Где — косинус угла между векторамии.
Если
векторы изображены в соответствии с
правилом треугольника и берется угол
по рисунку — между сторонами
треугольника — что не совпадает с
обычным определением угла между
векторами, а значит и с углом в приведенной
формуле, то последний член приобретает
знак минус, что соответствует теореме
косинусов в ее прямой формулировке.
Для суммы произвольного количества векторов применима аналогичная формула, в которой членов с косинусом больше: по одному такому члену существует для каждой пары векторов из суммируемого набора. Например, для трех векторов формула выглядит так:
Вычитание векторов
Два вектора и вектор их разности
Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:
Для получения вектора разности начала векторов соединяются и началом векторабудет конец, а концом — конец. Если записать, используя точки векторов, то.
Модуль разности векторов
Три вектора , как и при сложении, образуют треугольник, и выражение для модуля разности получается аналогичным:
где — косинус угла между векторамии
Отличие
от формулы модуля суммы в знаке перед
косинусом, при этом надо хорошо следить,
какой именно угол берется (вариант
формулы модуля суммы с углом между
сторонами треугольника при суммировании
по правилу треугольника по виду не
отличается от данной формулы для модуля
разности, но надо иметь в виду, что для
тут берутся разные углы: в случае суммы
берётся угол, когда вектор
переносится
к концу вектора,
когда же ищется модель разности, берётся
угол между векторами, приложенными к
одной точке; выражение для модуля суммы
с использованием того же угла, что в
данном выражении для модуля разности,
отличается знаком перед косинусом).
Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.
Определение 3
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Определение 4
Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.
Определение 5
Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:
$\overline{c}={m,n}$
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
Пример 1
Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.
Введем на плоскости декартову систему координат $xOy$.
2}$.
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Пример 2
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
Oxy
О А ОА .
, откуда ОА .
Таким образом, .
Рассмотрим пример.
Пример.
Решение.
:
Ответ:
Oxyz в пространстве.
А ОА будет диагональю.
В этом случае (так как ОА ОА .
Таким образом, длина вектора .
Пример.
Вычислите длину вектора
Решение.
, следовательно,
Ответ:
Прямая на плоскости
Общее уравнение
Ax + By + C ( > 0).
Вектор = (А; В) — нормальный вектор прямой.
В векторном виде: + С = 0 , где — радиус-вектор произвольной точки на прямой (рис. 4.11).
Частные случаи:
1) By + C = 0 — прямая параллельна оси Ox ;
2) Ax + C = 0 — прямая параллельна оси Oy ;
3) Ax + By = 0 — прямая проходит через начало координат;
4) y = 0 — ось Ox ;
5) x = 0 — ось Oy .
Уравнение прямой в отрезках
где a, b — величины отрезков, отсекаемых прямой на осях координат.
Нормальное уравнение прямой (рис. 4.11)
где — угол, образуемый нормально к прямой и осью Ox ; p — расстояние от начала координат до прямой.
Приведение общего уравнения прямой к нормальному виду:
Здесь — нормируемый множитель прямой; знак выбирается противоположным знаку C , если и произвольно, если C = 0 .
Нахождение длины вектора по координатам.
Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора.
Начнем с нахождения длины вектора на плоскости по координатам.
Введем на плоскости прямоугольную декартову систему координат Oxy . Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и .
Отложим от начала координат (от точки О ) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА .
В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, .
Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .
Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат.
Рассмотрим пример.
Пример.
Найдите длину вектора , заданного в декартовой системе координат.
Решение.
Сразу применяем формулу для нахождения длины вектора по координатам :
Ответ:
Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве.
Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.
В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .
Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат , то есть, находится по формуле .
Пример.
Вычислите длину вектора , где — орты прямоугольной системы координат.
Решение.
Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .
Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.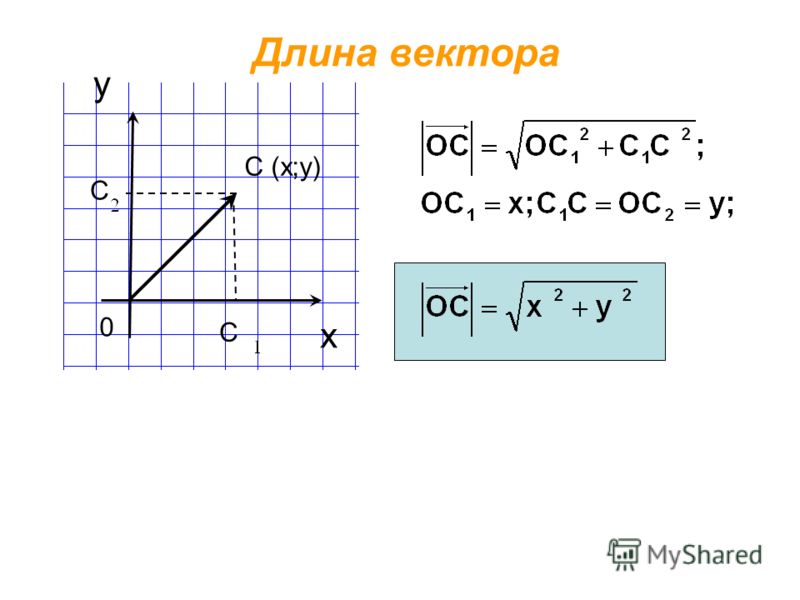
Определение 3
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Определение 4
Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.
Определение 5
Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:
$\overline{c}={m,n}$
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
Пример 1
Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$.
2}$.
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Пример 2
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья. Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре… Интересное: Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Стр 1 из 5Следующая ⇒ Нахождение длины вектора по координатам. Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора. Начнем с нахождения длины вектора на плоскости по координатам. Введем на плоскости прямоугольную декартову систему координат Oxy. Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и . Отложим от начала координат (от точки О) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА. В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, . Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид . Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат. Рассмотрим пример. Пример. Найдите длину вектора , заданного в декартовой системе координат. Решение. Сразу применяем формулу для нахождения длины вектора по координатам : Ответ: . Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве. Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю. В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, . Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле . Пример. Вычислите длину вектора , где — орты прямоугольной системы координат. Решение. Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем . Ответ: . Прямая на плоскости
Ax + By + C ( > 0). Вектор = (А; В) — нормальный вектор прямой. В векторном виде: + С = 0, где — радиус-вектор произвольной точки на прямой (рис. 4.11). Частные случаи: 1) By + C = 0 — прямая параллельна оси Ox; 2) Ax + C = 0 — прямая параллельна оси Oy; 3) Ax + By = 0 — прямая проходит через начало координат; 4) y = 0 — ось Ox; 5) x = 0 — ось Oy.
где a, b — величины отрезков, отсекаемых прямой на осях координат.
где — угол, образуемый нормально к прямой и осью Ox; p — расстояние от начала координат до прямой. Приведение общего уравнения прямой к нормальному виду: Здесь — нормируемый множитель прямой; знак выбирается противоположным знаку C, если и произвольно, если C = 0.
Нахождение длины вектора по координатам. Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора. Начнем с нахождения длины вектора на плоскости по координатам. Введем на плоскости прямоугольную декартову систему координат Oxy. Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и . Отложим от начала координат (от точки О) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА. В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, . Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид . Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат. Рассмотрим пример. Пример. Найдите длину вектора , заданного в декартовой системе координат. Решение. Сразу применяем формулу для нахождения длины вектора по координатам : Ответ: . Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве. Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, . Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле . Пример. Вычислите длину вектора , где — орты прямоугольной системы координат. Решение. Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем . Ответ: . 12345Следующая ⇒ Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций. Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
..
Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.
..Кратчайшая длина вектора
спросил
Изменено 9 лет, 9 месяцев назад
Просмотрено 4к раз
$\begingroup$
После прошлого экзамена я пришел к следующему вопросу: вектор $v = (k, k, 3 − k)$ зависит от переменной $k$.
Какова наименьшая длина вектора $v$? Я знаю, что ответ $\sqrt{6}$, но почему…? Как мне продолжить здесь, чтобы найти результат.
.
- векторные пространства
- векторный анализ
$\endgroup$
2
$\begingroup$
Вы можете написать формулу длины вектора?
Как насчет его квадрат 92-6k+9$ найдите производную $6k-6$, поэтому если $6k-6=0$, то подставьте $k=1$, чтобы найти минимальное расстояние $\sqrt 6$ по желанию. С уважением
$\endgroup$
2
$\begingroup$
Предполагая, что $k$ может варьироваться в пределах $\mathbb R$, и пусть $v_k=(k,k,3-k)$, начнем с рассмотрения функции $f(k)=\|v_k\|$ . Вам нужно найти минимум $f$. Теперь поработайте с определением длины вектора. Вы увидите, что оно содержит квадратный корень. Сделайте свою жизнь намного проще, заметив, что найти минимум функции $g(k)=\|v_k\|^2$ на самом деле та же самая проблема, так что теперь квадратный корень исчез.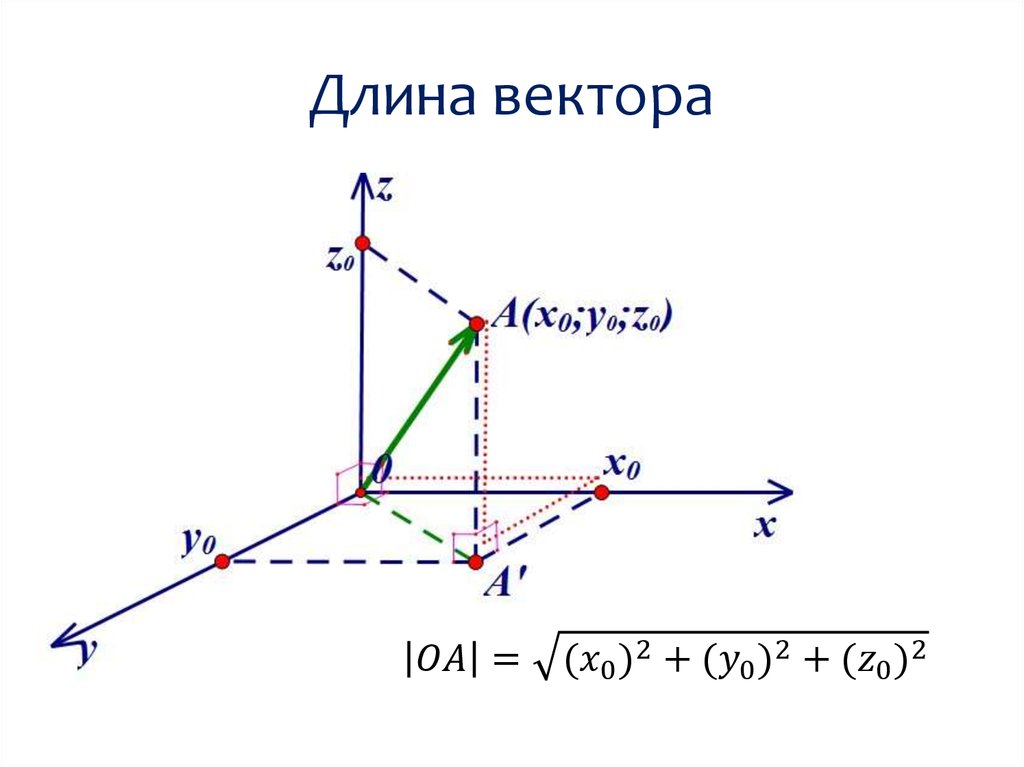
Теперь у вас есть довольно простая функция с действительным значением для одной переменной. Найдите его минимум, используя стандартные методы исчисления.
$\endgroup$
3
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Вопрос Видео: Нахождение длины проекции вектора на другой вектор
Стенограмма видео
Длина показанного куба равна 44, деленной на 17. Найдите скалярную проекцию 𝐎𝐀 на 𝐂𝐁, дав правильный ответ с точностью до двух знаков после запятой. .
Итак, глядя на этот куб, мы видим, что угол 𝑂 находится в начале 𝑥𝑦𝑧-системы координат. Мы также видим три других угла куба, помеченные 𝐴, 𝐵 и 𝐶. Мы хотим найти скалярную проекцию вектора 𝐎𝐀, показанного в нашем эскизе, на вектор 𝐂𝐁, который идет из угла 𝐶 нашего куба в угол 𝐵. Этот вектор будет выглядеть так. Чтобы начать работу над нашим решением, давайте вспомним, что скалярная проекция вектора 𝐀 на другой вектор 𝐁 равна скалярному произведению этих векторов, деленному на величину вектора, на который проецируется. В нашем случае мы хотим вычислить 𝐎𝐀 с точками 𝐂𝐁, деленное на величину вектора 𝐂𝐁.
Чтобы вычислить эту долю, нам нужно знать векторные компоненты этих двух векторов, 𝐎𝐀 и 𝐂𝐁.
Мы можем узнать их, работая с координатами наших четырех заданных точек. Мы можем начать с координат нашей точки 𝑂, которая, как мы видим, находится в начале координат. Из-за этого мы знаем, что 𝑥𝑦𝑧-координаты этой точки должны быть равны нулю, нулю, нулю.
Далее рассмотрим координаты точки 𝐴. Эта точка имеет 𝑥-значение, равное этой длине, длину стороны куба, которая, как нам сказали, равна сорок четырем семнадцатым, 𝑦-значение, равное этой длине, а также длину одной стороны куба. , а затем 𝑧-значение, равное этой длине, снова сорок четыре семнадцатых.
Теперь, когда мы знаем координаты этих двух точек, мы можем найти вектор 𝐎𝐀. Этот вектор равен координатам точки 𝐴 минус координаты точки 𝑂. Как мы видели, 𝑥-, 𝑦- и 𝑧-координаты точки 𝐴 равны сорок четырем семнадцатым, а координаты точки 𝑂 равны нулю. Это говорит нам о том, что компоненты вектора 𝐎𝐀 тоже одинаковы. Им всем сорок четыре семнадцатых. Зная это, теперь давайте выясним координаты двух других точек 𝐶 и 𝐵. Начиная с точки 𝐵, мы видим, что она имеет 𝑥-координату нуля, 𝑦-координату нуля, а затем 𝑧-координату сорок четыре семнадцатых.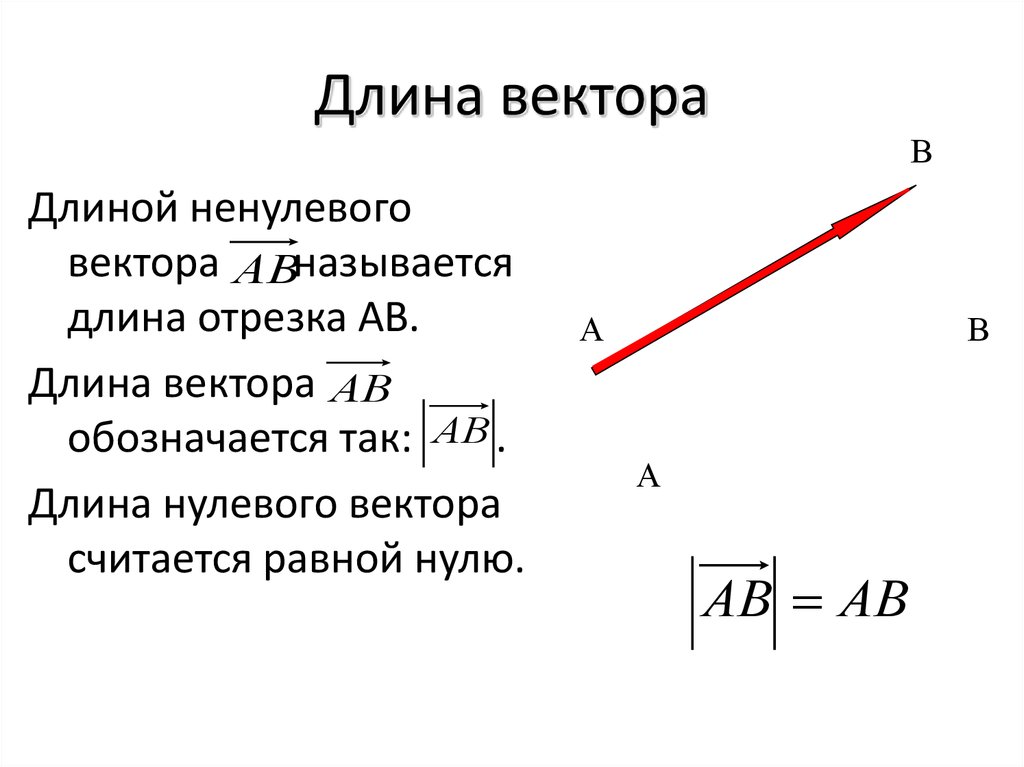
Тогда точка 𝐶 в некотором смысле противоположна. Он имеет 𝑥- и 𝑦-значения 44 больше 17, а 𝑧-значение равно нулю.
Вектор 𝐂𝐁 равен векторной форме координат 𝐵 за вычетом координат 𝐶. И когда мы подставляем эти значения и выполняем это вычитание, мы находим этот результат. 𝑥-компонента отрицательных сорока четырех семнадцатых, 𝑦-компонента того же и 𝑧-компонента положительных сорока четырех семнадцатых. Итак, у нас есть компоненты интересующих нас векторов, а это значит, что мы можем начать вычислять эту долю. Когда мы начнем, давайте очистим немного места на экране. А теперь подставим в эту дробь известные значения 𝐎𝐀 и 𝐂𝐁. Это дает нам это выражение, где мы вспомнили, что величина вектора равна квадратному корню из суммы квадратов его компонентов.
Следующим шагом в нашем числителе является умножение соответствующих компонентов этих векторов в 𝑥-, 𝑦- и 𝑧-направлениях. В нашем знаменателе мы можем возвести в квадрат эти различные компоненты вектора 𝐂𝐁. Когда мы делаем это, в нашем числителе мы получаем отрицательное количество сорок четыре семнадцатых в квадрате минус то же самое количество в квадрате плюс это количество в квадрате, а в нашем знаменателе квадратный корень из трех умноженных на 17 квадратов количества 44.