Как найти длину вектора формула: Как найти длину вектора? Ответ на webmath.ru

примеры и решения, формулы и теоремы

Основные понятия вектора

Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.

Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».

Определение

Вектор — это отрезок с определённой длиной и направлением.

Графическое изображение вектора — отрезок который имеет указание направления в виде стрелки.

Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.

Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.

• Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
• Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.

• Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
• Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
• Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
  Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.

Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.

Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.

Как найти длину вектора

Модуль вектора а будем обозначать .

Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy.  Допустим в данной системе будет задан, так вектор имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет  найти длину вектора , через известные нам координаты aₓ и aᵧ.

На взятой системе координат, от её начала отложим вектор В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.

Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует

Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора получаем 

Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:

Когда вектор дан в формате разложения по координатным векторам , то вычислить его можно по той же формуле , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат , в данной системе координат. 2 \) (из рисунка видно, что АО — диагональ прямоугольного параллелепипеда), поэтому

из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA=a , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:

Пример

Необходимо узнать длину вектора \( \left|\vec{a}\right|=2*\vec{i}+3*\vec{j}+4*\vec{k} \), в котором \( \vec{i}, \vec{j}, \vec{k} \), орты.

Решение

Получается, что дан вектор \( \left|\vec{a}\right| \) с координатами (2; 3; 4)

Применив выведенную ранее формулу получим

Ответ:

Длина вектора через координаты точек начала и конца

Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.

Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле

При этом формула вычисления длины вектора для трёхмерного пространства, с координатами и ), будет следующей:

Пример

Для прямой системы координат, найти длину вектора \( \overrightarrow{AB}\) , где A(1,√3) B(-3,1)

Решение

Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:

Существует второй вариант решения, где формулы применяются по очереди:

Ответ:

Пример

Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,\(λ^2\))

Решение

В первую очередь представим длину вектора в виде формулы. 2-2=-2
\)
\(
\lambda_1=-2, \lambda_2=2, \lambda_3=0.
\)

Ответ: \(
\lambda_1=-2, \lambda_2=2, \lambda_3=0.
\)

Длина вектора по теореме косинусов

Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.

К примеру, нам известны длины двух векторов \(\overrightarrow{AB}\)  и \(\overrightarrow{AC}\) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора \( \overrightarrow{BC} \) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.

Пример

Даны длины двух векторов \( \overrightarrow{AK}\) и \( \overrightarrow{AM}\) 2 и 4 соответственно, а угол между ними равен \( \frac{\pi}{3} \) . необходимо найти длину \( \overrightarrow{KM}\). 2}\) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.

В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.

Применение векторов в других сферах

Понятие и вычисление вектора важно не только в математике, но и других науках:

• в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
• в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
• в биологии.  Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
• географии. Вектором обозначается движение воздушных масс, или течение реки;

Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.  

примеры и решения, формулы и теоремы

Длина вектора — основные формулы

Длину вектора a→ будем обозначать a→. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат Oxy. Пусть в ней задан некоторый вектор a→ с координатами ax;ay. Введем формулу для нахождения длины (модуля) вектора a→ через координаты ax и ay.

От начала координат отложим вектор OA→=a→. Определим соответственные проекции точки A на координатные оси как Ax и Ay . Теперь рассмотрим прямоугольник OAxAAy с диагональю OA.

Из теоремы Пифагора следует равенство OA2=OAx2+OAy2, откуда OA=OAx2+OAy2. Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что OAx2=ax2 и OAy2=ay2, а по построению длина OA равна длине вектора OA→, значит, OA→=OAx2+OAy2.

Отсюда получается, что формула для нахождения длины вектора a→=ax;ay имеет соответствующий вид: a→=ax2+ay2.

Если вектор a→ дан в виде разложения по координатным векторам a→=ax·i→+ay·j→, то вычислить его длину можно по той же формуле a→=ax2+ay2, в данном случае коэффициенты ax и ay выступают в роли координат вектора a→ в заданной системе координат.

Пример 1

Вычислить длину вектора a→=7;e, заданного в прямоугольной системе координат.

Решение

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатамa→=ax2+ay2: a→=72+e2=49+e

Ответ: a→=49+e.

Формула для нахождения длины вектора a→=ax;ay;az по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

В данном случае OA2=OAx2+OAy2+OAz2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда OA=OAx2+OAy2+OAz2. Из определения координат вектора можем записать следующие равенства OAx=ax; OAy=ay; OAz=az; , а длина ОА равна длине вектора, которую мы ищем, следовательно, OA→=OAx2+OAy2+OAz2.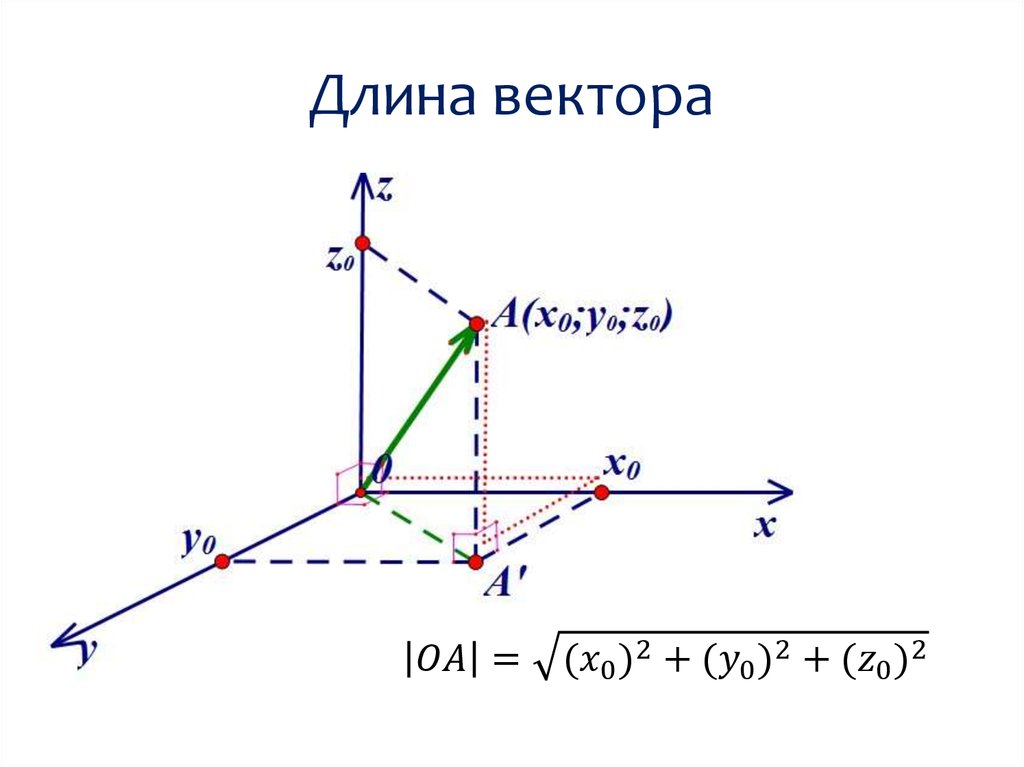

Отсюда следует, что длина вектора a→=ax;ay;az равна a→=ax2+ay2+az2.

Пример 2

Вычислить длину вектора a→=4·i→-3·j→+5·k→, где i→,j→,k→ — орты прямоугольной системы координат.

Решение

Дано разложение вектора a→=4·i→-3·j→+5·k→, его координаты равны a→=4,-3,5. Используя выше выведенную формулу получим a→=ax2+ay2+az2=42+(-3)2+52=52.

Ответ:a→=52.

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A(ax;ay) и B(bx;by), отсюда вектор AB→ имеет координаты (bx-ax; by-ay)значит, его длина может быть определена по формуле: AB→=(bx-ax)2+(by-ay)2

А если даны точки с заданными координатами A(ax;ay;az) и B(bx;by;bz) в трехмерном пространстве, то длину вектора AB→ можно вычислить по формуле

AB→=(bx-ax)2+(by-ay)2+(bz-az)2

Пример 3

Найти длину вектора AB→, если в прямоугольной системе координат A1, 3, B-3, 1.

Решение

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим AB→=(bx-ax)2+(by-ay)2: AB→=(-3-1)2+(1-3)2=20-23.

Второй вариант решения подразумевает под собой применение данных формул по очереди: AB→=(-3-1; 1-3)=(-4; 1-3); AB→=(-4)2+(1-3)2=20-23.-

Ответ: AB→=20-23.

Пример 4

Определить, при каких значениях  длина вектора AB→ равна 30, еслиA(0, 1, 2); B(5, 2, λ2) .

Решение

Для начала распишем длину вектора AB→ по формуле: AB→=(bx-ax)2+(by-ay)2+(bz-az)2=(5-0)2+(2-1)2+(λ2-2)2=26+(λ2-2)2

Затем полученное выражение приравняем к 30, отсюда найдем искомые λ:

 26+(λ2-2)2=3026+(λ2-2)2=30(λ2-2)2=4λ2-2=2 или λ2-2=-2  λ1=-2, λ2=2, λ3=0.

Ответ: λ1=-2, λ2=2, λ3=0.

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов AB→, AC→ и угол между ними (или косинус угла), а требуется найти длину вектора BC→ или CB→. В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ABC, вычислить длину стороны BC, которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Пример 5

Длины векторов AB→ и AC→ равны 3 и 7 соответственно, а угол между ними равен π3. Вычислить длину вектора BC→.

Решение

Длина вектора BC→ в данном случае равна длине стороны BC треугольника △ABC. Длины сторон AB и AC треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов:BC2=AB2+AC2-2·AB·AC·cos∠(AB,→AC→)=32+72-2·3·7·cosπ3=37 ⇒BC=37 Таким образом, BC→=37.

Ответ:BC→=37.

Итак, для нахождения длины вектора по координатам существуют следующие формулы a→=ax2+ay2 или a→=ax2+ay2+az2, по координатам точек начала и конца вектора AB→=(bx-ax)2+(by-ay)2 или AB→=(bx-ax)2+(by-ay)2+(bz-az)2, в некоторых случаях следует использовать теорему косинусов.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Векторы в двух- и трехмерных декартовых координатах

Во введении к векторам мы обсуждали векторы без привязки к какой-либо системе координат. Работая только с геометрическим определением величины и направления векторов, мы смогли определить такие операции, как сложение, вычитание, и умножение на скаляры. Мы также обсудили свойства этих операций.

Часто система координат оказывается полезной, потому что проще управлять координатами вектора, чем напрямую управлять его величиной и направлением. Когда мы выражаем вектор в системе координат, мы идентифицируем вектор с помощью списка чисел, называемых координатами или компонентами, которые определяют геометрию вектора в терминах системы координат.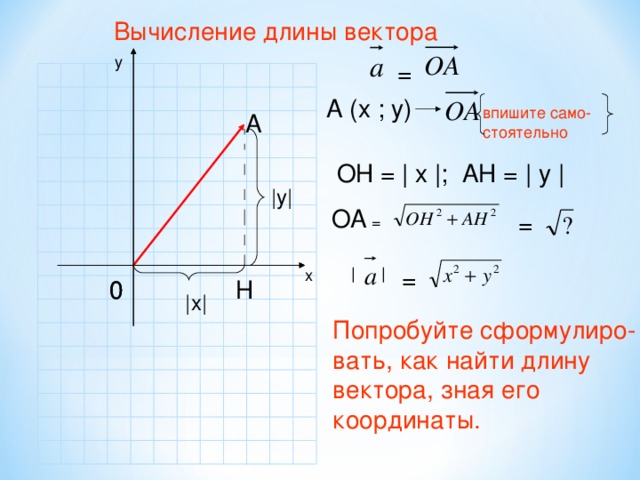

2$, чтобы обозначить, что его можно описать двумя действительными координатами. 92} = 5$.

Приведенный ниже апплет, повторяющийся из введения вектора, позволяет вам исследовать взаимосвязь между компонентами вектора и его величиной.

Величина и направление вектора. Синяя стрелка обозначает вектор $\vc{a}$. Два определяющих свойства вектора, величина и направление, показаны красной полосой и зеленой стрелкой соответственно. Длина красной полосы — это величина $\|\vc{a}\|$ вектора $\vc{a}$. Зеленая стрелка всегда имеет длину единицу, но ее направление совпадает с направлением вектора $\vc{a}$. Единственным исключением является случай, когда $\vc{a}$ является нулевым вектором (единственным вектором с нулевой величиной), для которого направление не определено. Вы можете изменить любой конец $\vc{a}$, перетащив его мышью. Вы также можете переместить $\vc{a}$, перетащив середину вектора; однако изменение положения $\vc{a}$ таким образом не меняет вектор, так как его величина и направление остаются неизменными.

Дополнительная информация об апплете.

Векторные операции, которые мы определили во введении к векторам, легко выразить в терминах этих координат. Если $\vc{a}=(a_1,a_2)$ и $\vc{b}=(b_1,b_2)$, их сумма просто $\vc{a}+\vc{b}=(a_1+b_1,a_2+b_2)$, как показано на рисунке ниже. Также легко видеть, что $\vc{b}-\vc{a} = (b_1-a_1,b_2-a_2)$ и $\lambda \vc{a} = (\lambda a_1, \lambda a_2)$ для любого скаляра $\lambda$.

Приведенный ниже апплет, который также повторяется из введения вектора, позволяет исследовать взаимосвязь между геометрическим определением сложения векторов и суммированием компонентов вектора.

Сумма двух векторов. Сумма $\vc{a}+\vc{b}$ вектора $\vc{a}$ (синяя стрелка) и вектора $\vc{b}$ (красная стрелка) показана зеленой стрелкой . Поскольку векторы не зависят от их начального положения, обе синие стрелки представляют один и тот же вектор $\vc{a}$, а обе красные стрелки представляют один и тот же вектор $\vc{b}$. Сумму $\vc{a}+\vc{b}$ можно составить, поместив хвост вектора $\vc{b}$ в начало вектора $\vc{a}$. То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки.

Дополнительная информация об апплете.

Вы могли заметить, что мы используем одни и те же обозначения для обозначения точки и вектора. Мы не склонны подчеркивать какое-либо различие между точкой и вектором. Вы можете думать о точке как о представлении вектора, хвост которого зафиксирован в начале координат. Вам придется выяснить по контексту, думаем ли мы о векторе или нет. как с фиксированным хвостом в начале координат.

Другой способ обозначения векторов — стандартные единичные векторы обозначаются $\vc{i}$ и $\vc{j}$. Единичный вектор — это вектор, длина которого равна единице. Вектор $\vc{i}$ является единичным вектором в направлении положительной оси $x$.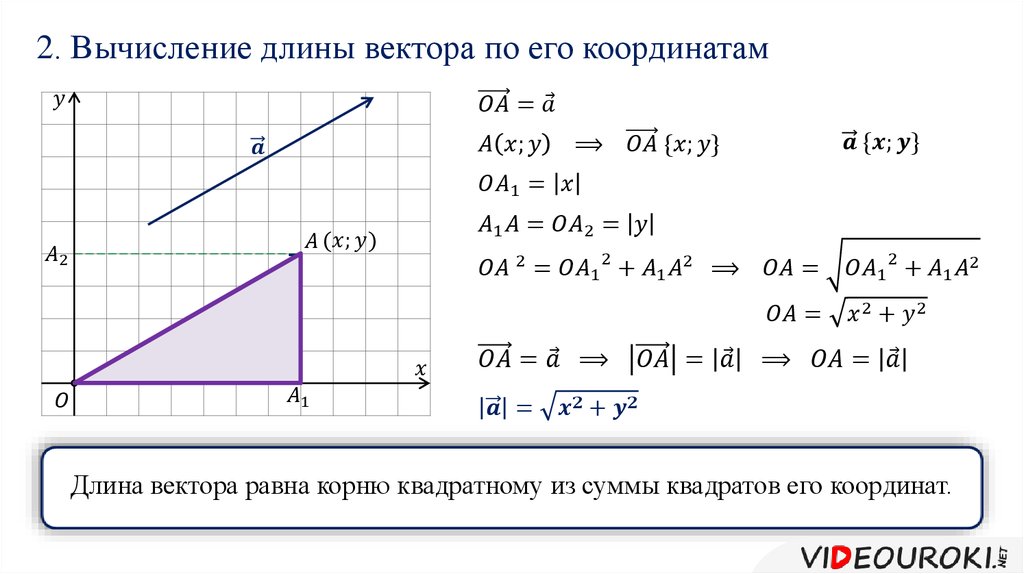 В координатах мы можем написать $\vc{i}=(1,0)$. Точно так же вектор $\vc{j}$ является единичным вектором в направлении положительной оси $y$: $\vc{j}=(0,1)$. Мы можем записать любой двумерный вектор в терминах этих единичных векторов как $\vc{a}=(a_1,a_2) = a_1\vc{i}+a_2\vc{j}$.

Векторы в трехмерном пространстве

В трехмерном пространстве существует стандартная декартова система координат $(x,y,z)$. Начиная с точки, которую мы называем началом координат, построим три взаимно перпендикулярные оси, которые мы называем осью $x$, осью $y$ и осью $z$. Вот один из способов изобразить эти оси. Встаньте в углу комнаты и посмотрите вниз, в точку, где стены соприкасаются с полом. Затем пол и стена слева от вас пересекаются по линии, являющейся положительной осью $x$. Пол и стена справа от вас пересекаются по линии, являющейся положительной осью $y$. Стены пересекаются по вертикальной линии, являющейся положительной осью $z$. Эти положительные оси изображены в приведенном ниже апплете и помечены как $x$, $y$ и $z$. Отрицательная часть каждой оси находится на противоположной стороне начала координат, где оси пересекаются.

Загрузка апплета

Трехмерные декартовы оси координат. Представление трех осей трехмерной декартовой системы координат. Положительная ось $x$, положительная ось $y$ и положительная ось $z$ — это стороны, помеченные $x$, $y$ и $z$. Начало — это пересечение всех осей. Ветвь каждой оси на противоположной стороне от начала координат (немаркированная сторона) является отрицательной частью. Вы можете перетащить фигуру с помощью мыши, чтобы повернуть ее.

Дополнительная информация об апплете.

Мы установили относительное расположение положительных осей $x$, $y$ и $z$ чтобы сделать систему координат правой системой координат . Обратите внимание, что если согнуть пальцы правой руки от положительной оси $x$ к положительной оси $y$, большой палец правой руки будет указывать в направлении положительной оси $z$.

Если вы поменяли местами положительную ось $x$ и положительную ось $y$, тогда у вас будет левосторонняя система координат. Если вы сделаете это, вы будете жить в математической вселенной, в которой некоторые формулы будут отличаться на знак минус от формулы во вселенной, которую мы здесь используем. Ваша вселенная будет такой же достоверной, как и наша, но будет много путаницы. Мы предлагаем вам жить в нашей вселенной, изучая эти страницы.

С помощью этих осей любой точке $\vc{p}$ в пространстве можно присвоить три координаты $\vc{p}=(p_1,p_2,p_3)$. Например, учитывая приведенную выше аналогию с углом комнаты, предположим, вы начинаете с угла комнаты и проходите четыре метра по оси $x$, затем поворачиваете налево и проходите три метра вглубь комнаты. Если ваш рост два метра, то ваша макушка находится в точке $(4,3,2)$. 93$ для обозначения того, что его можно описать тремя действительными координатами. Суммы, разности и скалярные умножения трехмерных векторов выполняются для каждого компонента. Если $\vc{a}=(a_1,a_2,a_3)$ и $\vc{b}=(b_1,b_2,b_3)$, то $\vc{a}+\vc{b}=(a_1+ b_1,a_2+b_2,a_3+b_3)$, $\vc{b}-\vc{a}=(b_1-a_1,b_2-a_2,b_3-a_3)$ и $\lambda\vc{a}= (\лямбда а_1, \лямбда а_2, \лямбда а_3)$.

Загрузка апплета

Вектор в трехмерном пространстве. Представление вектора $\vc{a}=(a_1,a_2,a_3)$ в трехмерной декартовой системе координат. Вектор $\vc{a}$ изображается в виде зеленой стрелки с хвостом, закрепленным в начале координат. Вы можете перетащить мышкой кончик зеленой стрелки, чтобы изменить вектор. Чтобы показать трехмерную перспективу, розовый треугольник соединяет вектор с его проекцией $(a_1,a_2,0)$ на $xy$-плоскость (серая стрелка). Фиолетовые векторы показывают проекции $\vc{a}$ на каждую ось и представляют координаты $a_1$, $a_2$ и $a_3$. Вы также можете перетаскивать головки фиолетовых векторов, чтобы изменить только одну из координат вектора. Или перетащите вершину серого вектора в плоскости $xy$, чтобы изменить только координаты $x$ и $y$.

Дополнительная информация об апплете.

Как и в двух измерениях, мы также можем обозначать трехмерные векторы is в терминах стандартных единичных векторов $\vc{i}$, $\vc{j}$ и $\vc{k}$. Эти векторы являются единичными векторами в положительных направлениях $x$, $y$ и $z$ соответственно. В терминах координат мы можем записать их как $\vc{i}=(1,0,0)$, $\vc{j}=(0,1,0)$ и $\vc{k}= (0,0,1)$. Мы можем выразить любой трехмерный вектор как сумму скалярных кратных этих единичных векторов в форме $\vc{a}=(a_1,a_2,a_3) = a_1\vc{i}+a_2\vc{j}+a_3\vc{k}$.

Загрузка апплета

Стандартные единичные векторы в трех измерениях. Стандартные единичные векторы в трех измерениях, $\vc{i}$ (зеленый), $\vc{j}$ (синий) и $\vc{k}$ (красный), представляют собой векторы длины один, которые указывают параллельно ось $x$, ось $y$ и ось $z$ соответственно. Перемещение их с помощью мыши не меняет вектора, поскольку они всегда указывают в положительном направлении соответствующей оси.

Дополнительная информация об апплете.

Какова длина вектора $\vc{a}=(a_1,a_2,a_3)$? Мы можем разложить вектор на $(a_1,a_2,a_3) = (a_1,a_2,0)+(0,0,a_3)$, где два вектора справа соответствуют двум зеленым сегментам линии в вышеуказанном апплете. Эти два отрезка образуют прямоугольный треугольник, гипотенуза — это вектор $\vc{a}$ (синий отрезок). 2}.$$ 9n$, где $n$ — некоторое натуральное число.

Перейти в более высокое измерение легко со списками чисел, хотя, конечно многомерные векторы нелегко (невозможно?) визуализировать. Вы можете прочитать больше о многомерных векторах или проверить примеры $n$-мерных векторы, которые иллюстрируют, как собираются размеры число выше трех может быть полезным во многих ситуациях.

`

Как вычислить длину дуги векторной функции — Криста Кинг Математика 92}\ дт???

где ???L??? длина дуги векторной функции, ???[a,b]??? интервал, определяющий дугу, и ???dx/dt???, ???dy/dt??? и ???dz/dt??? являются производными параметрических уравнений ???x???, ???y??? и ???з??? соответственно.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Чтобы определить длину дуги, нам понадобятся параметрические уравнения векторной функции. Задается ли наша векторная функция как ???r(t)=\langle{r(t)_1,r(t)_2,r(t)_3}\rangle??? или???r(t)=r(t)_1\bold i+r(t)_2\bold j+r(t)_3\bold k???, параметрические уравнения равны

???x=r(t)_1???

???y=r(t)_2???

???z=r(t)_3???

Получив эти параметрические уравнения, мы возьмем производную от каждого из них, чтобы получить ???dx/dt???, ???dy/dt??? и ???dz/dt??? . Предполагая, что нам дано ???[a,b]???, у нас будет все, что нам нужно, чтобы использовать формулу для длины дуги.

Как вычислить длину дуги векторной функции на определенном интервале

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

Узнать больше

Нахождение длины дуги вектор-функции

Пример

Нахождение длины дуги вектор-функции на интервале ???0\leq{t}\leq2???.

???r(t)=\left\langle{\sin{(2t)},\cos{(2t)},2t}\right\rangle???

Мы вытащим параметрические уравнения из векторной функции как

???x=\sin{(2t)}???

???y=\cos{(2t)}???

???z=2t???

Теперь возьмем производную от каждого из них.

???\frac{dx}{dt}=2\cos{(2t)}???

???\frac{dy}{dt}=-2\sin{(2t)}???

???\frac{dz}{dt}=2???

Чтобы определить длину дуги, нам понадобятся параметрические уравнения векторной функции.

Подстановка производных и заданного интервала ???0\leq{t}\leq2??? в формулу длины дуги получаем 92???

Вычисляя интервал, мы получаем

???L=2\sqrt{2}(2)-2\sqrt{2}(0)???

???L=4\sqrt{2}???

Длина дуги векторной функции на интервале ???0\leq{t}\leq2??? ???L=4\sqrt{2}???.

Получить доступ к полному курсу Calculus 3

Начать

Изучение математикиКриста Кинг 10 июня 2021 г.