Решение тригонометрических уравнений на промежутке
- Бахвалова Ольга Михайловна
Разделы: Математика
Цель урока:
а) закрепить умения решать простейшие тригонометрические уравнения;
б) научить выбирать корни тригонометрических уравнений из заданного промежутка
Ход урока.
1. Актуализация знаний.
а)Проверка домашнего задания: классу дано опережающее домашнее задание – решить уравнение и найти способ выбора корней из данного промежутка.
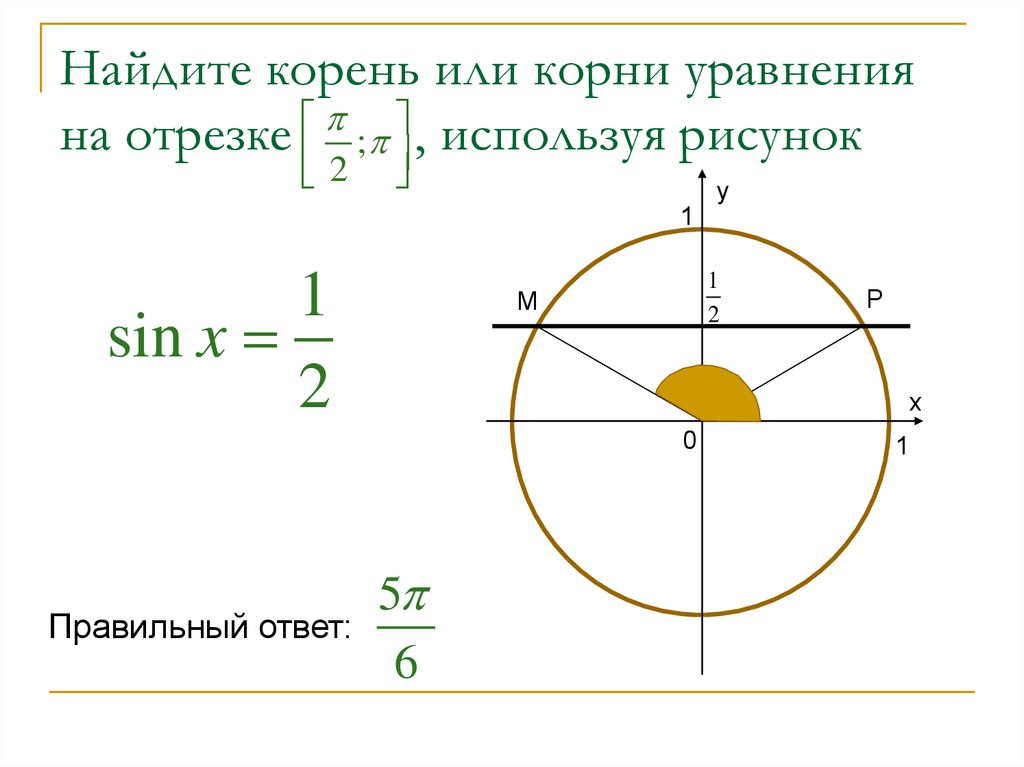
1)cos x = -0,5, где хI [- ].
Ответ: .
3)cos 2x = -, где хI [0;]. Ответ:
Ученики записывают решение на доске кто-то с помощью графика, кто-то методом подбора.
В это время класс работает устно.
Найдите значение выражения:
а) tg – sin + cos + sin . Ответ: 1.
б) 2arccos 0 + 3 arccos 1. Ответ: ?
в) arcsin + arcsin . Ответ: .
г) 5 arctg (-) – arccos (-). Ответ:– .
– Проверим домашнее задание, откройте свои тетради с домашними работами.
Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.
См. приложение 1
Приложение 2
Приложение 3
2.
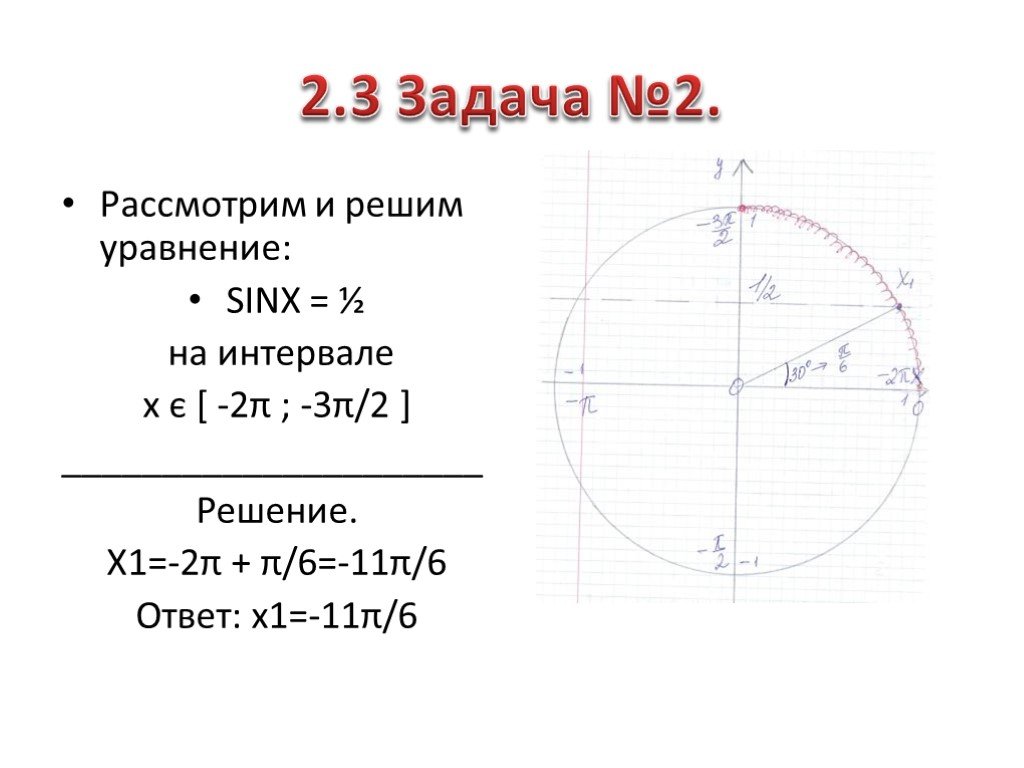Вывод о способах решения данных
заданий и постановка проблемы, т. е. сообщение
темы и цели урока.
– а) С помощью подбора решать сложно, если задан большой промежуток.
– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.
– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)
– Пример 1. (Ученик выходит к доске)
cos x = -0,5, где хI [- ].
Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске
х = + 2?k, где k R.
– Запишем это решение в виде совокупности:
– Как вы считаете, при какой записи
решения удобно выбирать корни на промежутке? (из
второй записи).
Но это ведь опять способ подбора.
Что нам необходимо знать, чтобы получить верный
ответ? (Надо знать значения k).
(Составим математическую модель для нахождения k).
— < k< , |
— < -k < , |
<k<, |
< k< , |
| так как kI Z, то k = 0, отсюда х = = | из данного неравенства видно, что целочисленныхзначений k нет. |
Ответ: .
Вывод: Чтобы выбрать корни из заданного промежутка при решении тригонометрического уравнения надо:
- для решения уравнения вида sin x = a, cos x = a
удобнее записать корни уравнения, как две серии
корней.
- для решения уравнений вида tg x = a, ctg x = a записать общую формулу корней.
- составить математическую модель для каждого решения в виде двойного неравенства и найти целое значение параметра k или n.
- подставить эти значения в формулу корней и вычислить их.
3. Закрепление.
Пример №2 и №3 из домашнего задания решить, используя полученный алгоритм. Одновременно у доски работают два ученика, с последующей проверкой работ.
4. Самостоятельная работа.
Самопроверка с выбором ответа. Выбрать № правильного ответа, получив закодированное число (312).
1) sin x = -, x
2) 3 tg x = -, x I [0; 2]
3) 2 cos , х [ ]
Приложение.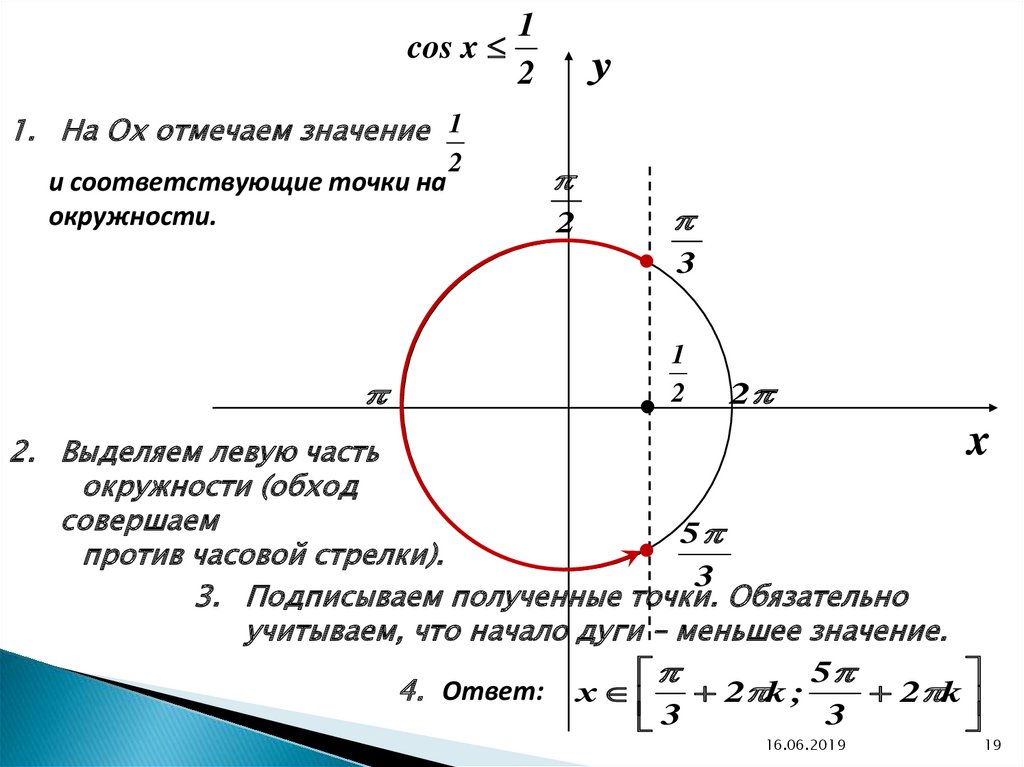
Ответы
к примерам
5. Домашнее задание:
1 уровень: № 295 (а,б), № 317 (а,б)
2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).
6. Итог урока.
Простая физика — EASY-PHYSIC
В этой статье научимся отбирать корни в задании 13 ЕГЭ с помощью двойного неравенства. Решать сами уравнения здесь не будем, только подробно разберем отбор корней.
Задача 1.
Предположим, вы решили тригонометрическое уравнение и ваш ответ на пункт а) такой: . Отбор нужно произвести на отрезке . Таким образом, точки, которые мы отберем, больше или равны , и меньше или равны . Запишем это двойным неравенством:
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке .
Очевидно, что подойдут значения , , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Ответ: б)
Задача 2.
Предположим, вы решили тригонометрическое уравнение и ваш ответ на пункт а) такой: . Отбор нужно произвести на отрезке . Таким образом, точки, которые мы отберем, больше или равны , и меньше или равны . Запишем это двойным неравенством:
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке . Очевидно, что подойдут значения , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Ответ: б)
Задача 3.
Предположим, вы решили тригонометрическое уравнение и ваш ответ на пункт а) такой: . Отбор нужно произвести на отрезке .
Таким образом, точки, которые мы отберем, больше или равны , и меньше или равны . Запишем это двойным неравенством для корня :
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке . Очевидно, что подойдут значения , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Теперь берем второй корень из серии и проделываем для него то же самое: снова составляем двойное неравенство
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке . Очевидно, что подойдут значения , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Берем вторую серию корней и повторяем все действия:
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке .
Очевидно, что подойдут значения, , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Теперь берем второй корень из серии и проделываем для него то же самое: снова составляем двойное неравенство
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке . Очевидно, что подойдут значения , , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Ответ: б) .
Таким образом, отбор двойным неравенством наиболее рационален тогда, когда промежуток длинный (больше трех четвертей круга) и решений, полученных в пункте а) не более двух. Иначе, при отборе для 4-х решений, как в задаче 3, расчетов уже получается много. Тем не менее любители алгебраизировать отбор очень любят этот способ и предпочитают его отбору на окружности.
Нахождение тригонометрических корней — тригонометрия
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Тригонометрия Помощь » Тригонометрические уравнения » Решение тригонометрических уравнений » Нахождение тригонометрических корней
Что из следующего является решением следующего уравнения таким образом, что
Возможные ответы:
Правильный ответ:
Объяснение:
Начнем с того, что приравняем правую часть уравнения к нулю.
Далее факторизуем.
Затем мы устанавливаем каждый фактор равным нулю и решаем.
или
Затем мы определяем углы, удовлетворяющие каждому решению за один оборот.
Углы и удовлетворяют первому, а удовлетворяют второму. Только является одним из вариантов ответа.
Сообщить об ошибке
Решите следующее уравнение для .
Возможные ответы:
Не существует решения
Правильный ответ:
Объяснение:
Самый быстрый способ решить эту проблему — заменить новую переменную. Позволять .Теперь уравнение принимает вид:
Итак, при каких углах функции синуса и косинуса равны. Это происходит по адресу
. Вы можете задаться вопросом: «Почему вы включили
, если они не находятся между и ?»
Причина в том, что после замены исходной переменной нам придется делить на 2. Это деление на 2 вернет два последних ответа в наш диапазон.
Разделив каждый ответ на 2, мы получим
Сообщить об ошибке
Решите уравнение для .
Возможные ответы:
Нет решения не существует
Правильный ответ:
Объяснение:
Начнем с замены новой переменной .
; Используйте тождество двойного угла для .
; вычесть с обеих сторон.
; Это выражение можно факторизовать.
; установить каждое выражение равным 0.
или ; решить каждое уравнение для
или ; Так как мы заменили новую переменную, мы можем видеть, что если , то мы должны иметь . Так как, значит.
Это важная информация, потому что она говорит нам, что когда мы решаем оба уравнения для u, наши ответы могут доходить не только до .
Таким образом, мы получаем
Разделите все на 2, чтобы получить наши окончательные решения
Сообщить об ошибке
Решите следующее уравнение для .
Возможные ответы:
Правильный ответ:
Объяснение:; Начнем с замены новой переменной. Позволять .
; Используйте тождество двойного угла для косинуса
; 1 отменяется, поэтому добавьте к обеим сторонам
; вынесите a из обоих терминов.
; установить каждое выражение равным 0.
или ; решить второе уравнение относительно sin u.
или ; возьмите арксинус, чтобы найти u (используйте круговую диаграмму или калькулятор)
; умножьте все на 2, чтобы найти х.
; Обратите внимание, что последние два решения не входят в наш диапазон . Так что единственное решение.
Сообщить об ошибке
Решите следующее уравнение для .
Возможные ответы:
Решение не существует
Правильный ответ:
; Сначала разделите обе части уравнения на 4
; Затем извлеките квадратный корень с обеих сторон.
Будь осторожен . Помните, что когда ВЫ извлекаете квадратный корень для решения уравнения, ответ может быть положительным или отрицательным. (Если квадратный корень уже был частью уравнения, обычно требуется только положительный квадратный корень. Например, решения равны 2 и -2, но если мы подставим 4 в функцию, ответ будет только 2. ) Итак,
; мы можем разделить это на два уравнения
и ; мы получаем
и
Сообщить об ошибке
Решите уравнение для .
Возможные ответы:
Правильный ответ:
Объяснение:
; Разделите обе части на 3
; Извлеките квадратный корень с обеих сторон. Как и в предыдущем вопросе, при извлечении квадратного корня ответ может быть положительным или отрицательным.
; Это можно записать в виде двух отдельных уравнений
и ; Возьмите арктангенс
и
Сообщите об ошибке
Решите следующее уравнение для .
Возможные ответы:
Правильный ответ:
Объяснение:
; Выражение похоже на квадратное выражение и может быть факторизовано.
; установите оба выражения равными 0. Поскольку они одинаковы, решения будут повторяться, поэтому я напишу это только один раз.
; возьмем арктангенс с обеих сторон
Сообщить об ошибке
Решите уравнение ниже для больше или равно и строго меньше .
Возможные ответы:
Только
и
и
только
Правильный ответ:
и
Объяснение:
Вызовите значения , для которых . Если это поможет, подумайте о синусе как о значениях на единичном круге.
Таким образом, допустимыми значениями были бы 0, 180, 360, 540 и т. д. Однако в нашем сценарии .
Таким образом, мы имеем и .
Любой другой ответ даст нам значения больше 90. При делении на 4 мы получим наши ответы:
и .
Сообщить об ошибке
Решите следующее уравнение. Найдите все решения такие, что .
Возможные ответы:
Нет решения
Правильный ответ:
Объяснение:
; Разделите обе части на 2, чтобы получить
; взять арксинус с обеих сторон
; левая часть сводится к x, поэтому
В этот момент либо используйте круговую диаграмму, либо калькулятор, чтобы найти значение.
Имейте в виду, что проблема требует всех решений между и .
Если вы используете калькулятор, вы получите только ответ.
Итак, нам нужно найти другой угол, удовлетворяющий уравнению.
Сообщить об ошибке
Решите следующее уравнение. Найдите все решения такие, что .
Возможные ответы:
Не существует решения
Правильный ответ:
Объяснение:
; Сначала используйте тождество двойного угла для .
; разделить обе части на 2
; вычесть с обеих сторон
; исключить
; Теперь у нас есть произведение двух выражений равно 0. Это может произойти только в том случае, если одно (или оба) выражения равны 0. Итак, пусть каждое выражение равно 0.
или ;
или ; Возьмем инверсию каждой функции для каждого выражения.
или ; Второе уравнение невозможно, поэтому не дает решения, но первое уравнение дает нам:
Сообщить об ошибке
← Предыдущая 1 2 3 Следующая →
Уведомление об авторских правах
Все ресурсы по тригонометрии 92 x — (p+3)\cos x + 2(p-1) = 0$ верно.
Теперь, поскольку $x$ должно быть реальным, мы знаем, что $\cos x$ также будет реальным.
(косинус любого действительного числа является действительным числом).
Точнее, $\cos x$ будет вещественным числом, принадлежащим отрезку $[-1,1].$
Но это может быть любое число в этом интервале; если мы позволим $x$ двигаться от $0$ до $\pi$, тогда $\cos x$ столкнется с каждым числом в $[-1,1].$Дело в том, что если мы должны начать беспокоиться о » interval $[-1,1]$» часть сразу, трудно понять, как решить проблему. Итак, давайте сначала побеспокоимся о части «действительного числа». Мы хотим знать, что существует реальное число, которое можно поставить вместо $\cos x$. в уравнении, которое делает уравнение верным. 92 — 16(п-1)} {4} = \frac{(p+3) \pm (p — 5)}{4}. $$
Если мы выберем $+$ вместо $\pm$, получим $y = (p — 1)/2$, а если выберем $-$, получим $y = 2.$
Очевидно, что $y = 2$ не годится, потому что $2$ не находится в интервале $[-1,1]$
поэтому это не может быть значением $\cos x.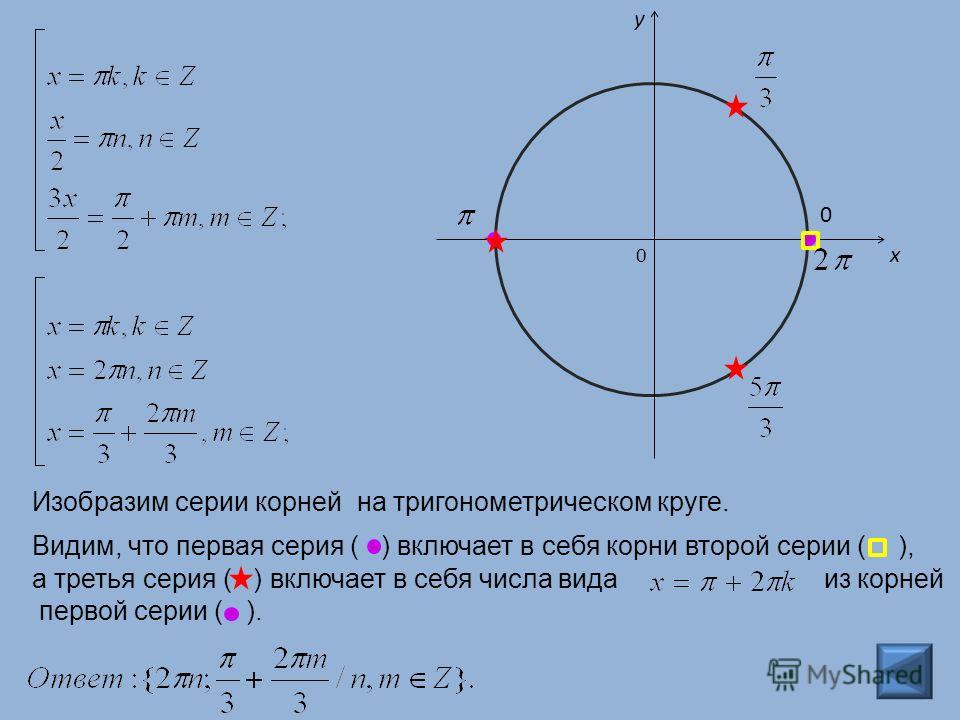
$
Поэтому наша единственная надежда состоит в том, что решение $y = (p — 1)/2.$
Для того, чтобы это было значением $\cos x$ (чтобы решить проблему, которая была задана изначально), должно быть верно, что
$-1 \leq (p — 1)/2 \leq 1.$
Остальная часть решения — это просто алгебра для упрощения этих неравенств.
Упрощенная версия $-1 \leq p \leq 3.$ 92 — 4ac \geq 0$ — это все, что вам нужно знать, потому что тогда будет реальный квадратный корень, и вы будете комбинировать его с другими действительными числами, чтобы в конце получить действительное число (или два).
(Я предполагаю, что вы работаете только с действительными числами, а не с комплексными числами. Если вы допускаете комплексные числа, то получается ненастоящий квадратный корень, и нам нужно проделать некоторую дополнительную работу, чтобы показать, что окончательный результат вычисления $y$ не является реальным.)
Поскольку на самом деле нам нужно больше узнать о $y $, чем просто то, что это реальное число,
нам нужно закончить вычисление формулы.