2 Решение матричных уравнений
2 Решение матричных уравнений2.1 Цель работы
1. Нахождение обратной матрицы. 2. Решение матричного уравнения c помощью обратной матрицы.
2.2 Теоретическое введение
Матрицей называется прямоугольная таблица чисел. При сложении матриц складываются их соответствующие элементы,а при умножения матрицы на число на него умножается каждый элемент этой матрицы. .
(2.1) |
Произведение матрицы A на матрицу B определено только в том случае, когда число столбцов матрицы A равно числу cтрок матрицы B. В результате умножения получается матрица C = A · B, у которой столько же строк, сколько в матрице A, и столько же столбцов, сколько в матрице B :
Матрица | A | B | C = A·B |
Число строк | m | n | m |
Число столбцов | n | l | l |
Запишем
матрицы A и B в
виде
.
Обозначим
элементы матрицы C
= A · B через c, .
Тогда
.
По
определению элемент ci
j ,
матрицы C
= A · B равен
скалярному произведению i-й
строки матрицы A (i –
первый индекс элемента ci
j )
на j-й
столбец матрицы B ( j —
второй индекс элемента ci
j ),
т.е.
ci j = (ai 1 , ai 2 ,…, ai n ) · (b1 j , b2 j ,…, bn j ) = ai 1 · b1 j + ai 2 · b2 j + …+ ai n · bn j | (2. |
2)Наряду с матрицей A будем рассматривать матрицу, столбцами которой являются строки матрицы A. Эту матрицу называюттранспонированной к A и обозначают через A
A·A-1 = A-1·A = E | (2. |
3)Если определитель |A| квадратной матрицы A не равен нулю, то существует и, притом единственная, матрица A-1.
Правило нахождения обратной матрицы Дополнительным
минором Mi
j к
элементу ai
j квадратной
матрицы A
n-го
порядка называется определитель
матрицы n —
1-го порядка, которая получается из
матрицы A путем
вычеркивания i-ой
строки и j-го
столбца (на пересечении которых стоит
элемент ai
j ). Алгебраическим
дополнением Ai
j , элемента ai
j называется
величина Ai
j
(2. |
4)Для матрицы A третьего порядка (3х3) обратная матрица A-1 имеет вид: . В типовом расчете рассматриваются матричные уравнения двух типов: X · A = B и A · X = B, где A – квадратная матрица с |A| ≠ 0. Рассмотрим сначала уравнение X · A = B. Умножим обе части этого уравнения справа на матрицу A-1, тогда по определению обратной матрицы уравнение X · A · A-1 = B · A-1 равносильно уравнению
X · E = B · A-1 или X = B · A-1 | (2.5) |
Если в условии варианта дано уравнение A · X = B, то умножим обе части этого уравнения слева на матрицу A-1, тогда уравнение A-1 · A · X = A-1 · B равносильно уравнению
E · X = A-1 · B или X = A-1 · B | (2. |
2.3 Содержание типового расчета
Заданы квадратная матрица A и прямоугольная матрица B. Решить матричное уравнение вида X · A = B или A · X = B, где X – искомая матрица. Конкретный вид уравнения задан в каждом варианте. Провести поэтапный контроль: расчета обратной матрицыA-1 умножением A на A-1; найденного решения X подстановкой в исходное уравнение.
2.4 Пример выполнения типового расчета
Условие типового расчета | |||||||||||||||||
Вариант Уравнение | Матрица A | Матрица B | |||||||||||||||
930207 A * X = B |
|
| |||||||||||||||
Выполнение типового расчета
1.
Найдем обратную матрицу A-1 по
формуле (4)
При
вычислении определителя использовано
разложение его по первой cтроке.
Получившиеся определители второго
порядка упрощены вынесением общего
множителя из какой-либо строки или
столбца. Затем найдем матрицу алгебраических
дополнений:
.
Тогда
Для
удобства дальнейших расчетов не будем
умножать матрицу на множитель, стоящий
перед ней.
Проведем
контроль расчетов, для этого перемножим
матрицы A и A-1.
Если расчеты проведены верно, результатом
должна быть единичная матрица.
При
умножении использована удобная форма
записи, при которой вторая матрица-сомножитель
записывается правее и ниже первой, а
правее первой и выше второй записывается
результат умножения. При такой записи
каждое число матрицы–результата стоит
на пересечении той строки первой матрицы
и того столбца второй матрицы, скалярное
произведение которых дает искомое
число.
3)
Решение X уравнения A
· X = B найдем
по формуле (2.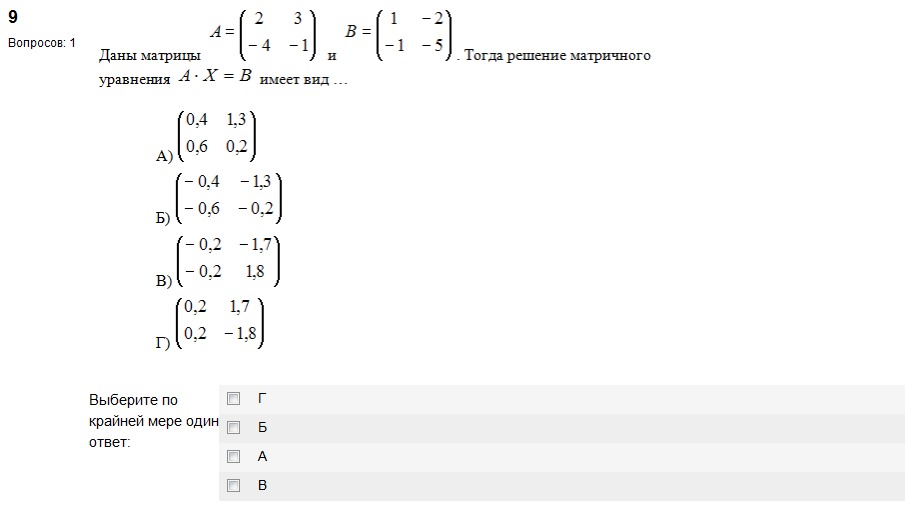
5).
X = B · A-1 = | |
X = . Теперь подставим матрицу X в исходное уравнение для проверки полученного результата: X · A = B
X·A = | = B |
2.5 Оформление отчета
В отчете по ТР должны быть представлены: расчет обратной матрицы A-1, проверка ее умножением матриц A на A-1, расчет искомой матрицы X, проверка найденного результата подстановкой матрицы X в исходное уравнение. В ответе необходимо записать определитель матрицы A и матрицу X : |A| = 5408 .
1.2 Решение матричного уравненияПорядок выполнения работы:
1.
Найти обратную матрицу A-1.
2.
Провести контроль расчетов перемножением
матриц А и A-1.
3.
С помощью матрицы A-1 найти
искомую матрицу X.
4.
Провести найденное решение подстановкой
матрицы X в
исходное уравнение.
Литература
1. Высшая математика. Раздел: Линейная алгебра и аналитическая геометрия. Учебное пособие по выполнению типовых расчетов. М., МИСиС, 1990, N 687, стр.9-16.
Как решить уравнение 2х. Решение матричных уравнений
Назначение сервиса . Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).
Инструкция . Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.
где А, В, С — задаваемые матрицы, Х — искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 .
Если задано выражение A·X — B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B (). Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат .
Рекомендуется также ознакомиться с основными действиями над матрицами .
Пример №1
. Задание . Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1
Обратная матрица A -1:
Найдем обратную матрицу B -1 .
Транспонированная матрица B T:
Обратная матрица B -1:
Матрицу X ищем по формуле: X = A -1 ·C·B -1
Ответ:
Пример №2
.
Задание. Решить матричное уравнение
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Пример №3
. Задание. Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T:
Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1
Ответ: >
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
возрастает.
{nm}:\]
Прибавляем к исходному уравнению:
Вынесем за скобки \
Выразим \
Поскольку степени одинаковые, отбрасываем их:
Ответ: \
Где можно решить показательное уравнение онлайн решателем?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения». Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений.
Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Готовьтесь к экзаменационному тестированию вместе со «Школково»!
При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул. Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.
Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.
Основные определения и формулы представлены в разделе «Теоретическая справка».
Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или . База упражнений на нашем сайте постоянно дополняется и обновляется.
Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.
Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!
Сервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям.
Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды.
2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные.
После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение.
Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.
Как решать уравнения?
В этом разделе мы вспомним (или изучим – уж кому как) самые элементарные уравнения. Итак, что такое уравнение? Говоря человеческим языком, это какое-то математическое выражение, где есть знак равенства и неизвестное.
Которое, обычно, обозначается буквой «х» . Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся.
Уравнения бывают всякие (вот удивил, да?). Но всё их бесконечное многообразие можно разбить всего на четыре типа.
4. Все остальные.)
Всех остальных, разумеется, больше всего, да…) Сюда входят и кубические, и показательные, и логарифмические, и тригонометрические и всякие другие. С ними мы в соответствующих разделах плотно поработаем.
Сразу скажу, что иногда и уравнения первых трёх типов так накрутят, что и не узнаешь их… Ничего. Мы научимся их разматывать.
И зачем нам эти четыре типа? А затем, что линейные уравнения решаются одним способом, квадратные другим, дробные рациональные — третьим, а остальные не решаются вовсе! Ну, не то, чтобы уж совсем никак не решаются, это я зря математику обидел.
) Просто для них существуют свои специальные приёмы и методы.
Но для любых (повторяю — для любых! ) уравнений есть надёжная и безотказная основа для решения. Работает везде и всегда. Эта основа — Звучит страшно, но штука очень простая. И очень (очень!) важная.
Собственно, решение уравнения и состоит из этих самых преобразований. На 99%. Ответ на вопрос: «Как решать уравнения? » лежит, как раз, в этих преобразованиях. Намёк понятен?)
Тождественные преобразования уравнений.
В любых уравнениях для нахождения неизвестного надо преобразовать и упростить исходный пример. Причем так, чтобы при смене внешнего вида суть уравнения не менялась. Такие преобразования называются тождественными или равносильными.
Отмечу, что эти преобразования относятся именно к уравнениям. В математике ещё имеются тождественные преобразования выражений. Это другая тема.
Сейчас мы с вами повторим все-все-все базовые тождественные преобразования уравнений.
Базовые потому, что их можно применять к любым уравнениям – линейным, квадратным, дробным, тригонометрическим, показательным, логарифмическим и т.д. и т.п.
Первое тождественное преобразование: к обеим частям любого уравнения можно прибавить (отнять) любое (но одно и то же!) число или выражение (в том числе и выражение с неизвестным!). Суть уравнения от этого не меняется.
Вы, между прочим, постоянно пользовались этим преобразованием, только думали, что переносите какие-то слагаемые из одной части уравнения в другую со сменой знака. Типа:
Дело знакомое, переносим двойку вправо, и получаем:
На самом деле вы отняли от обеих частей уравнения двойку. Результат получается тот же самый:
х+2 — 2 = 3 — 2
Перенос слагаемых влево-вправо со сменой знака есть просто сокращённый вариант первого тождественного преобразования. И зачем нам такие глубокие познания? – спросите вы. В уравнениях низачем.
Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить….
Второе тождественное преобразование : обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение. Здесь уже появляется понятное ограничение: на ноль умножать глупо, а делить и вовсе нельзя. Это преобразование вы используете, когда решаете что-нибудь крутое, типа
Понятное дело, х = 2. А вот как вы его нашли? Подбором? Или просто озарило? Чтобы не подбирать и не ждать озарения, нужно понять, что вы просто поделили обе части уравнения на 5. При делении левой части (5х) пятёрка сократилась, остался чистый икс. Чего нам и требовалось. А при делении правой части (10) на пять, получилась, знамо дело, двойка.
Вот и всё.
Забавно, но эти два (всего два!) тождественных преобразования лежат в основе решения всех уравнений математики. Во как! Имеет смысл посмотреть на примерах, что и как, правда?)
Примеры тождественных преобразований уравнений.
Основные проблемы.Начнём с первого тождественного преобразования. Перенос влево-вправо.
Пример для младшеньких.)
Допустим, надо решить вот такое уравнение:
3-2х=5-3х
Вспоминаем заклинание: «с иксами — влево, без иксов — вправо!» Это заклинание — инструкция по применению первого тождественного преобразования.) Какое выражение с иксом у нас справа? 3х ? Ответ неверный! Справа у нас — 3х ! Минус три икс! Стало быть, при переносе влево, знак поменяется на плюс. Получится:
3-2х+3х=5
Так, иксы собрали в кучку. Займёмся числами. Слева стоит тройка. С каким знаком? Ответ «с никаким» не принимается!) Перед тройкой, действительно, ничего не нарисовано. А это значит, что перед тройкой стоит плюс. Так уж математики договорились. Ничего не написано, значит, плюс. Следовательно, в правую часть тройка перенесётся с минусом. Получим:
-2х+3х=5-3
Остались сущие пустяки.
Слева — привести подобные, справа — посчитать. Сразу получается ответ:
В этом примере хватило одного тождественного преобразования. Второе не понадобилось. Ну и ладно.)
Пример для старшеньких.)
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
линейная алгебра — Найдите $X$ в матричном уравнении
спросил
Изменено 2 года, 8 месяцев назад
Просмотрено 4к раз
$\begingroup$
Как найти $X$ в этом матричном уравнении?
$$\begin{bmatrix}-3&-8\\-9&5\end{bmatrix} X + \begin{bmatrix}4&-7\\3&-2\end{bmatrix} = \begin{bmatrix}5&8\\-1&-1\end{bmatrix} X$$
Первый Я попробовал $AX + B = CX$, но тогда я не знаю, как решить для $X$, потому что независимо от того, что я делаю, я в конечном итоге избавляюсь от $X$.
- линейная алгебра
- матричные уравнения
$\endgroup$
1
$\begingroup$
9{2 \× 2}$. Векторизируя, можно получить линейную систему $4$ уравнений с $4$ неизвестными$$(I_2 \otimes A) \, \mbox{vec} (X) = \mbox{vec} (B)$$
Наконец, использовать исключение Гаусса.
$\endgroup$
$\begingroup$
Рассматривали ли вы, поскольку это матрицы 2 на 2, просто записать X как $\begin{bmatrix}a & b \\ c & d \end{bmatrix}$, а затем выполнить указанных операций?
$\begin{bmatrix}-3 & -8 \\ -9& 5\end{bmatrix}$$\begin{bmatrix}a & b \\ c & d \end{bmatrix}+ \begin{bmatrix}4 & -7 \\ 3 & -2 \end{bmatrix}$$ = \begin{bmatrix}5 и 8 \\ -1 и -1\end{bmatrix}\begin{bmatrix}a & b \\ c & d \end{bmatrix}$.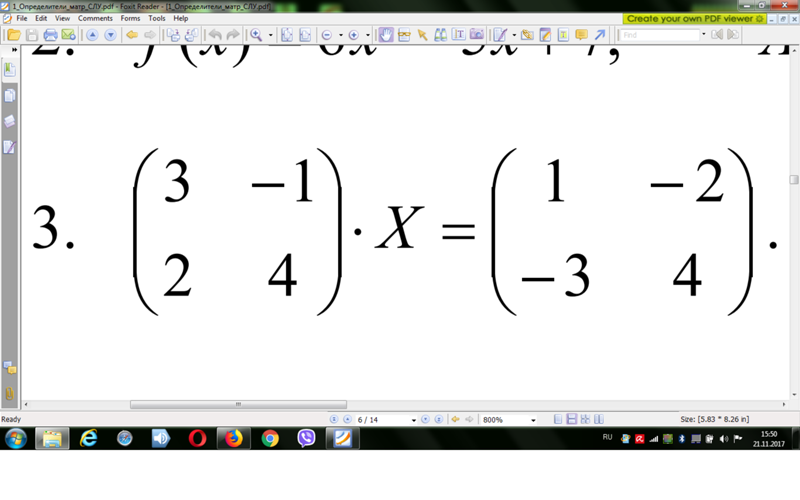
$\begin{bmatrix}-3a- 8c+ 4 & -3b- 8d- 7 \\ -9a+ 5b+ 3 & -9b+ 5d- 2\end{bmatrix}= \begin{bmatrix}5a+ 8c & 5b+ 8d \\ -a- c & -b- d\end{bmatrix}$.
Итак, мы имеем систему четырех уравнений
$$-3a- 8c+ 4= 5a+ 8c\\-9a+ 5b+ 3= -a- c\\-3b- 8d- 7= 5b+ 8d\\-9b+ 5d- 2= -b- d$$
Что легко решить относительно $a, b, c,$ и $д$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
92+AX=B$, где $A$ и $B$ — известные матрицы?Задавать вопрос
спросил
Изменено 4 года, 10 месяцев назад
Просмотрено 418 раз
$\begingroup$ 92=M$$, где $Y$ неизвестно, а $M$ задано.
$\endgroup$
0
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.