ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I.  ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ§ 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11.  n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 22. Производные различных порядков § 23.  x, sin x, cos xУпражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2.  Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратов§ 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  Формула Чебышева§ 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII |
7.3. Наибольшее и наименьшее значения функции на отрезке
Известно,
что если функция непрерывна на отрезке,
то она достигает на этом отрезке своего
наименьшего и наибольшего значения.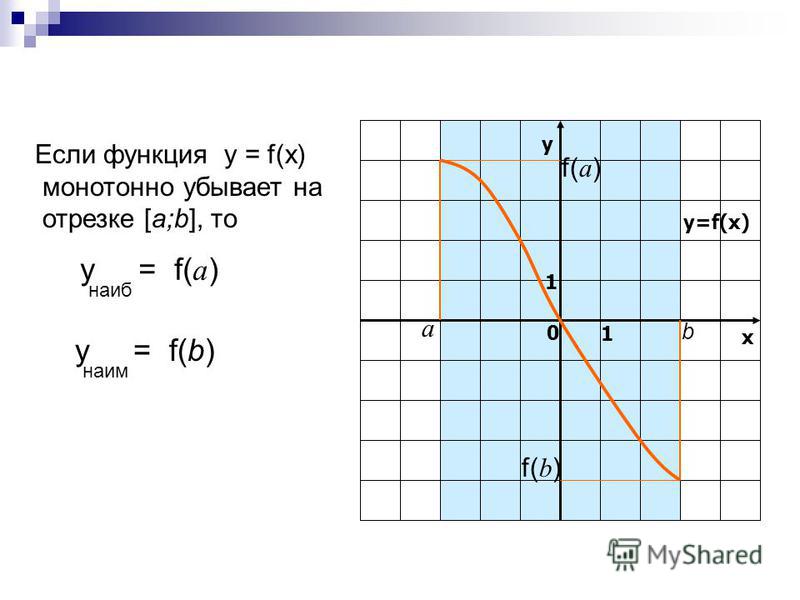
Иногда требуется найти наименьшее или
наибольшее значение такой функции.
Если на отрезке есть точки минимума и максимума функции , то наименьшее значение функция будет принимать либо в одной из точек минимума, либо на конце отрезка . Аналогично для наибольшего значения.
Сформулируем алгоритм нахождения наибольшего и наименьшего значения функции f(x), непрерывной на отрезке:
Найти критические точки x1, x2, …, xn функции . Для этого необходимо решить уравнение .
Отобрать все критические точки, принадлежащие отрезку .
Вычислить значения функции в этих критических точках и на концах отрезка.
Из этих значений выбрать самое большое и самое малое. Эти числа и будут наибольшим и наименьшим значениями на отрезке .
Пример 7.3. Найти наименьшее и наибольшее значения функции
Решение.
Найдем критические точки для данной функции:
;
при x1=0, x2 =–1, x3 =+1.
Все три критические точки принадлежат данному отрезку.
Вычислим значения функции в точках: :
4. Из найденных значений самое малое число 4, а самое большое число 13.
Таким образом, наименьшее значение функции равно 4, в точке х = 1, наибольшее значение равно 13, в точке х = 2 и в точке х = -2.
Пример 7.4. Найти наибольшее и наименьшее значения функции
на
отрезке
.
Решение.
, определена во всех точках;при.
На отрезке ,при.
Имеем три точки: ,,, в которых может достигаться наибольшее и наименьшее значения.
;
;
.
Итак, ,.
Пример 7.5. Найти наибольшее и наименьшее значения функции
на отрезке .
Решение.
Найдем критические точки функции из условия, что или такие, при которыхне существует:
.
Производная во всех точках существует,, когда.
Раскладывая левую часть на множители, получаем:
.
Отсюда находим критические точки: ,,.
Из этих точек отрезку принадлежат только две:и.
Найдем значения функции в этих точках и на концах отрезка, т. е. при ,,,:
;
;
=;
.
Итак, получили ,.
Среди многих применений производной функции одной переменной важное значение имеет решение так называемых задач на максимум (минимум).
Пример 7.6. Найти прямоугольный треугольник наибольшей площади, у которого сумма катета и гипотенузы равна .
Решение.
Обозначим один из катетов треугольника через , тогда гипотенуза будет равна, а другой катет, по теореме Пифагора будет равен:
.
Площадь треугольника , так какдолжна быть максимальной, тоилине существует. Находим производную:
.
не
существует, если
,
но тогда катет окажется равным гипотенузе,
что невозможно.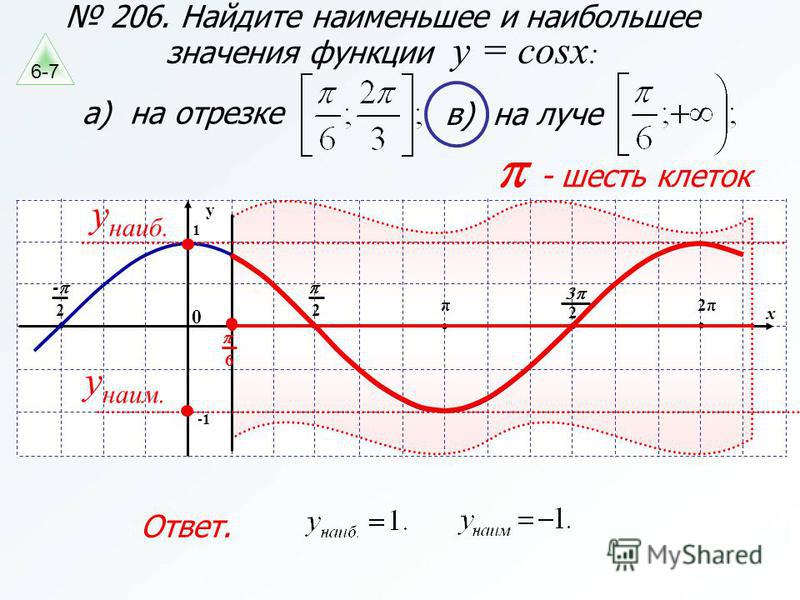
,
если.
Тогда.
Проверяем является ли эта точка точкой максимума. При , а при. Таким образом приплощадь треугольника будет наибольшей.
Гипотенуза будет равна , т. е., где– угол, прилежащий к катету. Значит,; другой угол будет.
Следовательно, искомый треугольник – это прямоугольный треугольник с углами и сторонами,и.
Пример 7.7. Из трех одинаковых досок изготовить симметричный желоб с наибольшей площадью поперечного сечения.
Решение.
Ширину данных досок обозначим через . Поперечное сечение желоба изображено на рис. 5,.
Обозначим через угол(), тогда,.
Площадь поперечного сечения (площадь трапеции) будет:
.
Наибольшее
значение эта функция принимает в точке
максимума, а необходимым условием того,
что точка
является точкой максимума функции,
является то, чтоилине существует.
Найдем:
.
Но всегда существует. Точки, в которых, находятся из уравнения:. Тогдаили. Если, то.
Но в этом случае никакого желоба не получится, так как . Остается случай, когда,, тогда, так как.
Проверим, является ли эта точка точкой максимума функции. При, производная функции принимает положительные значения, а при- отрицательные. То есть приплощадь поперечного сечения желоба будет наибольшей.
Таким образом, действительно точка максимума. А площадь поперечного сечения составит
.
макс. и мин. направленного отрезка
Исчисление Исчисление 3 Макс. и мин. сегмента направленной линии
Сью М.
спросил 24.06.16Пусть F= i + j.
Как разместить направленный отрезок C длины один так, чтобы значение ∫ c F *dr было равно
a. максимум
б. минимум
c.
ноль
д. каковы будут максимальное и минимальное значения интеграла?
Подписаться І 2
Подробнее
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Дэн Д. ответил 25.06.16
Репетитор
4.9 (433)
Репетитор для пациентов, сосредоточенный на вашем понимании математики
См. таких репетиторов
Смотрите таких репетиторов
Я предполагаю, что F = i + j определяет двумерное векторное поле, которое является постоянным с позицией (x, y),
и что i и j являются единичными векторами вдоль осей x и y соответственно.
Таким образом, в любой точке (x,y) F имеет длину √2 и указывает в направлении на 45 градусов от оси x, то есть параллельно линии y=x.
Теперь у нас есть C — отрезок длины 1, указывающий в каком-то направлении.
Интеграл линии, несомненно, является суммой точечного продукта между векторами F и DR , когда мы идем по курсу C:
∫ C F • DR
Когда F и dr находятся в одном направлении, мы получаем максимальный вклад, когда они противоположны, мы получаем минимальный (большое отрицательное значение) вклад, и если F и dr перпендикулярны, то мы получаем 0 вкладов от скалярного произведения.
Таким образом, для этого конкретного постоянного поля:
а) максимум, когда C указывает в направлении i + j . (45 градусов от оси X)
б) минимум, когда C находится в противоположном направлении: -i + -j . (225 градусов от оси X)
c) 0, когда C указывает перпендикулярно i + j, то есть в любом направлении: i — j или -i + j (+135 или -45 градусов от оси X)
d) Поскольку F имеет величину √2, а C имеет длину 1, мы получаем максимальное/минимальное значения +/- √2.