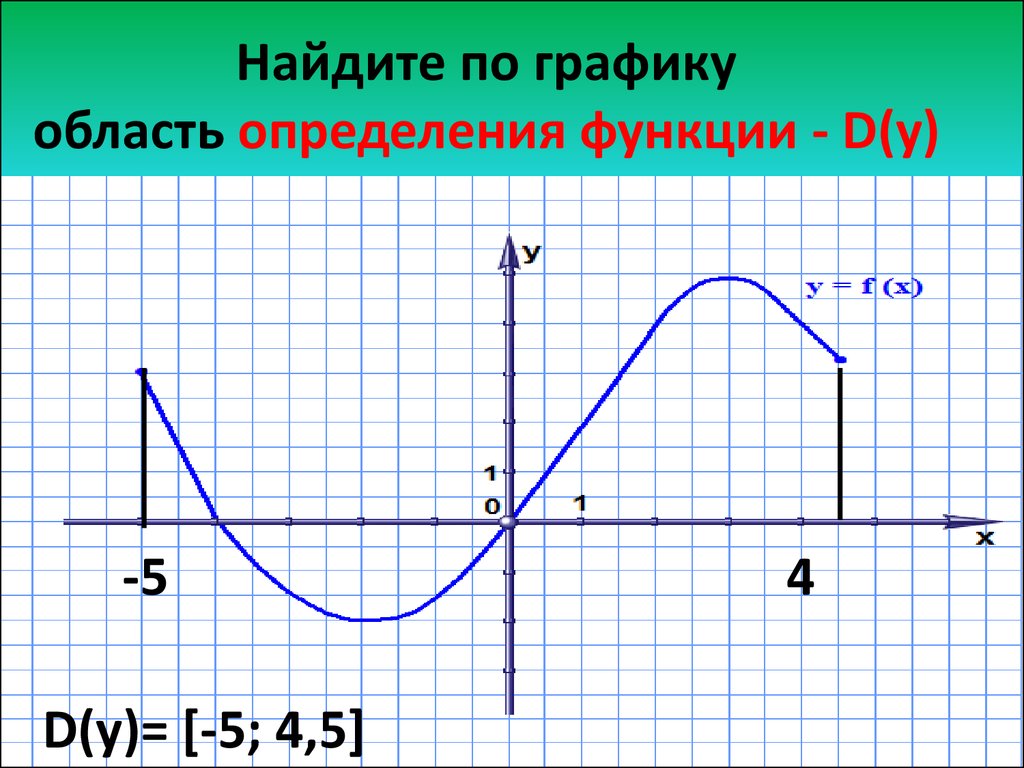
Исследование графика функции. Минимум и максимум
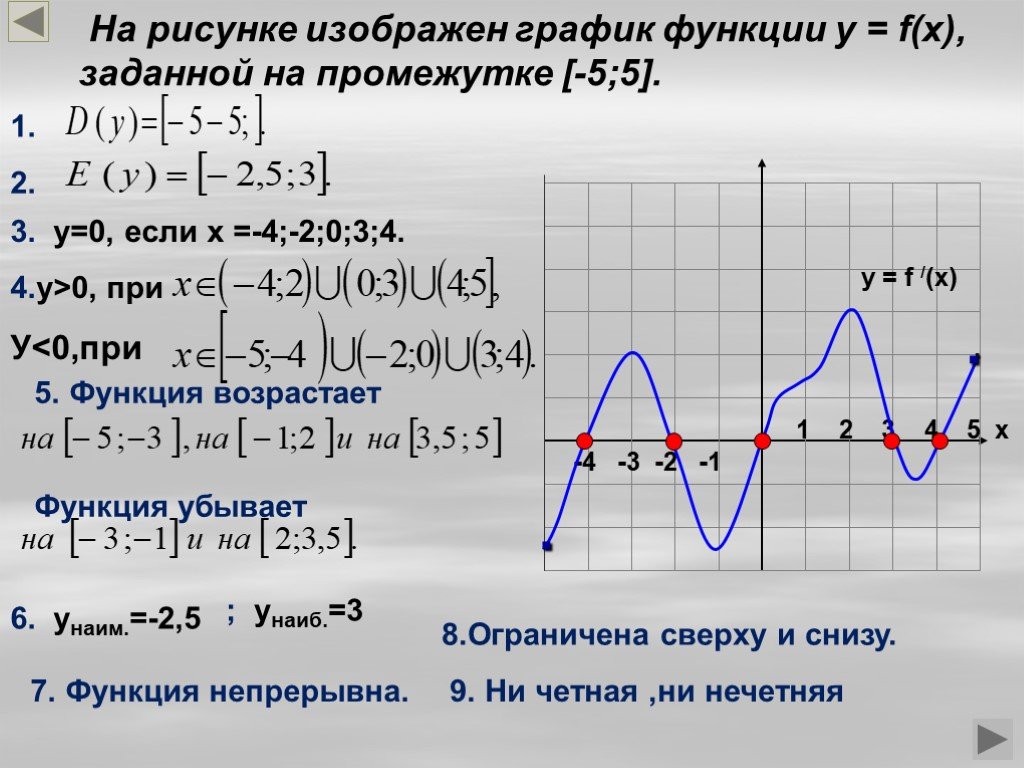
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции;
- область значений функции;
- нули функции;
- промежутки возрастания и убывания;
- точки максимума и минимума;
- наибольшее и наименьшее значение функции на отрезке.
Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.
Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно .
Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Исследование графика функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 08.04.2023
Область определения функции. Как найти, если функция задана графиком, таблицей, рисунком.
12+
6 месяцев назад
Математика от Баканчиковой293 подписчика
Алгебра 7-11 класс. Мы начинаем серию уроков о всех свойствах функции.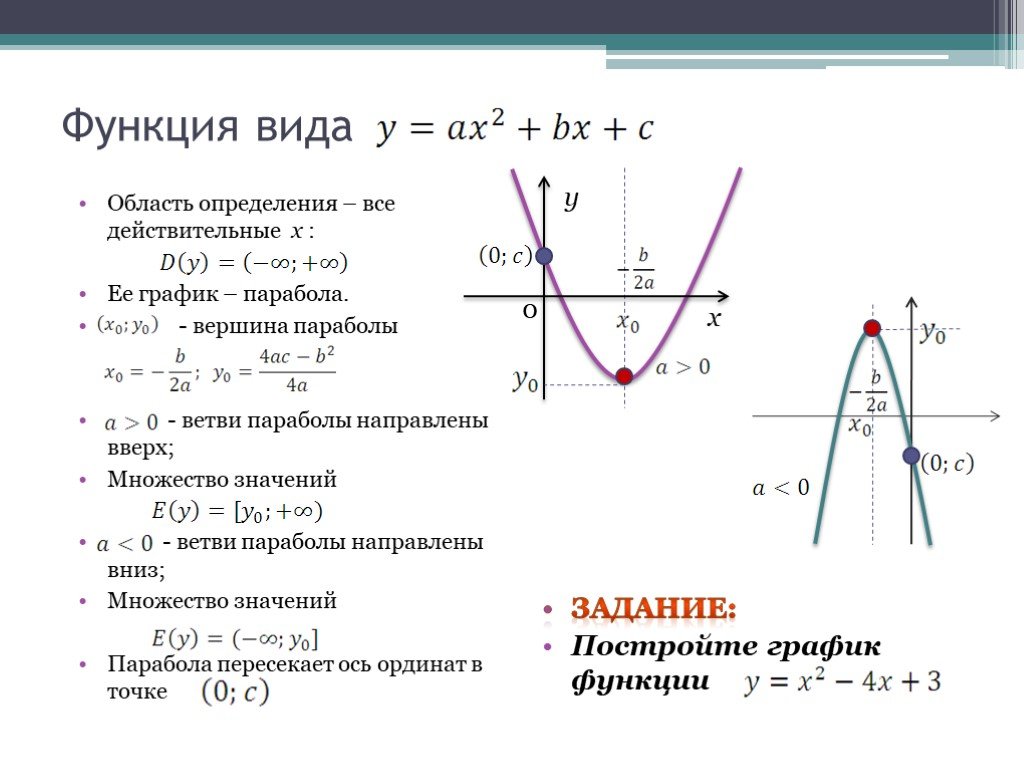
А начнём мы конечно же с области определения функции. Вначале мы коротко повторим определения функции и её компонентов, покажем, где находить область определения функции, если функция задана рисунком, таблицей и с помощью символа. Более подробное объяснение этих тем Вы можете найти в наших предыдущих уроках в плейлисте «Функция». Затем мы покажем Вам, как записывать область определения функции. Разберём, что такое допустимые значения аргумента. А потом на конкретных примерах подробно расскажем и покажем, как находить и записывать область определения функций, заданных различными графиками. Для закрепления материала, мы попросим Вас выполнить домашнее задание.
Подробный план урока Вы найдете в описании под видео.
00:00 Начало видео.
00:23 Совет Любовь Николаевны.
01:05 Повторим определение и компоненты функции.
03:00 Вспомним основные способы задания функции, где находится область определения функции и как её записать.
07:00 Что такое допустимые значения аргумента?
10:30 Вспомним графический способ задания функции.
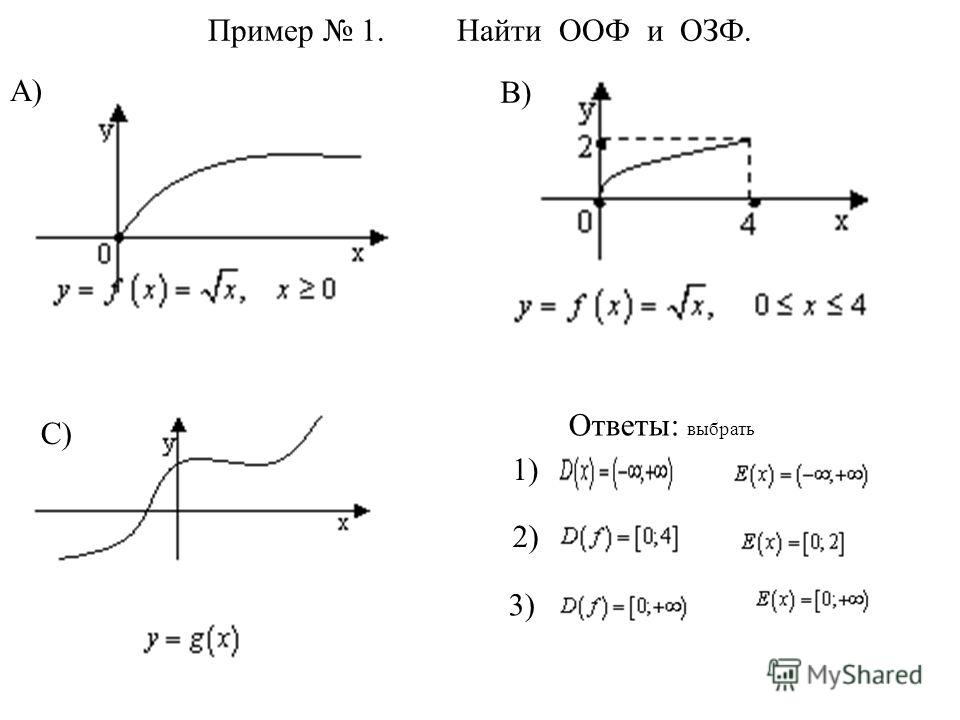
Определение домена и диапазона по графику
Результаты обучения
- Поиск домена и диапазона по графику и уравнению.
- Укажите домен и диапазон функций инструментария.
Другой способ определить домен и диапазон функций — использовать графики. Поскольку домен относится к набору возможных входных значений, домен графика состоит из всех входных значений, показанных на оси [latex]x[/latex]. Диапазон — это набор возможных выходных значений, которые показаны на оси [latex]y[/latex]. Имейте в виду, что если график выходит за пределы видимой части графика, домен и диапазон могут быть больше, чем видимые значения.
Мы можем заметить, что граф простирается по горизонтали от [латекс]-5[/латекс] вправо без границ, так что домен равен [латекс]\левый[-5,\infty \правый)[/латекс]. Вертикальный экстент графика — это все значения диапазона [latex]5[/latex] и ниже, поэтому диапазон равен [latex]\left(\mathrm{-\infty },5\right][/latex]. Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.
Пример: поиск домена и диапазона на графике
Найдите домен и диапазон функции [latex]f[/latex].
Показать раствор
Пример: нахождение области определения и диапазона по графику добычи нефти
Найдите область определения и диапазон функции [latex]f[/latex].
(кредит: модификация работы Управления энергетической информации США)
Показать решение
Попробуйте
Имея график, определите домен и диапазон, используя интервальную нотацию.
Показать решение
Вопросы и ответы
Могут ли домен и диапазон функции совпадать?
Да. Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел.
Домен и диапазон функций инструментария
Теперь мы вернемся к нашему набору функций набора инструментов, чтобы определить домен и диапазон каждой из них.
Для постоянной функции [latex]f\left(x\right)=c[/latex] область определения состоит из всех действительных чисел; ограничений на ввод нет. Единственным выходным значением является константа [latex]c[/latex], поэтому диапазоном является набор [latex]\left\{c\right\}[/latex], содержащий этот единственный элемент. В записи интервала это записывается как [латекс]\влево[с,с\право][/латекс], интервал, который начинается и заканчивается на [латекс]с[/латекс].
Для функции тождества [латекс]f\left(x\right)=x[/latex] ограничений на [latex]x[/latex] нет. И домен, и диапазон являются набором всех действительных чисел.
Для функции абсолютного значения [latex]f\left(x\right)=|x|[/latex] ограничений на [latex]x[/latex] нет. Однако, поскольку абсолютное значение определяется как расстояние от 0, выходное значение может быть только больше или равно 0.
{ 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа.
Для обратной функции [латекс]f\left(x\right)=\frac{1}{x}[/latex] мы не можем делить на 0, поэтому мы должны исключить 0 из области определения. Кроме того, 1, деленная на любое значение, никогда не может равняться 0, поэтому диапазон также не будет включать 0. В нотации построителя наборов мы могли бы также написать [латекс]\влево\{х|\текст{ }х\ne 0\вправо \}[/latex], множество всех вещественных чисел, не равных нулю. 9{2}}[/latex], мы не можем делить на [latex]0[/latex], поэтому мы должны исключить [latex]0[/latex] из домена.
Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа.
Для функции квадратного корня [latex]f\left(x\right)=\sqrt[]{x}[/latex] мы не можем извлечь квадратный корень из отрицательного действительного числа, поэтому домен должен быть 0 или выше. Диапазон также исключает отрицательные числа, поскольку квадратный корень из положительного числа [latex]x[/latex] определяется как положительный, хотя квадрат отрицательного числа [latex]-\sqrt{x}[/latex] также дает нам [латекс]x[/латекс].
Для функции кубического корня [latex]f\left(x\right)=\sqrt[3]{x}[/latex] домен и диапазон включают все действительные числа. Обратите внимание, что нет проблем с извлечением кубического корня или любого корня из нечетного целого числа из отрицательного числа, и результирующий результат будет отрицательным (это нечетная функция).
Попробуйте
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Как получить домен и диапазон из графика функции — Криста Кинг Математика
Определение области и диапазона
Областью являются все ???x???-значения или входные данные функции, а диапазоном являются все ???y???-значения или выходные данные функции.
При просмотре графика доменом являются все значения графика слева направо. Диапазон — это все значения графика снизу вверх.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Основные функции с ограничениями доменаНахождение домена и диапазона по графику функции
Пройти курс
Хотите узнать больше об Алгебре 1? У меня есть пошаговый курс для этого.
🙂Узнать больше
Область и область значений графика параболы
Пример
Каковы область определения и область значений функции? Предположим, что график не выходит за пределы показанного графика.
Начнем с домена. Помните, что домен — это то, как далеко график идет слева направо.
Начните с того, что посмотрите на самый левый край этого графика. Значение ???x??? в самой дальней левой точке равно ???x=-2???. Теперь продолжайте отслеживать график, пока не дойдете до точки, которая находится дальше всего справа. Значение ???x??? в этот момент равно ???2???. В графике слева направо нет разрывов, что означает, что он непрерывен от ???-2??? до ???2???.
Домен: ???[-2,2]??? также пишется как ???-2\leq x\leq 2???
Далее давайте посмотрим на диапазон. Помните, что диапазон — это то, как далеко график идет снизу вверх.
Посмотрите на самую дальнюю точку графика или нижнюю часть графика.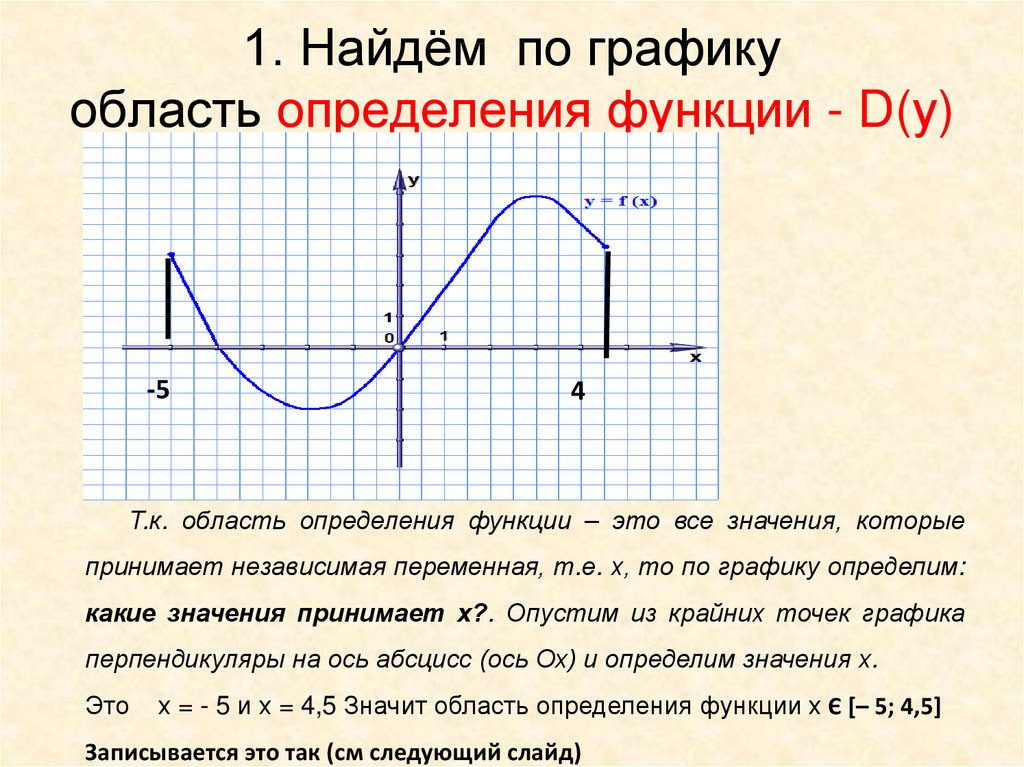
Значение ???y??? в этот момент равно ???y=1???. Теперь посмотрите, как далеко вверх идет график или вершина графика. Это когда ???x=-2??? или ???x=2???, но теперь мы находим диапазон, поэтому нам нужно посмотреть на ???y???-значение этой точки, которое находится в ???y=5??? . В графике сверху вниз нет разрывов, что означает, что он непрерывен.
Диапазон: ???[1,5]??? также пишется как ???1\leq y\leq 5???
Давайте попробуем еще один пример поиска домена и диапазона на графике.
Помните, что Домен — это все определенные значения x слева направо на графике.
Пример
Каковы домен и диапазон функции? Предположим, что график не выходит за пределы показанного графика.
Начнем с домена. Значение ???x??? в самой дальней левой точке равно ???x=-1???. Теперь продолжайте отслеживать график, пока не дойдете до точки, которая находится дальше всего справа.