Как найти область значений функции 10 класс: Область значений функции – Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения

Содержание

Область значений функции

Всем здравствуйте! Тренируемся находить область значений функции! Кто еще не понял, что такое область определения (а она нам тоже понадобится непременно), тому сюда.

Что же такое область значений функции? Это та “часть” оси ординат, та область, где можно наткнуться на какие-либо точки, принадлежащие функции. То есть можно сказать, что если область значений найдена, то все точки функции находятся в ней, не выше и не ниже. Это почти тоже самое, что и область определения, только теперь это “область определения по оси ординат”. Здесь никаких особых ограничений нет, поэтому, чтобы найти область значений, нужно иметь представление об элементарных функциях – например, как выглядят парабола или гипербола, как определить, направлены ли ветви параболы вверх или вниз и т.п. Все это рассказано и показано здесь.

Ну, поехали!

Примеры.

1. Найдите область значений функции

Решение: функция – квадратичная, представляет собой параболу с положительным старшим коэффициентом, ветви направлены вверх. Понятно тогда, что весь график располагается выше координаты своей вершины (вершина – самая низшая точка). Ордината вершины: $y_0=-D/{4a}=-100/4=25$ , тогда .

2. Найдите область значений функции $y=sqrt{x^2+4x-21}$

Решение: область определения функции D(f)= ( ] union [).

В точках (-7) и (3) двучлен обращается в ноль. Поскольку результат извлечения корня – величина положительная, то вся функция располагается выше оси абсцисс, и ее область значений E(f)= [)

3. Найти область значений функции $y=-1/{x^4}$

Область определения – вся числовая ось, кроме ноля. Можем подставить любое число из области определения, при этом функция всегда отрицательна.

Из графика также видно, что

4. Найти область значений функции: $y=1/{3^{sqrt{2x-x^2}}}$

Решение. Область определения:

0<=x<=2 0<=x<=2
На концах отрезка функция принимает значение 1, под корнем имеем квадратный двучлен, наибольшее значение он принимает в вершине, при x=1 , значит, функция будет принимать в этой точке наименьшее значение.

Подставив 1, получаем y=1/3

Ответ:

5. Найдите область значений функции: $y=x^2+5delim{$

Очевидно, что график данной функции может быть получен из графика обычной параболы , область значений которой легко найти: ветви направлены вверх, поэтому низшая точка – вершина параболы. Однако заметим также, что если аргумент функции под знаком модуля, то график такой функции может быть построен с помощью отражения части графика, лежащей в правой вертикальной полуплоскости, в левую полуплоскость(см. рисунок). Тогда от нашей параболы останется только часть, лежащая правее оси ординат, и именно она будет отражена относительно оси y, и тогда низшей точкой окажется та, в которой график пересечет ось ординат, а это – значение свободного члена (коэффициента с), который у нас равен (-6).

Область значений нашей функции E(f)= [)

6. Найдите область значений функции:

Очевидно, что график данной функции может быть получен из графика обычной параболы . Так как все выражение находится под знаком модуля, то для того, чтобы построить такой график, нужно отразить всю часть графика, расположенную ниже оси х, вверх, поэтому E(f)= [).

7. Найдите область значений функции:

Данная функция получена преобразованием обычной гиперболы. Данная функция не существует при 4x+1=0 , или . При второе слагаемое обращается в ноль, и функция стремится к значению y=2 , причем можно заметить, что при положительных больших значениях х данная функция приближается к 2 снизу, а при отрицательных – сверху.

Ответ:

8. Найти область значений функции: $y={0,7}^{sqrt{x+7}}$

Решение. Область определения:

При функция принимает наибольшее значение ,

При x, стремящемся к бесконечности, функция стремится к нулю. Но мы запишем область значений от меньшего к большему:

Ответ: (]

Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения

Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.

В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.

Начнем с базовых определений.

Определение 1
Множество значений функции y = f(x) на некотором интервале x представляет собой множество всех значений, которые данная функция принимает при переборе всех значений x∈X.
Определение 2
Область значений функции y=f(x) – это множество всех ее значений, которые она может принять при переборе значений x из области x∈(f).
Область значений некоторой функции принято обозначать E(f).
Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.
Важно также различать область значений и область допустимых значений переменной x для выражения в правой части y=f(x). Область допустимых значений x для выражения f(x) и будет областью определения данной функции.
Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.

Очевидно, что область значений функции можно получить при проецировании графика функции на ось Oy. При этом она может представлять собой как одно число, так и множество чисел, отрезок, интервал, открытый луч, объединение числовых
Область значений функции, теория и примеры
Область значений основных элементарных функций
Для линейной функции область значений .

Для обратной пропорциональности, то есть функции заданной формулой , область значений: .

Значение , где дискриминант, называется ординатой вершины параболы, задаваемой уравнением .

Действительно, абсцисса вершины параболы вычисляется по формуле , тогда

Итак, для квадратичной функции : если , то ветки параболы направлены вниз и значение является наибольшим значением функции, то есть ; если , то ветки направлены вверх и значение является наименьшим значением функции, то есть .

Для логарифмической функции область значений .

Для показательной функции область значений .

Для тригонометрических функции область значений , для область значений — множество всех действительных чисел.

Примеры решения задач
Понравился сайт? Расскажи друзьям!

Урок 1. область определения и множество значений тригонометрических функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №1. Область определения и множество значений тригонометрических функций.
Перечень вопросов, рассматриваемых в теме
Овладение понятиями «область определения», «область определения тригонометрических функций», «множество значений функции», «множество значений тригонометрических функций»;

Нахождение области определения и множества значений тригонометрических функций вида y=af(kx+b)+c и y=|f(k|x|+b)|, где f(x) — косинус, синус, тангенс или котангенс действительного числа от значения коэффициентов a, k, b.;
Объяснение зависимости области определения и множества значений функции вида y=af(kx+b)+c и y=|f(k|x|+b)|, где f(x) — косинус, синус, тангенс или котангенс действительного числа от значения коэффициентов a, k, b.
Глоссарий по теме
Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
Множеством значений функции y = sin x и y = cos x является отрезок -1 ≤ y ≤ 1. Данные функции ограничены сверху и снизу.
Областью определения функции y = tg x является множество чисел
x ≠ π/2 + πk, kЄ Z.
Областью определения функции y = сtg x является множество чисел x ≠ πk, kЄ Z.
Множеством значений функции y = tg x и y =сtg x является множество R всех действительных чисел, т.к. уравнения tg x = a и сtg x = a имеют корни при любом действительном значении a. Функции неограниченные.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения
Актуализация знаний
Вопросы:
Что такое функция?
Что такое область определения функции? Чем является область определения функции геометрически?
Что такое множество значений функции? Чем является множество значений функции геометрически?
Ответы на вопросы:
Если каждому значению x из некоторого множества чисел поставлено в соответствие по определенному правилу число y, то говорят, что на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у – зависимой переменной или функцией. Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают y=f(x).
Областью определения функции называют множество всех допустимых значений переменной x
. Геометрически – это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически – это проекция графика функции на ось Оy.
Найдите область определения функции и множество значений функции:
1) ; 2) ; 3) .
Ответы:
D(f): 1)
; 2) ; 3)
E(f): 1); 2) ; 3) .
Объяснение нового материала
С помощью единичной окружности сделайте выводы об области определения и множестве значений тригонометрических функций.

Заполните таблицу:
Функция
Область определения
Множество значений

Ответ:
Функция
Область определения
Множество значений
Итак, Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
Множеством значений функции y = sin x и y = cos x является отрезок -1 ≤ y ≤ 1. Данные функции ограничены сверху и снизу.
Областью определения функции y = tg x является множество чисел x ≠ π/2 + πk, kЄ Z.
Областью определения функции y = сtg x является множество чисел x ≠ πk, kЄ Z.
Множеством значений функции y = tg x и y =сtg x является множество R всех действительных чисел, т.к. уравнения tg x = a и сtg x = a имеют корни при любом действительном значении a. Функции неограниченные.
Примеры и разборы решения заданий тренировочного модуля:
Пример 1. Найти область определения функции .
;
;
;
Ответ: −.
Пример 2. Найти все решения уравнения
;
;
Ответ:
.
Функция. Область определения и область значений функции
Определение:
Зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение y, называют функцией.
В определении сказано, что только та зависимость является функцией, у которой каждому значению аргумента соответствует единственное значение функции.
Рассмотрим первый график. Видим, что одному значению x может соответствовать несколько значений y. Значит, данная зависимость не является функцией.
Обратимся ко второму случаю. Какие бы значения аргумента мы не брали, каждому из них соответствует только одно значение функции. Можно сказать, что эта зависимость является функцией.
В общем виде любую функцию можно записать так:
Например:
Понятно, что функция может принимать различные значения в зависимости от значения аргумента. Найдём значение каждой функции при заданном значении аргумента.
Вы заметили, что в этом задании функции названы разными буквами. Действительно, функцию можно называть любой буквой латинского алфавита.
Ранее вами были изучены несколько важных функций. Вспомним их.
Сейчас попробуем выяснить, как же получается график функции, и дадим определение этому понятию.
Можно записать её в таком виде:
Это линейная функция, графиком как вы помните, является прямая. Для изображения прямой достаточно двух точек.
Получаем точки с координатами (1;3) и (-1;-11).
Проведём прямую через полученные точки.
Мы изобразили график функции.
Определение:
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — значениям функции, называют графиком функции.
Все значения аргумента, т.е. переменной x образуют область определения функции, а все значения зависимой переменной, т.е. y, — область значений функции.
В данном случае x и y могут быть любыми числами, т.е. областью определения и областью значений является множество всех действительных чисел.
Потренируемся находить область определения и область значений функции по её графику.
Область определения можно находить не только по графику функции, но и по формуле, с помощью которой задана функция.
Область значений функции — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 июля 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 июля 2019; проверки требует 1 правка.
Область значений (или множество значений) функции — множество, состоящее из всех значений, которые принимает функция^[1]^[2]^[3].
Пусть на множестве X{\displaystyle X} задана функция f{\displaystyle f}, которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}, то есть: f:X→Y{\displaystyle f:X\to Y}. Тогда областью (или множеством) значений функции f{\displaystyle f} называется совокупность всех её значений, которая является подмножеством множества Y{\displaystyle Y} и обозначается f(X){\displaystyle f(X)}, E(f){\displaystyle E(f)}, R(f){\displaystyle R(f)} или ranf{\displaystyle \mathrm {ran} \,f} (от англ. range):
f(X)={y∈Y|y=f(x),x∈X}{\displaystyle f(X)=\{y\in Y|\,y=f(x),\,x\in X\}}.
Способы нахождения областей значений некоторых функций[править | править код]
последовательное нахождение значений сложных аргументов функции;
метод оценок;
использование свойств непрерывности и монотонности функции;
использование производной;
использование наибольшего и наименьшего значений функции;
графический метод;
метод введения параметра;
метод обратной функции.
В некоторых источниках различаются понятия области значений и множества значений функции. При этом областью значений функции называется её кодомен, то есть множество Y{\displaystyle Y} в обозначении функции f:X→Y{\displaystyle f:X\to Y}^[4], а множеством значений функции называется совокупность всех значений f(X){\displaystyle f(X)} функции f{\displaystyle f}.
Множество значений f(X){\displaystyle f(X)} называется также образом множества X{\displaystyle X} при отображении f{\displaystyle f}.
Иногда множество значений функции называют областью изменения функции^[3].
Функция. Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
И. А. Лавров, Л. Л. Максимова. Часть I. Теория множеств // Задачи по теории множеств, математической логике и теории алгоритмов. — 3-е изд.. — М.: Физматлит, 1995. — С. 13 — 21. — 256 с. — ISBN 5-02-014844-X.
А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14 — 18. — 256 с.
Дж. Л. Келли. Глава 0. Предварительные сведения // Общая топология. — 2-е изд.. — М.: Наука, 1981. — С. 19 — 27. — 423 с.
В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Функция // Математический анализ, часть I. — М.: Наука, 1981. — С. 23 — 36. — 544 с.
А. Н. Колмогоров. «Что такое функция» // «Квант». — М.: «Наука», 1970. — Вып. 1. — С. 27-36. — ISSN 0130-2221.
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
Понятие функции. Область определения функции. Множество значений функции
Определение. Пусть X – некоторое множество чисел. Говорят, что на множестве X задана числовая функция, если указано правило, с помощью которого каждому числу x из множества X ставится в соответствие некоторое число.
Это принято обозначать так:
y = f (x),
причем в этой записи x называют аргументом функции или независимой переменной, а y называют значением функции, соответствующим аргументу x .
Множество X называют областью определения функции f и обозначают D ( f ) . Множество Y всех возможных значений функции y = f (x) называют множеством значений функции f и обозначают E ( f ) (рис. 1).
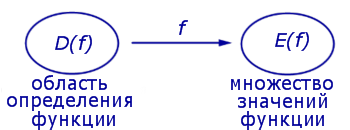
Рис.1
Примеры решения задач
Часто в задачах известна формула, задающая функцию f , и требуется найти наиболее широкое множество чисел, к которым данную формулу можно применить. В этом случае указанная задача формулируется так: «Найти область определения функции y = f (x)». В некоторых задачах требуется найти не только область опредения функции, но и множество ее значений.
Задача 1. Найти область определения функции
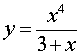
Решение. Указанная функцию представляет собой результат, полученный при делении числа x⁴ на число (3 + x) . Поскольку единственным ограничением является запрет деления на число 0 , то число (3 + x) не может равняться 0 , то есть .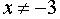
Ответ. .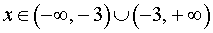
Задача 2. Найти область определения функции
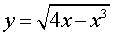
Решение. Поскольку квадратный корень можно извлекать только из неотрицательных чисел, то область определения данной функции задается неравенством
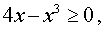
которое эквивалентно неравенству
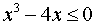
и может быть записано в виде
.
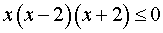Решая это неравенство с помощью метода интервалов, получим
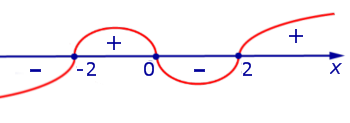
Ответ. .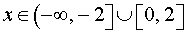
Задача 3. Найти область определения функции
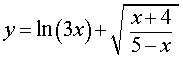
Решение. Исходя из определений логарифма и квадратного корня, область определения данной функции задается следующей системой неравенств
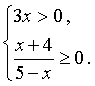(1)
Решая второе неравенство системы с помощью метода интервалов,
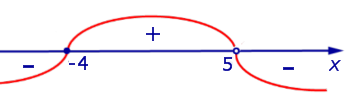
получим
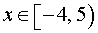
Таким образом, система (1) эквивалентна системе
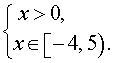
Решением этой системы является интервал
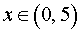
Ответ. .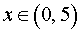
Задача 4 . Найти множество значений функции
y = 3sin x + 4cos x
Решение. Воспользовавшись формулой дополнительного угла (вспомогательного аргумента), получим
y = 5 sin (x + φ) ,
где
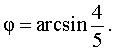
Поскольку множеством значений функции y = sin (x + φ) является отрезок [–1, 1], то множеством значений функции y = 5 sin (x +φ) будет отрезок [–5, 5].
Ответ. .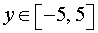
Задача 5 . Найти множество значений функции
y = x² + 6x + 8
Решение. Поскольку
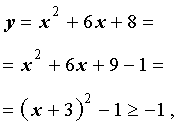
и для каждого числа 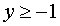существуют решения уравнения
x² + 6x + 8 = y ,
определяемые формулой
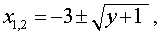
то множеством значений функции y = x² + 6x + 8 будет множество .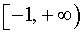
Ответ. .

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
No related posts.