Как найти основание треугольника зная среднюю линию: Как найти среднюю линию треугольника? Свойства, теорема

Как найти среднюю линию треугольника? Свойства, теорема

Поможем понять и полюбить математику

Начать учиться

162.8K

Не каждая геометрическая фигура может похвастаться таким количеством линий, как треугольник: медиана, средняя линия, биссектриса, высота, серединный перпендикуляр. В этот раз поговорим про среднюю линию и узнаем, зачем она нужна.

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Виды треугольников:

• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.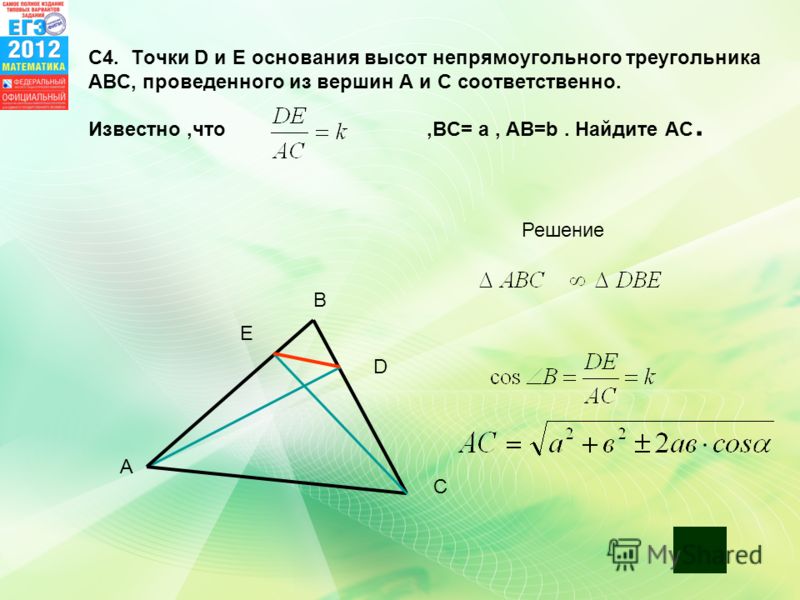

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

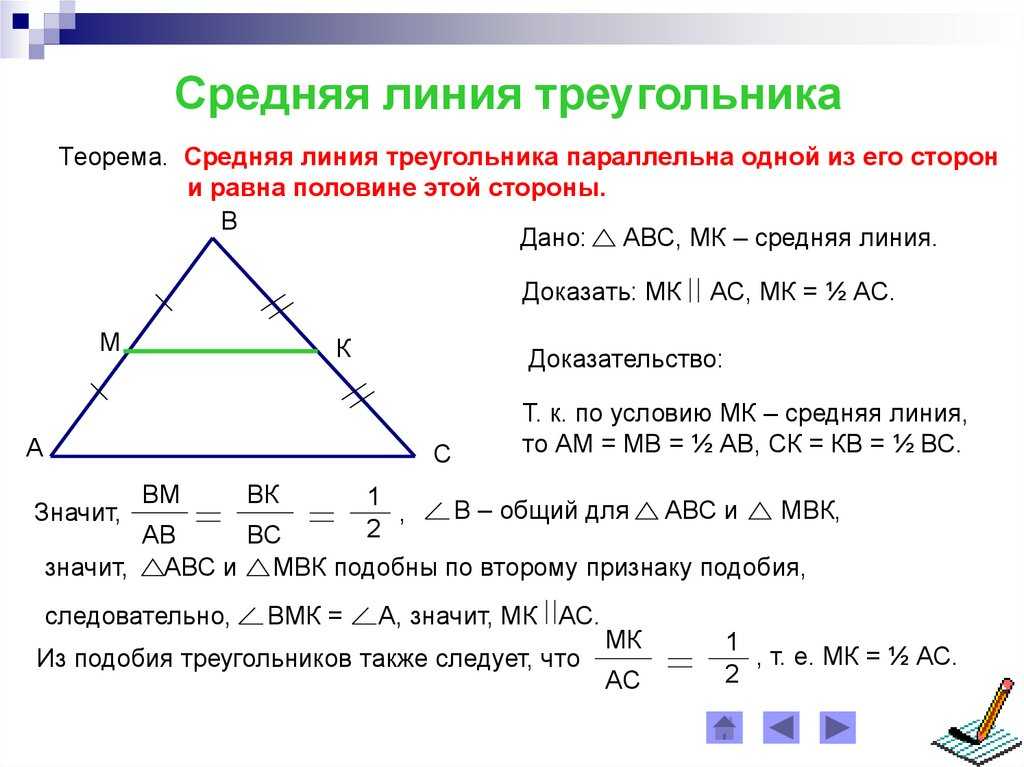
​Средняя линия треугольника — отрезок, который соединяет середины двух сторон.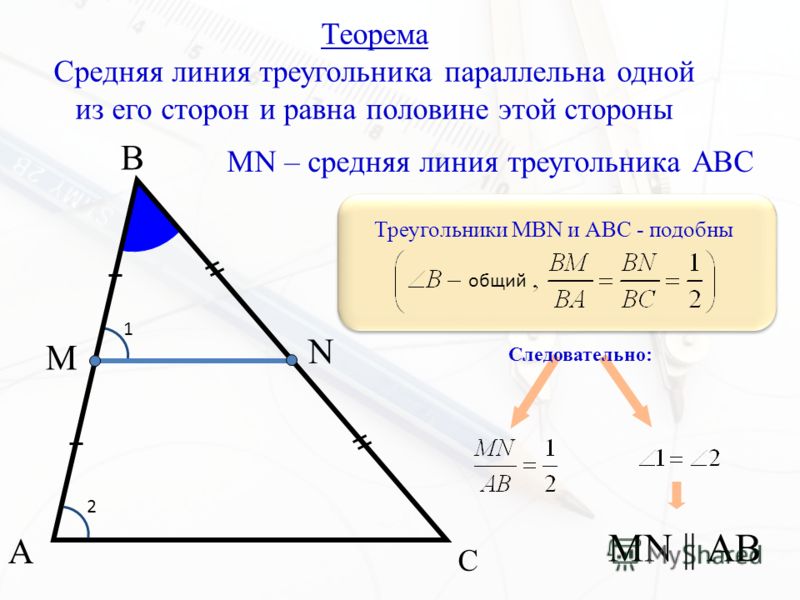 В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Запоминаем

Средняя линия параллельна третьей стороне, а ее длина равна половине длины этой стороны.

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.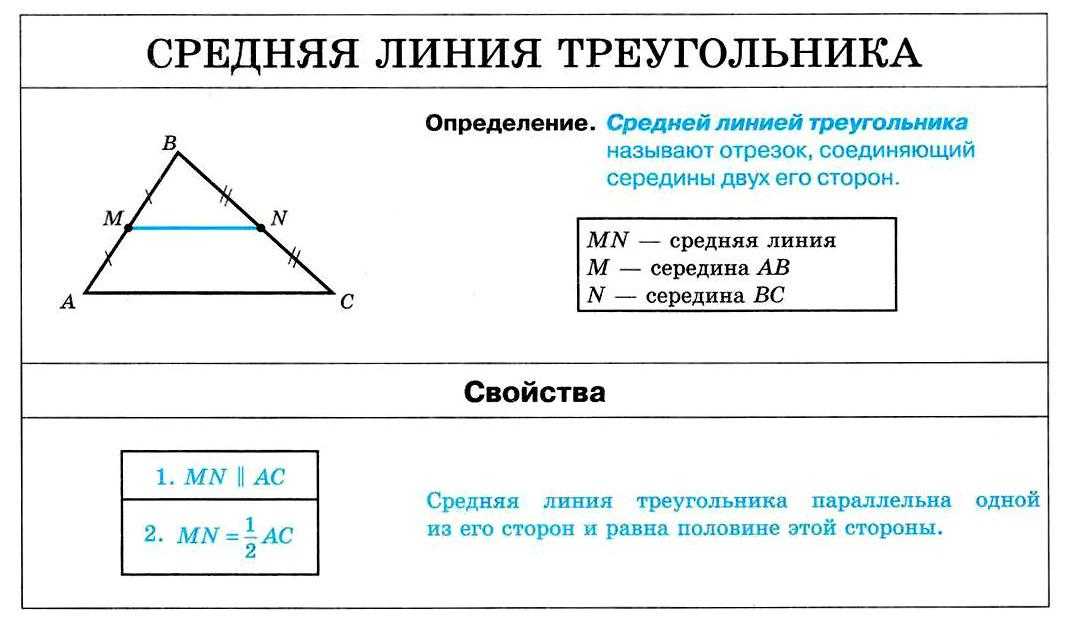

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Важное свойство

Средняя линия прямоугольного треугольника делит его на четыре прямоугольных треугольника.

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

 

1. Средняя линия равна половине длины основания и параллельна ему.


2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.


3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.


4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

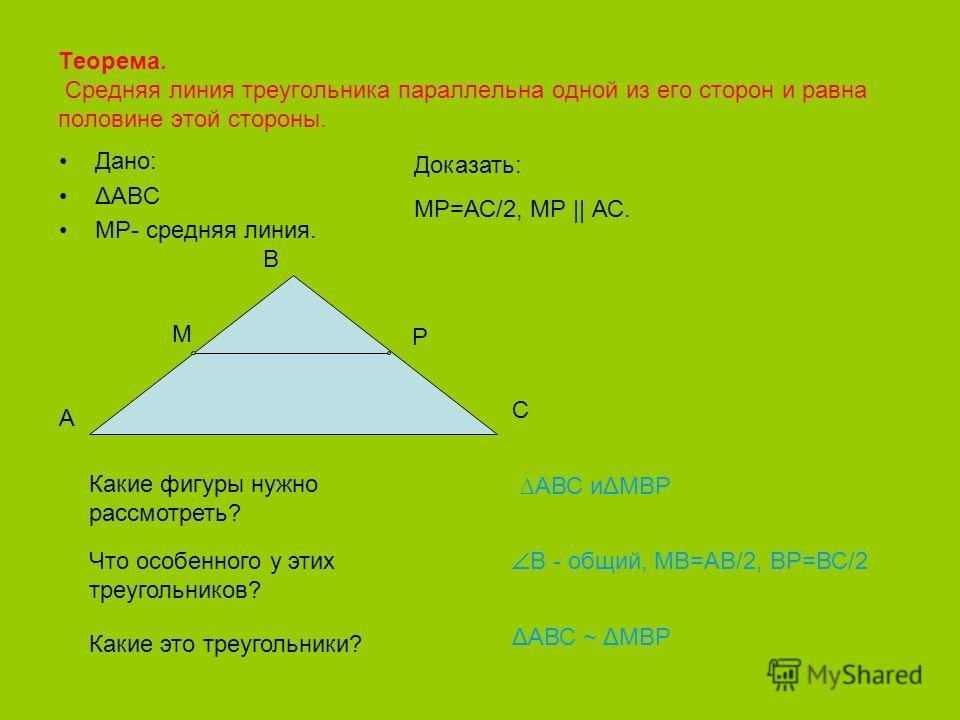
Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

 

1. По условию нам дано, что MA = MB, NA = NC

2. Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

   (по второму признаку подобия треугольников).

3. Так как △AMN ~ △ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.

4. Так как △AMN ~ △ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

   Параллельность средней линии и соответствующего ей основания доказана.

Теорема доказана.

Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Как найти периметр треугольника:

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Решение:

 

1. Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

   S = ½ × AC × BC

2. Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

   MN = ½ × AC

   Значит, AC = 2MN = 2 × 3 = 6.

3. Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

   NP = ½ × BC

   Значит, BC = 2NP = 2 × 4 = 8.

4. Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

   S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.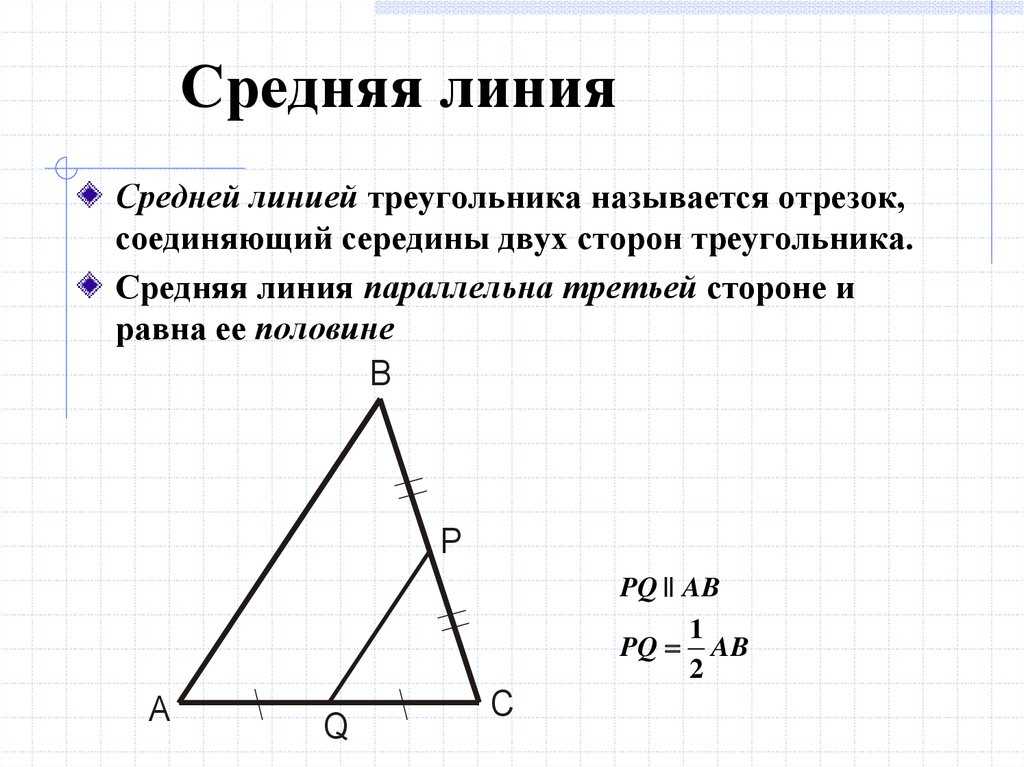

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

425.5K

Равнобедренный треугольник: свойства, признаки и формулы

К следующей статье

192.4K

Что такое рациональные числа?

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Средняя линия треугольника

Бизнес с Oriflame — рост и РАЗВИТИЕ!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2015-11-09

Средняя линия треугольника. Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была на блоге статья, в которой сии факты я предлагал просто запомнить, теперь подробнее…

Что такое средняя линия треугольника и каковы её свойства?

Определение. Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника.

Понятно, что средних линий в треугольнике три. Покажем их:

Без всяких доказательств вы уже, наверное, заметили, что все четыре образованные треугольника равны. Это так, но подробнее об этом поговорим далее.

 

Средняя линия треугольника. Теорема

 

Теорема. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.

Доказательство:

1. Давайте рассмотрим треугольники BMN и BAC. По условию у нас BM=MA, BN=NC. Можем записать:

Следовательно треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Что из этого следует? А то что:

По признаку параллельности прямых MN||AC.

2. Также из подобия треугольников следует, что

То есть MN в два раза меньше. Доказано!

 

Средняя линия треугольника. Задача

 

Решим типичную задачу.

Задача. В треугольнике ABC точки  M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.

Решение. Конечно, прежде всего следует проверить существование треугольника MNK (а значит и существование треугольника АВС). Сумма двух меньших сторон должна быть более третьей стороны, записываем 10+8>12. Выполнятся, следовательно треугольник существует.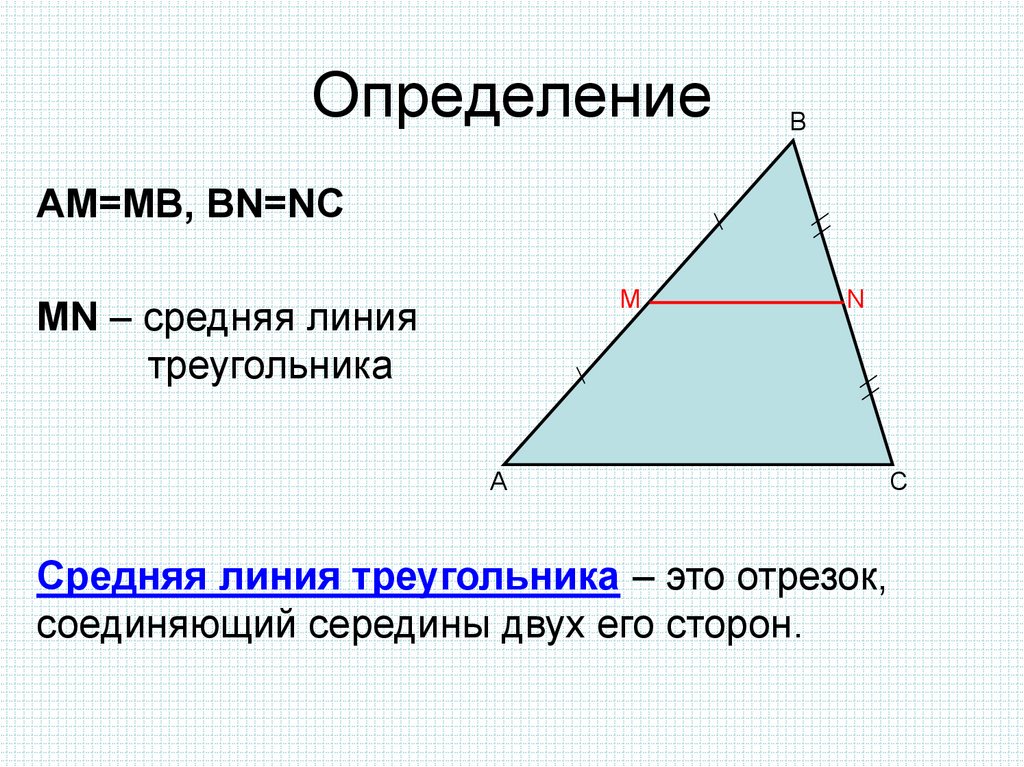

Построим эскиз:

Таким образом периметр треугольника АВС равен 24+20+16=60.

Ответ: 60

*Теперь подробнее о треугольниках полученных при построении всех трёх средних линий. Их равенство легко доказывается. Посмотрите:

Равны они по трём сторонам. Конечно, и другие признаки здесь применимы. Получаем, что

Как это свойство используется в заданиях включённых в состав экзамена? Особо хочется заострить внимание на задачах по стереометрии. Есть такие типы, в которых речь идет о треугольной призме.

Например, сказано что плоскость  проходит через середины сторон основания и она параллельна третьему ребру основания.  Ставятся вопросы о изменении площади поверхности призмы, её объёма и другие.

Так вот. Зная и понимая информацию изложенную выше вы сразу же определите, что эта плоскость отсекает от основания указанной призмы одну четвёртую часть и задачу решите устно. Вот статья на блоге с такими задачами.

На этом всё! Всего доброго!

Скачать материал статьи

С уважением, Александр Крутицких.

Делитесь информацией сайта в социальных сетях!

Категория: Формулы Теория | ТреугольникФормулы

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Средняя линия треугольника (теорема, формула и видео) Пол Маццола

Что такое средняя линия треугольника?

Средняя линия треугольника — это линия, построенная путем соединения середины любых двух сторон треугольника. В любом прямоугольном, равнобедренном или равностороннем треугольнике все три стороны треугольника можно разделить пополам (разрезать пополам), при этом точка, равноудаленная от любой вершины, будет серединой этой стороны.

В △ASH , внизу, сбоку AS и AH 24 см и 36 см соответственно.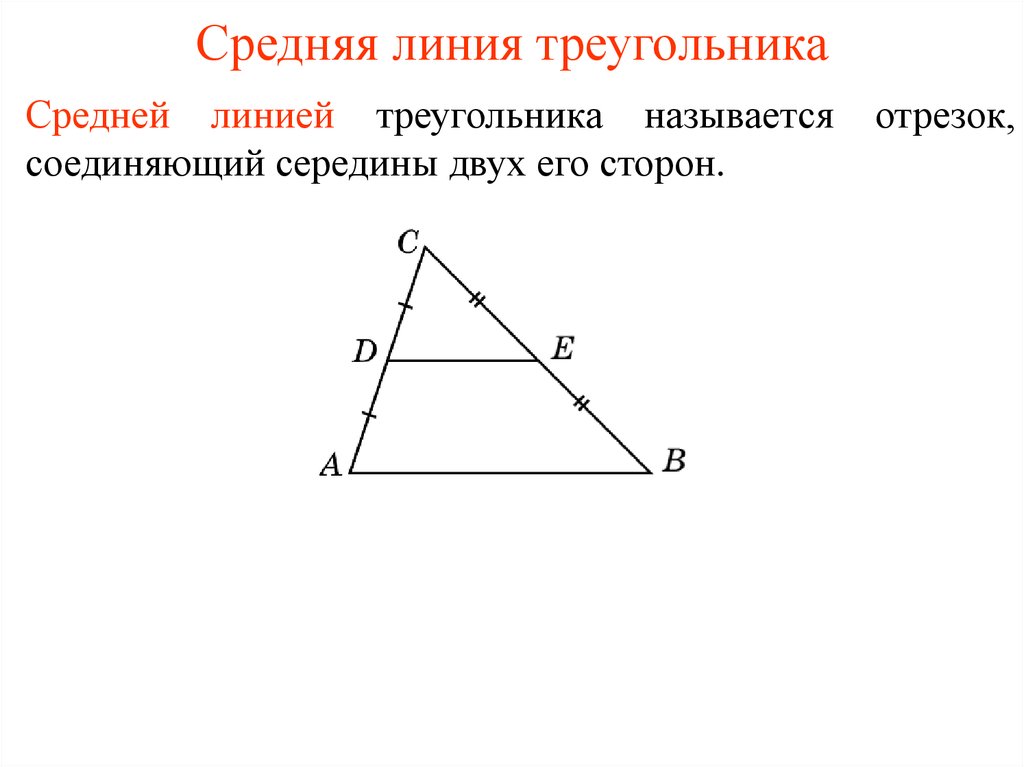 Поскольку мы знаем длины сторон, мы знаем, что точка C , середина стороны AS , точно равна 12 см с любого конца. Точка R на AH точно равна 18 см с любого конца.

Середина треугольника

Соединение середины сторон, Точки C и R , on  △ASH делает что-то кроме того, чтобы сделать всю нашу фигуру CRASH . Он создает средний сегмент, CR , который имеет пять удивительных особенностей.

Пять свойств срединного отрезка

Поскольку треугольники имеют три стороны, они могут иметь три срединных отрезка. Вы можете соединить любые две стороны в их средних точках. Один средний сегмент составляет половину длины основания (третья сторона не участвует в создании среднего сегмента). Это только одна интересная особенность. Это также:

• Всегда параллелен третьей стороне треугольника; основание

• Образует меньший треугольник, аналогичный исходному треугольнику

• Меньший аналогичный треугольник имеет четверть площади исходного треугольника

• Меньший аналогичный треугольник имеет половину площади периметр исходного треугольника

Поскольку меньший треугольник, созданный средней линией, подобен исходному треугольнику, соответствующие углы двух треугольников идентичны; соответствующие внутренние углы каждого треугольника имеют одинаковые измерения.

Из пяти атрибутов срединного отрезка два самых важных заключены в теореме о срединном отрезке, утверждении, которое было доказано математически (поэтому вам не нужно доказывать его снова; вы можете воспользоваться им, чтобы сэкономить время и работа).

Теорема о средней линии треугольника

Теорема о средней линии треугольника говорит нам, что средняя линия равна половине длины третьей стороны (основания) и также параллельна основанию.

Вам не нужно доказывать теорему о средней линии, но вы можете доказать ее, используя вспомогательную прямую, конгруэнтные треугольники и свойства параллелограмма.

Средний сегмент Formula

Средний сегмент || Основание треугольников

Формула среднего сегмента треугольника

Это мощный материал; за одну лишь стоимость рисования одного отрезка линии можно создать аналогичный треугольник с площадью в четыре раза меньше исходной, периметром в два раза меньше исходной и с гарантированно параллельным исходной и только вдвое короче.

Как найти середину треугольника

Нарисуйте любой треугольник, назовите его треугольником ABC. С помощью циркуля, карандаша и линейки найдите середины любых двух сторон треугольника. Вы делаете это в четыре шага:

1. Отрегулируйте циркуль для рисования так, чтобы он двигался по дуге, превышающей половину длины любой из сторон треугольника

2. Поместив стрелку компаса в каждую вершину, проведите дугу через сторону треугольника с обоих концов, создавая две противоположные стороны. , пересекающие дуги

3. Соедините точки пересечения обеих дуг с помощью линейки

4. Точка, в которой ваша линейка пересекает сторону треугольника, является серединой этой стороны)

Как найти середину треугольника

Соедините середины любых двух сторон, и вы получите середину треугольника. Независимо от того, какой средний отрезок вы создали, он будет составлять половину длины основания треугольника (сторона, которую вы не использовали), а средний отрезок и основание будут параллельными линиями!

Примеры теоремы о средней линии треугольника

Вот правильно △DOG , со стороной DO 46 дюймов и стороной DG 38,6 дюйма . Сторона 9{2}482,5 дюйма2.

Какие точки вы соедините, чтобы создать средний сегмент?

Пример теоремы о средней линии треугольника

Только соединив точек V и Y , можно создать среднюю линию треугольника. Это сделает сторону OG основой.

Вы должны быть в состоянии ответить на все эти вопросы:

1. Каков периметр оригинального △СОБАКА ?

2. Какова длина среднего сегмента ВЯ ?

3. Какова длина стороны DV ?

4. Какова длина стороны DY ?

5. Каков периметр вновь созданного аналога △DVY ?

6. Какова площадь недавно созданного △DVY ?

Вот наши ответы:

1. Добавьте длины: 46″ + 38,6″ + 25″ = 109,6″

9{2}120,625in2

Треугольник Серпинского

С помощью теоремы о среднем отрезке можно построить фигуру, используемую во фрактальной геометрии, треугольник Серпинского. Шаги просты, а результаты визуально приятны:

1. Нарисуйте три середины любого треугольника, хотя равносторонние треугольники работают очень хорошо треугольников осталось

2. Для каждого углового треугольника соедините три новых средних сегмента

3. Снова проигнорируйте (или закрасьте) каждый из их центральных треугольников и сосредоточьтесь на угловых треугольниках

4. Для каждого из этих угловых треугольников соедините три новые средние сегменты

Эта непрерывная регрессия создаст визуально мощную фрактальную фигуру:

Треугольник Серпинского

Калькулятор основания треугольника

Создано Komal Rafay

Отзыв от Anna Szczepanek, PhD

Последнее обновление: 30 октября 2022 г.

Содержание:

• Калькулятор основания треугольника
• Формула основания треугольника
• Как вычислить основание треугольника?
• Удивительный треугольник в Omni
• Часто задаваемые вопросы

Основа калькулятора треугольников — инструмент вашей мечты, если вы увлекаетесь математикой и геометрией.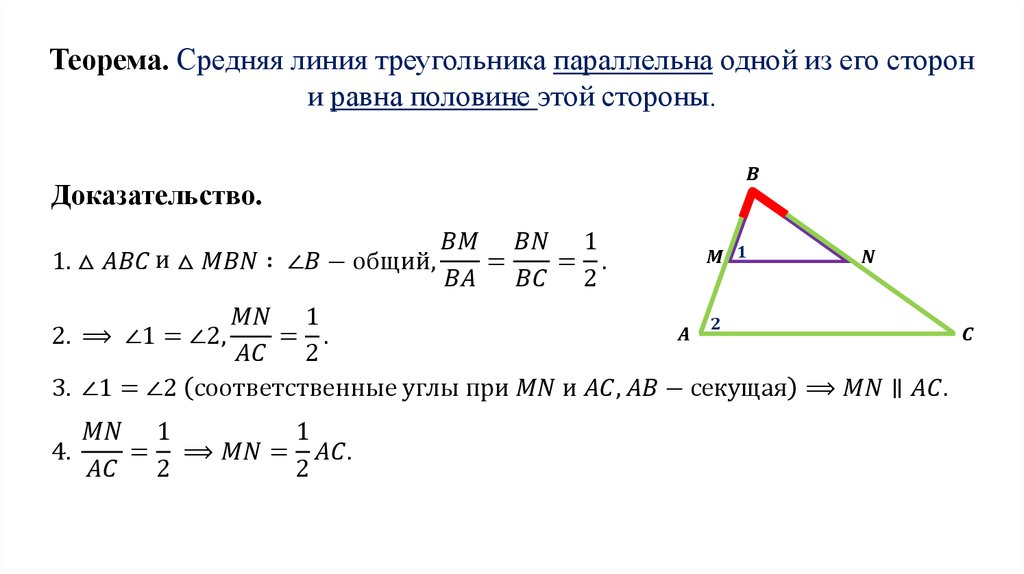 Даже если это не так, вы все равно найдете этот инструмент полезным.

Наиболее важные темы, которые мы рассмотрим:

• Формула основания треугольника; и
• Как вычислить основание треугольника.

Калькулятор основания треугольника

Калькулятор основания треугольника — это инструмент, который удобно и эффективно определит основание любого треугольника, используя его площадь. Но не волнуйтесь, это не все, для чего вы можете использовать этот инструмент. Если у вас уже есть основание и высота треугольника, вы все равно можете определить, если необходимо, площадь треугольника. Именно это мы имеем в виду, когда говорим «удобно».

Чтобы использовать наш инструмент:

• Введите площадь треугольника, вы можете выбрать единицу измерения по вашему выбору;
• Введите высоту треугольника; и
• Результат — основание треугольника.

💡 Вы можете вычислить любую из трех переменных треугольника, если у вас есть значение для любых двух.

Формула основания треугольника

Формула для определения основания треугольника получена из 9Формула 0307 для площади треугольника. Формула площади использует основание и высоту треугольника и выглядит следующим образом:

A=b⋅h3A = \frac {b \cdot h} {2} A=2b⋅h​

Теперь, если вы перетасуете формулу основания, она станет:

b=2⋅Ahb = \frac {2 \cdot A } {h}b=h3⋅A​

где :

• AAA — Площадь треугольника;
• hhh — Высота треугольника; и
• bbb — Основание треугольника.

Как вычислить основание треугольника?

Теперь, когда мы понимаем формулу основания треугольника , мы можем быстро определить ее, выполнив несколько простых шагов.

1. Запишите площадь треугольника и умножьте ее на 2;
2. Обратите внимание на высоту треугольника;
3. Разделить результат шага 1 на высоту;
4. Результат — основание треугольника.

Предположим, вы хотите сделать треугольную полку. Вы хотите, чтобы он покрывал площадь 60 см² на стене и должен быть Высота 15 см . Определим основу для вашей полки.

Площадь 60 см². Умножение на 2 дает нам 120.

60×2=12060×2 = 12060×2=120

Затем мы делим 120 на высоту треугольника.

b=12015\text b = \frac {120}{15} b=15120​

В результате получится основание вашей треугольной полки.

b=8 cm\text b =8 \text{ cm}b=8 cm

Треугольное великолепие в Omni

Треугольники — одна из самых распространенных форм, встречающихся в нашей повседневной жизни. Итак, чтобы отдать должное форме, у Omni есть длинный список инструментов, связанных с различными калькуляторами.

• Калькулятор площади треугольника;
• Калькулятор треугольников AAA;
• Средняя часть калькулятора треугольников;
• Калькулятор острого треугольника;
• Калькулятор центра окружности треугольника;
• Калькулятор сравнения треугольников;
• Калькулятор тупоугольных треугольников;
• Калькулятор косоугольного треугольника;
• Калькулятор треугольника AAS;
калькулятор треугольников SAS
• ;
• Калькулятор треугольников SSS; и
• Калькулятор треугольника ASA.

Часто задаваемые вопросы

Что такое основание треугольника?

Сторона , ​​перпендикулярная высоте треугольника, является его основанием .

Вы можете взять любую из трех сторон в качестве основания, если не забудете взять высоту в качестве перпендикуляра к этой стороне.

Как вычислить основание треугольника?

Формула для расчета основания треугольника:

b = 2A/h

где:

• б — Основание треугольника;
• A — Площадь треугольника; и
• h — Высота треугольника.

Итак, все, что вам нужно сделать, это:

1. Умножить площадь на 2;
2. Разделите ответ из шага 1 на высоту треугольника; и
3. Результат — основание вашего треугольника.

Чему равно основание треугольника, если его площадь равна 10 см²?

Основание треугольника площадью 10 см² равно 5 см, если его высота равна 4 см.