Конспект урока математики «Формулы периметра и площади прямоугольника» (3 класс) | План-конспект урока по математике (3 класс):
Дата: 14.02.2020 | ФИО учителя: Копотева Людмила Ильинична |
Школа: 104 | ФИ студента: Устинова Ульяна, 31 группа |
Класс: 3 «Б» | ФИО методиста: Серебренникова С.В. |
Кабинет: 206 | Подпись:______________ |
Конспект по математике
Тема: «Формулы периметра и площади прямоугольника»
Цели деятельности учителя: формирование у детей понятия формулы, умений записывать с помощью формул правила нахождения периметра, площади; умение выражать зависимость между величинами; совершенствование навыков решения составных уравнений и решения задач на нахождение площади прямоугольника и периметра.
Планируемые результаты:
Предметные:
Знать: единицы измерения площади, периметра, формулу нахождения периметра и площади прямоугольника; как устанавливать взаимосвязь между величинами площади и периметра прямоугольника.
Уметь: решать задачи на нахождение периметра и площади прямоугольника.
Личностные: принимать и осваивать социальную роль обучающегося; проявлять мотивы к учебной деятельности, навыки сотрудничества с взрослыми и сверстниками в разных социальных ситуациях; осознавать личностный смысл учения.
Тип урока: открытие нового знания
Оборудование: Л.Г. Петерсон, учебник «Математика», 3 класс, 2Ч. – Москва: «Ювента», 2012 – 96с., презентация.
Этап: | Время: | Деятельность учителя: | Деятельность учащихся: | УУД: |
Словесный метод: слово учителя | 1 мин | — Здравствуйте ребята! Меня зовут Ульяна Владимировна, и сегодня я проведу у вас урок математики. | Приветствуют учителя. | К: планирование учебного сотрудничества с учителем и сверстниками. |
Словесный метод: беседа | 4-5 мин | — Ребята, посмотрите на экран, как вы понимаете пословицу: «Краткость — сестра таланта»? — Математика — это точная наука. При решении различных примеров, уравнений, задач вы пользуетесь правилами, алгоритмами, памятками, которые используете в виде краткой записи. — Сегодня на уроке вы продолжите учиться использовать краткую запись в математике. — Что ожидает вас в пути во время открытий? — Какие шаги учебной деятельности вы выполняете, преодолевая трудности? — Итак, ребята, посмотрите на слайд. 12 • 3 + 8 • 3 30 + х = 60 х • 9 = 72 а = S : b а • b = S 4 • 16 — На какие группы можно разбить данные записи? — Назовите выражения. — Что общего в этих записях? — На какие группы их можно разбить? — Что такое уравнение? — Назовите уравнения. — Решите уравнения. (х = 8; х = 30.) | — Это рассказ самой важной и основной информации. — Мы столкнёмся с трудностями в учебной деятельности. — Сначала мы повторяем необходимое, потом будет задание на пробное действие. Мы постараемся его выполнить и, наверное, не получится. Мы подумаем, почему не получилось, поставим цель, составим план действий и, работая по плану, откроем новый способ. -Выражения, равенства. — 12 • 3+8 • 3; 4 • 16 -Это равенства, содержащие переменные. — Уравнения и не уравнения (формулы). — Равенство, содержащее переменную, значение которой нужно найти. — х • 9 = 72; 30 + х =60 Решают уравнения. | К: выражение своих мыслей с достаточной полнотой и точностью. |
Словесный метод: беседа Аналитико-синтетический: подводящий диалог Практический: решение задачи | 5 мин | — Что можно найти, используя данную запись: а • b = S? — Что можно найти, используя данную запись: а = S : b? — Данные равенства верны при любых значениях входящих в них букв. Их принято называть формулами. — Слово «формула» похоже на слово «форма», и это не случайно. Подобно тому, как формочка для песка помогает лепить из него пирожки, так и формулы помогают решать задачи, т.к. помогают вычислять значения одной из величин по известным значениям остальных величин.(Слайд) — Что же такое формула? Как вы понимаете? — Чем формулы отличаются от уравнений? — Для чего нужны формулы? -Посмотрите на слайд, перед вами задача. Вам нужно будет решить ее в тетради. Открываем тетрадь, отступаем 4 клетки от последней работы и на 5 строчке пишем сегодняшнее число. -Посмотрите на слайд, прочитайте задачу. Задача: Найдите площадь прямоугольника, если его периметр равен 16 см, а длина равна 6 см. -Попробуйте, решите данную задачу в тетрадь. — Итак, ребята, можете мне сказать, какое задание вы выполняли? -Кто-нибудь смог выполнить данную задачу? -Где возникло затруднение?
— Почему же возникло затруднение? — Кто-нибудь уже догадался, какова тема нашего сегодняшнего урока? | — Площадь прямоугольника. — Сторону прямоугольника.
Воспринимают информацию. — Выражение, с помощью которого можно решить пример. — В уравнениях буквы обозначают некоторые числа, а в формулах — значения величин; формулы верны для всех значений букв, а уравнения — только для корней. -Помогают при решении задач. Читают задачу. Выполняют задание. — Решали задачу на нахождение площади прямоугольника. — Нет. — При применении формулы площади, если не известна вторая сторона. — Потому что у нас нет нужной формулы для нахождения стороны прямоугольника по известному периметру. — Формулы периметра и площади прямоугольника. | П: прослушивание и восприятие художественного текста К: умение с достаточной полнотой выражать свои мысли |
Объяснительно-иллюстративный: беседа по формулам, презантация. Словесный: беседа Аналитико-синтетический: подводящий диалог Словесный: беседа Практический: Работа с задачей | 7-10 мин | — Верно, тема нашего сегодняшнего урока «Формулы периметра и площади треугольника». Кто может мне назвать цель нашего урока? — А чтобы построить формулу для нахождения стороны по периметру, какую формулу нужно хорошо знать? — Какова задача нашего урока? -Рисунок, какой геометрической фигуры поможет нам разобраться в данной теме? -Посмотрите внимательно на первую формулу. — Как вы прочитаете первую формулу? — Когда мы используем эту формулу? — А что помогут вычислить эти формулы? A = S:b b = S:a — Прочитайте их. — Что можно сказать о новых равенствах? — Теперь посмотрим, как связаны между собой периметр и стороны прямоугольника. Напомните, что такое периметр? — Какую формулу можно записать для периметра прямоугольника? — Любой из этих формул можно пользоваться для нахождения периметра. А какую из них удобнее использовать для решения задач? — Прочитайте последнюю формулу. — Опираясь на эту формулу, вы попробуете вывести формулу стороны прямоугольника по его периметру и второй стороне. С чего начнете? — Что вам напоминает эта запись? — Решите его.
— Теперь так же выведите формулу для нахождения ширины прямоугольника: b =Р : 2 -а — Прочитайте полученные формулы. — Что поможет вам проверить наши выводы? — Отройте учебник на странице 86. — Совпал ли ваш вывод с выводом учебника? -Давайте закрепим наши знания. Как найти площадь прямоугольника? — Какие единицы измерения площади вы знаете? — Как найти сторону прямоугольника? — Что означает формула периметра? — Какие единицы измерения периметра вы знаете? -Вернемся к задаче, которую мы не смогли решить в начале урока. -Сейчас вы сможете ее решить? — Что вам поможет? — Пользуясь, формулами площади и периметра найдите площадь прямоугольника, если его периметр равен 16см, а длина равна 6см. — Проверьте по подробному образцу: 1) 16 : 2 – 6 = 2 (см)- ширина. 2) 6 • 2 = 12(см2) Ответ: S = 12 см2 — Что вам позволяет новый способ? | — Построить формулу нахождения стороны по периметру. — Формулу нахождения периметра прямоугольника. — Построить формулу периметра и научиться, используя формулы, находить стороны прямоугольника. -Прямоугольник. — Площадь прямоугольника равна произведению длин его сторон. — Когда нужно найти площадь. — Длину стороны прямоугольника. — Длина стороны прямоугольника равна его площади, деленной на длину другой стороны. — В них длина и ширина выражены через площадь и длину другой стороны. — Сумма длин сторон фигуры. — Р = а + b + а + b или Р = а • 2 + b • 2 или Р = (а + b) • 2. — Последнюю, в ней всего 2 действия. — Периметр прямоугольника равен сумме его длины и ширины, умноженной на 2. -Выделим в формуле периметра прямоугольника одну из сторон, формулу, которой будем выводить, например, а. — Составное уравнение. (a + b) • 2 = P a + b = P : 2 a = P : 2 – b -Длина стороны прямоугольника равна разности половины периметра и длины другой его стороны. — Учебник Выполняют задание. — Да, мы сделали правильный вывод. — Чтобы найти площадь прямоугольника, надо длину умножить на ширину. — мм2, см2, дм2, м2 — Чтобы найти сторону прямоугольника, надо площадь разделить на другую сторону. — Периметр прямоугольника равен сумме его длины и ширины, умноженной на 2. — мм, см, дм, м -Да . — Формулы площади и периметра. Выполняют задание. Самопроверка. — Находить площадь, периметр, сторону по площади и периметру. | К: умение с достаточной полнотой выражать свои мысли П: определение основной и второстепенной информации. К: умение с достаточной полнотой выражать свои мысли К: умение с достаточной полнотой выражать свои мысли К: умение с достаточной полнотой выражать свои мысли П: осознание и произвольное построение речевого высказывания в письменной форме. |
Физминутка. | 1-2 мин | — Вы устали? Давайте встанем и разомнемся. Смотрите на экран и повторяйте движения. | Смотрят видеоролик и повторяют движения. | Л: комфортное ощущение в группе. |
Аналитико-синтетический: подводящий диалог Практический: Работа у доски, в парах | 5-7 мин | -Давайте перейдем к заданию 1, на стр. 86. Прочитайте задание. -Давайте решим вместе, одного ученика вызывает к доске, чтобы он решил один пример и так 3 примера. — Как найти площадь прямоугольника? 6 • 9 = 54 (м2) — площадь. -Как найти периметр прямоугольника? (6 + 9) • 2 = 30 (м) — периметр. б)58 дм и 70 дм. — Как найти площадь прямоугольника? 58 • 70 = 4060 (дм2) — площадь. -Как найти периметр прямоугольника? 58 • 2 + 70 • 2 = 116 + 140 = 256 (дм) — периметр. в)30 см и 80 см. — Как найти площадь прямоугольника? 30 • 80 = 2400 (см2) – площадь. -Как найти периметр прямоугольника? (30 + 80) • 2 = 220 (см) — периметр. -Следующее задание на стр. 87, номер 2. Вам предстоит выполнить в парах. Работа в парах. а)S = 4800 см2 b = S : а а = 60 см b = ? см b = 4800 : 60 = 80 (см) б)S = 1600 см2 а = 40 см b = ? см b = 1600: 40 = 40 (см)- данный прямоугольник — квадрат -Давайте сверимся с эталоном. (Слайд) | — Найди площадь и периметр прямоугольника со сторонами: а) 6 м и 9 м — Нужно умножить две стороны прямоугольника. -Чтобы найти периметр нужно сумму сторон умножить на 2. . — Нужно умножить две стороны прямоугольника. -Чтобы найти периметр нужно сумму сторон умножить на 2. — Нужно умножить две стороны прямоугольника. -Чтобы найти периметр нужно сумму сторон умножить на 2. Выполняют работу в парах. -Самопроверка. | П: определение основной и второстепенной информации. П: осознание и произвольное построение речевого высказывания в письменной форме. П: осознание и произвольное построение речевого высказывания в письменной форме. |
Практический: решение карточки. | 5-7 мин | — Сейчас каждый из вас получит карточку с заданием, вам нужно будет выполнить его самостоятельно (задание на стр. 87 номер 3) А) Напиши формулы периметра и площади квадрата со стороной а. Б) Найди периметр и площадь квадрата со стороной 30 см. В) Найди площадь квадрата, периметр которого равен 36 дм. -Все решили? Обменяйтесь листочками с соседом и проверьте с эталоном. Эталон для самопроверки. а) S = а • а Р = а + а + а + а или Р = а • 4 б) S = 30 • 30 = 900 (см2) Р = 30 • 4 = 120 (см) а = Р : 4 а = 36 : 4 = 9 (дм) S = 9 • 9 = 81 (дм2). — Оцените свою работу знаками «+» или «?» — У кого есть ошибки? Где вы допустили ошибку? — Над чем вам надо поработать, чтобы не допускать ошибок? — Не расстраивайтесь, у вас всё получится. -У кого ошибок нет? Хорошо. | Выполняют задание в карточке. Оценивают. Высказывают свое мнение. | Л: контроль и оценка процесса и результатов деятельности. |
Словесный: подводящий диалог. | 2 мин | — Какую цель вы перед собой ставили? — Достигли цели? Докажите. — Вспомним формулы. — Научились ли вы использовать новый способ? (Да.) | -Построить формулу нахождения стороны по периметру. — Мы узнали, что такое формула, вывели формулы площади и периметра, научились находить сторону по площади и периметру. -Да.
| К: выражение своих мыслей с достаточной полнотой и точностью. |
Частично-поисковый: самоанализ | 2-3 мин | — Вот и подошел к концу наш урок. -Давайте вспомним тему нашего урока. -Спасибо за урок, вы все хорошо работали. До свидание. | -Формулы периметра и площади прямоугольника. | Л: контроль и оценка процесса и результатов деятельности. |
Математика Площадь прямоугольника
Назовите фигуры, которые пришли вместе с Царицей Точкой?
Круг, квадрат, треугольник, прямоугольник.
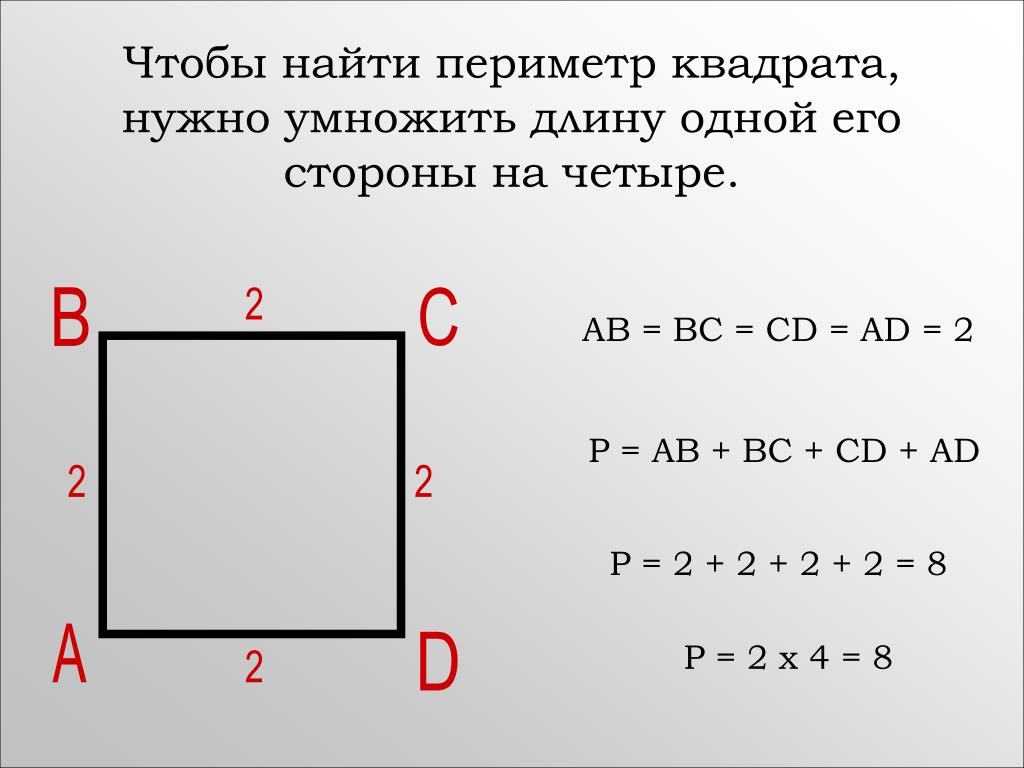
Вспомните, как найти периметр прямоугольника.
Чтобы найти периметр четырёхугольника, нужно сложить длины всех сторон или сложить длину и ширину и умножить на 2.
Найдите периметр прямоугольника, если его длина равна 6 см, а ширина 4 см
(6+4)·2
Периметр прямоугольника равен двадцати сантиметрам.
Кроме периметра у геометрической фигуры можно найти площадь.
В каких единицах измеряется площадь фигур?
Площадь фигуры измеряется в квадратных сантиметрах.
Что такое квадратный сантиметр?
Квадрат со стороной 1 см принято называть квадратным сантиметром.
Что значит найти площадь прямоугольника?
Чтобы найти площадь прямоугольника, нужно фигуру разделить на квадратные сантиметры.
Площадь прямоугольника равна двадцати четырём квадратным сантиметрам.
Этап усвоения новых знаний
Перед вами прямоугольник.
Длина прямоугольника 5 см. Значит,
по длине в одном ряду укладывается 5 квадратов со стороной 1 см.
Площадь такого ряда 5 сантиметров квадратных.
Сколько таких рядов?
Таких рядов 2. Значит, ширина равна двум сантиметрам. По ширине укладывается 2 квадрата со стороной 1 см. Площадь такого ряда 2 сантиметра квадратных.
Чтобы узнать площадь данного прямоугольника, нужно
Таким образом площадь прямоугольника будет равна 10 см²
Что такое 5 см?
Что такое 2 см?
5 см – это длина прямоугольника,
2 см – это ширина прямоугольника
Чтобы вычислить площадь прямоугольника нужно его длину умножить на ширину. Длина и ширина прямоугольника должны быть выражены в одинаковых единицах, площадь также будет выражена в соответствующих единицах.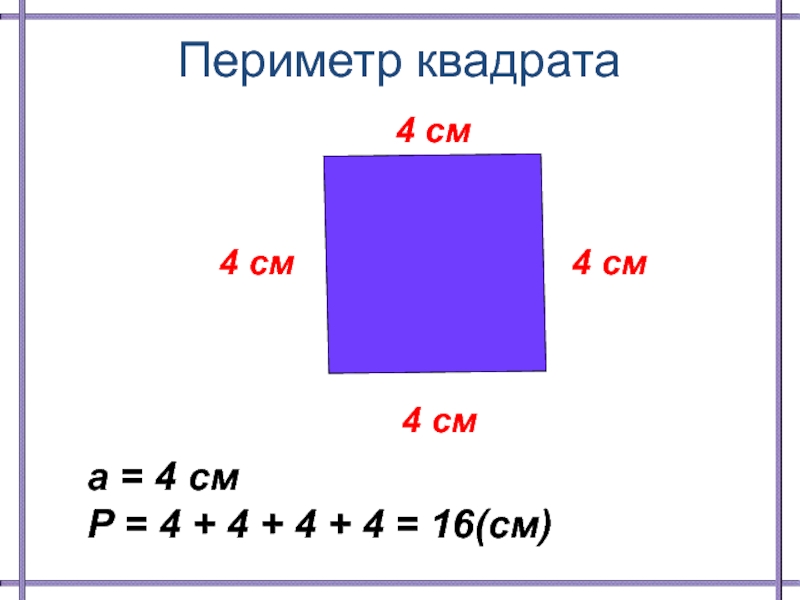
Площадь будем записывать латинской буквой S . Длину латинской a. Ширину — b.
Таким образом, площадь прямоугольника равна произведению длины на ширину.
Вычислим площадь нашего прямоугольника.
Чтобы вычислить площадь прямоугольника, нужно длину 5 см умножить на ширину 2 см, получится 10 см квадратных – площадь прямоугольника.
Площадь прямоугольника 10 см²
Закрепление материала
Задание
Начертите два квадрата: один со стороной 2 см, другой со стороной 3 см
Что мы знаем про квадрат?
У квадрата все стороны равны.
Найдите площадь квадратов.
Квадрат – это прямоугольник, у которого все стороны равны.
Чтобы вычислить площадь квадрата, нужно его длину умножить на ширину.
Сторона первого квадрата равна 2 см.
Длину 2 см умножим на ширину 2 см, получим 4 см квадратных – площадь первого квадрата.
Сторона второго квадрата равна 3 см.
Длину 3 см умножим на ширину 3 см, получим 9 см квадратных – площадь второго квадрата.
Самостоятельная работа
Задание
Начертите прямоугольник со сторонами 7 см и 3 см. Вычислите его периметр и площадь.
Проверьте себя и оцените свои успехи.
Периметр прямоугольника – это сумма длин его сторон: 7+3+7+3=20 см.
или каждую сторону умножить на 2 и произведения сложить: 7·2+3·2=20 см.
Площадь прямоугольника – произведение длины на ширину.
S=7·3=21 см²
Итог урока
Как вычислить площадь прямоугольника?
Какие латинские буквы используются при вычислении площади прямоугольника?
Рефлексия
Продолжите фразу:
сегодня я узнал
было интересно
было трудно
Связь площади и периметра — Математика 3 класса
Отличная работа! 🎊
Теперь давайте потренируемся решать задачи на площадь и периметр.
Пример 1: Тот же периметр, другая площадь
Фигуры ниже имеют одинаковый периметр , но разные площадь .
Какова площадь прямоугольника B?
👉 Начните , используя уже известную информацию.
У нас есть высота и ширина прямоугольника А. Мы можем использовать их, чтобы найти его периметр.
Мы делаем это с помощью , добавляя длину всех его сторон.
4 + 4 + 3 + 3 = 14 метров
Это означает, что периметр Прямоугольник B 9001 0 тоже 14 метров.
Мы еще не можем вычислить площадь B, потому что длина одной стороны все еще отсутствует. 😐
Как найти недостающую сторону? 🤔
👉 Работаем той стороной, которую знаем.
Мы знаем, что ширина 2 метра.
Поскольку напротив сторон равны равным , мы удваиваем чтобы получить сумму двух сторон.
2 + 2 = 4
Теперь мы вычитаем полученную сумму из общего периметра.
14 — 4 = 10
Это означает, что сумма из два 9 0010 неизвестно стороны 10 м. 👍
Мы делим на 2, чтобы получить длину каждой неизвестной стороны.
10 ÷ 2 = 5
👍 Теперь мы знаем, что высота прямоугольника B равна 5 метров!
Поскольку мы знаем высоту и ширину прямоугольника B, мы наконец можем найти его площадь .
Это просто, мы просто умножаем :
2 x 5 = 10 м²
009 10 м² ).
Пример 2: та же площадь, другой периметр
Прямоугольники ниже имеют одинаковую площадь , но разные периметр .
👆Что такое периметр Прямоугольник A ?
👉 Чтобы найти периметр прямоугольника, нам нужно знать его высоту и ширину.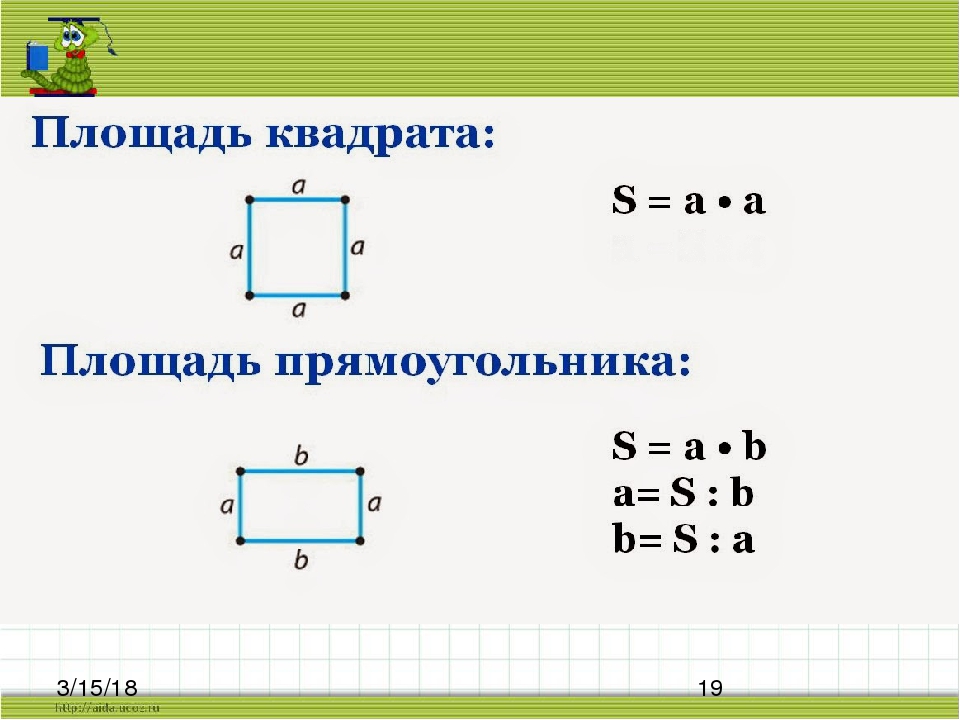
Мы знаем только ширину прямоугольника A — его высота отсутствует !
Как узнать его высоту? 🤔
Используя информацию, полученную из прямоугольника B.
Мы знаем, что площади двух прямоугольников равны. Если мы вычислим площадь прямоугольника B, то мы уже знаем площадь прямоугольника A.
Формула для площади : высота x ширина.
Используем это сейчас:
5 x 6 = 30 дюймов²
Площадь прямоугольника B равна 30 дюймов².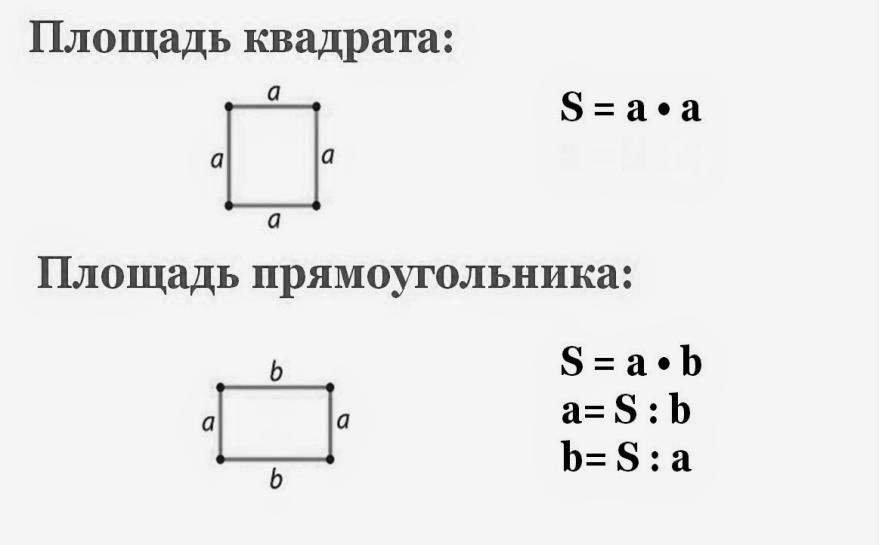
👍 Это означает, что площадь прямоугольника А также равна 30 дюймов².
👉 Наш следующий шаг — найти недостающую сторону прямоугольника А. Мы делаем это, используя информацию, которая у нас уже есть.
Мы знаем, что ширина прямоугольника А равна 3 дюймам, а его площадь равна 30 дюймов².
Наша формула:
H x W = Площадь
Итак, давайте заполним нашу формулу числами:
H x 3 = 30 900 10
Вы помните, как решить уравнение с переменной? Это просто так. 😃
😃
Наша переменная H (для высоты). Нам нужно добраться в одиночку с левой стороны.
Для этого нам нужно отменить умножение слева на , используя подразделение .
Делим обе стороны на 3!
Помните, что то, что вы делаете на одной стороне, должно быть сделано и на другой стороне. Это сохранит уравнение сбалансированным .
H x 3 ÷ 3 = 30 ÷ 3
H = 1 0 дюймов
Отсутствует сторона 10 дюймов .
Мы знаем, что это правильно, потому что когда мы умножьте на две стороны, чтобы получить его площадь, мы получим 30 дюймов². 👍 Это соответствует площади прямоугольника B!
👉 Теперь мы находим его периметр.
Это просто. Мы просто добавляем все стороны .
Помните, что противоположные стороны прямоугольника всегда равны.
Это означает, что мы удваиваем высоту, а также ширину.
3 + 3 + 10 + 10 = 26 дюймов
✅ периметр прямоугольника А равен 26 дюймов .
Отличная работа! А теперь попробуйте практические упражнения. 💪
Как найти площадь квадрата? Формула, определение
Площадь квадрата можно определить по тому, сколько пространства занимает внутри него квадрат. Проще говоря, пространство, находящееся в пределах границы квадрата, известно как площадь квадрата. В этой статье вы узнаете основные параметры квадрата. Кроме того, вы узнаете, как найти площадь квадрата, площадь формулы квадрата и площадь поверхности квадратной пирамиды.
Все ли мы знаем, что такое квадрат? Квадрат – это замкнутый четырехугольник. Четырехугольники – это фигуры, имеющие 4 стороны. Таким образом, квадрат — это четырехсторонняя фигура, у которой все четыре стороны равны. Если одна сторона квадрата равна 10 см, то и другие стороны равны 10 см. Давайте сначала изучим некоторые математические термины и понятия, связанные с квадратом:
- У квадрата все стороны равны.
 Отсюда следует, что противолежащая и прилежащая стороны квадрата равны друг другу.
Отсюда следует, что противолежащая и прилежащая стороны квадрата равны друг другу. - Противоположные стороны квадрата параллельны, что делает его параллелограммом.
- Смежные стороны квадрата перпендикулярны друг другу. Это означает, что любые две смежные стороны имеют между собой угол 90 градусов.
- Квадрат разделен на два равных прямоугольных треугольника.
- Квадрат — это частный случай прямоугольника.
- Периметр квадрата: Расстояние, пройденное границами квадрата, называется периметром квадрата. Он сформулирован следующим образом:
Периметр (квадрат) = s + s + s + s = 4 x s = 4s {где s — сторона квадрата}
В нашей повседневной жизни мы можем встретить квадраты повсюду. От наших домов до наших школ квадраты присутствуют на каждом углу. Плитка на вашей кухне квадратная. Шахматная доска представляет собой квадрат, состоящий из 64 черных и белых меньших квадратов. Самый распространенный пример — кубик Рубика. Каждая поверхность кубика Рубика квадратная.
Другие измерения, такие как диагональ и периметр квадрата, также могут использоваться для вычисления площади квадрата. В этой статье мы попытаемся узнать больше о площади квадрата.
Площадь квадрата
Площадь квадрата определяется как количество квадратных единиц, необходимых для заполнения этой фигуры. Другими словами, при вычислении площади квадрата мы учитываем длину его стороны. Поскольку все стороны фигуры равны, ее площадь равна произведению двух сторон. Наиболее распространенными единицами измерения площади квадрата являются квадратные метры, квадратные футы, квадратные дюймы и квадратные сантиметры.
Площадь квадрата также можно рассчитать, используя другие измерения, такие как диагональ и периметр квадрата. На этой странице мы попытаемся узнать больше о площади квадрата.
Какова площадь квадрата?
Квадрат — это двумерная замкнутая фигура, имеющая четыре равные стороны и четыре равных угла. Четыре угла при вершинах образованы четырьмя сторонами квадрата. Периметр квадрата — это сумма длин его сторон, а площадь квадрата — это площадь, занимаемая фигурой. Он обладает следующими свойствами четырехугольника.
Периметр квадрата — это сумма длин его сторон, а площадь квадрата — это площадь, занимаемая фигурой. Он обладает следующими свойствами четырехугольника.
Две стороны параллельны.
- Все четыре стороны одинаковые.
- Все углы 90 или .
Квадраты можно найти повсюду. Вот несколько примеров часто встречающихся объектов квадратной формы. Квадрат представлен шахматной доской, часами, доской и плиткой.
Иллюстрация: Рассмотрим квадрат длины 4 единицы. Теперь рассмотрим меньшие квадраты длиной 1 единица каждый. Как мы видим на рисунке ниже, 4 квадрата по 1 единице заполняют первый ряд большего квадрата. Аналогично по 4 квадрата 1 единицы заполняют второй, третий и четвертый ряд. Теперь большой квадрат заполнен. Если мы посчитаем количество меньших квадратов, то получим, что 16 квадратов из 1 единицы заполняют квадрат из 4 единиц. Следовательно, 16 единиц — это площадь квадрата.
Отсюда мы можем сделать вывод, что площадь квадрата равна произведению двух его сторон.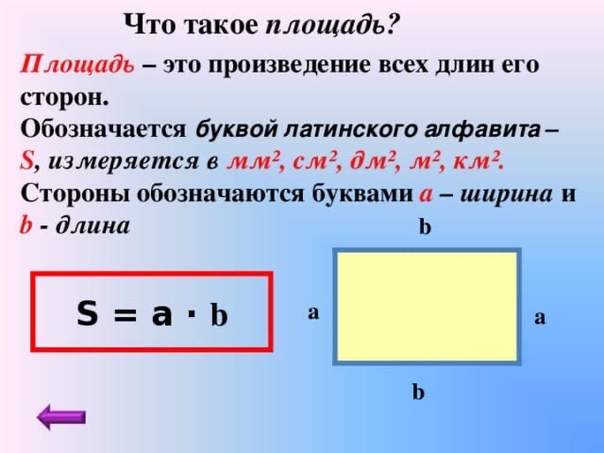 Как мы знаем, 16 = 4 х 4, а 4 единицы составляют одну сторону квадрата. В следующем разделе мы изучим и выведем формулу площади квадрата.
Как мы знаем, 16 = 4 х 4, а 4 единицы составляют одну сторону квадрата. В следующем разделе мы изучим и выведем формулу площади квадрата.
Формула площади квадрата
Из приведенного выше рисунка мы узнаем, что площадь квадрата равна произведению сторон. Это можно записать как «сторона х сторона». Следовательно, формула для любого квадрата с любой длиной стороны задается как
Площадь = (Сторона) 2
Давайте рассмотрим пример, чтобы понять эту формулу:
Пример: Найдите площадь квадрата со стороной 13 см.
Решение: При длине стороны = 13 см
Площадь квадрата = (Сторона) 2 = (13) 2 = 169 см 2 .
Площадь квадрата всегда выражается в квадратных единицах (квадратный сантиметр, квадратный метр, квадратный дюйм и т. д.)
Что если нам даны не стороны квадрата, а длина диагонали? Как найти площадь квадрата в этом случае?
Не волнуйтесь! Площадь квадрата можно вычислить, даже если известна длина диагонали. Вы можете найти площадь, используя формулу, написанную ниже:
Вы можете найти площадь, используя формулу, написанную ниже:
Площадь квадрата (с использованием диагоналей) = (D) 2 /2, где D представляет собой длину диагонали.
Примечание: Помните, что диагонали квадрата равны, поэтому площадь остается неизменной, если дана любая из диагоналей.
Пример: Найдите площадь квадрата, если длина диагонали равна 13 см.
Решение: Дано, диагональ = 13 см
Площадь квадрата = D = (13) 2 /2
= 169/2 см 2
Как найти площадь квадрата
До сих пор мы выучили 2 формулы, связанные с нахождением площади квадрата. Давайте узнаем, как вы будете подходить к вопросам, связанным с площадью любого квадрата.
1.
Когда дана чья-либо сторона:- Шаг 1: Запишите значение стороны, скажем «а».

- Шаг 2: Подставьте значение an в формулу -> Площадь (со стороной) = (Сторона) 2 = (a) 2
- Шаг 3: Запишите ответ в квадратных единицах.
Пример: Найдите площадь пластика, необходимую для покрытия квадратного стола длиной 8 м.
Решение: Учитывая, что длина стола = 8 м
Поэтому площадь пластика, необходимая для покрытия стола, = площади стола.
Площадь стола = (сторона) 2 = 8 2 = 64 м 10
- Шаг 1: Запишите значение диагонали длина, скажите «д».
- Шаг 2: Подставьте значение d в формулу -> Площадь (с диагональю) = (d)
- Шаг 3: Запишите результат в квадратных единицах.
Пример: Найдите площадь квадрата с диагональю 4 см
Решение: Учитывая, что длина диагонали = 4 см
Площадь квадрата = (4) 2 /2 = 16/2 = 8 см 2
Найдите площадь квадрата, зная периметр квадрата
В предыдущих разделах мы научились вычислять площадь квадрата, зная сторону или диагональ. Но, предположим, вам не предоставлен ни один из этих параметров, но задан периметр квадрата. Как найти площадь, если известен периметр квадрата? Давайте узнаем:
Но, предположим, вам не предоставлен ни один из этих параметров, но задан периметр квадрата. Как найти площадь, если известен периметр квадрата? Давайте узнаем:
- Шаг 1: Запишите периметр данного квадрата.
- Шаг 2: Мы знаем, что периметр квадрата равен 4 с. Следовательно, 4s = периметр.
- Шаг 3: Подставьте значение периметра и найдите сторону по формуле s = периметр/4
- Шаг 4: Теперь, когда мы знаем сторону квадрата. Найдите площадь, используя s2.
- Шаг 5: Запишите ответ в квадратных единицах.
Пример: Квадратный сад имеет периметр 64 см. Макс хочет посадить цветы и найти площадь этого сада, но не знает, как это сделать? Помогите ему определить площадь сада.
Решение: Мы знаем: Периметр сада = 64 см
Сначала вычислим длину сторон сада.
Используя формулу шага 3
Сторона (s) = периметр/4
= 64/4
= 16 см
Сейчас,
Площадь сада = (s) 2
= 16 2
9032 8 = 256 см 2Несколько советов с нашей стороны:
Обратите внимание на следующие факторы, которые следует учитывать иметь в виду, когда вы вычисляете площадь квадрата.
При вычислении площади квадрата мы часто ошибаемся, удваивая число. Это не вариант! Имейте в виду, что площадь квадрата не равна удвоенной стороне. Это всегда либо «сторона х сторона», либо сторона 2 .
Мы должны не забыть указать единицу измерения площади при ее представлении. Площадь квадрата всегда двумерна; следовательно, мы используем квадратные единицы. Например см 2 , м 2 , дюйм 2 и т. д.
Часто задаваемые вопросы
1. Что такое площадь квадрата в геометрии?
Площадь квадрата в геометрии является измерением поверхности. Он рассчитывается путем умножения длины на ширину.
2. Что такое формула площади квадрата?
Формула площади квадрата позволяет вычислить площадь квадрата. Формула площади квадрата: A = s2, где s представляет собой длину каждой стороны квадрата.
3. Как вычислить площадь квадрата?
Чтобы вычислить площадь квадрата, нужно умножить длину одной стороны на саму себя.

 Рада всех видеть, садитесь.
Рада всех видеть, садитесь.

 (14 февраля)
(14 февраля)
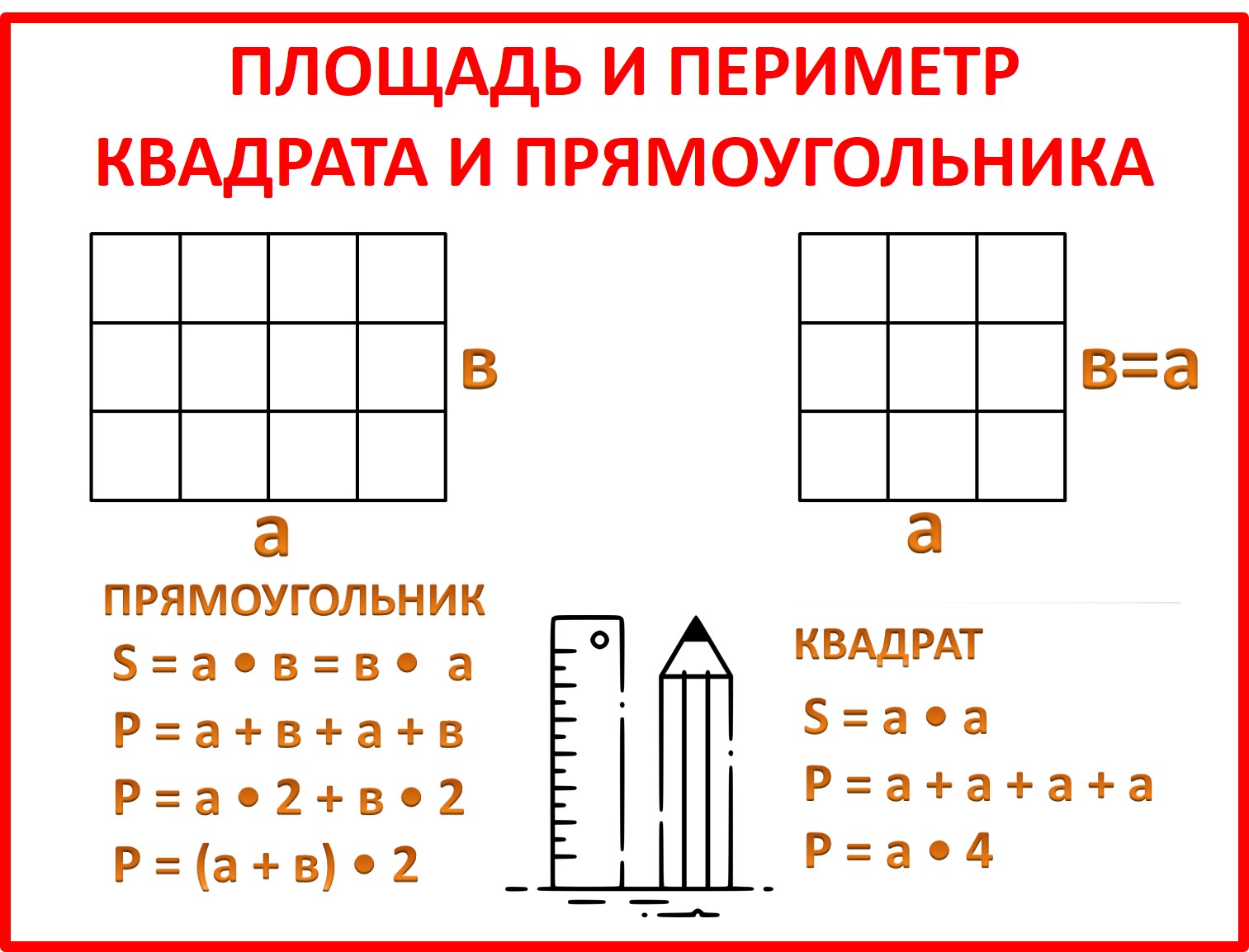 S = a • b
S = a • b Перед вами таблица с правилами, прочитайте правила.
Перед вами таблица с правилами, прочитайте правила.





 Отсюда следует, что противолежащая и прилежащая стороны квадрата равны друг другу.
Отсюда следует, что противолежащая и прилежащая стороны квадрата равны друг другу.