Как найти периметр прямоугольного треугольника: Как найти периметр треугольника 🔺 формула нахождения

Содержание

Как найти основание равнобедренного треугольника зная периметр. Периметр и площадь треугольника. Формула вычисления периметра

Словари. Энциклопедии. История. Литература. Русский язык » Литература » Как найти основание равнобедренного треугольника зная периметр. Периметр и площадь треугольника. Формула вычисления периметра

Предварительные сведения

Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон. Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.

Определение 1

Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).

Определение 2

Точки в рамках определения 1 будем называть вершинами треугольника.

Определение 3

Отрезки в рамках определения 1 будем называть сторонами треугольника.

Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.

В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.

Определение 4

Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.

Определение 5

Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.

Определение 6

Треугольник будем называть равносторонним, если все его стороны равняются друг другу.

Все виды этих треугольников Вы можете видеть на рисунке 2.

Как найти периметр разностороннего треугольника?

Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.

Вывод: Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.

Пример 1

Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.

$P=34+12+11=57$ см

Ответ: $57$ см.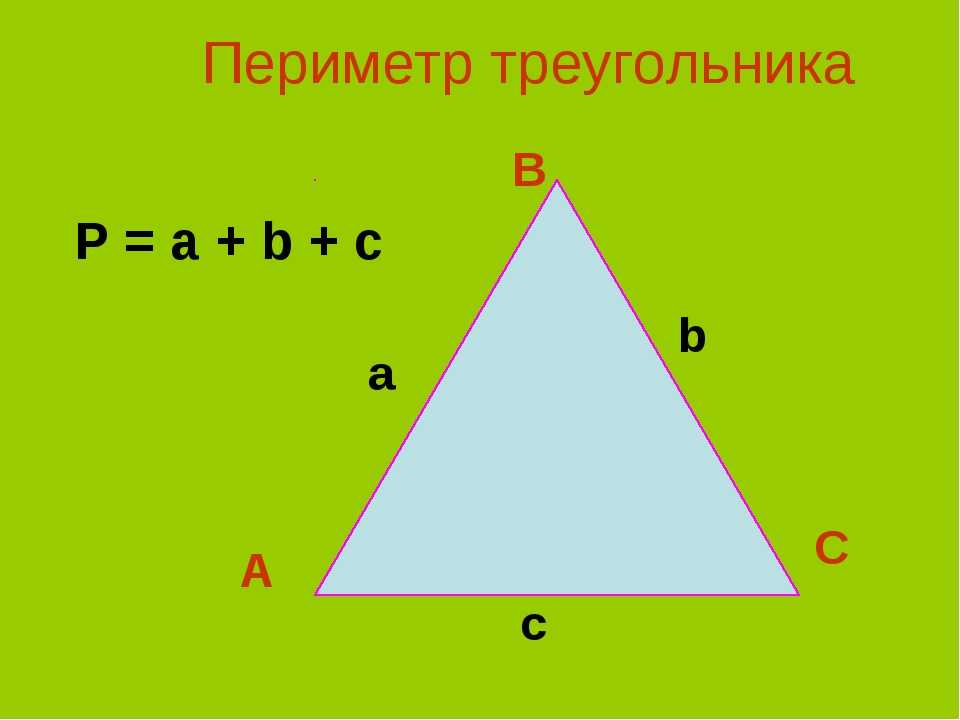

Пример 2

Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.

Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда

$α=10$ По правилу вычисления периметра разностороннего треугольника, получим

$P=10+8+6=24$ см

Ответ: $24$ см.

Как найти периметр равнобедренного треугольника?

Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+β=2α+β$

Вывод: Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.

Пример 3

Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.

По рассмотренному выше примеру, видим, что

$P=2\cdot 12+11=35$ см

Ответ: $35$ см.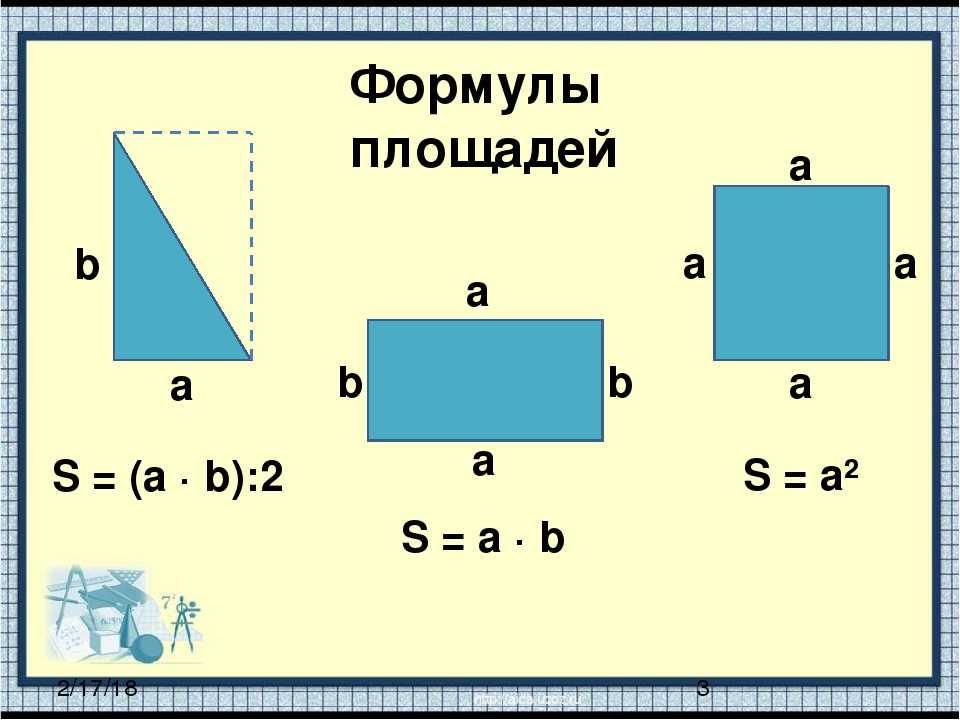

Пример 4

Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.

Рассмотрим рисунок по условию задачи:

Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.

По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда

По правилу вычисления периметра равнобедренного треугольника, получим

$P=2\cdot 10+12=32$ см

Ответ: $32$ см.

Как найти периметр равностороннего треугольника?

Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+α=3α$

Вывод: Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.

Пример 5

Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.

По рассмотренному выше примеру, видим, что

$P=3\cdot 12=36$ см

Периметром треугольника , как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.
Формула периметра треугольника выглядит так:

Пример расчета периметра треугольника. Пусть дан треугольник со сторонами a = 4см, b = 6 см, c = 7 см. подставим данные в формулу: см

Формула расчета периметра равнобедренного треугольника будет выглядеть так:

Формула расчета периметра равностороннего треугольника :

Пример расчета периметра равностороннего треугольника. Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см

В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по теореме Пифагора . К примеру, если известны длины катетов, то можно найти гипотенузу по формуле:

Рассмотрим пример расчета периметра равнобедренного треугольника при условии, что мы знаем длину катетов в прямоугольном равнобедренном треугольнике.
Дан треугольник с катетами a =b =5 см. Найти периметр. Для начала найдем недостающую сторону с . см
Теперь посчитаем периметр: см
Периметр прямоугольного равнобедренного треугольника будет равен 17 см.

В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле:
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле.

Предварительные сведения

Определение 1

Определение 2

Точки в рамках определения 1 будем называть вершинами треугольника.

Определение 3

Отрезки в рамках определения 1 будем называть сторонами треугольника.

Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.

Определение 4

Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.

Определение 5

Определение 6

Треугольник будем называть равносторонним, если все его стороны равняются друг другу.

Все виды этих треугольников Вы можете видеть на рисунке 2.

Как найти периметр разностороннего треугольника?

Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.

Пример 1

Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.

$P=34+12+11=57$ см

Ответ: $57$ см.

Пример 2

Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.

Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда

$α=10$ По правилу вычисления периметра разностороннего треугольника, получим

$P=10+8+6=24$ см

Ответ: $24$ см.

Как найти периметр равнобедренного треугольника?

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+β=2α+β$

Пример 3

Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.

По рассмотренному выше примеру, видим, что

$P=2\cdot 12+11=35$ см

Ответ: $35$ см.

Пример 4

Рассмотрим рисунок по условию задачи:

Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.

По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда

По правилу вычисления периметра равнобедренного треугольника, получим

$P=2\cdot 10+12=32$ см

Ответ: $32$ см.

Как найти периметр равностороннего треугольника?

Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+α=3α$

Пример 5

Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.

По рассмотренному выше примеру, видим, что

$P=3\cdot 12=36$ см

Периметр – это сумма всех сторон фигуры. Эта характеристика, наравне с площадью, одинаково востребована для всех фигур. Формула периметра равнобедренного треугольника логично вытекает из его свойств, но формула не столь сложна, как получение и закрепление практических навыков.

Формула вычисления периметра

Боковые стороны равнобедренного треугольника равны между собой. Это проистекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и проистекает формула периметра:

P=2a+b, где b-это основание треугольника, a-значение боковой стороны.

Рис. 1. Равнобедренный треугольник

Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон. Рассмотри несколько задач на нахождение периметра равнобедренного треугольника. 2}=\sqrt{9+16}=\sqrt{25}=5$$

Найдем периметр: P=AC+AB*2=6+5*2=16

Задача 2

В равнобедренном треугольнике высота, проведенная к основанию, равна 10, а острый угол при основании 30 градусам. нужно найти периметр треугольника.

Рис. 3. Рисунок к задаче 2

Эта задача осложнена отсутствием сведений о сторонах треугольника, но, зная значение высоты и угла, в прямоугольном треугольнике ABH можно найти катет AH, а после решение пойдет по тому же сценарию, что и в задаче 1.

Найдем AH через значение синуса:

$$sin (ABH)={BH\over AB}={1\over2}$$ — синус 30 градусов является табличным значением.

Выразим нужную сторону:

$$AB={{BH\over {1\over 2}}} =BH*2=10*2=20$$

Через котангенс найдем значение AH:

$$ctg(BAH)={AH\over BH}={1\over\sqrt{3}}$$

$$AH={BH\over\sqrt{3}}=10*\sqrt{3}=17,32$$ — получившееся значение округлим до сотых.

Найдем основание:

AC=AH*2=17,32*2=34,64

Теперь, когда все требуемые значения найдены, определим периметр:

P=AC+2*AB=34,64+2*20=74,64

Задача 3

В равнобедренном треугольнике ABC известна площадь, которая равна $$16\over\sqrt{3}$$ и острый угол при основании в 30 градусов. Найти периметр треугольника.

Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений

При такой постановке задачи может показаться, что решений нет, ведь сложно выразить одну из сторон или высоту из имеющихся данных. Попробуем решить по-другому.

Обозначим высоту и половину основания латинскими буквами: BH=h и AH=a

Тогда основание будет равно: AC=AH+HC=AH*2=2a

Площадь: $$S={1\over 2}*AC*BH={1\over 2}*2a*h=ah$$

С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно тангенс? Потому что в треугольнике ABH мы уже обозначили два катета a и h. Нужно выразить одно через другое. Два катета вместе связывают тангенс и котангенс. Традиционно к котангенсу и косинусу обращаются, только если не подходит тангенс или синус. Это не правило, можно решать так, как удобно, просто так принято. 2}=4,62$$

Подставим значения в формулу периметра:

P=AB*2+AH*2=4,62*2+4*2=17,24

Что мы узнали?

Мы разобрались подробно во всех тонкостях нахождения периметра равнобедренного треугольника. Решили три задачи разного уровня сложности, показав на примере, как решаются типовые задачи на решение равнобедренного треугольника.

Тест по теме

Оценка статьи

Средняя оценка: 4.4 . Всего получено оценок: 83.

Любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:

P = a + b + c

где P — это периметр треугольника, a , b и c — его стороны.

Можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:

P = 2a + b

где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.

Можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:

P = 3a

где P — это периметр равностороннего треугольника, a — любая из его сторон.

Площадь

Для измерения площади треугольника можно сравнить его с параллелограммом . Рассмотрим треугольник ABC :

Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:

В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.

Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна

Теперь рассмотрим прямоугольный треугольник:

Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:

Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.

Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2 . Общая формула для нахождения площади треугольников будет выглядеть так:

S =	ah a
	2

где S — это площадь треугольника, a — его основание, h a — высота, опущенная на основание a .

Как найти периметр треугольника если известны. Находим периметр треугольника различными способами

Как найти периметр треугольника? Таким вопросом задавался каждый из нас, учась в школе.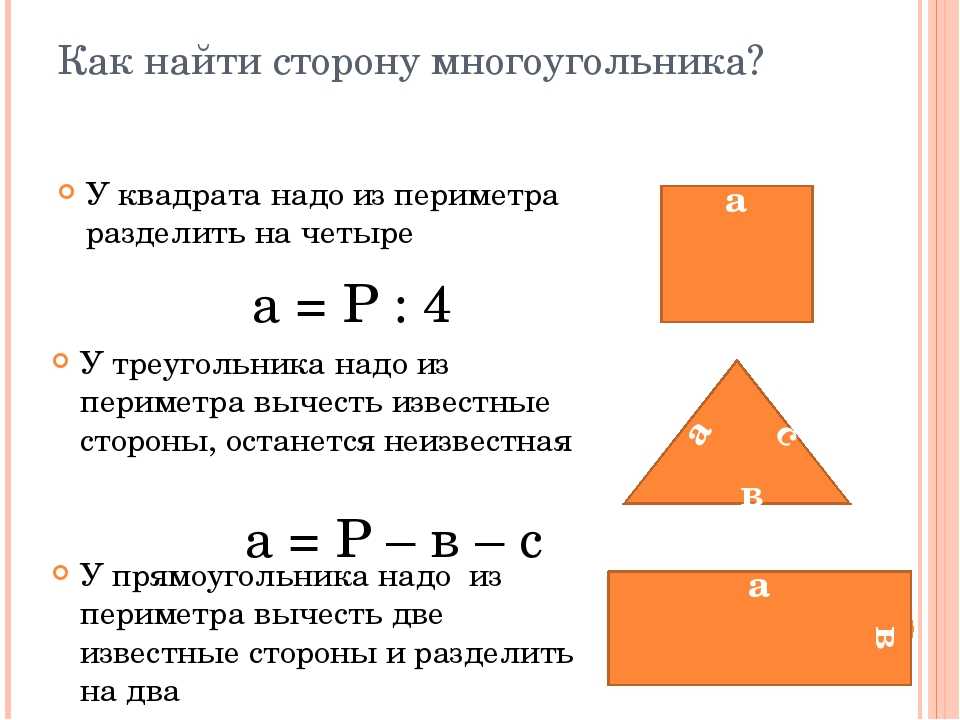 Попробуем вспомнить все, что мы знаем об этой удивительной фигуре, а также ответить на заданный вопрос.

Ответ на вопрос о том, как найти периметр треугольника, обычно является довольно-таки простым — требуется всего-лишь выполнить процедуру сложения длин всех его сторон. Однако есть ещё несколько простых методов искомой величины.

Советы

В том случае, если радиус (r) окружности, которая вписана в треугольник, и его площадь (S) известны, то ответить на вопрос о том, как найти периметр треугольника, довольно просто. Для этого вам необходимо воспользоваться обычной формулой:

Если известны два угла, допустим, α и β, которые прилегают к стороне, и сама длина стороны, то периметр можно найти с помощью весьма и весьма популярной формулы, которая имеет вид:

sinβ∙а/(sin(180° — β — α)) + sinα∙а/(sin(180° — β — α)) + а

Если вы знаете длины смежных сторон и угол β, находящийся между ними, то для того, чтобы найти периметр, требуется воспользоваться теоремой косинусов. Периметр вычисляется по формуле:

P = b + a + √(b2 + a2 — 2∙b∙а∙cosβ),

где b2 и а2 являются квадратами длин смежных сторон. Подкоренное выражение — это длина третьей стороны, которая неизвестна, выраженная посредством теоремы косинусов.

Если вы не знаете, как найти периметр равнобедренного треугольника, то здесь, на самом деле, нет ничего сложного. Вычислите его по формуле:

где b — основание треугольника, а — его боковые стороны.

Для нахождения периметра правильного треугольника следует воспользоваться простейшей формулой:

где а — длина стороны.

Как найти периметр треугольника, если известны только радиусы окружностей, которые описаны около него или вписаны в него? Если треугольник является равносторонним, то тогда следует применить формулу:

P = 3R√3 = 6r√3,

где R и r являются радиусами описанной и вписанной окружности соответственно.

Если треугольник является равнобедренным, то для него применима формула:

P=2R (sinβ + 2sinα),

где α — это угол, который лежит у основания, а β — угол, который противолежит основанию.

Зачастую для решения математических задач требуется глубочайший анализ и специфическое умение находить и выводить требуемые формулы, а это, как многим известно, довольно непростая работа. Хотя некоторые задачи можно решить всего лишь с помощью одной-единственной формулы.

Давайте рассмотрим формулы, которые являются базовыми для ответа на вопрос о том, как найти периметр треугольника, по отношению к самым разнообразным типам треугольников.

Безусловно, главное правило для нахождения периметра треугольника — это данное утверждение: для нахождения периметра треугольника требуется сложить длины всех его сторон по соответствующей формуле:

где b, a и с — это длины сторон треугольника, а Р — периметр треугольника.

Есть несколько частных случаев данной формулы. Допустим, ваша задача формулируется следующим образом: «как найти периметр прямоугольного треугольника?» В таком случае вам следует воспользоваться следующей формулой:

P = b + a + √(b2 + a2)

В этой формуле b и а являются непосредственными длинами катетов прямоугольного треугольника. Несложно догадаться, что вместо стороны с (гипотенузы) используется выражение, полученное по теореме великого ученного древности — Пифагора.

Если требуется решить задачу, где треугольники являются подобными, то логично было бы воспользоваться данным утверждением: отношение периметров соответствует коэффициенту подобия. Допустим, у вас есть два подобных треугольника — ΔABC и ΔA1B1C1. Тогда для нахождения коэффициента подобия необходимо разделить периметр ΔABC на периметр ΔA1B1C1.

В заключение можно отметить, что периметр треугольника можно найти при помощи самых различных методик, в зависимости от тех исходных данных, которые у вас имеются. Необходимо добавить, что существуют некоторые частные случаи для прямоугольных треугольников.

Треугольник являет собой одну из фундаментальных геометрических фигур, представляющих собой три пересекающихся отрезка прямых. Эта фигура была известна еще ученым Древнего Египта, Древней Греции и Древнего Китая, которые и вывели большинство формул и закономерностей, используемых учеными, инженерами и конструкторами до сих пор.

К основным составным частям треугольника относятся:

Вершины — точки пересечения отрезков.

Стороны — пересекающиеся отрезки прямых.

Исходя из этих составных частей, формулируют такие понятия, как периметр треугольника, его площадь, вписанная и описанная окружность. Еще со школы известно, что периметр треугольника представляет собой числовое выражение суммы всех трех его сторон. В то же время формул для нахождения данной величины известно великое множество, в зависимости от тех исходных данных, которые есть у исследователя в том или ином случае.

1. Самый простой способ нахождения периметра треугольника используется в том случае, когда известны числовые значения всех трех его сторон (x,y,z), как следствие:

2. Периметр равностороннего треугольника можно найти, если вспомнить, что у данной фигуры все стороны, впрочем, как и все углы, равны. Зная длину этой стороны, периметр равностороннего треугольника можно определить по формуле:

3. У равнобедренного треугольника, в отличие от равностороннего, только две боковые стороны имеют одно и то же числовое значение, поэтому в этом случае в общем виде периметр будет находиться следующим образом:

4. Следующие способы необходимы в тех случаях, когда известны числовые значения не всех сторон. Например, если в исследовании есть данные о двух сторонах, а также известен угол между ними, то периметр треугольника может быть найден с помощью определения третьей стороны и известного угла. В этом случае эта третья сторона будет найдена по формуле:

z= 2x+2y-2xycosβ

Исходя из этого, периметр треугольника будет равен:

P= x+y+2x+(2y-2xycos β)

5. В том случае, когда изначально дана длина не более чем одной стороны треугольника и известны числовые величины двух углов прилегающих к ней, то периметр треугольника можно вычислить, опираясь на теорему синусов:

P = x+sinβ х/(sin(180°-β)) + sinγ x/(sin(180°-γ))

6. Бывают случаи, когда для нахождения периметра треугольника используются известные параметры вписанной в него окружности. Данная формула также известна большинству еще со школьной скамьи:

P= 2S/r (S — площадь окружности, тогда как r — ее радиус).

Из всего вышеприведенного видно, что величина периметра треугольника может быть найдена множеством способов, исходя из тех данных, которыми владеет исследователь. Кроме того, есть еще несколько частных случаев нахождения данной величины. Так, периметр является одной из важнейших величин и характеристик прямоугольного треугольника.

Как известно, таким треугольником называют фигуру, две стороны которой образуют прямой угол. Периметр прямоугольного треугольника находится через числовое выражение суммы обоих катетов и гипотенузы. В том случае, если исследователю известны данные только о двух сторонах, оставшуюся можно вычислить с помощью знаменитой теоремы Пифагора: z= (x2 + y2), если известны оба катета, или x= (z2 — y2), если известна гипотенуза и катет.

В том случае, если известна длина гипотенузы и один из прилежащих у ней углов, то две другие стороны находятся по формулам: х= z sinβ , y= z cosβ. В этом случае периметр будет равен:

P= z(cosβ + sinβ +1)

Также частным случаем является вычисление периметра правильного (или равностороннего) треугольника, то есть такой фигуры, у которой все стороны и все углы равны. Вычисление периметра такого треугольника по известной стороне никакой проблемы не составляет, однако, зачастую исследователю известны какие-то другие данные. Так, если известен радиус вписанной окружности, периметр правильного треугольника находится по формуле:

А если дана величина радиуса описанной окружности, периметр правильного треугольника будет найден следующим образом:

Формулы нужно запомнить, чтобы успешно применть на практике.

Содержимое:

Периметр – это общая длина границ двумерной формы. Если вы хотите найти периметр треугольника, то вы должны сложить длины всех его сторон; если вы не знаете длину хотя бы одной стороны треугольника, необходимо найти ее. Эта статья расскажет вам, (а) как найти периметр треугольника по трем известным сторонам; (б) как найти периметр прямоугольного треугольника, когда известны только две стороны; (в) как найти периметр любого треугольника, когда даны две стороны и угол между ними (используя теорему косинусов).

Шаги

1 По трем данным сторонам

1 Для нахождения периметра используйте формулу: Р = a + b + c, где a, b, c – длины трех сторон, Р – периметр.
2 Найдите длины всех трех сторон. В нашем примере: a = 5, b = 5, с = 5.
- Это равносторонний треугольник, так как все три стороны имеют одинаковую длину. Но вышеуказанная формула применяется к любому треугольнику.
3 Сложите длины всех трех сторон, чтобы найти периметр. В нашем примере: 5 + 5 + 5 = 15, то есть Р = 15.
- Другой пример: a = 4, b = 3, с = 5. Р = 3 + 4 + 5 = 12.
4 В ответе не забывайте указывать единицу измерения. В нашем примере стороны измеряются в сантиметрах, поэтому ваш окончательный ответ также должен включать сантиметры (или единицы измерения, указанные в условии задачи).
- В нашем примере каждая сторона равна 5 см, поэтому окончательный ответ: Р = 15 см.

2 По двум данным сторонам прямоугольного треугольника

1 Вспомните теорему Пифагора. Эта теорема описывает соотношение между сторонами прямоугольного треугольника и является одной из наиболее известных и применяемых теорем математики. Теорема гласит, что в любом прямоугольном треугольнике стороны связаны следующим соотношением: a 2 + b 2 = c 2 , где а, b – катеты, с – гипотенуза.
2 Нарисуйте треугольник и обозначьте стороны как a, b, c. Самая длинная сторона прямоугольного треугольника – это гипотенуза. Она лежит напротив прямого угла. Обозначьте гипотенузу как «с». Катеты (стороны, прилежащие к прямому углу) обозначьте как «a» и «b».
3 Подставьте значения известных сторон в теорему Пифагора (a 2 + b 2 = c 2). Вместо букв подставьте числа, данные в условии задачи.
- Например, а = 3 и b = 4. Подставьте эти значения в теорему Пифагора: 3 2 + 4 2 = c 2 .
- Другой пример: а = 6 и с = 10. Тогда: 6 2 + b 2 = 10 2
4 Решите полученное уравнение, чтобы найти неизвестную сторону. Для этого сначала возведите в квадрат известные длины сторон (просто умножьте данное вам число само на себя). Если вы ищете гипотенузу, сложите квадраты двух сторон и из полученной суммы извлеките квадратный корень. Если вы ищете катет, вычтите квадрат известного катета из квадрата гипотенузы и из полученного частного извлеките квадратный корень.
- В первом примере: 3 2 + 4 2 = c 2 ; 9 + 16 = c 2 ; 25= c 2 ; √25 = с. Таким образом, c = 25.
- Во втором примере: 6 2 + b 2 = 10 2 ; 36 + b 2 = 100. Перенесите 36 на правую сторону уравнения и получите: b 2 = 64; b = √64. Таким образом, b = 8.
5
- В нашем первом примере: P = 3 + 4 + 5 = 12.
- В нашем втором примере: P = 6 + 8 + 10 = 24.

3 По двум данным сторонам и углу между ними

1 Любую сторону треугольника можно найти по теореме косинусов, если вам даны две стороны и угол между ними. Эта теорема применяется к любым треугольникам и является очень полезной формулой. Теорема косинусов: c 2 = a 2 + b 2 — 2abcos(C), где a, b, c – стороны треугольника, А, B, С – углы, противолежащие соответствующим сторонам треугольника.
2 Нарисуйте треугольник и обозначьте стороны как a, b, c; обозначьте противолежащие соответствующим сторонам углы как A, B, C (то есть угол, противолежащий стороне «а», обозначьте как «А» и так далее).
- Например, дан треугольник со сторонами 10 и 12 и углом между ними в 97°, то есть a = 10, b = 12, C = 97°.
3 Подставьте данные вам значения в формулу и найдите неизвестную сторону «с». Сначала возведите в квадрат длины известных сторон и сложите полученные значения. Затем найдите косинус угла С (с помощью калькулятора или онлайн-калькулятора). Умножьте длины известных сторон на косинус данного угла и на 2 (2abcos(C)). Полученное значение вычтите из суммы квадратов двух сторон (a 2 + b 2), и вы получите c 2 . Из этой величины извлеките квадратный корень, чтобы найти длину неизвестной стороны «с». В нашем примере:
- c 2 = 10 2 + 12 2 — 2 × 10 × 12 × cos(97)
- c 2 = 100 + 144 – (240 × -0,12187)
- c 2 = 244 – (-29,25)
- c 2 = 244 + 29,25
- c 2 = 273,25
- c = 16,53
4 Сложите длины трех сторон, чтобы найти периметр. Напомним, что периметр вычисляется по формуле: P = a + b + c.
- В нашем примере: Р = 10 + 12 + 16,53 = 38,53.

Периметр любого треугольника — это длина линии, ограничивающей фигуру. Чтобы его вычислить, нужно узнать сумму всех сторон этого многоугольника.

Вычисление по данным значениям длины сторон

Когда известны их значения, то сделать это несложно. Обозначив эти параметры буквами m, n, k, а периметр буквой P, получим формулу для вычисления: P = m+n+k. Задание: Известно, что треугольник имеет стороны длиной 13,5 дециметров, 12,1 дециметров и 4,2 дециметра. Узнать периметр. Решаем: Если стороны данного многоугольника — a = 13,5 дм, b = 12,1 дм, c = 4,2 дм, то P = 29,8 дм. Ответ: P = 29,8 дм.

Периметр треугольника, который имеет две равные стороны

Такой треугольник называется равнобедренным. Если эти равные стороны имеют длину a сантиметров, а третья сторона — b сантиметров, то периметр легко узнать: P =b+2a. Задание: треугольник имеет две стороны по 10 дециметров, основание 12 дециметров. Найти P. Решение: Пусть боковая сторона a = c = 10 дм, основание b = 12 дм. Сумма сторон P = 10 дм + 12 дм + 10 дм = 32 дм. Ответ: P = 32 дециметра.

Периметр равностороннего треугольника

Если все три стороны треугольника имеют равное количество единиц измерения, он называется равносторонним. Еще одно название — правильный. Периметр правильного треугольника находят при помощи формулы: P = a+a+a = 3·a. Задача: Имеем равносторонний треугольный земельный участок. Одна сторона равна 6 метрам. Найти длину забора, которым можно обнести этот участок. Решение: Если сторона этого многоугольника a= 6м, то длина забора P = 3·6 = 18 (м). Ответ: P = 18 м.

Треугольник, у которого есть угол 90°

Его называют прямоугольным. Наличие прямого угла дает возможность находить неизвестные стороны, пользуясь определением тригонометрических функций и теоремой Пифагора. Самая длинная сторона называется гипотенуза и обозначается c. Имеются еще две стороны, a и b. Следуя теореме, носящей имя Пифагора, имеем c 2 = a 2 + b 2 . Катеты a = √ (c 2 — b 2) и b = √ (c 2 — а 2). Зная длину двух катетов a и b, вычисляем гипотенузу. Затем находим сумму сторон фигуры, сложив эти значения. Задание: Катеты прямоугольного треугольника имеют длину 8,3 сантиметра и 6,2 сантиметра. Периметр треугольника нужно вычислить. Решаем: Обозначим катеты a = 8,3 см, b = 6,2 см. За теоремой Пифагора гипотенуза c = √ (8,3 2 + 6,2 2) = √ (68,89 + 38,44) = √107,33 = 10,4 (см). P = 24,9 (см). Или P = 8,3 + 6,2 + √ (8,3 2 + 6,2 2) = 24,9 (см). Ответ: P = 24,9 см. Значения корней брали с точностью до десятых. Если нам известны значения гипотенузы и катета, то значение Р получим, вычислив Р=√ (c 2 — b 2) + b + c. Задача 2: Отрезок земельного участка, лежащий против угла в 90 градусов, 12 км, один из катетов — 8 км. За какое время можно обойти весь участок, если двигаться со скоростью 4 километра в час? Решение: если наибольший отрезок — 12 км, меньший b = 8 км, то длина всего пути составит P = 8 + 12 + √ (12 2 — 8 2) = 20 + √80 = 20 + 8,9 = 28,9 (км). Время найдем, разделив путь на скорость. 28,9:4 = 7,225 (ч). Ответ: можно обойти за 7,3 ч. Значение квадратных корней и ответа берем с точностью до десятых. Можно найти сумму сторон прямоугольного треугольника, если дана одна из сторон и значение одного из острых углов. Зная длину катета b и значение противолежащего ему угла β, найдем неизвестную сторону a = b/ tg β. Находим гипотенузу c = a: sinα. Периметр такой фигуры находим, сложив полученные значения. P = a + a/ sinα + a/ tg α, или P = a(1 / sin α+ 1+1 / tg α). Задание: В прямоугольном Δ АВС с прямым углом С катет ВС имеет длину 10 м, угол А — 29 градусов. Нужно найти сумму сторон Δ АВС. Решение: Обозначим известный катет ВС = a = 10 м, угол, лежащий напротив него, ∟А = α = 30°, тогда катет АС = b = 10: 0,58 = 17,2 (м), гипотенуза АВ = c = 10: 0,5 = 20 (м). Р = 10 + 17,2 + 20 = 47,2 (м). Или Р = 10 · (1 + 1,72 + 2) = 47,2 м. Имеем: P = 47,2 м. Значение тригонометрических функций берем с точностью до сотых, значение длины сторон и периметра округляем до десятых. Имея значение катета α и прилежащего угла β, узнаем, чему равен второй катет: b = a tg β. Гипотенуза в таком случае будет равна катету, разделенному на косинус угла β. Периметр узнаем по формуле P = a + a tg β + a: cos β = (tg β + 1+1: cos β)·a. Задание: Катет треугольника с углом 90 градусов 18 см, прилежащий угол — 40 градусов. Найти P. Решение: Обозначим известный катет ВС = 18 см, ∟β = 40°. Тогда неизвестный катет АС = b = 18 · 0,83 = 14,9 (см), гипотенуза АВ = c = 18: 0,77 = 23,4 (см). Сумма сторон фигуры равна Р = 56,3 (см). Или Р = (1 + 1,3+0,83)*18 = 56,3 см. Ответ: P = 56,3 см. Если известна длина гипотенузы c и какой-нибудь угол α, то катеты будут равны произведению гипотенузы для первого — на синус и для второго — на косинус этого угла. Периметр этой фигуры P = (sin α + 1+ cos α)*c. Задание: Гипотенуза прямоугольного треугольника АВ = 9,1 сантиметр, а угол 50 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим гипотенузу: AB = c = 9,1 см, ∟A= α = 50°, тогда один из катетов BC имеет длину a = 9,1 · 0,77 = 7 (см), катет АС = b = 9,1 · 0,64 = 5,8 (см). Значит периметр этого многоугольника равен P = 9,1 + 7 + 5,8 = 21,9 (см). Или P = 9,1·(1 + 0,77 + 0,64) = 21,9 (см). Ответ: P = 21,9 сантиметров.

Произвольный треугольник, одна из сторон которого неизвестна

Если мы имеем значения двух сторон a и c, и угла между этими сторонами γ, третью находим теоремой косинусов: b 2 = с 2 + a 2 — 2 ас cos β, где β — угол, лежащий между сторонами а и с. Затем находим периметр. Задание: Δ АВС имеет отрезок АВ длиной 15 дм, отрезок АС, длина которго 30,5 дм. Значение угла между этими сторонами 35 градусов. Вычислить сумму сторон Δ АВС. Решение: Теоремой косинусов вычислим длину третей стороны. BC 2 = 30,5 2 + 15 2 — 2·30,5·15·0,82 = 930,25 + 225 — 750,3 = 404,95. BC = 20,1 см. P = 30,5 + 15 + 20,1 = 65,6 (дм).Имеем: P = 65,6 дм.

Сумма сторон произвольного треугольника, у которого длины двух сторон неизвестны

Когда знаем длину только одного отрезка и значение двух углов, можно узнать длину двух неизвестных сторон, пользуясь теоремой синусов: «в треугольнике стороны всегда пропорциональны значениям синусов противоположных углов».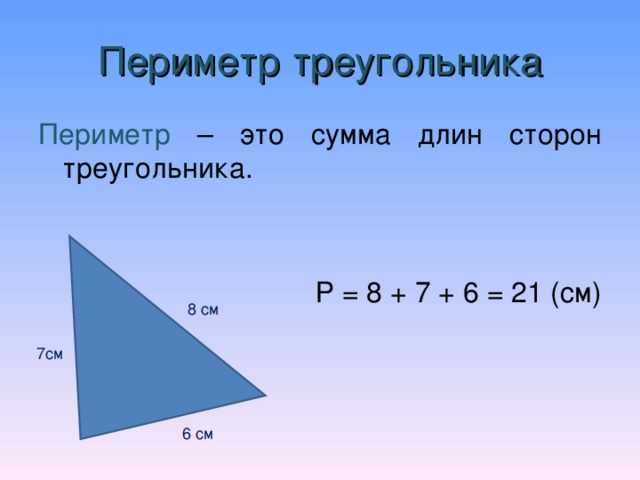 Откуда b = (a* sin β)/ sin a. Аналогично c = (a sin γ): sin a. Периметр в таком случае будет P = а + (а sin β)/ sin a + (a sin γ)/ sin a. Задание: Имеем Δ ABC. В нем длина стороны BC 8,5 мм, значение угла C — 47°, а угла B — 35 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим длины сторон BC = a = 8,5 мм, AC = b, AB = c, ∟ A = α= 47°, ∟B = β = 35°, ∟ C = γ = 180° — (47° + 35°) = 180° — 82° = 98°. Из соотношений, полученных из теоремы синусов, находим катеты AC = b = (8,5·0,57): 0,73= 6,7 (мм), AB = c = (7 · 0,99): 0,73 = 9,5 (мм). Отсюда сумма сторон этого многоугольника равна P = 8,5 мм + 5,5 мм + 9,5 мм = 23,5 мм. Ответ: P = 23,5 мм. В случае, когда есть только длина одного отрезка и значения двух прилежащих углов, сначала вычисляем угол, противоположный известной стороне. Все углы этой фигуры в сумме имеют 180 градусов. Поэтому ∟A = 180° — (∟B + ∟C). Дальше находим неизвестные отрезки, используя теорему синусов. Задание: Имеем Δ ABC. Он имеет отрезок BC, равный 10 см. Значение угла B равно 48 градусов, угол C равен 56 градусов. Найти сумму сторон Δ ABC. Решение: Сначала найдем значение угла A, противолежащего стороне BC. ∟A = 180° — (48° + 56°) = 76°. Теперь с теоремой синусов вычислим длину стороны AC = 10·0,74: 0,97 = 7,6 (см). AB = BC* sin C/ sin A = 8,6. Периметр треугольника Р = 10 + 8,6 + 7,6 = 26,2 (см). Результат: P = 26,2 см.

Вычисление периметра треугольника с использованием радиуса окружности, вписанной в него

Иногда из условия задачи не известна ни одна сторона. Зато есть значение площади треугольника и радиуса окружности, вписанной в него. Эти величины связаны: S = r p. Зная значение площади треугольника, радиуса r, можем найти полупериметр p. Находим p = S: r. Задача: Участок имеет площадь 24 м 2 , радиус r равен 3 м. Найти количество деревьев, которое нужно высадить равномерно по линии, ограждающей этот участок, если между двумя соседними должно быть расстояние 2 метра. Решение: Сумму сторон данной фигуры находим так: P = 2 · 24: 3 = 16 (м). Затем делим на два. 16:2= 8. Итого: 8 деревьев.

Сумма сторон треугольника в декартовых координатах

Вершины Δ АВС имеют координаты: A (x 1 ; y 1), B (x 2 ; y 2), C(x 3 ; y 3). Найдем квадраты каждой из сторон AB 2 = (x 1 — x 2) 2 + (y 1 — y 2) 2 ; ВС 2 = (x 2 — x 3) 2 + (y 2 — y 3) 2 ; АС 2 = (x 1 — x 3) 2 + (y 1 — y 3) 2 . Чтобы найти периметр, достаточно сложить все отрезки. Задание: Координаты вершин Δ ABC: B (3; 0), A (1; -3), C (2; 5). Найти сумму сторон этой фигуры. Решение: поставив значения соответствующих координат в формулу периметра, получим P = √(4 + 9) + √(1 + 25) + √(1 + 64) = √13 + √26 + √65 = 3,6 + 5,1 + 8,0 = 16,6. Имеем: P = 16,6. Если фигура находится не на плоскости, а в пространстве, то каждая из вершин имеет три координаты. Поэтому формула суммы сторон будет иметь еще одно слагаемое.

Векторный метод

Если фигура задана координатами вершин, периметр можно вычислить, используя векторный метод. Вектор — отрезок, имеющий направление. Его модуль (длина) обозначается символом ǀᾱǀ. Расстояние между точками — это и есть длина соответствующего вектора, или модуль вектора. Рассмотрим треугольник, лежащий на плоскости. Если вершины имеют координаты А (х 1 ; у 1), М(х 2 ; у 2), Т (х 3 ; у 3), то длину каждой из сторон находим по формулам: ǀАМǀ = √ ((х 1 — х 2) 2 + (у 1 — у 2) 2), ǀМТǀ = √ ((х 2 — х 3) 2 + (у 2 — у 3) 2), ǀАТǀ = √ ((х 1 — х 3) 2 + (у 1 — у 3) 2). Периметр треугольника получим, сложив длины векторов. Аналогично находят сумму сторон треугольника в пространстве.

Предварительные сведения

Определение 1

Определение 2

Точки в рамках определения 1 будем называть вершинами треугольника.

Определение 3

Отрезки в рамках определения 1 будем называть сторонами треугольника.

Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.

Определение 4

Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.

Определение 5

Определение 6

Треугольник будем называть равносторонним, если все его стороны равняются друг другу.

Все виды этих треугольников Вы можете видеть на рисунке 2.

Как найти периметр разностороннего треугольника?

Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.

Пример 1

Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.

$P=34+12+11=57$ см

Ответ: $57$ см.

Пример 2

Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.

Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда

$α=10$ По правилу вычисления периметра разностороннего треугольника, получим

$P=10+8+6=24$ см

Ответ: $24$ см.

Как найти периметр равнобедренного треугольника?

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+β=2α+β$

Пример 3

Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.

По рассмотренному выше примеру, видим, что

$P=2\cdot 12+11=35$ см

Ответ: $35$ см.

Пример 4

Рассмотрим рисунок по условию задачи:

Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.

По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда

По правилу вычисления периметра равнобедренного треугольника, получим

$P=2\cdot 10+12=32$ см

Ответ: $32$ см.

Как найти периметр равностороннего треугольника?

Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+α=3α$

Пример 5

Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.

По рассмотренному выше примеру, видим, что

$P=3\cdot 12=36$ см

Периметр прямоугольного треугольника Формула, методы и примеры

Прямоугольный треугольник — это особый вид треугольника, в котором один из углов равен 90 градусов. Сумма углов двух других равна 90 градусов. Основание треугольника и перпендикулярные стороны включают прямой угол. Самая длинная из трех сторон, известная как гипотенуза, является третьей стороной. Полная длина границы геометрической формы известна как ее периметр. Таким образом, периметр прямоугольного треугольника равен сумме всех его сторон.

Что такое периметр прямоугольного треугольника?

Периметр прямоугольного треугольника равен сумме длин всех трех сторон, включая гипотенузу, высоту (высоту) и основание. Если прямоугольный треугольник имеет стороны a, b и c, то его периметр будет равен (a + b + c).

Учитывая, что это прямоугольный треугольник, можно сказать, что длина окружности треугольника равна произведению длин двух его сторон и гипотенузы.

Пример: Прямоугольный треугольник со сторонами a, b и c в следующем примере. a, b — стороны, которые в сумме составляют 9угол 0°. Три стороны можно обозначить следующими именами: высота (а), основание (б) и гипотенуза (в).

Периметр прямоугольного треугольника Формула

Периметр прямоугольного треугольника, стороны которого равны a, b и c.

Формула периметра прямоугольного треугольника = a + b + c, где a, b и c — размеры его трех сторон.

Пример:

a = 4 см, b = 3 см, c = 5 см

Периметр этого прямоугольного треугольника будет равен = a + b + c = 4 + 3 + 5 = 12 см.

Узнайте о периметре разностороннего треугольника

Как найти периметр прямоугольного треугольника

Мы можем найти периметр прямоугольного треугольника, используя 3 метода, приведенные ниже:

Метод 1: Периметр прямоугольного треугольника с данным вершины
Метод 2: Периметр прямоугольного треугольника с заданными двумя сторонами
Метод 3: Периметр прямоугольного треугольника с площадью

Периметр прямоугольного треугольника с заданными вершинами 9{2}} \)
Теперь, используя три вершины, мы добавляем три длины для вычисления периметра:
P = AB + AC + BC
Периметр прямоугольного треугольника с заданными двумя сторонами
В этом В этом случае мы сначала определяем периметр прямоугольного треугольника, а затем применяем теорему Пифагора для определения недостающей стороны. {2}} = \sqrt{20} \) 9{2}} = \sqrt{13} \)
Шаг: 3 Длины трех сторон складываются для определения периметра. Чтобы рассчитать периметр, сложите три значения расстояния, полученные на шаге 2.
Периметр = $ AB + BC + AC = \sqrt{20} + \sqrt{29} + \sqrt{13} = 13,46$
Решенные примеры на периметр прямоугольного треугольника
Пример 1: Определить периметр прямоугольного треугольника
Решение: Дано, a = 3, b = 4, c = 5 9{2} \)
$ 225-25 = \sqrt{205}$
Высота = 14,317 ед.
Периметр прямоугольного треугольника равен 5 + 15+ 14,3 = 34,3 ед.
Если вы хотите хорошо сдать экзамен по математике, то вы попали по адресу. Здесь вы получите еженедельную подготовку к тестам, живые уроки и серию экзаменов. Загрузите приложение Testbook прямо сейчас, чтобы подготовить умную и высокорейтинговую стратегию к экзамену.
Часто задаваемые вопросы о периметре прямоугольного треугольника
В. 1 Как найти периметр прямоугольного треугольника? 9{2}} \)
Q.2 Что такое теорема Пифагора для прямоугольного треугольника?
Ответ 2 Согласно теореме Пифагора, «квадрат гипотенузы равен сумме квадратов двух других сторон» для всех прямоугольных треугольников.
Q.3 В чем разница между площадью и периметром прямоугольного треугольника?
Ответ 3 Внутреннее пространство фигуры измеряется площадью. Периметр фигуры — это окружающее ее пространство.
Q.4 Как найти периметр прямоугольного треугольника с двумя сторонами и гипотенузой?
Ans.4 мы можем найти периметр прямоугольного треугольника с двумя сторонами и гипотенузой, используя следующую формулу: P = a+ b + h.
В.5 Как найти периметр прямоугольного треугольника без гипотенузы?
Ответ 5 Периметр прямоугольного треугольника без гипотенузы можно найти по следующей формуле: P = a + b + c.
Скачать публикацию в формате PDF
Читать Подробные посты
Кластерный анализ: определение, типы, сравнения и примеры
Бокс.
Скалярное произведение: формула, свойства и примеры решения
Много одна функция: определение, свойства и примеры решения
Как найти периметр треугольника 30-60-90?
Геометрия — это раздел математики, изучающий размеры, формы, положения, углы и размеры вещей. Плоские формы, такие как квадраты, круги и треугольники, являются частью плоской геометрии и называются двумерными фигурами. Эти формы имеют только 2 измерения: длину и ширину.
Геометрия — один из старейших разделов математики. Он касается свойств пространства, связанных с расстоянием, формой, размером и относительным положением фигур. Математик, работающий в области геометрии, называется геометром.
Что такое треугольник?
Треугольник — это простой замкнутый многоугольник с тремя ребрами и тремя вершинами. Это одна из основных фигур в геометрии.
Основная форма треугольника
Свойства:
Имеет три стороны.
Имеет три угла.
Имеет три вершины.
Формулы треугольников
Площадь треугольника = 1/2 * основание * высота
Периметр треугольника = сумма всех трех сторон
Типы треугольников
По сторонам
Равносторонний треугольник: Когда все три стороны треугольника равны, такой треугольник называется равносторонним. Каждый из углов равностороннего треугольника равен 60°.
Равнобедренный треугольник: Когда две стороны треугольника равны, такой треугольник называется равнобедренным. Углы, лежащие при равных сторонах, в равнобедренном треугольнике равны.
Разносторонний треугольник: В этом типе треугольника нет двух сторон, равных друг другу, и нет двух углов, равных друг другу.
На основании угла
Остроугольный треугольник: Когда все углы треугольника острые, то есть их мера меньше 90°, такой треугольник называется остроугольным или остроугольным. .
остроугольный треугольник
тупоугольный треугольник: Когда один из углов треугольника равен 90°, он называется прямоугольным треугольником или прямоугольным треугольником.
тупоугольный треугольник
Прямоугольный треугольник: Если один из углов треугольника является тупым, то есть его мера больше 90°, такой треугольник называется тупоугольным или тупоугольным.
прямоугольный треугольник
30-60-90 Треугольник
Это особый тип прямоугольного треугольника, в котором кроме угла 90° один угол равен 30°, а другой угол равен 60°.
или, другими словами, мы можем сказать, что углы находятся в соотношении 30:60:90
= 1: 2: 3
, как мы знаем и теорема Пифагора.
Мы знаем, что
Периметр треугольника = сумма всех трех сторон
Итак, прежде всего мы вычислим его стороны.
пусть основание будет x.
tanθ = P/B
tan 30° = P/x
P = x * tan 30°
P = x * 1/√3
P = x / √3
Сейчас,
3 = H/B
сек 30° = H/x
H = x * сек 30°
H = x * 2/√3
H = 2x / √3
Итак, мы вычислили стороны
первая сторона=x
вторая сторона=2x/√3
третья сторона = x/√3
Теперь мы можем обобщить формулы для вычисления периметра,
Периметр треугольника = сумма трех сторон
= первая сторона + вторая сторона + третья сторона
= x + 2x/√3 + x/√3
= (√3x + 2x + x)/√3
= (3x + √3x) / √3
= √3x + x
= (√3 + 1) x
Пример Вопросы
Вопрос 1: Найдите периметр 30 60 90 треугольник, основание которого равно 5 м.
Решение:
Периметр 30-60-90 Треугольник = (√3+1) x
= (√3+1)*5
= (5√3+5) m.
Итак, периметр треугольника 30-60-90 с основанием 5 м равен (5√3+5)м.
Вопрос 2: Периметр треугольника 30 60 90 равен (12√3 + 12) м. Найдите его высоту.
Решение:
Периметр 30-60-90 Треугольник = (√3+1) x
(12√3+12) m = (√3+1)*x
x = 12 (√3+1) / (√3+1)
x = 12 м
Итак, основание равно 12 м.
Высота треугольника составляет x / √3 = 12 / √3
= 12√3 / 3
= 4√3 м
Итак, высота треугольника составляет 4√3 м.
Вопрос 3: Найдите периметр треугольника 30-60-90. Учитывая сумму двух сторон, отличных от гипотенузы, как 7 + 7 √ 3 см.
Решение:
Сумма двух сторон, отличных от гипотенузы = основание + перпендикуляр
7 + 7 √3 = x + x/√3
Умножение всего уравнения на √3,
21 + 7 √ 3 = х + √3x
x (1 + √3) = 7√3 (1 + √3)
x = 7чина 3 )
= 21 + 7 √3 см
Итак, периметр треугольника равен (21 + 7√3) см.
Вопрос 4: Найдите периметр треугольника ABC. Если АВ = 4 см, ВС = 5 см и СА = 6 см.
Решение:
Периметр треугольника = сумма сторон
= AB + BC + CA
= 4 + 5 + 6
= 15 см
С. Периметр Triandgle ABC — 15CM.
Вопрос 5: Дан периметр треугольника 15см. Найдите третью сторону, если сумма двух соседних сторон равна 8 см.
Решение:
Периметр треугольника = сумма сторон
Пусть третья сторона равна х
х + 8 = 15
х = 7 см
Итак, длина третьей стороны равна 7 см.
Вопрос 6: Если гипотенуза прямоугольного равнобедренного треугольника равна 6√2 м. Найдите его периметр.
Решение:
Периметр треугольника = сумма сторон
Пусть длины равнобедренного треугольника равны l , l , √2l , так как они удовлетворяют условиям прямоугольного равнобедренного треугольника.
No related posts.