Как найти периметр прямоугольной трапеции: Периметр трапеции если известна площадь. Как найти периметр прямоугольной трапеции

alexxlab / / Разное

Периметр трапеции в задачах ЕГЭ: что такое периметр трапеции

Главная » Геометрия » Периметр трапеции

Геометрия

Автор Ольга Викторовна Опубликовано

Периметр трапеции часто нужно определить в задачах по геометрии. Периметр трапеции определяется также как и периметр любой другой фигуры на плоскости:

Периметр плоской фигуры – есть сумма всех сторон фигуры.

Периметр трапеции

Периметр трапеции – есть сумма всех сторон трапеции.

Чему равен периметр равнобедренной трапеции – то же самое – сумме всех ее сторон.

Содержание

В задачах ЕГЭ вы найдете периметр трапеции. Например,

Задача 1

Около окружности описана трапеция, периметр которой равен 60. Найдите длину ее средней линии.

Решение:

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противолежащих сторон равны:

 

АD+CD=DC+AB=PABCD /2,

Где PABCD  – периметр трапеции. В самом деле PABCD =AD+CB+DC+AB=2(DC+AB), а значит, DC+AB=PABCD /2

Средняя линия трапеции – это полусумма ее оснований, то есть MN=(DC+AB)/2=(PABCD /2)/2=PABCD /4 = 60/4=15 .

Ответ: 15.

Задача 2

Около окружности описана трапеция, периметр которой равен 44. Найдите длину ее средней линии.

Решение. Рассуждаем аналогично и получаем MN=(DC+AB)/2=(PABCD /2)/2=PABCD /4 = 44/4=11.

Ответ: 11.

То есть мы сами с вами вывели лайфхак для решения этой задачи:

Лайфхак 1

Если в трапецию вписана окружность, и дан периметр трапеции, то для того чтобы найти среднюю линию трапеции, нужно периметр разделить на 4.

И обратный лайфхак:

Лайфхак 2

Если в трапецию можно вписать окружность, и дана средняя линия трапеции (l), то формула периметра трапеции P:

P=4l

Применим наш лайфхак 1 к решению следующей задачи?

Задача 3

Около окружности описана трапеция, периметр которой равен 30.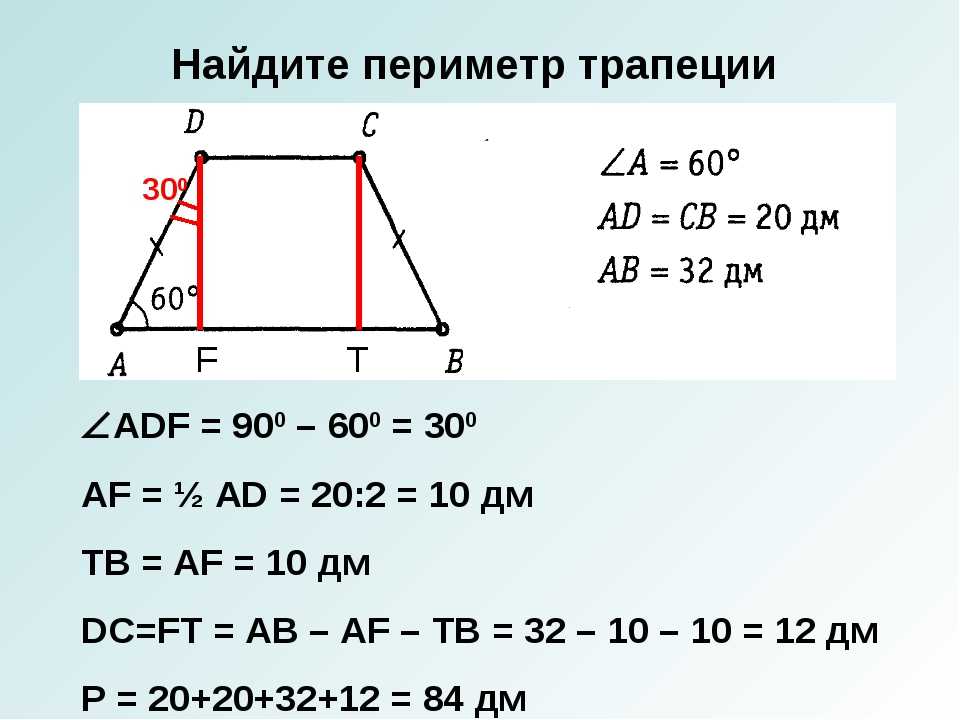 Найдите длину ее средней линии.

Вычисление

Делим периметр на 4 и получаем среднюю линию трапеции: 30/4=7,5.

Ответ: 7,5.

Задача 4

Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 37, найдите радиус окружности.

Решение. Периметр трапеции равен:  АD+DC+CB+AB=PABCD       (1)

В трапецию можно вписать окружность, если суммы длин противоположных сторон равны. То есть, имеем: AD+CB=DC+AB   (2)

С учетом (2) равенство (1) можно записать в виде:  2(АD+CB)=PABCD       (3)

Теперь давайте посмотрим на вот такой рисунок:

Видно, что сторона AD=2R, где R – радиус окружности.

Тогда, AD+CB=2R+37, тогда равенство (3): 2(2R+37)=100.

Решаем уравнение, относительно R:

4R+74=100

4R=100-74

4R=26

R=26/4

R= 6,5

Ответ: 6,5

Задача 5

Из сборника ЕГЭ по математике профильный уровень 2020 год вариант 19 задание 6.
Около окружности описана трапеция, периметр которой равен 28. Найдите длину ее средней линии.
Решение: пользуясь лайфхаком, который мы вывели выше, вычисляем длину средней линии трепеции: делим периметр трапеции на 4.
Получаем 28:4=7
Ответ: 7.

 

( 3 оценки, среднее 5 из 5 )

Поделиться с друзьями

Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции

Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции

Навигация по странице: Определение прямоугольной трапеции Признаки прямоугольной трапеции Основные свойства прямоугольной трапеции Стороны прямоугольной трапеции Средняя линия прямоугольной трапеции

Определение.

Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.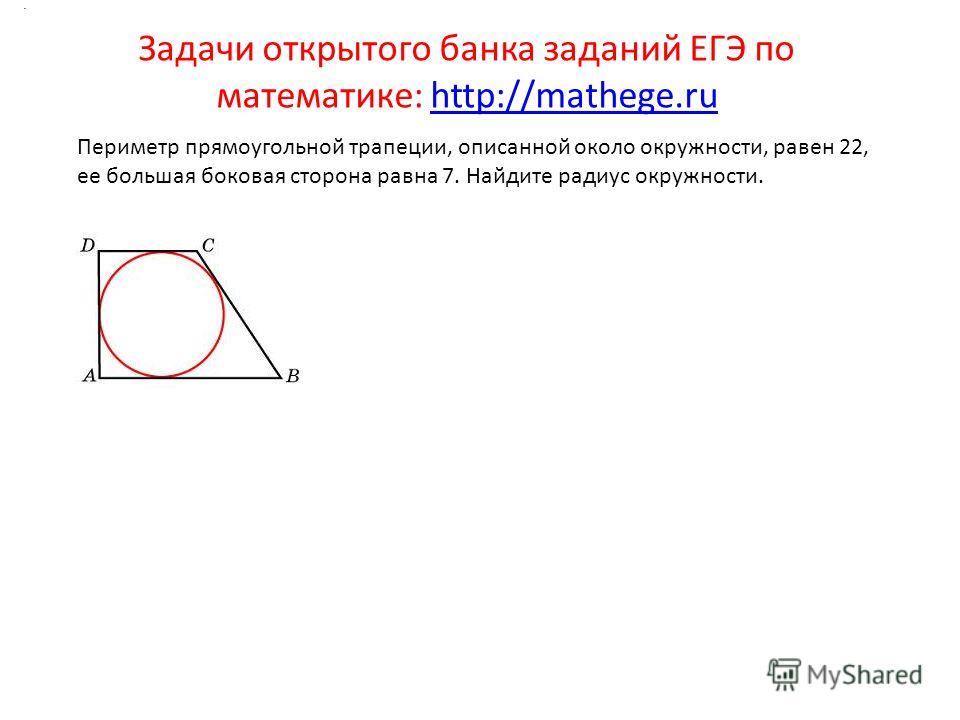

Рис.1

Признаки прямоугольной трапеции

Трапеция будет прямоугольной если выполняется одно из этих условий:

1. В тапеции есть два смежных прямых угла:

∠BAD = 90° и ∠ABC = 90°

2. Одна боковая сторона перпендикулярна основам:

AB ┴ BC, AB ┴ AD


Основные свойства прямоугольной трапеции

1. В трапеции есть два смежных прямых угла:

∠BAD = ∠ABC = 90°

2. Одна боковая сторона перпендикулярна основам:

AB ┴ BC ┴ AD

3. Высота равна меньшей боковой стороне:

h = AB


Стороны прямоугольной трапеции

Формулы длин сторон прямоугольной трапеции:

1. Формулы длины оснований через стороны и угол при нижнем основании:

a = b + d cos α = b + c ctg α = b + √d 2 — c2

b = a — d cos α = a — c ctg α = a — √d 2 — c2

2. Формулы длины оснований через стороны, диагонали и угол между ними:

a = d1d2 · sin γ — b = d1d2 · sin δ — b
cc
b = d1d2 · sin γ — a = d1d2 · sin δ — a
cc

3. Формулы длины оснований трапеции через площадь и другие стороны:

a = 2S — b      b = 2S — a
cc

4. Формула боковой стороны через другие стороны и угол при нижнем основании:

c = √d 2 — (a — b)2 = (a — b) tg α = d sin α

5. Формулы боковой стороны через основы, диагонали и угол между ними:

c = d1d2 · sin γ = d1d2 · sin δ
a + ba + b

6. Формулы боковой стороны через площадь, основы и угол при нижнем основании:

c = S = 2S
ma + b
d = S = 2S
m sin α(a + b) sin α

7. Формула боковой стороны через другие стороны, высоту и угол при нижнем основании:

d = a — b = c = h = √c2 + (a — b)2
cos αsin αsin α


Средняя линия прямоугольной трапеции

Формулы длины средней линии прямоугольной трапеции:

1. Формулы средней линии через основание, высоту (она же равна стороне c ) и угол α при нижнем основании:

m =  a — h ·ctg α = b + h ·ctg α
22

2.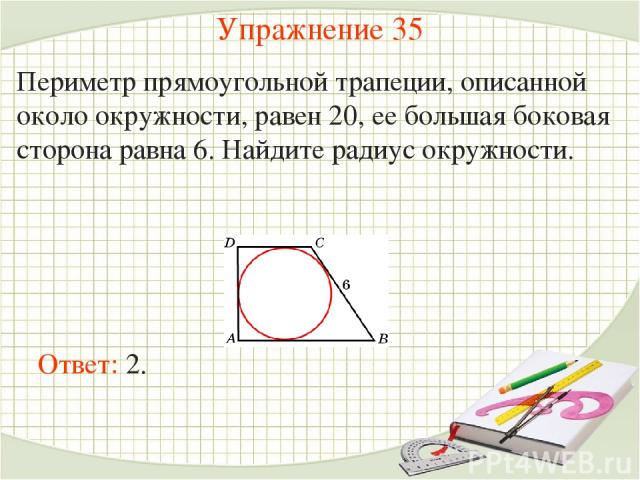 Формулы средней линии через основания и боковые стороны сторону:

m = a —√d 2 — c2 = b +√d 2 — c2
22


Все таблицы и формулы

Трапезионный калькулятор

, созданный Luis Hoyos

Последнее обновление: 21 июля, 2022

СОДЕРЖАНИЕ:
  • Трапезионный периметр и углы
  • Как рассчитать трапецию
  • Как найти высоту трапезоида

к калькулятору трапеций, инструменту, с помощью которого вы сможете:

  • Рассчитать площадь трапеции ;
  • Найти трапецию высотой ;
  • Рассчитать трапецию периметр ; и
  • Рассчитать трапецию углов .

Читайте дальше, если хотите узнать, как найти высоту, площадь или периметр трапеции с помощью формул.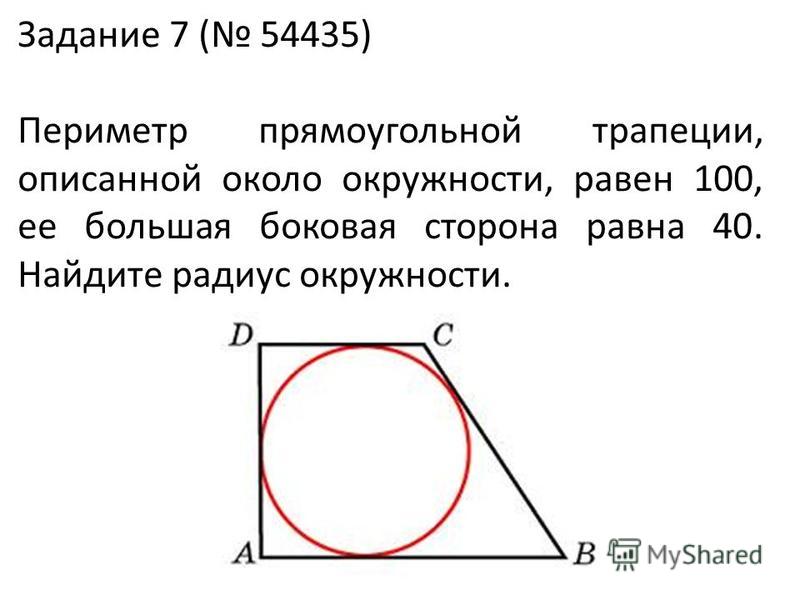

Периметр трапеции и углы

Периметр

Периметр многоугольника, правильного или неправильного, равен сумме длин его сторон , и трапеции не являются исключением. Следовательно, периметров трапеции — это сумма четырех ее сторон :

P = a + b + c + d

Углы

Как и в любом другом четырехугольнике, сумма углов в трапеции равна 360 градусам (или 2π радианам). Однако то, что трапеция является трапецией (т. е. имеет пару параллельных сторон), требует дополнительного свойства, согласно которому пара углов вдоль одного из катетов является дополнительными углами. Следовательно, их сумма должна равняться 180 градусам (или π радианам), что в обозначениях по цифре калькулятора переводится как:

α + 𝛾 = β + δ = 180°

Как вычислить площадь трапеции

Трапеция похожа на прямоугольник, который немного «упал». Поэтому вычисляем его площадь аналогично площади прямоугольника.

Для расчета площади трапеции используйте следующую формулу:

A = h × (a + b)/2

где:

  • A 9 площадь трапеции;
  • h — Высота трапеции; и
  • а
    и б — Трапециевидные основания.

Вы можете посмотреть размеры на следующем изображении:

Например, чтобы рассчитать площадь трапеции, основания которой a = 6 в и b = высота h = 4 дюйма :

A = 4 in × (6 in + 5 in)/2
A = 4 in × (11 in)/2
A = 4 in × 5.5 in
A = 22 в 2

Если формула кажется вам запутанной, вы можете выполнить следующие шаги, чтобы получить результат:

  1. Суммируйте основания трапеции. В этом случае: a + b
    = 6 дюймов + 5 дюймов = 11 дюймов
  2. Разделите предыдущий результат на два. В этом случае: (11 дюймов)/2 = 5,5 дюйма
  3. Умножить предыдущий результат на высоту. В данном случае: 4 дюйма × 5,5 дюйма = 22 дюйма

Но что, если вы не знаете h ? Посмотрим, как найти высоту трапеции.

Как найти высоту трапеции

Уравнение для нахождения высоты основано на тригонометрических функциях. Формула:

h = c × sin(α) = d × sin(δ)

Как видите, для расчета высоты нужно знать:

  • Сторона c и угол α ; или
  • Сторона d и угол δ .

Острая трапеция

Тупоугольная трапеция

Например, чтобы вычислить высоту треугольника с c = 5 в и α = 22 degrees :

h = 5 in × sin(22°)
h = = 5 in × 0. 3746
h = = 1,873 в

Вы можете узнать больше о тригонометрических функциях с помощью нашего калькулятора тригонометрических функций.

Луис Ойос

Видео по геометрии

Введение в основы геометрии: точки, линии, сегменты, плоскости, углы и многоугольники

Точки, линия и плоскости
Определить и назвать точку, линию, луч, сегмент и угол
Определить, является ли измерение одномерным, двухмерным или трехмерным

Постулат линейки и постулат сложения сегментов
Определить длину в сантиметрах, миллиметрах и дюймы
Середина сегмента и биссектриса сегмента
Основы углов
Назовите и классифицируйте типы углов
Анимация:  Типы углов
Анимация:  Измерение углов с помощью транспортира
Взаимосвязи углов и типы треугольников
Определение меры недостающих углов по фигуре
Назовите типы треугольников и определите недостающий внутренний угол
Введение в многоугольники
Классификация многоугольников
Внутренние и внешние углы многоугольника
Свойства многоугольников и четырехугольников
Введение в подобия
Подобные треугольники и Многоугольники
Конгруэнтные и подобные треугольники
Определение отношений сторон, периметров и площадей подобных многоугольников
Подобные многоугольники: поиск недостающей площади по отношению периметров
Подобные многоугольники: найти недостающий периметр по отношению площадей
Масштабный коэффициент, подобные треугольники и пропорции
Начертить аналогичный многоугольник, используя масштабный коэффициент 3
Теорема Пифагора
Теорема Пифагора и обращение к теореме Пифагора
Используя Пифагор для определения длины гипотенузы
Решение приложений с помощью теоремы Пифагора (только c)
Анимация: сумма внутренних углов треугольника
Пример 2B. Нахождение меры внутреннего угла треугольника
Пример: Найдите внутренние углы треугольника из выражений для углов
Дополнительный, дополнительный и вертикальный углы
Определите дополнение и дополнение заданного угла
Определите меру вертикальных углов и углов из фигуры
Пример: Напишите Выражения для дополнительных углов и дополнительных углов (основной)
Пример: Напишите выражения и определите меру дополнительных углов
Пример: Напишите выражения и определите меру дополнительных углов
Биссектриса угла
Упражнения на биссектрису и середину — пример 1
Упражнения на биссектрису и середину — пример 2
Пример: середина отрезка
Пример: нахождение конца отрезка по средней и одной конечной точкам

Введение в доказательство

Индуктивное рассуждение
Введение в дедуктивное рассуждение
Введение в доказательство с использованием свойств равенства
Введение в доказательство с использованием свойств сравнения

Параллельные и перпендикулярные прямые

Параллельные и перпендикулярные прямые и плоскости
Постулат о параллельных линиях
Постулат о перпендикулярных линиях
Углы и сечения
Свойства параллельных прямых
Доказательство: чередующиеся внутренние углы равны
Доказательство: последовательные внутренние углы являются дополнительными плоскостями
Доказательства: параллельные плоскости Формирование параллельных линий
Доказательство: Две линии, параллельные третьей, являются параллельными
Пример 1: Свойства параллельной линии
Пример 2: Свойства параллельной линии
Доказательство: включающая две пары параллельных линий

Параллельные линии, вырезанные по поперечным

Соответствующее угол Конверс
Доказательство: альтернативные внутренние углы Конверсии
Доказательство: альтернативные внешние углы.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *