Как найти площадь треугольника ABC?
Как найти площадь треугольника ABC?
Площадь треугольника через вписанную окружность и стороны. S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности. Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом: S = r * p, где p — полупериметр.
Как найти площадь прямоугольника в 4 классе?
Для вычисления площади прямоугольника нужно умножить его длину на ширину. Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Как найти площадь и периметр прямоугольника 4 класс?
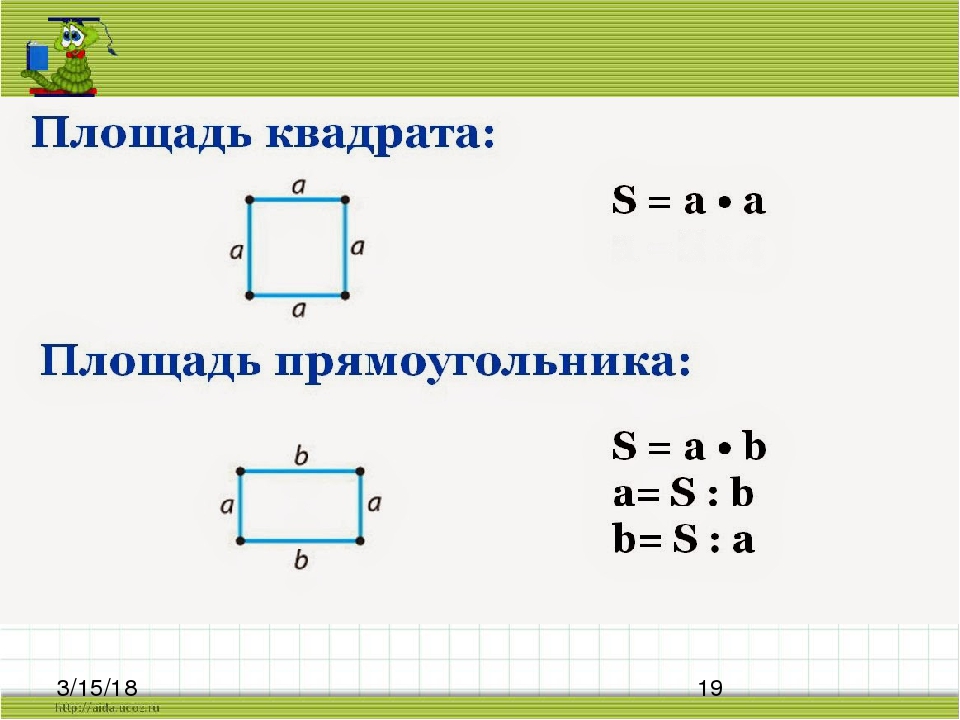
Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = ( + b) · 2, где P — периметр, — длина, b — ширина прямоугольника.
Что такое площадь фигуры в математике?
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Как найти формулу площади квадрата?
Формулы площади квадрата
- Формула площади квадрата по длине стороны Площадь квадрата равна квадрату длины его стороны. S = a2
- Формула площади квадрата по длине диагонали Площадь квадрата равна половине квадрата длины его диагонали. S = d2 где S — площадь квадрата, a — длина стороны квадрата, d — длина диагонали квадрата.
Как найти площадь квадрата в 3 классе?
Площадь квадрата равна квадрату его стороны. Периметр квадрата равен сумме его четырех сторон.
Как найти площадь квадрата в третьем классе?
Теоретический материал для самостоятельного изучения
- Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см.
 Площадь этой геометрической фигуры составляет 18 квадратов. …
Площадь этой геометрической фигуры составляет 18 квадратов. … - Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2 …
- S = a ∙ b. S – площадь
Как найти периметр квадрата 3 класс?
Формула для вычисления периметра квадрата: P = 4s, где s – длина стороны квадрата. Определите длину одной стороны квадрата и умножьте ее на 4, чтобы найти периметр. Чтобы определить длину стороны, измерьте ее линейкой или посмотрите ее значение в учебнике (задаче).
Что такое S в математике 3 класс?
В вычислениях обозначается латинской буквой S. Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Как найти площадь и периметр треугольника 3 класс?
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности. Если известны две стороны и угол между ними, вычислить периметр треугольника можно так: P = √ b2 + с2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.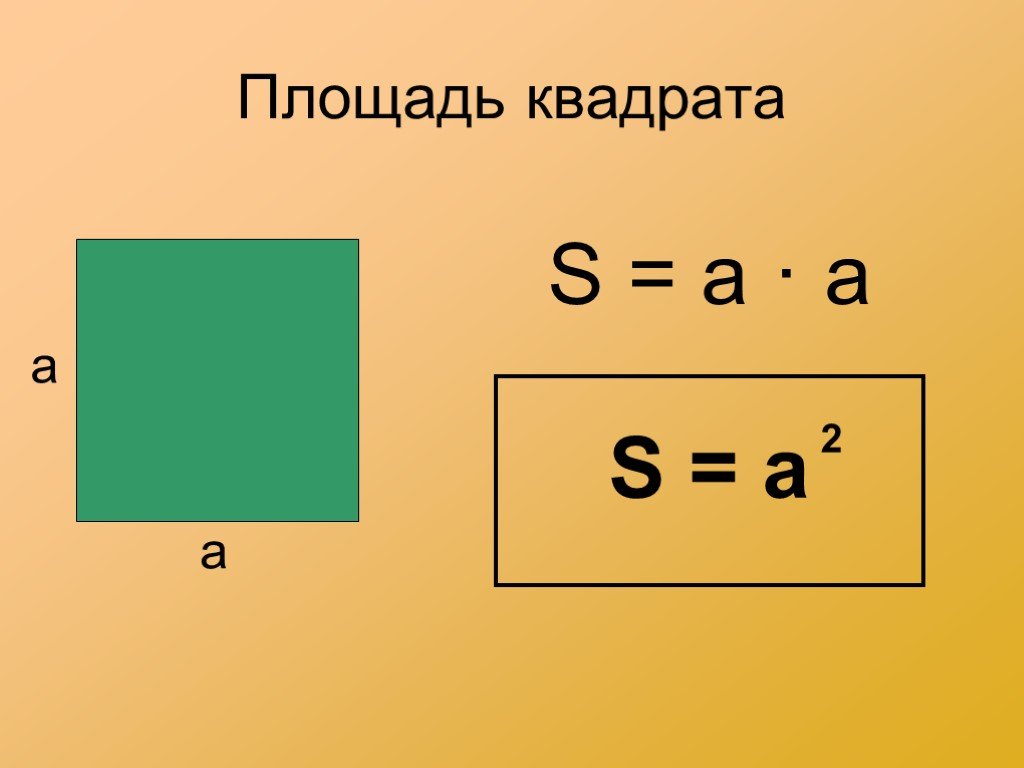
Что такое Что такое периметр треугольника?
Треугольник это многоугольник с тремя сторонами. Стороны треугольника обозначаются малыми буквами, соответствующими обозначению противоположных вершин. Периметр треугольника равен сумме длин его сторон: 1.
Как вычислить площадь и периметр треугольника?
P = a + b + c, где P — это периметр треугольника, a, b и c — его стороны.
Как найти площадь и периметр ромба?
Формулы :
- Площадь Ромба = a * h.
- Площадь Ромба = ½ * d1 * d2
- Площадь Ромба = a² * SinA.
- Периметр Ромба = 4(a)
Как найти площадь по периметру?
Данные необходимые для того чтобы найти периметр
- Площадь = длина стороны во второй степени. …
- Длина стороны = корень квадратный от площади
- Так длина стороны при площади 4 квадратных метров, будет 2 метра, а при 16 квадратных метров 4 метра.

- Периметр = длина квадрата умноженная на 4.
Что такое Полупериметр треугольника?
Центр Шпикера является центром тяжести сторон треугольника. Прямая, проходящая через центр вписанной окружности треугольника делит периметр пополам в том и только в том случае, когда она делит пополам площадь. Полупериметр треугольника равен периметру его медианного треугольника.
Площадь квадрата
Для полной функциональности сайта желательно включить JavaScript в настройках Вашего браузера.
Главная
→
Геометрия
→
Площадь квадрата
Площадь квадрата – это численная характеристика, характеризующая размер плоскости, ограниченной четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами равен 90 градусов.
Для вычисления площади квадрата применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь или проверить уже выполненные вычисления.
Таблица с формулами площади квадрата (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
1
Площадь квадрата через его сторону
… подготовка …
a — сторона
2
Площадь квадрата через его диагональ
… подготовка …
d — диагональ
3
Площадь квадрата через периметр
… подготовка …
P — периметр
4
Площадь квадрата через отрезок проведенный из вершины квадрата к середине противоположной стороны
. .. подготовка …
.. подготовка …
k — отрезок
5
Площадь квадрата через радиус вписанной окружности
… подготовка …r — радиус вписанной окружности
6
Площадь квадрата через радиус описанной окружности
… подготовка …
R — радиус описанной окружности
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади квадрата
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| 1 | сторона | ||
| 2 | диагональ | ||
| 3 | периметр | ||
| 4 | отрезок проведенный из вершины квадрата к середине противоположной стороны | ||
| 5 | радиус вписанной окружности | ||
| 6 | радиус описанной окружности |
Определения
Квадрат – это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами равен 90 градусов.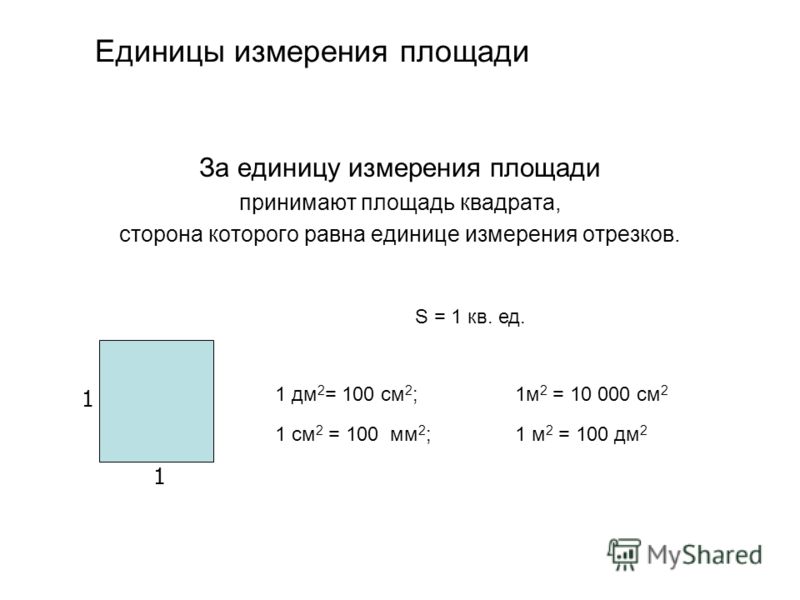
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км 2, м2, см2, мм2 и т.д.
Объяснение урока: Площади прямоугольников и квадратов
В этом объяснении мы научимся находить площади прямоугольников и квадратов, используя формулу с дробями и десятичными знаками, и решать реальные задачи.
Определение: площадь, длина, ширина, единица площади
- Площадь – это количество квадратных единиц, необходимых для покрытия поверхности.
- Длина прямоугольника равна длине его наибольшей стороны, а ширина равна длина его наименьшей стороны.
- Единичный квадрат — это квадрат, сторона которого равна 1 единице длины. Площадь блока квадрат равен 1 квадратной единице.
Мы измеряем площадь в квадратных единицах; в зависимости от единицы, используемой для измерения длины, эти
могут быть квадратные сантиметры, квадратные дюймы, квадратные мили или что-то еще. Мы уже знаем, что площадь
прямоугольника можно найти, подсчитав, сколько единичных квадратов составляют фигуру.
Мы уже знаем, что площадь
прямоугольника можно найти, подсчитав, сколько единичных квадратов составляют фигуру.
Например, если у нас есть прямоугольник, длина которого 3 единицы, а ширина 2 единицы, то есть 2 группы по 3 квадратных единицы или 3 группы по 2 квадратных единицы.
Следовательно, мы умножаем длину на ширину, чтобы найти площадь, 𝐴=2×3=6.squareunits
Площадь прямоугольника
Площадь 𝐴 прямоугольника равна его длине 𝑙 умножить на его ширину 𝑤.
Формула площади: 𝐴=𝑙𝑤.
Иногда вместо длины и ширины размеры называют основанием и высотой. Итак, если прямоугольник имеет высоту ℎ и длину основания 𝑏, тогда его площадь 𝐴=𝑏ℎ.
Помните, что площадь измеряется в квадратных единицах.
Например, площадь этого прямоугольника 4×3=12 квадратных единиц.
Пример 1. Нахождение площади прямоугольника
Найдите площадь прямоугольника 𝐴𝐵𝐶𝐷.
Ответ
Используйте формулу площади прямоугольника: площадьпрямоугольникадлинаширинасмсмсм=×=8×6=48.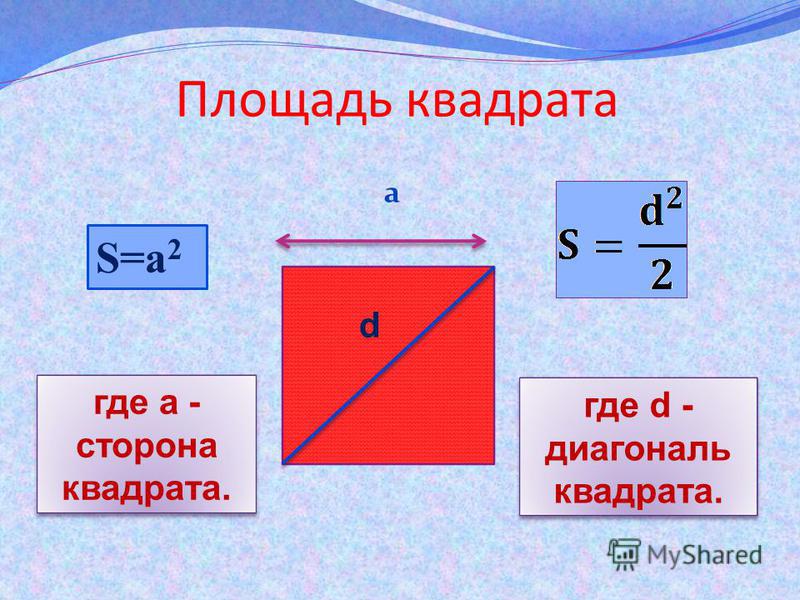
Зная площадь прямоугольника, мы можем легко вывести формулу площади прямоугольника. площадь. Поскольку квадрат также является прямоугольником, его площадь равна 𝐴=𝑙𝑤 где длина равна ширине; поэтому для квадрата 𝐴=𝑙×𝑙.
Следовательно, мы можем вычислить площадь квадрата, используя только длину одной из сторон.
Площадь квадрата
Площадь 𝐴 квадрата равна квадрату длины 𝑙 одной из его сторон.
Формула площади: 𝐴=𝑙.
Помните, что площадь измеряется в квадратных единицах.
Например, площадь этого квадрата 4×4=4=16 квадратных единиц.
Пример 2. Нахождение площади квадрата
Найдите площадь квадрата.
Ответ
Используйте формулу площади квадрата: площадьквадратасторонадлинасторонадлинасмсмсм=×=5×5=25.
Закончим рассмотрением еще двух примеров.
Пример 3. Решение текстовых задач с использованием формулы площади прямоугольников
Размер детских футбольных полей зависит от возрастной группы игроков. Использовать
таблица для определения разницы между площадью футбольного поля для детей до 14 лет
по сравнению с полем для детей до 12 лет.
Использовать
таблица для определения разницы между площадью футбольного поля для детей до 14 лет
по сравнению с полем для детей до 12 лет.
| возрастная группа | до 10S | до 12S | до 14S |
|---|---|---|---|
| Длина поля). | 50 |
Ответ
Мы можем начать с наброска того, что мы знаем. Из таблицы видно, что до 12 лет играют на прямоугольном поле размером 80 на 50 ярдов, а юноши до 14 лет играют на прямоугольное поле размером 100 м на 60 м.
Сначала мы посчитаем площадь каждого поля, используя площадь прямоугольника равно длине, умноженной на ширину. Отметим также, что, поскольку длины указаны в ярды (ярд), единицей измерения площади будет квадратных ярдовyd.
Площадь поля для детей до 12 лет составляет 80×50=4000,ярдов
Площадь поля для детей до 14 лет составляет 100×60=6000,ярдов
Затем мы вычисляем разницу в площадях как 6000− 4000=2000 ярдов
Пример 4.
 Решение текстовых задач с использованием формулы площади прямоугольников и квадратов
Решение текстовых задач с использованием формулы площади прямоугольников и квадратовПрямоугольный ковер размером 4 м по 3 м помещается в квадратную комнату длиной 9 м. какая площадь пола не покрыта ковром?
Ответ
Шаг 1 : Найдите площадь прямоугольного ковра: площадьпрямоугольникадлинаширинаm=×=4×3=12.Шаг 2 : Найдите площадь квадратного пола: площадь квадрата×9=81.
Шаг 3 : Найдите площадь непокрытого пола.
Вычесть площадь прямоугольного ковра из площади квадратного пола: непокрытая область = 81−12 = 69.
Площадь прямоугольников и квадратов
Главная > Математика > Геометрия > Разделы по геометрии > Площадь прямоугольников и квадратов
Посмотрите на диаграмму ниже. Сколько квадратов внутри?
Если вы посчитаете все квадраты, то увидите, что их 48.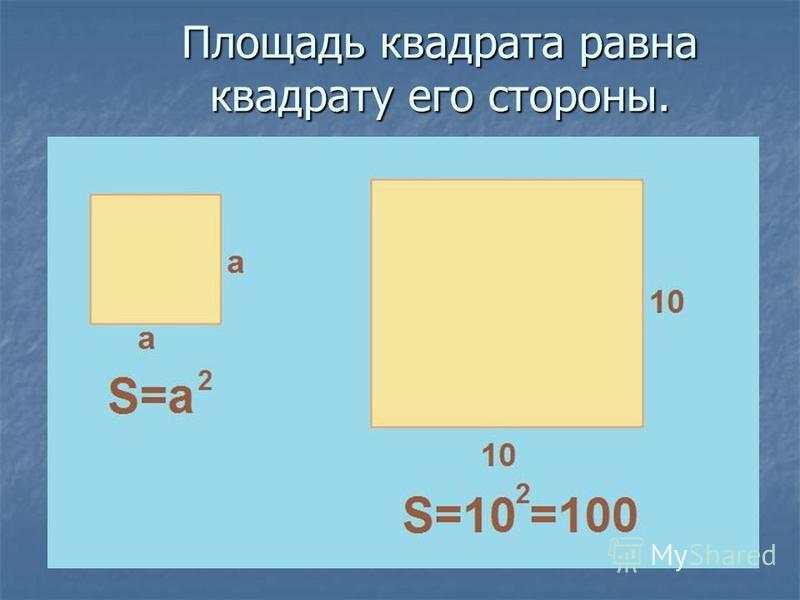 Это означает, что площадь 9 квадратов0123 прямоугольник или пространство, покрывающее прямоугольник, составляет 48 квадратных единиц.
Это означает, что площадь 9 квадратов0123 прямоугольник или пространство, покрывающее прямоугольник, составляет 48 квадратных единиц.
Однако подсчет квадратов не очень эффективный способ определения площади. Существует лучший способ.
А = лв
А = 8 шт. x 6 шт.
A = 48 квадратных единиц или 48 единиц.
Поскольку стороны равны, когда мы умножаем длину и ширину, мы получаем число, умноженное на само себя, или число в квадрате.
Итак, для квадратов мы можем упростить формулу и
использовать A = s 2 .
A = S 2
A = (8 единиц) 2
A = 64 единицы 2
. длина 4 и ширина 9 единиц.
Решение: A = lw
A = (4 единицы)(9 единиц)
A = 36 единиц 2
2.) Определить площадь прямоугольника
Решение: A = lw
A = (3 дюйма) (18 дюймов)
A = 54 дюйма 2
3.
Решение: Поскольку нам дана площадь, действуйте в обратном порядке путем деления.
A = lw
30 см 2 = (6 см)w
30 см 2 ÷ 6 см = w
5 см = w
4) Найдите площадь квадрата. длина стороны 10 см.
A = s 2
A = (10 см) 2
A = 100 см 2
5) Определить площадь показанной фигуры.
A = S 2
A = (7 мм) 2
A = 49 мм 2
6.) Площадь квадрата 144 в 2 . Какова длина каждой стороны?
Решение: Поскольку нам дана площадь, действуйте в обратном порядке, извлекая квадратный корень.
a = S 2
144 в 2 = S 2
√144 в 2 = √s 2
9000 12 12 in = S 2 9000 3 9000 12 12 in = S 2 9000 3 12 in = S 2 9000 31.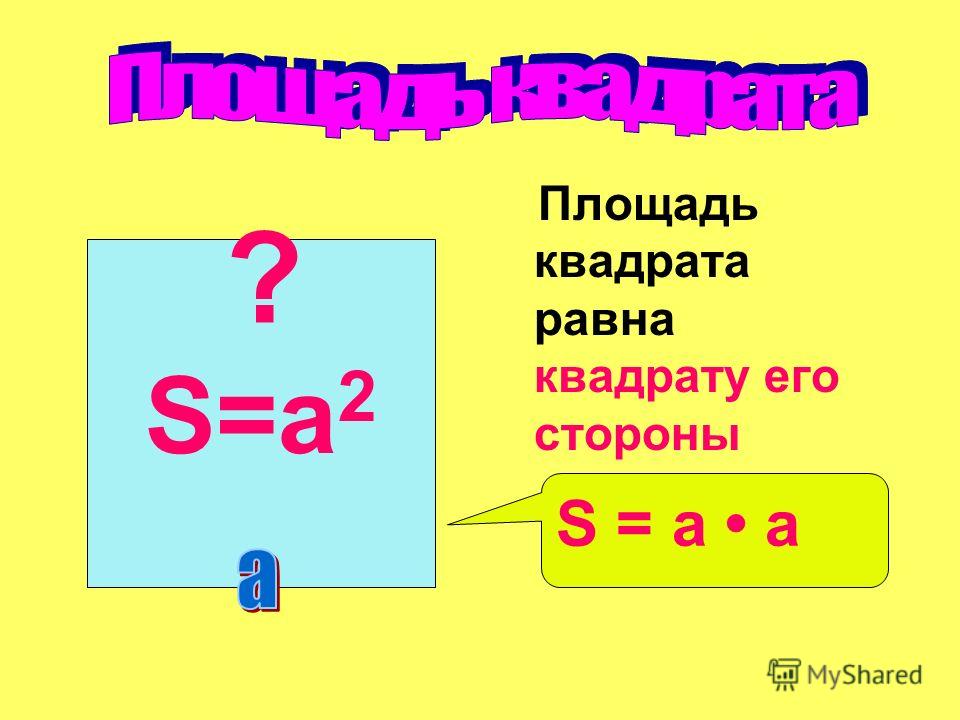

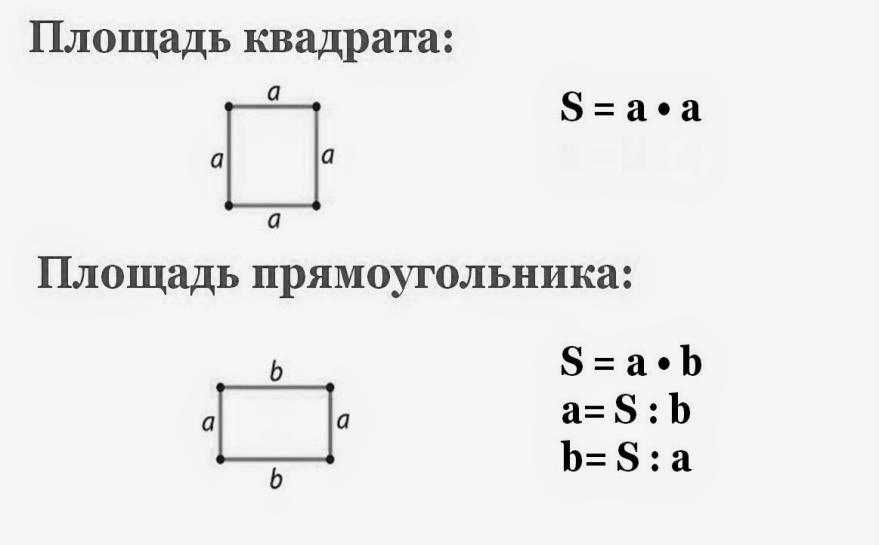 Площадь этой геометрической фигуры составляет 18 квадратов. …
Площадь этой геометрической фигуры составляет 18 квадратов. …