Как найти разложение вектора по векторам: Разложение вектора по векторам

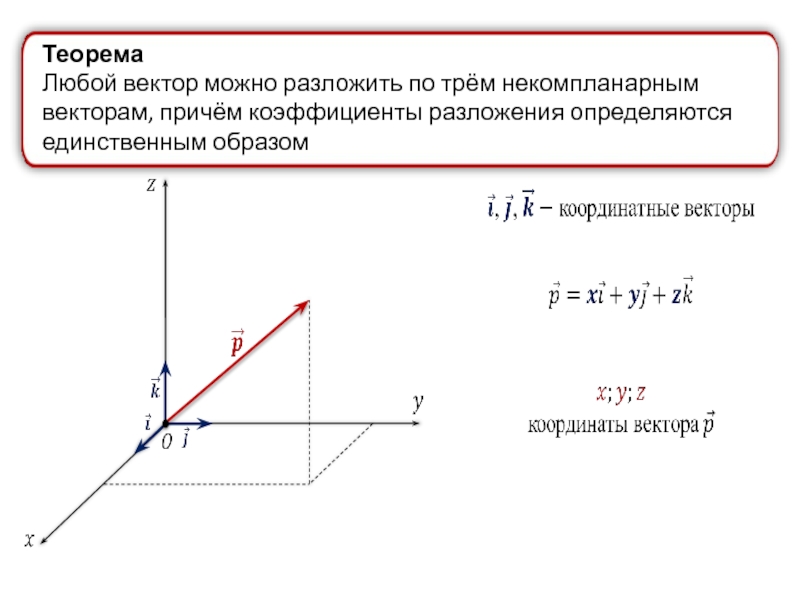
Разложение вектора по базису. Контрольные онлайн



Образовательные онлайн сервисы: теория и практика

• Главная
• Примеры
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
• Видео-уроки
  • Математический анализ
  • Векторная алгебра и Аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование. Методы оптимизации
• Готовые работы
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
  • Другое
• Контакты

Полезные материалы:

• Учебники
• Справочники
• Онлайн калькуляторы

• Помощь в решении
• Онлайн занятия в Zoom

Разложение вектора по базису

Задача 1. Написать разложение вектора x по векторам


Задача 2. В стандартном базисе пространства  даны векторы
, , ,  и
Требуется:
а) убедиться, что векторы  образуют базис пространства ;
б) найти разложение вектора  по этому базису;
в) найти угол между векторами  и .
Решение
а) Векторы  образуют базис пространства , если
их линейная комбинация  равна нулю, только при .

Уравнению  соответствует система  уравнений  

Эта однородная система имеет только нулевое (тривиальное) решение , если её определитель не равен нулю, то есть
Вычислим определитель, разложив его по элементам второй строки
.
Следовательно, заданные векторы  образуют базис пространства .
б) Найдем координаты вектора  в базисе  из векторного уравнения .
Этому векторному уравнению соответствует система
.
Решив систему, находим .
Следовательно, разложение вектора  по базису :
.
в) Если скалярное произведение в  определено аналогично тому, как это было в , то
.

   Следовательно, , то есть векторы  и  ортогональны.



Задать вопрос
Заказать помощь

Отзывы

+7-911-7987704

vk.com/id286009794

Написать в Whatsapp

Написать в Viber

@matem96

Skype: matem96.ru



Разложение вектора по базису — онлайн калькулятор

• Справочник
• Онлайн-калькуляторы
• Тесты с ответами

В основе нашего сервиса лежит теорема о разложении вектора по базису. По ней любой вектор векторного пространства раскладывается по его базису. Способ разложения всегда только 1. Вы получаете точный ответ сразу после ввода данных.

Разложить вектор по базису онлайн потребуется студентам, ученикам школ старших классов. Вы сможете свериться с самостоятельно полученным ответом и увидеть пошаговые вычисления.

1. Укажите размерность вектора. Для изменения размерности используйте кнопки «+», «-».
   
2. Введите значения базисных векторов в соответствующие поля.  
   
3. Введите значение вектора, который нужно разложить по базису. Отправьте задание на вычисление кнопкой «Рассчитать».
   
4. Для решения задачи записывается векторное уравнение, находится определитель матрицы. Определитель матрицы не равен 0, поэтому система векторов является базисом. Смотрите подробное решение после нажатия кнопки.
   
5. Решим уравнение методом Гаусса
   
6. Подставляем полученное значение в уравнение и вычисляем ответ.
   

Материалы, которые помогут вам лучше разобраться в теме:

• Векторы на плоскости и в пространстве — основные определения
• Координаты вектора в декартовой системе координат (ДСК)
• Нахождение длины вектора, примеры и решения
• Нахождение координат вектора через координаты точек

Ответ:

Решение

Ответ:

• list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

• Длина вектора. Модуль вектора
• Векторное произведение векторов
• Умножение вектора на число
• Угол между векторами
• Смешанное произведение векторов
• Сложение и вычитание двух векторов
• Скалярное произведение векторов
• Определение вектора по двум точкам
• Проверить являются ли вектора базисом
• Ортогональность векторов
• Компланарность векторов
• Коллинеарность векторов
• Проекция вектора на вектор
• Площадь треугольника, построенного на векторах
• Площадь параллелограмма, построенного на векторах

Как быстро разложить вектор по базису

Вам не придется искать нужные формулы и высчитывать результаты промежуточных действий. Разложение вектора по базису происходит автоматически. Zaochnik дает возможность учащимся осуществлять подготовку к занятиям по сложным темам, быстрее осваивать новый и непонятный материал. Сервисом пользуются, потому что:

• Услуга предоставляется бесплатно. Не всегда есть возможность нанимать репетитора. Теперь повышать свой уровень образования можно без дополнительных трат.
• Не нужна регистрация. Ничто не мешает получить ответ максимально быстро. А это так важно учащимся во время урока, семинара, зачета.
• Количество вводимых примеров не ограничивается. Наша команда разработала сервис, чтобы учащимся было легче справляться с заданиями. Калькулятор позволяет осуществлять самопроверку столько раз, сколько необходимо. 
• Широкий охват тем. Мы максимально учли запросы по вычислениям и создали программы по решению задач для школ и университетов.

Если у вас возникли вопросы по использованию калькулятора, напишите консультанту. Он оперативно ответит на ваш вопрос, связанный с разложением вектора по базису онлайн, или предложит помощь опытного преподавателя по выгодной цене.

Понравился калькулятор? Поделись с друзьями!

Разделы калькуляторов

• Процент
• Решение матриц
• Точка, прямая, плоскость
• Конвертеры
• Объем фигур
• Калькуляторы площади фигур
• Решение уравнений
• Операции над векторами
• Периметр фигур

Поможем с любой работой

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Решение задач
• Отчеты по практике

Все наши услуги

Узнай бесплатно стоимость работы

Не получается написать работу самому?

Доверь это кандидату наук!

Глава 5 Векторная геометрия: углы, проекция и разложение

В этой главе вы познакомитесь с некоторыми дополнительными идеями геометрии векторов. Опять же, хотя иллюстрация этих концепций ограничена двумерным пространством, все эти идеи могут быть расширены до n -мерностей.

5.1 Угол между векторами

Может оказаться весьма полезным определить угол между двумя векторами. Например, каков угол между вектором а и б где,

\[ \mathbf{a} = \begin{bmatrix} 2\3 \end{bmatrix} \quad \mathrm{and} \quad \mathbf{b}= \begin{bmatrix} -4\1 \end{bmatrix} \]

На рис. 5.1 показаны оба вектора, отображаемые в одной и той же двумерной базовой системе координат.

Рисунок 5.1: График, показывающий два вектора a (красный) и b (синий) в пространстве измерений R1–R2. Угол между ними обозначается как \(\theta\). Для удобства мы расположили хвосты обоих векторов в начале координат.

Угол между этими векторами обозначается как \(\theta\) и может быть найден с помощью следующего:

\[ \cos (\ theta) = \frac{\mathbf{a}\bullet\mathbf{b}}{\lvert\lvert\mathbf{a}\rvert\rvert\times\lvert\lvert\mathbf{b}\rvert \rверт} \]

То есть косинус угла между двумя векторами равен скалярному произведению векторов, деленному на произведение их длин. Чтобы найти угол (\(\theta\)), мы можем вычислить арккосинус этого отношения. В нашем примере 9{\circ}\). Ниже приведен синтаксис R для вычисления этого угла.

 # Создание векторов
a = матрица (данные = c (2, 3), ncol = 1)
b = матрица (данные = c (-4, 1), ncol = 1)
# Вычисление скалярного произведения между a и b
a_dot_b = сумма (а * б)
# Вычисление длин векторов
l_a = sqrt (сумма (а * а))
l_b = sqrt (сумма (b * b))
# Вычислить тета (в радианах)
acos(a_dot_b / (l_a * l_b)) 

 [1] 1.91382 

 # Вычислить тета (в градусах)
acos(a_dot_b / (l_a * l_b)) * 180 / pi 

 [1] 109,6538 

Манипулирование формулой для вычисления угла между двумя векторами дает общую формулу для определения скалярного произведения между двумя векторами.

\[ \начать{разделить} \ cos (\ theta) & = \ frac {\ mathbf {a} \ bullet \ mathbf {b}} {\ lvert \ lvert \ mathbf {a} \ rvert \ rvert \ times \ lvert \ lvert \ mathbf {b} \ rvert\rvert} \\[2ex] \mathbf{a}\bullet\mathbf{b} &= \lvert\lvert\mathbf{a}\rvert\rvert\times\lvert\lvert\mathbf{b}\rvert\rvert \cos(\theta) \конец{разделить} \] То есть скалярное произведение между векторами a и b равно произведению их модулей и косинуса угла между ними.

5.1.1 Ортогональные векторы 9\circ\) угол равен 0, если

a и b ортогональны, то

\[ 0 = \ frac {\ mathbf {a} \ bullet \ mathbf {b}} {\ lvert \ lvert \ mathbf {a} \ rvert \ rvert \ times \ lvert \ lvert \ mathbf {b} \ rvert \ rvert} \]

Например, рассмотрим следующие два элементарных вектора

\[ \mathbf{e}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \qquad \mathbf{e}_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \]

Скалярное произведение между этими двумя векторами равно 0, что означает, что косинус угла между ними также должен быть равен 0, указывая на то, что \(\mathbf{e}_1\) и \(\mathbf{e}_2 \) ортогональны. 9\circ\) угол равен 1, если a и b коллинеарны, то

\[ 1 = \ frac {\ mathbf {a} \ bullet \ mathbf {b}} {\ lvert \ lvert \ mathbf {a} \ rvert \ rvert \ times \ lvert \ lvert \ mathbf {b} \ rvert \ rvert} \]

Например, рассмотрим следующие два вектора

\[ \mathbf{a} = \begin{bmatrix} 2 \\ 1 \end{bmatrix} \qquad \mathbf{b} = \begin{bmatrix} 6 \\ 3 \end{bmatrix} \]

\[ \начать{разделить} \frac{\mathbf{a}\bullet\mathbf{b}}{\lvert\lvert\mathbf{a}\rvert\rvert\times\lvert\lvert\mathbf{b}\rvert\rvert} &= \frac {14}{\sqrt{5}\times\sqrt{45}} \\[2ex] &= \frac{14}{\sqrt{225}} \\[2ex] &= \frac{14}{14} \\[2ex] &= 1 \конец{разделить} \]

Это означает, что a и b лежат на одной прямой. Два вектора коллинеарны, если один можно представить в виде линейной комбинации другого. В нашем примере

\[ \mathbf{b} = 3\mathbf{а} \] Геометрически коллинеарные векторы параллельны друг другу (помните, что расположение в опорном пространстве удобно).

5.2 Ортогональная проекция

Ортогональная проекция вектора a на вектор b получается путем опускания перпендикулярной линии от конечной точки до до пересечения с x2.

Рисунок 5.2: Ортогональная проекция вектора a (красно-красный) на вектор b (черный). Обратите внимание, что проекция создает угол 90 градусов с вектором b . Результатом проекции является вектор p (синий).

Результатом является вектор p , который коллинеарен вектору b , но имеет другую длину. Чтобы вычислить длину p , мы используем тот факт, что проекция создает прямоугольный треугольник с гипотенузой a и смежный отрезок p до угла \(\theta\). Затем

\[ \начать{разделить} \cos(\theta) &= \frac{\lvert\lvert\mathbf{p}\rvert\rvert}{\lvert\lvert\mathbf{a}\rvert\rvert} \\[2em] \lvert\lvert\mathbf{p}\rvert\rvert &= \lvert\lvert\mathbf{a}\rvert\rvert \times \cos(\theta) \конец{разделить} \]

Поскольку \(\theta\) — это угол между a и b ,

\[ \начать{разделить} \lvert\lvert\mathbf{p}\rvert\rvert &= \lvert\lvert\mathbf{a}\rvert\rvert \times \cos(\theta) \\[2em] &= \lvert\lvert\mathbf{a}\rvert\rvert\times\frac{\mathbf{a}\bullet\mathbf{b}}{\lvert\lvert\mathbf{a}\rvert\rvert\times\ lvert\lvert\mathbf{b}\rvert\rvert}\\[2em] & = \ гидроразрыва {\ mathbf {a} \ пуля \ mathbf {b}} {\ lvert \ lvert \ mathbf {b} \ rvert \ rvert} \конец{разделить} \]

То есть величина проекции p представляет собой отношение скалярного произведения векторов a и b к величине b . Рассмотрим следующие два вектора:

\[ \mathbf{a} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} \qquad \mathbf{b} = \begin{bmatrix} 2 \\ -1 \end{bmatrix} \]

Проецирование a на b , геометрически,

Рисунок 5. 3: Ортогональная проекция вектора a (выделены красным) на вектор b (синий). Результатом проекции является вектор p (черный цвет).

Мы можем найти величину p , используя нашу формулу:

\[ \начать{разделить} \lvert\lvert\mathbf{p}\rvert\rvert &= \frac{\mathbf{a}\bullet\mathbf{b}}{\lvert\lvert\mathbf{b}\rvert\rvert} \\[2ex ] &= \frac{1}{\sqrt{5}} \\[2ex] &= 0,447 \конец{разделить} \]

 # Создание векторов
а = с (2, 3)
б = с (2, -1)
# Вычисление скалярного произведения a и b
a_dot_b = сумма (а * б)
# Вычислить длину b
l_b = sqrt (сумма (b * b))
# Вычислить длину p
l_p = a_dot_b / l_b
л_п 

 [1] 0,4472136 

В дальнейшем будем обозначать проекцию вектора a на вектор b как:

\[ \mathbf{p}_{\mathbf{a}\perp\mathbf{b}} \]

5.3 Ортогональное разложение

Ортогональное проецирование вектора приводит к геометрическому разложению вектора на две аддитивные компоненты. На рис. 5.4 показано разложение вектора a на две аддитивные компоненты, \(\mathbf{p}_1\) и \(\mathbf{p}_2\). то есть

\[ \mathbf{a} = \mathbf{p}_1 + \mathbf{p}_2 \]

Рисунок 5.4: Две ортогональные проекции вектора a (киноварь). Первая ортогональная проекция — это вектор a на вектор b (горизонтальный черный), а вторая ортогональная проекция — вектор a на вектор o (вертикальный черный). Результатом проекций являются векторы \(\mathbf{p}_1\) (синяя горизонталь) и \(\mathbf{p}_2\) (синяя вертикаль).

Вектор \(\mathbf{p}_1\) является той же ортогональной проекцией из предыдущего примера, а именно \(\mathbf{p}_{\mathbf{a}\perp\mathbf{b}}\). Вектор \(\mathbf{p}_1\) является второй проекцией a на вектор o (\(\mathbf{p} _{\mathbf{a}\perp\mathbf{o}} \)). Вектор o по определению ортогонален вектору b .

Длины двух выступов соответствуют длинам сторон прямоугольного треугольника, где гипотенуза равна и . А именно ⁴ ,

\[ \начать{разделить} \ lvert \ lvert \ mathbf {p} _ {\ mathbf {a} \ perp \ mathbf {b}} \ rvert \ rvert & = \ lvert \ lvert \ mathbf {a} \ rvert \ rvert \ times \ cos (\ theta ) \\[2em] \ lvert \ lvert \ mathbf {p} _ {\ mathbf {a} \ perp \ mathbf {o}} \ rvert \ rvert & = \ lvert \ lvert \ mathbf {a} \ rvert \ rvert \ times \ sin (\ theta ) \конец{разделить} \]

В качестве примера мы можем разложить на Используя два наших предыдущих примера векторов:

\[ \mathbf{a} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} \qquad \mathbf{b} = \begin{bmatrix} 2 \\ -1 \end{bmatrix} \] 9\circ) \\[2em] &= 3,58 \конец{разделить} \]

 # Вычислить длину
l_a = sqrt (сумма (а * а))
# Вычислить тета (в радианах)
тета = acos (a_dot_b / (l_a * l_b))
theta 

 [1] 1.446441 

 # Вычисление длины проекции a на o
l_p2 = l_a * грех (тета)
l_p2 

 [1] 3,577709 

Мы можем использовать теорему Пифагора, чтобы проверить вычисление длин двух проекций. Так как квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его сторон, то 92

 [1] TRUE 

Окончательная система показана на рис. 5.5.

Рисунок 5.5: Ортогональная проекция вектора a (красный) на вектор b (синий). Результатом проекции является вектор \(\mathbf{p}_1\) (черный). Второй проекцией является вектор \(\mathbf{p}_2\) (черный) на вектор o , который ортогонален b .

---

4. Существуют и другие способы вычисления длины \(\mathbf{p}_{\mathbf{a}\perp\mathbf{o}}\). Например, с o ортогонален b , угол между o и a равен \(\phi=90-\theta\). Тогда \(\lvert\lvert\mathbf{p}_{\mathbf{a}\perp\mathbf{o}}\rvert\rvert=\lvert\lvert\mathbf{a}\rvert\rvert \times \cos( \фи)\).↩︎

Векторная композиция и разложение | Каналы для Pearson+

Патрик Форд

Было ли это полезно?

Привет, ребята. Итак, до сих пор мы могли использовать векторную математику для многих наших векторов без использования сеток или квадратов, поэтому мы могли разбить это на треугольник. Мы можем посчитать коробки, чтобы вычислить ножки, например, три и четыре и тому подобное. К сожалению, многих векторов, которые мы увидим, не будет на диаграммах, где нет сетки или квадрата. И нам придется заняться векторной математикой без их использования. Итак, в этом видео я покажу вам, что на самом деле нам нужны четыре уравнения, чтобы описать все, что нам нужно знать о векторе. Эти четыре уравнения составляют математические уравнения треугольника. Они называются уравнениями векторной композиции и декомпозиции. Давайте проверим это. Итак, ребята, есть три вещи, которые нам нужны для описания вектора. Когда у нас есть сетка, которой нет, вы знаете, когда у нас есть ах, диаграмма не имеет сетки квадратов. Таким образом, у векторов есть величина длины этой стрелки прямо здесь. Векторы также имеют направление, и без сетки мы указываем это направление с помощью угла относительно оси X, называемого тета X. И последнее, что векторы также являются треугольниками, что означает, что у них есть стороны. Эти ноги просто получили причудливое имя. Они называются компонентами. В общем, вот этот вектор, этот треугольник можно разбить на части. Эти ножки просто называются компонентами. Итак, я упомянул, что есть четыре уравнения, и на самом деле они просто разбиваются на две разные ситуации, называемые векторной композицией и декомпозицией. И действительно, разница в том, что вам дано и что вы пытаетесь найти. Векторная композиция — это когда вам даны одномерные компоненты или стороны треугольника, и вы пытаетесь выяснить, какая величина и направление отличается от декомпозиции новостей с большим банком, что противоположно. Это наше, когда тебе уже заданы величина и направление, и теперь ты пытаешься выяснить, каковы стороны вектора. Ребята, давайте проверим это более подробно, когда мы делали векторную композицию, это точно так же, как мы делали, когда добавляли перпендикулярные векторы, такие как три и четыре. Поэтому, когда мы добавили три и четыре, мы просто объединили их. Бен, у нас был результирующий или кратчайший путь от начала до конца, чтобы вычислить этот вектор, который я назову здесь. Мы просто используем теорию Пифагора, потому что получился треугольник. Таким образом, три и четыре, новость о большом банке просто возводится в квадрат три в квадрате на четыре в квадрате, и это m. Итак, вот эти компоненты, эти ноги три и четыре, просто получили причудливое название. Они называются компонентами. И так моя тройка это моя бывшая составляющая. Это то, какая часть этого вектора не является. Буква А находится на оси X, а вот эти четыре — в компонентах «Почему моя жена?». Это то, какая часть вектора лежит в направлении Y. И они объединились, чтобы сформировать вектор величины. А. Итак, я пошел в этом направлении. Это что-то вроде Зиффа. Я прошел три, а потом четыре в этом направлении. Единственное, о чем мы еще не говорили, это то, что этот вектор указывает на некоторое направление, называемое тета X. И способ, которым мы вычисляем эти данные X здесь, — это просто использование другого набора математических уравнений треугольника, называемого Саката. Итак, в основном, чтобы вычислить этот угол здесь, все, что мне нужно использовать, это просто новое уравнение, которое ваши учебники и ваши профессора выведут. Данные X — это арктангенс или арктангенс моих белых компонентов по моим бывшим компонентам. Итак, в этом примере у моей жены компонентов для X три. Это означает, что моя тета X здесь будет просто арктангенсом. Так что вы можете найти это в своих калькуляторах, и это будет 4/3. И эта тета X составляет всего 53 градуса. Убедитесь, что ваш калькулятор находится в режиме градусов. И на самом деле это просто угол, который выше положительной оси X. Так что это угол, который идет вот так. Ладно, ребята, на этом все. Вот только эти два уравнения, и это когда у вас есть стороны треугольника, и вы пытаетесь вычислить величину и направление. Другое дело — векторное разложение. Это в основном обратный процесс. Итак, здесь у меня есть величина угла. Теперь я хочу выяснить ноги, поэтому мы хотим выяснить, что такое мой бывший, и я хочу выяснить, каковы мои компоненты A Y. И действительно, все сводится к этим двум уравнениям, которые мы пришли из Китона. Итак, теперь мы хотим разложить a на его компоненты a X и A y. Так вот в чем дело. Пока этот фатальный угол X обращен к ближайшей оси x, мы будем использовать здесь эти уравнения. Мой бывший будет умножен на косинус угла. Таким образом, это величина, умноженная на знак угла, умноженная на CO, а A Y будет умноженной на знак угла. Так, например, если бы мне дали такой угол, как вот эти данные, это данные, которые относятся к направлению Y. Это плохо. Я не могу использовать это. Ну, я не буду использовать это в своих уравнениях. Это этот угол закончился. С другой стороны, Data X хорош. Так что это то, что я включаю в свои уравнения. Так, например, через X будет величина, умноженная на косинус. Итак, величина равна пяти. Косинус угла равен 53 градусам, поэтому я возьму три. И затем, если вы подставите y, вы получите звездную величину, которая в пять раз превышает, извините, не береговую линию знака 53. А если вы подставите это, вы получите четыре. Обратите внимание, что мы в основном только что придумали те же числа три и четыре, что и здесь. И это не должно быть сюрпризом, потому что мы в основном только что образовали точно такой же треугольник, как и здесь. Просто мы начали с катетов треугольника вот здесь, а здесь мы начали с величины и направления. Так что неудивительно, что мы получили одинаковые цифры. Ладно, ребята, на этом все. Вы просто будете использовать эти уравнения, основываясь на том, что вы пытаетесь найти, и на том, что вам дано. Итак, давайте продолжим и попрактикуемся в каждом из следующих действий. Вы нарисуете вектор, а затем найдёте недостающие переменные. Итак, мои бывшие съели мои A и шесть, пытаясь определить величину и направление, так что мне дали компоненты. Итак, позвольте мне просто нарисовать вот этот маленький вектор. У меня есть стороны треугольника, так что я знаю, что это восьмерки, а это шесть. Это мой бывший. Это мой Ай. И теперь я на самом деле пытаюсь найти величину и направление. Это значит, что я буду использовать свои векторные уравнения композиции. Так что, чтобы вычислить мою А, мне просто нужно использовать теорему Пифагора. Я просто использую восемь в квадрате плюс шесть в квадрате. И если я это сделаю, я получу 10. Так что это моя величина. А теперь про угол. Помните углы, нарисованные относительно оси X? Это мой тха X, и вот этот фатальный X будет арктангенсом, арктангенсом моих белых компонентов, который на шесть больше моего бывшего компонента, который равен восьми. И если вы продолжите и проработаете это, вы должны получить 37 градусов. Вот мой угол теперь 37 градусов. Хорошо, давайте перейдем к части B, которая теперь у меня есть угол, или теперь у меня есть величина 13 и у меня есть угол 67,4, и теперь я хочу вычислить компоненты. Итак, давайте нарисуем этот вектор здесь. Это не компонент. На самом деле это просто вектор. Так что я просто нарисую это вот так.