Как найти разность прогрессии арифметической: Арифметическая прогрессия — Умскул Учебник

Как найти разность прогрессии формула?

Как найти разность прогрессии формула?

Соответственно, чтобы найти разность арифметической прогрессии, отнимем от последнего члена первый и разделим на количество членов прогрессии за вычетом одного.

Что значит найти разность арифметической прогрессии?

Арифметическая прогрессия – это числовая последовательность, каждый член которой равен сумме предыдущего числа и определенного фиксированного числа. … Другими словами, разность (шаг) арифметической прогрессии – разность между последующим и предыдущим членом.

Чему равна разность прогрессии?

Арифметическая прогрессия – это последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и некоторого фиксированного числа, называемого разностью арифметической прогрессии.

Что такое Q в арифметической прогрессии?

Геометрическая прогрессия Последовательность чисел {an} называется геометрической прогрессией, если отношение последующего члена к предыдущему равно одному и тому же постоянному числу q, называемому знаменателем геометрической прогрессии. Таким образом, an+1an=q или an+1=qan для всех членов геометрической прогрессии.

Чему равна сумма бесконечно убывающей геометрической прогрессии?

Сумма бесконечно убывающей геометрической прогрессии равна первому члену этой прогрессии, деленному на разность между единицей и знаменателем этой прогрессии. Полученная формула используется для вывода правил обращения чистых и смешанных периодических десятичных дробей в обыкновенные дроби.

Чему равен D в арифметической прогрессии?

Определение арифметической прогрессии an+1= an + d, где d — это разность арифметической прогрессии. Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.

Как решать алгебраические прогрессии?

Формулы арифметической прогрессии:

1. an = a1 + d(n — 1) — формула n-го члена арифметической прогрессии;
2. 2an = an-1 + an+1 — характеристическое свойство арифметической прогрессии для трех последовательных чисел;
3. an = ak + d(n — k) — формула нахождения n-го члена арифметической прогрессии через k -ый член прогрессии;

Как найти n ый член арифметической прогрессии?

a n = a 1 + d ( n − 1 ) , где n — порядковый номер члена прогрессии, a 1 — первый член прогрессии, d — разность. Это равенство называется общей формулой арифметической прогрессии.

Как найти количество чисел в арифметической прогрессии?

Сумма всех членов арифметической прогрессии равна половине произведения суммы её крайних членов на количество всех её членов. где S — это сумма всех членов, a1 — первый член прогрессии, an — последний член, а n — количество членов в данной прогрессии. = 165.

Как составить формулу n го члена последовательности?

Получим новую формулу: an = 3 + 2n. Это тоже формула n—го члена арифметической прогрессии! Только не общая, а для конкретной прогрессии.

Как найти формулу N го числа последовательности?

an = a1 + d(n – 1). Это формула n—го члена арифметической прогрессии.

Какие последовательности являются расходящимися?

Числовая последовательность {xn} называется расходящейся, если она не имеет конечного предела, т. е. если она либо имеет бесконечный предел, либо у нее вообще нет предела. В частности всякая неограниченная числовая последовательность расходится.

Какая последовательность называется монотонной?

Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств.

Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Определение арифметической прогрессии.
Формула n-го члена арифметической
прогрессии
Цель:
1.Научиться определять арифметическую прогрессию
2.Научиться находить члены , разность , порядковые
номера членов арифметической прогрессии
3.Вывести формулу n-го члена арифметической

прогрессии
4.Познакомиться с характеристическим свойством
арифметической прогрессии .
Повторение. Устные упражнения.
1.
1. Что называется числовой последовательностью?
2. Каким способом можно задать последовательность?
3. Какие члены последовательности (bn) расположены
между: а)
b638 и b645 ,
в) bn-6 и bn–2 ?
б)
bn+2 и bn+5,
4. Последовательность задана формулой
Найдите:
а 5,
5. Дано: с1 = — 20,
а10, аk .
сn+1 = сn + 10.
Найдите : с₂, с₃,с₄.
аn = 4n – 1.
2.
Продолжить
последовательности :
а) 2; 4; 6; 8; …
б) — 3; — 5; — 7; — 9; …
в) — 2; — 4; — 8; — 16; …
г) 1; 2; 3; 4; …
д) 2; 5; 8; 11; …
Какие последовательности образованы с
помощью одного и того же правила?
3. Определение:
Числовая последовательность, каждый член
которой, начиная со второго, равен
предыдущему, сложенному с одним и тем же
числом, называется арифметической
прогрессией.
аn + 1 = аn + d, d – некоторое число.
Для нахождения d , получим формулу
d = аn + 1 – аn — разность арифметической
прогрессии
4. Устно решить упражнения:
1.Назовите первые пять членов
арифметической прогрессии:
а) а₁ = 5,d = 3
1 вариант
Ответ: а₁=5, а₂= 8, а₃ = 11, а₄=14, а₅=17.
б) а₁ = 5,d = — 3
2 вариант
Ответ: а₁=5, а₂= 2, а₃ =-1 , а₄=-4, а₅=-7.
в) а₁ = 5,d = 0
3 вариант
Ответ: а₁=5, а₂= 5, а₃ = 5, а₄=5, а₅=5.
5. Дано: (аn)- арифметическая прогрессия.
1 вариант:
Ответ: d = 2
а) а₁ = 4, а₂= 6.
Найти: d
2 вариант:
Ответ: d = -2
б) а₃ = 7, а₄= 5.
Найти: d
3 вариант:
в) а₇ = 10, а₈ = -2. Найти: d
Ответ: d = -12
6. Вывод формулы n-го члена арифметической
прогрессии
Дано: (аn) – арифметическая прогрессия,
a1- первый член прогрессии, d – разность.
• a2 = a 1 + d
• a3 = a2 + d =(a1 + d) + d = a1+2d
• a4 = a3 + d =(a1+2d) +d = a1+3d
• a5 = a4 + d =(a1+3d) +d = a1+4d
. . .
• an = a1+ (n-1)d
Записать в тетрадь формулу: an = a1+ d (n-1)

9. Тест Задание №1

• 1.Арифметичекая прогрессия – это числовая
последовательность, в которой каждый член
начиная со второго, равен предыдущему
• Выберите правильный ответ
• а) сложенному с одним и тем же числом
• б) умноженному на одно и то же число
• в) разделенному на одно и то же число
• г) возведенному в квадрат

10. Задание №2

• 2. Что бы найти разность арифметической
прогрессии , надо:
• Выберите правильный ответ
• а) из первого члена вычесть второй
• б) второй член разделить на первый
• в) первый член умножить на второй
• г) из последующего члена вычесть
предыдущий

11.

Задание № 3; 4• 3. Укажите формулу n – го члена арифметической
прогрессии:
• а) an = a1 ∙ d (n-1)
• б) an = a1+ d (n-1)
• в) an = a1: d (n-1)
• г) an = d + a1 (n-1)
• 4.Какая из последовательностей чисел является
арифметической прогрессией
• а) 1; -1; 1; -1; 1; -1;…
• б) -1; 3; 7; 11; 15; 19;…
• в) -1; -3; -9; -27; — 81; — 243…
• г) -1; 3; — 7; 11; — 15; 19;…

12. Задание № 5; 6; 7

• 5. Первый член арифметической прогрессии
а₁; а₂; 4; 8;…
равен
а) 1
б) 12
в) -4
г) -1
• 6. Найдите разность арифметической
прогрессии , если а₃ = 4, а₄ = 8
а) -4
б) 0,5
в) 6
г) 4
• 7. Найдите четвертый член арифметической
прогрессии , если
а₁ = 10; d = — 0,1
а) 97
б) 9,7 в) -97
г) – 9,7

13. Задание № 8; 9; 10

• 8. Третий член арифметической прогрессии
равен 6, а пятый равен 10. Найдите первый
член этой прогрессии.
а) 1
б) -1
в) 2
г) 0
• 9. Число -15,8 является членом
арифметической прогрессии:
8,2; 6,6 … . Его порядковый номер
а) 16
б) 17
в) 13
г) 14
• 10. Найдите bк ,если (bn ) арифметическая
прогрессия 4; bк; 9 …
а) 5,5
б) 7,5 в) 8.5
г) 6.5
Проверка теста:
правильный ответ -1 балл.
1. а
2. г
3. б
4. б
5. в
6. г
7. б
8. в
9. а
10. г
Домашнее задание:
п.31
№576, №578
Спасибо за урок

English     Русский Правила

Как найти общую разность арифметической прогрессии 5, 9, 13, 17,….?

Последняя обновленная дата: 07 -й февраля 2023

•

Всего просмотров: 219,3K

•

Просмотр сегодня: 6.10K

Ответ

Проверено

219,3K+ виды

HINT: . тема последовательности и серии. В этом вопросе мы сначала узнаем, как найти общую разность любой арифметической прогрессии. После этого найдем общую разность арифметической прогрессии, которая задана в вопросе.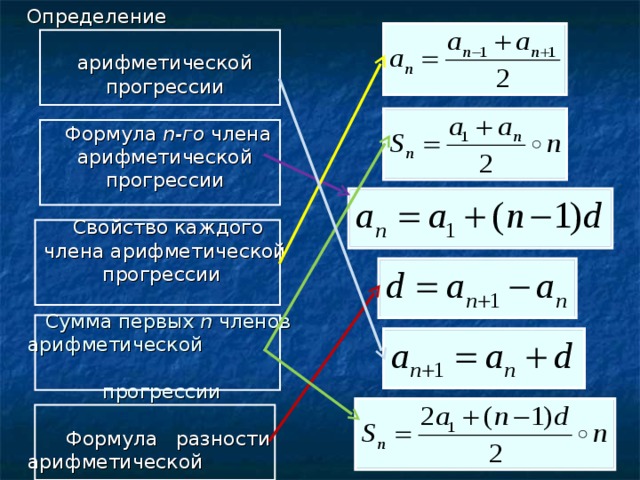 После этого мы увидим еще один способ решения этого вопроса. 9{th}}\] член последовательности, \[a\] — первый член, \[d\] — общая разность, а \[n\] — общее количество членов.
Для нахождения общих различий воспользуемся этой формулой.
В данной последовательности последний или четвертый член равен 17, а первый член равен 5, а общее количество членов равно 4, поэтому, используя приведенную выше формулу, мы можем написать
\[17=5+\left( 4-1 \right) d\]
\[\Rightarrow 17-5=\left( 3 \right)d\]
\[\Rightarrow 12=3d\]
\[\Rightarrow d=4\]
Итак, мы получили, что общий разность данной последовательности равна 4. 9{th}}\] член арифметической прогрессии, a — первый член арифметической прогрессии, d — общая разность арифметической прогрессии, n — общее количество членов и \[{{S}_{n}}\] — сумма n слагаемых.
Мы можем решить этот вопрос другим способом.
Итак, давайте сначала выясним разницу между последовательными числами.
Найдем разницу между 5 и 9.
9-5=4
Найдем разницу между 9 и 13.
13-9=4
Найдем разницу между 13 и 17.
17-13=4
Итак, мы получили, что разница между последовательными числами одинакова. И мы знаем, что разница между последовательными числами равна 4.
Следовательно, мы нашли общую разность арифметической последовательности 5, 9, 13, 17,….
Общая разница равна 4.

Недавно обновлено Страницы

Если пружина имеет период T и разрезана на n равных 11 класс физики CBSE

Планета движется вокруг Солнца по почти круговой орбите 11 класс физики CBSE

В любом треугольнике AB2 BC4 CA3 и D является серединой математического класса 11 JEE_Main

В треугольнике ABC 2asin dfracAB+C2 равно IIT Отборочный класс 11 математики JEE_Main

Если в aDelta ABCangle A 45circ угол C 60circ тогда класс 11 maths JEE_Main

Если в треугольнике rmABC сторона a sqrt 3 + 1rmcm и угол класс 11 maths JEE_Main

Если пружина имеет период T и разрезана на n равный класс 11 физика CBSE

Планета движется вокруг солнца на почти круговой орбите 11 класс физики CBSE

В любом треугольнике AB2 BC4 CA3 и D является серединой математического класса 11 JEE_Main

В треугольнике ABC 2asin dfracAB+C2 равно IIT Отборочный класс 11 математики JEE_Main

Если в aDelta ABCangle A 45circ угол C 60circ тогда класс 11 Математика JEE_MAIN

Если в треугольнической стороне RMABC A SQRT 3 + 1RMCM и CONGE CLASS 11 MATHS JEE_MAIN

Трендовые сомнения. геометрические последовательности на уроках математики. В этой статье мы обсудим арифметические последовательности. Мы также будем реализовывать программы для выполнения различных операций над арифметической последовательностью в Python.

Что такое арифметическая последовательность?

Арифметическая последовательность — это последовательность чисел, в которой любые два последовательных числа имеют фиксированную разность. Эта разница также известна как общая разница между членами арифметической последовательности.

Например, 3,5,7,9,11,13,… — это арифметическая последовательность с общей разностью 2 между последовательными элементами.

N-й член арифметической последовательности

Если нам дан первый член A ₁ и общая разность D, мы можем записать второй член как A 1 +D , третий член как A 1 +2D , четвертый член как A 1 +3D и так далее. N-й член будет записан как A 1 +(N-1)D Чтобы найти N-й член арифметической последовательности в python, мы можем просто добавить общую разность (N-1) раз к первым терминам A ₁ с помощью цикла for следующим образом.

 общая разница = 2
print("Общая разница в арифметической последовательности:", commonDifference)
первыйтермин = 3
print("Первый член арифметической последовательности:", firstTerm)
# вычисление 100-го члена
N = 100
nthTerm = первыйтермин
для i в диапазоне (1, N):
    nthTerm = nthTerm + commonDifference
print("100-й член арифметической последовательности равен:", nthTerm)
 

Выход:

 Общий Разница в арифметической последовательности: 2
Первый член арифметической последовательности: 3
100-й член арифметической последовательности: 201 

В качестве альтернативы, мы можем напрямую вычислить N-й член, используя следующие формулы.

 общая разница = 2
print("Общая разница в арифметической последовательности:", commonDifference)
первыйтермин = 3
print("Первый член арифметической последовательности:", firstTerm)
# вычисление 100-го члена
N = 100
nthTerm = firstTerm + (N - 1) * commonDifference
print("100-й член арифметической последовательности равен:", nthTerm) 

Выход:

 Общий Разница в арифметической последовательности: 2
Первый член арифметической последовательности: 3
Сотый термин в арифметической последовательности: 201 

Сумма N терминов в арифметической последовательности В Python

Чтобы найти сумму N терминов в арифметическом выражении, мы можем просто сложить каждый термин, используя цикл for.

В цикле for мы сначала найдем каждый термин, используя формулы, рассмотренные выше. После этого мы добавим каждый член, чтобы вычислить сумму N членов следующим образом.

 общая разница = 2
print("Общая разница в арифметической последовательности:", commonDifference)
первыйтермин = 3
print("Первый член арифметической последовательности:", firstTerm)
# вычисление суммы 50 слагаемых
N = 50
сумма терминов = 0
для i в диапазоне (1, N + 1):
    ithTerm = firstTerm + (i - 1) * commonDifference
    сумма терминов = сумма терминов + ithTerm
print("Сумма 50 слагаемых в арифметической последовательности:", sumOfTerms) 

Вывод:

 Общее Разница в арифметической последовательности: 2
Первый член арифметической последовательности: 3
Сумма 50 членов арифметической прогрессии: 2600 

В качестве альтернативы мы также можем вывести математическое выражение для вычисления суммы N членов арифметической прогрессии.

Мы знаем, что сумма N чисел будет равна  N * (среднее значение всех слагаемых). Здесь мы можем очень легко найти среднее значение всех условий.

Для арифметической последовательности с первым членом A ₁ и N-м членом A _N среднее значение всех членов определяется как (A 1 + A N )/2 . Как А ₁ и общая разность D будет дана в программе, найдем A N = A 1 + (N-1)*D .

Следовательно, среднее всех чисел в арифметической последовательности станет (2A 1 + (N-1)*D)/2 .

Следовательно, сумма N членов арифметической последовательности станет N*((2A 1

+ (N-1)*D)/2) .

Мы можем вычислить сумму N слагаемых в арифметическом уравнении, используя эту формулу в python, следующим образом.

 общая разница = 2
print("Общая разница в арифметической последовательности:", commonDifference)
первыйтермин = 3
print("Первый член арифметической последовательности:", firstTerm)
# вычисление суммы 50 слагаемых
N = 50
sumOfTerms = (N * (2 * firstTerm + (N - 1) * commonDifference)) // 2
print("Сумма 50 слагаемых в арифметической последовательности:", sumOfTerms) 

Вывод:

 Общее Разница в арифметической последовательности: 2
Первый член арифметической последовательности: 3
Сумма 50 членов арифметической прогрессии: 2600 

Заключение

В этой статье мы обсудили основы и формулы арифметических последовательностей.