Как найти точку максимума функции по уравнению: Как найти экстремум (точки минимума и максимума) функции

как найти по уравнению, поиск минимума

Содержание:

• Минимум и максимум функции
  • Точка минимума, минимум функции
  • Точка максимума, максимум функции
• Исследование функций на экстремумы
• Примеры задач

Содержание

• Минимум и максимум функции
  • Точка минимума, минимум функции
  • Точка максимума, максимум функции
• Исследование функций на экстремумы
• Примеры задач

Минимум и максимум функции

Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом: 

• \(y_{min}, y_{max}\) — минимум, максимум функции или экстремумы;
• \(x_{min}, x_{max}\) — точки минимума, максимума функции;
• \(y_{наиб}, y_{наим}\) — наибольшее (максимальное), наименьшее (минимальное) значение функции.

Точка минимума, минимум функции

Точка минимума — такая точка \(x_0\), если у неё существует окрестность, для всех точек которой выполняется неравенство \(f(x)\geq f(x_0)\)

Минимум функции — значение функции в точке минимума \(x_0\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.

Точка максимума, максимум функции

Точка максимума — такая точка \(x_0\), если у неё существует окрестность, для всех точек которой выполняется неравенство \(f(x)\leq f(x_0)\)

Максимум функции — значение функции в точке максимума \(x_0\)

Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.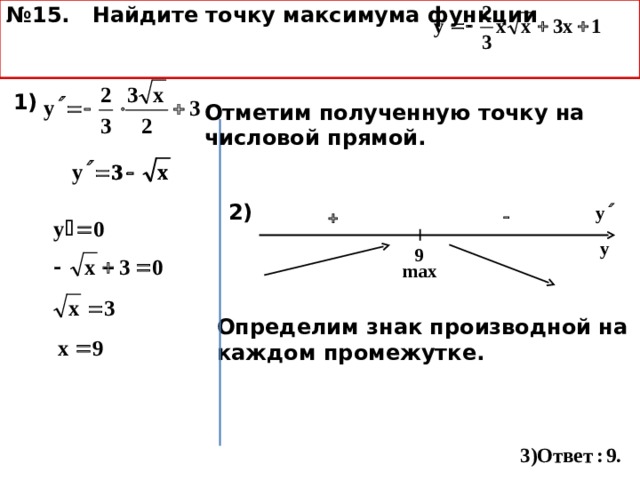

4+6x\)

3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках \((-\infty;0)\) и \((0;+\infty)\). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.

Утверждение доказано

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 3)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Нахождение точек максимума функции. Логарифмы.

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2013-04-15

   Здравствуйте, Дорогие друзья! Продолжаем рассматривать задания связанные с исследованием функций. Рекомендую повторить теорию, необходимую для решения задач на нахождение максимального (минимального) значения функции и на нахождение точек максимума (минимума) функции.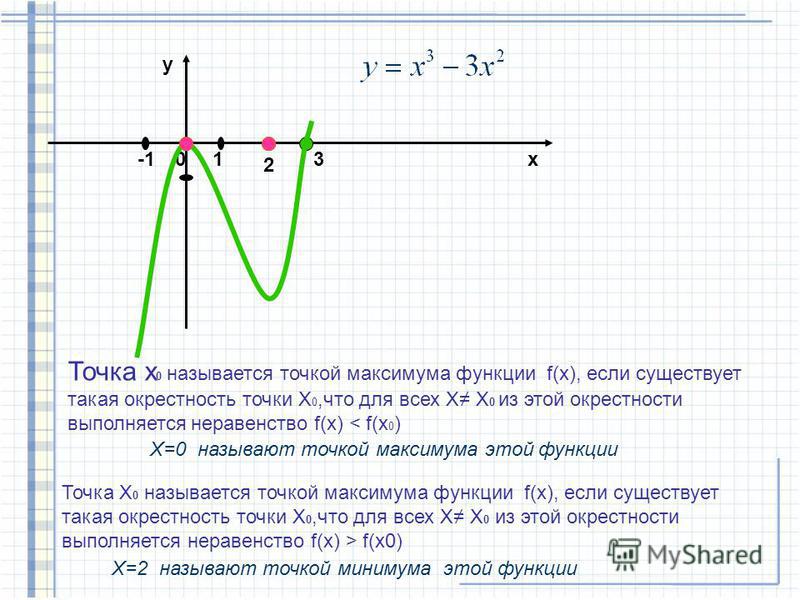

Задачи с логарифмами на нахождение наибольшего (наименьшего) значения функции мы уже рассмотрели. В этой статье рассмотрим три задачи, в которых стоит вопрос нахождения точек максимума (минимума) функций, при чём в заданной функции присутствует натуральный логарифм.  

Теоретический момент:

По определению логарифма – выражение стоящее под знаком логарифма должно быть больше нуля. *Это обязательно нужно учитывать не только в данных задачах, но и при решении уравнений и неравенств содержащих логарифм.

Алгоритм нахождения точек максимума (минимума) функции:

1. Вычисляем производную функции.

2. Приравниваем её к нулю, решаем уравнение.

3. Полученные корни отмечаем на числовой прямой. *Также на ней отмечаем точки, в которых производная не существует. Получим интервалы, на которых функция возрастает или убывает.

4. Определяем знаки производной на этих интервалах (подставляя произвольные значения из них в производную).

5. Делаем вывод.

Найдите точку максимума функции у = ln (х–11)–5х+2

Сразу  запишем, что х–11>0 (по определению логарифма), то есть х > 11.

Рассматривать функцию будем на интервале (11;∞).

Найдём производную заданной функции:

Найдем нули производной:

Точка х = 11 не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси две точки 11 и 11,2. Определим знаки производной функции, подставляя произвольные значения из интервалов (11;11,2) и (11,2;+∞) в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х=11,2 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума.

Ответ: 11,2  

Решите самостоятельно:

Найдите точку максимума функции у=ln (х+5)–2х+9.

Посмотреть решение

Найдите точку минимума функции у=4х– ln (х+5)+8

Сразу запишем, что х+5>0 (по свойству логарифма), то есть х>–5.

Рассматривать функцию будем на интервале  (– 5;+∞).

Найдём производную заданной функции:

Найдем нули производной:

Точка х = –5  не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси две точки –5 и –4,75. Определим знаки производной функции, подставляя произвольные значения из интервалов (–5;–4,75) и (–4,75;+∞) в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х= –4,75  производная функции меняет знак с отрицательного на положительный,  значит это искомая точка минимума.

Ответ: – 4,75   

Решите самостоятельно:

Найдите точку минимума функции у=2х–ln (х+3)+7.

Посмотреть решение

Найдите точку максимума функции у = х²–34х+140lnх–10

По свойству логарифма выражение, стоящее под его знаком больше нуля, то есть х > 0.

Функцию будем рассматривать на интервале (0; +∞).

Найдём производную заданной функции:

Найдем нули производной:

Решая квадратное уравнение, получим: D = 9    х₁ = 10   х₂ = 7.

Точка х = 0  не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси три точки 0, 7 и 10.

Ось ох разбивается на интервалы:  (0;7),  (7;10), (10; +∞).

Определим знаки производной функции, подставляя произвольные значения из полученных интервалов в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х = 7 производная функции меняет знак с положительного на  отрицательный,  значит это искомая точка максимума.

Ответ: 7

Решите самостоятельно:

Найдите точку максимума функции у = 2х² –13х+9lnх+8

Посмотреть решение

В данной рубрике продолжим рассматривать задачи, не пропустите!

На этом всё. Успехов вам!

С уважением, Александр Крутицких 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Функции MAX MIN | ЕГЭ-№11Производная

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Как найти максимальную прибыль (Максимизация прибыли)

Решение задач расчета > > Как найти максимальную прибыль

Как найти максимальную прибыль: Содержание:

1. Обзор максимизации
2. Максимизация прибыли (данная функция прибылей и убытков)
3. Нахождение минимальной прибыли

Для максимизировать функция означает найти свое максимальное значение в заданном диапазоне значений.

Есть два способа найти максимальную прибыль: с помощью графика или с помощью исчисления.

Графически , вы ищете глобальный максимум.

• Глобальный максимум — это максимум во всем диапазоне функции what. На графике это самый высокий пик.
• Локальные максимумы возникают в точках перегиба (где график меняет направление).
• В максимуме функции градиент или наклон функции равен нулю.

С помощью исчисления вы можете найти производную функции, чтобы найти точки, где градиент (наклон) равен нулю, но это могут быть либо максимумов, либо , либо минимумов.

• Если уклон увеличивается в точке поворота, он минимален.
• Если наклон уменьшается в точке поворота, значит, вы нашли максимум функции.

Максимизация прибыли с учетом функций прибыли и затрат

Посмотрите видео с пошаговым примером:

Найдите максимальную прибыль (функции затрат и спроса) с помощью исчисления

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Максимизация прибыли — одна из тем, которые, вероятно, будут тестироваться в разделе кратких ответов экзамена AP Calculus . Он равен выручке предприятия за вычетом затрат, понесенных при получении этой выручки . Максимизация прибыли важна, потому что предприятия управляются для получения максимально возможной прибыли. Расчет можно использовать для расчета количества произведенных единиц продукции, максимизирующего прибыль.

Найдите максимальную прибыль в исчислении: Пример бизнеса

Пример вопроса: Найдите уравнение прибыли бизнеса с функцией дохода 2000x – 10x ² и функцией затрат 2000 + 500x.

Шаг 1: Установите прибыль равной выручке за вычетом затрат. Например, уравнение выручки 2000x – 10x ² и уравнение затрат 2000 + 500x можно объединить так: прибыль = 2000x – 10x ² – (2000 + 500x) или прибыль = -10x 9. 0979 2 + 1500x – 2000.

Шаг 2: Найдите производную уравнения прибыли (вот список распространенных производных). Например, уравнение прибыли -10x ² + 1500x – 2000 становится -20x + 1500.

Шаг 3: Приравняйте уравнение к нулю :
-20x + 1500 = 0

Шаг 4: Используйте алгебру , чтобы найти, сколько единиц произведено из уравнения, которое вы написали на шаге 3.
20x = 1500
x = 75.

Шаг 5: Рассчитайте максимальная прибыль с использованием количества произведенных единиц, рассчитанного на предыдущем шаге. В этом примере подстановка x = 75 в уравнение прибыли -10x ² + 1500x – 2000 дает -10(75) ² + 1500(75) – 2000 или 54 250 прибыли.
Вот как найти максимальную прибыль в расчетах!

Совет:
Для ответа на этот тип вопросов на экзамене AP по математическому анализу обязательно запишите эту цифру, используя единицы измерения, представленные в задаче на краткий ответ. Для задач с коротким ответом на экзамене AP Calculus по максимизации прибыли этой единицей измерения почти наверняка являются доллары США или доллары США. Некоторые уравнения могут представлять более одного возможного ответа. Некоторые из этих ответов можно выбрать и отбросить, руководствуясь здравым смыслом, но чаще всего к ним нельзя относиться одинаково. В этих случаях вставьте все возможные ответы в уравнение прибыли, чтобы рассчитать их прибыль, а затем выберите ответ, который дает наибольшую прибыль как количество произведенных единиц, максимизирующее прибыль.

Как найти максимальную прибыль: пример с функцией и алгеброй

Пример задачи: найти локальное максимальное значение y = 4x ³ + 2x ² + 1.

Шаг 1: Продифференцировать функцию, используя силовое правило . Постоянные члены исчезают при дифференцировании.
d/dx (4x ³ + 2x ² + 1) = 12x ² + 4x
Результат, 12x ² + 4x, представляет собой градиент функции. Это имеет два нуля, которые можно найти с помощью факторинга.
12x ² + 4x = 4x(3x+1), что равно нулю, когда x = 0 или x = -1/3

Шаг 2: Проверьте каждую точку поворота (при x = 0 и x = -1/3 ), чтобы выяснить, является ли оно максимальным или минимальным. Для этого продифференцируем второй раз и подставим в значение x каждой поворотной точки.
d/dx (12x ² + 4x) = 24x + 4
При x = 0 24x + 4 = 4, что больше нуля. Это минимум.
При x = -1/3, 24x + 4 = -4, что меньше нуля. Это максимум.

Шаг 3: Найдите соответствующие координаты y для значения x (максимума), которое вы нашли на шаге 2, путем подстановки обратно в исходную функцию.
При x = -1/3, y = 4x ³ + 2x ² + 1 = -4/27 + 2/9 + 1 = 29/27
Следовательно, функция имеет максимальное значение при (- 1/3, 29/27).

Совет : Вы можете проверить свой ответ, нарисовав график и найдя самые высокие и самые низкие точки.

Одним из многих практических применений исчисления является определение максимум или минимум значений функции. Нахождение этого минимального значения — это то, как найти минимальную прибыль.

Если вы когда-нибудь занимались математикой, то наверняка видели немало графиков с прикрепленными функциями. Многие графики имеют определенные точки, которые мы можем определить как «максимумы» и «минимумы», которые являются самыми высокими или самыми низкими точками на графике. Довольно часто возникает проблема, связанная с функцией без прикрепленного графика , поэтому может быть полезно знать метод получения этих значений.

Как найти минимальную прибыль с помощью вычислений: шаги

Пример задачи: Определите минимальную прибыль для компании x, функция прибыли которой:
f(t) = 100t ² – 50t + 9,
где f(t) — это выигранные деньги, а t — это время.

Шаг 1: Дифференцируйте свою функцию. В то время как сама функция представляет общую сумму полученных денег, дифференцированная функция дает вам скорость приобретения денег. Это будет полезно на следующем шаге.
Здесь я использую степенное правило:
f(t) = 100t ² – 50t + 9 дифференцируется, чтобы получить f ‘(t) = 200t – 50.

Шаг 2: Приравняйте уравнение к нулю и решить для т . 0 = 200t – 50
→ 50 = 200t,
Решив t, вы получите t = 1/4.
Это значение означает наличие либо максимума, либо минимума при t = 1/4.

Шаг 3: Проверьте окружающие значения t (в исходном уравнении), чтобы решить, является ли ваше значение максимумом или минимумом.

1. Подставьте свое значение «t» в исходное уравнение.
   Для t = 1/4:
   f(t) = 100(1/4) ² – 50(1/4) + 9 = 2,75.
2. Выберите две точки, очень близкие к нашим экстремумам (t = 1/4). Важно выбрать одно значение больше и меньше ваших экстремумов. Обычно разумно выбирать быстрые и простые значения для этой части процедуры. Например, 0 и 1 — отличный выбор не только потому, что они очень близки, но и потому, что они позволяют вам производить вычисления в уме.
   При t = 0 уравнение принимает вид f(t) = 100(0) ² – 50(0) + 9 = 9.
   При t = 1 уравнение принимает вид 100(1) ² – 50( 1) + 9 = 59.

Шаг 4: Сравните результаты. Если бы вы начертили три точки данных, это выглядело бы примерно так:
(0, 9), (1/4, 2,75), (2,59).
Вы должны быть в состоянии быстро нарисовать грубый набросок того, как это выглядит — вы обнаружите, что минимум составляет 1/4. Этот факт подтверждается тем фактом, что точки данных сразу слева и справа от этого значения выше. Если бы они были ниже, точка была бы максимумом, а если бы один был выше, а другой ниже, это была бы просто точка, где наклон функции равен нулю.

Вот как найти минимальную прибыль!

Предупреждение: поиск минимумов функции довольно прост, но будьте осторожны, в более сложных уравнениях может быть довольно сложно получить все значения для «t», когда функция равна нулю.

No related posts.