Урок математики по теме:»Упрощение выражений»,5 класс
Тема: «Упрощение выражений»
5 класс, учебник Виленкина Н.Я.
Цели: развивать умение упрощать выражения, учить решать уравнения, в которых требуется найти два неизвестных числа, учить решать задачи способом составления уравнения, в которых требуется найти два неизвестных числа.
Оборудование: учебники, тетради, компьютер, презентация, дидактические материалы, раздаточный материал.
Ход урока
I. Организационный момент.
Здравствуйте, ребята! Сегодня у нас на уроке присутствуют гости.
Вы не бойтесь, повернитесь,
Им легонько улыбнитесь
И тихонечко садитесь.
Я хочу начать сегодня наш урок словами великого русского писателя Л.Н.Толстого «Знание только тогда знание, когда оно приобретено усилием свой мысли…». Итак, «включаем» свои мысли и начинаем урок.
Итак, «включаем» свои мысли и начинаем урок.
II. Устный счет
Внимание на экран.
Упростите выражение – упрощаете выражение и называете какое свойство вы для этого применяете.
1)
Распределительно свойство умножение относительно сложения и вычитания
14х+6х
2)
3)
4)
5)
6)
6й пример вызовет затруднение у учащихся.
III. Формулировка темы и цели урока.
Итак, пять выражений вы упростили, а с 6ым не справились (если кто-то сразу догадался – похвалить и сказать, что большинство не справились).
Почему вы не смогли упростить последнее выражение (новое, мы такое не упрощали), вы хотите справиться с этим заданием (да). Тогда попытайтесь сформулировать тему нашего урока(тема – упрощение выражений) , а цель нашего урока.
Цели: 1) научиться упрощать новые выражения; 2) применять упрощении выражений при решении уравнений и задач, решаемых с помощью уравнений.
IV. Объяснение нового материала.
Откройте тетради и запишите число и тему урока (тема на доске). Обратимся к примеру, который у вас вызвал затруднение. Запишите его в тетрадь.
4t+2t+3 (учитель записывает на доске)
Прочитайте выражение (сумма выражений 4t, 2t и числа 3), назовите слагаемые этой суммы (4t, 2t, 3).
Какие из них можно объединить по какому-то признаку? (4t и 2t, т.к. у них одинаковая буква). Совершенно верно! Эти слагаемые содержат одинаковую букву, поэтому их называют подобными. Для удобства упрощения подобные слагаемые можно подчеркнуть.
4t+2t+3=6t+3
Что можно сделать с подчеркнутыми слагаемыми (применить распеделительное свойство умножения относительно сложения), можно еще что-нибудь сделать с этим выражением? (нет). Объясните, какую ошибку можно допустить.
V. Закрепление.
А теперь вы сами упростите следующие выражения: (задания на доске 2 ученика закрытые)
1) 9a-5a+17=4a+17
2) 5x+10+7x+3=12x+13
А теперь, ребята, выясним как вы подружились с подобными слагаемыми.
Обменяйтесь тетрадями и проверьте ответы соседа, пользуясь готовыми ответами.
Кто выполнил задание без ошибок? Поднимите руку.
А кто допустил 1 ошибку? Поставьте себе оценку по количеству «+».
VII. Закрепление материала.
Где мы можем применять упрощение выражений? (при решении уравнений)
Решаем №574 (а, б*)
а) 3х+7х+18=178
Вызвать по желанию одного ученика. Какое это уравнение? (сложное)
Что неизвестно? (?)
Что можно сделать с левой частью? (упростить)
10х+18=178
10х=178-18
10х=160
х=160:10
х=16
Ответ:16
Учитель ходит по классу и смотрит за выполнением.
б)* Если кто-то успел решить два уравнения, отметить это. (оценку)
б) 6y-2y+25=65
4y+25=65
4y=65-25
4y=40
y=40:4
y=10
Ответ: 10
Молодцы, ребята! А теперь давайте применим знания на практике: решим задачу.
Внимание на экран. Читаем условия задачи. О чем говорится в задаче? (о домах на улице). Что сказано о домах, расположенных на левой стороне улицы (на правой)? Что еще известно? (построили 12) Сколько всего домов? (99). Прочитайте вопрос (два неизвестных числа).
Читаем условия задачи. О чем говорится в задаче? (о домах на улице). Что сказано о домах, расположенных на левой стороне улицы (на правой)? Что еще известно? (построили 12) Сколько всего домов? (99). Прочитайте вопрос (два неизвестных числа).
Повесить памятку.
Запомни!
Обозначай за х то, что требуется найти.
Если в задаче несколько неизвестных, обозначай за х то, что меньше.
Что следует обозначать за х в этой задаче? Почему? Давайте решим задачу. Пишем:
Левая х домов
Правая 2х домов
Построили 12 домов
Стало (х+2х+12) домов
99 домов
Составим и решим уравнение.
х+2х+12=99
Закончите решение задачи самостоятельно.
3х+12=99
3х=99-12
3х=87
х=29
Значит, 29 домов было на левой стороне улицы, а на правой 1) 29*2=58 (домов).
Ответ: 29 домов, 58 домов.
Проверить решение на слайде (дети самостоятельно)
Кто верно решил задачу?
VII. Рефлексия.
А теперь ребята давайте подведем итоги нашего урока.
Попробуйте закончить фразы:
Сегодня на уроке я научился… (упрощать новые выражения, содержащие подобные слагаемые, решать уравнения, в которых нужно упростить выражения)
Теперь я могу
Мне было трудно
Мне было интересно
Мне захотелось… (придумать задачу или пример)
VIII. Домашнее задание.
А теперь запишите домашнее задание: №573, 574 (в,г), придумать задачу по данной теме и оформить с рисунками на листе А4, решение приложить на отдельном листе.
Просмотр содержимого документа
«Урок математики по теме:»Упрощение выражений»,5 класс »
Тема: «Упрощение выражений»
5 класс, учебник Виленкина Н. Я.
Я.
Цели: развивать умение упрощать выражения, учить решать уравнения, в которых требуется найти два неизвестных числа, учить решать задачи способом составления уравнения, в которых требуется найти два неизвестных числа.
Оборудование: учебники, тетради, компьютер, презентация, дидактические материалы, раздаточный материал.
Ход урока
I. Организационный момент.
Здравствуйте, ребята! Сегодня у нас на уроке присутствуют гости.
Вы не бойтесь, повернитесь,
Им легонько улыбнитесь
И тихонечко садитесь.
Я хочу начать сегодня наш урок словами великого русского писателя Л.Н.Толстого «Знание только тогда знание, когда оно приобретено усилием свой мысли…». Итак, «включаем» свои мысли и начинаем урок.
II. Устный счет
Устный счет
Внимание на экран.
Упростите выражение – упрощаете выражение и называете какое свойство вы для этого применяете.
1
Распределительно свойство умножение относительно сложения и вычитания
4х+6хm+12m
10y-2y
13n-n
8b+3b-2b
4t+2t+3
6й пример вызовет затруднение у учащихся.
III. Формулировка темы и цели урока.
Итак, пять выражений вы упростили, а с 6ым не справились (если кто-то сразу догадался – похвалить и сказать, что большинство не справились).
Почему вы не смогли упростить последнее выражение (новое, мы такое не упрощали), вы хотите справиться с этим заданием (да). Тогда попытайтесь сформулировать тему нашего урока(тема – упрощение выражений) , а цель нашего урока.
Цели: 1) научиться упрощать новые выражения; 2) применять упрощении выражений при решении уравнений и задач, решаемых с помощью уравнений.
IV. Объяснение нового материала.
Откройте тетради и запишите число и тему урока (тема на доске). Обратимся к примеру, который у вас вызвал затруднение. Запишите его в тетрадь.
4t+2t+3 (учитель записывает на доске)
Прочитайте выражение (сумма выражений 4t, 2t и числа 3), назовите слагаемые этой суммы (4t, 2t, 3).
Какие из них можно объединить по какому-то признаку? (4t и 2t, т.к. у них одинаковая буква). Совершенно верно! Эти слагаемые содержат одинаковую букву, поэтому их называют подобными. Для удобства упрощения подобные слагаемые можно подчеркнуть.
4t+2t+3=6t+3
Что можно сделать с подчеркнутыми слагаемыми (применить распеделительное свойство умножения относительно сложения), можно еще что-нибудь сделать с этим выражением? (нет).
Обменяйтесь тетрадями и проверьте ответы соседа, пользуясь готовыми ответами.
Кто выполнил задание без ошибок? Поднимите руку.
А кто допустил 1 ошибку? Поставьте себе оценку по количеству «+».
VII. Закрепление материала.
Где мы можем применять упрощение выражений? (при решении уравнений)
Решаем №574 (а, б*)
а) 3х+7х+18=178
Вызвать по желанию одного ученика. Какое это уравнение? (сложное)
Что неизвестно? (?)
Что можно сделать с левой частью? (упростить)
10х+18=178
10х=178-18
10х=160
х=160:10
х=16
Ответ:16
Учитель ходит по классу и смотрит за выполнением.
б)* Если кто-то успел решить два уравнения, отметить это. (оценку)
б) 6y-2y+25=65
4y+25=65
4y=65-25
4y=40
y=40:4
y=10
Ответ: 10
Молодцы, ребята! А теперь давайте применим знания на практике: решим задачу.
Внимание на экран. Читаем условия задачи. О чем говорится в задаче? (о домах на улице). Что сказано о домах, расположенных на левой стороне улицы (на правой)? Что еще известно? (построили 12) Сколько всего домов? (99). Прочитайте вопрос (два неизвестных числа).
Повесить памятку.
Запомни!
Обозначай за х то, что требуется найти.
Если в задаче несколько неизвестных, обозначай за х то, что меньше.
Что следует обозначать за х в этой задаче? Почему? Давайте решим задачу. Пишем:
Пишем:
Левая х домов
Правая 2х домов
Построили 12 домов
Стало (х+2х+12) домов
99 домов
Составим и решим уравнение.
х+2х+12=99
Закончите решение задачи самостоятельно.
3х+12=99
3х=99-12
3х=87
х=29
Значит, 29 домов было на левой стороне улицы, а на правой 1) 29*2=58 (домов).
Ответ: 29 домов, 58 домов.
Проверить решение на слайде (дети самостоятельно)
Кто верно решил задачу?
VII. Рефлексия.
А теперь ребята давайте подведем итоги нашего урока.
Попробуйте закончить фразы:
Сегодня на уроке я научился… (упрощать новые выражения, содержащие подобные слагаемые, решать уравнения, в которых нужно упростить выражения)
Теперь я могу
Мне было трудно
Мне было интересно
Мне захотелось… (придумать задачу или пример)
VIII. Домашнее задание.
Домашнее задание.
А теперь запишите домашнее задание: №573, 574 (в,г), придумать задачу по данной теме и оформить с рисунками на листе А4, решение приложить на отдельном листе.
Как упростить выражение и вычислить его значение. Преобразование выражений
Вам понадобится
- — понятие одночлена многочлена;
- — формулы сокращенного умножения;
- — действия с дробями;
- — основные тригонометрические тождества.
Инструкция
Если в выражении имеются одночлены с , найдите сумму коэффициентов при них и умножьте на единый для них множитель. Например, если есть выражение 2 а-4 а+5 а+а=(2-4+5+1)∙а=4∙а.
В том случае, если выражение представляет собой натуральную дробь, выделите из числителя и знаменателя общий множитель и сократите дробь на него. Например, если нужно сократить дробь (3 a²-6 a b+3 b²)/(6∙a²-6∙b²), вынесите из числителя и знаменателя общие множители в числителе это будет 3, в знаменателе 6.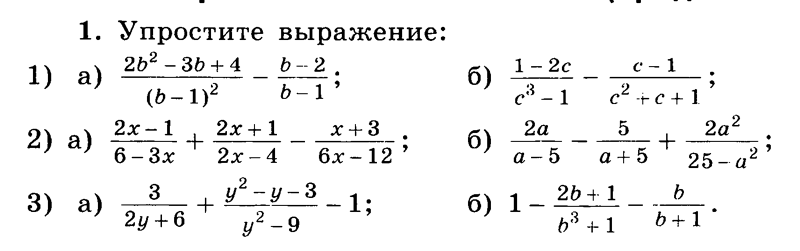 Получите выражение (3 (a²-2 a b+b²))/(6∙(a²-b²)). Сократите числитель и знаменатель на 3 и примените к оставшимся выражениям формулы сокращенного умножения. Для числителя это квадрат разности, а для знаменателя разность квадратов. Получите выражение (a-b)²/(2∙ (a+b)∙(a-b)) сократив его на общий множитель a-b, получите выражение (a-b)/(2∙ (a+b)), которое при конкретных значениях переменных гораздо легче посчитать.
Получите выражение (3 (a²-2 a b+b²))/(6∙(a²-b²)). Сократите числитель и знаменатель на 3 и примените к оставшимся выражениям формулы сокращенного умножения. Для числителя это квадрат разности, а для знаменателя разность квадратов. Получите выражение (a-b)²/(2∙ (a+b)∙(a-b)) сократив его на общий множитель a-b, получите выражение (a-b)/(2∙ (a+b)), которое при конкретных значениях переменных гораздо легче посчитать.
Если одночлены имеют одинаковые множители, возведенные в степень, то при их суммировании следите, чтобы степени были равны, иначе сводить подобные нельзя. Например, если есть выражение 2∙m²+6 m³-m²-4 m³+7, то при сведении подобных получится m²+2 m³+7.
При упрощении тригонометрических тождеств используйте формулы для их преобразования. Основное тригонометрическое тождество sin²(x)+cos²(x)=1, sin(x)/cos(x)=tg(x), 1/ tg(x)= ctg(x), формулы суммы и разности аргументов, двойного, тройного аргумента и другие. Например, (sin(2∙x)- cos(x))/ ctg(x). Распишите формулу двойного аргумента и котангенса, как отношения косинуса на синус. Получите (2∙ sin(x) cos(x)- cos(x)) sin(x)/cos(x). Вынесите общий множитель, cos(x) и сократите дробь cos(x) (2∙ sin(x) — 1) sin(x)/cos(x)= (2∙ sin(x) — 1) sin(x).
Получите (2∙ sin(x) cos(x)- cos(x)) sin(x)/cos(x). Вынесите общий множитель, cos(x) и сократите дробь cos(x) (2∙ sin(x) — 1) sin(x)/cos(x)= (2∙ sin(x) — 1) sin(x).
Видео по теме
Источники:
- формула упрощения выражения
Краткость, как говорится, — сестра таланта. Каждому хочется блеснуть талантом, но вот его сестра — штука сложная. Гениальные мысли почему-то сами собой облекаются в сложноподчинённые предложения со множеством деепричастных оборотов. Однако в ваших силах упростить свои предложения и сделать их понятными и доступными всем.
Инструкция
Чтобы облегчить адресату (будь то слушатель или читатель) , постарайтесь заменять причастные и деепричастные обороты короткими придаточными предложениями, особенно если вышеуказанных оборотов слишком много в одном предложении. «Пришедший домой кот, только что съевший мышь, громко мурлыча, ласкался к хозяину, пытаясь заглянуть ему в глаза, надеясь выпросить рыбу, принесённую из магазина» — не пойдёт. Разбейте подобную конструкцию на несколько частей, не торопитесь и не пытайтесь сказать всё одним предложением, вам счастье.
Разбейте подобную конструкцию на несколько частей, не торопитесь и не пытайтесь сказать всё одним предложением, вам счастье.
Если вы задумали гениальное высказывание, но в нём оказалось слишком много придаточных предложений (тем более с одним ), то лучше разбить высказывание на несколько отдельных предложений или опустить какой-то элемент. «Мы решили, что он расскажет Марине Васильевне, что Катя скажет Вите, что…» — можно продолжать бесконечно. Вовремя остановитесь и вспомните о том , кто будет это читать или выслушивать.
Однако подводные камни кроются не только в структуре предложения. Обратите внимание на лексику. Иноязычные слова, длинные термины, слова, почерпнутые из художественной литературы 19 века — всё это только осложнит восприятие. Необходимо уточнить для себя, для какой аудитории вы составляете текст: технари, конечно, поймут и сложные термины, и специфические слова; но если вы те же слова предложите учительнице литературы, вряд ли она вас поймёт.
Талант — великая вещь. 2*b*c)=2/(a*c). Но помните, что сокращать можно только множители. Если числитель и знаменатель алгебраической дроби умножать на одно и то же число, отличное от нуля, то при этом значение дроби не изменится. Преобразовывать рациональные выражения можно двумя способами: цепочкой и по действиям. Предпочтительней второй способ, т.к. легче проверить результаты промежуточных действий.
2*b*c)=2/(a*c). Но помните, что сокращать можно только множители. Если числитель и знаменатель алгебраической дроби умножать на одно и то же число, отличное от нуля, то при этом значение дроби не изменится. Преобразовывать рациональные выражения можно двумя способами: цепочкой и по действиям. Предпочтительней второй способ, т.к. легче проверить результаты промежуточных действий.
Нередко в выражениях необходимо извлекать корни. Корни четной степени извлекаются только из неотрицательных выражений или чисел. Корни нечетной степени извлекаются из любых выражений.
Источники:
- упрощение выражений со степенями
«Выражением» в математике обычно называют набор арифметических и алгебраических действий с числами и переменными значениями. По аналогии с форматом записи чисел такой набор называют «дробным» в том случае, когда он содержит операцию деления. К дробным выражениям, как и к числам в формате обыкновенной дроби, применимы операции упрощения.
Инструкция
Начните с нахождения общего множителя для , стоящих в числителе и — это одинаково как для численных соотношений, так и для содержащих неизвестные переменные. Например, если в числителе стоит выражение 45*X, а в знаменателе 18*Y, то наибольшим общим множителем будет число 9. После выполнения этого шага числитель можно записать как 9*5*X, а знаменатель — как 9*2*Y.
Например, если в числителе стоит выражение 45*X, а в знаменателе 18*Y, то наибольшим общим множителем будет число 9. После выполнения этого шага числитель можно записать как 9*5*X, а знаменатель — как 9*2*Y.
Если выражения в числителе и знаменателе содержат комбинацию основных математических операций ( , деление, сложение и вычитание), то сначала придется вынести за скобки общий множитель для каждого из них в отдельности, а затем вычленить из этих чисел наибольший общий делитель. Например, для выражения 45*X+180, стоящего в числителе, за скобки следует вынести множитель 45: 45*X+180 = 45*(X+4). А выражение 18+54*Y в знаменателе надо привести к виду 18*(1+3*Y). Затем, как в предыдущем, шаге найдите наибольший общий делитель вынесенных за скобки множителей: 45*X+180 / 18+54*Y = 45*(X+4) / 18*(1+3*Y) = 9*5*(X+4) / 9*2*(1+3*Y). В этом примере он тоже равен девятке.
Сократите найденный на предыдущих шагах общий множитель выражений в числителе и знаменателе дроби. Для примера из первого шага всю операцию упрощения можно записать так: 45*X / 18*Y = 9*5*X / 9*2*Y = 5*X / 2*Y.
Не обязательно при упрощении сокращаемым общим делителем должно быть число, это может быть и выражение, содержащее переменную. Например, если в числителе дроби стоит (4*X + X*Y + 12 + 3*Y), а в знаменателе (X*Y + 3*Y — 7*X — 21), то наибольшим общим делителем будет выражение X+3, которое и следует сократить для упрощения выражения: (4*X + X*Y + 12 + 3*Y) / (X*Y + 3*Y — 7*X — 21) = (X+3)*(4+Y) / (X+3)*(Y-7) = (4+Y) / (Y-7).
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Зачастую в задачах требуется привести упрощенный ответ. Хотя и упрощенный, и неупрощенный ответы являются верными, преподаватель может снизить вашу оценку, если вы не упростите ответ. Более того, с упрощенным математическим выражением гораздо легче работать. Поэтому очень важно научиться упрощать выражения.
Шаги
Правильный порядок выполнения математических операций
Запомните правильный порядок выполнения математических операций. При упрощении математического выражения необходимо соблюдать определенный порядок действий, так как некоторые математические операции имеют приоритет над другими и должны быть сделаны в первую очередь (на самом деле несоблюдение правильного порядка выполнения операций приведет вас к неправильному результату).
 Запомните следующий порядок выполнения математических операций: выражение в скобках, возведение в степень, умножение, деление, сложение, вычитание.
Запомните следующий порядок выполнения математических операций: выражение в скобках, возведение в степень, умножение, деление, сложение, вычитание.- Обратите внимание, что знание правильного порядка выполнения операций позволит вам упростить большинство простейших выражений, но для упрощения многочлена (выражения с переменной) необходимо знать специальные приемы (смотрите следующий раздел).
Начните с решения выражения в скобках. В математике скобки указывают на то, что заключенное в них выражение должно быть выполнено в первую очередь. Поэтому при упрощении любого математического выражения начинайте с решения выражения, заключенного в скобки (при этом неважно, какие операции нужно выполнить внутри скобок). Но помните, что работая с выражением, заключенным в скобки, следует соблюдать порядок проведения операций, то есть члены в скобках сначала перемножаются, делятся, складываются, вычитаются и так далее.
- Например, упростим выражение 2x + 4(5 + 2) + 3 2 — (3 + 4/2) .
 Здесь начнем с выражений в скобках: 5 + 2 = 7 и 3 + 4/2 = 3 + 2 =5.
Здесь начнем с выражений в скобках: 5 + 2 = 7 и 3 + 4/2 = 3 + 2 =5.- Выражение во второй паре скобок упрощается до 5, потому что сначала нужно разделить 4/2 (согласно правильному порядку выполнения операций). Если не соблюдать этот порядок, то вы получите неправильный ответ: 3 + 4 = 7 и 7 ÷ 2 = 7/2.
- Если в скобках есть еще одна пара скобок, начните упрощение с решения выражения во внутренних скобках, а затем переходите к решению выражения во внешних скобках.
- Например, упростим выражение 2x + 4(5 + 2) + 3 2 — (3 + 4/2) .
Возведите в степень. Решив выражения в скобках, перейдите к возведению в степень (помните, что у степени есть показатель степени и основание степени). Возведите соответствующее выражение (или число) в степень и подставьте результат в данное вам выражение.
- В нашем примере единственным выражением (числом) в степени является 3 2: 3 2 = 9. В данном вам выражении вместо 3 2 подставьте 9 и вы получите: 2x + 4(7) + 9 — 5.
Умножьте. Помните, что операция умножения может обозначаться следующими символами: «х», «∙» или «*».
 Но если между числом и переменной (например, 2х) или между числом и числом в скобках (например, 4(7)) нет никаких символов, то это также является операцией умножения.
Но если между числом и переменной (например, 2х) или между числом и числом в скобках (например, 4(7)) нет никаких символов, то это также является операцией умножения.- В нашем примере присутствуют две операции умножения: 2x (два умножить на переменную «х») и 4(7) (четыре умножить на семь). Мы не знаем значения х, поэтому выражение 2х оставим как есть. 4(7) = 4 х 7 = 28. Теперь вы можете переписать данное вам выражение так: 2x + 28 + 9 — 5.
Разделите. Помните, что операция деления может обозначаться следующими символами: «/», «÷» или «–» (последний символ вы можете встретить в дробях). Например 3/4 – это три, деленное на четыре.
- В нашем примере операции деления больше нет, так как вы уже разделили 4 на 2 (4/2) при решении выражения в скобках. Поэтому вы можете перейти к следующему шагу. Помните, что в большинстве выражений нет сразу всех математических операций (только некоторые из них).
Сложите. При сложении членов выражения вы можете начать с самого крайнего (слева) члена, или можете сначала сложить те члены выражения, которые легко складываются.
 Например, в выражении 49 + 29 + 51 +71 сначала легче сложить 49 + 51 = 100, потом 29 + 71 = 100 и, наконец, 100 + 100 = 200. Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.
Например, в выражении 49 + 29 + 51 +71 сначала легче сложить 49 + 51 = 100, потом 29 + 71 = 100 и, наконец, 100 + 100 = 200. Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.- В нашем примере 2x + 28 + 9 + 5 присутствуют две операции сложения. Начнем с самого крайнего (слева) члена: 2x + 28; вы не можете сложить 2х и 28, потому что не знаете значения переменной «х». Поэтому сложите 28 + 9 = 37. Теперь выражение можно переписать так: 2х + 37 — 5.
Вычтите. Это последняя операция в правильном порядке выполнения математических операций. На этом этапе вы также можете прибавлять отрицательные числа или же делать это на этапе сложения членов – это никак не отразится на конечном результате.
- В нашем примере 2х + 37 — 5 присутствует только одна операция вычитания: 37 — 5 = 32.
На этом этапе, проделав все математические операции, вы должны получить упрощенное выражение. Но если данное вам выражение содержит одну или несколько переменных, то помните, что член с переменной останется таким, как есть.
 Решение (а не упрощение) выражения с переменной подразумевает нахождение значения этой переменной. Иногда выражения с переменной можно упростить, используя специальные методы (смотрите следующий раздел).
Решение (а не упрощение) выражения с переменной подразумевает нахождение значения этой переменной. Иногда выражения с переменной можно упростить, используя специальные методы (смотрите следующий раздел).- В нашем примере окончательный ответ: 2х + 32. Вы не сможете сложить два члена, пока не узнаете значение переменной «х». Узнав значение переменной, вы с легкостью упростите этот двучлен.
Упрощение сложных выражений
Сложение подобных членов. Помните, что вычитать и складывать можно исключительно подобные члены, то есть члены с одинаковой переменной и одинаковым показателем степени. Например, можно сложить 7x и 5x, но нельзя складывать 7x и 5x 2 (так как здесь показатели степени разные).
- Это правило распространяется и на члены с несколькими переменными. Например, можно сложить 2xy 2 и -3xy 2 , но нельзя складывать 2xy 2 и -3x 2 y или 2xy 2 и -3y 2 .
- Рассмотрим пример: x 2 + 3x + 6 — 8x. Здесь подобными членами являются 3x и 8x, поэтому их можно сложить.
 Упрощенное выражение выглядит так: x 2 — 5x + 6.
Упрощенное выражение выглядит так: x 2 — 5x + 6.
Упростите числовую дробь. В такой дроби и в числителе, и в знаменателе находятся числа (без переменной). Числовая дробь упрощается несколькими способами. Во-первых, просто разделите знаменатель на числитель. Во-вторых, разложите числитель и знаменатель на множители и сократите одинаковые множители (так как при делении числа на само себя вы получите 1). Другими словами, если и у числителя, и у знаменателя есть один и тот же множитель, его можно отбросить и получить упрощенную дробь.
- Например, рассмотрим дробь 36/60. При помощи калькулятора разделите 36 на 60 и получите 0,6. Но вы можете упростить эту дробь и по-другому, разложив числитель и знаменатель на множители: 36/60 = (6х6)/(6х10) = (6/6)*(6/10). Так как 6/6 = 1, то упрощенная дробь: 1 х 6/10 = 6/10. Но эту дробь также можно упростить: 6/10 = (2х3)/(2*5) = (2/2)*(3/5) = 3/5.
Если дробь содержит переменную, можно сократить одинаковые множители с переменной.
 Разложите и числитель, и знаменатель на множители и сократите одинаковые множители, даже если они содержат переменную (помните, что здесь одинаковые множители могут содержать или не содержать переменную).
Разложите и числитель, и знаменатель на множители и сократите одинаковые множители, даже если они содержат переменную (помните, что здесь одинаковые множители могут содержать или не содержать переменную).- Рассмотрим пример: (3x 2 + 3x)/(-3x 2 + 15x). Это выражение можно переписать (разложить на множители) в виде: (x + 1)(3x)/(3x)(5 — x). Так как член 3x находится и в числителе, и в знаменателе, его можно сократить, и вы получите упрощенное выражение: (х + 1)/(5 — х). Рассмотрим другой пример: (2x 2 + 4x + 6)/2 = (2(x 2 + 2x + 3))/2 = x 2 + 2x + 3.
- Обратите внимание, что вы не можете сокращать любые члены – сокращаются только одинаковые множители, которые присутствуют как в числителе, так и в знаменателе. Например, в выражении (х(х + 2))/х переменная (множитель) «х» находится и в числителе, и в знаменателе, поэтому «х» можно сократить и получить упрощенное выражение: (х + 2)/1 = х + 2. Тем не менее, в выражении (х + 2)/х переменную «х» сокращать нельзя (так как в числителе «х» не является множителем).

Раскройте скобки. Для этого умножьте член, стоящий за скобкой, на каждый член в скобках. Иногда это помогает упростить сложное выражение. Это относится как к членам, которые являются простыми числами, так и к членам, которые содержат переменную.
- Например, 3(x 2 + 8) = 3x 2 + 24, а 3x(x 2 + 8) = 3x 3 + 24x.
- Обратите внимание, что в дробных выражениях скобки раскрывать не нужно, если и в числителе, и в знаменателе присутствует одинаковый множитель. Например, в выражении (3(x 2 + 8))/3x скобки раскрывать не нужно, так как здесь можно сократить множитель 3 и получить упрощенное выражение (x 2 + 8)/x. С этим выражением легче работать; если бы вы раскрыли скобки, то получили бы следующее сложное выражение: (3x 3 + 24x)/3x.
Упрощение алгебраических выражений является одним из ключевых моментов изучения алгебры и чрезвычайно полезным навыком для всех математиков. Упрощение позволяет привести сложное или длинное выражение к простому выражению, с которым легко работать. Базовые навыки упрощения хорошо даются даже тем, кто не в восторге от математики. Соблюдая несколько простых правил, можно упростить многие из наиболее распространенных типов алгебраических выражений без каких-либо специальных математических знаний.
Базовые навыки упрощения хорошо даются даже тем, кто не в восторге от математики. Соблюдая несколько простых правил, можно упростить многие из наиболее распространенных типов алгебраических выражений без каких-либо специальных математических знаний.
Шаги
Важные определения
Подобные члены . Это члены с переменной одного порядка, члены с одинаковыми переменными или свободные члены (члены, не содержащие переменную). Другими словами, подобные члены включают одну переменную в одной и той же степени, включают несколько одинаковых переменных или не включают переменную вовсе. Порядок членов в выражении не имеет значения.
- Например, 3x 2 и 4x 2 — это подобные члены, так как они содержат переменную «х» второго порядка (во второй степени). Однако х и x 2 не являются подобными членами, так как содержат переменную «х» разных порядков (первого и второго). Точно так же -3yx и 5хz не являются подобными членами, так как содержат разные переменные.

- Например, 3x 2 и 4x 2 — это подобные члены, так как они содержат переменную «х» второго порядка (во второй степени). Однако х и x 2 не являются подобными членами, так как содержат переменную «х» разных порядков (первого и второго). Точно так же -3yx и 5хz не являются подобными членами, так как содержат разные переменные.
Разложение на множители . Это нахождение таких чисел, произведение которых приводит к исходному числу. Любое исходное число может иметь несколько множителей. Например, число 12 может быть разложено на следующий ряд множителей: 1 × 12, 2 × 6 и 3 × 4, поэтому можно сказать, что числа 1, 2, 3, 4, 6 и 12 являются множителями числа 12. Множители совпадают с делителями, то есть числами, на которые делится исходное число.
- Например, если вы хотите разложить на множители число 20, запишите это так: 4 × 5.
- Обратите внимание, что при разложении на множители переменная учитывается. Например, 20x = 4(5x) .
- Простые числа не могут быть разложены на множители, потому что они делятся только на себя и на 1.
Запомните и соблюдайте порядок выполнения операций во избежание ошибок.
- Скобки
- Степень
- Умножение
- Деление
- Сложение
- Вычитание
Приведение подобных членов
Запишите выражение.
 Простейшие алгебраические выражения (которые не содержат дробей, корней и так далее) можно решить (упростить) всего за несколько шагов.
Простейшие алгебраические выражения (которые не содержат дробей, корней и так далее) можно решить (упростить) всего за несколько шагов.- Например, упростите выражение 1 + 2x — 3 + 4x .
Определите подобные члены (члены с переменной одного порядка, члены с одинаковыми переменными или свободные члены).
- Найдите подобные члены в этом выражении. Члены 2x и 4x содержат переменную одного порядка (первого). Кроме того, 1 и -3 — это свободные члены (не содержат переменную). Таким образом, в этом выражении члены 2х и 4x являются подобными, и члены 1 и -3 тоже являются подобными.
Приведите подобные члены. Это значит сложить или вычесть их и упростить выражение.
- 2x + 4x = 6х
- 1 — 3 = -2
Перепишите выражение с учетом приведенных членов. Вы получите простое выражение с меньшим количеством членов. Новое выражение равно исходному.

- В нашем примере: 1 + 2x — 3 + 4x = 6х — 2 , то есть исходное выражение упрощено и с ним легче работать.
Соблюдайте порядок выполнения операций при приведении подобных членов. В нашем примере было легко привести подобные члены. Однако в случае сложных выражений, в которых члены заключены в скобки и присутствуют дроби и корни, привести подобные члены не так просто. В этих случаях соблюдайте порядок выполнения операций.
- Например, рассмотрим выражение 5(3x — 1) + х((2x)/(2)) + 8 — 3x. Здесь было бы ошибкой сразу определить 3x и 2x как подобные члены и привести их, потому что сначала необходимо раскрыть скобки. Поэтому выполните операции согласно их порядку.
- 5(3x-1) + x((2x)/(2)) + 8 — 3x
- 15x — 5 + x(x) + 8 — 3x
- 15x — 5 + x 2 + 8 — 3x. Теперь , когда в выражении присутствуют только операции сложения и вычитания, вы можете привести подобные члены.
- x 2 + (15x — 3x) + (8 — 5)
- x 2 + 12x + 3
- Например, рассмотрим выражение 5(3x — 1) + х((2x)/(2)) + 8 — 3x. Здесь было бы ошибкой сразу определить 3x и 2x как подобные члены и привести их, потому что сначала необходимо раскрыть скобки. Поэтому выполните операции согласно их порядку.
Вынесение множителя за скобки
Найдите наибольший общий делитель (НОД) всех коэффициентов выражения.
 НОД — это наибольшее число, на которое делятся все коэффициенты выражения.
НОД — это наибольшее число, на которое делятся все коэффициенты выражения.- Например, рассмотрим уравнение 9x 2 + 27x — 3. В этом случае НОД=3, так как любой коэффициент данного выражения делится на 3.
Разделите каждый член выражения на НОД. Полученные члены будут содержать меньшие коэффициенты, чем в исходном выражении.
- В нашем примере разделите каждый член выражения на 3.
- 9x 2 /3 = 3x 2
- 27x/3 = 9x
- -3/3 = -1
- Получилось выражение 3x 2 + 9x — 1 . Оно не равно исходному выражению.
- В нашем примере разделите каждый член выражения на 3.
Запишите исходное выражение как равное произведению НОД на полученное выражение. То есть заключите полученное выражение в скобки, а за скобки вынесите НОД.
- В нашем примере: 9x 2 + 27x — 3 = 3(3x 2 + 9x — 1)
Упрощение дробных выражений с помощью вынесения множителя за скобки. Зачем просто выносить множитель за скобки, как это было сделано ранее? Затем, чтобы научиться упрощать сложные выражения, например дробные выражения.
 В этом случае вынесение множителя за скобки может помочь избавиться от дроби (от знаменателя).
В этом случае вынесение множителя за скобки может помочь избавиться от дроби (от знаменателя).- Например, рассмотрим дробное выражение (9x 2 + 27x — 3)/3. Воспользуйтесь вынесением множителя за скобки, чтобы упростить это выражение.
- Вынесите множитель 3 за скобки (как вы делали это ранее): (3(3x 2 + 9x — 1))/3
- Обратите внимание, что теперь и в числителе, и в знаменателе присутствует число 3. Его можно сократить, и вы получите выражение: (3x 2 + 9x – 1)/1
- Так как любая дробь, у которой в знаменателе находится число 1, равна просто числителю, то исходное дробное выражение упрощается до: 3x 2 + 9x — 1 .
- Например, рассмотрим дробное выражение (9x 2 + 27x — 3)/3. Воспользуйтесь вынесением множителя за скобки, чтобы упростить это выражение.
Дополнительные методы упрощения
Упрощение дробных выражений. Как отмечалось выше, если и в числителе, и в знаменателе присутствуют одинаковые члены (или даже одинаковые выражения), то их можно сократить. Для этого нужно вынести за скобки общий множитель у числителя или у знаменателя, или как у числителя, так и у знаменателя.
 Или можно разделить каждый член числителя на знаменатель и таким образом упростить выражение.
Или можно разделить каждый член числителя на знаменатель и таким образом упростить выражение.- Например, рассмотрим дробное выражение (5x 2 + 10x + 20)/10. Здесь просто разделите каждый член числителя на знаменатель (10). Но учтите, что член 5x 2 не делится на 10 нацело (так как 5 меньше 10).
- Поэтому запишите упрощенное выражение так: ((5x 2)/10) + x + 2 = (1/2)x 2 + x + 2.
- Например, рассмотрим дробное выражение (5x 2 + 10x + 20)/10. Здесь просто разделите каждый член числителя на знаменатель (10). Но учтите, что член 5x 2 не делится на 10 нацело (так как 5 меньше 10).
Упрощение подкоренных выражений. Выражения, стоящие под знаком корня, называются подкоренными выражениями. Они могут быть упрощены через их разложение на соответствующие множители и последующий вынос одного множителя из-под корня.
- Рассмотрим простой пример: √(90). Число 90 можно разложить на следующие множители: 9 и 10, а из 9 извлечь квадратный корень (3) и вынести 3 из-под корня.
- √(90)
- √(9×10)
- √(9)×√(10)
- 3×√(10)
- 3√(10)
- Рассмотрим простой пример: √(90). Число 90 можно разложить на следующие множители: 9 и 10, а из 9 извлечь квадратный корень (3) и вынести 3 из-под корня.
Упрощение выражений со степенями.
 В некоторых выражениях присутствуют операции умножения или деления членов со степенью. В случае умножения членов с одним основанием их степени складываются; в случае деления членов с одним основанием их степени вычитаются.
В некоторых выражениях присутствуют операции умножения или деления членов со степенью. В случае умножения членов с одним основанием их степени складываются; в случае деления членов с одним основанием их степени вычитаются.- Например, рассмотрим выражение 6x 3 × 8x 4 + (x 17 /x 15). В случае умножения сложите степени, а в случае деления – вычтите их.
- 6x 3 × 8x 4 + (x 17 /x 15)
- (6 × 8)x 3 + 4 + (x 17 — 15)
- 48x 7 + x 2
- Далее приведено объяснение правила умножения и деления членов со степенью.
- Умножение членов со степенями равносильно умножению членов на самих себя. Например, так как x 3 = x × x × x и x 5 = x × x × x × x × x, то x 3 × x 5 = (x × x × x) × (x × x × x × x × x), или x 8 .
- Аналогично, деление членов со степенями равносильно делению членов на самих себя. x 5 /x 3 = (x × x × x × x × x)/(x × x × x). Так как подобные члены, находящиеся и в числителе, и в знаменателе, могут быть сокращены, то в числителе остается произведение двух «х», или x 2 .

- Например, рассмотрим выражение 6x 3 × 8x 4 + (x 17 /x 15). В случае умножения сложите степени, а в случае деления – вычтите их.
Замечание 1
Логическую функцию можно записать с помощью логического выражения, а затем можно перейти к логической схеме. Упрощать логические выражения надо для того, чтобы получить как можно более простую (а значит, и более дешёвую) логическую схему. По сути, логическая функция, логическое выражение и логическая схема −это три разных языка, рассказывающие об одной сущности.
Для упрощения логических выражений используют законы алгебры логики .
Какие-то преобразования похожи на преобразования формул в классической алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), а другие преобразования основаны на свойствах, которыми операции классической алгебры не обладают (использование распределительного закона для конъюнкции, законов поглощения, склеивания, правил де Моргана и др.).
Законы алгебры логики формулируются для базовых логических операций — “НЕ” – инверсия (отрицание), “И” – конъюнкция (логическое умножение) и “ИЛИ” – дизъюнкция (логическое сложение).
Закон двойного отрицания означает, что операция “НЕ” обратима: если применить ее дважды, то в итоге логическое значение не изменится.
Закон исключенного третьего гласит, что любое логическое выражение либо истинно, либо ложно (“третьего не дано”). Поэтому если $A=1$, то $\bar{A}=0$ (и наоборот), а, значит, конъюнкция этих величин всегда равно нулю, а дизъюнкция равна единице.
$((A + B) → C) \cdot (B → C \cdot D) \cdot C.$
Упростим эту формулу:
Рисунок 3.
Отсюда следует, что $A = 0$, $B = 1$, $C = 1$, $D = 1$.
Ответ: в шахматы играют ученики $B$, $C$ и $D$, а ученик $A$ не играет.
При упрощении логических выражений можно выполнять такую последовательность действий :
- Заменить все “небазовые” операции (эквивалентность, импликацию, исключающее ИЛИ и др.) на их выражения через базовые операции инверсию, конъюнкцию и дизъюнкцию.
- Раскрыть инверсии сложных выражений по правилам де Моргана таким образом, чтобы операции отрицания остались только у отдельных переменных.

- Затем упростить выражение, используя раскрытие скобок, вынесение общих множителей за скобки и другие законы алгебры логики.
Пример 2
Здесь последовательно использованы правило де Моргана, распределительный закон, закон исключенного третьего, переместительный закон, закон повторения, вновь переместительный закон и закон поглощения.
Как упростить математическое выражение: 13 шагов
‘).insertAfter(«#intro»),$(‘
‘).insertBefore(«.youmightalsolike»),$(‘
‘).insertBefore(«#quiz_container»),$(‘
‘).insertBefore(«#newsletter_block_main»),fa(! 0),b=document.getElementsByClassName(«scrolltomarker»),a=0;a
В этой статье:
Правильный порядок выполнения математических операций
Упрощение сложных выражений
Дополнительные статьи
Зачастую в задачах требуется привести упрощенный ответ. Хотя и упрощенный, и неупрощенный ответы являются верными, преподаватель может снизить вашу оценку, если вы не упростите ответ. Более того, с упрощенным математическим выражением гораздо легче работать. Поэтому очень важно научиться упрощать выражения.
Хотя и упрощенный, и неупрощенный ответы являются верными, преподаватель может снизить вашу оценку, если вы не упростите ответ. Более того, с упрощенным математическим выражением гораздо легче работать. Поэтому очень важно научиться упрощать выражения.
Шаги
1
Запомните правильный порядок выполнения математических операций. При упрощении математического выражения необходимо соблюдать определенный порядок действий, так как некоторые математические операции имеют приоритет над другими и должны быть сделаны в первую очередь (на самом деле несоблюдение правильного порядка выполнения операций приведет вас к неправильному результату). Запомните следующий порядок выполнения математических операций: выражение в скобках, возведение в степень, умножение, деление, сложение, вычитание.
- Обратите внимание, что знание правильного порядка выполнения операций позволит вам упростить большинство простейших выражений, но для упрощения многочлена (выражения с переменной) необходимо знать специальные приемы (смотрите следующий раздел).

- Обратите внимание, что знание правильного порядка выполнения операций позволит вам упростить большинство простейших выражений, но для упрощения многочлена (выражения с переменной) необходимо знать специальные приемы (смотрите следующий раздел).
2
Начните с решения выражения в скобках. В математике скобки указывают на то, что заключенное в них выражение должно быть выполнено в первую очередь. Поэтому при упрощении любого математического выражения начинайте с решения выражения, заключенного в скобки (при этом неважно, какие операции нужно выполнить внутри скобок). Но помните, что работая с выражением, заключенным в скобки, следует соблюдать порядок проведения операций, то есть члены в скобках сначала перемножаются, делятся, складываются, вычитаются и так далее.
- Например, упростим выражение 2x + 4(5 + 2) + 32 — (3 + 4/2). Здесь начнем с выражений в скобках: 5 + 2 = 7 и 3 + 4/2 = 3 + 2 =5.
- Выражение во второй паре скобок упрощается до 5, потому что сначала нужно разделить 4/2 (согласно правильному порядку выполнения операций). Если не соблюдать этот порядок, то вы получите неправильный ответ: 3 + 4 = 7 и 7 ÷ 2 = 7/2.
- Если в скобках есть еще одна пара скобок, начните упрощение с решения выражения во внутренних скобках, а затем переходите к решению выражения во внешних скобках.

- Например, упростим выражение 2x + 4(5 + 2) + 32 — (3 + 4/2). Здесь начнем с выражений в скобках: 5 + 2 = 7 и 3 + 4/2 = 3 + 2 =5.
3
Возведите в степень. Решив выражения в скобках, перейдите к возведению в степень (помните, что у степени есть показатель степени и основание степени). Возведите соответствующее выражение (или число) в степень и подставьте результат в данное вам выражение.
- В нашем примере единственным выражением (числом) в степени является 32: 32 = 9. В данном вам выражении вместо 32 подставьте 9 и вы получите: 2x + 4(7) + 9 — 5.
4
Умножьте. Помните, что операция умножения может обозначаться следующими символами: «х», «∙» или «*». Но если между числом и переменной (например, 2х) или между числом и числом в скобках (например, 4(7)) нет никаких символов, то это также является операцией умножения.
- В нашем примере присутствуют две операции умножения: 2x (два умножить на переменную «х») и 4(7) (четыре умножить на семь).
 Мы не знаем значения х, поэтому выражение 2х оставим как есть. 4(7) = 4 х 7 = 28. Теперь вы можете переписать данное вам выражение так: 2x + 28 + 9 — 5.
Мы не знаем значения х, поэтому выражение 2х оставим как есть. 4(7) = 4 х 7 = 28. Теперь вы можете переписать данное вам выражение так: 2x + 28 + 9 — 5.
- В нашем примере присутствуют две операции умножения: 2x (два умножить на переменную «х») и 4(7) (четыре умножить на семь).
5
Разделите. Помните, что операция деления может обозначаться следующими символами: «/», «÷» или «–» (последний символ вы можете встретить в дробях). Например 3/4 – это три, деленное на четыре.
- В нашем примере операции деления больше нет, так как вы уже разделили 4 на 2 (4/2) при решении выражения в скобках. Поэтому вы можете перейти к следующему шагу. Помните, что в большинстве выражений нет сразу всех математических операций (только некоторые из них).
6
Сложите. При сложении членов выражения вы можете начать с самого крайнего (слева) члена, или можете сначала сложить те члены выражения, которые легко складываются. Например, в выражении 49 + 29 + 51 +71 сначала легче сложить 49 + 51 = 100, потом 29 + 71 = 100 и, наконец, 100 + 100 = 200.
 Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.
Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.- В нашем примере 2x + 28 + 9 + 5 присутствуют две операции сложения. Начнем с самого крайнего (слева) члена: 2x + 28; вы не можете сложить 2х и 28, потому что не знаете значения переменной «х». Поэтому сложите 28 + 9 = 37. Теперь выражение можно переписать так: 2х + 37 — 5.
7
Вычтите. Это последняя операция в правильном порядке выполнения математических операций. На этом этапе вы также можете прибавлять отрицательные числа или же делать это на этапе сложения членов – это никак не отразится на конечном результате.
- В нашем примере 2х + 37 — 5 присутствует только одна операция вычитания: 37 — 5 = 32.
8
На этом этапе, проделав все математические операции, вы должны получить упрощенное выражение. Но если данное вам выражение содержит одну или несколько переменных, то помните, что член с переменной останется таким, как есть.
 Решение (а не упрощение) выражения с переменной подразумевает нахождение значения этой переменной. Иногда выражения с переменной можно упростить, используя специальные методы (смотрите следующий раздел).
Решение (а не упрощение) выражения с переменной подразумевает нахождение значения этой переменной. Иногда выражения с переменной можно упростить, используя специальные методы (смотрите следующий раздел).- В нашем примере окончательный ответ: 2х + 32. Вы не сможете сложить два члена, пока не узнаете значение переменной «х». Узнав значение переменной, вы с легкостью упростите этот двучлен.
Реклама
1
Сложение подобных членов. Помните, что вычитать и складывать можно исключительно подобные члены, то есть члены с одинаковой переменной и одинаковым показателем степени. Например, можно сложить 7x и 5x, но нельзя складывать 7x и 5x2 (так как здесь показатели степени разные).
- Это правило распространяется и на члены с несколькими переменными. Например, можно сложить 2xy2 и -3xy2, но нельзя складывать 2xy2 и -3x2y или 2xy2 и -3y2.

- Рассмотрим пример: x2 + 3x + 6 — 8x. Здесь подобными членами являются 3x и 8x, поэтому их можно сложить. Упрощенное выражение выглядит так: x2 — 5x + 6.
- Это правило распространяется и на члены с несколькими переменными. Например, можно сложить 2xy2 и -3xy2, но нельзя складывать 2xy2 и -3x2y или 2xy2 и -3y2.
2
Упростите числовую дробь. В такой дроби и в числителе, и в знаменателе находятся числа (без переменной). Числовая дробь упрощается несколькими способами. Во-первых, просто разделите знаменатель на числитель. Во-вторых, разложите числитель и знаменатель на множители и сократите одинаковые множители (так как при делении числа на само себя вы получите 1). Другими словами, если и у числителя, и у знаменателя есть один и тот же множитель, его можно отбросить и получить упрощенную дробь.
- Например, рассмотрим дробь 36/60. При помощи калькулятора разделите 36 на 60 и получите 0,6. Но вы можете упростить эту дробь и по-другому, разложив числитель и знаменатель на множители: 36/60 = (6х6)/(6х10) = (6/6)*(6/10). Так как 6/6 = 1, то упрощенная дробь: 1 х 6/10 = 6/10.
 Но эту дробь также можно упростить: 6/10 = (2х3)/(2*5) = (2/2)*(3/5) = 3/5.
Но эту дробь также можно упростить: 6/10 = (2х3)/(2*5) = (2/2)*(3/5) = 3/5.
- Например, рассмотрим дробь 36/60. При помощи калькулятора разделите 36 на 60 и получите 0,6. Но вы можете упростить эту дробь и по-другому, разложив числитель и знаменатель на множители: 36/60 = (6х6)/(6х10) = (6/6)*(6/10). Так как 6/6 = 1, то упрощенная дробь: 1 х 6/10 = 6/10.
3
Если дробь содержит переменную, можно сократить одинаковые множители с переменной. Разложите и числитель, и знаменатель на множители и сократите одинаковые множители, даже если они содержат переменную (помните, что здесь одинаковые множители могут содержать или не содержать переменную).
- Рассмотрим пример: (3x2 + 3x)/(-3x2 + 15x). Это выражение можно переписать (разложить на множители) в виде: (x + 1)(3x)/(3x)(5 — x). Так как член 3x находится и в числителе, и в знаменателе, его можно сократить, и вы получите упрощенное выражение: (х + 1)/(5 — х). Рассмотрим другой пример: (2x2 + 4x + 6)/2 = (2(x2 + 2x + 3))/2 = x2 + 2x + 3.
- Обратите внимание, что вы не можете сокращать любые члены – сокращаются только одинаковые множители, которые присутствуют как в числителе, так и в знаменателе.
 Например, в выражении (х(х + 2))/х переменная (множитель) «х» находится и в числителе, и в знаменателе, поэтому «х» можно сократить и получить упрощенное выражение: (х + 2)/1 = х + 2. Тем не менее, в выражении (х + 2)/х переменную «х» сокращать нельзя (так как в числителе «х» не является множителем).
Например, в выражении (х(х + 2))/х переменная (множитель) «х» находится и в числителе, и в знаменателе, поэтому «х» можно сократить и получить упрощенное выражение: (х + 2)/1 = х + 2. Тем не менее, в выражении (х + 2)/х переменную «х» сокращать нельзя (так как в числителе «х» не является множителем).
4
Раскройте скобки. Для этого умножьте член, стоящий за скобкой, на каждый член в скобках. Иногда это помогает упростить сложное выражение. Это относится как к членам, которые являются простыми числами, так и к членам, которые содержат переменную.
- Например, 3(x2 + 8) = 3x2 + 24, а 3x(x2 + 8) = 3x3 + 24x.
- Обратите внимание, что в дробных выражениях скобки раскрывать не нужно, если и в числителе, и в знаменателе присутствует одинаковый множитель. Например, в выражении (3(x2 + 8))/3x скобки раскрывать не нужно, так как здесь можно сократить множитель 3 и получить упрощенное выражение (x2 + 8)/x.
 С этим выражением легче работать; если бы вы раскрыли скобки, то получили бы следующее сложное выражение: (3x3 + 24x)/3x.
С этим выражением легче работать; если бы вы раскрыли скобки, то получили бы следующее сложное выражение: (3x3 + 24x)/3x.
5
Разложите на множители многочлены. При помощи этого метода можно упростить некоторые выражения и многочлены. Разложение на множители – это операция, противоположная раскрытию скобок, то есть выражение записывается в виде произведения двух выражений, каждое из которых заключено в скобки. В некоторых случаях разложение на множители позволяет сократить одинаковое выражение. В особых случаях (как правило, с квадратными уравнениями) разложение на множители позволит вам решить уравнение.
- Рассмотрим выражение x2 — 5x + 6. Оно раскладывается на множители: (x — 3)(x — 2). Таким образом, если, например, дано выражение (x2 — 5x + 6)/(2(x — 2)), то вы можете переписать его в виде (x — 3)(x — 2)/(2(x — 2)), сократить выражение (х — 2) и получить упрощенное выражение (х — 3)/2.

- Разложение многочленов на множители применяется для решения (нахождения корней) уравнений (уравнение – это многочлен, приравненный к 0). Например, рассмотрим уравнение x2 — 5x + 6 = 0. Разложив его на множители, вы получите (х — 3)(х — 2) = 0. Так как любое выражение, умноженное на 0, равно 0, то мы можем записать так: х — 3 = 0 и х — 2 = 0. Таким образом, х = 3 и х = 2, то есть вы нашли два корня данного вам уравнения.
Реклама
- Рассмотрим выражение x2 — 5x + 6. Оно раскладывается на множители: (x — 3)(x — 2). Таким образом, если, например, дано выражение (x2 — 5x + 6)/(2(x — 2)), то вы можете переписать его в виде (x — 3)(x — 2)/(2(x — 2)), сократить выражение (х — 2) и получить упрощенное выражение (х — 3)/2.
Об этой статье
На других языках
Как упростить математическое выражение — Wiki How Русский
Зачастую в задачах требуется привести упрощенный ответ. Хотя и упрощенный, и неупрощенный ответы являются верными, преподаватель может снизить вашу оценку, если вы не упростите ответ. Более того, с упрощенным математическим выражением гораздо легче работать. Поэтому очень важно научиться упрощать выражения.
Эту страницу просматривали 28 489 раз.
Реклама
Упрощение выражений — Алгебра II
Все ресурсы по Алгебре II
10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 Следующая →
Алгебра II Помощь » Базовая алгебра с одной переменной » Выражения » Упрощение выражений
Упростить x(4 – x) – x(3 – x).
Возможные ответы:
1
x
3x
0
x 2
Правильный ответ:
x
Объяснение:
Вы должны умножить первый набор скобок (распределить), и вы получите 4x – x 2 . Затем умножьте второй набор, и вы получите –3x + x 2 . Объедините одинаковые термины, и вы получите x.
х(4 – х) – х(3 – х)
4х – х 2 – х(3 – х)
4х – х 2 — (3x — x 2 )
4x — x 2 — 3x + x 2 = x
Отчет о ошибке
Разделение:
. Правильный ответ:
Правильный ответ:
Объяснение:
Разложить на множители числитель и знаменатель:
Отменить множители, которые появляются как в числителе, так и в знаменателе:
Сообщить об ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
Объяснение:
и сократить, оставив в числителе. 5 и 25 сокращаются, оставляя 5 в знаменателе
Сообщить об ошибке
Упростите следующее:
Возможные ответы:
Правильный ответ:
5
5 Объяснение:
Сначала, давайте учитываем число:
Отчет о ошибке
Найдите продукт:
Возможные ответы:
Правильный ответ:
Правильный ответ:
. Объяснение:
Объяснение:
Во-первых, умножьте моном на первый член многочлена:
Во-вторых, умножьте моном на второй член многочлена:
Добавить термины вместе:
Отчет о ошибке
Умножение, выражая продукт в простейшей форме:
Возможные ответы:
Правильный ответ:
. Объяснение:
Сократите коэффициенты, разделив 15 и 25 на 5, а 14 и 21 на 7:
Теперь используйте правило отношения переменных путем вычитания показателей степени:
Сообщить об ошибке
Упростите следующее:
Возможные ответы:
Правильный ответ:
Пояснение:
В этой задаче нужно умножить две дроби. Вы можете сначала упростить коэффициенты в числителях и знаменателях. Вы можете разделить и сократить 2 и 14 каждое на 2, а 3 и 15 каждое на 3:
Вы можете сначала упростить коэффициенты в числителях и знаменателях. Вы можете разделить и сократить 2 и 14 каждое на 2, а 3 и 15 каждое на 3:
Вы можете умножить два числителя и два знаменателя, имея в виду, что при умножении подобных переменных с показателями степени вы упрощаете на сложение показателей вместе:
Любые переменные, находящиеся как в числителе, так и в знаменателе, можно упростить, вычитая показатель степени числителя на показатель степени знаменателя. Если в числителе показатель степени отрицательный, можно переместить переменную в знаменатель, чтобы показатель степени оставался положительным:
Сообщить об ошибке
Разложить выражение на множители:
Возможные ответы:
5
Правильный ответ:Объяснение:
Чтобы найти наибольший общий множитель, нам нужно разбить каждый член на его простые множители:
Глядя на то, какие термины являются общими для всех трех выражений; таким образом, GCF равен . Затем мы учитываем это: .
Затем мы учитываем это: .
Сообщить об ошибке
Развернуть:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы расширить, умножьте 8x на оба члена в выражении (3x + 7).
8x умножить на 3x будет 24x².
8х умножить на 7 будет 56х.
Следовательно, 8x(3x + 7) = 24x² + 56x.
Сообщить об ошибке
Упрощение:
Возможные ответы:
Ни один из других ответов не является правильным.
Правильный ответ:
Объяснение:
Сначала распределите -5 через круглые скобки, умножив оба члена на -5.
Затем объедините одноименные переменные (–5x и –3x).
Сообщить об ошибке
← Предыдущая 1 2 3 4 5 6 7 8 Следующая →
Уведомление об авторских правах 630 практических тестов Вопрос дня Карточки Учитесь по концепции
Объяснение урока: Упрощение выражений: Правила экспоненты
В этом объяснении мы научимся упрощать алгебраические выражения, используя правила экспонентов.
Алгебраическое выражение будет вести себя очень похоже на выражение с участием чисел. Это связано с тем, что неизвестные переменные в алгебраическом выражение — неизвестные числа. Мы можем использовать эту идею для упрощения алгебраического выражения, включающие показатели степени; мы можем рассмотреть, как бы мы упростили выражение, включающее показатели степени числа.
Например, рассмотрим 22. Мы можем оценить это с помощью калькулятора;
однако мы также можем сделать это вручную. Напомним, что возведение числа 𝑏 в
положительный целочисленный показатель степени 𝑛 означает умножение
𝑛 много 𝑏. Мы можем использовать это, чтобы
расширить полномочия как продукты. Мы знаем, что 2 — это произведение 5 лотов.
из 2 и 2 является произведением 3 лотов по 2:
2=2×2×2×2×2,2=2×2×2.
Мы можем использовать это, чтобы
расширить полномочия как продукты. Мы знаем, что 2 — это произведение 5 лотов.
из 2 и 2 является произведением 3 лотов по 2:
2=2×2×2×2×2,2=2×2×2.
Подставляя их в частное, мы получаем 22=2×2×2×2×22×2×2.
Теперь мы можем отменить три общих множителя 2 в числителе и знаменатель, чтобы получить
Мы можем применить этот же процесс, даже если мы не знаем основы выражения. Например, если у нас есть 𝑏𝑏, то мы можем следовать точно таким же рассуждениям: 𝑏𝑏=𝑏×𝑏×𝑏×𝑏×𝑏𝑏×𝑏×𝑏=𝑏=𝑏.
Мы можем следовать этим же рассуждениям, чтобы показать много полезных результатов при упрощении экспоненциальные выражения. Они известны как законы показателей.
Закон: Законы экспонентов
Для любых оснований 𝑎 и 𝑏 и натуральных чисел 𝑚 и 𝑛 имеем следующее:
- Правило произведения для показателей: 𝑏×𝑏=𝑏
- Факторное правило для показателей: 𝑏𝑏=𝑏
- Мощность степенного правила для показателей степени: (𝑏)=𝑏×
- Сила правила произведения для показателей: (𝑎𝑏)=𝑎𝑏
Стоит отметить, что эти правила всегда остаются верными при условии, что мы можем
оценить выражения. Например, мы не можем делить на 0, поэтому мы не можем применить
правило отношения для показателей степени, если основание равно 0,
Например, мы не можем делить на 0, поэтому мы не можем применить
правило отношения для показателей степени, если основание равно 0,
Мы действительно можем доказать все эти законы, расширяя продукты и используя свойства мощностей и произведений. Например, мы можем переписать 𝑏×𝑏 путем расширения каждой степени:
У нас есть произведение 𝑚 множителей 𝑏 и 𝑛 факторы 𝑏. Заметим, что это произведение 𝑚+𝑛 коэффициенты 𝑏, которые можно переписать как 𝑏:
Мы можем следовать тому же процессу, чтобы показать все эти законы.
В нашем первом примере мы будем использовать законы экспонент, чтобы упростить произведение из двух мономов.
Пример 1. Упрощение произведения двух алгебраических выражений
Упростить 𝑥×𝑥.
Ответ
Чтобы упростить произведение двух мономов, сначала напомним, что произведение
правило для показателей говорит нам, что
𝑏×𝑏=𝑏. Мы можем применить это правило с
𝑏=𝑥, 𝑚=2 и 𝑛=3, чтобы получить
𝑥×𝑥=𝑥=𝑥.
В нашем следующем примере мы будем использовать законы показателей, чтобы упростить частное двух мономов.
Пример 2. Упрощение деления двух алгебраических выражений
Упростить 𝑥𝑥.
Ответ
Нас просят упростить частное двух мономов. Мы можем сделать это с помощью напоминая, что это похоже на правило частных для показателей, которое говорит, что для положительных целых чисел 𝑚 и 𝑛𝑏𝑏=𝑏.
В этом случае мы имеем 𝑏=𝑥, 𝑚=7 и 𝑛=6. Таким образом новый показатель находится вычитанием степеней: 𝑥𝑥=𝑥=𝑥.
Наконец, напомним, что при возведении числа в степень 1 выходит оно без изменений. Итак, 𝑥=𝑥, и мы показали, что 𝑥𝑥=𝑥.
В следующем примере мы упростим произведение двух мономов, используя законы показателей.
Пример 3. Упрощение умножения двух алгебраических выражений
Упростить 7𝑥×8𝑥.
Ответ
Нас просят упростить произведение двух мономов. Мы можем сделать это с помощью
отметив, что это похоже на правило произведения для показателей степени, которое гласит, что
для положительных целых чисел 𝑚 и 𝑛
𝑏×𝑏=𝑏.
Мы можем сделать это с помощью
отметив, что это похоже на правило произведения для показателей степени, которое гласит, что
для положительных целых чисел 𝑚 и 𝑛
𝑏×𝑏=𝑏.
Мы не можем напрямую применить этот закон, так как есть также постоянные факторы. Вместо этого давайте начнем с перестановки произведения таким образом, чтобы одинаковые термины умножаются вместе: 7𝑥×8𝑥=(7×8)×𝑥×𝑥.
Мы можем вычислить, что 7×8=56, и мы можем упростить 𝑥×𝑥 с помощью правила произведения для показателей. У нас есть 𝑏=𝑥, 𝑚=4 и 𝑛=7: (7×8)×𝑥×𝑥=56𝑥=56𝑥.
В нашем следующем примере мы будем использовать законы экспонент, чтобы упростить частное многочлена и монома.
Пример 4. Деление многочлена на одночлен
Упростить −43𝑥+12𝑥−6𝑥𝑥.
Ответ
Чтобы упростить частное многочлена и монома, мы сначала
нужно разделить деление на каждый член в числителе:
−43𝑥+12𝑥−6𝑥𝑥=−43𝑥𝑥+12𝑥𝑥−6𝑥𝑥.
Теперь мы видим, что каждый член является частным мономов. Мы можем упростить каждый член, используя правило отношения для показателей, которое говорит, что 𝑏𝑏=𝑏. Мы помним, что 𝑥=𝑥, и мы перепишем каждый член следующим образом: −43𝑥𝑥+12𝑥𝑥−6𝑥𝑥=−43𝑥𝑥+12𝑥𝑥−6𝑥𝑥.
Теперь мы можем упростить каждое частное, используя правило отношения для показателей степени. У нас есть −43𝑥𝑥+12𝑥𝑥 — 6𝑥𝑥 = −43𝑥+12𝑥 — 6𝑥 = −43𝑥+12𝑥 — 6𝑥 = −43𝑥+12𝑥 — 6𝑥.
В нашем следующем примере мы упростим алгебраическое выражение, включающее распределение произведения одночлена над двучленом.
Пример 5. Умножение одночлена на двучлен и упрощение
Вычислить −2𝑥𝑥+𝑥.
Ответ
Мы хотим разложить произведение одночлена на двучлен. Мы можем сделать это путем распределения произведения по каждому члену бинома. Мы делаем это в точно так же, как мы распределили бы произведение постоянной над биномом:
Мы можем упростить каждый термин, заметив, что каждый из них включает произведение
силы. Мы можем использовать правило произведения для показателей степени, которое гласит, что
𝑏×𝑏=𝑏.
Мы можем использовать правило произведения для показателей степени, которое гласит, что
𝑏×𝑏=𝑏.
Перепишем каждый термин, чтобы показать произведение степеней и применить законы показателей: −2𝑥×𝑥+−2𝑥×𝑥=−2𝑥×𝑥−2𝑥×𝑥=−2𝑥−2𝑥=−2𝑥−2𝑥.
В нашем последнем примере мы применим несколько законов экспонент, чтобы упростить алгебраическое выражение.
Пример 6. Упрощение выражения с использованием правил возведения в степень
Упрощение 2𝑥4𝑥×𝑥.
Ответ
Мы можем упростить это выражение, сначала упростив числитель и знаменатель отдельно, используя законы показателей. Начнем с числитель. Заметим, что это мощность произведения, поэтому воспользуемся правилом (𝑎𝑏)=𝑎𝑏 с 𝑎=2, 𝑏=𝑥 и 𝑛=4: 2𝑥=2𝑥.
Мы можем упростить это, заметив, что
𝑥
это сила власти. Мы можем использовать закон экспонент, который гласит, что
(𝑏)=𝑏×, чтобы упростить это:
2𝑥=16𝑥=16𝑥. ×
×
В знаменателе произведение степеней, поэтому можно упростить это с использованием закона показателей, который гласит, что 𝑏×𝑏=𝑏. У нас есть 4𝑥×𝑥=4𝑥×𝑥=4𝑥=4𝑥.
Теперь мы можем подставить выражения для числителя и знаменателя в частное, чтобы получить 2𝑥4𝑥×𝑥=16𝑥4𝑥.
Мы можем сократить общий множитель 4 и использовать правило отношения для показателей степени 𝑏𝑏=𝑏 для дальнейшего упрощения. Мы переписываем частное, чтобы упростить применение этих правил: 16𝑥4𝑥=164×𝑥𝑥.
Теперь оценим каждое частное. У нас есть 164×𝑥𝑥=4×𝑥=4𝑥.
Давайте закончим повторением некоторых важных моментов из этого объяснения.
Ключевые точки
- Для любых оснований 𝑎 и 𝑏 и натуральных чисел 𝑚 и
𝑛 имеем следующее:
- Правило произведения для показателей: 𝑏×𝑏=𝑏
- Факторное правило для показателей: 𝑏𝑏=𝑏
- Мощность степенного правила для показателей степени: (𝑏)=𝑏×
- Сила правила произведения для показателей степени: (𝑎𝑏)=𝑎𝑏

- Мы можем разложить произведение алгебраических выражений, а затем применить законы степени, чтобы найти эквивалентное выражение для произведения. Точно так же мы может использовать законы показателей, чтобы найти эквивалентные выражения для частных алгебраических выражений.
Упрощение выражений — Алгебра — GCSE Maths
Что такое упрощение выражений
Рабочие листы для упрощения выражений
Как упростить выражения
Распространенные заблуждения
Практические вопросы по упрощению выражений
Упрощение выражений Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Что такое упрощение выражений
Рабочие листы для упрощения выражений
Как упростить выражения
Распространенные заблуждения
Практические вопросы по упрощению выражений
Упрощение выражений Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Вот все, что вам нужно знать об упрощении алгебраических выражений для выпускных экзаменов по математике (Edexcel, AQA и OCR). Вы научитесь собирать одинаковые термины, писать и упрощать выражения, а также упрощать алгебраические дроби.
Вы научитесь собирать одинаковые термины, писать и упрощать выражения, а также упрощать алгебраические дроби.
Обратите внимание на рабочие листы для упрощения выражений с правильными ответами, задачами и экзаменационными вопросами в конце.
Что означает упрощение выражения
Упрощение алгебраического выражения — это когда мы используем различные методы, чтобы сделать алгебраические выражения более эффективными и компактными — в их простейшей форме — без изменения значения исходного выражения.
Что означает упрощение выражения?
Рабочие листы по упрощению выражений
Получите бесплатный рабочий лист по упрощению выражений, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочие листы по упрощению выражений
Получите бесплатный рабочий лист по упрощению выражений, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Как упростить выражения
Чтобы упростить выражения, сначала раскройте любые скобки, затем умножьте или разделите любые члены и при необходимости используйте законы индексов, затем соберите одинаковые члены, сложив или вычитая, и, наконец, перепишите выражение.
Например, чтобы упростить
\[8 x+4+3(2 x-3) \]
- Раскройте скобки
\[8 x+4+6 x-9 \]
2Собрать похожие термины
\[\begin{aligned} 8 х+6 х&=14 х \\ 4-9&=-5 \end{выровнено} \]
3Перепишите выражение
\[\begin{align}8 x+4+3(2 x-3) \\ =14 х-5\конец{выровнено} \]
Какие 5 методов используются для упрощения выражений?
Как упростить выражение, собирая одинаковые термины
Чтобы упростить алгебраическое выражение, нам нужно ‘ собрать похожие термины ‘, сгруппировав похожие термины:
Когда мы выделяем похожие термины, мы должны поставить знак перед термином и, при необходимости, определить отрицательные числа.
+8x ✔
8x ✘
-2y✔
2y✘
Что такое термины?
Подобные термины имеют одинаковую комбинацию переменных и/или чисел, но коэффициенты могут быть другими.
Например…
4 и 9 подобны терминам ✔
3x и 5x подобны терминам ✔
2ab и -5ab подобны терминам ✔
НО
9004 90 и 3x не похожи термины ✔ 2x не похожи ✘
x 2 и x не похожи ✘
Способы упрощения выражений
+4-2 x+8 y-7\]
1 Определите похожие термины
Термины, включающие x, подобны терминам. Термины, включающие y, подобны терминам. Постоянные термины подобны терминам.
Знак плюс (или минус) относится к термину перед ним.
2 Сгруппируйте одинаковые термины
\[5 x-2 x+3 y+8 y+4-7\]
3 Объедините похожие термины, добавляя или вычитая
\begin{align} 5 х-2 х=3 х \\\\ 3 г+8 г=11 г \\\\ 4-7=-3 \end{выровнено}
Итак,
\begin{выровнено} 5 х+3 у+4-2 х+8 у-7 \\\\ =3 х+11 у-3 \end{выровнено} 9{2} b c \div 2 a=6 a b c\]
Итак,
\[\frac{3 a b \times 4 a c}{2 a}=6 a b c\]
3.
 Раскрывающие скобки
Раскрывающие скобкиПример раскрывающиеся скобки:
\[3(2 x+5)\]
1 Умножить член за скобками на первый член в скобках
\[3 \times 2 x=6 x\]
2 Умножьте член вне скобок на второй член в скобках.
\[3 х 5=15\]
Итак,
\[3(2 х+5)=6 х+15\]
Пошаговое руководство: Раскрывающие скобки
См. также: Расширить и упростить
4. Алгебраические дроби
Пример алгебраических дробей
Упростить
90}{x12 \fracy{8×12} [0}{8×12] \]1 Найдите наибольший общий множитель (ОПК) числителя и знаменателя.
HCF 12xy и 8x равен 4 x
2 Разделите числитель и знаменатель на это значение.
Числитель
\[12xy \div 4x=3y\]
Знаменатель
\[8x\div 4x=2\]
3 Переписать упрощенную дробь
\[\frac{12xy}{8x}\]
\ [=\frac{3y}{2}\]
Пошаговое руководство: Алгебраические дроби
См. также o: Упрощение алгебраических дробей
также o: Упрощение алгебраических дробей
5. Напишите и упростите алгебраические выражения
Мы можем написать алгебраические выражения для упрощения задач. Мы часто сможем составить линейное уравнение или квадратное уравнение и решить его.
Пример написания и упрощения выражения
Напишите выражение для периметра фигуры.
- Внимательно прочитайте вопрос и выделите ключевую информацию.
Ключевые слова:
Выражение : набор терминов, объединенных с помощью (+, −, ✕ и ÷)
Периметр : расстояние вокруг края фигуры 9 0 0 0 9 чтобы сложить вместе каждую из длин фигуры.
2Напишите выражение и упростите его.
Затем мы упрощаем следующее выражение, добавляя и вычитая члены.
\[\begin{выровнено} Периметр&=\color{#00BC89}{2x}\color{#7C4DFF}{+3}\color{#00BC89}{+x}\color{#7C4DFF}{-2}\color{#00BC89}{+2x }\color{#7C4DFF}{+3}\color{#00BC89}{+x}\color{#7C4DFF}{-2}\\ &=\цвет{#00BC89}{6x}\цвет{#7C4DFF}{+2} \end{aligned}\]
Примеры упрощения выражений
Пример 1: сбор одинаковых термов с одной переменной и одной константой
Упростить
\[8x+5-2x+6\]
- Подчеркните похожие члены в выражении и соедините их.

\begin{align}8 x-2 x=6 x \\\\\ 5+6=11 \end{aligned}
2Перепишите выражение.
\begin{выровнено} 8 х+5-2 х+6 \\\\ =6 х+11 \end{align}
Пример 2: сбор похожих термов с несколькими переменными и одной константой
Упростить
\[5xy+3y-4-2xy-8y+7\]
Подчеркнуть похожие термины в выражении 9{2}-9}\]
\[=\frac{x-5}{x-3}\]
Пошаговое руководство: Факторизация квадратичных уравнений
Пошаговое руководство направляющая: Разность двух квадратов
Пример 7: выражение для площади
Напишите выражение для площади фигуры.
Внимательно прочитайте вопрос и выделите ключевую информацию.
Ключевые слова:
Выражение : набор терминов, объединенных с помощью (+, −, ✕ и ÷) 9{2}+5x+2\]
Пример 8: сформулированная задача
Софи x лет,
Эмили на три года моложе Софи
Амейла в четыре раза старше Софи.
Напишите выражение для каждого возраста.
Внимательно прочитайте вопрос и подчеркните ключевую информацию.
Нам сказали, что Софи х лет
Эмили на три года моложе Софи, поэтому на три меньше х равно х — 3
Амейла в четыре раза старше Софи, поэтому четыре партии х — 3 4 (х — 3).
Нам нужны скобки, потому что мы умножаем все x − 3 на 4
Напишите выражение и упростите его.
Софи х лет
Эмили х — 3 года
Амейле 4(х — 3) = 4х — 12 лет
Распространенные заблуждения
- является его частью
Когда мы подчеркиваем подобные термины, мы должны поставить знак перед 9{2}\\
\end{выровнено} При сложении и умножении порядок вычислений не имеет значения и Это не относится к вычитанию и делению. Для того, чтобы два термина были «подобными терминам», им нужна одинаковая комбинация переменных. 3×2 и 5×2 похожи друг на друга 2a2b и -5a2bare, как и термины , но 3×2 и 5x не похожи на термины 2a2b, а -5ab не похожи на термины 4. нужно использовать скобки, чтобы каждое слагаемое умножалось. Для постоянных членов имеем 7-9=-2 Для переменных членов имеем 9{2}+14x+15 2(x+11) Возраст Стива = x Возраст Рэйчел = x+11 Возраст Барри = 2(x+11)=2x+22 Всего возрастов =x+x+11+2x+ 22 \\ \frac{3ab}{2} \frac{3}{2} \frac{6ab}{4} Наибольший общий делитель числителя и знаменателя равен 6 , поэтому мы делим числитель и знаменатель на 6 , что приводит к упрощенной дроби. 2x+3x=3x+2x=5x
2a3b=3b2a=6ab

2(у+4)\\
2\раз у+4
Практические вопросы по упрощению выражений
& =4x+33
\end{выровнено} [/katex]


 Запомните следующий порядок выполнения математических операций: выражение в скобках, возведение в степень, умножение, деление, сложение, вычитание.
Запомните следующий порядок выполнения математических операций: выражение в скобках, возведение в степень, умножение, деление, сложение, вычитание. Здесь начнем с выражений в скобках: 5 + 2 = 7 и 3 + 4/2 = 3 + 2 =5.
Здесь начнем с выражений в скобках: 5 + 2 = 7 и 3 + 4/2 = 3 + 2 =5. Но если между числом и переменной (например, 2х) или между числом и числом в скобках (например, 4(7)) нет никаких символов, то это также является операцией умножения.
Но если между числом и переменной (например, 2х) или между числом и числом в скобках (например, 4(7)) нет никаких символов, то это также является операцией умножения.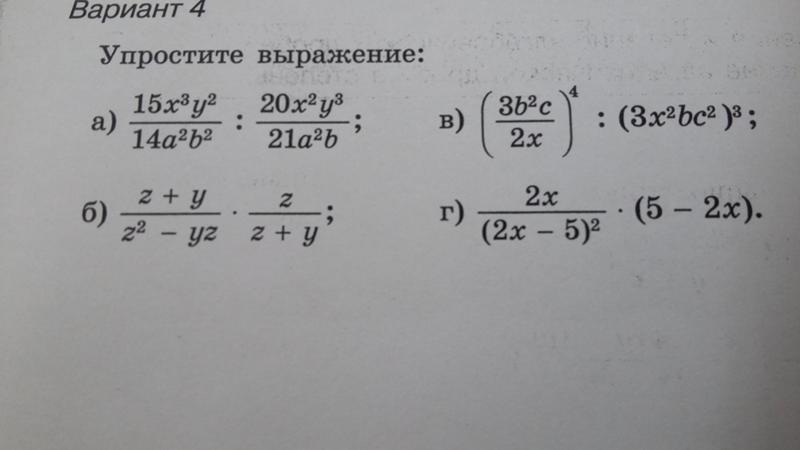 Например, в выражении 49 + 29 + 51 +71 сначала легче сложить 49 + 51 = 100, потом 29 + 71 = 100 и, наконец, 100 + 100 = 200. Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.
Например, в выражении 49 + 29 + 51 +71 сначала легче сложить 49 + 51 = 100, потом 29 + 71 = 100 и, наконец, 100 + 100 = 200. Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200. Решение (а не упрощение) выражения с переменной подразумевает нахождение значения этой переменной. Иногда выражения с переменной можно упростить, используя специальные методы (смотрите следующий раздел).
Решение (а не упрощение) выражения с переменной подразумевает нахождение значения этой переменной. Иногда выражения с переменной можно упростить, используя специальные методы (смотрите следующий раздел). Упрощенное выражение выглядит так: x 2 — 5x + 6.
Упрощенное выражение выглядит так: x 2 — 5x + 6. Разложите и числитель, и знаменатель на множители и сократите одинаковые множители, даже если они содержат переменную (помните, что здесь одинаковые множители могут содержать или не содержать переменную).
Разложите и числитель, и знаменатель на множители и сократите одинаковые множители, даже если они содержат переменную (помните, что здесь одинаковые множители могут содержать или не содержать переменную).

 Простейшие алгебраические выражения (которые не содержат дробей, корней и так далее) можно решить (упростить) всего за несколько шагов.
Простейшие алгебраические выражения (которые не содержат дробей, корней и так далее) можно решить (упростить) всего за несколько шагов.
 НОД — это наибольшее число, на которое делятся все коэффициенты выражения.
НОД — это наибольшее число, на которое делятся все коэффициенты выражения. В этом случае вынесение множителя за скобки может помочь избавиться от дроби (от знаменателя).
В этом случае вынесение множителя за скобки может помочь избавиться от дроби (от знаменателя). Или можно разделить каждый член числителя на знаменатель и таким образом упростить выражение.
Или можно разделить каждый член числителя на знаменатель и таким образом упростить выражение. В некоторых выражениях присутствуют операции умножения или деления членов со степенью. В случае умножения членов с одним основанием их степени складываются; в случае деления членов с одним основанием их степени вычитаются.
В некоторых выражениях присутствуют операции умножения или деления членов со степенью. В случае умножения членов с одним основанием их степени складываются; в случае деления членов с одним основанием их степени вычитаются.



 Мы не знаем значения х, поэтому выражение 2х оставим как есть. 4(7) = 4 х 7 = 28. Теперь вы можете переписать данное вам выражение так: 2x + 28 + 9 — 5.
Мы не знаем значения х, поэтому выражение 2х оставим как есть. 4(7) = 4 х 7 = 28. Теперь вы можете переписать данное вам выражение так: 2x + 28 + 9 — 5. Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.
Гораздо сложнее складывать так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200. Решение (а не упрощение) выражения с переменной подразумевает нахождение значения этой переменной. Иногда выражения с переменной можно упростить, используя специальные методы (смотрите следующий раздел).
Решение (а не упрощение) выражения с переменной подразумевает нахождение значения этой переменной. Иногда выражения с переменной можно упростить, используя специальные методы (смотрите следующий раздел).
 Но эту дробь также можно упростить: 6/10 = (2х3)/(2*5) = (2/2)*(3/5) = 3/5.
Но эту дробь также можно упростить: 6/10 = (2х3)/(2*5) = (2/2)*(3/5) = 3/5. Например, в выражении (х(х + 2))/х переменная (множитель) «х» находится и в числителе, и в знаменателе, поэтому «х» можно сократить и получить упрощенное выражение: (х + 2)/1 = х + 2. Тем не менее, в выражении (х + 2)/х переменную «х» сокращать нельзя (так как в числителе «х» не является множителем).
Например, в выражении (х(х + 2))/х переменная (множитель) «х» находится и в числителе, и в знаменателе, поэтому «х» можно сократить и получить упрощенное выражение: (х + 2)/1 = х + 2. Тем не менее, в выражении (х + 2)/х переменную «х» сокращать нельзя (так как в числителе «х» не является множителем). С этим выражением легче работать; если бы вы раскрыли скобки, то получили бы следующее сложное выражение: (3x3 + 24x)/3x.
С этим выражением легче работать; если бы вы раскрыли скобки, то получили бы следующее сложное выражение: (3x3 + 24x)/3x.

