проверка функции на четность и нечетность
Что такое четность и нечетность функции
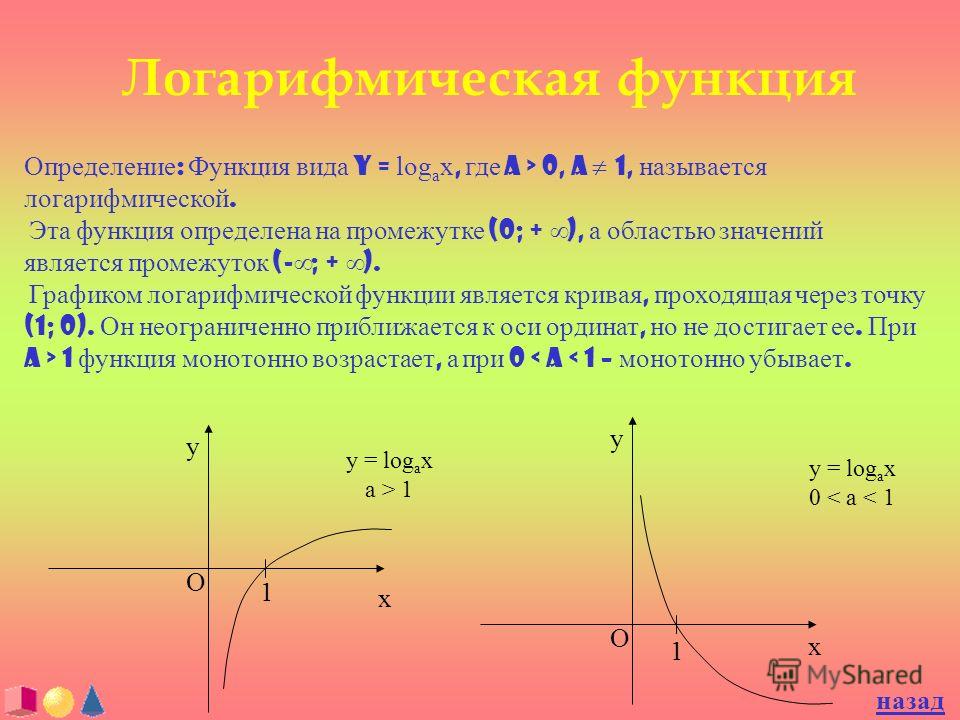
Если проанализировать графики функций, можно заметить, что некоторые из них симметричны либо относительно оси ординат, либо относительно точки начала координат.
Симметрия графика отражается в такой характеристики функции как четность или нечетность.
Исследование на четность и нечетность имеет важное значение в разделах математического анализа, описывающих разложение в числовые ряды (степенные, ряды Фурье).
Определение 1Не все функции можно отнести к четным или нечетным. Такие функции, не являющимися четными или нечетными, принято называть функциями общего вида.
Четная функция
Дадим определение четной функции.
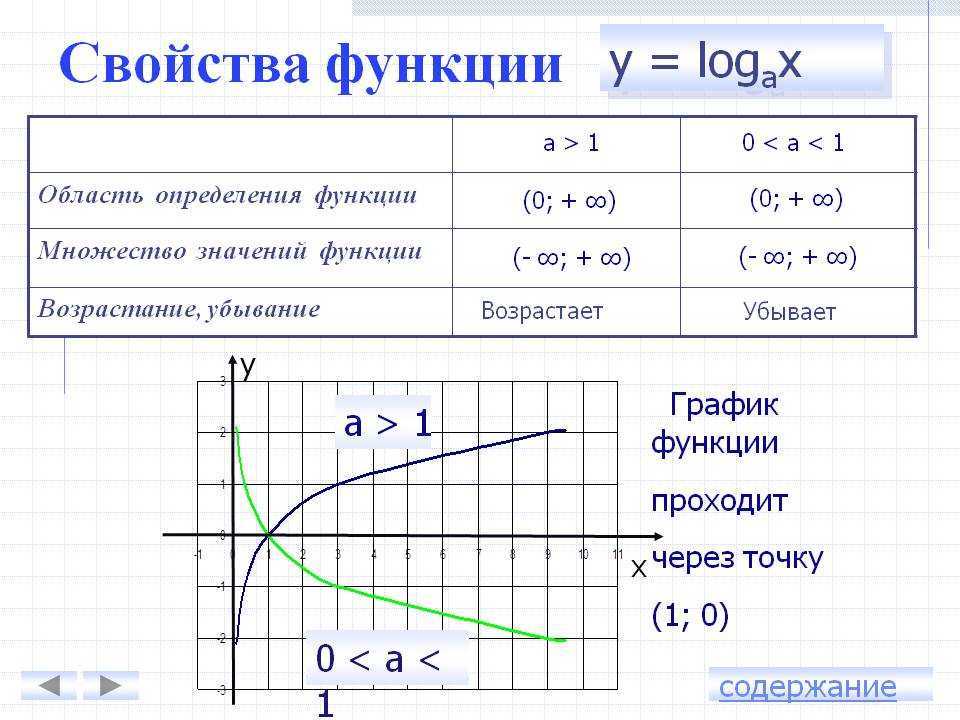
Определение 2Функцию считают четной, если выполняется следующее условие: f(-x)=f(x) для x∈X, где X — область допустимых значений.
Четные функции симметричны относительно оси ординат.
Квадратичная парабола, заданная уравнением y=ax2+b, является четной функции. В доказательство этого утверждения приведем график параболы.
В доказательство этого утверждения приведем график параболы.
Из рисунка видно, что график симметричен относительно оси Y. Проверим функцию на соответствие условию четности. В уравнении параболы y=ax2+b заменим x на (–x):y(-x)=a(-x)2+b=ax2+b. Получим y(-x)=y(x), значит, функция четна.
К четным относится также функция модуля y=|x|.
В тригонометрии четной является функция косинуса, так как косинус обладает свойством cos(-α)=cos(α).
Сформулируем необходимые условия четности функции:
- область определения должна быть симметрична относительно оси ординат;
- должно выполняться равенство f(-x)=f(x).
Условие о симметричности области определения подразумевает полную симметрию. Если на области допустимых значений имеются исключенные точки или промежутки, они также должны быть симметричны относительно оси Y.
Нечетная функция
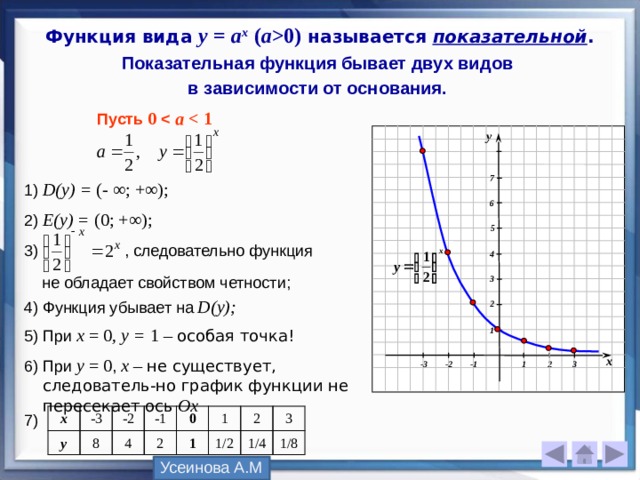
Определение 3Функцию считают нечетной, если выполняется следующее условие: f(-x)=-f(x) для x∈X, где X — область допустимых значений.
Нечетные функции симметричны относительно начала координат.
Примером нечетной функции можно назвать кубическую параболу вида y=ax3.
Выясним, соблюдается ли условие нечетности, для чего подставим в формулу параболы значение (–x):y(-x)=a(-x)3=-ax3. Получили, что y(-x)=-y(x).
Из тригонометрических функций к нечетным относится функция синуса, так как для синуса справедливо тождество sin(-α)=-sin(α)
Необходимые условия нечетности функции:
- область определения симметрична относительно начала координат;
- для всех х из области допустимых значений выполняется равенство f(-x)=-f(x).
Замечание относительно симметричности аналогично замечанию о четных функциях.
Свойства четных и нечетных функций
Четные и нечетные функции обладают следующими свойствами:
- Результатом сложения или вычитания четных функций является четная функция, нечетных — нечетная функция.
- При взятии производной результат будет противоположным.
 В случае четной функции производная будет нечетной, и наоборот.
В случае четной функции производная будет нечетной, и наоборот. - Умножение четных функций дает четную функцию, как и умножение нечетных функций.
- Произведение четной и нечетной функций есть нечетная функция.
Примеры на исследование функции
Прежде чем приступить к рассмотрению примеров, перечислим два способа определения четности:
- графический;
- аналитический.
При использовании графического способа строят график функции. По графику узнают о симметричности области определения, после чего делают вывод о четности функции.
В аналитическом способе в уравнении функции делают замену x на (–x). Выражение функции упрощают и проверяют соблюдения условия f(-x)=f(x) или f(-x)=-f(x).
В основном, при решении задач комбинируют два перечисленных способа.
Пример 1Графически определить, является ли функция y=cos2x+2 четной или нечетной.
Решение
Построим график заданной функции.
Из рисунка видно, что график симметричен относительно оси ординат, значит, функция четна.
Ответ: функция четна.
Пример 2Без построения определить, четна или нет функция y=1x+4-10.
Решение
В выражении функции имеется дробь. Нахождение точек, не входящих в область определения, сводится к решению уравнения x+4=0. Получим D(f)=(-∞; -4)∪(-4; +∞). Функция имеет одну точку разрыва, то есть область определения не симметрична относительно оси ординат. Функция не может быть четной.
Проверим четность еще раз, сделав замену x на (–х).
y(-x)=1(-x)+4-10=14-x-10
Получили, что y(-x)≠y(x) и y(-x)≠-y(x).
Ответ: функция общего вида.
Пример 3Без построения графика выяснить, является функция y=x2+3×5 четной.
Решение
Область определения имеет одну точку разрыва x=0, так как в этом случае знаменатель обращается в ноль. Указанная точка совпадает с началом координат. Сделаем замену x на (–х).
y(-x)=(-x)2+3(-x)5=x2+3-x5=-x2+3×5
Получили, что y(-x)=-y(x).
Ответ: функция нечетная.
Виды функций (четные, нечетные, общего вида, периодические функции) — Студопедия
Поделись
Глава 1.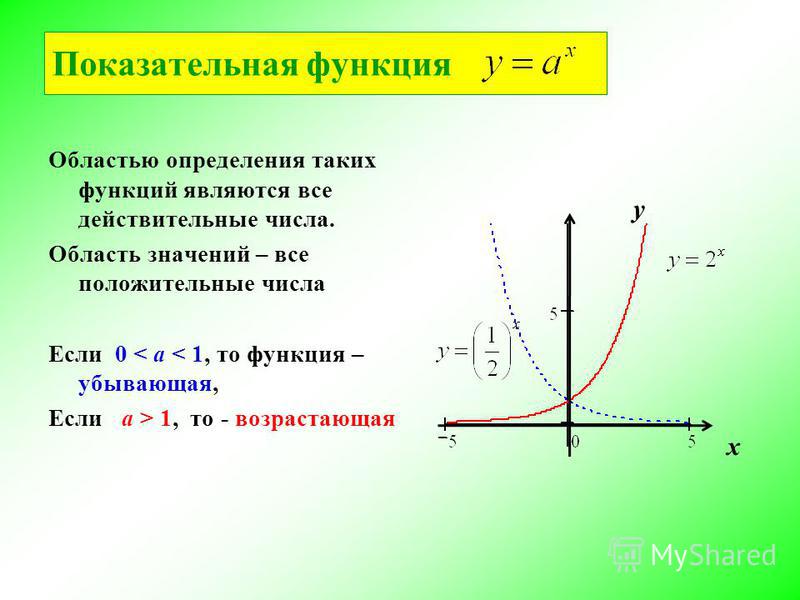 Развитие понятия функции
Развитие понятия функции
Изучение свойств функции и построение ее графика являются одним из самых замечательных приложений производной. Этот способ исследования функции неоднократно подвергался тщательному анализу. Основная причина состоит в том, что в приложениях математики приходилось иметь дело со все более и более сложными функциями, появляющимися при изучении новых явлений. Появились исключения из разработанных математикой правил, появились случаи, когда вообще созданные правила не годились, появились функции, не имеющие ни в одной точке производной.
Развитие функциональных представлений в курсе изучения алгебры и начал анализа на старшей ступени обучения помогает получить наглядные представления о непрерывности и разрывах функций, узнать о непрерывности любой элементарной функции на области ее применения, научиться строить их графики и обобщить сведения об основных элементарных функциях и осознать их роль в изучении явлений реальной действительности, в человеческой практики.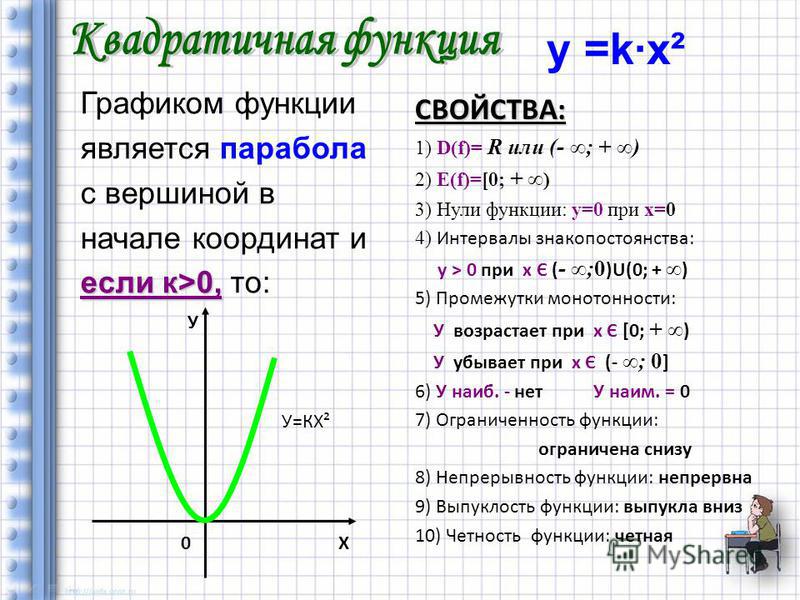
Начиная с XVIII века одним из важнейших понятий является понятие функции. Оно сыграло и поныне играет большую роль в познании реального мира.
Необходимые предпосылки к возникновению понятия функции были созданы, когда возникла аналитическая геометрия, характеризующаяся активным привлечением алгебры к решению геометрических задач.
Идея функциональной зависимости возникла в глубокой древности. Она содержится уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур и геометрических тел.
Однако явное и вполне сознательное применение понятия функции и систематическое изучение функциональной зависимости берет свое начало в XVII веке в связи с проникновением в математику идеи переменных.
Четкого представления понятия функции в XVII веке еще не было, однако путь к первому такому определению проложил Декарт. Постепенно понятие функции стало отождествляться с понятием аналитического выражения – формулы.
Явное определение функции было впервые дано в 1718 году Иоганном Бернулли: «Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
Во второй половине XIX века понятие функции формулируется следующим образом: если каждому элементу х множества А поставлен в соответствие некоторый определенный элемент у множества В, то говорят, что на множестве А задана функция y = f(x), или что множество А отображено на множество В.
Общее понятие функции применимо, конечно, не только к величинам и числам, но и к другим математическим объектам, например, к геометрическим фигурам.
Краткий обзор развития понятия функции приводит к мысли о том, что эволюция еще далеко не закончена и, вероятно, никогда не закончится, как никогда не закончится и эволюция математики в целом.
Глава 2. Основные свойства функции
Определение функции и графика функции. Область определения и область значений функции.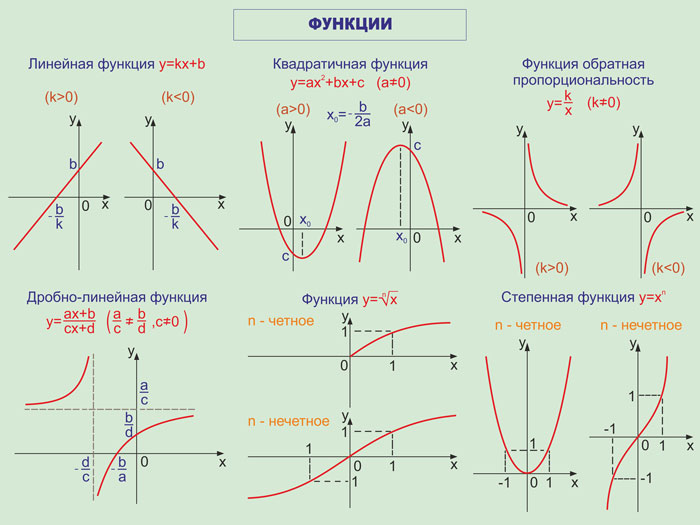 Нули функции
Нули функции
функция график экономический
Умение изображать геометрически функциональные зависимости, заданные формулами, особенно важно для успешного усвоения курса высшей математики.
Как известно, функциональной зависимостью называют закон, по которому каждому значению величины х из некоторого множества чисел, называемого областью определения функции, ставится в соответствие одно вполне определенное значение величины у; совокупность значений, которые принимает зависимая переменная у, называется областью изменения функции.
Независимую переменную х называют также аргументом функции. Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f(x).
Функцию можно задать тремя способами: аналитический, табличный, графический.
Аналитический – с помощью формул.
Табличный – с помощью таблиц, где можно указать значения функции, однако лишь для конечного набора значений аргумента.
Графический способ задания функции очень удобен: он дает возможность наглядно представить свойства функции.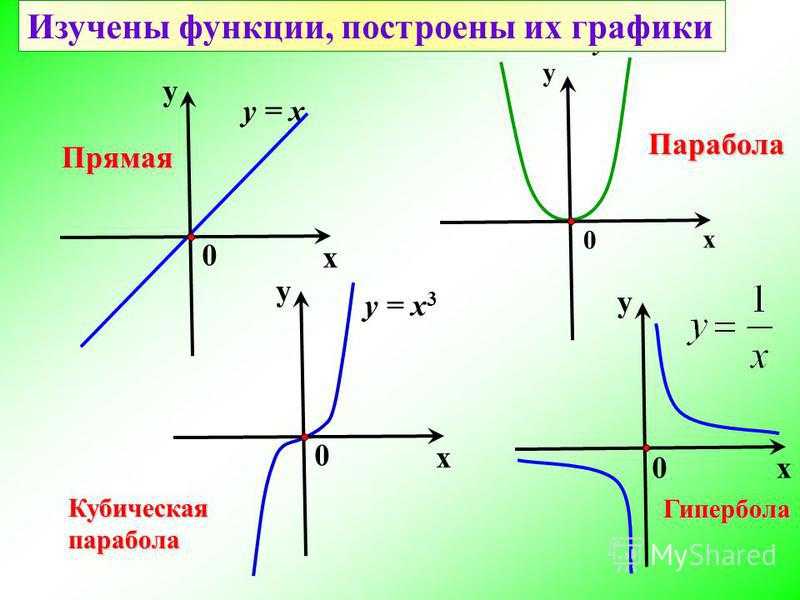
Графиком функции f называют множество всех точек (х;у) координатной плоскости, где y=f(x), а х «пробегает» всю область определения функции f.
Пример 1. Найти область определения функции
y = lg (2x-3) у = lg(2x-3)
D(y): 2x-3 > 0
2x > 3
х > 1,5
Ответ: D(y) = (1,5; +∞ ).
Одним из понятий для исследования функции является нули функции.
Нули функции – это точки, в которых функция принимает значение нуля.
Пример 2. Найти нули функции
y = 4x-8
у = 4x-8
D(y) = R
По определению:
у = 0,
тогда
4х-8 = 0
4x = 8
х = 2
Ответ: нулями этой функции является точка х = 2.
Виды функций (четные, нечетные, общего вида, периодические функции)
Рассмотрим функции, области определения которых симметричны относительно начала координат, то есть для любого х из области определения число (-х) также принадлежит области определения. Среди таких функций выделяют четные и нечетные.
Среди таких функций выделяют четные и нечетные.
Определение: Функция f называется четной, если для любого х из ее области определения f(-x) = f(x).
График четной функции симметричен относительно оси ординат.
Пример 3. Определить вид функции
y = 2cos2x.
у = 2cos2x,
D(y) = R
y(-x) = 2cos2(-x) = -2cos2x = 2cos2x = y(x) – четная.
Пример 4. Определить вид функции
y = x4 — 2×2 + 2.
Y = x4 — 2×2 + 2,
D(y) = R.
y(-x) = (-x)4 — 2(-x)2 + 2 = x4 — 2×2 + 2 = y(x) – четная.
Определение: Функция f называется нечетной, если для любого х из ее области определения f(-x) = -f(x).
График нечетной функции симметричен относительно начала координат.
Пример 5. Определить вид функции
y = 2sin2x.
у = 2sin2x,
D(y) = R
y(-x) = 2sin2(-x) = -2sin2x = -y(x) – нечетная.
Пример 6. Определить вид функции
y = 3x + 1/3x.
у = 3x + 1/3x
y(-x) = 3(-x) + 1/3(-x) = -3x — 1/3x = -(3x + 1/3x) = -y(x) – нечетная.
Определение: Функцию f называют периодической с периодом Т≠ 0, если для любого х из области определения значения этой функции в точках х, х -Т и х+Т равны, то есть f(x+T) = f(x) = f(x-T).
Пример 7. Определить период функции
y = cos2x.
cos2x = cos2(x+T) = cos(2x+2T),
где 2T = 2π, т.е. Т = π.
Для построения графика периодической функции с периодом Т достаточно провести построение на отрезке длиной Т и затем полученный график параллельно перенести на расстояния nT вправо и влево вдоль оси Ох.
Пример 8. Построить график периодической функции
f(x) = sin2x.
f(x) = sin2x,
sin2x = sin2(x+T) = sin(2x+2T),
где 2Т = 2π, т.е. Т = π.
Tutorial: Начало работы с дженериками
Этот туториал знакомит с основами дженериков в Go. С помощью дженериков вы можете
объявлять и использовать функции или типы, которые написаны для работы с любым набором
типов, предоставляемых вызывающим кодом.
В этом руководстве вы объявите две простые необобщенные функции, а затем та же логика в одной универсальной функции.
Вы пройдете следующие разделы:
- Создайте папку для своего кода.
- Добавить необобщенные функции.
- Добавьте общую функцию для обработки нескольких типов.
- Удалить аргументы типа при вызове универсальной функции.
- Объявите ограничение типа.
Примечание: Другие учебные пособия см. в разделе Учебные пособия.
Примечание: При желании вы можете использовать игровая площадка Go в режиме «Go dev branch» вместо этого редактировать и запускать вашу программу.
Предпосылки
- Установка Go 1.18 или более поздней версии. Инструкции по установке см. Установка Го.
- Инструмент для редактирования вашего кода. Любой текстовый редактор, который у вас есть, будет работать нормально.

- Командный терминал. Go хорошо работает с любым терминалом на Linux и Mac, и на PowerShell или cmd в Windows.
Создайте папку для вашего кода
Для начала создайте папку для кода, который вы будете писать.
Откройте командную строку и перейдите в свой домашний каталог.
В Linux или Mac:
$ кд
В Windows:
C:\> компакт-диск %HOMEPATH%
В остальной части руководства в качестве подсказки будет отображаться символ $. Команды, которые вы используете будет работать и в Windows.
В командной строке создайте каталог для своего кода с именем generics.
$ mkdir дженерики $ cd дженерики
Создайте модуль для хранения вашего кода.
Запустите команду
go mod init, указав путь к модулю вашего нового кода.$ go mod init пример/универсальные go: создание нового go.mod: пример модуля/дженерики
Примечание.
 Для производственного кода следует указать более конкретный путь к модулю.
к вашим собственным потребностям. Чтобы узнать больше, обязательно посмотрите
Управление зависимостями.
Для производственного кода следует указать более конкретный путь к модулю.
к вашим собственным потребностям. Чтобы узнать больше, обязательно посмотрите
Управление зависимостями.
Далее вы добавите простой код для работы с картами.
Добавить необобщенные функции
На этом шаге вы добавите две функции, каждая из которых суммирует значения карту и вернуть общее количество.
Вы объявляете две функции вместо одной, потому что работаете с двумя
различные типы карт: одна, которая хранит значения int64
значения float64 .Напишите код
Используя текстовый редактор, создайте файл с именем main.go в дженериках. каталог. Вы будете писать свой код Go в этом файле.
В файл main.go в верхней части файла вставьте следующий пакет декларация.
пакет основной
Автономная программа (в отличие от библиотеки) всегда находится в пакете
main.
Под объявлением пакета вставьте следующие две функции декларации.
// SumInts суммирует значения m. func SumInts(m map[string]int64) int64 { переменная int64 для _, v := диапазон m { с += v } вернуть с } // SumFloats суммирует значения m. func SumFloats(m map[string]float64) float64 { переменная с плавающей запятой64 для _, v := диапазон m { с += v } вернуть с }В этом коде вы:
- Объявить две функции для сложения значений карты и возврата
сумма.
-
SumFloatsпреобразуетстрокив значенияfloat64. -
SumIntsберет карту изстрокв значенияint64.
-
- Объявить две функции для сложения значений карты и возврата
сумма.
В верхней части main.go под объявлением пакета вставьте следующее
основная функциядля инициализации двух карт и использования их в качестве аргументов при вызов функций, которые вы объявили на предыдущем шаге.
функция main () { // Инициализировать карту для целочисленных значений целые числа: = карта [строка] int64 { «первая»: 34, "второй": 12, } // Инициализируем карту для значений с плавающей запятой поплавки: = карта [строка] float64 { «первый»: 35,98, «секунда»: 26,99, } fmt.Printf("Необщие суммы: %v и %v\n", SumInts(целые), SumFloats(плавает)) }В этом коде вы:
- Инициализировать карту из
значений float64и карту изint64значения, каждое с двумя входами. - Вызовите две объявленные ранее функции, чтобы найти сумму каждой из них. значения карты.
- Распечатать результат.
- Инициализировать карту из
В верхней части main.go, прямо под объявлением пакета, импортируйте package, который вам понадобится для поддержки кода, который вы только что написали.
Первые строки кода должны выглядеть так:
пакет основной импортировать "фмт"
Сохранить main.
 go.
go.
Запустите код
Из командной строки в каталоге, содержащем main.go, запустите код.
$ беги. Необщие суммы: 46 и 62,97.
С помощью дженериков здесь можно написать одну функцию вместо двух. Далее вы будете добавьте одну общую функцию для карт, содержащих либо целочисленные значения, либо значения с плавающей запятой.
Добавьте общую функцию для обработки нескольких типов
В этом разделе вы добавите одну универсальную функцию, которая может получать карту содержащие либо целые числа, либо значения с плавающей запятой, фактически заменяя два функции, которые вы только что написали с помощью одной функции.
Для поддержки значений любого типа этой единственной функции потребуется способ объявить, какие типы он поддерживает. С другой стороны, для вызова кода потребуется способ указать, вызывается ли он с целочисленной или плавающей картой.
Для поддержки этого вы напишете функцию, которая объявляет параметры типа в
в дополнение к своим обычным параметрам функции. Эти параметры типа делают
универсальная функция, позволяющая ей работать с аргументами разных типов. Ты будешь
вызвать функцию с 9Аргументы типа 0193 и обычные аргументы функций.
Эти параметры типа делают
универсальная функция, позволяющая ей работать с аргументами разных типов. Ты будешь
вызвать функцию с 9Аргументы типа 0193 и обычные аргументы функций.
Каждый параметр типа имеет ограничение типа , которое действует как своего рода метатип для параметра типа. Каждое ограничение типа указывает допустимый тип аргументы, которые вызывающий код может использовать для соответствующего параметра типа.
Хотя ограничение параметра типа обычно представляет собой набор типов, в во время компиляции параметр типа обозначает один тип — предоставленный тип в качестве аргумента типа вызывающим кодом. Если тип аргумента типа не допускается ограничением параметра типа, код не будет компилироваться.
Имейте в виду, что параметр типа должен поддерживать все операции универсального
код выполняется на нем. Например, если код вашей функции пытается
выполнить строковых операций (таких как индексация) над параметром типа,
ограничение включало числовые типы, код не компилировался.
В коде, который вы собираетесь написать, вы будете использовать ограничение, позволяющее либо целочисленные или плавающие типы.
Напишите код
Под двумя ранее добавленными функциями вставьте следующий общий функция.
// SumIntsOrFloats суммирует значения карты m. Он поддерживает как int64, так и float64. // как типы для значений карты. func SumIntsOrFloats[K сопоставимый, V int64 | float64](m map[K]V) V { вар с V для _, v := диапазон m { с += v } вернуть с }В этом коде вы:
- Объявите функцию
SumIntsOrFloatsс двумя параметрами типа (внутри квадратные скобки),KиV, и один аргумент, использующий тип параметры,мтипакарта[К]В. Функция возвращает значение типВ. - Укажите для параметра типа
Kограничение типа, сопоставимое. Предназначенное специально для таких случаев, ограничение, сопоставимое с. предварительно объявлено в Go. Он позволяет использовать любой тип, значения которого могут использоваться в качестве
операнд операторов сравнения
предварительно объявлено в Go. Он позволяет использовать любой тип, значения которого могут использоваться в качестве
операнд операторов сравнения ==и!=. Go требует эту карту ключи сопоставимы. Итак, объявлениеKкаксопоставимыйнеобходим так что вы можно использоватьKв качестве ключа в переменной карты. Это также гарантирует, что вызов код использует допустимый тип для ключей карты. - Укажите для параметра типа
Vограничение, которое представляет собой объединение двух типы:int64иfloat64. Использование|указывает объединение двух типы, что означает, что это ограничение допускает любой тип. Любой тип будет разрешено компилятором в качестве аргумента в вызывающем коде. - Укажите, что аргумент
mимеет типmap[K]V, гдеKиVявляются типами, уже указанными для параметров типа. Обратите внимание, что мы
know
Обратите внимание, что мы
know map[K]Vявляется допустимым типом карты, посколькуKявляется сопоставимым типом. Если мы не объявилиKсопоставимыми, компилятор отклонил бы ссылка на карту[K]V.
- Объявите функцию
В main.go под уже имеющимся кодом вставьте следующий код.
fmt.Printf("Общие суммы: %v и %v\n", SumIntsOrFloats[строка, int64](целые), SumIntsOrFloats[строка, float64](плавает))В этом коде вы:
Вызов только что объявленной универсальной функции, передавая каждую из карт вы создали.
Укажите аргументы типа — имена типов в квадратных скобках — которые ясно о типах, которые должны заменить параметры типа в функция, которую вы вызываете.
Как вы увидите в следующем разделе, часто можно опустить тип аргументы в вызове функции. Go часто может вывести их из вашего кода.
Вывести суммы, возвращаемые функцией.
Запустите код
Из командной строки в каталоге, содержащем main. go, запустите код.
go, запустите код.
$ беги. Необщие суммы: 46 и 62,97. Общие суммы: 46 и 62,97
Чтобы запустить ваш код, в каждом вызове компилятор заменял параметры типа на конкретные типы, указанные в этом вызове.
При вызове универсальной функции, которую вы написали, вы указали аргументы типа, которые сообщает компилятору, какие типы использовать вместо параметров типа функции. Как вы увидите в следующем разделе, во многих случаях вы можете опустить эти типы. аргументы, потому что компилятор может их вывести.
Удалить аргументы типа при вызове универсальной функции
В этом разделе вы добавите модифицированную версию универсального вызова функции, внесение небольшого изменения для упрощения вызывающего кода. Вы удалите тип аргументы, которые в данном случае не нужны.
Вы можете опустить аргументы типа в вызывающем коде, если компилятор Go может вывести
типы, которые вы хотите использовать. Компилятор выводит аргументы типа из типов
аргументы функции.
Обратите внимание, что это не всегда возможно. Например, если вам нужно позвонить универсальная функция без аргументов, вам нужно будет включить тип аргументы в вызове функции.
Напишите код
В main.go под уже имеющимся кодом вставьте следующий код.
fmt.Printf("Общие суммы, выведенные параметры типа: %v и %v\n", SumIntsOrFloats(целые), SumIntsOrFloats(плавает))В этом коде вы:
- Вызов универсальной функции без аргументов типа.
Запустить код
Из командной строки в каталоге, содержащем main.go, запустите код.
$ беги. Необщие суммы: 46 и 62,97. Общие суммы: 46 и 62,97 Общие суммы, предполагаемые параметры типа: 46 и 62,97
Далее вы еще больше упростите функцию, захватив объединение целых чисел и плавает в ограничение типа, которое вы можете повторно использовать, например, из другого кода.
Объявить ограничение типа
В этом последнем разделе вы переместите ограничение, которое вы определили ранее, в его
собственный интерфейс, чтобы вы могли повторно использовать его в нескольких местах. Объявление
ограничения таким образом помогают упростить код, например, когда ограничение
более сложный.
Объявление
ограничения таким образом помогают упростить код, например, когда ограничение
более сложный.
Вы объявляете ограничение типа как интерфейс. Ограничение позволяет любое тип, реализующий интерфейс. Например, если вы объявляете ограничение типа интерфейс с тремя методами, затем используйте его с параметром типа в универсальном функции, аргументы типа, используемые для вызова функции, должны иметь все эти методы.
Интерфейсы ограниченийтакже могут ссылаться на определенные типы, как вы увидите в этом примере. раздел.
Напишите код
чуть выше
main, сразу после операторов импорта вставьте следующий код для объявления ограничения типа.тип Номер интерфейса { интервал64 | поплавок64 }В этом коде вы:
Объявите тип интерфейса
Numberдля использования в качестве ограничения типа.Объявить объединение
int64иfloat64внутри интерфейса.
По сути, вы перемещаете объединение из объявления функции в ограничение нового типа. Таким образом, когда вы хотите ограничить тип параметр либо
int64илиfloat64, вы можете использовать этот номерint64 | поплавок64.
Под уже имеющимися функциями вставьте следующий общий
Функция SumNumbers.// SumNumbers суммирует значения карты m. Он поддерживает оба целых числа // и плавает как значения карты. func SumNumbers[K сопоставимый, V Number](m map[K]V) V { вар с V для _, v := диапазон m { с += v } вернуть с }В этом коде вы:
- Объявить универсальную функцию с той же логикой, что и универсальная функция вы объявили ранее, но с новым типом интерфейса вместо union как ограничение типа. Как и раньше, вы используете параметры типа для типов аргументов и возвращаемых значений.
В main.
 go под уже имеющимся кодом вставьте следующий код.
go под уже имеющимся кодом вставьте следующий код.fmt.Printf("Общие суммы с ограничением: %v и %v\n", СуммаЧисла (целые), СуммаЧисла(с плавающей запятой))В этом коде вы:
Вызов
SumNumbersс каждой картой, печать суммы из значений каждый.Как и в предыдущем разделе, вы опускаете аргументы типа (тип имена в квадратных скобках) при вызовах универсальной функции. Идти компилятор может вывести аргумент типа из других аргументов.
Запустите код
Из командной строки в каталоге, содержащем main.go, запустите код.
$ беги . Необщие суммы: 46 и 62,97. Общие суммы: 46 и 62,97 Общие суммы, предполагаемые параметры типа: 46 и 62,97 Общие суммы с ограничением: 46 и 62,97
Заключение
Отлично сделано! Вы только что познакомились с дженериками в Go.
Предлагаемые следующие темы:
- Go Tour — отличный пошаговый
введение в основы Go.

- Вы найдете полезные рекомендации по Go, описанные в Эффективное движение и Как написать код на Go.
Завершенный код
Вы можете запустить эту программу в Иди на детскую площадку. На площадка просто нажмите кнопку Run .
пакет основной
импортировать "фмт"
тип числовой интерфейс {
интервал64 | поплавок64
}
основная функция () {
// Инициализировать карту для целочисленных значений
целые числа: = карта [строка] int64 {
«первая»: 34,
"второй": 12,
}
// Инициализируем карту для значений с плавающей запятой
поплавки: = карта [строка] float64 {
«первый»: 35,98,
«второй»: 26,99,
}
fmt.Printf("Необщие суммы: %v и %v\n",
SumInts(целые),
SumFloats(плавает))
fmt.Printf("Общие суммы: %v и %v\n",
SumIntsOrFloats[строка, int64](целые),
SumIntsOrFloats[строка, float64](плавает))
fmt.Printf("Общие суммы, выведенные параметры типа: %v и %v\n",
SumIntsOrFloats(целые),
SumIntsOrFloats(плавает))
fmt. Printf("Общие суммы с ограничением: %v и %v\n",
СуммаЧисла (целые),
СуммаЧисла(с плавающей запятой))
}
// SumInts суммирует значения m.
func SumInts(m map[string]int64) int64 {
переменная int64
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumFloats суммирует значения m.
func SumFloats(m map[string]float64) float64 {
переменная с плавающей запятой64
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumIntsOrFloats суммирует значения карты m. Он поддерживает как числа с плавающей запятой, так и целые числа.
// как значения карты.
func SumIntsOrFloats[K сопоставимый, V int64 | float64](m map[K]V) V {
вар с V
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumNumbers суммирует значения карты m. Он поддерживает оба целых числа
// и плавает как значения карты.
func SumNumbers[K сопоставимый, V Number](m map[K]V) V {
вар с V
для _, v := диапазон m {
с += v
}
вернуть с
}
Printf("Общие суммы с ограничением: %v и %v\n",
СуммаЧисла (целые),
СуммаЧисла(с плавающей запятой))
}
// SumInts суммирует значения m.
func SumInts(m map[string]int64) int64 {
переменная int64
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumFloats суммирует значения m.
func SumFloats(m map[string]float64) float64 {
переменная с плавающей запятой64
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumIntsOrFloats суммирует значения карты m. Он поддерживает как числа с плавающей запятой, так и целые числа.
// как значения карты.
func SumIntsOrFloats[K сопоставимый, V int64 | float64](m map[K]V) V {
вар с V
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumNumbers суммирует значения карты m. Он поддерживает оба целых числа
// и плавает как значения карты.
func SumNumbers[K сопоставимый, V Number](m map[K]V) V {
вар с V
для _, v := диапазон m {
с += v
}
вернуть с
}
Функциональное программирование.
 Можно ли создать «общую» функцию в Standard ML?
Можно ли создать «общую» функцию в Standard ML? Одной из главных особенностей SML является составная модульная система. Вместо использования параметрического полиморфизма и передачи функции nubOrd функции сравнения порядка вы можете создать модуль, который принимает другой модуль в качестве параметра (функтор ).
Во-первых, давайте определим подпись для модулей, представляющих порядок типов:
подпись ОРД = знак тип т val сравнить: t * t -> порядок конец
(Обратите внимание, что перед t нет ' .)
Это означает, что любой может создать структуру ... end : ORD , указав t и соответствующую функцию сравнения для t s. Многие встроенные типы имеют предопределенные функции сравнения : int имеет Int.compare и real имеет Real.compare .
Затем определите древовидную структуру данных множества; Я использовал бинарное дерево поиска и пропустил большинство функций, кроме тех, которые строго необходимы для выполнения этого трюка. В идеале вы могли бы расширить интерфейс и использовать лучший тип дерева, например, самобалансирующееся дерево. (К сожалению, поскольку вы пометили эти вопросы и ответы как SML/NJ и Moscow ML, я не был уверен, какой модуль использовать, поскольку они по-разному расширяют стандартную библиотеку, когда речь идет о сбалансированных деревьях.)
В идеале вы могли бы расширить интерфейс и использовать лучший тип дерева, например, самобалансирующееся дерево. (К сожалению, поскольку вы пометили эти вопросы и ответы как SML/NJ и Moscow ML, я не был уверен, какой модуль использовать, поскольку они по-разному расширяют стандартную библиотеку, когда речь идет о сбалансированных деревьях.)
функтор TreeSet (X : ORD) =
структура
тип t = X.t
тип данных 'дерево = Лист | Ветвь дерева * 'a * 'дерево
val пустой = лист
забавный член (x, Leaf) = false
| член (х, ветвь (слева, у, справа)) =
case X.compare (x, y) of
РАВНО => истина
| МЕНЬШЕ => элемент (x, слева)
| БОЛЬШЕ => член (x, справа)
забавная вставка (x, лист) = ветвь (лист, x, лист)
| вставить (х, ветвь (слева, у, справа)) =
case X.compare (x, y) of
РАВНО => Ветвь (влево, у, вправо)
| МЕНЬШЕ => Ветвь (вставить (x, слева), y, справа)
| БОЛЬШЕ => Ветвь (слева, у, вставка (х, справа))
конец
Наконец, функтор ListUtils содержит служебную функцию nubOrd . Функтор принимает структуру
Функтор принимает структуру X : ORD точно так же, как и функтор TreeSet . Он создает структуру XSet путем специализации функтора TreeSet с использованием того же модуля упорядочения. Затем он использует этот XSet от до эффективно, сохраняет запись элементов, которые он видел раньше.
функтор ListUtils (X : ORD) =
структура
структура XSet = TreeSet(X)
fun nubOrd (xs : список X.t) =
позволять
val init = ([], XSet.пусто)
весело идти (x, (ys, видел)) =
если XSet.member(x, видно)
тогда (да, видел)
иначе (x::ys, XSet.insert (x, видно))
in rev (#1 (foldl go init xs))
конец
конец
Использование этого функтора для удаления дубликатов в списке int :
структура IntListUtils = ListUtils(struct
тип т = целое число
val сравнение = Int.compare
конец)
пример val = IntListUtils. nubOrd [1,1,2,1,3,1,2,1,3,3,2,1,4,3,2,1,5,4,3,2,1]
(* [1, 2, 3, 4, 5] *)
nubOrd [1,1,2,1,3,1,2,1,3,3,2,1,4,3,2,1,5,4,3,2,1]
(* [1, 2, 3, 4, 5] *)
Цель всего этого бардака — nubOrd без прямого параметра дополнительной функции.
К сожалению, для того, чтобы это расширилось до int list list , вам необходимо создать функцию compare для этого типа, поскольку в отличие от Int.compare в стандартной библиотеке также нет универсальной функции. . (Здесь Haskell намного более эргономичен.)
Итак, вы можете пойти и написать общую функцию сравнения лексикографических списков: если вы знаете, как сравнивать два элемента типа 'a , вы знаете, как сравнить два списка из них, независимо от типа элемента:
fun listCompare _ ([], []) = EQUAL (* пустые списки равны *)
| listCompare _ ([], ys) = LESS (* пустой всегда меньше непустого *)
| listCompare _ (xs, []) = БОЛЬШЕ (* пустое всегда меньше непустого *)
| listCompare сравнить (x::xs, y::ys) =
случай сравнения (x, y) из
EQUAL => listCompare сравнить (xs, ys)
| МЕНЬШЕ => МЕНЬШЕ
| БОЛЬШЕ => БОЛЬШЕ
А теперь
структура IntListListUtils = ListUtils(struct тип t = список int val compare = listCompare Int.

 В случае четной функции производная будет нечетной, и наоборот.
В случае четной функции производная будет нечетной, и наоборот.
 Для производственного кода следует указать более конкретный путь к модулю.
к вашим собственным потребностям. Чтобы узнать больше, обязательно посмотрите
Управление зависимостями.
Для производственного кода следует указать более конкретный путь к модулю.
к вашим собственным потребностям. Чтобы узнать больше, обязательно посмотрите
Управление зависимостями.
 go.
go. предварительно объявлено в Go. Он позволяет использовать любой тип, значения которого могут использоваться в качестве
операнд операторов сравнения
предварительно объявлено в Go. Он позволяет использовать любой тип, значения которого могут использоваться в качестве
операнд операторов сравнения  Обратите внимание, что мы
know
Обратите внимание, что мы
know 
 go под уже имеющимся кодом вставьте следующий код.
go под уже имеющимся кодом вставьте следующий код.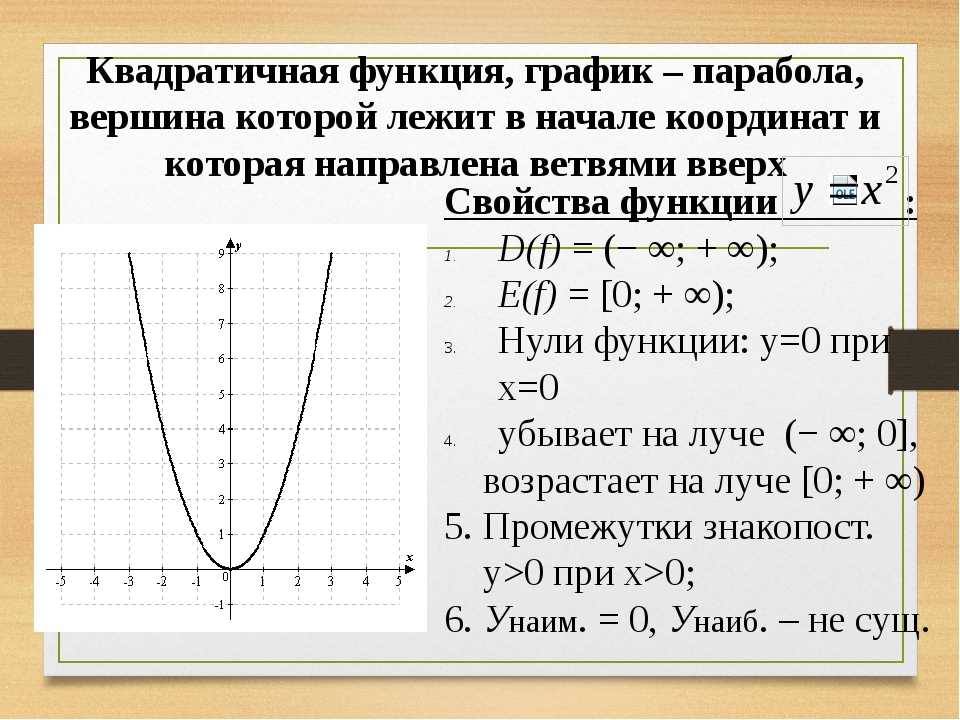
 Printf("Общие суммы с ограничением: %v и %v\n",
СуммаЧисла (целые),
СуммаЧисла(с плавающей запятой))
}
// SumInts суммирует значения m.
func SumInts(m map[string]int64) int64 {
переменная int64
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumFloats суммирует значения m.
func SumFloats(m map[string]float64) float64 {
переменная с плавающей запятой64
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumIntsOrFloats суммирует значения карты m. Он поддерживает как числа с плавающей запятой, так и целые числа.
// как значения карты.
func SumIntsOrFloats[K сопоставимый, V int64 | float64](m map[K]V) V {
вар с V
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumNumbers суммирует значения карты m. Он поддерживает оба целых числа
// и плавает как значения карты.
func SumNumbers[K сопоставимый, V Number](m map[K]V) V {
вар с V
для _, v := диапазон m {
с += v
}
вернуть с
}
Printf("Общие суммы с ограничением: %v и %v\n",
СуммаЧисла (целые),
СуммаЧисла(с плавающей запятой))
}
// SumInts суммирует значения m.
func SumInts(m map[string]int64) int64 {
переменная int64
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumFloats суммирует значения m.
func SumFloats(m map[string]float64) float64 {
переменная с плавающей запятой64
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumIntsOrFloats суммирует значения карты m. Он поддерживает как числа с плавающей запятой, так и целые числа.
// как значения карты.
func SumIntsOrFloats[K сопоставимый, V int64 | float64](m map[K]V) V {
вар с V
для _, v := диапазон m {
с += v
}
вернуть с
}
// SumNumbers суммирует значения карты m. Он поддерживает оба целых числа
// и плавает как значения карты.
func SumNumbers[K сопоставимый, V Number](m map[K]V) V {
вар с V
для _, v := диапазон m {
с += v
}
вернуть с
}
 nubOrd [1,1,2,1,3,1,2,1,3,3,2,1,4,3,2,1,5,4,3,2,1]
(* [1, 2, 3, 4, 5] *)
nubOrd [1,1,2,1,3,1,2,1,3,3,2,1,4,3,2,1,5,4,3,2,1]
(* [1, 2, 3, 4, 5] *)
