§ Как найти координаты точки. Как записать координаты точек
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность.
 Площадь круга
Площадь круга - Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Лень закаляет характер, если вспомнить, сколько
требуется усилий, чтобы её побороть.
на главную
Введите тему
Русский язык Поддержать сайт
Оси координат. Координатные четверти Как найти и записать координаты точки
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на первом месте стоит абсцисса, а на втором — ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
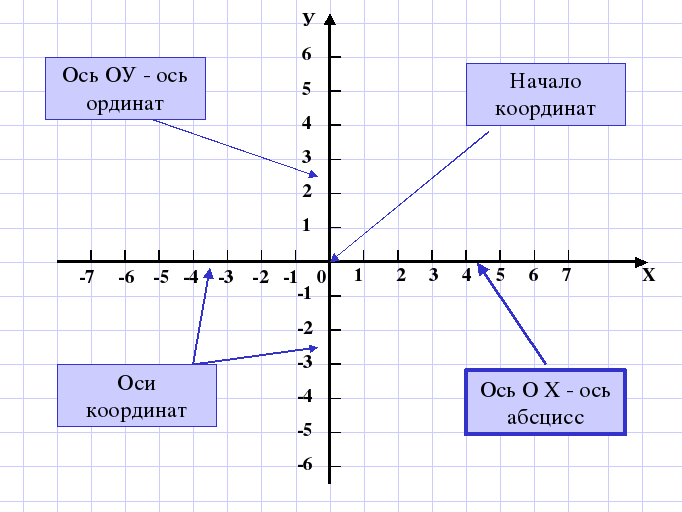
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором — ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Найти точку в системе координат можно двумя способами.
Первый способ
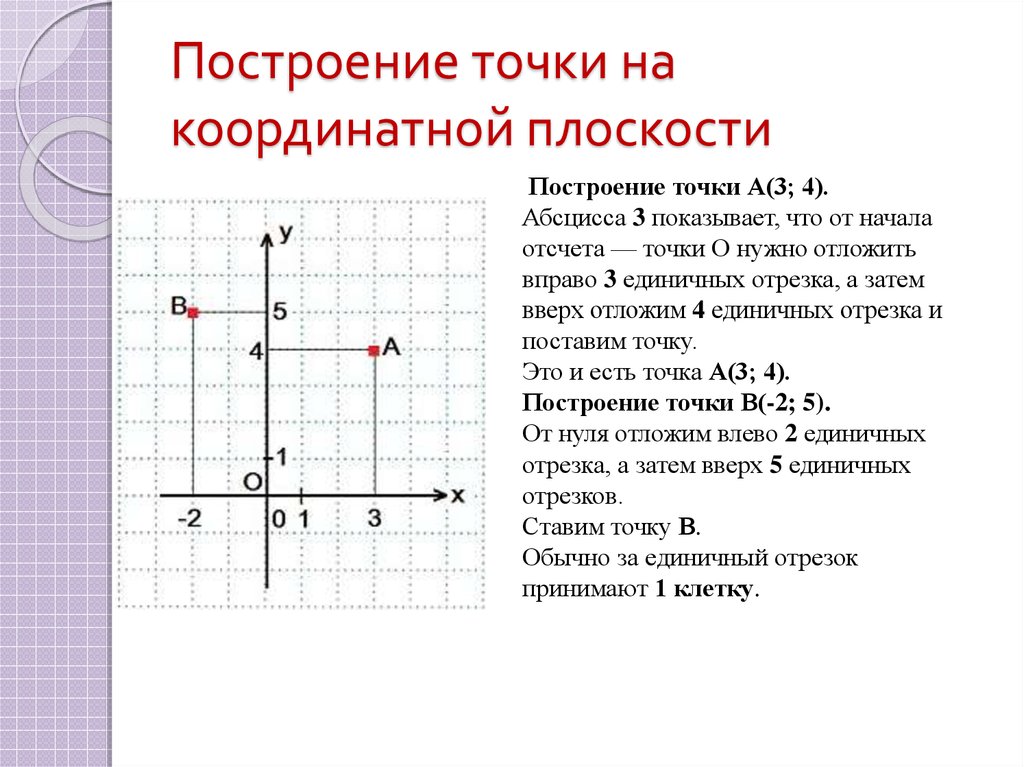
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой «−4», и провести через неё прямую перпендикулярную оси «Ox».
- Отметить на оси «Oy», точку с координатой 2, и провести через неё прямую перпендикулярную оси «Oy».
- Точка пересечения перпендикуляров (·) D — искомая точка. У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4 стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.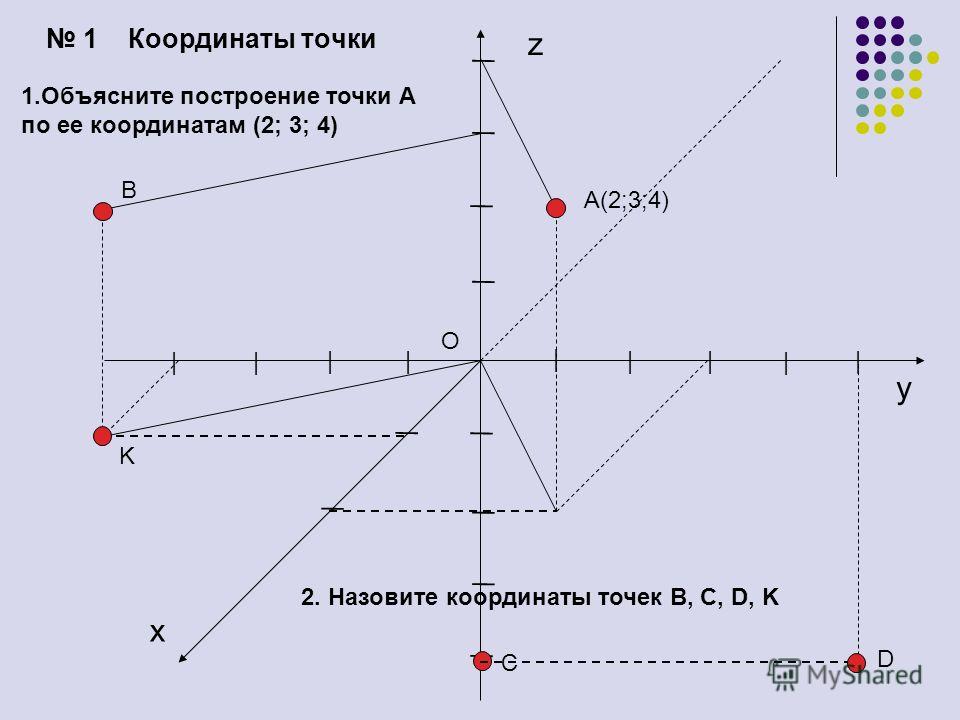
Оси координат. Координатные четверти Как найти и записать координаты точки
Открытая Математика. Функции и Графики. Декартова система координат
Декартова система координат
Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. В конкретной невырожденной координатной системе каждой точке соответствует один и только один набор координат.
Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат (в честь французского математика Рене Декарта).
В элементарной математике чаще всего рассматривается двухмерная или трехмерная декартова система координат; координаты обычно обозначаются латинскими буквами x, y, z и называются, соответственно, абсциссой, ординатой и аппликатой.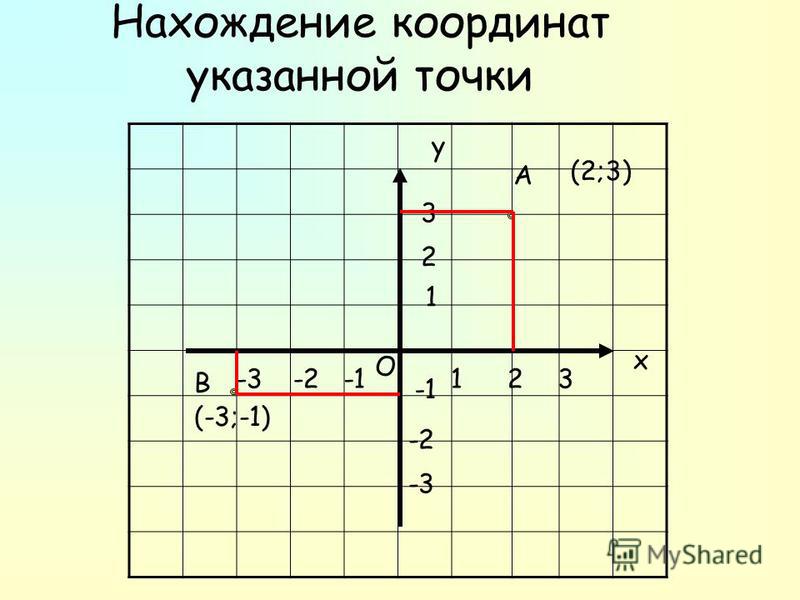 Координатная ось OX называется осью абсцисс, ось OY – осью ординат, ось OZ – осью аппликат. Положительные направления отсчета по каждой из осей обозначаются стрелками.
Координатная ось OX называется осью абсцисс, ось OY – осью ординат, ось OZ – осью аппликат. Положительные направления отсчета по каждой из осей обозначаются стрелками.
Как определить координаты точки в декартовой системе координат? Проведем через точку A прямые (в трехмерном случае – плоскости), перпендикулярные осям. Расстояния от точек пересечения построенных прямых (плоскостей) с осями абсцисс, ординат (аппликат) до начала координат, взятые со знаком «+», если точки лежат на положительных полуосях, и со знаком «–», если они лежат на отрицательных полуосях, и будут координатами точки A. Координаты точки записываются в скобках: например, A (–3; 2) или B (x0; y0).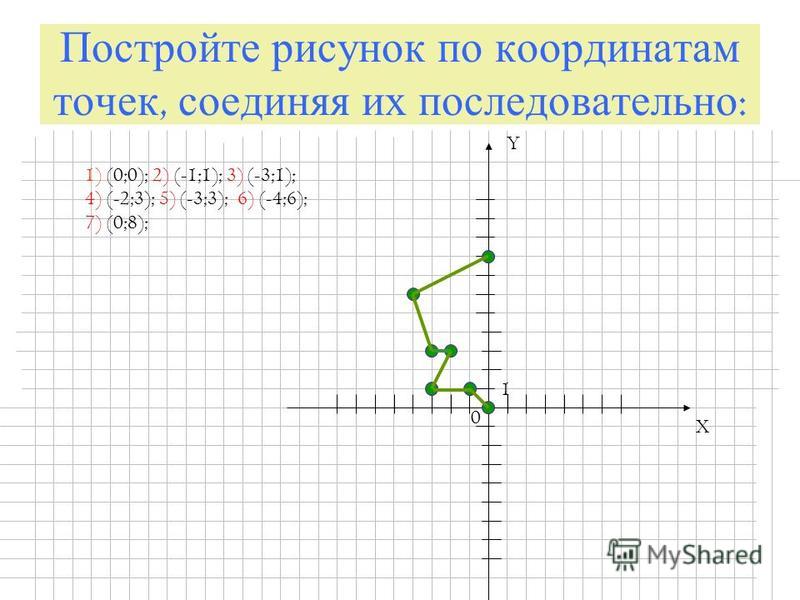 В трехмерном пространстве координаты точки в декартовой системе координат записываются тремя числами, например, C (5; 0,2; –6)
В трехмерном пространстве координаты точки в декартовой системе координат записываются тремя числами, например, C (5; 0,2; –6)
В двухмерной системе координат все точки, лежащие над (под) осью OX, образуют верхнюю (нижнюю) координатную полуплоскость. Все точки, лежащие правее (левее) оси OY образуют правую (левую) координатную полуплоскость.
В конце этого параграфа приведем некоторые очевидные формулы.
- Расстояние от точки A (x0; y0) до оси OX равно |y0|.
- Расстояние от точки A (x0; y0) до оси OY равно |x0|.
- Расстояние от точки
A(x0; y0)
до начала координат равно
x02+y02.

- Расстояние |AB| между точками A (x1; y1) и B (x2; y2) равно x2-x12+y2-y12.
- Точка M, которая является серединой отрезка AB, где A (x1; y1) и B (x2; y2), имеет координаты x1+x22, y1+y22.
На случай трехмерного пространства эти формулы обобщаются следующим образом:
- Расстояние от точки A (x; y; z) до плоскости OYZ равно |x|.
- Расстояние от точки A (x; y; z) до начала координат равно x2+y2+z2.
- Расстояние |AB| между точками A (x1; y1; z1) и B (x2; y2; z2) равно (x2-x1)2+(y2-y1)2+(z2-z1)2.
- Координаты точки M, которая является серединой отрезка AB, где A (x1; y1; z1) и B (x2; y2; z2) равны
x1+x22; y1+y22; z1+z22.

Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».
Построение трехмерных точек — Криста Кинг Математика
Как наносить точки в трех измерениях
Чтобы наносить точки в трехмерном координатном пространстве, мы начнем с трехмерной системы координат, где ось ???x??? ???y???-ось движется вправо, а ???z???-ось совершенно вертикальна.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Если нам нужно рассмотреть отрицательные значения ???x???, ???y??? или ???z???, то мы должны знать, что отрицательное направление ???x?? ?-ось следует прямой положительной оси ???x???-от нас, что отрицательное направление оси ???y???-оси смещается влево, а отрицательное направление ???z???-ось совершенно вертикальна, простираясь ниже положительного направления ???z???-оси.
Таким же образом, как мы наносим точки в двумерном координатном пространстве, перемещаясь по оси ???x???-к нашему ???x??? значения, а затем двигаясь параллельно оси ???y???, пока не найдем нашу точку, в трехмерном пространстве мы будем двигаться вдоль оси ???x???, затем параллельно оси ?? ?y???-оси, затем параллельно ???z???-оси, пока мы не достигнем нашей точки координат.
Видеоинструкция по построению четырех разных точек в трехмерном пространстве
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂
Учить больше
Еще один пример построения точки в трех измерениях
Пример
Нанесение точки в трехмерной системе координат.
???(4,2,3)???
Начнем с рисования осей, затем будем двигаться от начала координат вдоль оси ???x???, пока не дойдем до ???x=4???.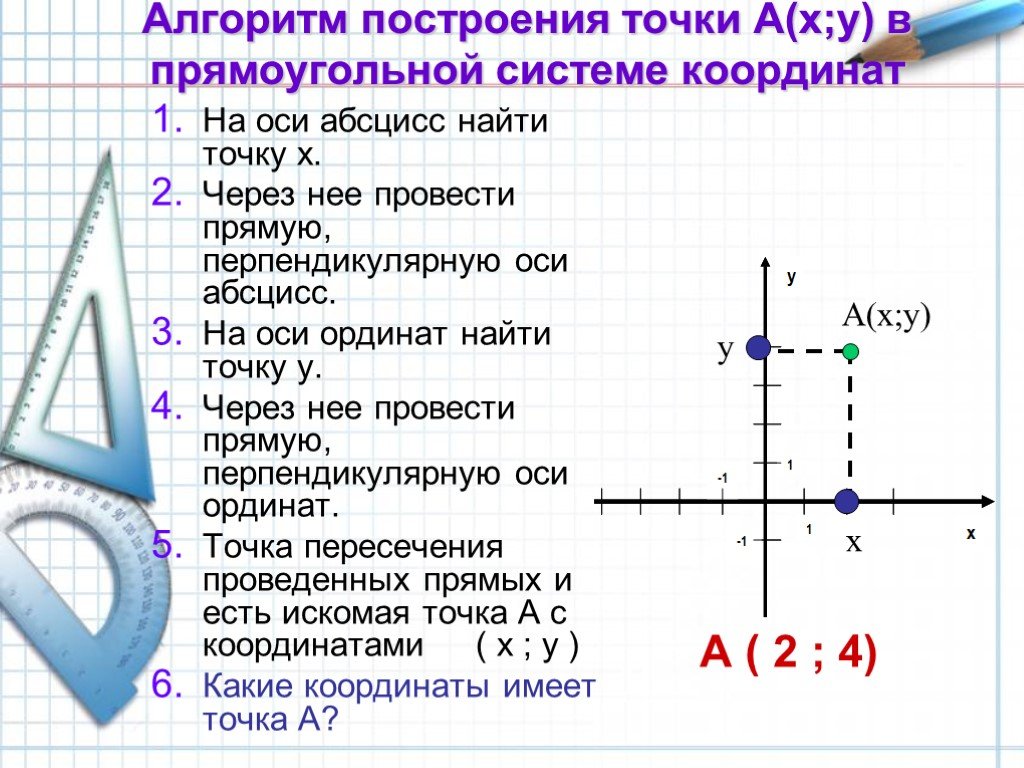
Чтобы добраться до ???(4,2)??? в плоскости ???xy??? мы начнем с того места, где остановились на оси ???x???, и будем двигаться параллельно оси ???y???, пока не дойдем до ???у=2???.
Чтобы добраться до ???(4,2,3)??? в трехмерном пространстве мы начнем с того места, где остановились в координатной плоскости ???xy???, и будем двигаться параллельно оси ???z???, пока не доберемся до ???z= 3???.
в трехмерном пространстве мы будем двигаться вдоль оси x, затем параллельно оси y, затем параллельно оси z, пока не достигнем нашей координатной точки.
Если мы нанесем только точку и ничего больше, может быть трудно или невозможно определить местоположение трехмерной точки на двухмерном листе бумаги. Чтобы решить эту проблему, мы можем заполнить трехмерный блок, поместив один угол блока в начало координат, а противоположный угол в точку координат, которую мы только что нанесли.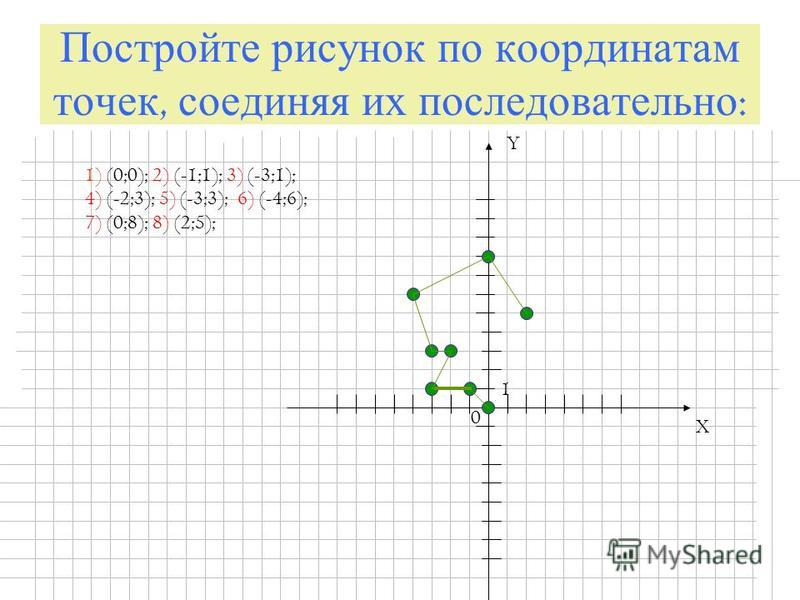
Несмотря на то, что наносить и маркировать координатную точку необходимо только технически, вы можете видеть, как рисование линий, которые мы использовали, чтобы добраться до точки, и прямоугольник, соединяющий начало координат с точкой координат, действительно помогает нам получить некоторые перспектива.
Получить доступ к полному курсу Calculus 3
Начать
Учим математикуКриста Кинг точек построения в трех измерениях
0 лайковДекартова плоскость координат и график (видео и практика)
TranscriptPractice
Если вы когда-либо создавали веб-сайт раньше, вы знаете, что под всеми изображениями, кнопками и меню находятся строки и строки компьютерного кода. Кодирование носит текстовый характер, то есть состоит из слов, чисел и фраз, но в результате получается физические изображения, строки, блоки и макеты, которые вы видите на веб-сайте.
Кодирование носит текстовый характер, то есть состоит из слов, чисел и фраз, но в результате получается физические изображения, строки, блоки и макеты, которые вы видите на веб-сайте.
Точно так же числа, уравнения и выражения, с которыми вы знакомы из своего опыта в алгебре, также могут быть выражены в визуальном формате, например, в виде линий и других фигур .
Как это достигается? Это именно то, что мы рассмотрим сегодня в этом видео о декартовой координатной плоскости.
Рене Декарт был французским философом, который придумал плоскость, на которой можно было рисовать числа и уравнения. Легенда гласит, что, лежа в постели, Декарт заметил муху на потолке и развернул свою плоскость, чтобы указать положение мухи.
Плоскость состоит из двух пересекающихся перпендикулярных линий, одна горизонтальная, а другая вертикальная. Горизонтальная линия называется осью x , а вертикальная линия называется осью y .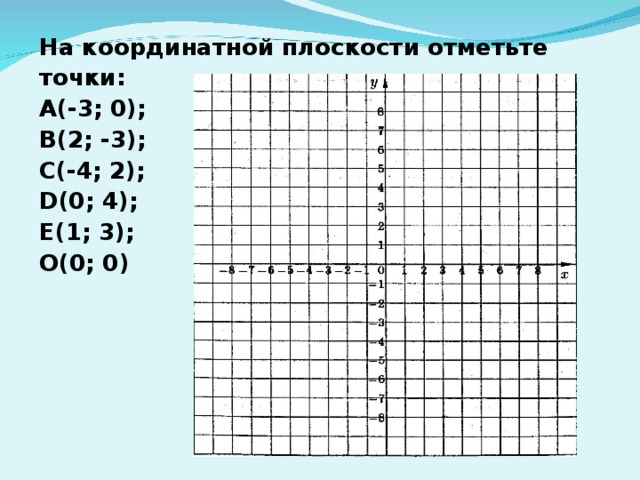 Ось x используется для обозначения горизонтального положения точек на плоскости, тогда как ось y используется для обозначения вертикального положения точек на плоскости. Линии пересекаются в так называемом начале координат , прямо там, которое имеет нулевое значение.
Ось x используется для обозначения горизонтального положения точек на плоскости, тогда как ось y используется для обозначения вертикального положения точек на плоскости. Линии пересекаются в так называемом начале координат , прямо там, которое имеет нулевое значение.
Давайте внимательнее посмотрим на ось x. Мы начнем с левой стороны и назовем ее -3, -2 и -1. После начала координат, которое, как мы уже упоминали, имеет нулевое значение, мы продолжим с 1, 2 и 3. Это может показаться вам знакомым, поскольку напоминает традиционную числовую прямую, которую вы, возможно, использовали для решения математических задач. То же самое делаем с осью Y, начиная с самого низа, -3, -2 и -1. Затем мы перемещаемся выше начала координат и делаем 1, 2 и 3.
Как видите, точки слева от начала координат имеют отрицательное значение x, тогда как точки справа от начала координат имеют положительное значение x. ценность. Точно так же точки ниже начала координат имеют отрицательное значение y, тогда как точки выше начала координат имеют положительное значение y.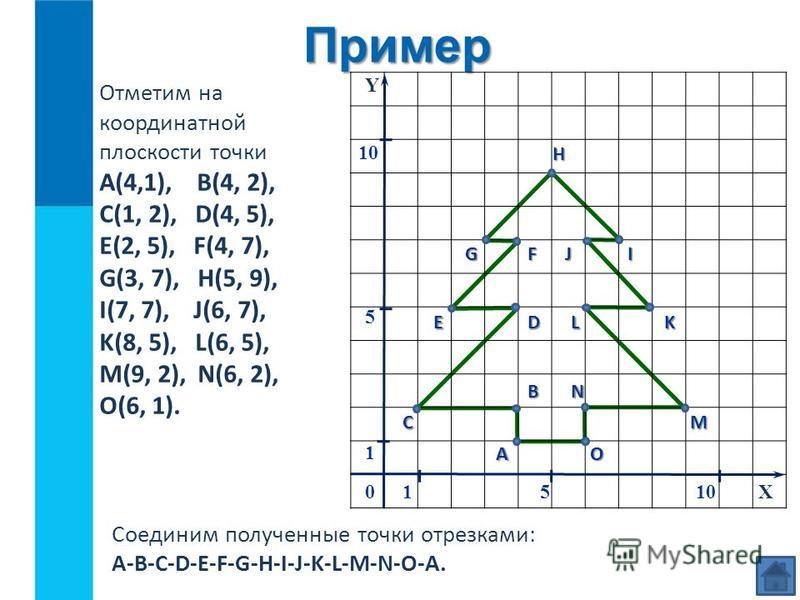
Каждая точка, нанесенная на плоскость, имеет набор координат, записанных следующим образом: (x, y). Это означает, что для любой заданной точки мы сначала пишем ее местоположение по оси x, а затем за ней следует местоположение по оси y.
Возможно, вы заметили, что плоскость с пересечением осей x и y состоит из четырех «квадратов». Итак, прямо здесь. Каждый из этих квадратов называется квадрантом . Верхний правый — это первый квадрант, верхний левый — второй квадрант, нижний левый — третий квадрант, а нижний правый — четвертый квадрант. Как видите, квадранты обычно обозначаются римскими цифрами.
Чтобы собрать все воедино, давайте рассмотрим несколько примеров. Скажем, вам дали координаты (1, -2). Нашим первым шагом было бы найти 1 на оси x. Затем опускаемся до -2 по оси Y, затем отмечаем нашу точку (1, -2). Давайте попробуем еще, скажем, вы хотели найти скажем (-3, 2). Сначала мы находим -3 по оси X, которая здесь. А затем продолжайте до 2 по оси Y, прямо там, и мы отмечаем нашу точку.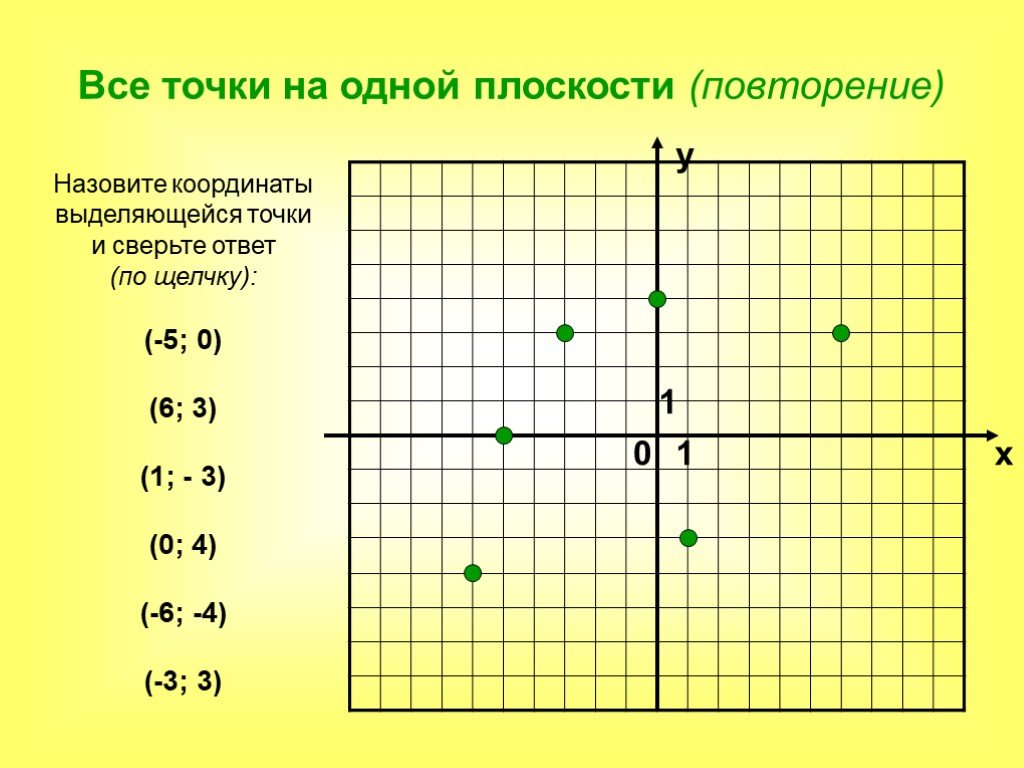 Важно отметить, что наша первая точка расположена в четвертом квадранте, тогда как наша вторая точка находится во втором квадранте.
Важно отметить, что наша первая точка расположена в четвертом квадранте, тогда как наша вторая точка находится во втором квадранте.
Давайте сделаем еще один шаг и нарисуем очень простое уравнение. Нам понадобится расширенная плоскость, поэтому давайте создадим такую, которая изменяется от -5 до 5 по осям x и y.
Допустим, вы хотите построить график y = 2x + 1.
Первое, что мы сделаем, это нарисуем таблицу с одним столбцом для значений x и другим столбцом для наших значений y:
Начнем с подстановки значений для x и посмотреть, каким будет соответствующее значение y. Начнем со значения x, равного -3. Итак, если у нас есть -3, мы, по сути, подключаем его к нашему уравнению здесь, поэтому я сделаю это здесь. Таким образом, у равно 2(-3)+1. 2 умножить на -3 равно -6, плюс 1, у равно -5. Итак, мы подставляем сюда -5. Это наша первая точка (-3, -5). Подойдя к нашей плоскости, мы сначала найдем -3 по оси x, затем -5 по оси y, и так далее, и нанесем нашу точку.
Теперь давайте попробуем значение x равное -1.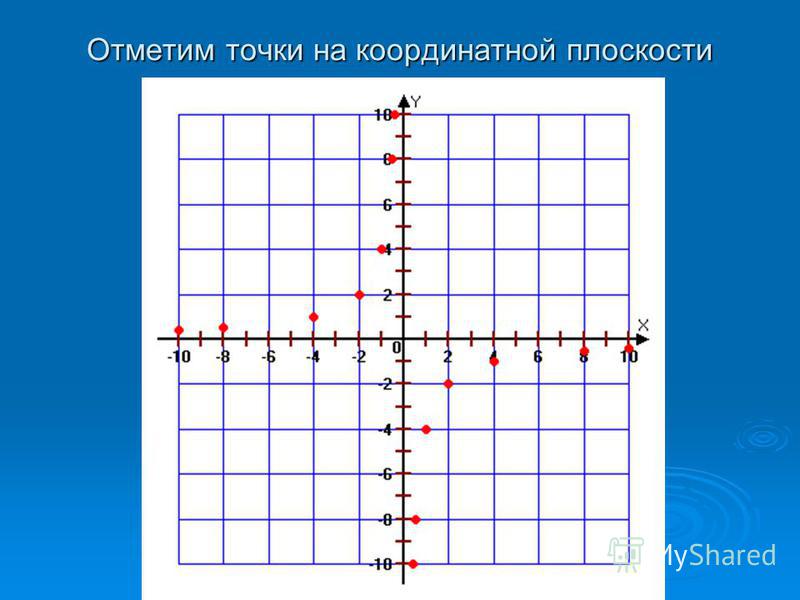 Еще раз пишем -1 в столбце x. -1, поэтому теперь нам нужно найти соответствующее значение y, подставив его в наше уравнение. Итак, мы получаем 2(-1) + 1. Таким образом, у равно -2 плюс 1, что дает нам у равно -1. Поэтому мы ставим -1 прямо здесь. Итак, теперь у нас есть следующая координата (-1, -1). Итак, сначала мы идем к нашей оси X, находим -1 и опускаемся до -1, и рисуем нашу метку.
Еще раз пишем -1 в столбце x. -1, поэтому теперь нам нужно найти соответствующее значение y, подставив его в наше уравнение. Итак, мы получаем 2(-1) + 1. Таким образом, у равно -2 плюс 1, что дает нам у равно -1. Поэтому мы ставим -1 прямо здесь. Итак, теперь у нас есть следующая координата (-1, -1). Итак, сначала мы идем к нашей оси X, находим -1 и опускаемся до -1, и рисуем нашу метку.
Давайте быстро нанесем еще две точки. Мы попробуем значение x равное 1. Итак, теперь у нас есть следующий набор координат, это (1, 3). Итак, мы идем и находим 1 по оси x, затем поднимаемся до 3 по оси y. Мы закончим со значением x, равным 2. Поэтому мы помещаем 2 в наш столбец x, а затем подставляем его в наше уравнение. Итак, это дает нам наш следующий набор координат, который равен (2, 5). Таким образом, мы находим 2 по оси x, а затем идем до 5 по оси y.
Теперь, когда у нас есть четыре точки на графике, мы возвращаем время вспять к играм, в которые играли до появления смартфонов, и «соединяем точки», чтобы сформировать линию.
Линия идеально показывает, как мы графически изобразим y = 2x +1. Это визуальное представление уравнения, которое выводит наше понимание алгебры и геометрии на новый уровень.
Я надеюсь, что этот обзор Декартовой координатной плоскости был полезен! Спасибо за просмотр и удачной учебы!
Вопрос №1:
Посмотрите на декартов график ниже. Какие координаты описывают положение красной точки на плоскости?
\((4,1)\)
\((-1,4)\)
\((4,-1)\)
\((1,4)\)
Показать Ответ
Ответ:
Чтобы увидеть это, нам сначала нужно определить размер точки x . Где находится точка на горизонтальной оси x ? Точка прямо под 4, так что 4 это x -значение. Во-вторых, мы определяем значение y точки, видя, где она лежит на вертикальной оси y .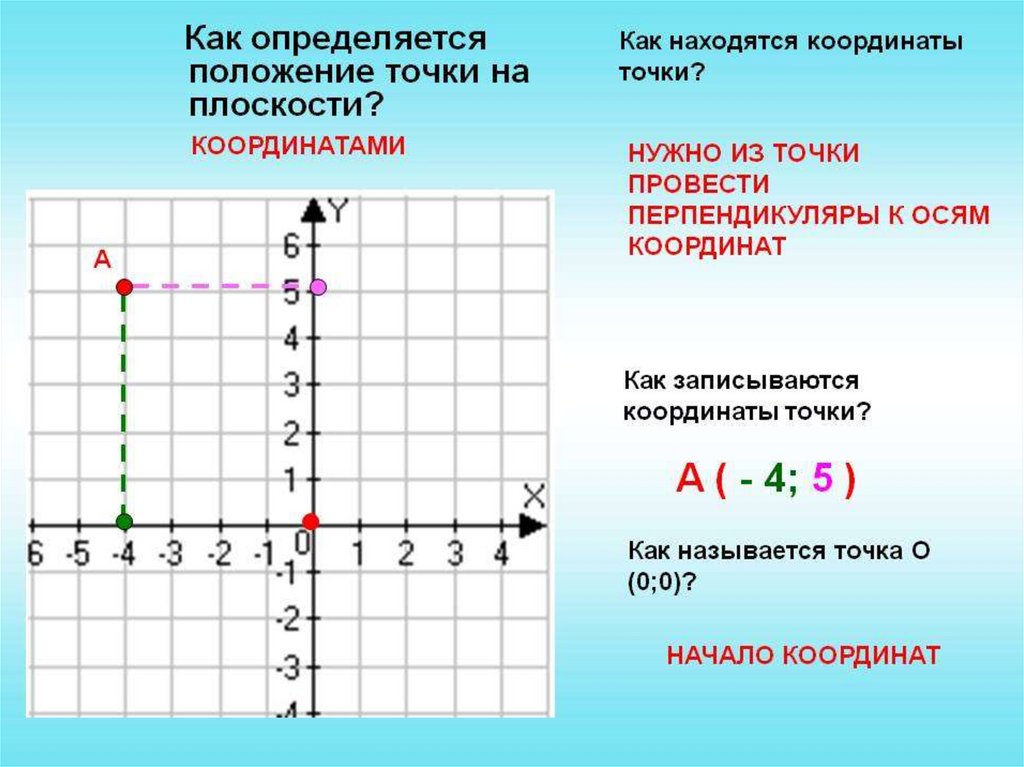 Обратите внимание, что точка находится справа от -1 на оси y , и мы также можем видеть, что точка находится на один «квадрат» или на одну единицу ниже оси x . Наконец, помните, что мы указываем значение x перед значением y при записи декартовых координат. Таким образом, соответствующие координаты для этой точки равны \((4,-1)\).
Обратите внимание, что точка находится справа от -1 на оси y , и мы также можем видеть, что точка находится на один «квадрат» или на одну единицу ниже оси x . Наконец, помните, что мы указываем значение x перед значением y при записи декартовых координат. Таким образом, соответствующие координаты для этой точки равны \((4,-1)\).
Скрыть ответ
Вопрос №2:
Внутри какого квадранта находится точка \((4,-1)\)?
I
II
III
IV
Показать ответ
Ответ:
Посмотрите еще раз на график и на то, где мы нанесли точку.
Поскольку точка \((4,-1)\) имеет положительное значение x , она лежит справа от вертикальной оси. И потому что у него отрицательное y — значение, оно лежит ниже горизонтальной оси. Квадранты декартовой плоскости упорядочены, начиная с правого верхнего «угла» и двигаясь против часовой стрелки, как показано ниже. Тогда наша точка находится в квадранте IV.
Квадранты декартовой плоскости упорядочены, начиная с правого верхнего «угла» и двигаясь против часовой стрелки, как показано ниже. Тогда наша точка находится в квадранте IV.
Скрыть ответ
Вопрос №3:
В каком квадранте находится точка \((-1,-2)\)?
I
II
III
IV
Показать ответ
Ответ:
Для начала посмотрим, где точка \((-1,-2.)\) лежит на плоскости Находим -1 по горизонтали x -ось, затем спуститесь на две единицы вниз, пока мы не окажемся на той же высоте, что и -2 по вертикальной оси y .
Теперь, когда мы знаем, где находится точка, снова вспомним, что квадранты упорядочены, начиная с правого верхнего «угла» и двигаясь против часовой стрелки, как показано ниже.
Из этих двух рисунков легко увидеть, что точка \((-1,-2)\) находится в третьем квадранте.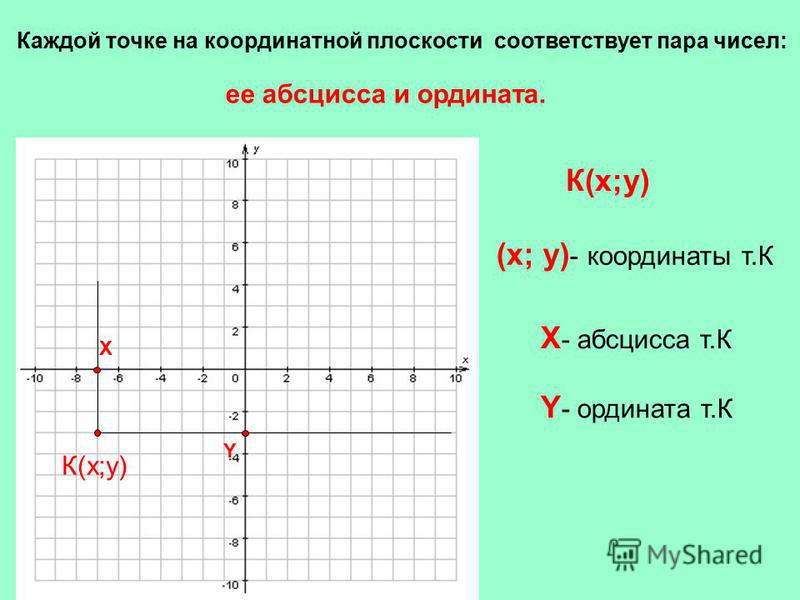 Однако по мере того, как вы лучше знакомитесь с квадрантами и их порядком, вам будет легче определять точки в первом и третьем квадрантах. Точки в квадранте I имеют положительные значения для обоих x — и y -координаты, в то время как точки в квадранте III имеют отрицательные значения для обеих.
Однако по мере того, как вы лучше знакомитесь с квадрантами и их порядком, вам будет легче определять точки в первом и третьем квадрантах. Точки в квадранте I имеют положительные значения для обоих x — и y -координаты, в то время как точки в квадранте III имеют отрицательные значения для обеих.
Скрыть ответ
Вопрос № 4:
Рассмотрим уравнение \(y=\frac{1}{2}x+2\) и найдем y -значение, когда \(x=1 \) to complete the table below:
| x | y |
| -2 | 1 |
| -1 | 1.5 |
| 0 | 2 |
| 1 | ??? |
| 2 | 3 |
\ (y = 1 \)
\ (y = 2,5 \)
\ (y = 3,5 \)
\ (y = 1,155
\ (y = 3,5 \)
\ (y = 1,155
\ (y = 3,5 \)
Ответ:
Ответ:
Чтобы получить это решение, подставим \(x=1\) в полученное уравнение.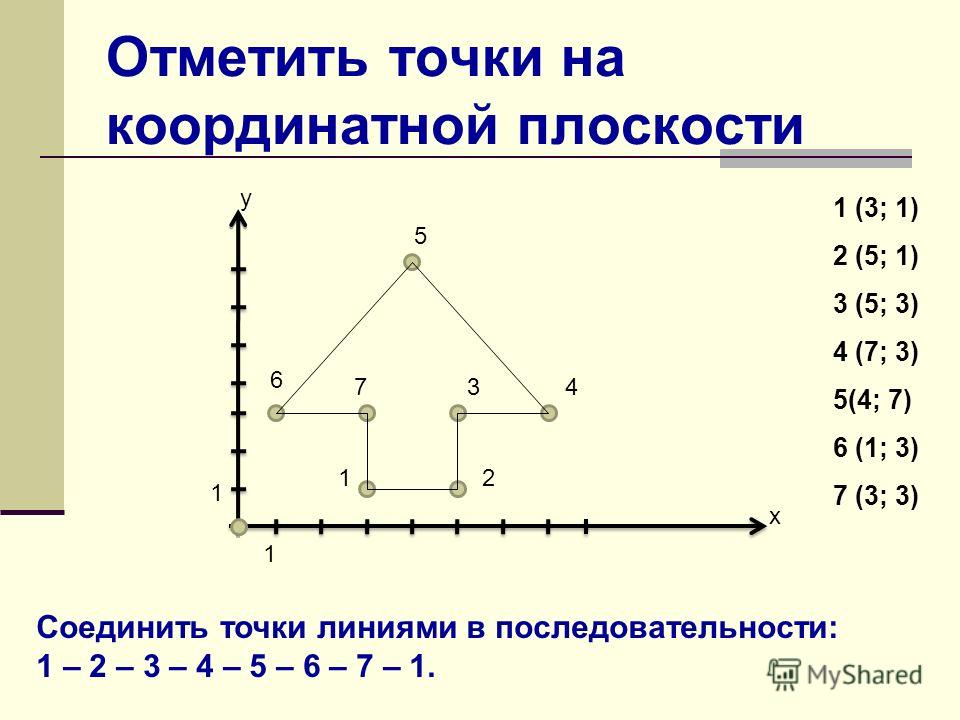
\(y=\frac{1}{2}(1)+2\)
\(y=\frac{1}{2}+2\)
\(y=2.5\)
Мы также можем угадайте это решение, заметив закономерность в и — значения, указанные в таблице. Для каждого приращения на 1 по оси x значения y увеличиваются на 0,5. Мы не удивлены, увидев, что наше решение на 0,5 больше, чем предыдущее y -значение (2), и на 0,5 меньше, чем следующее y -значение (3). (Эта интересная закономерность получается из дроби \(\frac{1}{2}\) прямо перед x в нашем уравнении. Подобные коэффициенты называются «наклоном» линии, и вы узнать больше об их полезности в следующих уроках.)
Скрыть ответ
Вопрос №5:
Какая из следующих точек не лежит на прямой, описываемой уравнением \(y=-x+3\)?
Подсказка: вы можете проверить, находится ли каждая точка на линии, подставив координату x в уравнение, а затем проверив, соответствует ли оно правильному значению y (вторая координата).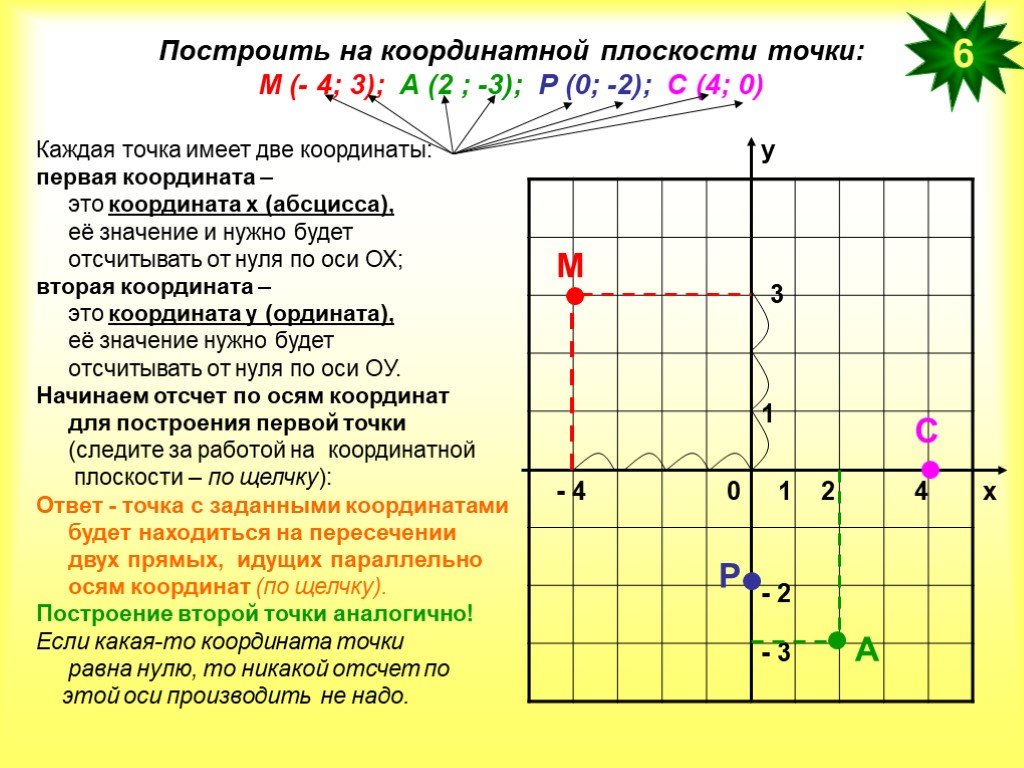

 Площадь круга
Площадь круга