Перемножение корней с разными степенями. Умножение корней: методы и применение
Известно, что знак корня является квадратным корнем из некоторого числа. Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Yandex.RTB R-A-339285-1
Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:
- без множителей;
- с множителями;
- с разными показателями.
Метод умножения корней без множителей
Алгоритм действий:
Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.
Пример
Пример 1: 18 × 2 = ?
Пример 2: 10 × 5 = ?
Пример
Пример 1: 18 × 2 = 36
Пример 2: 10 × 5 = 50
Пример 3: 3 3 × 9 3 = 27 3
Упростить подкоренные выражения.
Пример
Пример 1: 36 = 6 . 36 — квадратный корень из шести (6 × 6 = 36) .
Пример 2: 50 = (25 × 2) = (5 × 5) × 2 = 5 2 . Число 50 раскладываем на произведение 25 и 2 . Корень из 25 — 5 , поэтому выносим 5 из-под знака корня и упрощаем выражение.
Пример 3: 27 3 = 3 . Кубический корень из 27 равен 3: 3 × 3 × 3 = 27 .
Метод умножения показателей с множителями
Алгоритм действий:
Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:
Пример
Пример 1: 3 2 × 10 = 3 ? 3 × 1 = 3
Пример 2: 4 3 × 3 6 = 12 ? 4 × 3 = 12
Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Пример
Пример 1: 3 2 × 10 = 3 (2 × 10) = 3 20
Пример 2: 4 3 × 3 6 = 12 (3 × 6) = 12 18
Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
Пример
Пример 1: 3 20 = 3 (4 × 5) = 3 (2 × 2) × 5 = (3 × 2) 5 = 6 5
Пример 2: 12 18 = 12 (9 × 2) = 12 (3 × 3) × 2 = (12 × 3) 2 = 36 2
Метод умножения корней с разными показателями
Алгоритм действий:
Найти наименьшее общее кратное (НОК) показателей. Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.
Пример
Необходимо найти НОК показателей для следующего выражения:
Показатели равны 3 и 2 . Для этих двух чисел наименьшим общим кратным является число 6 (оно делится без остатка и на 3 , и на 2). Для умножения корней необходим показатель 6 .
Записать каждое выражение с новым показателем:
Найти числа, на которые нужно умножить показатели, чтобы получить НОК.
В выражении 5 3 необходимо умножить 3 на 2 , чтобы получить 6 . А в выражении 2 2 — наоборот, необходимо умножить на 3 , чтобы получить 6 .
А в выражении 2 2 — наоборот, необходимо умножить на 3 , чтобы получить 6 .
Возвести число, которое стоит под знаком корня, в степень равную числу, которое было найдено в предыдущем шаге. Для первого выражения 5 нужно возвести в степень 2 , а втором — 2 в степень 3:
2 → 5 6 = 5 2 6 3 → 2 6 = 2 3 6
Возвести в степень выражения и записать результат под знаком корня:
5 2 6 = (5 × 5) 6 = 25 6 2 3 6 = (2 × 2 × 2) 6 = 8 6
Перемножить числа под корнем:
(8 × 25) 6
Записать результат:
(8 × 25) 6 = 200 6
По возможности необходимо упростить выражение, но в данном случае оно не упрощается.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Остальное — брехня и пустая трата времени.
Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)
Вы ведь тоже ещё не вкурили?
Урок получился довольно большим, поэтому я разделил его на две части:
- Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
- Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще. С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.
Основное правило умножения
Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:
Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:
Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:
\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]
Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Примеры. Рассмотрим сразу четыре примера с числами:
\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}. \\ \end{align}\]
Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу .
Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.
Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.
Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:
\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}.
\\ \end{align}\]
И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.
Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка.
Случай произвольного показателя
Итак, с квадратными корнями разобрались. А что делать с кубическими? Или вообще с корнями произвольной степени $n$? Да всё то же самое. Правило остаётся прежним:
Чтобы перемножить два корня степени $n$, достаточно перемножить их подкоренные выражения, после чего результат записать под одним радикалом.
В общем, ничего сложного. {2n}}}=\left| a \right|. \\ \end{align}\]
{2n}}}=\left| a \right|. \\ \end{align}\]
Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:
Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?
При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)
Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.
Умножение корней с разными показателями
Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt{23}$? Можно ли вообще это делать?
Да конечно можно. Всё делается вот по этой формуле:
Правило умножения корней.
{2}}}=\sqrt{5}. \\ \end{align}\]
Но тогда получается какая-то хрень:
\[\sqrt{-5}=\sqrt{5}\]
Этого не может быть, потому что $\sqrt{-5} \lt 0$, а $\sqrt{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
- Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
- Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.
{2}}}=\sqrt{75}. \end{align}\]
Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
a m ·a n = a m + n .
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
(a/b) n = a n /b n .
5. Возводя степень в степень, показатели степеней перемножают:
(a m) n = a m n .
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .
Например . a 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .
Сложение корней с разными степенями. Сложение и вычитание корней, примеры. Что такое квадратный корень
Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение.
Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.Шаг 1. Извлечение квадратных корней
Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .
Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней.
Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .
Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.
В наше время современных электронных вычислительных машин вычисление корня из числа не представляется сложной задачей. Например, √2704=52, это вам подсчитает любой калькулятор. К счастью, калькулятор есть не только в Windows, но и в обычном, даже самом простеньком, телефоне. Правда если вдруг (с малой долей вероятности, вычисление которой, между прочим, включает в себя сложение корней) вы окажитесь без доступных средств, то, увы, придется рассчитывать только на свои мозги.
Тренировка ума никогда не помещает. Особенно для тех, кто не так часто работает с цифрами, а уж тем более с корнями. Сложение и вычитание корней — хорошая разминка для скучающего ума. А еще я покажу поэтапно сложение корней. Примеры выражений могут быть следующие.
Уравнение, которое нужно упростить:
√2+3√48-4×√27+√128
Это иррациональное выражение. Для того чтобы его упростить нужно привести все подкоренные выражения к общему виду. Делаем поэтапно:
Первое число упростить уже нельзя.
2×2)
Переписываем выражение с упрощенными слагаемыми:
√2+12×√3-12×√3+8×√2
Теперь складываем числа одним и тем же подкоренным выражением. Нельзя складывать или вычитать выражения с разными подкоренными выражениями. Сложение корней требует соблюдение этого правила.
Ответ получаем следующий:
√2+12√3-12√3+8√2=9√2
√2=1×√2 — надеюсь, то, что в алгебре принято опускать подобные элементы, не станет для вас новостью.
Выражения могут быть представлены не только квадратным корнем, но так же и с кубическим или корнем n-ной степени.
Сложение и вычитание корней с разными показателями степени, но с равнозначным подкоренным выражением, происходит следующим образом:
Если мы имеем выражение вида √a+∛b+∜b, то мы можем упростить это выражение так:
∛b+∜b=12×√b4 +12×√b3
12√b4 +12×√b3=12×√b4 + b3
Мы привели два подобных члена к общему показателю корня. Здесь использовалось свойство корней, которое гласит: если число степени подкоренного выражения и число показателя корня умножить на одно и то же число, то его вычисление останется неизменным.
На заметку: показатели степени складываются только при умножении.
Рассмотрим пример, когда в выражении присутствуют дроби.
5√8-4×√(1/4)+√72-4×√2
Будем решать по этапам:
5√8=5*2√2 — мы выносим из-под корня извлекаемую часть.
4√(1/4)=-4 √1/(√4)= — 4 *1/2= — 2
Если в тело корня представлено дробью, то часто этой дроби не измениться, если извлечь квадратный корень из делимого и делителя. В итоге мы получили описанное выше равенство.
√72-4√2=√(36×2)- 4√2=2√2
10√2+2√2-2=12√2-2
Вот и получился ответ.
Главное помнить, что из отрицательных чисел не извлекается корень с четным показателем степени. Если четной степени подкоренное выражение является отрицательным, то выражение является нерешаемым.
Сложение корней возможно только при совпадении подкоренных выражений, так как они являются подобными слагаемыми. То же самое относиться и к разности.
Сложение корней с разными числовыми показателями степени производиться посредством приведения к общей корневой степени обоих слагаемых.
Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.
Если в подкоренном выражении имеется число, возведенное в степень, то это выражение можно упростить при условии, что между показателем корня и степени существует общий знаменатель.
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Шаги
Часть 1 из 2: Определение корней
Обозначение корней. Выражение под знаком корня () означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: (27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5 (2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
Запомните, какие корни можно складывать, а какие нельзя. Так же, как нельзя складывать разные члены выражения, например, 2а + 2b 4ab, вы не можете складывать разные корни.
Нельзя складывать корни с разными подкоренными выражениями, например, (2) + (3) (5). Но вы можете сложить числа, стоящие под одним корнем, например, (2 + 3) = (5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236). Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, (64) + (64) (эта сумма не равна (64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297). Часть 2 из 2: Упрощение и сложение корней
Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2 (3) + (81) + 2 (50) + (32) + 6 (3)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2 (3) + 2 (50) + (32) + 6 (3) + (81)- Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2 (50) + (32) + 2 (3) + 6 (3) + (81)Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1. Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81)
Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3. Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10 (2) + 4 (2) + 2 (3)+ 6 (3) + 3 (3) Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
10 (2) + 4 (2) = 14 (2). 2 (3)+ 6 (3) = 8 (3). Окончательное упрощенное выражение: 14 (2) + 8 (3) + 3 (3)
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Внимание, только СЕГОДНЯ!
Все интересное
Число, которое находится под знаком корня, часто мешает решению уравнения, с ним неудобно работать.
Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Корнем из числа x называется такое число, которое при возведении в степень корня будет равно x. Множителем называется умножаемое число. То есть, в выражении вида x*ª-&radic-y нужно внести x под корень. Инструкция 1Определите степень…
Если подкоренное выражение содержит набор математических действий с переменными, то иногда в результате его упрощения есть возможность получить относительно простое значение, часть которого можно вынести из под корня. Бывает полезно такое упрощение…
Арифметические действия с корнями различной степени могут значительно упростить расчеты в физике и технике и сделать их более точными. При умножении и делении удобнее не извлекать корень из каждого сомножителя или делимого и делителя, а сначала…
Квадратным корнем из числа x называют число a, которое при умножении само на себя дает число x: a * a = a^2 = x, x = a.
Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
Корень в математике может иметь два значения: это арифметическое действие и каждое из решений уравнения, алгебраического, параметрического, дифференциального или любого другого. Инструкция 1Корень n-ной степени из числа a — это такое число, что…
При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные выражения. Для упрощения расчетов может понадобиться вынести множитель за знак радикала или внести под него. Это действие можно…
Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную перед знаком корня степень должно дать число, указанное под этим самым знаком. Часто для решения задач, в которых присутствуют…
Знаком корня в математических науках называется условное обозначение для корней. Число, находящееся под знаком корня, называется подкоренным выражением.
n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)
Вы ведь тоже ещё не вкурили?
Урок получился довольно большим, поэтому я разделил его на две части:
- Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
- Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще.
С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.
Основное правило умножения
Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:
Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:
\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]
Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Примеры. Рассмотрим сразу четыре примера с числами:
\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}.
\\ \end{align}\]
Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу .
Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.
Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.
Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:
\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]
И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.
Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка.
{2n}}}=\left| a \right|. \\ \end{align}\]
Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:
Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?
При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)
Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.
Умножение корней с разными показателями
Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt{23}$? Можно ли вообще это делать?
Да конечно можно. Всё делается вот по этой формуле:
Правило умножения корней.
{2}}}=\sqrt{5}. \\ \end{align}\]
Но тогда получается какая-то хрень:
\[\sqrt{-5}=\sqrt{5}\]
Этого не может быть, потому что $\sqrt{-5} \lt 0$, а $\sqrt{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
- Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
- Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.
2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
Инструкция
1. Во-первых, при сложении квадратных корней испробуйте извлечь эти корни. Это будет допустимо, если числа под знаком корня являются полными квадратами. Скажем, пускай задано выражение?4 + ?9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: ?4 + ?9 = 2 + 3 = 5.
2. Если под знаком корня нет полных квадратов, то испробуйте перенести из под знака корня множитель числа. Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 – множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.
3. Пускай сумма 2-х квадратных корней является знаменателем дроби, скажем, A / (?a + ?b). И пускай перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда дозволено воспользоваться дальнейшим методом. Умножьте числитель и знаменатель дроби на выражение?a – ?b. Таким образом в знаменателе получится формула сокращенного умножения: (?a + ?b) * (?a – ?b) = a – b. По аналогии, если в знаменателе дана разность корней: ?a – ?b, то числитель и знаменатель дроби нужно умножить на выражение?a + ?b. Для примера, пускай дана дробь 4 / (?3 + ?5) = 4 * (?3 – ?5) / ((?3 + ?5) * (?3 – ?5)) = 4 * (?3 – ?5) / (-2) = 2 * (?5 – ?3).
4. Разглядите больше непростой пример избавления от иррациональности в знаменателе. Пускай дана дробь 12 / (?2 + ?3 + ?5). Нужно умножить числитель и знаменатель дроби на выражение?2 + ?3 – ?5:12 / (?2 + ?3 + ?5) = 12 * (?2 + ?3 – ?5) / ((?2 + ?3 + ?5) * (?2 + ?3 – ?5)) = 12 * (?2 + ?3 – ?5) / (2 * ?6) = ?6 * (?2 + ?3 – ?5) = 2 * ?3 + 3 * ?2 – ?30.
5. И наконец, если вам нужно только примерное значение, то дозволено посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для всего числа и запишите с нужной точностью (скажем, два знака позже запятой). А после этого совершите требуемые арифметические операции, как с обыкновенными числами. Скажем, пускай нужно узнать примерное значение выражения?7 + ?5 ? 2,65 + 2,24 = 4,89.
Видео по теме
Обратите внимание!
Квадратные корни ни в коем случае невозможно складывать как примитивные числа, т.е. ?3 + ?2 ? ?5!!!Полезный совет
Если вы раскладываете число на множители, дабы перенести квадрат из под знака корня, то совершите обратную проверку – перемножьте все получившиеся множители и получите изначальное число.Как ⚠️ корень умножить на корень с одинаковыми основаниями, но разными степенями
Как происходит перемножение корней с одинаковыми основаниями
Определение
Теорема умножения корней с одинаковыми основаниями: корень из произведения пары неотрицательных чисел определяется, как произведение квадратных чисел.
2 \cdot 3 cdot 7 =84\)
Ответ: 84
Задача 3
Определить корень:
\(\sqrt{25}\cdot \sqrt{4}\)
Решение:
\(\sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10\)
Ответ: 10
Задача 4
Вычислить корень:
\(\sqrt{32}\cdot \sqrt{2}\)
Решение:
\(\sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8\)
Ответ: 8
Задача 5
Рассчитать корень:
\(\sqrt{54}\cdot \sqrt{6}\)
Решение:
\(\sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18\)
Ответ: 18
Задача 6
Найти корень:
\(\sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}\)
Решение:
\(\sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}\)
Ответ: \(\frac{1}{3}\)
Решение примеров с помощью обобщения теоремы
Решение типичных задач на применение теоремы умножения корней основано на упрощении иррациональных выражений. При извлечении корней из 32 и 2 было получено произведение, которое являлось точным квадратом, корень из которого определяется рациональным числом.
Отдельно вычислить \(\sqrt{32}\) и \(\sqrt{2}\) не представляется возможным. В последнем примере в обоих подкоренных выражениях находятся дробные числа. С помощью произведения удалось сократить многие из множителей, что позволило оптимально преобразовать все выражение.
Умножать можно не только пары, но и несколько корней. Правило справедливо и в этом случае. Целесообразно рассмотреть применение теоремы на примерах:
\(\sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6\)
\(\sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}\)
Примечание
Во втором выражении третий множитель имеет под корнем десятичную дробь. В процессе преобразований она была заменена обычной дробью, что позволило выполнить сокращение. Благодаря исключению из иррациональных выражений десятичных дробей, существенно упрощается их решение.
В задачах нередко встречаются корни с произвольной степенью n.
{3}}} \)
Деление корней с разными степенями: Умножение корней с разными показателями. Деление корней: правила, методы, примеры — ЭкоДом: Дом своими руками
Этого не может быть, потому что $\sqrt{-5} \lt 0$, а $\sqrt{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.{2}}}=\sqrt{75}. \end{align}\]
Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?
Известно, что знак корня является квадратным корнем из некоторого числа.
Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Yandex.RTB R-A-339285-1
Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:
- без множителей;
- с множителями;
- с разными показателями.
Метод умножения корней без множителей
Алгоритм действий:
Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.
Пример
Пример 1: 18 × 2 = ?
Пример 2: 10 × 5 = ?
Пример
Пример 1: 18 × 2 = 36
Пример 2: 10 × 5 = 50
Пример 3: 3 3 × 9 3 = 27 3
Упростить подкоренные выражения.
Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:Пример
Пример 1: 36 = 6 .
36 — квадратный корень из шести (6 × 6 = 36) .
Пример 2: 50 = (25 × 2) = (5 × 5) × 2 = 5 2 . Число 50 раскладываем на произведение 25 и 2 . Корень из 25 — 5 , поэтому выносим 5 из-под знака корня и упрощаем выражение.
Пример 3: 27 3 = 3 . Кубический корень из 27 равен 3: 3 × 3 × 3 = 27 .
Метод умножения показателей с множителями
Алгоритм действий:
Умножить множители.
Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:Пример
Пример 1: 3 2 × 10 = 3 ? 3 × 1 = 3
Пример 2: 4 3 × 3 6 = 12 ? 4 × 3 = 12
Умножить числа под знаком корня.
Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:Пример
Пример 1: 3 2 × 10 = 3 (2 × 10) = 3 20
Пример 2: 4 3 × 3 6 = 12 (3 × 6) = 12 18
Упростить подкоренное выражение.
Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня.После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
Пример
Пример 1: 3 20 = 3 (4 × 5) = 3 (2 × 2) × 5 = (3 × 2) 5 = 6 5
Пример 2: 12 18 = 12 (9 × 2) = 12 (3 × 3) × 2 = (12 × 3) 2 = 36 2
Метод умножения корней с разными показателями
Алгоритм действий:
Найти наименьшее общее кратное (НОК) показателей.
Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.Пример
Необходимо найти НОК показателей для следующего выражения:
Показатели равны 3 и 2 . Для этих двух чисел наименьшим общим кратным является число 6 (оно делится без остатка и на 3 , и на 2). Для умножения корней необходим показатель 6 .
Записать каждое выражение с новым показателем:
Найти числа, на которые нужно умножить показатели, чтобы получить НОК.
В выражении 5 3 необходимо умножить 3 на 2 , чтобы получить 6 . А в выражении 2 2 — наоборот, необходимо умножить на 3 , чтобы получить 6 .
Возвести число, которое стоит под знаком корня, в степень равную числу, которое было найдено в предыдущем шаге.
Для первого выражения 5 нужно возвести в степень 2 , а втором — 2 в степень 3:2 → 5 6 = 5 2 6 3 → 2 6 = 2 3 6
Возвести в степень выражения и записать результат под знаком корня:
5 2 6 = (5 × 5) 6 = 25 6 2 3 6 = (2 × 2 × 2) 6 = 8 6
Перемножить числа под корнем:
(8 × 25) 6
Записать результат:
(8 × 25) 6 = 200 6
По возможности необходимо упростить выражение, но в данном случае оно не упрощается.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)В предыдущем уроке мы разобрались, что такое квадратный корень .
Пришла пора разобраться, какие существуют формулы для корней
, каковы свойства корней
, и что со всем этим можно делать.Формулы корней, свойства корней и правила действий с корнями
— это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Иррациональные выражения. Преобразование иррациональных выражений
Выражения, содержащие корень, который нельзя извлечь, называются иррациональными или радикальными.
Примеры:
— иррациональные выражения.
Сложение и вычитание корней
При сложении или вычитании иррациональных выражений их пишут одно за другим с сохранением их знаков.
Примеры:
В некоторых случаях с помощью преобразования можно сделать иррациональные выражения подобными, то есть, имеющими одинаковые показатели корней и подкоренные числа (или выражения), а затем сделать приведение.
Примеры:
Умножение и деление корней
При умножении иррациональных выражений с одинаковыми показателями корней перемножаются их подкоренные числа или выражения:
При делении иррациональных выражений с одинаковыми показателями корней подкоренное число или выражение делимого делится на подкоренное число или выражение делителя:
Примеры:
Возведение корня в степень
Чтобы возвести в степень иррациональное выражение, следует возвести в степень подкоренное число или выражение:
Примеры:
При возведении в n-ю степень знак корня отбрасывается, так как возведение числа (или выражения) в n-ю степень и извлечение из него корня n-ой степени — это взаимно сокращающиеся действия:
Извлечение корня
Чтобы извлечь корень из иррационального выражения, следует показатели корней перемножить:
, так как
Пример.

С помощью таких преобразований можно упростить извлечение корней 4-й, 6-й, 8-й, 9-й и т. п. степеней из чисел.
Примеры:
Сокращение корней
Величина иррационального выражения не изменится, если показатель корня и подкоренного выражения умножить или разделить на одно и то же число:
так как извлечение корня и возведение в степень — это взаимно сокращающиеся действия, если их показатели равны.
На этом свойстве основано сокращение корней и приведение их к общему показателю.
Сокращение корней — это деление показателей корня и подкоренного числа (или выражения) на одно и то же число, если оно является общим множителем для всех показателей.
Примеры:
Приведение корней к общему показателю
Приведение корней к общему показателю имеет большое сходство с приведением дробей к общему знаменателю. Рассмотрим два способа:
- Показатели корней не имеют общих множителей. В этом случае показатель каждого корня и его подкоренное число (или выражение) умножают на произведение остальных корней.

Рассмотрим три выражения:
,
Так как у данных показателей нет общего множителя, то просто перемножаем все показатели между собой. Полученный результат и станет общим показателем. После приведения к общему показателю выражения будут иметь следующий вид:
- Показатели корней имеют общий множитель. В этом случае надо найти НОК показателей и умножить показатель каждого корня на недостающий множитель.
Рассмотрим два выражения:
,
НОК (4, 6) = 12, значит, для первого выражения дополнительным множителем будет 3, а для второго 2. После приведения к общему показателю выражения будут иметь следующий вид:
При умножении и делении иррациональных выражений с разными показателями их приводят к общему показателю, а затем уже умножают или делят их подкоренные числа или выражения.
Примеры:
Как складывать корни с разными показателями. Правила вычитания корней
Квадратным корнем из числа X
называется число A
, которое в процессе умножения самого на себя (A * A
) может дать число X
.
Т.е. A * A = A 2 = X
, и √X = A
.Над квадратными корнями (√x
), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y
).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.Шаг 1. Извлечение квадратных корней
Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9
. Первое число 4
является квадратом числа 2
.Второе число 9
является квадратом числа 3
. Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5
.
Все, пример решен. Но так просто бывает далеко не всегда.Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54
.Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3
,
54 = 2 * 3 * 3 * 3
.В числе 24
мы имеем множитель 4
, его можно вынести из-под знака квадратного корня. В числе 54
мы имеем множитель 9
.Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6
.Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b)
.
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b
.Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b
.Аналогично, если в знаменателе имеется разность корней: √a — √b
, числитель и знаменатель дроби умножаем на выражение √a + √b
.Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3)
.Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5)
.
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5
.Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.

Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5
.В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89
.Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо.2=400\\
\hline \end{array}\]Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\)
Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть
\[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\]
Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\)
, то первоначально вы должны найти значения \(\sqrt{25}\)
и \(\sqrt{49}\)
, а затем их сложить.Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\]
Если значения \(\sqrt a\)
или \(\sqrt b\)
при сложении \(\sqrt
a+\sqrt b\)
найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt
2+ \sqrt {49}\)
мы можем найти \(\sqrt{49}\)
– это \(7\)
, а вот \(\sqrt
2\)
никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt
2+7\)
. Дальше это выражение, к сожалению, упростить никак нельзя
\(\bullet\)
Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad
\sqrt a:\sqrt b=\sqrt{a:b}\]
(при условии, что обе части равенств имеют смысл
)
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot
2}=\sqrt{64}=8\)
;
\(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\)
;
\(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}=
5\cdot 8=40\)
.
\(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\)
. Так как \(44100:100=441\)
, то \(44100=100\cdot 441\)
. По признаку делимости число \(441\)
делится на \(9\)
(так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\)
, то есть \(441=9\cdot 49\)
.
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}=
\sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\]
Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}=
\sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{
\dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot
\sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]\(\bullet\)
Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\)
(сокращенная запись от выражения \(5\cdot
\sqrt2\)
).Так как \(5=\sqrt{25}\)
, то \
Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\)
,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)3) \(\sqrt a+\sqrt a=2\sqrt a\)
.2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\)
и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\)
(число “пи”, приблизительно равное \(3,14\)
), \(e\)
(это число называют числом Эйлера, приблизительно оно равно \(2,7\)
) и т.д.
\(\bullet\)
Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел.
Обозначается это множество буквой \(\mathbb{R}\)
.
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.Факт 5.
\(\bullet\)
Модуль вещественного числа \(a\)
– это неотрицательное число \(|a|\)
, равное расстоянию от точки \(a\)
до \(0\)
на вещественной прямой.2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3
\(\bullet\)
Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\
&\sqrt 3\approx 1,7 \end{aligned}\]
Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\)
Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа.2=168\cdot 168=28224\)
.
Следовательно, \(\sqrt{28224}=168\)
. Вуаля!Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор
. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.- Потому что это развивает интеллект
. Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
Тема про квадратные корни является обязательной в школьной программе курса математики. Без них не обойтись при решении квадратных уравнений. А позже появляется необходимость не только извлекать корни, но и выполнять с ними другие действия. Среди них достаточно сложные: возведение в степень, умножение и деление. Но есть и достаточно простые: вычитание и сложение корней. Кстати, они только на первый взгляд кажутся такими. Выполнить их без ошибок не всегда оказывается просто для того, кто только начинает с ними знакомиться.
Что такое математический корень?
Это действие возникло в противовес возведению в степень.
Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Если в степени стоит двойка, то и корень будет квадратным. Он является самым распространенным в школьной математике. У него даже нет указания, что он квадратный, то есть возле него не приписывается цифра 2. Математическая запись этого оператора (радикала) представлена на рисунке.
Из описанного действия плавно вытекает его определение. Чтобы извлечь квадратный корень из некоторого числа, нужно выяснить, какое даст при умножении на себя подкоренное выражение. Это число и будет квадратным корнем. Если записать это математически, то получится следующее: х*х=х 2 =у, значит √у=х.
Какие действия с ними можно выполнять?
По своей сути корень — это дробная степень, у которой в числителе стоит единица. А знаменатель может быть любым. Например, у квадратного корня он равен двум.
Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
И требования к этим действиям у них одинаковые. Если умножение, деление и возведение в степень не встречают затруднений у учеников, то сложение корней, как и их вычитание, иногда приводит в замешательство. А все потому что хочется выполнить эти операции без оглядки на знак корня. И здесь начинаются ошибки.
По каким правилам выполняется их сложение и вычитание?
Сначала нужно запомнить два категорических «нельзя»:
- нельзя выполнять сложение и вычитание корней, как у простых чисел, то есть невозможно записать подкоренные выражения суммы под один знак и выполнять с ними математические операции;
- нельзя складывать и вычитать корни с разными показателями, например квадратный и кубический.
Наглядный пример первого запрета: √6 + √10 ≠ √16, но √(6 + 10) = √16
.Во втором случае лучше ограничиться упрощением самих корней. А в ответе оставить их сумму.
Теперь к правилам
- Найти и сгруппировать подобные корни. То есть те, у которых не только стоят одинаковые числа под радикалом, но и они сами с одним показателем.
- Выполнить сложение корней, объединенных в одну группу первым действием. Оно легко осуществимо, потому что нужно только сложить значения, которые стоят перед радикалами.
- Извлечь корни в тех слагаемых, в которых подкоренное выражение образует целый квадрат. Другими словами, не оставлять ничего под знаком радикала.
- Упростить подкоренные выражения. Для этого нужно разложить их на простые множители и посмотреть, не дадут ли они квадрата какого-либо числа. Понятно, что это справедливо, если речь идет о квадратном корне. Когда показатель степени три или четыре, то и простые множители должны давать куб или четвертую степень числа.
- Вынести из-под знака радикала множитель, который дает целую степень.
- Посмотреть, не появилось ли опять подобных слагаемых. Если да, то снова выполнить второе действие.
В ситуации, когда задача не требует точного значения корня, его можно вычислить на калькуляторе. Бесконечную десятичную дробь, которая высветится в его окошке, округлить. Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Это вся информация о том, как выполняется сложение корней. Примеры, расположенные ниже, проиллюстрируют вышесказанное.
Первое задание
Вычислить значение выражений:
а) √2 + 3√32 + ½ √128 — 6√18;
б) √75 — √147 + √48 — 1/5 √300;
в) √275 — 10√11 + 2√99 + √396.
а) Если следовать приведенному выше алгоритму, то видно, что для первых двух действий в этом примере ничего нет. Зато можно упростить некоторые подкоренные выражения.
Например, 32 разложить на два множителя 2 и 16; 18 будет равно произведению 9 и 2; 128 — это 2 на 64. Учитывая это, выражение будет записано так:
√2 + 3√(2 * 16) + ½ √(2 * 64) — 6 √(2 * 9).
Теперь нужно вынести из-под знака радикала те множители, которые дают квадрат числа.
Это 16=4 2 , 9=3 2 , 64=8 2 . Выражение примет вид:
√2 + 3 * 4√2 + ½ * 8 √2 — 6 * 3√2.
Нужно немного упростить запись. Для этого производится умножение коэффициентов перед знаками корня:
√2 + 12√2 + 4 √2 — 12√2.
В этом выражении все слагаемые оказались подобными. Поэтому их нужно просто сложить. В ответе получится: 5√2.
б) Подобно предыдущему примеру, сложение корней начинается с их упрощения. Подкоренные выражения 75, 147, 48 и 300 будут представлены такими парами: 5 и 25, 3 и 49, 3 и 16, 3 и 100. В каждой из них имеется число, которое можно вынести из-под знака корня:
5√5 — 7√3 + 4√3 — 1/5 * 10√3.
После упрощения получается ответ: 5√5 — 5√3. Его можно оставить в таком виде, но лучше вынести общий множитель 5 за скобку: 5 (√5 — √3).
в) И снова разложение на множители: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. После вынесения множителей из-под знака корня имеем:
5√11 — 10√11 + 2 * 3√11 + 6√11. После приведения подобных слагаемых получим результат: 7√11.
Пример с дробными выражениями
√(45/4) — √20 — 5√(1/18) — 1/6 √245 + √(49/2).
На множители нужно будет разложить такие числа: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
3/2 √5 — 2√5 — 5/ 3 √(½) — 7/6 √5 + 7 √(½) = (3/2 — 2 — 7/6) √5 — (5/3 — 7) √(½) = — 5/3 √5 + 16/3 √(½).
Это выражение требует того, чтобы избавиться от иррациональности в знаменателе. Для этого нужно умножить на √2/√2 второе слагаемое:
5/3 √5 + 16/3 √(½) * √2/√2 = — 5/3 √5 + 8/3 √2.
Для полноты действий нужно выделить целую часть у множителей перед корнями. У первого она равна 1, у второго — 2.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
Инструкция
1.
Во-первых, при сложении квадратных корней испробуйте извлечь эти корни. Это будет допустимо, если числа под знаком корня являются полными квадратами. Скажем, пускай задано выражение?4 + ?9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: ?4 + ?9 = 2 + 3 = 5.2.
Если под знаком корня нет полных квадратов, то испробуйте перенести из под знака корня множитель числа.Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 – множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.
3.
Пускай сумма 2-х квадратных корней является знаменателем дроби, скажем, A / (?a + ?b). И пускай перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда дозволено воспользоваться дальнейшим методом. Умножьте числитель и знаменатель дроби на выражение?a – ?b. Таким образом в знаменателе получится формула сокращенного умножения: (?a + ?b) * (?a – ?b) = a – b. По аналогии, если в знаменателе дана разность корней: ?a – ?b, то числитель и знаменатель дроби нужно умножить на выражение?a + ?b. Для примера, пускай дана дробь 4 / (?3 + ?5) = 4 * (?3 – ?5) / ((?3 + ?5) * (?3 – ?5)) = 4 * (?3 – ?5) / (-2) = 2 * (?5 – ?3).4.
Разглядите больше непростой пример избавления от иррациональности в знаменателе. Пускай дана дробь 12 / (?2 + ?3 + ?5). Нужно умножить числитель и знаменатель дроби на выражение?2 + ?3 – ?5:12 / (?2 + ?3 + ?5) = 12 * (?2 + ?3 – ?5) / ((?2 + ?3 + ?5) * (?2 + ?3 – ?5)) = 12 * (?2 + ?3 – ?5) / (2 * ?6) = ?6 * (?2 + ?3 – ?5) = 2 * ?3 + 3 * ?2 – ?30.5.
И наконец, если вам нужно только примерное значение, то дозволено посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для всего числа и запишите с нужной точностью (скажем, два знака позже запятой). А после этого совершите требуемые арифметические операции, как с обыкновенными числами. Скажем, пускай нужно узнать примерное значение выражения?7 + ?5 ? 2,65 + 2,24 = 4,89.Видео по теме
Обратите внимание!
Квадратные корни ни в коем случае невозможно складывать как примитивные числа, т.е. ?3 + ?2 ? ?5!!!Полезный совет
Если вы раскладываете число на множители, дабы перенести квадрат из под знака корня, то совершите обратную проверку – перемножьте все получившиеся множители и получите изначальное число.b}\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) или \( {\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a > 1}\\{x \wedge y\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \)
Также можем добавить правило про логарифмы с разными основаниями и одинаковым аргументом:
\( \displaystyle \begin{array}{l}a>b>1\ \ \Leftrightarrow \ \ {{\log }_{a}}x<{{\log }_{b}}x\\1>a>b>0\ \ \Leftrightarrow \ \ {{\log }_{a}}x>{{\log }_{b}}x\end{array}\)
Объяснить его можно так: чем больше основание, тем в меньшую степень его придется возвести, чтобы получить один и тот же \( x\). Если же основание меньше \( 1\), то все наоборот, так как соответствующая функция монотонно убывающая.
Пример.
Сравните числа: \( {{\log }_{3}}5\) и \( {{\log }_{8}}26\).
Решение:
Согласно вышеописанным правилам:
\( \displaystyle \left. \begin{array}{l}{{\log }_{8}}26>{{\log }_{8}}25\\{{\log }_{8}}25>{{\log }_{9}}25={{\log }_{3}}5\text{ }\end{array} \right|\Rightarrow \text{ }{{\log }_{8}}26>{{\log }_{3}}5\)
А теперь формула для продвинутых.
{2}14<2,25}}\end{array}\)
§1 Корень n-степени и его свойства. Алгебра и начала математического анализа, 10 класс: уроки, тесты, задания.
1.
Произведение иррациональных чисел
Сложность:
лёгкое
2.
Действия с иррациональными числами
Сложность:
лёгкое
3.
Деление иррациональных чисел
Сложность:
лёгкое
4.
Корень степени n
Сложность:
лёгкое
5.
Вычисление корня степени n
Сложность:
лёгкое
6.
Подкоренное число и показатель степени
Сложность:
лёгкое
7.
Корень n-й степени (десятичные дроби)
Сложность:
лёгкое
8.
Корень n-й степени (обыкновенные дроби)
Сложность:
лёгкое
9.
Корень из произведения, десятичные дроби и целые числа
Сложность:
лёгкое
10.
Корень из произведения, целые числа и обыкновенные дроби
Сложность:
лёгкое
11.
Корень из частного, обыкновенные дроби
Сложность:
лёгкое
12.
Корень из произведения
Сложность:
лёгкое
13.
Корень из корня
Сложность:
лёгкое
14.
Извлечение корня из степени
Сложность:
лёгкое
15.
Показатели корня
Сложность:
лёгкое
16.
Корни с разными показателями
Сложность:
лёгкое
17.
Корень из корня степени
Сложность:
лёгкое
18.
Корень n-й степени (целые числа)
Сложность:
среднее
19.
Сравнение иррациональных чисел
Сложность:
среднее
20.
Уравнение (степень)
Сложность:
среднее
21.
Корень n-й степени (целые числа и десятичные дроби)
Сложность:
среднее
22.
Область определения функции корня n-й степени, чётная и нечётная степени
Сложность:
сложное
23.
Область определения функции корня n-й степени (нечётная степень)
Сложность:
среднее
24.
Область определения функции корня n-й степени (четная степень)
Сложность:
среднее
25.
Область определения функции, противоположный квадратный трёхчлен (чётная степень)
Сложность:
среднее
26.
Возрастание функции корня n-й степени
Сложность:
среднее
27.
Область значений функции корня n-й степени
Сложность:
среднее
28.
Решение уравнения графически (нечётная степень)
Сложность:
среднее
29.
Возрастание функции корня n-й степени вида y=f(x+m) или y=f(x)+b (чётная степень)
Сложность:
среднее
30.
Область значений функции вида y=f(x+m) или y=f(x)+b (нечётная степень)
Сложность:
среднее
31.
Область определения функции корня n-й степени, дробь (чётная степень)
Сложность:
среднее
32.
Область определения функции, квадратный трёхчлен (чётная степень)
Сложность:
среднее
33.
Корень из произведения степеней, корень в степени (целые числа)
Сложность:
среднее
34.
Корень из дроби
Сложность:
среднее
35.
Произведение корней
Сложность:
среднее
36.
Частное корней
Сложность:
среднее
37.
Произведение корня из произведения степеней и корня из степени
Сложность:
среднее
38.
Корень из частного степеней
Сложность:
среднее
39.
Корень из степени
Сложность:
среднее
40.
Сравнение корней
Сложность:
среднее
41.
Произведение корней с разными показателями
Сложность:
среднее
42.
Частное корней с разными показателями
Сложность:
среднее
43.
Произведение корней с разными показателями из произведений степеней
Сложность:
среднее
44.
Степень произведения (число и корень)
Сложность:
среднее
45.
Степень произведения (одночлен и корень)
Сложность:
среднее
46.
Корень из произведения степеней (десятичные дроби)
Сложность:
среднее
47.
Возведение в степень произведения (переменная и корень)
Сложность:
среднее
48.
Возведение в степень произведения (степень и корень)
Сложность:
среднее
49.
Произведение корней из произведений степеней
Сложность:
среднее
50.
Вычиcление выражения
Сложность:
среднее
51.
Уравнение n-ой степени
Сложность:
среднее
52.
Область определения функции, сумма корней (чётная степень)
Сложность:
сложное
53.
Область определения функции, дробь (нечётная степень)
Сложность:
сложное
54.
Область определения функции корня n-й степени, сумма корней
Сложность:
сложное
Что такое квадратный корень? Формулы и Примеры
Что такое квадратный корень
Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Определение квадратного корня также можно представить в виде формул:
√a = x
x2 = a
x ≥ 0
a ≥ 0Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из √-16
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Если — 4, то -4 * -4 = 16, (минус на минус всегда дает плюс).
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Здесь могут возникнуть резонные вопросы, почему, например, в примере x2 = 16, x = 4 и x = -4.
Чтобы вопросы отпали, и все встало на свои места, нужно разобраться, в чем разница между квадратным уравнением и арифметическим квадратным корнем. В детской школе Skysmart ученики вникают в тонкости математической вселенной вместе с красочными героями комиксов и в интерактивном формате.
Приходите вместе с ребенком на бесплатный вводный урок: познакомимся и покажем, как решать задачки весело и эффективно.
Разница между квадратным корнем и арифметическим квадратным уравнением
Прежде всего, чтобы разграничить эти два понятия, запомните:
- x2 = 16 не равно x = √16.
Это два нетождественных друг другу выражения.
- x2 = 16 — это квадратное уравнение.
- x = √ 16 — арифметический квадратный корень.
Из выражения x2 = 16 следует, что:
- |x| = √16, это значит, что x = ±√16 = ±4, x1 = 4, x2 = -4.
Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.
В то же самое время, из выражения x = √16 следует, что x = 4.
Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:
- Пример решен неверно
- Это квадратное уравнение.
Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.
Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.
Даны два выражения:
- x2 = 36
- x = √36
Первое выражение — квадратное уравнение.
|x| = √36
x1 = +6
x2 = -6.Второе выражение — арифметический квадратный корень.
√36 = 6
x = 6.Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.
Запись иррациональных чисел с помощью квадратного корня
Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.
Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.
Примеры иррациональных чисел:
√2 = 1,414213…;
π = 3,141592…;
e = 2,718281…. .
Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.
Дано уравнение: x2 = 2.
Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.
Переберем числа, чтобы удостовериться в этом:
1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.
Решение следующее:
Строим график функции y = x2.
Отмечаем решения на графике: -√2; √2.Если попробовать извлечь квадратный корень из 2 с помощью калькулятора, то результат будет следующий: √2 = 1,414213… .
В таком виде ответ не записывают — нужно оставить квадратный корень.
x2 = 2.
x = √2
x = -√2.Извлечение корней
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.
Таблица квадратов
Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:
- 1.
Извлеките квадратный корень: √289
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Влево — 1, вверх — 7.
Ответ: √289 = 17.
- 2. Извлеките квадратный корень: √3025
Ищем в таблице число 3025.
Влево — 5, вверх — 5.Ответ: √3025 = 55.
- 3. Извлеките квадратный корень: √7396
Ищем в таблице число 7396.
Влево — 8, вверх — 6.
Ответ: √7396 = 86.
- 4. Извлеките корень: √9025
Ищем в таблице число 9025.
Влево — 9, вверх — 5.
Ответ: √9025 = 95.
- 5. Извлеките корень √1600
Ищем в таблице число 1600.
Влево — 4, вверх — 0.
Ответ: √1600 = 40.
Извлечением корня называется нахождение его значение.
Свойства арифметического квадратного корня
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
- Корень произведения равен произведению корней
- Извлечь корень из дроби — это извлечь корень из числителя и из знаменателя
- Чтобы возвести корень в степень, нужно возвести в степень значение под корнем
Давайте потренируемся и порешаем примеры на все три свойства. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.
Умножение арифметических корней
Для умножения арифметических корней используйте формулу:
Примеры:
Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.
Если нет возможности извлечь корни из чисел, то поступаем так:
- Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:
Добрая напоминалочка
Чтобы решать примеры быстрее, не забывайте пользоваться таблицей квадратов.
Деление арифметических корней
Для деления арифметических корней используйте формулу:
Примеры:
Ответ: смешанную дробь превращаем в неправильную (16 * 3) + 1 = 49
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.
Возведение арифметических корней в степень
Для возведения арифметического корня в степень используйте формулу:
Примеры:
Эти две формулы нужно запомнить:
Повторите свойства степеней, чтобы без труда решать такие примеры.
Внесение множителя под знак корня
Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.
А теперь давайте разберемся, как вносить множитель под знак корня.
Дано выражение: 7√9
Число семь умножено на квадратный корень из числа девять.
Извлечем квадратный корень и умножим его на 7.
√9= 3.
7√9 = 7*3 = 21
В данном выражение число 7 — множитель. Давайте внесем его под знак корня.
Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.
Вы помните, что (√a)2 = a
Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.
7√9 = √72* 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.
Формула внесения множителя под знак корня:
Запоминаем:
Нельзя вносить отрицательные числа под знак корня.
Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.
Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
- √28
Раскладываем подкоренное выражение на множители 28 = 7*4.
Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.
- Ответ: по правилу извлечения квадратного корня из произведения,
Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.
- Вынесите множитель из-под знака корня в выражении: √24
Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.
- Упростите выражение:
Вынесем в двух последних выражения множитель из-под знака корня.
Умножаем (-4 * 4) = -16. Все остальное выражение записываем в неизменном виде.
Мы видим, что во всем выражении есть один общий множитель — √5.
Выносим общий множитель за скобки:Далее вычисляем все, что в скобках:
Давайте тренироваться вместе: в современном формате и под присмотром внимательных учителей. Учиться в удовольствие — это реально.
Запишите ребенка на бесплатный урок математики в Skysmart: покажем, как все устроено на платформе и поможем ребенку поверить в себя.
Сравнение квадратных корней
Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда.
Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.
Если:
- √a < √b, то a < b
- √a = √b, то a = b
Давайте разберем на примере.
Сравните два выражения: √70 и 8√2
Первым делом преобразуем второе выражение: 8√2 = √64 * √2 = √64*2 = √128.
70 < 128.
Это значит, что √70 < 8√2.
Запоминаем
Чем больше число под знаком корня, тем больше сам корень.
Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.
- Сравните два выражения: √50 и 9√5
Ответ: преобразовываем выражение 9√5.
9√5 = √81 * √5 = √81*5 = √405
50 < 405
Это значит, что √50 < 9√5.
- Сравните два выражения: 6√5 и √18
Ответ: преобразовываем выражение 6√5.
6√5 = √36 * √5 = √36*5= √180
180 > 18
Это значит, что 6√5 > √18.
- Сравните два выражения: 7√12 и √20
Ответ: преобразовываем выражение 7√12.
7√12 = √49 * √12 = √49*12 = √588
588 >20
Это значит, что 7√12 > √20.
Как видите, ничего сложного в сравнении арифметических квадратных корней нет.
Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.
Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.
Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.
Таких калькуляторов в интернете много, вот один из них.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука.
С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
- Определить «сотни», между которыми оно стоит.
- Определить «десятки», между которыми оно стоит.
- Определить последнюю цифру в этом числе.
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
102 = 100
202 = 400
302 = 900
402 = 1600
502 = 2500
Мы видим что, 2116 больше 1600, но меньше 2500.
Это значит, что число 2116 находится между 402и 502.
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.
Как пользоваться таблицей
12 = 1
22 = 4
32 = 9
42 = 16 ⇒ 6
52 = 25 ⇒ 5
62 = 36 ⇒ 6
72 = 49 ⇒ 9
82 = 64 ⇒ 4
92 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Таким образом, у нас остаются два варианта: 442 и 462.
Далее вычисляем: 44 * 44 = 1936.
46 * 46 = 2116.
Ответ: √2116 = 46
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
11666 : 4 = 2916
2916 : 4 = 729
729 : 3 = 243
243 : 3 = 81
11664
4
2916
4
729
3
243
3
81
81
Запишем выражение в следующем виде:
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит.
Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
В 8 классе примеров с корнями очень много. Это значит, что ничего не остается, как выучить все формулы и натренироваться так, чтобы самый оголтелый квадратный корень выпустил белый флаг и запросил пощады.
На уроках математики в онлайн-школе Skysmart ваш ребенок научится извлекать самые неподатливые и громоздкие корни. Записывайтесь на бесплатный вводный урок и учите алгебру с удовольствием.
Корень и его свойства | ПОЛЕЗНЫЕ ПРОГРАММЫ ДЛЯ УЧЕБЫ И РАБОТЫ
Тема в математике «Корень и его свойства» нередко вызывает затруднения у школьников, особенно при решении примеров. В данной статье описаны основные свойства корней, а также правила сложения, вычитания, умножения и деления. Наглядные примеры помогаю понять, как решать задания с корнями.
Определение «Корень»
Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √64 = 8 (√64 равно числу 8).Формула: √a2 = a
Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.Извлечение корней: примеры
Извлечь корень — значит найти значение корня (то есть найти число, при возведении которого в степень, получается подкоренное значение).

Например, извлечь корень из 64 – значит найти √64.Найти корень из числа можно одним из следующих способов:
- Использование таблицы квадратов, таблицы кубов и т.д. В данном случае нужно просто найти нужное число в таблице и посмотреть, какому значению оно соответствует.
- Разложение подкоренного выражения (числа) на простые множители.
Порядок нахождения корня в этом случае будет следующим:
1. Разложение подкоренного значения на простые множители,
2. Объединение одинаковых множителей и их представление в виде степени с необходимым показателем.
Например, √144 = √2х2х2х2х3х3 = √(2х2)х(2х2)х(3х3) = √22х22х32 = √122 = 12
3. В случае, если невозможно найти корень из числа, то можно упростить подкоренное выражение (число). В этом случае применяется следующее правило: корень из произведения чисел равен произведению корней этих чисел.
Например, √72 = √2х2х2х3х3 = √(2х2)х2х(3х3) = √22х2х32 = √62х2 = 6√2- Когда невозможно получить два одинаковых числа под знаком корня, это значит, что упростить такой корень нельзя.
Например, √130=√13х5х2 – упростить нельзя.
- Извлечение корня из дроби. В этом случае применяются следующие правила:
1. дробное число должно быть записано в виде обыкновенной дроби;
2. корень из дроби равен частному от деления корня числителя на корень знаменателя.
Например, √3,24 = √324/100 = √81/25 = √81 / √25 = 9/5 = 1,8.- Извлечение нечетной степени из отрицательных чисел. Чтобы извлечь корень нечетной степени из отрицательного числа необходимо извлечь его из положительного числа и поставить перед ним знак минус.
Например, чтобы найти корень третьей степени из (-125), нужно найти корень третьей степени из 125 (будет 5) и подставить знак минуса (будет -5).
Приведение корней с разными показателями
Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.
Для этого воспользуемся следующим свойством дроби: a = n√an.
Например, есть квадратный корень (второй степени √2 ) и кубический корень (третьей степени 3√3).
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n√an: √2 = 2√2 = 6√23 = 6√8; 3√3 = 6√32 = 6√9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.Корень: сложение и вычитание корней
Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.

Примеры:
2√3 + 3√3 = 5√3
2√3 + 2√4 – не выполняется.При этом, нужно рассмотреть возможность упростить выражения.
Пример: 2√3 + 3√12 = 2√3 + 3√2х2х3 = 2√3 + 3√ 22х3 = 2√3 + 6√3 = 8√3.Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!Корень: умножение
Умножение корней без множителей
Произведение корней из чисел равно корню из произведения этих чисел.

√a*b=√a*√b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√2 х √3 = √6
√6 х √3 = √18 = √3х3х2 = 3√2Умножение корней с множителями
При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√2 х √5 = (3х1) √(2*5) = 3√10
4√2 х 3√3 = (3х4) √(2х3) = 12√6Корень: деление
Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√a:b=√a:√b
В процессе деления квадратных корней дроби упрощаются.Деление корней без множителей
Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √21:√3=√21:3=√7Деление квадратных корней с множителями
При делении корней с множителями нужно отдельно разделить множители и подкорневые выражения (числа). Подкорневые числа можно делить между собой только в том случае, если они имеют одинаковые степени. В случае отсутствия множителя, он равен единице.
Пример. 12√32 : 6√16 = (12:6) √(32:16) = 2√2.Примеры для практики
Чтобы попрактиковаться решать примеры на вычисление квадратный корней, можно скачать программу «Корни квадратные«
Умножение радикалов разных корней — концепция
Чтобы упростить два радикала с разными корнями, мы сначала перепишем корни как рациональные показатели.
Прежде чем члены можно будет перемножить, мы меняем показатели, чтобы они имели общий знаменатель. Таким образом, основания теперь имеют одни и те же корни, и их члены можно умножать вместе. Затем мы пишем задачу, используя корневые символы, а затем упрощаем.
Итак, мы знаем, как умножить квадратные корни вместе, когда у нас есть тот же индекс, тот же корень, с которым мы имеем дело.Мы не знаем, как их умножить, если у нас другой корень. Вот о чем мы и поговорим прямо сейчас.
Итак, если у нас есть квадратный корень из 3, умноженный на квадратный корень из 5. Они оба являются квадратными корнями, мы можем просто объединить наши члены и получить квадратный корень 15. Хорошо? Это достаточно просто. На самом деле мы не знаем, что делать, когда наши корни другие. Итак, у меня есть кубический корень и квадратный корень, хорошо? Мы не можем их комбинировать, потому что имеем дело с разными корнями.Но есть способ манипулировать ими, чтобы их можно было комбинировать. И как я всегда это делаю, так это переписываю свои корни как экспоненты, хорошо? Так что превратите это в 2 к одной трети умножить на 3 к половине.Хорошо. И помните, что когда мы имеем дело с долей экспонент, это власть над корнем. Чтобы умножить наши радикалы вместе, наши корни должны быть одинаковыми. Итак, нам нужно как-то манипулировать этими двумя корнями, 3 и квадратом, 3 и 2, чтобы они были одним и тем же корнем, хорошо? Так что подумайте, какое у нас наименьшее общее кратное.2 и 3, 6. Хорошо? Итак, мы хотим переписать обе эти степени с корнем со знаменателем 6. Итак, 6, 2 вы получите 6. Нам просто нужно умножить это на 2 на 2, так что мы получим 2 на 6, а затем 3, нужно чтобы сделать половину со знаменателем 6, чтобы получилось 3 на 6. Хорошо. Итак, то, что у нас действительно есть сейчас, — это корень шестой степени из 2, умноженный на корень шестой степени из 3 в третьем. Хорошо? Таким образом, мы вообще не изменили нашу задачу, а просто изменили нашу экспоненту на небольшую, но большую дробь.Это прекрасно. И теперь у нас одинаковые корни, поэтому мы можем перемножить, оставив нам корень шестой степени из 2 в квадрате, умноженного на 3 куба.
Хорошо. Часто эти числа будут довольно уродливыми и довольно большими, поэтому иногда вы можете просто оставить их вот так. 2 в квадрате и 3 в кубе — не такие уж большие числа. 2 в квадрате равно 4, 3 в квадрате равно 27, 4 умноженное на 27, я считаю, 108. Таким образом, это становится корнем шестой степени из 108.
Небольшое примечание, вам не обязательно переходить от переписывания его показателей дроби к ваши радикалы.Часто это помогает людям точно увидеть, что у них есть, так что видя, что у вас одни и те же корни, вы можете приумножить их, но если вам удобно, вы можете просто перейти от этого шага прямо к этому. Это прекрасно.
Таким образом, всякий раз, когда вы умножаете радикалы с разными индексами, разными корнями, вам всегда нужно сделать ваши корни одинаковыми, и вы делаете это, просто меняя свою дробь на общий знаменатель [IB].Корни или нули многочленов степени выше 2
13
Фактор теорема
Основная теорема алгебры
Стратегия поиска корней
Теорема о целочисленном корне
Сопряженные пары
Доказательство теоремы о множителях
Доказательство теоремы о целочисленном корне
В ЭТОЙ ТЕМЕ мы увидим, как найти корни многочлена степени больше 2.
Это будет зависеть от предыдущей темы: Синтетическое деление.
Мы видели в этой теме то, что называется теоремой о факторах.
Факторная теорема. x — r является множителем полинома P ( x ) тогда и только тогда, когда r является корнем из P ( x ).
Это означает, что если многочлен можно разложить на множители, например, следующим образом:
P ( x ) = ( x — 1) ( x + 2) ( x + 3)
, то теорема говорит нам, что корни равны 1, −2 и −3.
И наоборот, если мы знаем, что корни многочлена равны −2, 1 и 5, то многочлен имеет следующие множители:
( x + 2) ( x — 1) ( x — 5).
Затем мы могли бы перемножить и узнать многочлен, имеющий эти три корня.
Ниже мы увидим, как доказать факторную теорему.
Задача 1.
a) Используйте теорему о множителях, чтобы доказать: ( x + 1) множитель x 5 + 1.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!−1 является корнем из x 5 + 1. Для (−1) 5 + 1 = −1 + 1 = 0.
Следовательно, согласно теореме о множителях,
[ x — (- 1)] = ( x + 1) является множителем.б) Используйте синтетическое деление, чтобы найти другой фактор.
Следовательно, x 5 + 1 = ( x + 1) ( x 4 — x 3 + x 2 — x + 1)
Следуя той же процедуре, мы можем доказать:
( x + a ) — коэффициент x 5 + a 5 ,
и полностью в целом:
( x + a ) является множителем x n + a n , где n является нечетным.
Основная теорема алгебры
Следующее называется основной теоремой алгебры:
Многочлен степени n имеет по крайней мере один корень, действительный или комплексный.

Это на первый взгляд простое утверждение позволяет сделать вывод:
Многочлен P ( x ) степени n имеет ровно n корней, действительных или комплексных.
Если старший коэффициент P ( x ) равен 1, то теорема о факторах позволяет нам сделать вывод:
P ( x ) = ( x — r n ) ( x — r n — 1 ). . . ( x — r 2 ) ( x — r 1 )
Следовательно, многочлен третьей степени, например, будет иметь три корня.А если все они настоящие, то его график будет выглядеть примерно так:
For, три корня — это три интерцепта x .
Примечание: Если представить, что график начинается слева от
y — ось, тогда этот график начинается с ниже по оси x . Почему? Потому что в любом полиноме главный член в конечном итоге будет доминировать.Если ведущий член положительный, а полином равен нечетным градусам, тогда, когда x является большим отрицательным числом , то есть далеко слева от начала координат, тогда нечетная степень отрицательного числа сам по себе отрицательный.График будет ниже оси x .
Что касается многочлена четвертой степени, то у него будет четыре корня. А если все они настоящие, то его график будет выглядеть примерно так:
Здесь крайний левый график — это над по оси x . Поскольку, когда полином равен и даже градусам (и старший коэффициент положителен), тогда четная степень отрицательного числа будет положительной .График будет выше оси x .
Пример 1. Напишите многочлен с целыми коэффициентами, имеющий следующие корни: −1, ¾.
Решение . Поскольку -1 — корень, то ( x + 1) — множитель. Что касается корня, то у нас было бы решение
x = 3
4, что подразумевает 4 x = 3 4 x — 3 = 0 Коэффициенты равны (4 x — 3) ( x + 1).
Полином равен 4 x 2 + x — 3.
Задача 2. Определите многочлен, корни которого равны −1, 1, 2, и нарисуйте его график.
Факторы: ( x + 1) ( x — 1) ( x — 2). При умножении получается многочлен ( x 2 — 1) ( x — 2) =
x 3 — 2 x 2 — x + 2.
Вот график:
Пересечение y является постоянным членом 2. В каждом полиноме перехват y является постоянным членом, потому что постоянный член — это значение y , когда x = 0.
Задача 3. Определите многочлен с целыми коэффициентами, корни которых равны −½, −2, −2, и нарисуйте график.
Факторы: (2 x + 1) ( x + 2) 2 .При умножении многочлен равен (2 x + 1) ( x 2 + 4 x + 4) =
2 x 3 + 9 x 2 + 12 x + 4.
Вот график:
−2 — двойной корень.
График не пересекает ось x .
Вопрос. Если r является корнем многочлена p ( x ), то после деления p ( x ) на x — r , какой остаток вам следует ожидать?
0.Поскольку r является корнем, тогда x — r — это фактор из p ( x ).
Задача 4. Является ли x = 2 корнем этого многочлена:
x 6 — 3 x 5 + 3 x 4 — 3 x 3 + 3 x 2 −3 x + 2?
Используйте синтетическое деление, чтобы разделить многочлен на x — 2, и посмотрите на остаток.
Остаток равен 0. 2 — корень многочлена.
Урок 12
Пример 2. Найдите три корня из
.
P ( x ) = x 3 — 2 x 2 — 9 x + 18,
с учетом того
корень 3.Решение. Поскольку 3 является корнем из P ( x ), то согласно теореме о множителях x — 3 является множителем. Следовательно, разделив P ( x ) на x — 3, мы можем найти другой квадратичный множитель.
У нас
x 3 — 2 x 2 — 9 x + 18 = ( x 2 + x — 6) ( x — 3) = ( x — 2) ( x + 3) ( x — 3) Три корня: 2, −3, 3.
Опять же, поскольку x — 3 является фактором из P ( x ), остаток равен 0.
Задача 5. Нарисуйте график этого многочлена,
.
y = x 3 — 2 x 2 — 5 x + 6,
, учитывая, что один корень равен -2.
Поскольку −2 является корнем, то ( x + 2) является множителем.
Чтобы найти другой, квадратичный множитель, разделите многочлен на x + 2. Обратите внимание, что корень −2 помещается в поле:
У нас
x 3 — 2 x 2 — 5 x + 6 = ( x 2 — 4 x + 3) ( x + 2) = ( x — 1) ( x — 3) ( x + 2) Три корня: 1, 3, −2.Вот график:
Стратегия поиска корней
Что же тогда представляет собой стратегия нахождения корней многочлена степени n > 2?
Нам нужно дать или угадать корень r . Затем мы можем разделить многочлен на x — r и, следовательно, получить коэффициент полинома , который будет на один градус меньше. Если мы сможем найти корень этого фактора, мы сможем продолжить процесс, уменьшая степень каждый раз, пока не достигнем квадратичного значения, которое мы всегда сможем решить.
Вот теорема, которая поможет нам угадать корень.
Теорема о целочисленном корне. Если целое число является корнем многочлена, коэффициенты которого являются целыми числами, а старший коэффициент равен ± 1, то это целое число является коэффициентом постоянного члена.
Мы докажем это ниже.
Эта теорема о целочисленном корне является примером более общей теоремы о рациональном корне:
Если рациональное число об / с является корнем многочлена, коэффициенты которого являются целыми числами, то целое число r является множителем постоянного члена, а целое число s является множителем старшего коэффициента.
Пример 3. Каковы возможные целочисленные корни x 3 — 4 x 2 + 2 x + 4?
Ответ. Если есть целые корни, они будут множителями постоянного члена 4; а именно: ± 1, ± 2, ± 4.
Итак, 1 — это корень? Чтобы ответить, мы разделим многочлен на x — 1 и надеемся на остаток 0.
1 — 4 + 2 + 4 | 1 + 1 — 3 — 1 ———————————————— ————————————————— —— 1 — 3 — 1 + 3 Остаток не равен 0.1 не является корнем. Давайте попробуем −1:
1 — 4 + 2 + 4 | -1 — 1 + 5 — 7 ———————————————— ————————————————— —— 1 — 5 + 7 — 3 Остаток снова не равен 0.Попробуем 2:
1 — 4 + 2 + 4 | 2 + 2 — 4 — 4 ———————————————— ————————————————— —— 1 — 2 — 2 + 0 Да! 2 — это корень.
У нас
x 3 — 4 x 2 + 2 x + 4 = ( x 2 — 2 x — 2) ( x — 2)
Теперь мы можем найти корни квадратичного, завершив квадрат. Как мы обнаружили в теме 11:
.
х = 1 ±
Следовательно, три корня:
1+, 1 -, 2.
Проблема 6.
а) Каковы возможные целые корни этого многочлена?
x 3 — 2 x 2 — 3 x + 1
± 1. Это единственные факторы постоянного члена.
б) Имеет ли этот многочлен целые корни?
Нет, потому что ни 1, ни -1 не сделают этот многочлен равным 0. Синтетическое деление на оба ± 1 не дает остатка 0.
Задача 7. Разложите этот многочлен на произведение линейных множителей.
x 3 + 2 x 2 — 5 x — 6
Мы должны найти корни. Возможные целые корни: ± 1, ± 2, ± 3, ± 6. Синтетическое деление показывает, что -1 — это корень.
Следовательно,
x 3 + 2 x 2 — 5 x — 6 = ( x + 1) ( x 2 + x — 6) = ( x + 1) ( x + 3) ( x −2) Сопряженные пары
Если иррациональное число a + является корнем, то его сопряженное число a — также является корнем.(См. «Навыки алгебры», Урок 28.) И если комплексное число a + bi является корнем, то и его сопряженное число a — bi .
Пример 4. Многочлен P ( x ) имеет следующие корни:
−2, 1 +, 5 и .
Какую наименьшую степень может иметь P ( x )?
Ответ .5. Ибо, поскольку 1 + — корень, то и сопряженный с ним 1 -. И поскольку 5 i является корнем, то же самое и его сопряжение, −5 i .
P ( x ) имеет как минимум эти 5 корней:
−2, 1 ±, ± 5 и .
Задача 8. Постройте многочлен со следующим корнем:
а) 2 +
Поскольку 2 + является корнем, то 2 — также. Следовательно, согласно теореме суммы и произведения корней, они являются корнями x 2 — 4 x + 1.
Тема 10
б) 2 — 3 и
Поскольку 2 — 3 i — это корень, то 2 + 3 i — тоже. Опять же, согласно теореме суммы и произведения корней, они являются корнями x 2 — 4 x + 13.
См. Тему 10, пример 7.
Задача 9. Построить многочлен с корнями 1 и 5 i .
Поскольку 5 i является корнем, то также и его сопряженный элемент, −5 i . Они будут корнями квадратичного множителя многочлена. Сумма этих корней равна 0. Произведение равно 25. Следовательно, квадратичный коэффициент равен ( x 2 + 25).
Далее, поскольку 1 — это корень, тогда ( x — 1) является множителем. Следовательно, многочлен
( x — 1) ( x 2 + 25) = x 3 — x 2 + 25 x — 25.
Задача 10. Пусть f ( x ) = x 5 + x 4 + x 3 + x 2 — 12 x — 12. Один корень равно, а другой — −2 i .
Если f ( x ) имеет целочисленные корни, сколько их может быть?
Один. Это многочлен 5-й степени, имеющий 5 корней. Два и -.И два — 2 i и −2 i .
Задача 11. Может ли многочлен 5-й степени иметь 2 действительных корня и 3 мнимых корня?
Нет это не так. Поскольку мнимые корни всегда попадают в пары, то, если есть какие-то мнимые корни, их всегда будет четное число.
Рассмотрим график многочлена 5-й степени с положительным старшим членом. Когда x — большое отрицательное число, график находится ниже оси x .Когда x — большое положительное число, оно находится выше оси x . Следовательно, график должен хотя бы один раз пересечь ось x . Теперь вы можете нарисовать график так, чтобы он пересекал ось x ровно дважды? Нет, ты не можешь.
Многочлен нечетной степени должен иметь нечетное число действительных корней.
Доказательство теоремы о множителях
x — r является множителем полинома P ( x )
тогда и только тогда, когда
r является корнем из P ( x ).Во-первых, если ( x — r ) является множителем P ( x ), тогда P ( r ) будет иметь множитель ( r — r ), который равно 0. Это сделает P ( r ) = 0. Это означает, что r является корнем.
И наоборот, если r является корнем из P ( x ), то P ( r ) = 0. Но согласно теореме об остатках P ( r ) = 0 означает что при делении P ( x ) на x — r остаток равен 0. x — r , следовательно, это коэффициент P ( x ).
Это то, что мы хотели доказать.
Доказательство теоремы о целочисленном корне
Если целое число является корнем многочлена, коэффициенты которого являются целыми числами, а старший коэффициент равен ± 1, то это целое число является коэффициентом и постоянного члена.
Пусть целое число r будет корнем этого многочлена:
P ( x ) = ± x n + a n −1 x n −1 + a n −2 x n −2 +.. . + a 2 x 2 + a 1 x + a 0 ,
, где и — целые числа. Тогда, поскольку r является корнем,
P ( r ) =
± r n +
a n −1 r n −1 + a n −2 r n −2 +.. . + a 2 r 2 + a 1 r + a 0 = 0,Преобразуйте постоянный член в 0 и множите на из оставшихся членов:
r (± r n −1 + a n −1 r n −2 +.
+ a 2 r + a 1 ) = — a 0
Теперь все и являются целыми числами; поэтому выражение в скобках является целым числом, которое для удобства назовем — q:
r (−q) = — a 0 ,
или,
rq = a 0 .
Таким образом, постоянный член a 0 может быть разложен на множители как rq , если r и q являются целыми числами. Таким образом, в этих условиях r является множителем постоянного члена.
Это то, что мы хотели доказать.
Следующая тема: Множественные корни
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
корней с более высоким индексом | Purplemath
Purplemath
Операции с кубическими корнями, корнями четвертой степени и другими корнями с более высоким индексом работают аналогично квадратным корням, хотя в некоторых случаях нам нужно немного расширить наше мышление.
Я объясню по ходу дела.
Упрощение терминов с более высоким индексом
На предыдущих страницах мы упростили квадратные корни, исключив из радикала любой множитель, встречающийся в наборах по два. Для второго корня нам понадобилась вторая копия.
Для корней с более высоким индексом рассуждения те же. Если у нас есть кубический корень, мы можем исключить любой фактор, встречающийся в наборах по три; из корня четвертой степени мы вычитаем любой фактор, который встречается в наборах по четыре; из корня пятой степени мы исключаем любой фактор, встречающийся в наборах по пять штук; и так далее.Например:
MathHelp.com
Упростить
Раньше я мог извлечь из квадратного корня все, что у меня было две копии.Таким же образом теперь я могу извлечь из корня четвертой степени все, что у меня есть четыре копии. Поскольку 16 = 2 4 , то:
Я беру кубический корень. Затем я могу вывести из радикала любой фактор, который встречается трижды.
Поскольку 8 = 2 3 , то этот радикал полностью упростится.
Мой первый шаг — полностью учесть это:
54 = 2 · 27 = 2 · (3 · 3 · 3)
У меня есть три копии 3, поэтому я могу вытащить 3 из корня куба, оставив 2 внутри.
Упростить:
Опять же, начну с факторинга:
48 = 3 · 16 = 3 · 2 · 2 · 2 · 2
У меня есть четыре копии фактора 2, но это кубический корень, поэтому я могу извлечь 2 только для трех из этих копий.3 и четвертая 2 останутся внутри радикала.
Упростить:
Я знаю, что 27 = 3 3 , поэтому кубический корень упростится до целого числа. Потом закончу умножением.
Упростить:
Мне дали переменные внутри этого радикала, но процесс работает так же, как всегда.Я беру пятый корень, поэтому могу вытащить из радикала все, для чего у меня есть пять копий.
32 — это 2 5 , так что это будет радикал.
x 10 = ( x 2 ) 5 , поэтому выйдет x 2 . y 6 = ( y 5 ) ( y 1 ), поэтому я смогу вытащить y , оставив последние y внутри корня.И z 7 = ( z 5 ) ( z 2 ), поэтому я смогу вытащить z , оставив z 2 внутри.
Моя работа выглядит так:
Примечание. Когда вы упрощаете радикальные выражения с помощью переменных, если радикал является корнем с четным индексом (например, квадратный корень или корень четвертой степени), они, вероятно, укажут, что вы должны «предполагать, что все переменные неотрицательны. «(или» положительный «).Это сделано для того, чтобы не принимать во внимание, необходимы ли столбцы абсолютных значений для вашего ответа. Если вы не уверены, о чем я говорю, проверьте здесь.
Умножение корней с более высоким индексом
Это умножение работает так же, как умножение квадратных корней, в том смысле, что произведение двух одинаковых корней с более высоким индексом может быть преобразовано в корень с более высоким индексом произведения.
Затем я упрощаю как обычно.
Упростите продукт:
В данном случае они дали мне продукт четвертого корня. Я могу превратить продукт радикалов в радикал продукта. Тогда я могу упростить.
Добавление корней с более высоким индексом
Упростить:
Термины в этом выражении являются кубическими корнями, но я могу объединить их, только если они кубические корни одного и того же значения.Прямо сейчас это не так. Поэтому я сначала упрощу радикалы, а затем посмотрю, смогу ли я пойти дальше.
Замечу, что 8 = 2 3 и 64 = 4 3 , так что я действительно смогу полностью упростить радикалы.
Упростить:
Я вообще не могу упростить второй радикал.Но я могу упростить первый радикал, потому что 81 = 3 4 = (3 3 ) (3). Итак, я получу сумму двух корней третьих из трех, которые я могу объединить.
Разделение корней с более высоким индексом
Знаменатель — это куб, равный 27 = 3 3 , поэтому я могу легко упростить и прийти к «рационализированному» знаменателю:
Это похоже на предыдущее упражнение, но здесь куб (то есть 27) находится в числителе.Я не могу упростить это выражение должным образом, потому что я не могу упростить радикал в знаменателе до целых чисел:
Чтобы рационализировать знаменатель, содержащий квадратный корень, мне потребовались две копии любых множителей внутри радикала. Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.
У меня есть одна копия множителя 5 в знаменателе.Я умножу сверху и снизу на кубический корень из 25, что даст две дополнительные копии 5, которые мне нужны, чтобы рационализировать знаменатель.
Это последнее выражение, возможно, ненамного «проще», чем исходное выражение. В этом контексте «упростить» означало «рационализировать знаменатель».
Часто «правильный» ответ будет не намного, если вообще, «проще», чем тот, с которого вы начали.
Упростить:
Поскольку 72 = 8 × 9 = (2 × 2 × 2) × (3 × 3), у меня есть только три двойки и две тройки. Другими словами, при нынешней дроби мне не хватит каких-либо факторов знаменателя, чтобы избавиться от радикала.
Чтобы извлечь что-либо из корня четвертой степени, мне нужно по четыре копии каждого фактора.Для радикала этого знаменателя мне понадобятся еще две тройки и еще одна 2. Итак, я умножу верхнюю и нижнюю часть на корень четвертой степени из 3 · 3 · 2 = 18.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в работе с выражениями с более высоким индексом. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.
)
URL: https://www.purplemath.com/modules/radicals6.htm
радикалов | Безграничная алгебра
Введение в радикалы
Радикальные выражения дают корни и являются обратными экспоненциальным выражениям.
Цели обучения
Опишите корень числа в порядке возведения в степень
Основные выводы
Ключевые моменты
- Корни — это операция, обратная возведению в степень.3 = у [/ латекс].
Ключевые термины
- корень : число, возведение которого в указанную степень дает указанное число или выражение.
- радикальное выражение : математическое выражение, содержащее корень, записанный в форме [латекс] \ sqrt [n] {a} [/ latex].
- кубический корень : корень степени 3, записанный в форме [латекс] \ sqrt [3] {a} [/ latex].
- квадратный корень : корень степени 2, записанный в форме [латекс] \ sqrt {a} [/ latex].
2 = 7 \ cdot 7 = 49 [/ латекс]
Поскольку корни являются обратной операцией возведения в степень, они позволяют нам работать в обратном направлении от решения экспоненциального выражения к числу в основе выражения. {n} = a [/ latex].4 = 7 \ cdot 7 \ cdot 7 \ cdot 7 = 2401 [/ латекс].
Сложение, вычитание и умножение радикальных выражений
Радикалы и экспоненты предъявляют особые требования к сложению и вычитанию, тогда как умножение выполняется более свободно.
Цели обучения
Различать правильное и неправильное использование операций над радикальными выражениями
Основные выводы
Ключевые моменты
- Чтобы добавить радикалы, подкоренное выражение (число под радикалом) должно быть одинаковым для каждого радикала.
- Вычитание выполняется по тем же правилам, что и сложение: подкоренное выражение должно быть таким же.
- Умножение радикалов просто требует, чтобы мы умножили член под радикальными знаками.
Ключевые термины
- radicand : число или выражение, квадратный корень или другой корень которого рассматривается; например, 3 дюйма [латекс] \ sqrt [n] {3} [/ latex].
Проще говоря, число под корнем.
- радикальное выражение : выражение, представляющее корень числа или величины.
Корни — это операция, обратная экспонентам. Выражение с корнями называется радикальным выражением . Вычислить экспоненты с учетом корня легко, хотя, возможно, и утомительно. Например [латекс] 7 \ cdot7 \ cdot7 \ cdot7 = 49 \ cdot49 = 2401 [/ латекс]. Итак, мы знаем, что корень четвертой степени из 2401 равен 7, а квадратный корень из 2401 равен 49. Что такое корень третьей степени из 2401? Найти значение для конкретного корня сложно. Это связано с тем, что возведение в степень — это другой вид функции, чем сложение, вычитание, умножение и деление.
Давайте рассмотрим некоторые основные математические операции с радикалами и показателями.
Сложение и вычитание радикальных выражений
Чтобы добавить радикалы, подкоренное число и (число под корнем) должно быть одинаковым для каждого радикала, поэтому общее уравнение будет иметь вид:
[латекс] a \ sqrt {b} + c \ sqrt {b} = (a + c) \ sqrt {b} [/ латекс]
Давайте подставим некоторые числа вместо переменных:
[латекс] \ sqrt 3 +2 \ sqrt 3 = 3 \ sqrt 3 [/ латекс]
Вычитание выполняется по тем же правилам, что и сложение:
[латекс] a \ sqrt b — c \ sqrt b = (a-c) \ sqrt b [/ латекс]
Например:
[латекс] 3 \ sqrt 3 -2 \ sqrt 3 = \ sqrt 3 [/ латекс]
Умножение радикальных выражений
Умножение радикалов просто требует, чтобы мы умножили переменную под знаками радикала.
[латекс] \ sqrt a \ cdot \ sqrt b = \ sqrt {a \ cdot b} [/ латекс]
Несколько примеров с действительными числами:
[латекс] \ sqrt 3 \ cdot \ sqrt 6 = \ sqrt {18} [/ латекс]
Это уравнение можно еще больше упростить; мы рассмотрим упрощение в другом разделе.
Упрощение радикальных выражений
Радикальное выражение можно упростить, если:
- значение под знаком корня можно записать как показатель степени,
- есть дроби под знаком корня,
- в знаменателе стоит радикальное выражение.2} {3}} = 4 \ sqrt {\ frac {1} {3}} [/ латекс]
Тогда можно обратиться к дроби под знаком корня и упростить радикал в числителе.
[латекс] \ displaystyle 4 \ sqrt {\ frac {1} {3}} = \ frac {4 \ sqrt {1}} {\ sqrt {3}} = \ frac {4} {\ sqrt {3}} [/ латекс]
Наконец, нужно вычеркнуть радикал из знаменателя.
[латекс] \ displaystyle \ frac {4} {\ sqrt {3}} = \ frac {4} {\ sqrt {3}} \ cdot \ frac {\ sqrt {3}} {\ sqrt {3}} = \ frac {4 \ sqrt {3}} {3} = \ frac {4} {3} \ sqrt {3} [/ latex]
Дроби, содержащие радикалы
Рационализация корня — это процесс, с помощью которого исключаются любые корни в знаменателе иррациональной дроби.
Цели обучения
Преобразование между дробями с рационализированным знаменателем и без него
Основные выводы
Ключевые моменты
- Чтобы рационализировать знаменатель, умножьте числитель и знаменатель на радикал в знаменателе.
Ключевые термины
- рационализация : Процесс удаления радикалов в знаменателе дроби.
В математике нам часто дают члены в виде дробей с радикалами в числителе и / или знаменателе.Когда нам задают выражения, которые включают радикалы в знаменателе, это упрощает вычисление выражения, если мы переписываем его таким образом, чтобы радикал больше не был в знаменателе. Этот процесс называется , рационализируя знаменатель .
Прежде чем мы начнем, помните, что все, что мы делаем с одной стороной алгебраического уравнения, мы должны делать и с другой стороной. Тот же принцип можно применить и к дробям: что бы мы ни делали с числителем, мы должны делать и со знаменателем, и наоборот.
2}} = {\ frac {10 \ sqrt {3}} {3}} [/ латекс]
Мнимые числа
Не существует такого значения, возведение которого в квадрат дает отрицательное значение; поэтому мы классифицируем корни отрицательных чисел как «мнимые».2 = -1 [/ latex] для [latex] x [/ latex] приводит к «числу», которое не будет действительным числом, называемым мнимым числом.
- Мнимое число [latex] i [/ latex] определяется как квадратный корень из -1: [latex] i = \ sqrt {-1} [/ latex].
Ключевые термины
- мнимое число : квадратный корень из -1.
- подкоренное выражение : значение под знаком корня.
Радикальное выражение представляет собой корень заданной величины.2 = -1 [/ latex] истинное утверждение.
Вот здесь и появляются мнимые числа. Когда подкоренное выражение (значение под знаком радикала) отрицательно, корень этого значения считается мнимым числом. В частности, мнимое число , [latex] i [/ latex], определяется как квадратный корень из -1: таким образом, [latex] i = \ sqrt {-1} [/ latex].
Мы можем записать квадратный корень из любого отрицательного числа через [латекс] i [/ латекс]. Вот несколько примеров:
- [латекс] \ sqrt {-25} = \ sqrt {25 \ cdot-1} = \ sqrt {25} \ cdot \ sqrt {-1} = 5i [/ латекс]
- [латекс] \ sqrt {-18} = \ sqrt {2 \ cdot9 \ cdot-1} = \ sqrt {2} \ cdot \ sqrt {9} \ cdot \ sqrt {-1} = 3i \ sqrt {2} [/ латекс]
Деление и взаимные значения радикальных выражений — стенограмма видео и урока
Деление радикалом
Мы собираемся разделить наши радикалы двумя разными способами в зависимости от того, какую проблему разделения мы видим.Напомним, что у каждого радикала есть порядковый номер, который представляет собой маленькое число, написанное в углублении символа радикала. Если наша задача деления имеет один и тот же индекс для числителя и знаменателя, и если знаменатель делится на числитель поровну, то мы продолжим и разделим числитель и знаменатель, объединяя их под одним и тем же радикальным символом.
Так, например, третий корень из 24, деленный на третий корень из 4, становится третьим корнем из 24, деленным на 4, что является третьим корнем из 6.Теперь, если бы у нас был третий корень из 4, разделенный на третий корень из 8, мы бы фактически продолжили и вычислили третий корень из 8, потому что это устранило бы один из радикалов, тем самым упростив наше выражение. Итак, у нас будет третий корень из 4, разделенный на 2. Итак, правило здесь заключается в том, что если мы можем продолжить и оценить радикал, удаляя таким образом радикал, то мы обязательно должны это сделать. Теперь, если у нас есть другой случай, когда у нас все еще есть радикал в знаменателе, тогда нам придется упростить наш радикал, чтобы у нас не было радикала в знаменателе.Об этом мы и поговорим сейчас.
Упрощение радикалов
Одно из правил упрощения радикалов состоит в том, что мы должны удалить радикалы из знаменателя. В знаменателе не может быть радикалов. Итак, если либо наша противоположность радикалу, либо наше разделение на радикал дает нам радикал в знаменателе, который мы не можем оценить, тогда нам придется использовать метод, который я собираюсь показать вам прямо сейчас, чтобы удалить его.
.
Этот метод заключается в умножении числителя и знаменателя на радикал в знаменателе.Итак, если 1 разделить на квадратный корень из 24, я умножу 1 на квадратный корень из 24, а мы умножим квадратный корень из 24 на квадратный корень из 24. Что произойдет, если мы умножим радикал сам на себя? Получаем число внутри радикала. Таким образом, квадратный корень из 24, умноженный на квадратный корень из 24, дает нам 24. Итак, 1, деленная на квадратный корень из 24, упрощается до квадратного корня из 24, деленного на 24. Мы еще не закончили. Нам все еще нужно проверить наши радикалы, чтобы увидеть, можем ли мы их еще больше упростить.Квадратный корень мы можем еще больше упростить, потому что мы можем разделить его на квадратный корень из 4, умноженный на квадратный корень из 6, который становится 2-кратным квадратным корнем из 6. Теперь мы видим, что у нас есть 2 вместо 24, поэтому мы можем на самом деле упростите это еще больше, разделив 2 и 24. Итак, наш окончательный ответ — квадратный корень из 6 из 12.
Еще один пример
Давайте посмотрим на последний пример. Допустим, мы делим квадратный корень из 11 на квадратный корень из 3. Я не могу объединить их в один радикал, потому что 3 не делится на 11 равномерно.Я также не могу вычислить квадратный корень из 3 в знаменателе. Это означает, что мне нужно упростить задачу деления, умножив числитель и знаменатель на радикал в знаменателе — квадратный корень из 3. Умножение числителя на квадратный корень из 3 дает мне квадратный корень из 11, умноженный на квадрат. корень из 3, который становится квадратным корнем из 33. Знаменатель — это квадратный корень из 3, умноженный на квадратный корень из 3, который становится 3. Я не могу больше ничего упрощать, поэтому мой ответ — квадратный корень из 33 делится на 3.
Краткое содержание урока
Что мы узнали? Мы узнали, что когда дело доходит до деления на радикал или при делении числа на радикал , деление числа 1 на ваш радикал, мы должны стремиться удалить радикал в знаменателе.
Если индексы радикала числителя и радикала знаменателя совпадают, мы должны увидеть, делятся ли числа равномерно друг на друга. Или, если мы можем оценить любого из радикалов, то мы тоже должны это сделать. Наша цель — устранить радикал в знаменателе.Если мы не можем легко удалить радикал из знаменателя, то мы должны упростить наш радикал, умножив числитель и знаменатель на радикал в знаменателе. Это удаляет радикал в знаменателе, оставляя нам значение внутри радикала. Числитель будет умножен на этот радикал. Все это часть упрощения нашего радикала.
Результат обучения
Просмотрите этот видео-урок, чтобы укрепить свои способности:
- Определите обратное радикалу
- Понять процесс деления на радикальное число
- Запомните шаги, необходимые для упрощения радикального выражения
Как разделить радикалы | Sciencing
Обновлено 20 ноября 2020 г.
Крис Дезил
В математике радикал — это любое число, которое включает знак корня (√).
Число под знаком корня является квадратным корнем, если перед знаком корня нет верхнего индекса, кубический корень — это верхний индекс 3 перед ним ( 3 √), корень четвертой степени, если ему предшествует 4 ( 4 √) и т. на. Многие радикалы нельзя упростить, поэтому деление на один требует специальных алгебраических методов. Чтобы использовать их, запомните эти алгебраические равенства:
\ sqrt {\ frac {a} {b}} = \ frac {\ sqrt {a}} {\ sqrt {b}}
\ sqrt {a × b } = \ sqrt {a} × \ sqrt {b}
Числовой квадратный корень в знаменателе
Обычно выражение с числовым квадратным корнем в знаменателе выглядит так:
\ frac {a} { \ sqrt {b}}
Чтобы упростить эту дробь, вы рационализируете знаменатель, умножив всю дробь на √ b / √ b .2} = b
\ frac {a \ sqrt {b}} {b}
1. Рационализируйте знаменатель дроби
\ frac {5} {\ sqrt {6}}
Решение: Умножьте дробь на √6 / √6
\ frac {5 \ sqrt {6}} {\ sqrt {6} \ sqrt {6}} \\ \, \\ \ frac {5 \ sqrt {6}} {6} \ text {или} \ frac {5} {6} × \ sqrt {6}
\ frac {6 \ sqrt {32}} {3 \ sqrt {8}}
Решение: В этом случае вы можете упростить, разделив числа вне знака корня и числа внутри него двумя отдельными операциями:
\ frac {6} {3} = 2 \\ \, \\ \ frac {\ sqrt {32} } {\ sqrt {8}} = \ sqrt {4} = 2
Выражение сводится к
2 × 2 = 4
Деление на кубические корни
Та же общая процедура применяется, когда радикал в знаменателе куб, корень четвертой или более высокой степени.
2}}
\ frac {5} {\ sqrt [3] {5}}
Умножьте числитель и знаменатель на 3 √25.
\ frac {5 × \ sqrt [3] {25}} {\ sqrt [3] {5} × \ sqrt [3] {25}} \\ \, \\ = \ frac {5 \ sqrt [3 ] {25}} {\ sqrt [3] {125}} \\ \, \\ = \ frac {5 \ sqrt [3] {25}} {5}
Цифры вне знака корня отменяют, а ответ:
\ sqrt [3] {25}
Переменные с двумя членами в знаменателе
Когда радикал в знаменателе включает два члена, вы обычно можете упростить его, умножив на его сопряжение.2 — 3}
College Algebra
Учебник 37: Synthetic Division и
Теоремы об остатке и множителеЦели обучения
По завершении этого руководства вы сможете:
- Чтобы разделить многочлен на двучлен вида x — c , используя синтетическое деление.
- Используйте теорему об остатке в сочетании с синтетическим делением, чтобы найти
функциональная ценность.- Используйте теорему о факторах в сочетании с синтетическим делением, чтобы найти факторы
и нули полиномиальной функции.Введение
В этом уроке мы рассмотрим синтетическое деление.
Вы можете использовать синтетическое деление всякий раз, когда вам нужно разделить многочлен
функцию двучленом вида x — c .
Мы можем использовать это, чтобы найти несколько вещей. Один — фактическое частное
а остаток вы получите, если разделите полиномиальную функцию на x — c . Кроме того, теорема об остатке утверждает, что
остаток, который мы получаем при применении синтетического деления на самом деле
дает нам функциональную ценность. Другое использование — поиск факторов и
нули.Факторная теорема утверждает, что если функциональное значение равно
0 при некотором значении c , затем x — c — коэффициент, а c — ноль. Вы можете не только найти эту функциональную ценность, используя синтетические
деление, но и найденное частное может помочь в процессе факторинга.
Похоже, синтетическое деление может помочь нам по нескольким различным типам
проблем. Я думаю, вы готовы открыть для себя
чудесный мир синтетического деления.Учебник
Синтетическое деление — это еще один способ разделить полином на бином x — c , где c равно
константа.
Шаг 1. Установите синтетический
разделение.
Простой способ сделать это — сначала настроить его, как если бы вы долго
подразделение, а затем создайте свое синтетическое подразделение.Если вам нужен обзор постановки задачи деления в столбик, не стесняйтесь
перейти к Урок 36: Длинный
Разделение.Делитель (то, на что вы делите) находится снаружи коробки.
Дивиденд (то, на что вы делите) идет внутри коробки.Когда вы выписываете дивиденд, убедитесь, что вы записываете его в порядке убывания
полномочия, и вы вставляете 0 для любых пропущенных терминов. Например, если
у тебя была проблема,
многочлен,
начинается с степени 4, затем следующая высшая степень — 1. Отсутствует
степени 3 и 2. Итак, если бы мы поместили его в ячейку деления, мы
написал бы это так:.
Это позволит вам выстроить в очередь условия, когда вы решите проблему.
Когда вы настраиваете это с помощью синтетического деления, напишите c для делителя x — c .
Затем напишите коэффициенты дивиденда справа вверху.
Включите любые 0, которые были вставлены вместо отсутствующих терминов.
Шаг 2: Вниз
ведущий коэффициент в нижнюю строку.
Шаг 3: Умножьте c на значение, только что записанное в нижней строке.
Поместите это значение сразу под следующим коэффициентом в дивиденде:
Шаг 4: Добавьте
столбец, созданный на шаге 3.
Запишите сумму в нижней строке:
Шаг 5: Повторить
пока не готово.
Шаг 6: Запишите
отвечать.
Числа в последней строке составляют ваши коэффициенты частного
а также остаток. Окончательное значение справа — это остаток.
Работая справа налево, следующее число — ваша константа, следующее — значение
коэффициент для x , следующий коэффициент
для x в квадрате и т. д.Степень частного на единицу меньше степени дивиденда.
Например, если степень дивиденда равна 4, то степень дивиденда
частное 3.
Пример
1 : Разделить с помощью синтетического деления:.
Синтетическое подразделение будет выглядеть так:
* Привести 2
* (- 1) (2) = -2
* Поместите -2 в следующий столбец
* -3 + (-2) = -5
Числа в последней строке составляют ваши коэффициенты частного
а также остаток.Окончательное значение справа — это остаток.
Работая справа налево, следующее число — ваша константа, следующее — значение
коэффициент для x , следующий коэффициент
для x в квадрате и т. д.
Пример
2 : Разделить с помощью синтетического деления:
Синтетическое подразделение будет выглядеть так:
* Привести 1
* (1) (1) = 1
* Поместите 1 в следующий столбец
* 0 + 1 = 1
Числа в последней строке составляют ваши коэффициенты частного
а также остаток.Окончательное значение справа — это остаток.
Работая справа налево, следующее число — ваша константа, следующее — значение
коэффициент для x , следующий коэффициент
для x в квадрате и т. д.
Теорема об остатке Если многочлен f ( x )
делится на x — c , затем
напоминание будет f ( c ).
Это означает, что мы можем применить синтетическое деление и последнее число
справа, то есть остаток, расскажет нам, какой функционал
значение c есть.
Пример
3 : Дано,
используйте теорему об остатке, чтобы найти f (-2).
Используя синтетическое деление, чтобы найти остаток, мы получаем:
Опять же, на этот раз наш ответ — не частное, а остаток.
Окончательный ответ: f (-2) = -27
Теорема о множителях Если f ( x ) является полиномом И
1) f ( c ) = 0, тогда x — c является множителем f ( x ).
2) x — c — коэффициент f ( x ),
тогда f ( c ) = 0.
Имейте в виду, что алгоритм деления
делимое = делитель (частное) + напоминание
Итак, если напоминание равно нулю, вы можете использовать это, чтобы помочь вам разложить многочлен на множители.
Если x — c является фактором,
вы можете переписать исходный многочлен как ( x — c ) (частное).Вы можете использовать синтетическое разделение, чтобы помочь вам с этим типом проблемы.

Теорема об остатке утверждает, что f ( c )
= остаток. Итак, если остаток оказывается равным 0, когда вы подаете заявку
синтетическое деление, тогда x — c — коэффициент f ( x ).
Пример
4 : используйте синтетическое деление, чтобы разделить на x — 2. Используйте результат, чтобы найти
все нули f .
Используя синтетическое деление, чтобы найти частное, мы получаем:
Обратите внимание, что остаток равен 0. Это означает, что ( x — 2) множитель.
Перезапись f ( x )
как ( x -2) (частное) получаем:Нам нужно закончить эту проблему, установив это равным нулю и
решение:
* Установить 1-й коэффициент = 0
* Установить 2-й коэффициент = 0
* Установить 3-й коэффициент = 0
Нули этой функции: x = 2,
-3 и -1.
Пример
5 : Решите уравнение
учитывая, что 3/2 является нулем (или корнем) из.
Используя синтетическое деление, чтобы найти частное, мы получаем:
Обратите внимание, что остаток равен 0. Это означает, что ( x — 3/2) является множителем.
Перезапись f ( x )
как ( x — 3/2) (частное) получаем:Нам нужно закончить эту проблему, установив это равным нулю и
решение:
* Учесть разницу во мнениях
квадратов* Обратите внимание, что 1-й множитель — 2, который является константой,
, который никогда не может быть = 0* Установить 2-й коэффициент = 0
* Установить 3-й коэффициент = 0
* Установить 4-й коэффициент = 0
Решение или нули этой функции: x = 3/2, -1 и 1.

Практические задачи
Это практические задачи, которые помогут вам перейти на следующий уровень.
Это позволит вам проверить и понять, понимаете ли вы эти
типы проблем. Математика работает как и все
в противном случае, если вы хотите добиться успеха в этом, вам нужно практиковать это.
Даже лучшие спортсмены и музыканты получали помощь и много
практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте.
На самом деле не бывает слишком много практики.Чтобы получить от них максимальную отдачу, вы должны решить проблему
свой, а затем проверьте свой ответ, щелкнув ссылку для ответа / обсуждения
для этой проблемы . По ссылке вы найдете ответ
а также любые шаги, которые позволили найти этот ответ.Практика
Задача 1a: Разделите с помощью синтетического деления.
Практика
Проблема 2a: Учитывая функцию f ( x ), используйте остаток
Теорема для нахождения f (-1).Практика
Задача 3a: Решите данное уравнение, учитывая, что 1/2 — ноль (или
корень) из.Нужна дополнительная помощь по этим темам?
Последний раз редактировал Ким Сьюард 15 марта 2012 г.
Авторские права на все содержание (C) 2002 — 2012, WTAMU и Kim Seward. Все права защищены..
Сложение корней с числами. Как вынести множитель из-под корня? Почему подкоренные выражения должны быть неотрицательными
Тема про квадратные корни является обязательной в школьной программе курса математики. Без них не обойтись при решении квадратных уравнений. А позже появляется необходимость не только извлекать корни, но и выполнять с ними другие действия.
Среди них достаточно сложные: возведение в степень, умножение и деление. Но есть и достаточно простые: вычитание и сложение корней. Кстати, они только на первый взгляд кажутся такими. Выполнить их без ошибок не всегда оказывается просто для того, кто только начинает с ними знакомиться.
Что такое математический корень?
Это действие возникло в противовес возведению в степень. Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Если в степени стоит двойка, то и корень будет квадратным. Он является самым распространенным в школьной математике. У него даже нет указания, что он квадратный, то есть возле него не приписывается цифра 2. Математическая запись этого оператора (радикала) представлена на рисунке.
Из описанного действия плавно вытекает его определение. Чтобы извлечь квадратный корень из некоторого числа, нужно выяснить, какое даст при умножении на себя подкоренное выражение.
Это число и будет квадратным корнем. Если записать это математически, то получится следующее: х*х=х 2 =у, значит √у=х.
Какие действия с ними можно выполнять?
По своей сути корень — это дробная степень, у которой в числителе стоит единица. А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
И требования к этим действиям у них одинаковые. Если умножение, деление и возведение в степень не встречают затруднений у учеников, то сложение корней, как и их вычитание, иногда приводит в замешательство. А все потому что хочется выполнить эти операции без оглядки на знак корня. И здесь начинаются ошибки.
По каким правилам выполняется их сложение и вычитание?
Сначала нужно запомнить два категорических «нельзя»:
- нельзя выполнять сложение и вычитание корней, как у простых чисел, то есть невозможно записать подкоренные выражения суммы под один знак и выполнять с ними математические операции;
- нельзя складывать и вычитать корни с разными показателями, например квадратный и кубический.
Наглядный пример первого запрета: √6 + √10 ≠ √16, но √(6 + 10) = √16 .
Во втором случае лучше ограничиться упрощением самих корней. А в ответе оставить их сумму.
Теперь к правилам
- Найти и сгруппировать подобные корни. То есть те, у которых не только стоят одинаковые числа под радикалом, но и они сами с одним показателем.
- Выполнить сложение корней, объединенных в одну группу первым действием. Оно легко осуществимо, потому что нужно только сложить значения, которые стоят перед радикалами.
- Извлечь корни в тех слагаемых, в которых подкоренное выражение образует целый квадрат. Другими словами, не оставлять ничего под знаком радикала.
- Упростить подкоренные выражения. Для этого нужно разложить их на простые множители и посмотреть, не дадут ли они квадрата какого-либо числа. Понятно, что это справедливо, если речь идет о квадратном корне. Когда показатель степени три или четыре, то и простые множители должны давать куб или четвертую степень числа.
- Вынести из-под знака радикала множитель, который дает целую степень.
- Посмотреть, не появилось ли опять подобных слагаемых. Если да, то снова выполнить второе действие.
В ситуации, когда задача не требует точного значения корня, его можно вычислить на калькуляторе. Бесконечную десятичную дробь, которая высветится в его окошке, округлить. Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Это вся информация о том, как выполняется сложение корней. Примеры, расположенные ниже, проиллюстрируют вышесказанное.
Первое задание
Вычислить значение выражений:
а) √2 + 3√32 + ½ √128 — 6√18;
б) √75 — √147 + √48 — 1/5 √300;
в) √275 — 10√11 + 2√99 + √396.
а) Если следовать приведенному выше алгоритму, то видно, что для первых двух действий в этом примере ничего нет. Зато можно упростить некоторые подкоренные выражения.
Например, 32 разложить на два множителя 2 и 16; 18 будет равно произведению 9 и 2; 128 — это 2 на 64.
Учитывая это, выражение будет записано так:
√2 + 3√(2 * 16) + ½ √(2 * 64) — 6 √(2 * 9).
Теперь нужно вынести из-под знака радикала те множители, которые дают квадрат числа. Это 16=4 2 , 9=3 2 , 64=8 2 . Выражение примет вид:
√2 + 3 * 4√2 + ½ * 8 √2 — 6 * 3√2.
Нужно немного упростить запись. Для этого производится умножение коэффициентов перед знаками корня:
√2 + 12√2 + 4 √2 — 12√2.
В этом выражении все слагаемые оказались подобными. Поэтому их нужно просто сложить. В ответе получится: 5√2.
б) Подобно предыдущему примеру, сложение корней начинается с их упрощения. Подкоренные выражения 75, 147, 48 и 300 будут представлены такими парами: 5 и 25, 3 и 49, 3 и 16, 3 и 100. В каждой из них имеется число, которое можно вынести из-под знака корня:
5√5 — 7√3 + 4√3 — 1/5 * 10√3.
После упрощения получается ответ: 5√5 — 5√3. Его можно оставить в таком виде, но лучше вынести общий множитель 5 за скобку: 5 (√5 — √3).
в) И снова разложение на множители: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36.
После вынесения множителей из-под знака корня имеем:
5√11 — 10√11 + 2 * 3√11 + 6√11. После приведения подобных слагаемых получим результат: 7√11.
Пример с дробными выражениями
√(45/4) — √20 — 5√(1/18) — 1/6 √245 + √(49/2).
На множители нужно будет разложить такие числа: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
3/2 √5 — 2√5 — 5/ 3 √(½) — 7/6 √5 + 7 √(½) = (3/2 — 2 — 7/6) √5 — (5/3 — 7) √(½) = — 5/3 √5 + 16/3 √(½).
Это выражение требует того, чтобы избавиться от иррациональности в знаменателе. Для этого нужно умножить на √2/√2 второе слагаемое:
5/3 √5 + 16/3 √(½) * √2/√2 = — 5/3 √5 + 8/3 √2.
Для полноты действий нужно выделить целую часть у множителей перед корнями. У первого она равна 1, у второго — 2.
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня.
Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Шаги
Часть 1 из 2: Определение корней
Обозначение корней. Выражение под знаком корня () означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: (27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5 (2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
Запомните, какие корни можно складывать, а какие нельзя. Так же, как нельзя складывать разные члены выражения, например, 2а + 2b 4ab, вы не можете складывать разные корни.
Нельзя складывать корни с разными подкоренными выражениями, например, (2) + (3) (5). Но вы можете сложить числа, стоящие под одним корнем, например, (2 + 3) = (5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236). Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, (64) + (64) (эта сумма не равна (64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297). Часть 2 из 2: Упрощение и сложение корней
Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения.
Например, рассмотрим выражение:
2 (3) + (81) + 2 (50) + (32) + 6 (3)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2 (3) + 2 (50) + (32) + 6 (3) + (81)- Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2 (50) + (32) + 2 (3) + 6 (3) + (81)Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1. Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81) Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3. Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10 (2) + 4 (2) + 2 (3)+ 6 (3) + 3 (3)
Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
10 (2) + 4 (2) = 14 (2). 2 (3)+ 6 (3) = 8 (3). Окончательное упрощенное выражение: 14 (2) + 8 (3) + 3 (3)
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Внимание, только СЕГОДНЯ!
Все интересное
Число, которое находится под знаком корня, часто мешает решению уравнения, с ним неудобно работать. Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Корнем из числа x называется такое число, которое при возведении в степень корня будет равно x.
2 = x, x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
Корень в математике может иметь два значения: это арифметическое действие и каждое из решений уравнения, алгебраического, параметрического, дифференциального или любого другого. Инструкция 1Корень n-ной степени из числа a — это такое число, что…
При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные выражения. Для упрощения расчетов может понадобиться вынести множитель за знак радикала или внести под него. Это действие можно…
Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную перед знаком корня степень должно дать число, указанное под этим самым знаком. Часто для решения задач, в которых присутствуют…
Знаком корня в математических науках называется условное обозначение для корней. Число, находящееся под знаком корня, называется подкоренным выражением.
n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
Корень из числа проще всего вычесть с помощью калькулятора. Но, если у вас нет калькулятора, тогда надо знать алгоритм вычисления квадратного корня. Дело в том, что под корнем сидит число в квадрате. Например, 4 в квадрате — это 16. То есть корень квадратный из 16 будет равен четырем. Так же 5 в квадрате — это 25. Поэтому корень из 25 будет 5. И так далее.
Если число небольшое, то его можно легко вычесть устно, к примеру, корень из 25 будет равен 5, а корень из 144-12. Также на калькуляторе можно посчитать, есть специальный значок корня, нужно вбить число и нажать на значок.
Поможет также таблица квадратных корней:
Есть еще способы, которые более сложные, однако очень эффективные:
Корень из какого либо числа можно вычесть с помощью калькулятора, тем более они есть в каждом телефоне на сегодняшний день.
Можно попробовать примерно прикинуть как может получится данное число, умножив одно число само на себя.
Вычислить корень квадратный из числа не сложно, особенно, если есть специальная таблица. Всем хорошо известная таблица еще с уроков алгебры. Такая операция называется извлечение квадратного корня из числа quot;aquot;, другими словами решение уравнения. Почти все калькуляторы, в смартфонах имеют функцию определения квадратного корня.
Результатом извлечения квадратного корня из известного числа будет другое число, которое, при возведении во вторую степень (квадрат), даст то самое число, которое нам известно. Рассмотрим одно из описаний расчтов, которое представляется кратким и понятным:
Вот видео по теме:
Вычеслить корень квадратный из числа можно несколькими способами.
Самым популярным способом — является использование специальной таблицы кореня (смотрите ниже).
Также на каждом калькуляторе есть функция при помощи которой можно узнать корень.
Или при помощи специальной формулы.
Извлечь квадратный корень из числа можно несколькими способами.
Один из них — самый быстрый, с помощью калькулятора.
Но если нет калькулятора, то можно это сделать вручную.
Результат получится точным.
Принцип практически такой же как деление столбиком:
Попробуем без калькулятора найти значение квадратного корняот числа, к примеру, 190969.
Таким образом, вс предельно просто. В вычислениях главное придерживаться определнных простых правил и логически размышлять.
Для этого нужна таблица квадратов
Вот например, корень из 100 = 10, из 20 = 400 из 43 = 1849
Сейчас практически все калькуляторы, в том числе и на смартфонах умеют высчитывать квадратный корень из числа. НО если калькулятора у вас нет, то можно найти корень из числа несколькими простыми способами:
Разложение на простые множители
Разложите подкоренное число на множители, являющиеся квадратными числами.
В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа числа, из которых можно извлечь целый квадратный корень. Множители числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как 25 = 5, 36 = 6, 49 = 7. Квадратные множители это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 это квадратное число. Разделив 400 на 25, вы получите 16, которое также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
Запишите это как: 400 = (25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть (а х b) = a x b .
Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
В нашем примере извлеките корень из 25 и из 16.
Если подкоренное число не раскладывается на два квадратных множителя (а это происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
Теперь вы можете оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу.
Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (1 = 1) и 4 (4 = 2). Таким образом, значение 3 расположено между 1 и 2. Та как значение 3, вероятно, ближе к 2, чем к 1, то наша оценка: 3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Этот метод также работает с большими числами. Например, рассмотрим 35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (25 = 5) и 36 (36 = 6). Таким образом, значение 35 расположено между 5 и 6. Та как значение 35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что 35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ разложите подкоренное число на простые множители.
Простые множители числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, 45 = (3 х 3 х 5). 3 можно вынести за знак корня: 45 = 35. Теперь можно оценить 5.
Рассмотрим другой пример: 88.
= (2 х 4 х 11)
= (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
2(2 х 11) = 22 х 11. Теперь можно оценить 2 и 11 и найти приблизительный ответ.
Может быть полезным будет еще это обучающее видео:
Чтобы извлечь корень из числа следует воспользоваться калькулятором, либо если нет подходящего, советую зайти вот на этот сайт и решить задачу с помощью онлайн калькулятора, который за секунды выдаст правильное значение.
Факт 1.
\(\bullet\) Возьмем некоторое неотрицательное число \(a\) (то есть \(a\geqslant 0\) ).2=400\\ \hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\) , то первоначально вы должны найти значения \(\sqrt{25}\) и \(\sqrt{49}\) , а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\) или \(\sqrt b\) при сложении \(\sqrt a+\sqrt b\) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt 2+ \sqrt {49}\) мы можем найти \(\sqrt{49}\) – это \(7\) , а вот \(\sqrt 2\) никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt 2+7\) . Дальше это выражение, к сожалению, упростить никак нельзя \(\bullet\) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad \sqrt a:\sqrt b=\sqrt{a:b}\] (при условии, что обе части равенств имеют смысл )
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot 2}=\sqrt{64}=8\) ; \(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\) ; \(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}= 5\cdot 8=40\) .\(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\) . Так как \(44100:100=441\) , то \(44100=100\cdot 441\) . По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\) , то есть \(441=9\cdot 49\) .
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}= \sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}= \sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{ \dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot \sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\) Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\) (сокращенная запись от выражения \(5\cdot \sqrt2\) ). Так как \(5=\sqrt{25}\) , то \ Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\) ,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\) .2\) , поэтому \(\sqrt{16}=4\) . А вот извлечь корень из числа \(3\) , то есть найти \(\sqrt3\) , нельзя, потому что нет такого числа, которое в квадрате даст \(3\) .
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\) и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\) ), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\) ) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\) .
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.Факт 5.
\(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\) , равное расстоянию от точки \(a\) до \(0\) на вещественной прямой.2\\ &2>2,25 \end{aligned}\] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3 \(\bullet\) Следует запомнить, что \[\begin{aligned} &\sqrt 2\approx 1,4\\ &\sqrt 3\approx 1,7 \end{aligned}\] Знание приблизительного значения данных чисел поможет вам при сравнении чисел! \(\bullet\) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа.2=168\cdot 168=28224\) .
Следовательно, \(\sqrt{28224}=168\) . Вуаля!Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
В математике любое действие имеет свою пару-противоположность – в сущности, это представляет собою одно из проявлений гегелевского закона диалектики: «единство и борьба противоположностей». Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня.
Извлечь из числа корень такой-то степени – это значит вычислить, какое число необходимо возвести в соответствующую степень, чтобы в итоге получилось данное число.
Две степени имеют свои отдельные названия: вторая степень называется «квадратом», а третья – «кубом». Соответствено, корни данных степеней приятно именовать квадратным корнем и кубическим. Действия с кубическими корнями – тема для отдельного разговора, а сейчас поговорим о сложении квадратных корней.
Начнем с того, что в ряде случаев квадратные корни проще сначала извлечь, а потом уже складывать результаты. Предположим, нам необходимо найти значение такого выражения:
Ведь совсем не сложно вычислить, что корень квадратный из 16 равен 4, а из 121 – 11. Следовательно,
√16+√121=4+11=15
Впрочем, это самый простой случай – здесь речь идет о полных квадратах, т.е. о таких числах, которые получаются при возведении в квадрат целых чисел. Но так бывает не всегда. Например, число 24 – это не полный квадрат (не найти такого целого числа, которое при возведении его во вторую степень дало бы в результате 24). То же самое относится к такому числу, как 54… Что делать, если нам необходимо сложить корни квадратные из этих чисел?
В таком случае мы получим в ответе не число, а другое выражение.
Максимум, что мы можем тут сделать – это максимально упростить исходное выражение. Для этого придется вынести множители из-под корня квадратного. Посмотрим, как это делается, на примере упомянутым чисел:
Для начала разложим на множители 24 – таким образом, чтобы из одного из них легко можно было извлечь корень квадратный (т.е., чтобы он был полным квадратом). Такое числи есть – это 4:
Теперь проделаем то же самое с 54. В его составе таким числом будет 9:
Т.о., у нас получается следующее:
√24+√54=√(4*6)+ √(9*6)
Теперь извлечем корни из того, из чего можем их извлечь: 2*√6+3*√6
Здесь есть общий множитель, который мы можем вынести за скобки:
(2+3)* √6=5*√6
Это и будет результатом сложения – больше ничего тут извлечь нельзя.
Правда, можно прибегнуть к помощи калькулятора – правда, результат будет приблизительным и с огромным количеством знаков после запятой:
√6=2,449489742783178
Постепенно округляя его, мы получим приблизительно 2,5.
Если нам все-таки хотелось бы довести до логического завершения решение предыдущего примера, мы можем умножить этот результат на 5 – и получится у нас 12,5. Более точного результата при таких исходных данных получить нельзя.
Использование предлога in в английском языке
Употребление и произношение in
Свойства степеней и корней. Чудо-конспект
Быстренько вспоминаем, что такое степень – это свёрнутая запись произведения:
, при этом называется основанием степени, а – показателем степени или тоже степенью. Особый случай: , если .Повторим важные свойства степеней. Некоторыми из них мы уже вовсю пользовались, в частности:
Для того чтобы возвести в степень произведение, нужно возвести в эту степень каждый множитель: . Правило работает для любого количества множителей.
Например: и т.п.
Следующее очевидное свойство следует из определения степени:Чтобы умножить степени с одинаковыми основаниями, нужно основание оставить таким же, а показатели сложить: .
! Не путать с «похожими» действиями! Для разных оснований – правило не работает! Для суммы – тоже нет!
Например:, при этом степень может быть и «навороченной»: – важно только, чтобы у них были одинаковые основания.
Чтобы возвести степень в степень нужно перемножить показатели:
Примеры: , и более замысловатые, но такие же естественные: .
При переносе степени из знаменателя в числитель (или наоборот) у показателя следует сменить знак:
Да, показатель степени может быть и отрицательным! Например: . Числа и называют взаимно обратными, их произведение равно: .
Другие примеры: , ну и можно ещё немножко поизвращаться: , такое тоже встречается J.
Следующее свойство вытекает из предыдущих:Деление степеней с одинаковыми основаниями:
Например: , и если присмотреться, то это обычное сокращение дроби: .
Разумеется, все правила работают и в обратном направлении, только что вот я «расщепил» степень на множители: . Довольно часто приходится выделять степень в степени: , а также «сбрасывать» степень в знаменатель: и тому подобное.
Но и это ещё не все секреты! На самом деле корень – это тоже степень:
Радикал (корень) можно записать в виде , где – положительная рациональная дробь . При получается квадратный корень: . Если же дробь отрицательна, то речь идёт о корне, который находится в знаменателе:
, таким образом: .Обращаю ваше внимание, что здесь не проводится никаких алгебраических действий: и – это две разные ЗАПИСИ одного и того же корня.
Например:
и давайте что-нибудь страшненькое: .Корень часто записывают в виде для того, чтобы с комфортом взять от него производную или интеграл.
И, кроме того, это мощнейший инструмент для перемножения «разношёрстных» степеней и корней, поскольку рассмотренные выше свойства работают и для дробных показателей:
, после чего результат обычно снова представляют в виде корня: (с помощью той же формулы ).Главное, уметь приводить дроби к общему знаменателю:
так же легко выполняется почленное деление числителя на знаменатель:
и приведение к общему знаменателю:
– полученный результат как раз можно проверить с помощью почленного деления.Теперь повторим факты, которые касаются именно корней:
Если – чётное число, бОльшее нуля, то корень определён только для неотрицательных значений ; если – нечётное число, бОльшее единицы, то корень определён для всех .
Корни вида определены только для неотрицательных значений «икс» (вне зависимости от того, чётное или нечётное).
При этом по возможности их можно (и нужно) сокращать: .
Например: .
Вы спрОсите, а что не так с корнем ? Вроде всё хорошо: .
А дело вот в чём: показатель можно записать в виде несократимой дроби , и тогда . Но дроби и задают одно и то же число! Во избежание этого парадокса и принято считать, что такие корни определены лишь для . Далее:Если делится на , то корень определён для всех значений , при этом , если – нечётное, и, если – чётное.
В частности, при : , если – чётное и, если – нечётное.Самый популярный случай: , например: — как мы помним, модуль уничтожает возможный знак «минус». А вот здесь модуль не нужен: – поскольку «икс квадрат» и так неотрицателен. К слову, при частичном вынесении модуль тоже не нужен: , ибо отрицательным здесь «икс» быть не может.

Другие примеры: и т.п.
Следует добавить, что все перечисленные факты справедливы и в том случае, если корень расположен в знаменателе.Среди «вычислительных» свойств наиболее важнЫ следующие, и ими мы тоже пользовались:
Если, то , и если , то
Если множители отрицательны, то возможны варианты. Так, корень «расщеплять» категорически нельзя. Но вот с корнем это вполне себе «прокатывает».
Другие практически значимые свойства:
Для натуральных и справедливо следующее:
Эти факты элементарно выводятся из свойства степеней: .Например: , впрочем, в высшей математике такие действия приходится выполнять редко.
Кроме того, есть и другие свойства, но они тоже не особо актуальны, порешаем лучше примеры:
Задание 4
а) Упростить:
б) Выполнить действия и записать результат в виде корня:
.в) Разделить почленно:
г) Привести к общему знаменателю:
д) Преобразовать:
Решения и ответы в конце книги.
И местечко тут даже на странице ещё осталось, наверное, какого-то свойства не хватает… или просто умной мысли – подумаю и обязательно добавлю, если надумаю – в следующем переиздании книги 🙂
1.8.1. Арифметическая прогрессия
1.6.4. Как представить сумму в виде произведения?
| Оглавление |
операций над радикальными выражениями | Начальная алгебра
Результаты обучения
- Умножение и деление подкоренных выражений
- Использование свойств показателей степени для умножения и деления подкоренных выражений
- Сложение и вычитание радикальных выражений
- Определите радикалы, которые можно добавить или вычесть
- Добавить подкоренные выражения
- Вычитание подкоренных выражений
- Рационализировать знаменатели
- Определить иррациональный и рациональный знаменатели
- Удалить радикалы из знаменателя одного члена
Умножение и деление
Вы можете сделать больше, чем просто упростить подкоренных выражений .
Их тоже можно умножать и делить. Умножение радикалов очень просто, если индексы всех радикалов совпадают. Правило произведения радикалов можно обобщить следующим образом:
Произведение, возведенное в степень Правило
Для любых чисел 9{\frac{1}{x}}}[/latex]
Для любых чисел a и b и любого положительного целого числа x : [латекс] \sqrt[x]{ab}=\sqrt[ x]{a}\cdot \sqrt[x]{b}[/latex]
Правило произведения в степени важно, поскольку его можно использовать для умножения подкоренных выражений. Обратите внимание, что корни одинаковы — вы можете комбинировать, например, квадратные корни с квадратными корнями или кубические корни с кубическими корнями. Но вы не можете умножать квадратный корень и кубический корень, используя это правило.
В следующем примере мы умножаем два квадратных корня
Используя правило произведения, возведенного в степень, вы можете взять, казалось бы, сложное выражение, [latex] \sqrt{18}\cdot \sqrt{16}[/latex] , и превратить его во что-то более управляемое, [latex] 12\sqrt{2}[/latex].
Вы могли также заметить, что и [латекс] \sqrt{18}[/латекс], и [латекс] \sqrt{16}[/латекс] могут быть записаны как произведения, включающие совершенные квадратные множители. Как изменится выражение, если вы сначала упростите каждый радикал, перед умножением ?
В обоих случаях вы получите один и тот же продукт, [латекс] 12\sqrt{2}[/латекс]. Неважно, умножаете ли вы подкоренные или сначала упрощаете каждый радикал.
Таким же образом вы умножаете подкоренные выражения, содержащие переменные. Пока корни подкоренных выражений одинаковы, вы можете использовать правило произведения, возведенного в степень, для умножения и упрощения. Посмотрите на два следующих примера. В обеих задачах сразу используется правило произведения, возведенное в степень, а затем выражение упрощается. 92}[/latex]
Показать решение
В следующем видео мы представляем больше примеров умножения кубических корней.
youtube.com/embed/cxRXofdelIM?feature=oembed» frameborder=»0″ gesture=»media» allow=»encrypted-media» allowfullscreen=»»>Разделение подкоренных выражений
Вы можете использовать те же идеи, чтобы понять, как упростить и разделить подкоренные выражения. Напомним, что правило продукта, возведенное в степень, гласит, что [латекс] \sqrt[x]{ab}=\sqrt[x]{a}\cdot \sqrt[x]{b}[/latex]. Что, если вы имеете дело с частным вместо произведения?
Для этого тоже есть правило. 9{\frac{1}{x}}}}[/latex]
Для любых действительных чисел a и b ( b ≠ 0) и любого положительного целого числа x : [латекс] \sqrt[ x]{\frac{a}{b}}=\frac{\sqrt[x]{a}}{\sqrt[x]{b}}[/latex]
Как и с умножением, вы начнете с некоторыми примерами с целыми числами, прежде чем перейти к радикалам с переменными.
Как и в случае с умножением, основная идея здесь заключается в том, что иногда имеет смысл разделить, а затем упростить, а иногда имеет смысл упростить, а затем разделить.
Однако какой бы порядок вы ни выбрали, вы должны прийти к одному и тому же конечному выражению. 9{4}}}}[/латекс].
Это потому, что числитель представляет собой квадратный корень, а знаменатель – корень в четвертой степени. В этом последнем видео мы покажем больше примеров упрощения частного с помощью радикалов.
Сложение и вычитание радикальных выражений
Сложение и вычитание радикалов очень похоже на объединение одинаковых терминов с переменными. Мы можем складывать и вычитать выражения с такими переменными:
[латекс]5x+3y — 4x+7y=x+10y[/латекс]
Есть два ключа к объединению радикалов путем сложения или вычитания: посмотрите на индекс , и посмотрите на подкоренное число и . Если они одинаковы, то возможно сложение и вычитание. Если нет, то вы не можете объединить два радикала.
Ключи
Помните, что индекс — это степень корня, а подкоренное число — это термин или выражение под радикалом. На приведенной ниже диаграмме индекс равен n, а подкоренное число равно 100. Подкоренное число помещается под корневым символом, а индекс размещается вне корневого символа слева:
Индекс и подкоренное число
Потренируйтесь определять радикалы, совместимые для сложения и вычитания, глядя на индекс и радикал корней в следующем примере.
Пример
Определите корни, имеющие одинаковый индекс и подкоренное число.
[латекс] 10\sqrt{6}[/латекс]
[латекс] -1\sqrt[3]{6}[/латекс]
[латекс] \sqrt{25}[/латекс]
[латекс] 12\sqrt{6}[/латекс]
[латекс] \frac{1}{2}\sqrt[3]{25}[/латекс]
[латекс] -7\sqrt[3] {6}[/латекс]
Показать решение
Давайте воспользуемся этой концепцией, чтобы добавить несколько радикалов.
Когда вы добавляете и вычитаете слова, вам может помочь придумать радикальные термины.
Последний пример можно прочитать как «три квадратных корня из одиннадцати плюс 7 квадратных корней из одиннадцати».
Следующий пример содержит дополнительные дополнения. Обратите внимание, что вы можете комбинировать как члены (радикалы, которые имеют один и тот же корень и индекс), но вы не можете комбинировать в отличие от членов.
Обратите внимание, что выражение в предыдущем примере упрощено, несмотря на то, что оно состоит из двух элементов: [латекс] 7\sqrt{2}[/латекс] и [латекс] 5\sqrt{3}[/латекс]. Было бы ошибкой пытаться объединить их дальше! (Некоторые ошибочно полагают, что [латекс] 7\sqrt{2}+5\sqrt{3}=12\sqrt{5}[/latex]. Это неверно, потому что [латекс] \sqrt{2}[/latex ] и [latex]\sqrt{3}[/latex] не похожи на радикалы, поэтому их нельзя добавлять.)
Иногда вам может понадобиться добавить и упростить радикал. Если радикалы разные, попробуйте сначала упростить — возможно, вы сможете объединить радикалы в конце, как показано в следующих двух примерах.
Вычитание радикалов
Вычитание радикалов следует тому же набору правил и подходов, что и сложение — подкоренные и индексы (множественное число от индекса) должны быть одинаковыми для вычитания двух (или более) радикалов.
В следующем видео-примере мы покажем больше примеров того, как складывать и вычитать радикалы, которые не нужно предварительно упрощать.
В следующем видео показано, как складывать и вычитать радикалы, которые можно заранее упростить.
Рационализация знаменателей
Хотя радикалы подчиняются тем же правилам, что и целые числа, часто бывает трудно вычислить значение выражения, содержащего радикалы. Например, вы, вероятно, хорошо понимаете, сколько [латекс] \frac{4}{8},\ 0,75[/latex] и [латекс] \frac{6}{9}[/latex], но что о количествах [латекс] \frac{1}{\sqrt{2}}[/latex] и [латекс] \frac{1}{\sqrt{5}}[/latex]? Их намного сложнее визуализировать.
Вы можете использовать метод под названием , рационализируя знаменатель , чтобы исключить радикал. Смысл рационализации знаменателя состоит в том, чтобы облегчить понимание того, что на самом деле представляет собой величина, путем удаления радикалов из знаменателя.
Напомним, что числа 5, [латекс] \frac{1}{2}[/латекс] и [латекс] 0,75[/латекс] известны как рациональные числа — каждое из них может быть выражено как отношение двух целые числа ([латекс] \frac{5}{1},\frac{1}{2}[/latex] , и [латекс] \frac{3}{4}[/latex] соответственно). Некоторые радикалы являются иррациональными числами, потому что их нельзя представить в виде отношения двух целых чисел. В результате смысл рационализации знаменателя состоит в том, чтобы изменить выражение так, чтобы знаменатель стал рациональным числом.
Вот несколько примеров иррационального и рационального знаменателей.
Иррациональный
Рационал
[латекс] \frac{1}{\sqrt{2}}[/latex]
=
[латекс] \frac{\sqrt{2}}{2}[/латекс]
[латекс] \frac{2+\sqrt{3}}{\sqrt{3}}[/latex]
=
[латекс] \frac{2\sqrt{3}+3}{3}[/латекс]
Теперь давайте рассмотрим, как перейти от иррациональных знаменателей к рациональным.
Начнем с дроби [латекс] \frac{1}{\sqrt{2}}[/latex]. Его знаменатель — [латекс] \sqrt{2}[/латекс], иррациональное число. Это затрудняет определение значения [latex] \frac{1}{\sqrt{2}}[/latex].
Вы можете переименовать эту дробь без изменения ее значения, если умножите ее на 1. В этом случае установите 1 равной [латекс] \frac{\sqrt{2}}{\sqrt{2}}[/latex] . Смотрите, что происходит.
[латекс] \ frac {1} {\ sqrt {2}} \ cdot 1 = \ frac {1} {\ sqrt {2}} \ cdot \ frac {\ sqrt {2}} {\ sqrt {2} } = \ frac {\ sqrt {2}} {\ sqrt {2 \ cdot 2}} = \ frac {\ sqrt {2}} {\ sqrt {4}} = \ frac {\ sqrt {2}} {2 }[/latex]
Знаменатель новой дроби больше не радикал (обратите внимание, однако, что числитель).
Так зачем умножать [латекс] \frac{1}{\sqrt{2}}[/latex] на [латекс] \frac{\sqrt{2}}{\sqrt{2}}[/latex] ? Вы знали, что квадратный корень из числа, умноженный на себя, будет целым числом. В алгебраических терминах эта идея представлена как [латекс] \sqrt{x}\cdot \sqrt{x}=x[/latex].
Вернемся к знаменателям произведения [латекс] \frac{1}{\sqrt{2}}\cdot 1[/latex]. Вы видите, где [латекс] \sqrt{2}\cdot \sqrt{2}=\sqrt{4}=2[/латекс]?
Вот еще несколько примеров. Обратите внимание, что значение дроби совсем не меняется — оно просто умножается на 1.
В следующем видео-примере мы показываем больше примеров того, как рационализировать знаменатель с помощью целочисленного подкоренного числа.
Вы можете использовать тот же метод для рационализации знаменателей, чтобы упростить дроби с радикалами, которые содержат переменную. Пока вы умножаете исходное выражение на другое имя для 1, вы можете удалить радикал в знаменателе, не изменяя значение самого выражения.
Следующее видео показывает больше примеров того, как рационализировать знаменатель с мономом подкоренного числа.
youtube.com/embed/EBUzRctmgyk?feature=oembed» frameborder=»0″ gesture=»media» allow=»encrypted-media» allowfullscreen=»»>Резюме
Когда вы сталкиваетесь с дробью, которая содержит радикал в знаменателе, вы можете удалить радикал, используя процесс, называемый рационализацией знаменателя. Чтобы рационализировать знаменатель, вам нужно найти количество, которое при умножении на знаменатель создаст рациональное число (без радикалов) в знаменателе. Когда знаменатель содержит один член, например [латекс] \frac{1}{\sqrt{5}}[/latex], дробь умножается на [латекс] \frac{\sqrt{5}}{\sqrt{ 5}}[/latex] удалит радикал из знаменателя.
Резюме
Правило произведения в степени и правило возведения в степень можно использовать для упрощения подкоренных выражений, если корни подкореней одинаковы. Правило произведения гласит, что произведение двух или более чисел, возведенных в степень, равно произведению каждого числа, возведенного в ту же степень. То же самое относится и к корням: [латекс] \sqrt[x]{ab}=\sqrt[x]{a}\cdot \sqrt[x]{b}[/latex].
При делении подкоренных выражений правила, регулирующие частные, аналогичны: [латекс] \sqrt[x]{\frac{a}{b}}=\frac{\sqrt[x]{a}}{\sqrt[x]{ б}}[/латекс].
Объединение радикалов возможно, когда индекс и подкоренное число двух или более радикалов совпадают. Радикалы с одинаковым индексом и подкоренным числом называются подобными радикалами. Часто бывает полезно обращаться с радикалами так же, как с переменными: одинаковые радикалы можно добавлять и вычитать точно так же, как можно добавлять и вычитать одинаковые переменные. Иногда вам нужно будет упростить подкоренное выражение, прежде чем можно будет добавить или вычесть похожие термины.
10.5: Радикалы со смешанными индексами
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 45138
- Darlene Diaz
- Santiago Canyon College через ASCCC Open Educational Resources Initiative
93y}&\text{Радикальный в редуцированной форме с корнем }4\end{массив}\nonumber\]Уменьшить радикалы
Обратите внимание, что мы уменьшили индекс, разделив индекс и все показатели степени в подкоренном члене на одно и то же число, например, \(2\) в примере 10.
p}\nonumber\] 9{11}}&\text{Продукт с общим корнем}12\end{массив}\nonumber\]
Чтобы перемножить радикалы с разными индексами, нам нужно найти общий знаменатель, который является наименьшим общим кратным (НОК) между корнями. Как только мы получим LCM, мы можем умножить каждый корень и показатель степени в подкоренном члене, чтобы получить LCM, и переписать как один радикал.
Умножение радикалов с разными индексами
Пусть \(n\), \(p\), \(m\) — положительные целые числа, отличные от нуля, а наименьшее общее кратное равно \(m\), т. е. \( НОК(п, р) = т\), тогда 95(y+z)}&\text{Произведение с общим корнем }6\text{ и извлеченными множителями} \\ &3\text{ и }(y+z)\end{массив}\nonumber\]
Примечание
Первоначально радикал был просто галочкой, а остальная часть выражения радикала заключалась в скобки. В 1637 году Рене Декарт первым поставил черту над всем корневым выражением.
Деление радикалов с разными индексами
К счастью, для деления радикалов со смешанными индексами используется тот же процесс, что и для умножения радикалов со смешанными индексами.
Так как окончательное выражение не может иметь радикалов в знаменателе, то может быть дополнительный шаг рационализации знаменателя. 92}}\)
Эта страница под названием 10.5: Radicals with Mixed Indices распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Дарлин Диаз (Инициатива открытых образовательных ресурсов ASCCC) через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дарлин Диас
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- Программа ASCCC OERI
- Показать страницу Содержание
- нет
- Теги
- source@https://www.
sccollege.edu/OER/Documents/MATH 105/Математика для студентов, изучающих гуманитарные науки (2017).pdf
Умножение подкоренных выражений — ChiliMath
ПоискВ этом уроке мы будем иметь дело только с квадратными корнями, которые являются особым типом радикальных выражений с индексом \color{red}2. Если вы видите радикальный символ без явно написанного индекса, считается, что он имеет индекс \color{red}2.
Ниже приведены основные правила умножения подкоренных выражений.
Подкоренное число — это член, находящийся внутри квадратного корня. Мы умножаем радикалы, перемножая их подкоренные вместе, сохраняя при этом их произведение под одним и тем же радикальным символом. Что произойдет тогда, если подкоренные выражения имеют числа, расположенные снаружи?
Нам просто нужно изменить приведенную выше формулу. Но ключевая идея состоит в том, что произведение чисел, находящихся вне подкоренных символов, также остается снаружи.
Давайте рассмотрим несколько примеров, чтобы увидеть, как применяются эти два основных правила.
Примеры умножения подкоренных выражений
Пример 1 : Упростить путем умножения.
Умножить подкоренные, сохраняя произведение внутри квадратного корня.
Произведение представляет собой полный квадрат, поскольку 16 = 4 · 4 = 4 2 , а это означает, что квадратный корень из \color{blue}16 – это просто целое число.
Пример 2 : Упростить путем умножения.
Можно умножать числа, если они оба находятся под радикалом. После умножения подкоренных посмотрите, можно ли еще упростить.
Пример 3 : Упростите путем умножения.
Возьмите число за скобками и распределите его между числами внутри. Мы просто применяем распределительное свойство умножения.
Далее выполните обычное умножение радикалов. Будьте осторожны здесь. Умножать можно только числа равные внутри радикальные символы.
Точно так же вы можете использовать только числа, которые за пределами радикальных символов.
При умножении числа внутри и вне подкоренного символа просто поместите их рядом.
Пример 4 : Упростить путем умножения.
Как и в примере 3, мы собираемся распределить число вне круглых скобок на числа внутри. Но обязательно умножайте числа только в том случае, если их «местоположения» совпадают. То есть умножьте числа вне подкоренных символов независимо от чисел внутри подкоренных символов.
Отсюда мне просто нужно упростить продукты.
Пример 5 : Упростите путем умножения.
Решение :
Пример 6 : Упростите путем умножения двух двучленов с подкоренными членами.
В этой задаче нам нужно перемножить два двучлена, содержащие радикальные члены. Примените метод FOIL для упрощения.
- F : Умножьте первые члены.
- O : умножьте внешних терминов.
- I : умножьте внутренних слагаемых.
- L : умножьте последних слагаемых.
После применения свойства дистрибутивности методом FOIL я их упрощу как обычно.
Пример 7 : Упростите путем умножения двух двучленов с радикалами.
Как и в предыдущем примере, давайте применим метод FOIL для упрощения произведения двух двучленов.
- F : умножьте первых слагаемых.
- O : умножьте внешних членов.
- I : умножьте внутренних слагаемых.
- L : умножьте последних слагаемых.
С этого момента упрощайте как обычно. Обратите внимание, что два средних члена взаимно компенсируют друг друга.
Пример 8 : Упростите путем умножения двух двучленов с подкоренными членами.
Давайте решим это шаг за шагом:
- Умножьте вместе, используя метод FOIL.
- Упростите продукт.
- Упростите знаки.
- Добавить аналогичные радикалы. Пример 9
Пример 7 -2 × 6 -3Давайте решим это шаг за шагом:
- Разложите произведение биномов с помощью FOIL.
- Получите квадратные корни из чисел с полным квадратом, равных \color{red}36 и \color{red}9.
- Найдите коэффициент совершенного квадрата для 24 .
- Разложите его как произведение квадратных корней.
- Упростите квадратный корень из 4.
- Вычтите одинаковые радикалы, а также вычтите числа без радикалов.
Пример 10 : Упростить путем умножения.
Мы собираемся умножить эти двучлены, используя «матричный метод».
Напишите члены первого бинома (синим) в крайнем левом столбце, а члены второго бинома (красным) в верхнем ряду.
Умножьте номера соответствующих сеток. Смотрите анимацию ниже.
Далее упростите произведение внутри каждой сетки.
Наконец, добавьте все продукты во все четыре сетки и упростите, чтобы получить окончательный ответ.
Пример 11 : Упростить путем умножения.
Поместите члены первого двучлена в крайний левый столбец, а члены второго двучлена в верхнюю строку. Затем умножьте соответствующие квадратные сетки.
Наконец, сложите значения в четырех сетках и максимально упростите, чтобы получить окончательный ответ.
Вас также может заинтересовать:
Решение уравнений с радикалами
Упрощение выражений с радикалами
Сложение и вычитание подкоренных выражений
Рационализация знаменателяУмножение показателей — Правила | Умножение показателей
Перемножение двух членов с показателями степени называется умножением показателей степени .
Умножение показателей степени включает определенные правила в зависимости от основания и мощности. Иногда нам нужно умножать отрицательные показатели или умножать показатели с одинаковым основанием или с разными основаниями. Во всех этих случаях мы следуем разным правилам. Давайте узнаем больше об умножении показателей в этой статье.
1. Что такое умножение показателей? 2. Умножение показателей степени с одинаковым основанием 3. Умножение показателей с разным основанием 4. Часто задаваемые вопросы о умножении показателей степени Что такое умножение показателей?
Прежде чем исследовать концепцию умножения показателей степени, давайте вспомним значение показателей степени. Показатель степени можно определить как количество раз, когда величина умножается сама на себя.
Например, когда 2 умножается трижды само на себя, это выражается как 2 × 2 × 2 = 2 3 . Здесь 2 — это основание , а 3 — степень или показатель степени . Читается как «2 в степени 3».
Теперь давайте обсудим, что означают показатели степени умножения. Когда любые два члена с показателями умножаются, это называется умножением показателей. Давайте рассмотрим различные случаи с помощью примеров, чтобы лучше понять концепцию.
Умножение показателей степени с одинаковым основанием
Рассмотрим два члена с одинаковым основанием, то есть н и м . Здесь основание равно «а». Когда члены с одинаковым основанием перемножаются, степени складываются, т. е. a m × a n = a {m+n}
Давайте рассмотрим несколько примеров, чтобы понять, как добавляются силы.
Пример 1: Умножить 2 4 × 2 2
Решение: Здесь основание такое же, т.
е. 2. По правилу сложим степени, 2 4 × 2 2 = 2 (4+2) = 2 6 = 64.
Проверим ответ. 2 4 × 2 2 = (2 × 2 × 2 × 2) × (2 × 2) = 2 × 2 × 2 × 2 × 2 × 2 = 2 6 = 64
Пример 2: Найдите произведение 10 45 и 10 39
Решение: В данном вопросе основание одно и то же, то есть 10. По правилу сложим степени 10 45 × 10 39 = 10 (45+39) = 10 84 .
Будет ли правило оставаться прежним, если базы будут другими? Давайте посмотрим на это в следующем разделе.
Умножение показателей степени с разным основанием
Когда два числа или переменные имеют разные основания, мы можем умножать выражения, следуя некоторым основным правилам возведения в степень. Здесь у нас есть два сценария, как указано ниже.
Когда базы разные, а силы одинаковые.

Рассмотрим два выражения с разным основанием и одинаковой степенью a n и b n . Здесь основания равны a и b, а мощность равна n. При умножении показателей степени с разными основаниями и одинаковыми степенями сначала умножаются основания. Математически его можно записать как n × b n = (a × b) n
Пример: 0036 Здесь базы разные, но силы одинаковые. Итак, применяя правило, сначала умножим основания, то есть 5 2 × 8 2 = (5 × 8) 2 = 40 2 = 1600
Когда основания и степени равны другой.
Рассмотрим два выражения с разными основаниями и степенями a n и b m . Здесь основаниями являются a и b. Степени равны n и m. При перемножении выражений с разными основаниями и разной степенью каждое выражение вычисляется отдельно, а затем перемножается. Это может быть записано математически как N × B M = (A N ) × (B M )
Пример: .
базы и полномочия разные. Поэтому каждое условие будет решаться отдельно. 10 3 × 7 2 = 1000 × 49 = 49000.
Вспомним правила умножения показателей степени с одинаковым основанием и с разными основаниями на следующем рисунке.
Умножение отрицательных показателей
Отрицательные показатели говорят нам, сколько раз нам нужно умножить обратную величину основания. Другими словами, мы можем преобразовать отрицательную экспоненту в положительную, написав обратную величину данного члена, а затем мы можем решить его как положительный член. Например, 2 -3 можно записать как 1/2 3 . Для умножения отрицательных показателей нам необходимо следовать определенным правилам, которые приведены в следующей таблице.
Чемоданы Правила Когда базы одинаковые. a -n × a -m = a -(n+m) = 1/a {n+m} Когда основания разные, а отрицательные степени одинаковы. а -n × b -n = (a × b) -n = 1/(a × b) n Когда основания и отрицательные степени различны. а -n × b -m = (a -n ) × (b -m ) Теперь давайте разберемся в этих правилах с помощью следующих примеров.
Пример 1: Найдите произведение 2 -3 и 2 -9
Решение: Здесь одно и то же основание, то есть 2. Степени отрицательны и различны. Таким образом, 2 -3 × 2 -9 = 2 -(3+9) = 2 -12 = 1/2 12 = 1/4096 ≈ 0,000244
Пример 2: Умножение 6 -3 × 3 -3
Решение: ЗДЕСЬ. отрицательные силы одинаковы. Таким образом, 6 -3 × 3 -3 = (6 × 3) -3 = 18 -3 = 1/18 3 = 1/5832 ≈ 0,0001715 3p
Решение: Здесь разные основания и отрицательные степени.
Таким образом, 7 -2 × 6 -3 = 1/7 2 × 1/6 3 = 1/(7 2 × 6 3 ) ≈ 9,45 × -5 3 ) ≈ 9,45 × -5 3 ) ≈ 9,45 × -5 3 ). с переменными
Если основанием термина является переменная, мы используем те же правила умножения степени, что и для чисел.
Когда основания переменных одинаковы, степени складываются.
Пример: Найдите произведение 4 и 10
Решение: Переменное основание такое же, то есть «а». Итак, мы добавим показатели степени, a 4 × a 10 = a 4 + 10 = a 14
. .
Пример: Умножить a 17 × b 17
Решение: Переменные основания разные, а степени одинаковые, то есть a 17 × b 17 = (a × b) 17 = (ab) 17
Когда переменные основания и степени различаются, члены вычисляются отдельно, а затем перемножаются.

Пример: Найдите произведение x 8 и y 9 .
Решение: Переменные основания и степени различны, то есть x 8 × y 9 = x 8 y 9
Умножение показателей степени с квадратным корнем
В этом разделе мы рассмотрим умножение показателей степени, где основания имеют квадратный корень. Следует отметить, что правила экспоненты остаются теми же, если основаниями являются квадратные корни.
Помимо этого, следует помнить один важный момент: мы можем преобразовать радикалы в рациональные показатели, а затем умножить данные выражения. Например, квадратный корень из положительного числа √a можно выразить в виде рационального показателя следующим образом. √а = а 1/2 . Теперь, когда нам нужно переписать данный экспоненциальный член как рациональный показатель, мы умножаем существующую степень на 1/2. Например, если нам нужно перепишем √5 3 как рациональный показатель, мы сначала преобразуем радикал √5 в 5 1/2 , затем умножим степень 3 на 1/2, что составит 3/2.
Теперь радикал √5 3 преобразуется в рациональный показатель и записывается как 5 3/2 .
Правила умножения показателей степени с квадратным корнем
Теперь давайте воспользуемся правилами умножения показателей степени, применимыми к выражениям, в которых основанием являются квадратные корни.
Когда основания квадратного корня совпадают, степени складываются.
Пример: Найдите произведение (√5) 2 и (√5) 7 .
Решение: Основания квадратного корня одинаковы. Таким образом, (√5) 2 × (√5) 7 = (√5) 2+7 = (√5) 9 = (5) 1/2 × 9 = (5) 9/2
Если основания квадратного корня разные, а степени одинаковые, сначала умножаются основания.
Пример: Умножить (√5) 3 × (√7) 3
Решение: Основания квадратного корня разные, а степени одинаковые.
Таким образом, (√5) 3 и (√7) 3 = (√5 × √7) 3 = [√(5×7)] 3 = (√35) 3 = ( 35) 3/2
Когда основания квадратного корня и степени различаются, показатели степени оцениваются отдельно, а затем перемножаются.
Пример: Найдите произведение (√5) 3 и (√7) 4
Решение: Основания квадратного корня и степени различны. Таким образом, (√5) 3 × (√7) 4 = 11,18 × 49 ≈ 547,82
Правила умножения показателей степени на дроби
Если основанием выражения является дробь, возведенная в степень, мы используйте те же правила экспоненты, которые используются для оснований, являющихся целыми числами. Обратите внимание на следующую таблицу, чтобы увидеть различные сценарии.
Чемоданы Правила Когда основания дробей одинаковы. (а/б) н × (а/б) м = (а/б) н+м Когда основания дробей разные, а степени одинаковые. (a/b) n × (c/d) n = (a/b × c/d) n Когда основания дробей и степени различны. (a/b) n × (c/d) m = (a n × c m )/(b n × d m ) Давайте рассмотрим несколько решенных примеров, чтобы лучше понять это.
Пример 1: Найдите произведение (2/3) 2 и (15/8) 2
Решение: Здесь дробные основания разные, но степени одинаковы. Таким образом, применяя указанное выше правило, (2/3) 2 × (15/8) 2 = (2/3 × 15/8) 2 = (5/4) 2 = 5 2 /4 2 = 25/16
3 Пример 2: Умножить (2/3) 2 × (2/3) 5
Решение: Здесь основания дробей одинаковы.
(2/3) 2 × (2/3) 5 = (2/3) 2+5 = Таким образом, (2/3) 7 = 2 7 /3 7 = 128/2187.
Пример 3: Умножить (3/4) 2 × (2/3) 3
Решение: Здесь дробные основания и степени разные. Итак, сначала будем решать каждое слагаемое отдельно, а потом двигаться дальше. (3/4) 2 × (2/3) 3 = Таким образом, (3 2 × 2 3 )/(4 2 × 3 3 ) = (9 × 8)/ (16 × 27) = 1/6.
Как умножать дробные степени?
Когда термин имеет дробную степень, он называется дробным показателем. Например, 2 3/5 — дробный показатель. Давайте разберемся с правилами, применяемыми для умножения дробных показателей, с помощью следующей таблицы.
Ящики Правила Когда базы одинаковые. а н/м × а к/й = а н/м+к/й Когда основания разные, но дробные степени одинаковы. a н/м × b н/м = (a×b) н/м Когда основания и дробные степени разные. а н/м × b к/дж = (а н/м ) × (б к/дж ) Давайте разберемся в этих правилах с помощью следующих примеров.
Пример 1: Умножить 2 1/2 и 2 3/2
Решение: Здесь базы одинаковые. Таким образом, 2 1/2 × 2 3/2 = 2 1/2+3/2 = 2 4/2 = 2 2 = 4
Пример 3. Найдите произведение 90. из 2 1/2 и 3 1/2
Решение: Здесь основания разные, но дробные степени одинаковы. Таким образом, 2 1/2 × 3 1/2 = (2×3) 1/2 = 6 1/2 = √6
Пример 3: Умножьте 4 2/3 × 2 1/3
Решение: Здесь основания и дробные степени разные.
Таким образом, 4 2/3 × 2 1/3 ≈ 2,52 × 1,26 = 3,1752
Советы по умножению показателей степени:
- Ноль в любой степени (кроме 0) равен 0.
- Любое число, возведенное в нулевую степень, равно 1.
- Показатель степени — это способ выражения многократного умножения.
☛ Похожие темы
- Экспоненциальные уравнения
- Иррациональные Показатели
- Экспоненциальная функция
- Операции с экспоненциальными членами
Часто задаваемые вопросы о умножении показателей степени
Как работает умножение показателей степени?
Умножение показателей означает нахождение произведения двух членов, имеющих показатели степени. Поскольку существуют разные сценарии, такие как разные базы или разные силы, для их решения применяются разные правила экспоненты. Ниже приведены некоторые основные правила, которые используются почти во всех случаях.
- При перемножении членов с одинаковым основанием степени складываются, т.е.
- Для умножения терминов с разными основаниями и одинаковыми степенями сначала умножаются основания. Математически это можно записать как
- При перемножении терминов с разными основаниями и разной степенью каждый термин оценивается отдельно, а затем умножается. можно записать как n × b m = (a n ) × (b m )
Можно ли умножать степени с разными коэффициентами?
Да, выражения с разными коэффициентами можно перемножать. Коэффициенты умножаются отдельно, как показано в примере. Например, 3a 2 × 4a 3 = (3 × 4) × (a 2 × a 3 ) = 12a 5 .
При умножении степеней вы складываете степени?
При перемножении показателей степени с одинаковыми основаниями степени складываются. Например, 3 4 × 3 5 = 3 ( 4+5) = 3 9
Как умножать степени с разными основаниями?
Для умножения показателей степени с разными основаниями и одинаковыми степенями основания умножаются, а степень записывается вне скобок.
а n × b n = (a × b) n . Например, 2 2 × 3 2 = (2 × 3) 2 = 6 2 = 36. Однако, когда мы умножаем показатели степени с разными основаниями и разными степенями, каждый показатель степени решается отдельно, а затем они умножаются. n × b м = (a n ) × (b м ). Например, 2 2 × 5 4 = (2) 2 × (5) 4 = 4 × 625 = 2500.
Что означает умножение показателей степени с одинаковым основанием?
Умножение степеней с одинаковым основанием означает, что основания одинаковы, а степени разные. В этом случае основание остается общим, а разные степени добавляются, т. е. a m × a n = a (м+п) . Например, 2 3 × 2 4 = 2 (3 + 4) = 2 7 = 128
Как умножать числа в скобках?
Когда показатели степени умножаются на скобки, степень вне скобок умножается на каждую степень внутри скобок.
Например, (2a 2 b 3 ) 2 = 2 2 × a (2 × 2) × b (3 × 2) = 4a 4 0 b 9 b
Каковы правила умножения показателей степени?
Существуют разные правила умножения показателей степени. Основные правила умножения показателей приведены ниже.
- При перемножении выражений с одинаковым основанием степени складываются, т.е.
- При перемножении выражений с разными основаниями и одинаковыми степенями общая степень записывается вне скобок, т.е.0879 н
- При перемножении выражений с разными основаниями и разными степенями каждое слагаемое вычисляется отдельно, а затем умножается, т. е.
Как умножать степени с отрицательными степенями?
Умножение показателей с отрицательными степенями следует тому же набору правил, что и умножение показателей с положительными степенями. Единственная разница здесь в том, что мы должны быть осторожны со сложением и вычитанием целых чисел для него.
Например, 2 -3 × 2 -9 = 2 -(3+9) = 2 -12 = 1/2 12 = 1/4096 ≈ 0,000244
Чтобы умножить показатели степени на переменные, мы используем те же правила, что и для чисел. Например, давайте умножим y 5 × y 3 . По экспоненциальному правилу умножения с одинаковым основанием складываем степени. Это означает, что будет y 5 × y 3 = y 5 + 3 = у 8 .
Умножение радикалов – полный урок с подведением итогов · Математика
В этом уроке вы узнаете все об умножении радикалов и их различных типах.
Не волнуйтесь, если вы не знаете, что такое радикал, вы, вероятно, видели их раньше! Это числа, содержащие символ √ , который называется радикалом или корневым символом .
Радикалы — это аккуратный способ записи чисел с десятичными расширениями, которые продолжаются бесконечно, поэтому вы должны быть в состоянии использовать их уверенно.
Умножение радикалов часто лучше рассматривать как упрощение радикального выражения, которое переписывает как можно проще!
Но сначала давайте освоимся с правильными словами.
Содержание
Части подкоренных и квадратных корней
Умножение подкоренных чисел
Метод 1: Использование подкоренных обозначений
Метод 2: Использование дробных показателей
Какой метод использовать
Как упростить подкоренные выражения
Резюме
Зачем использовать подкоренные?
квадратных корней
Cube Roots и более
до суммы (каламбур)Части радикальных и квадратных корней
Радикан и , A +3, находится внутри Radical Symbol , 555 +3, расположен внутри Radical Symbol , 55555559. . Радикальный символ просто помогает вам ясно видеть, что происходит!
квадратный корень из — это тип радикала, с которым вы, вероятно, знакомы!
Показатель степени квадратного корня опущен — если вы когда-нибудь встретите подкоренной символ без числа для его корня, то это квадратный корень.
Если вы не уверены в том, как работают радикалы, или хотите освежить в них знания перед тем, как приступить к умножению, перейдите к разделу «Обзор» и вернитесь сюда, когда закончите.
Умножение радикалов
Если вы предпочитаете читать, а не смотреть видео, или хотите делать и то, и другое, то вперед!
Теперь, когда вы знаете, какие бывают типы и части подкоренных выражений и как их упростить, вы готовы начать их перемножать!
Существует два полезных метода умножения радикалов: 93\справа)\)
Метод 1: Использование подкоренной записи
Есть несколько простых правил, которые помогают при умножении одного подкоренного выражения на другое. Мы пройдемся по ним по очереди.
Правило 1: подкоренные умножаются вместе и остаются внутри подкоренного символа.
\(
\sqrt{5}\times\sqrt{2}=\sqrt{10}
\)\(
\sqrt{8}\times\sqrt{2}=\sqrt{16 }
\)Но 16 — красивое квадратное число, поэтому его можно упростить.
\(
\sqrt{16}=4
\)Потому что 4 2 = 4 × 4 = 16.
Правило 2: Любые числа вне подкоренного символа умножаются вместе и остаются вне подкоренного символа .
\(
3\sqrt{5}\times2\sqrt{2}=6\sqrt{10}
\)\(
5\sqrt{8}\times2\sqrt{2}=10 \sqrt{16}
\)Опять же, 16 — квадратное число, так что это тоже можно упростить.
\(
\eqalign{
10\sqrt{16}&=10\times4\\
&=40
}
\)Правило 3: Вы должны применить радикал к числу, чтобы взять его вне подкоренной.
Видите, как это работает для квадратного корня? Число a 2 можно было бы удалить, потому что его мощность равна 2, а число обратное корня, но число b 3 не соответствует корню, поэтому оно остается внутри.
То же самое относится к кубам или любому другому порядку, если уж на то пошло.
В этом случае a 2 остается внутри, потому что это не кубическое число, а b 3 было, поэтому его можно вывести.
\(
\eqalign{
\sqrt{50}&=\sqrt{25\times2}\\
&=\sqrt{25}\times\sqrt{2}
}
\)И квадрат корень из 25 равен 5, потому что 5 2 = 5 × 5 = 25. Итак…
\(
\sqrt{25}\times\sqrt{2}=5\sqrt{2}
\)Это так же просто, как это радикальное выражение.
\(
\sqrt[3]{108}=\sqrt[3]{27}\times\sqrt[3]{4}
\)Кубический корень из 27 равен 3, потому что 3 3 = 3 × 3 × 3 = 27.
\(
\sqrt[3]{27}\times\sqrt[3]{4}=3\sqrt[3]{4}
\)Метод 2 : Использование дробных показателей
Во-первых, что такое дробный показатель?!
Дробная означает дробь с числителем вверху (множитель) и знаменателем внизу (делитель).
Показатель степени — это еще одно слово, обозначающее мощность или индекс.
Сложите их вместе, и у вас будет дробная экспонента — удобный способ показать подкоренное выражение, потому что он позволяет вам видеть степени или корни как простые дроби.
При использовании этого метода необходимо знать одно из правил экспоненциального произведения .
С помощью этого правила power -ful у вас теперь есть ключи к умножению радикалов всех видов!
Вот рабочий пример.
Какой метод использовать при умножении радикалов?
Оба метода будут работать в любом случае, как только вы поймете, что они делают, но какой из них проще всего использовать?
Ответ на ваш выбор.
Однако!! Эта быстрая проверка даст вам минимум работы:
- Если показатели степени (корни/индексы/степени) одинаковы, то радикальный метод является самым простым.
- Если подкоренные (основания) одинаковые, то проще всего использовать метод дробных показателей
Вот и все, что осталось.
..
Как упростить подкоренные выражения
Упрощение подкоренных выражений является обязательным шагом для представления вашего окончательного ответа. Не делать этого было бы все равно, что показывать 2/4 вместо 1/2.
Обратное правило радикального умножения. Давайте попробуем это вместе.
75 не является квадратным числом, так что вы можете сделать, чтобы упростить его?
75 можно разложить на 25 и 3, потому что 25 × 3 = 75. Возможно, вы заметили, что 25 это квадратное число!
Итак, если мы воспользуемся первым правилом умножения радикалов в обратном порядке:
\(
\sqrt{75}=\sqrt{25}\times\sqrt{3}
\)\(\sqrt{3 }\) нельзя упростить, но \(\sqrt{25}=5\) поэтому \(\sqrt{75}\) можно упростить до
\(
\sqrt{75}=5\ sqrt{3}
\)Давайте сделаем еще одно вместе, прежде чем вы сделаете это сами, на этот раз с кубическими корнями.
Сначала мы должны найти число в кубе, которое делит 250.
Вы можете посмотреть числа кубиков; первые несколько — 8, 27, 64, 125, 196,…
250 делится на 125, а 125 — число в кубе. Идеальный!
Итак, снова используя первое правило умножения радикалов:
\(
\eqalign{
\sqrt[3]{250}&=\sqrt[3]{125\times2}\\
&=\sqrt[ 3]{125}\times\sqrt[3]{2}
}
\)Теперь \(\sqrt[3]{125}=5\) и \(\sqrt[3]{2}\) не может быть упрощено, поэтому:
\(
\sqrt[3]{125}\times\sqrt[3]{2}=5\sqrt[3]{2}
\)Чтобы определить квадратные множители, которые могут помочь упростить радикалы, используйте наш список множителей для всех чисел до 100.
Резюме
Зачем использовать радикал?
Ответ: посмотрите на квадратный корень из любого числа, кроме квадратного числа, например 7.
\(
\sqrt{7}=2,64575131\ldots
\)Это десятичное число продолжается… и продолжается … и далее… НАВСЕГДА!
Числа типа \(\sqrt{7}\) известны как surds , если они используют радикальное обозначение, или иррациональные числа в противном случае.
Корень или подкоренной символ помогают нам легко их записывать, чтобы уравнения не были заполнены десятичными числами.
Квадратные корни
Если из — положительное число, то квадратный корень из из из — это число, которое дает из при возведении в квадрат или умножении само на себя. Вот так:
\(
\sqrt{25}=5
\)Потому что 5, умноженное само на себя, равно 25.
Что произойдет, если вы возведете квадратный корень в квадрат? 91
\)Таким образом, квадратный корень действует противоположно возведению числа в квадрат.
Произведите впечатление на учителя, сказав ему, что квадратный корень — это , обратное квадратной функции. Просто убедитесь, что вы можете объяснить, что это значит!
Кубические корни и многое другое
Кубический корень спрашивает: «Какое число нужно умножить само на себя 3 раза, чтобы получить подкоренное число?»
Это выглядит так:
Как видите, ответ для кубического корня из 8 равен 2, потому что
2 3 = 2 × 2 × 2 = 8
Корень четвертой степени выглядит как \(\sqrt[4]{16}\)
Он спрашивает: «Какое число нужно умножить на себя 4 раза, чтобы получить радикал?»
Ответ на \(\sqrt[4]{16}\) равен 2, потому что 2 4 =2×2×2×2=16
место.
Вернитесь к разделу с практическими рекомендациями по умножению радикалов
Подведение итогов (каламбур)
Символ радикала √ — это еще один способ записи дробного показателя степени 9.0035 a 1 ⁄ 2
Подкоренное число — это число внутри подкоренного символа.
Радикалы с корнем x задайте вопрос: «Какое число раз умножить само себя x , чтобы получилось подкоренное».
Чтобы упростить подкоренное выражение, найдите число, на которое делится подкоренное число. Используйте нашу таблицу множителей и множителей, чтобы помочь с этим.
При умножении корней:
- Если они имеют один и тот же показатель степени (корень), используйте радикальный метод. Числа вне корня умножаются и остаются снаружи. Числа внутри подкоренных умножаются и остаются внутри подкоренных.
- Если они имеют одинаковые подкоренные числа, преобразовать в дробные степени.
Показатель степени складываются, а подкоренное число, которое теперь называется основанием, остается прежним.
Если что-то из этого не имеет для вас смысла, если вы застряли или вам просто понравился урок, оставьте комментарий ниже, и мы сможем помочь!
6.1 Упрощение выражений с помощью корней и дробных показателей — Алгебра среднего уровня
Цели обучения
- Введение в корни
- Определение и вычисление главных квадратных корней
- Определить и оценить корни n-й степени
- Оценка несовершенных корней
- Подкоренные выражения и дробные показатели
- Определение и идентификация подкоренного выражения
- Преобразование радикалов в выражения с дробными показателями 92}=|x|\), и применить его при упрощении подкоренных выражений
Знаете ли вы, что из числа можно извлечь корень шестой степени? Вы, наверное, слышали о квадратном корне, который пишется как \(\sqrt{\,\,\,}\), но вы также можете взять корень третьей, четвертой и даже 5000-й степени (если вам действительно нужно).
В этом уроке мы узнаем, как определяется квадратный корень, а затем мы будем опираться на это, чтобы сформировать представление о корнях n-й степени. Мы будем использовать факторинг и правила для показателей, чтобы упростить математические выражения, содержащие корни. 9{\text{n}}}\)
Название: «Три в квадрате» или «Три в второй степени», «Четыре в пятой степени», « x в кубе», « x в степени n -я степень»
Повторное умножение: \( 3\cdot 3\), \( 4\cdot 4\cdot 4\cdot 4\cdot 4\), \( x\cdot x\cdot x\ ), \( \underbrace{x\cdot x\cdot x…\cdot x}_{n\text{times}}\).
И наоборот, когда вы пытаетесь найти квадратный корень из числа (скажем, 25), вы пытаетесь найти число, которое можно умножить само на себя, чтобы получить исходное число. В случае 25 вы можете обнаружить, что \(5\cdot5=25\), поэтому 5 должно быть квадратным корнем.
Квадратные корни
Символ квадратного корня называется радикальным символом и выглядит следующим образом: \(\sqrt{\,\,\,}\).
Выражение \( \sqrt{25}\) читается как «квадратный корень из двадцати пяти» или «корень из двадцати пяти». Число, записанное под подкоренным знаком, называется подкоренным числом и .
В следующей таблице показаны различные радикалы и их эквивалентные письменные и упрощенные формы.
Радикальный Имя Упрощенная форма \( \sqrt{36}\) «Квадратный корень из тридцати шести»
«Корень тридцать шесть»
\(\sqrt{36}=\sqrt{6\cdot 6}=6\) \( \sqrt{100}\) «Квадратный корень из ста»
«Корневая сотня»
\(\sqrt{100}=\sqrt{10\cdot 10}=10\) \( \sqrt{225}\) «Квадратный корень из двухсот двадцати пяти»
«Корень двести двадцать пять»
\(\sqrt{225}=\sqrt{15\cdot 15}=15\) Снова рассмотрим \( \sqrt{25}\).
Вы можете заметить, что есть еще одно значение, которое при умножении само на себя также дает 25. Это число равно \(-5\).
\( \begin{array}{r}5\cdot 5=25\\-5\cdot -5=25\end{array}\)
По определению, символ квадратного корня всегда означает нахождение положительного корень, называемый основным корнем . Таким образом, хотя \(5\cdot5\) и \(-5\cdot-5\) равны 25, только 5 является основным корнем. Вы также должны знать, что ноль особенный, потому что он имеет только один квадратный корень: сам (поскольку \(0\cdot0=0\)).
В нашем первом примере мы покажем вам, как использовать радикальную запись для вычисления главных квадратных корней.
Пример
Найдите главный корень каждого выражения.
- \(\sqrt{100}\)
- \(\sqrt{\sqrt{16}}\)
- \(\sqrt{25+144}\)
- \(\sqrt{49}-\sqrt{81}\\\)
- \(-\sqrt{81}\)
- \(\sqrt{-9}\)
Показать ответ
В следующем видео мы представляем больше примеров того, как найти главный квадратный корень.
Последний пример, который мы показали, приводит к важной характеристике квадратных корней. Извлекать квадратный корень можно только из неотрицательных значений.
Домен квадратного корня
\(\sqrt{-a}\) определен не для всех действительных чисел, a. Таким образом, \(\sqrt{a}\) определяется для \(a\ge0\)Подумайте об этом
Имеет ли \(\sqrt{25}=\pm 5\)? Напишите свои идеи и предложение, чтобы защитить их, в поле ниже, прежде чем вы посмотрите на ответ.
Показать ответ 9{3}=8\), мы говорим, что 2 — это кубический корень из 8. В следующем примере мы будем вычислять кубические корни некоторых совершенных кубов.
Как мы видели в последнем примере, есть один интересный факт о кубических корнях, который не относится к квадратным корням. Отрицательные числа не могут иметь квадратные корни из действительных чисел, но отрицательные числа могут иметь кубические корни из действительных чисел! Чему равен кубический корень из \(-8\)? \( \sqrt[3]{-8}=-2\) потому что \(-2\cdot -2\cdot -2=-8\).
{3}}}=-1\).
В следующем видео мы покажем больше примеров нахождения кубического корня.
N-ые корни
Кубический корень числа записывается с маленькой цифрой 3, называемой индексом , сразу за радикальным символом и над ним. Это выглядит как \(\sqrt[3]{{}}\). Эта маленькая цифра 3 отличает кубические корни от квадратных корней, которые записываются без маленькой цифры снаружи и над корневым символом.
Ту же идею можно применить к любому показателю степени и соответствующему корню. 9{5}=243\). Если \(a\) является вещественным числом с хотя бы одним n -м корнем, то главный n -й корень из \(a\) является числом с тем же знаком, что и \(a\), что , возведенный в степень n , равен \(a\).
Главный n -й корень \(a\) записывается как \(\sqrt[n]{a}\), где \(n\) — натуральное число, большее или равное 2. В подкоренное выражение, \(n\) называется индексом подкореня.
Определение: Директор
n -й кореньЕсли \(a\) является вещественным числом с хотя бы одним n -м корнем, то главный n -й корень из \(a\), записанный как \(\sqrt [n]{a}\) — число с тем же знаком, что и \(a\), которое при возведении в n -ю степень равно \(a\). индекс радикала равен \(n\).
Пример
Оценить каждое из следующих значений:
- \(\sqrt[5]{-32}\)
- \(\sqrt[4]{81}\)
- \(\sqrt[8]{-1}\)
Показать ответ
В следующем видео мы покажем больше примеров того, как вычислить и n-й корень.
Вы можете найти нечетный корень отрицательного числа, но вы не можете найти четный корень отрицательного числа и получить действительный ответ. Это означает, что вы можете вычислять радикалы \(\sqrt[3]{-81},\\sqrt[5]{-64}\) и \(\sqrt[7]{-2187}\), но не можете вычислить радикалы \( \sqrt[{}]{-100},\ \sqrt[4]{-16}\) или \( \sqrt[6]{-2500}\) и получить ответ, который настоящий номер.
Позже мы научимся справляться с этими радикалами, а пока просто скажем, что они не определены.
Оценка корней
Подход к обработке несовершенных корней (квадратов, кубов и т. д.) заключается в их аппроксимации путем сравнения значений с совершенными квадратами, кубами или корнями n-й степени. Предположим, вы хотите узнать квадратный корень из 17. Давайте посмотрим, как вы можете его аппроксимировать.
Это приближение довольно близко. Если бы вы продолжали использовать эту стратегию проб и ошибок, вы могли бы продолжать извлекать квадратный корень с точностью до тысячных, десятитысячных и сотен тысячных, но со временем это стало бы слишком утомительно, чтобы делать это вручную.
По этой причине, когда вам нужно найти более точное приближение квадратного корня, вы должны использовать калькулятор. В большинстве калькуляторов есть клавиша квадратного корня \( (\sqrt{{}})\), которая позволяет быстро вычислить квадратный корень. На простом четырехфункциональном калькуляторе вы, скорее всего, наберете число, из которого хотите извлечь квадратный корень, а затем нажмете клавишу квадратного корня.
Попробуйте найти \( \sqrt{17}\) с помощью калькулятора. Обратите внимание, что вы не сможете получить «точный» ответ, потому что \( \sqrt{17}\) — иррациональное число, число, которое нельзя представить в виде дроби, а десятичная дробь никогда не заканчивается и не повторяется. Чтобы точно зафиксировать значение \(\sqrt{17}\), вам потребуется бесконечная точность. До девяти знаков после запятой \(\sqrt{17}\) приблизительно равно 4,123105626. Калькулятор может сэкономить много времени и получить более точный квадратный корень, когда вы имеете дело с числами, которые не являются идеальными квадратами.
В следующем видео показан еще один пример вычисления квадратного корня.
Подкоренные выражения и дробные показатели
Квадратные корни чаще всего записываются с использованием подкоренного знака, например, \( \sqrt{4}\). Но есть и другой способ их представления. Вы можете использовать дробные показатели степени вместо радикала. А 9{4}}y}\)
Запишите выражение с дробным показателем степени в качестве корня
Радикалы и дробные показатели представляют собой альтернативные способы выражения одного и того же.
В таблице ниже показаны эквивалентные способы выражения радикалов: с корнем, с дробным показателем и в виде главного корня.
Радикальная форма
Форма экспонента
Основной корень
\( \sqrt{16}\) 9{\ гидроразрыва {1} {2}}}} \) 10 Давайте рассмотрим еще несколько примеров, но на этот раз с кубическими корнями. Помните, что кубирование числа возводит его в степень три. Обратите внимание, что в примерах в таблице ниже знаменатель дробного показателя степени равен 3.
Радикальная форма
Форма экспонента
Основной корень
\( \sqrt[3]{8}\) 9{\ гидроразрыва {1} {п}}} \) В приведенной выше таблице обратите внимание, как знаменатель дробного показателя степени определяет индекс корня.
Таким образом, показатель степени \( \frac{1}{2}\) переводится в квадратный корень, показатель степени \( \frac{1}{5}\) переводится в корень пятой степени или \( \sqrt[5 ]{{}}\), а \( \frac{1}{8}\) преобразуется в корень восьмой степени или \( \sqrt[8]{{}}\).
Помните, что показатели степени относятся только к количеству непосредственно слева от них, если только не используется символ группировки. Пример ниже очень похож на предыдущий с одним важным отличием: здесь нет скобок! Посмотрите, что происходит.
Запишите подкоренное выражение в виде выражения с дробным показателем
Мы можем записывать подкоренные выражения с дробными показателями, и, как мы увидим, когда будем упрощать более сложные подкоренные выражения, это может упростить задачу. Наличие различных способов выражения и записи алгебраических выражений позволяет нам иметь гибкость при их решении и упрощении. Это похоже на тезаурус, когда вы пишете, вы хотите иметь варианты для самовыражения!
Пример
Запишите \( \sqrt[4]{81}\) как выражение с дробным показателем степени.
93}\)
Показать решение
В нашем последнем примере мы перепишем выражения с дробными показателями как радикалы. Эта практика поможет нам, когда мы будем упрощать более сложные радикальные выражения, и когда мы научимся решать радикальные уравнения. Обычно легче упростить, когда мы используем дробные показатели степени, но это упражнение предназначено для того, чтобы помочь вам понять, как числитель и знаменатель показателя степени являются показателем степени подкоренного и индексом подкореня.
9{\ гидроразрыва {4} {7}} \)Показать ответ
В следующем видео мы покажем больше примеров записи подкоренных выражений с дробными показателями и выражений с дробными показателями в качестве подкоренных выражений.
Мы будем использовать это обозначение позже, поэтому вернитесь к практике, если вы забудете, как писать радикал с дробным показателем.
Упрощение подкоренных выражений
Подкоренные выражения — это выражения, содержащие подкоренные.
{4}}y} \). 9{\frac{1}{2}}}\)
А поскольку вы знаете, что возведение числа в степень \(\frac{1}{2}\) равносильно извлечению квадратного корня из этого числа, вы также можете написать это таким образом.
\( \sqrt{3x}=\sqrt{3}\cdot \sqrt{x}\)
Посмотрите на это: любое число под радикалом можно представить как произведение отдельных множителей , собственный радикал.
Продукт, преобразованный в степенное правило или иногда называемый квадратным корнем из правила продукта
Для любых действительных чисел a и b , \( \sqrt{ab}=\sqrt{a}\cdot \sqrt{b}\).
Например: \( \sqrt{100}=\sqrt{10}\cdot \sqrt{10}\) и \( \sqrt{75}=\sqrt{25}\cdot \sqrt{3}\ )
Это правило важно, потому что оно помогает вам думать об одном радикале как о произведении нескольких радикалов. Если вы можете идентифицировать правильные квадраты внутри радикала, как с \( \sqrt{(2\cdot 2)(2\cdot 2)(3\cdot 3})\), вы можете переписать выражение как произведение нескольких совершенных квадраты: \( \sqrt{{{2}^{2}}}\cdot \sqrt{{{2}^{2}}}\cdot \sqrt{{{3}^{2}}}\).
Квадратный корень из правила произведения поможет нам упростить несовершенные корни, как показано в следующем примере.
Пример
Упрощение. \( \sqrt{63}\)
Показать решение
Окончательный ответ \( 3\sqrt{7}\) может показаться немного странным, но он в упрощенной форме. Вы можете прочитать это как «три корня из семи» или «три умножить на квадратный корень из семи».
В следующем видео показано больше примеров того, как упростить квадратные корни, которые не имеют идеальных квадратных корней. 9{2}}\)
\(\влево|х\вправо|\) \(-5\) 25 5 5 \(-2\) 4 2 2 0 0 0 0 6 36 6 6 10 100 10 10 Примечание: в случаях, когда 92\) всегда будет неотрицательным.
Включение столбцов абсолютных значений было бы излишним. Один совет, чтобы узнать, когда применять абсолютное значение после упрощения любого даже индексированного корня, — это посмотреть на конечный показатель степени в ваших переменных терминах. Если показатель степени нечетный, включая 1, добавьте абсолютное значение. Это относится к упрощению любого корня с четным индексом, как мы увидим в последующих примерах.
В следующем видео вы увидите больше примеров того, как упростить радикальные выражения с переменными.
Мы покажем другой пример, где упрощенное выражение содержит переменные как с нечетными, так и с четными степенями.
В нашем следующем примере мы начнем с выражения, записанного с дробным показателем степени. Вы увидите, что вы можете использовать аналогичный процесс — разложение членов на множители и сортировку по квадратам — для упрощения этого выражения.
Вот еще один пример с идеальными квадратами.
Упрощение кубических корней
Мы можем использовать те же методы, которые мы использовали для упрощения квадратных корней, для упрощения корней более высокого порядка.
Например, чтобы упростить кубический корень, цель состоит в том, чтобы найти множители под радикалом, которые являются идеальными кубами, чтобы вы могли извлечь их кубический корень. Нам больше не нужно беспокоиться о том, определили ли мы главный корень, поскольку теперь мы находим кубические корни. Сосредоточьтесь на поиске идентичных трио факторов по мере упрощения. 9{3}}\конец{массив}\)
Вы также можете пропустить шаг разложения отрицательного числа на множители, когда освоитесь с определением кубов.
В следующем видео мы покажем больше примеров упрощения кубических корней.
Упрощение корней четвертой степени
Теперь давайте перейдем к упрощению корней четвертой степени. Независимо от того, какой корень вы упрощаете, применяется одна и та же идея: найдите кубы для кубических корней, степени четырех для четвертых корней и т. д. Вспомните, что когда ваше упрощенное выражение содержит четный индексированный радикал и переменный множитель с нечетным показателем, вам нужно применить абсолютное значение (если только контекст вашей проблемы не позволяет вам «предполагать, что \(x \ge 0\)»).
{4}}}}\) . В этом выражении две переменные, дробь и радикал. Давайте рассмотрим это шаг за шагом и посмотрим, может ли использование дробных показателей помочь нам упростить его.
Начнем с упрощения знаменателя, так как именно здесь находится подкоренной знак. Напомним, что показатель степени в знаменателе или дроби можно переписать как отрицательный показатель степени.Ну, это заняло некоторое время, но вы сделали это. Вы применили свои знания о дробных показателях, отрицательных показателях и правилах показателей, чтобы упростить выражение.
В нашем последнем видео мы показываем, как использовать дробные показатели для упрощения радикальных выражений.
Резюме
Квадратный корень числа — это число, которое при умножении само на себя дает исходное число. Основные квадратные корни всегда положительны, а квадратный корень из 0 равен 0. Вы можете брать квадратный корень только из значений, которые больше или равны 0. Квадратный корень из полного квадрата будет целым числом.




 {2}}}=\sqrt{5}. \\ \end{align}\]
{2}}}=\sqrt{5}. \\ \end{align}\] {2}}}=\sqrt{75}. \end{align}\]
{2}}}=\sqrt{75}. \end{align}\]

 Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ). 

 Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
 2×2)
2×2)
 Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.
Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.

 Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81)
Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81) Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из… Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция … n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.… С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм. \\ \end{align}\]
\\ \end{align}\]
 {2n}}}=\left| a \right|. \\ \end{align}\]
{2n}}}=\left| a \right|. \\ \end{align}\] {2}}}=\sqrt{5}. \\ \end{align}\]
{2}}}=\sqrt{5}. \\ \end{align}\] 2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.

 2 \cdot 3 cdot 7 =84\)
2 \cdot 3 cdot 7 =84\)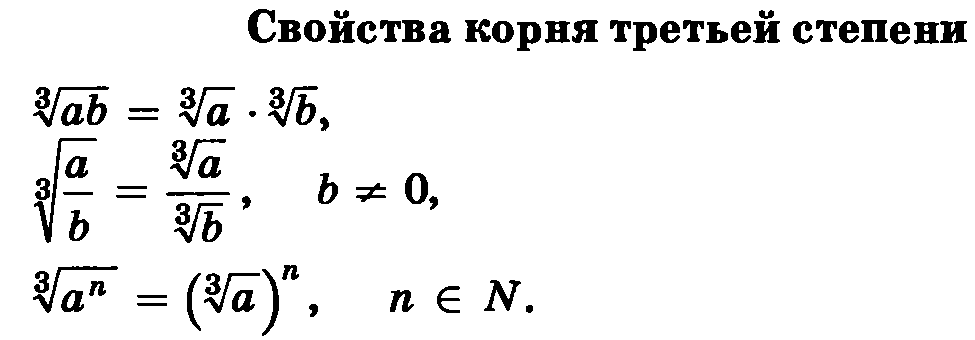 Отдельно вычислить \(\sqrt{32}\) и \(\sqrt{2}\) не представляется возможным. В последнем примере в обоих подкоренных выражениях находятся дробные числа. С помощью произведения удалось сократить многие из множителей, что позволило оптимально преобразовать все выражение.
Отдельно вычислить \(\sqrt{32}\) и \(\sqrt{2}\) не представляется возможным. В последнем примере в обоих подкоренных выражениях находятся дробные числа. С помощью произведения удалось сократить многие из множителей, что позволило оптимально преобразовать все выражение. {3}}} \)
{3}}} \) Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров. 36 — квадратный корень из шести (6 × 6 = 36) .
36 — квадратный корень из шести (6 × 6 = 36) . После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
 Пришла пора разобраться, какие существуют формулы для корней
Пришла пора разобраться, какие существуют формулы для корней



 Второе число 9
Второе число 9

 Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\]
Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\]
 Так как \(5=\sqrt{25}\)
Так как \(5=\sqrt{25}\)
 2=168\cdot 168=28224\)
2=168\cdot 168=28224\)
 Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
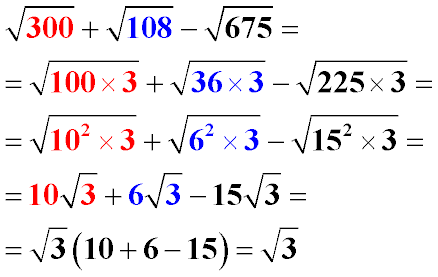
 Это 16=4 2 , 9=3 2 , 64=8 2 . Выражение примет вид:
Это 16=4 2 , 9=3 2 , 64=8 2 . Выражение примет вид:



 Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 – множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.
Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 – множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.
 b}\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) или \( {\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a > 1}\\{x \wedge y\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \)
b}\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) или \( {\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a > 1}\\{x \wedge y\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) {2}14<2,25}}\end{array}\)
{2}14<2,25}}\end{array}\)







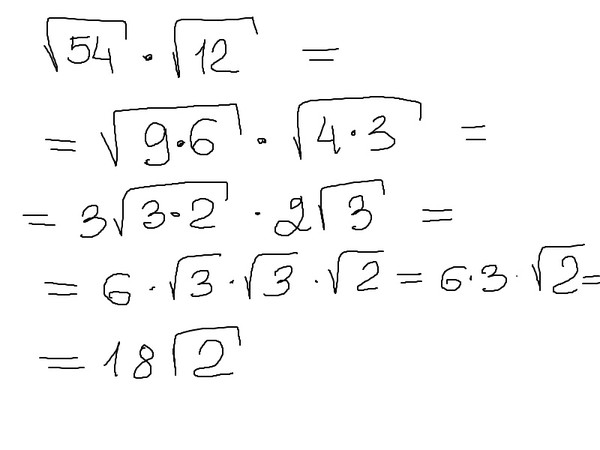


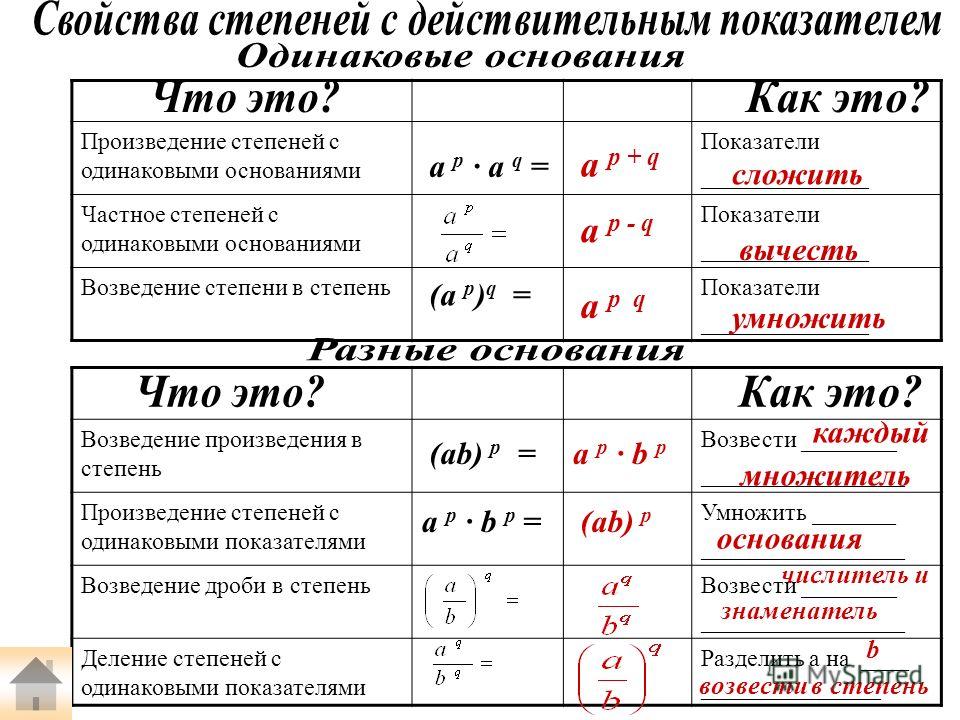



 Извлеките квадратный корень: √289
Извлеките квадратный корень: √289




 Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Осталось научиться сравнивать корни и стать непобедимым теоретиком.
 С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

 Например, для контрольной или ЕГЭ.
Например, для контрольной или ЕГЭ.






 Прежде чем члены можно будет перемножить, мы меняем показатели, чтобы они имели общий знаменатель. Таким образом, основания теперь имеют одни и те же корни, и их члены можно умножать вместе. Затем мы пишем задачу, используя корневые символы, а затем упрощаем.
Прежде чем члены можно будет перемножить, мы меняем показатели, чтобы они имели общий знаменатель. Таким образом, основания теперь имеют одни и те же корни, и их члены можно умножать вместе. Затем мы пишем задачу, используя корневые символы, а затем упрощаем. Хорошо. И помните, что когда мы имеем дело с долей экспонент, это власть над корнем. Чтобы умножить наши радикалы вместе, наши корни должны быть одинаковыми. Итак, нам нужно как-то манипулировать этими двумя корнями, 3 и квадратом, 3 и 2, чтобы они были одним и тем же корнем, хорошо? Так что подумайте, какое у нас наименьшее общее кратное.2 и 3, 6. Хорошо? Итак, мы хотим переписать обе эти степени с корнем со знаменателем 6. Итак, 6, 2 вы получите 6. Нам просто нужно умножить это на 2 на 2, так что мы получим 2 на 6, а затем 3, нужно чтобы сделать половину со знаменателем 6, чтобы получилось 3 на 6. Хорошо. Итак, то, что у нас действительно есть сейчас, — это корень шестой степени из 2, умноженный на корень шестой степени из 3 в третьем. Хорошо? Таким образом, мы вообще не изменили нашу задачу, а просто изменили нашу экспоненту на небольшую, но большую дробь.Это прекрасно. И теперь у нас одинаковые корни, поэтому мы можем перемножить, оставив нам корень шестой степени из 2 в квадрате, умноженного на 3 куба.
Хорошо. И помните, что когда мы имеем дело с долей экспонент, это власть над корнем. Чтобы умножить наши радикалы вместе, наши корни должны быть одинаковыми. Итак, нам нужно как-то манипулировать этими двумя корнями, 3 и квадратом, 3 и 2, чтобы они были одним и тем же корнем, хорошо? Так что подумайте, какое у нас наименьшее общее кратное.2 и 3, 6. Хорошо? Итак, мы хотим переписать обе эти степени с корнем со знаменателем 6. Итак, 6, 2 вы получите 6. Нам просто нужно умножить это на 2 на 2, так что мы получим 2 на 6, а затем 3, нужно чтобы сделать половину со знаменателем 6, чтобы получилось 3 на 6. Хорошо. Итак, то, что у нас действительно есть сейчас, — это корень шестой степени из 2, умноженный на корень шестой степени из 3 в третьем. Хорошо? Таким образом, мы вообще не изменили нашу задачу, а просто изменили нашу экспоненту на небольшую, но большую дробь.Это прекрасно. И теперь у нас одинаковые корни, поэтому мы можем перемножить, оставив нам корень шестой степени из 2 в квадрате, умноженного на 3 куба. Хорошо. Часто эти числа будут довольно уродливыми и довольно большими, поэтому иногда вы можете просто оставить их вот так. 2 в квадрате и 3 в кубе — не такие уж большие числа. 2 в квадрате равно 4, 3 в квадрате равно 27, 4 умноженное на 27, я считаю, 108. Таким образом, это становится корнем шестой степени из 108.
Хорошо. Часто эти числа будут довольно уродливыми и довольно большими, поэтому иногда вы можете просто оставить их вот так. 2 в квадрате и 3 в кубе — не такие уж большие числа. 2 в квадрате равно 4, 3 в квадрате равно 27, 4 умноженное на 27, я считаю, 108. Таким образом, это становится корнем шестой степени из 108.  Это будет зависеть от предыдущей темы: Синтетическое деление.
Это будет зависеть от предыдущей темы: Синтетическое деление.

 Если ведущий член положительный, а полином равен нечетным градусам, тогда, когда x является большим отрицательным числом , то есть далеко слева от начала координат, тогда нечетная степень отрицательного числа сам по себе отрицательный.График будет ниже оси x .
Если ведущий член положительный, а полином равен нечетным градусам, тогда, когда x является большим отрицательным числом , то есть далеко слева от начала координат, тогда нечетная степень отрицательного числа сам по себе отрицательный.График будет ниже оси x .