Синус и косинус 11 градусов и 32,7 минут как вычислить?
Автор Admin На чтение 4 мин Просмотров 37 Опубликовано
Всех сильно умных даунов, которые считают, что их дети при рождении будут вылезать оттуда же, откуда вылезли они, только с калькуляторами в руках, предлагаю кастрировать. Девочки, вы хотите об таких размножаться? После родов эти идиоты будут у вас спрашивать, куда вы калькулятор за ныкали.
Когда я учился в школе, мне приходилось пользоваться таблицей Брадиса для нахождения синусов, косинусов, тангенсов и котангенсов. Уже забыл, как этой таблицей пользоваться. Но сегодня мы живем в компьютерном веке, а что такое компьютер? Правильно, это такой большой калькулятор. А в каждом большом калькуляторе должен быть калькулятор маленький. Вот этим калькулятором и нужно воспользоваться. У меня операционная система Windows XP, на экране слева, внизу, есть кнопочка «Пуск«.
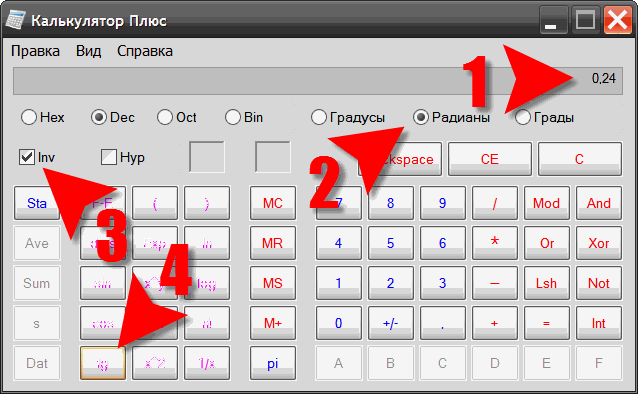
Сам калькулятор обычно не имеет синусов и косинусов. Нужно нажать кнопочку «Вид» в верхней панельке калькулятора и выбрать «Инженерный«. В инженерном калькуляторе есть нужные нам кнопочки синус «sin«, косинус «cos» и тангенс «tg«.
После этого нужно проследить, что бы в калькуляторе была включена десятичная система счисления и градусы для углов. Для этого нужно нажать пыптик «Dec» и пыптик «Градусы«, как на картинке показано. Наш инструмент для нахождения синусов и косинусов готов. Теперь приступим непосредственно к процессу добычи полезных тригонометрических ископаемых.
Если вам не удалось выковырять калькулятор из своего компьютера, не отчаивайтесь! Специально для вас я разместил в этом блоге «Математика для блондинок» калькулятор бесплатно, которым вы можете воспользоваться прямо здесь и сейчас!
Сперва минуты нужно перевести в градусы.
Для этого 32,7 делим на 60. В результате получаем 0,545 градуса. На 60 делим потому, что в одном градусе 60 минут. К полученной циферке прибавляем 11 градусов, которые у нас уже есть, и получаем 11,545 градусов. Вот из такого угла на калькуляторе можно уже извлекать синусы и косинусы. Для этого нужно просто нажать кнопочку «sin» или «cos«.
Весь процесс нажимания кнопочек выглядит так:
32,7 / 60 + 11 = sin
В результате в окошке калькулятора появится число 0,20013750391127021629780041181162
Математически это записывается так:
sin (11° 32,7′) = sin 11,545° = 0,2001
Для косинуса угла 11 градусов 32,7 минут значение равно почти единице и запишется так:
cos (11° 32,7′) = cos 11,545° = 0,9798
Для тангенса выполняется всё точно также, только в самом конце вместо кнопочки «sin» нажимается кнопочка «tg«. Вот с котангенсами, кажется, проблема.
Нет такой кнопочки в калькуляторе! Но мы умные, и помним, что тригонометрическая функция котангенс является обратной тригонометрической функцией по отношению к тангенсу (столько умных слов за один раз — аж самому страшно!). На практике это выглядит очень просто: сперва находим тангенс, как описано выше. Когда циферки тангенса появились в окошке калькулятора, нажимаем на кнопочку «1/х«. Циферки тангенса поменяются на циферки котангенса. А эта дополнительная волшебная кнопочка называется «число, обратное введенному». Ради прикола, введите число 2, нажмите эту волшебную кнопочку и у вас появится число 0,5 что равно 1/2.
Для перевода секунд в минуты, секунды так же нужно разделить на 60, поскольку в каждой минуте 60 секунд. Для перевода в градусы, полученные минуты нужно ещё раз разделить на 60:
1″ = 0.016667′ = 0,00027778°
Вот, кажется, всё о том, как вычислить синус и косинус 11 градусов и 32,7 минут. Если у кого-то остались вопросы, пишите в комменты.
Для своих любимых блондинок могу дать несколько маленьких подсказок. Синус 6 градусов 30 минут нужно на калькуляторе набирать как 6,5 градусов, потом нажать кнопочку синуса.
Теперь примерчик посложнее, с секундами: косинус 6 градусов 7 минут 9 секунд. 9 секунд делим на 60, прибавляем 7 минут, снова делим на 60, прибавляем 6 градусов. Должно получиться число 6,11916666… градусов. Теперь нажимаем кнопочку косинуса «
9 / 60 + 7 / 60 + 6 = cos
Математически пересчет градусов, минут и секунд в градусы для 6 градусов 7 минут 9 секунд можно записать так:
(9 : 60 + 7) : 60 + 6 = 6,11916666…
В общем виде для угла в x градусов, y минут, z секунд формула перевода в градусы будет выглядеть так:
(z : 60 + y) : 60 + x = градусы
Надеюсь, эта формула вам пригодится.
2.
Что такое грех в математике? Синус одного из углов прямоугольного треугольника (часто сокращенно «sin») равен отношение длины стороны треугольника, противоположной углу, к длине гипотенузы треугольника.
Что такое синус?
Тангенс x определяется как его синус, деленный на его косинус:… Секанс x равен 1, деленному на косинус x: sec x = 1 cos x, а косеканс x определяется как 1, деленный на синус из x: csc х = 1 грех х .
Как мне узнать, есть ли у меня SOH CAH TOA? SOHCAHTOA — это мнемоническое устройство, помогающее запомнить, какое соотношение соответствует какой функции.
- SOH = Синус противоположен гипотенузе.
- CAH = косинус смежен с гипотенузой.
- TOA = Касательная противоположна соседнему.
Как вы оцениваете грех 2? Значение sin 2 градуса можно рассчитать по формуле построение угла 2 ° с осью x, а затем найти координаты соответствующей точки (0.9994, 0.0349) на единичной окружности. Значение sin 2° равно координате y (0.
2)? Конвенция такова. Это никогда не означает. Лучше было бы спросить, может ли это означать , потому что в некоторых контекстах повторяющаяся композиция функции с самой собой обозначается показателем степени.
Также Что такое формула Sinx? грех (π/2 – х) = потому что х. соз (π / 2 — х) = грех х.
Каково значение синуса?
Значение синуса изменяется при изменении угла между основанием и гипотенузой прямоугольного треугольника. Обычно используемые значения синуса: sin 0 = 0, грех π/6 = 1/2, sin π/4 = 1/√2, sin π/3 = √3/2 и sin π/2 = 1. Мы можем определить эти значения, используя формулу синуса, заданную как sin x = перпендикуляр/гипотенуза.
Чему равен грех? В контексте прямого угла функция синуса, записанная как sinθ, равна равно делению противоположной стороны опорного угла (θ) на гипотенузу, или длинная сторона треугольника.
Как посчитать грех вручную?
Как найти sin 0 без калькулятора?
На единичной окружности координата x в каждой позиции является косинусом заданного угла, а координата y — синусом.
При θ = 0, самая правая точка, координатная пара равна (1, 0). Координата Y равна 0, поэтому грех (0) = 0 .
Можно ли использовать Sohcahtoa на любом треугольнике? Q: Sohcahtoa только для прямоугольных треугольников? В: Да, это относится только к прямоугольным треугольникам. … A: У прямоугольного треугольника гипотенуза всегда противоположна углу 90 градусов и является самой длинной стороной.
Как решить задачу Сохкахтоа?
Какова цена греха? Определение синуса с точки зрения Sin 0
| Синус градусы/радианы | Ценности |
|---|---|
| Грех 90 0 or Sinπ/2 | 1 |
| Sin 180°c или Sin π | 0 |
| Sin 270° или Sin 3π/2 | -1 |
| Sin 360° или Sin 2π | 0 |
Как вы оцениваете грех 3?
Значение sin 3 градуса можно рассчитать, построив угол 3° с осью x и затем найдя координаты соответствующей точки (0.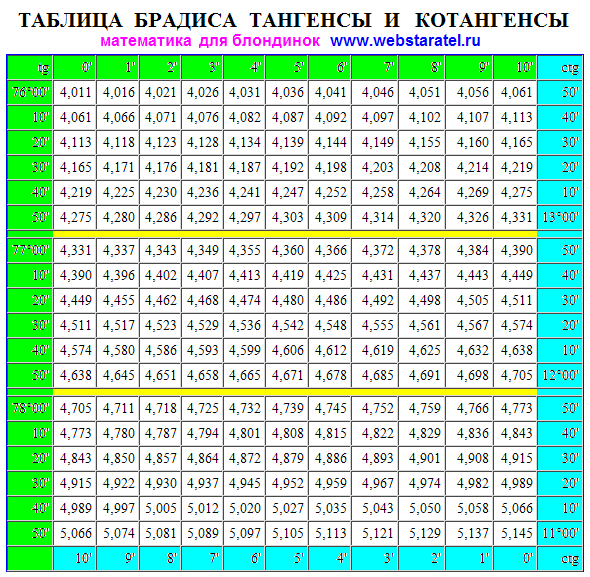
2 x = квадрат синуса угла x.
Как построить график sin 2x?
Как калькулятор находит синус угла?
В этом уравнении следует отметить две вещи:
- Чтобы найти синус, нам нужно работать с многочленом, и
- Этот многочлен бесконечен. Калькулятор будет только оценивать ответ, поэтому, чем сложнее наш калькулятор, тем больше знаков после запятой он сможет отображать. (Для тех из нас, кто не знаком с восклицательным знаком, используемым в этом уравнении, у меня есть еще один блог о факториальной функции.)
Процесс преобразования синусоидальной функции в многочлен выше называется разложением в ряд Тейлора или Маклорена; это полезный инструмент, который преподается в углубленном исчислении (студенты, изучающие AP Исчисление BC или Анализ и подход более высокого уровня в IB, будут изучать его в течение курса).
Давайте посмотрим, как теперь мы можем «вычислить» синус произвольного угла с помощью простого четырехфункционального калькулятора (который может только складывать, вычитать, умножать и делить).
Сначала мы придумаем угол. Возьмем 53°. Для справки, результат синуса 53° равен 0,79663551005… Поскольку в большинстве вопросов нам потребуется округлить только до трех значащих цифр, давайте округлим его до 4 ст.ф. в качестве сравнения, что даст нам эталонное значение 0,7966.
Используя только стандартный калькулятор с четырьмя функциями, мы сначала переведем угол из градусов в радианы. Для этого нам нужно будет умножить 53 на π, а затем разделить на 180. Поскольку в большинстве четырехфункциональных калькуляторов нет числа π, мы оценим его, используя 3,14159.. Таким образом, угол в радианах следует оценивать как 0,925023722.
Далее применим расширение. Мы будем работать только с первыми тремя терминами, чтобы увидеть, насколько близко мы подходим.
Нахождение результата факториала должно быть довольно простым даже с помощью калькулятора с четырьмя функциями, так как нам просто нужно умножать одно число за раз.
Самая сложная часть — мощность. Опять же, большинство четырехфункциональных калькуляторов не имеют функции «степени». Тем не менее, большинство этих калькуляторов имеют встроенный короткий путь для нахождения результата степени положительного целого числа. Для этого вы дважды нажимаете кнопку умножения, а затем нажимаете знак равенства «n» минус один раз, где «n» — это степень, которую мы ищем. Например, чтобы найти 4 5 , начнем с 4, затем дважды нажмем кратное и четыре раза нажмем равно. Таким образом, мы должны получить следующее:
x = 0,925023722
x 3 = 0,791514017
x 5 = 0,677273917
9 0002 Наконец, вычисляем результат второго и третьего членов:2 nd член = 0,791514017 / 6 = 0,131919002
3 rd член = 0,677273917 / 120 = 0,005643943
Складывая все эти члены вместе после расширения, мы имеем:
0,925023722 – 0,131919002 + 0,005643943 = 0,798748664
По сравнению с округленным значением 0,7966 (4 ст.
ф.), мы видим, что результат, скорее всего, будет считаться неверным. Это может быть связано с округлением при расчете каждого шага и с тем, что мы используем только три термина для оценки ответа.
В конце концов, никому из нас не будет смысла делать это вручную. Калькуляторы в настоящее время могут обрабатывать числа с молниеносной скоростью, поэтому мы должны просто позволить им выполнять тяжелую работу. Интересно то, что какой бы сложной или продвинутой ни была концепция в математике, по своей сути она все равно, скорее всего, представляет собой набор арифметических операций.
Калькулятор тригонометрии
Этот калькулятор тригонометрии позволяет вычислять функции тригонометрического угла (sin, cos, tan, sec, csc, tan) в градусах или радианах. Не только это, но и калькулятор sohcahtoa с шагами будет применять эту конкретную мнемонику для точного определения тригонометрических отношений углов, тем самым также представляя график.
Тригонометрический калькулятор прямоугольного треугольника: Вы можете определить любые соотношения тригонометрических функций, используя этот онлайн-калькулятор шести тригонометрических функций.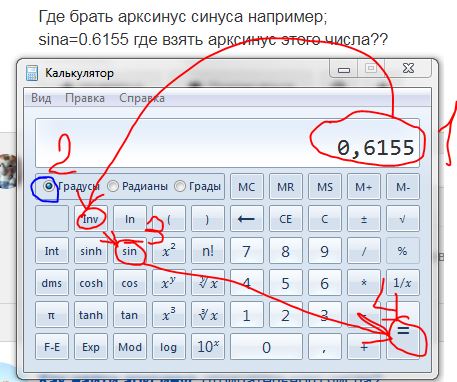
Ввод:
- В первом поле введите из первого раскрывающегося списка, выберите триггерную функцию для вычисления.
- В следующем поле введите величину угла.
- Теперь нажмите кнопку «Рассчитать».
Вывод:
Наш калькулятор коэффициента триггера выполняет следующие вычисления:
- Вычисляет коэффициент триггерного угла как в градусах, так и в радианах.
- Показывает графическую интерпретацию угловой функции.
Помимо углов, вы также можете определить стороны прямоугольного треугольника, используя другой калькулятор закона синусов.
Что такое тригонометрия и тригонометрические отношения? Изучение трех углов треугольника называется тригонометрией. Наш бесплатный треугольник-калькулятор триггеров также подходит для определения всех взаимосвязанных угловых соотношений за пару мгновений.
Ниже приведены стандартные отношения тригонометрических функций, которые также можно вычислить для любого угла с помощью нашего онлайн-калькулятора тригонометрических отношений:
Синус:Отношение длины перпендикуляра к гипотенузе называется синусом.
Формула:
Синус = Перпендикуляр/Гипотенуза
Точное значение синуса углов может быть вычислено с помощью этого треугольника тригонометрического калькулятора.
Косинус:В тригонометрии отношение основания треугольника к гипотенузе известно как функция косинуса, которую можно в деталях понять с помощью бесплатного калькулятора косинуса.
Формула:
Косинус = Основание/Гипотенуза
Тангенс:Отношение перпендикуляра к основанию треугольника известно как функция тангенса.
Формула:
Тангенс = Перпендикуляр/Основание
Секанс: Секанс прямо противоположен синусу.
Другими словами, оно соответствует отношению гипотенузы к перпендикуляру.
Формула:
Секанс = гипотенуза/перпендикуляр
Косеканс:Подобно синусу и секансу, косеканс представляет собой отношение, обратное отношению косинуса. Проще говоря, отношение гипотенузы к основанию треугольника называется косекансом.
Формула:
Косеканс = гипотенуза/основание
Котангенс:Отношение основания треугольника к перпендикуляру называется функцией котангенса.
Формула:
Котангенс = Основание/Перпендикуляр 9{-1}x
Все эти триггерные функции дают разные значения в градусах или радианах для разных мер по азимуту. И довольно сложно рассчитать для каждого значения отдельно. Но здесь на помощь приходит наш бесплатный калькулятор тригонометрии прямоугольного треугольника. Так что используйте этот калькулятор и начните решать для разных углов.
Сводка тригонометрических функций:| Функция | Описание | ||
Найдите значение каждого тригонометрического соотношения для треугольника, указанного ниже:
Решение:
Синус(θ) = Перпендикуляр/Гипотенуза
Синус(θ) = 0,8 ( для расчета угла коснитесь калькулятора синуса)
Косинус (θ) = основание/гипотенуза
косинус (θ) = 0,6 (для расчета угла коснитесь калькулятора косинуса)
Тангенс (θ) = перпендикуляр/основание
Тангенс(θ) = 1,33 (для расчета угла коснитесь калькулятора тангенса)
Секанс(θ) = гипотенуза/перпендикуляр
Секанс(θ) = 1,25 (для расчета угла коснитесь калькулятора секанса)
Косеканс(θ) = Гипотенуза/основание
Косеканс(θ) = 1,67 (для расчета угла коснитесь калькулятора csc)
Котангенс(θ) = основание/перпендикуляр
Котангенс(θ) = 0,75 (для расчета угла коснитесь калькулятора котангенса)
Которые являются необходимыми тригонометрическими отношениями для данного треугольника, а также могут быть перепроверены с помощью онлайн-калькулятора точного значения тригонометрической функции.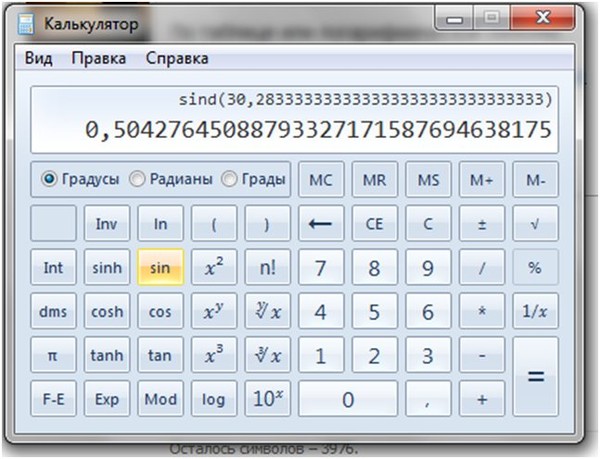
Вот как можно преобразовать десятичную дробь в градусы в тригонометрии:
- Найдите отношение тригонометрии с помощью SOHCATOA.
- Вы можете получить результат, взяв обратное тождество десятичной дроби.
Найти высоту треугольника с помощью тригонометрии очень просто, смотрите ниже.
- Прежде всего, нарисуйте треугольник и разделите его на два меньших треугольника, затем отметьте высоту.
- Вы можете решить оставшиеся треугольники с помощью тригонометрии и найти высоту треугольника.
- Найдя высоту, вы можете сравнить свой ответ с ответом онлайн-калькулятора тригонометрии.
Ниже приведены реальные применения тригонометрии:
- Спутниковые системы
- Картография
- Астрофизика
- Проекты наклона крыши
- Машиностроение
- Химия
Тригонометрия — это изучение природы углов в любом треугольнике.