Окружность и круг – различия (6 класс, математика)
4.7
Средняя оценка: 4.7
Всего получено оценок: 588.
4.7
Средняя оценка: 4.7
Всего получено оценок: 588.
Окружность и круг – это две разные фигуры, которые частенько путают в математике 6 класса. Поэтому имеет смысл обсудить эту тему более подробно.
Определения
Круг – это часть пространства, ограниченная окружностью. Окружность – это множество точек, равноудаленных от одной точке, называемой центром окружности.
Различия
Окружность – это линия. Круг – это плоская фигура. Окружность не может иметь площади, тогда как круг ее имеет.
Рис. 1. Круг и окружность.На этом, пожалуй, различия круга и окружности заканчиваются. Но стоит сказать еще и о том, что в геометрии чаще звучит название окружности.
Круг имеет площадь, но в задачах мы чаще ищем длину окружности. На длину окружности завязаны некоторые свойства вписанной и описанной окружности треугольника, поэтому сложилась некая традиция использования окружности вместо круга.
Вспомним, что
$R={D\over{2}}$-то есть радиус равен половине диаметра. Соответственно это равенство можно подставить в формулу площади и получить еще одну формулу. Или просто найти диаметр или радиус через эту формулу и подставить в уже приведенную формулу.
Существует формула, которая позволяет найти длину окружности. Что такое длина окружности? Если условно распрямить линию окружности, то получится прямая, длину которой можно найти по формуле:
$L=\pi*d$ – диаметр, так же, как и в площади можно заменить диаметром.
Рис. 2. Длина окружности.Окружность и прямая
Положение окружности и прямой на плоскости это отдельная тема для разговора. Прямая на плоскости может:
- Пересекать окружность
- Не пересекать окружность
- Касаться окружности
Прямая, пересекающая окружность зовется секущей и имеет две общие точки с окружностью.
Отдельный интерес имеет касательная прямая, то есть прямая, которая имеет одну общую точку с окружностью.
Запомните, радиус, проведенный в точку касания перпендикулярен касательной.
Рис. 3. Окружность и прямая.Окружность и угол
Окружность и угол связаны, потому как окружность это наиболее яркий пример полного угла. То есть, если провести какой либо отрезок и повернуть его вокруг своего начала на 360 градусов, то получится окружность.
Углом в окружности измеряется дуга. Дуга это часть окружности, ограниченная двумя радиусами. Два радиуса и дуга представляют собой сектор.
Что мы узнали?
Из статьи мы узнали о том, что круг – это плоская фигура, а окружность – это линия. Мы познакомились с характеристиками этих понятий и узнали свойства круга и окружности.
Тест по теме
Доска почёта
Владимир Найда
10/10
Вет Громов
9/10
Шварева Наталья
8/10
Ольга Журавлёва
10/10
Оценка статьи
4.
7
Средняя оценка: 4.7
Всего получено оценок: 588.
А какая ваша оценка?
Как найти радиус 40? – Обзоры Вики
1 Ответ
- г = 402π
- г = 20π
- Поэтому r = ок. 203.14159 = 6.37 дюйма.
Точно так же, каков диаметр круга? Диаметр круга
Диаметр длина линии, проходящей через центр, которая касается двух точек на краю круга.
Чему равен радиус 40 диаметра? Площадь круга равна π⋅r2. Если ваш диаметр 40 м, то ваш радиус должен быть 20m, так как радиус круга всегда равен половине диаметра.
Чему равна длина окружности, если радиус равен 40 см? Круги (базовые)
| Диаметр | Окружность (приблизительно) | Длина окружности |
|---|---|---|
| 20 см | 60 см | 62.8cm |
| 40 см | 120 см | 125.6cm |
| 3m | 9m | 9. 42m |
| 5 см | 15.7 см | 15.7cm |
Во-вторых, какова окружность 40-дюймового круга? Что такое окружность? Запишите свой ответ, используя число Пи. Я знаю, что ответ 125.6, но я понятия не имею, как это написать с помощью pi.
Как определить диаметр?
Формула для определения диаметра устанавливает соотношение между диаметром и радиусом. Диаметр состоит из двух сегментов, каждый из которых имеет радиус. Следовательно, формула такова: Диаметр = 2 * измерение радиуса. Вы можете сократить эту формулу как d = 2r.
тогда как мне измерить диаметр? Чтобы вычислить диаметр круга, умножьте радиус на 2. Если у вас нет радиуса, разделите длину окружности на π, чтобы получить диаметр.
Что такое радиус 40 метров?
Поскольку диаметр в два раза больше радиуса, если диаметр равен 40 метрам, радиус окружности равен 20 метров.
Каков радиус круга диаметром 10 см? 2π10=20π см золота Около 62.8 см. Надеюсь это поможет!
Как мы находим радиус окружности?
Как найти радиус круга?
- Когда диаметр известен, формула Радиус = Диаметр/2.
- Когда длина окружности известна, формула Радиус = Окружность/2π.
- Когда площадь известна, формула для радиуса: Радиус = ⎷(Площадь круга/π).
Как перевести см в диаметр? Разделите окружность на π. Это диаметр круга, в данном случае 31.8 сантиметра. Разделить на 2.
Какой диаметр 60 см?
Таким образом, 60 см равняется 23.62 дюймов.
Как определить диаметр?
Формула для определения диаметра устанавливает соотношение между диаметром и радиусом. Диаметр состоит из двух сегментов, каждый из которых имеет радиус. Следовательно, формула такова: Диаметр = 2 * измерение радиуса. Вы можете сократить эту формулу как d = 2r.
Чему равна окружность круга диаметром 30 см? Ответ: Длина окружности диаметром 30 см будет равна 94.
25 сантиметры.
Как преобразовать радиус в длину окружности?
Для расчета длины окружности вам понадобится радиус окружности:
- Умножьте радиус на 2, чтобы получить диаметр.
- Умножьте результат на π или 3.14 для оценки.
- Вот и все; вы нашли окружность круга.
Является ли диаметр половиной окружности? Диаметр – это хорда, проходящая через центр окружности. … Центр круга — это середина его диаметра. То есть делит его на две равные части, каждая из которых является радиусом окружности. Чай radius составляет половину диаметра.
Как найти диаметр окружности?
Диаметр круга с использованием радиуса
Радиус — это длина отрезка прямой от центра окружности до конечной точки окружности, а диаметр в два раза больше радиуса окружности. Используя это определение, формула диаметра выглядит так: D = Радиус × 2.
Какого диаметра можно нарисовать круг? бесконечный диаметр можно нарисовать по кругу.
Как вы измеряете диаметр в см?
Например, если радиус 5 см, диаметр будет 10 см. Разделите окружность на пи, если вы знаете длину окружности.. Это измерение внешней стороны круга. Если окружность 21.98 см, диаметр 9 см.
Вычислить окружность — диаметр радиуса окружности площади
Тема Круг ﹣ Калькулятор
Здесь все вращается по кругу: определения, формулы и расчеты радиуса, диаметра, длины окружности и площади круга с единицами разной величины завершают тему. С помощью калькулятора круга вы можете рассчитать наиболее важные свойства круга, то есть радиус, диаметр, длину окружности и площадь круга. В тексте справки калькулятора кругов каждое преобразование для отдельных свойств круга выводится с использованием соответствующей формулы круга.
Калькулятор ↑Содержание ↑
Окружность представляет собой геометрическую фигуру и определяется как множество всех точек на плоскости, находящихся на одинаковом расстоянии от точки М, центра окружности. Это расстояние от каждой точки на линии круга или на краю круга до центра круга называется радиусом. Математически круг является кривой и, следовательно, одномерным. Однако круг обычно интерпретируется как двумерная поверхность или круговой диск, который заключен в линию окружности.
К основным свойствам круга относятся радиус, диаметр круга, длина окружности круга и площадь круга. Вычисление этих свойств окружности и их преобразование с использованием формул окружности удобно выполнять с помощью Калькулятора окружности, что более подробно будет рассмотрено ниже.
В связи с вычислениями и формулами для круга и вычислением кругов мы неоднократно встречаем Пи или греческую букву π. Число окружности Пи соответствует, независимо от размера окружности, точному отношению длины окружности к диаметру. Пи имеет бесконечное число знаков после запятой и начинается с 3,14159.26. Следовательно, длина окружности всегда примерно в 3,14 раза больше ее диаметра.
Калькулятор ↑Содержание ↑
- Диаметр: d = 2 × r
- Радиус: r = ½ × d
- Окружность: C = 2 × r × π или C = d × π
- Площадь: A = r² × π или A = (d² × π)/4 = ¼ × d² × π
Калькулятор ↑Содержание ↑
Калькулятор для расчета круга содержит несколько полей ввода, которые более подробно описаны ниже:
Выберите здесь соответствующую единицу размера, чтобы отобразить ее для отдельных полей ввода. Вы можете выбрать мм, см, дм, м, км, дюймы, футы, ярды или мили.
А вот как работает калькулятор: Вы можете заполнить любое поле ввода ниже.
Остальные значения затем рассчитываются и заполняются автоматически с использованием формулы для расчета окружности. Справочные тексты для радиуса, диаметра, длины окружности и площади всегда содержат текущий вывод текущего расчета. Как только вы снова измените одно из значений, выполняется новый расчет оставшихся значений и обновление текстов справки для получения нового расчета.
Введите радиус, чтобы рассчитать диаметр, длину окружности и площадь круга. «Справочные тексты» рассчитанных свойств круга будут обновлены, чтобы включить соответствующую формулу круга, а также вывод вычисления из введенного радиуса в соответствующее свойство.
Пожалуйста, введите диаметр, чтобы рассчитать радиус, длину окружности и площадь круга. Затем обновляются справочные тексты рассчитанных свойств окружности, которые содержат соответствующую формулу расчета, а также вывод расчета от введенного диаметра к соответствующему свойству.
Введите длину окружности, чтобы рассчитать радиус, диаметр и площадь круга.
Справочные тексты рассчитанных свойств окружности обновляются, и каждый из них содержит конкретный вывод текущего расчета, т. е. от длины окружности до радиуса, до диаметра или до площади окружности.
Введите площадь для расчета радиуса, диаметра и длины окружности. Точно так же при расчете радиуса, диаметра и окружности их справочные тексты обновляются, чтобы можно было понять вывод преобразования в каждом случае.
Эскиз показывает выбранное свойство окружности. Это дает вам представление о том, как определяются радиус, диаметр, длина окружности и площадь круга. Отображение меняется, как только вы нажимаете на поле ввода для свойств круга или выбираете соответствующую кнопку справки.
Калькулятор ↑Содержание ↑
Как уже было сказано, окружность определяется как множество всех точек плоскости, находящихся на равном расстоянии от точки М, центра окружности. Это расстояние от центра круга до края круга называется радиусом.
Радиус r или радиус — это расстояние между центральной точкой M окружности и линией окружности.
Калькулятор ↑Содержание ↑
Диаметр окружности d или ⌀ представляет собой длину соединительного расстояния двух точек линии окружности, проходящей через центр окружности M.
Таким образом, диаметр — это максимально возможное расстояние между двумя точками на окружности.
Диаметр d соответствует удвоенному радиусу r
д = 2 × г
Калькулятор ↑Содержание ↑
Длина окружности C равна длине окружности.
Длина окружности C вычисляется путем умножения диаметра d на число Pi (π = 3,1415…).
С = д × π
Калькулятор ↑Содержание ↑
Площадь круга A — это площадь, ограниченная линией окружности.
Площадь круга A вычисляется путем умножения квадрата радиуса r на число Пи (π = 3,1415…).
А = г² × π
Видео, демонстрирующее вывод формулы площади круга
Вот еще одно видео на тему «Окружности, окружность и площадь» от Math Antics.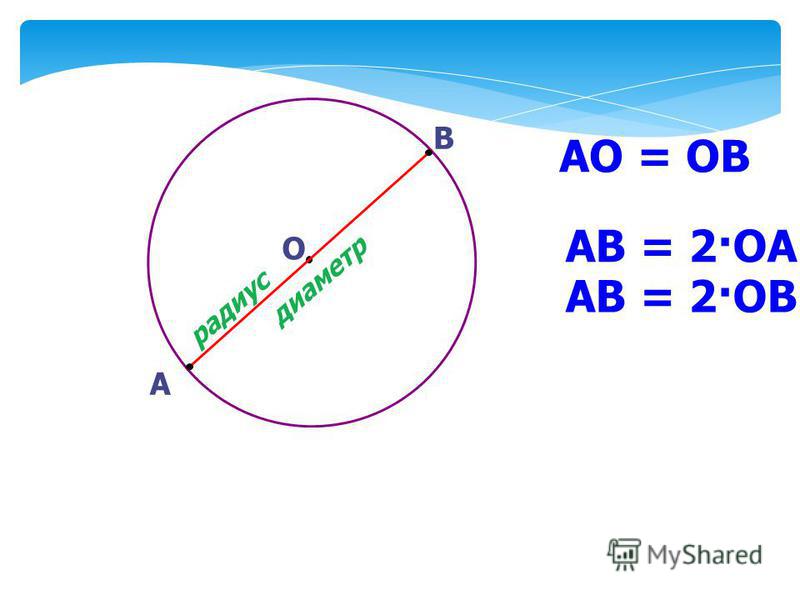
Калькулятор ↑Содержание ↑
Четыре свойства круга, описанные на этой странице, — радиус, диаметр, длина окружности и площадь — можно рассчитать, указав одно значение другого свойства в каждом случае. Например, если вы хотите вычислить площадь круга, это можно сделать, используя одно из трех других свойств в каждом случае, то есть используя радиус, диаметр или длину окружности.
Поэтому ниже мы покажем вам три примера для расчета радиуса, диаметра, длины окружности и площади круга с использованием трех других свойств круга в каждом случае.
В следующих трех примерах показано вычисление радиуса с использованием свойств круга диаметра, длины окружности и площади.
Дан круг с диаметром d 20 в . Ищем радиус r.
Расчет
Радиус r равен половине диаметра d, поэтому r = d / 2 .
Заменив 20 дюймов, выбранных в примере, на диаметр d, радиус окружности r = 20 дюймов / 2 = 10 дюймов .
Дан круг с длиной окружности C 30 в . Ищем радиус r.
Расчет
Формула длины окружности: C = 2 × r × π . Когда мы преобразуем эту формулу в r, мы получаем r = C / π / 2, что составляет половину длины окружности, деленную на Pi (π = 3,1415…), таким образом r = C / π / 2 .
Если мы заменим 30 в выбранном в примере для окружности C, радиус круга r = 30 дюймов / π / 2 = 4,77 дюймов .
Видео для расчета радиуса по окружности
Вот еще одно видео на тему «Вычисление длины окружности с учетом радиуса» мистера Дж.: В видео также показано, как преобразовать формулу длины окружности в r, чтобы рассчитать радиус на основе заданной длины окружности.
Начиная с 3:09 следуют еще два примера преобразования.
Дано круглых площадей A размером 100 дюймов2 . Ищем радиус r.
Расчет
Общая формула площади круга A: A = r² × π . Если мы преобразуем эту формулу в r, радиус r будет равен квадратному корню из результата площади круга A, деленному на Pi (π = 3,1415…), таким образом r = A / π .
Если мы вставим 100 дюймов², выбранные в примере для площади A, радиус круга будет r = 100 дюймов / π = 5,64 дюйма .
Видео для расчета радиуса по круглой площади
В целях иллюстрации, вот еще одно видео на тему «Найти радиус» Брайана Маклогана: Здесь также объясняется преобразование формулы площади круга в r, чтобы можно было вычислить соответствующий радиус для заданного круглая площадь.
Калькулятор ↑Содержание ↑
В следующих примерах показано вычисление диаметра с использованием свойств окружности радиуса, длины окружности и площади.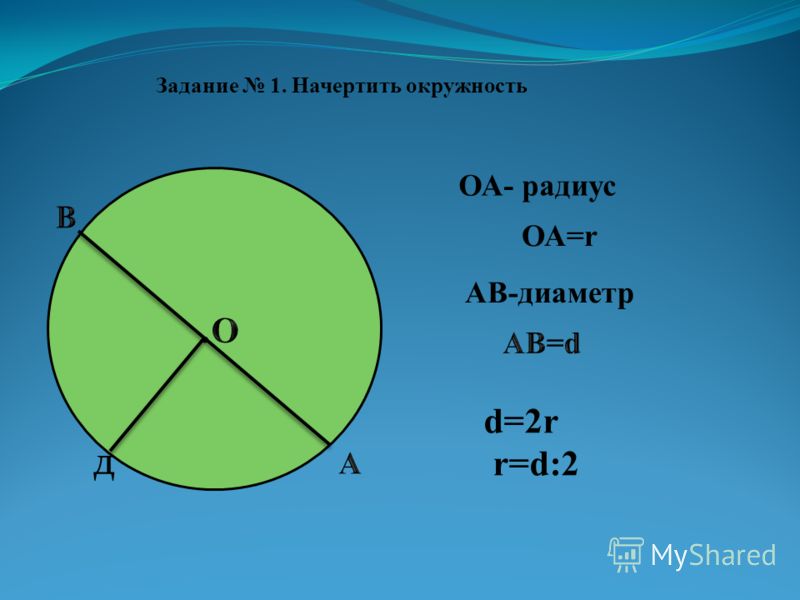
Дана окружность с радиусом r 10 в . Ищем диаметр d.
Расчет
Диаметр d соответствует удвоенному радиусу r, то есть d = 2 × r .
Если 10 дюймов, выбранных в примере, используются для радиуса r, диаметр круга равен d = 2 × 10 дюймов = 20 в .
Дан круг с длиной окружности C 30 в . Ищем диаметр d.
Расчет
Формула длины окружности: C = d × π . Если мы преобразуем эту формулу в d, диаметр d будет равен длине окружности, деленной на число Пи (π = 3,1415…), таким образом d = C / π .
Если мы заменим 30 в выбранном в примере для окружности C, диаметр круга d = 30 дюймов / π = 9,55 дюйма .
Дан круг с площадью A 100 дюймов² . Ищем диаметр d.
Расчет
Общая формула площади круга A: A = r² × π . Поскольку диаметр d соответствует удвоенному радиусу r, формула поэтому A = (d / 2)² × π .
Если мы преобразуем эту формулу в d, диаметр d будет равен удвоенному квадратному корню из площади круга A, деленному на Pi (π = 3,1415.
..), таким образом d = 2 × A / π .
Если мы вставим 100 дюймов², выбранные в примере для площади A, диаметр круга будет d = 2 × 100 дюймов / π = 11,28 дюймов .
Калькулятор ↑Содержание ↑
Следующие примеры иллюстрируют вычисление длины окружности с использованием радиуса, диаметра и площади окружности.
Дана окружность с радиусом r 10 в . Ищем окружность U.
Расчет
Окружность C соответствует удвоенному радиусу r, умноженному на число Pi (π = 3,1415…), таким образом С = 2 × r × π .
Если мы вставим 10 в выбранный в примере радиус r, длина окружности будет равна C = 2 × 10 дюймов × π = 62,83 дюйма .
Дан круг с диаметром d 20 в . Ищем окружность U.
Расчет
Длина окружности C соответствует диаметру d, умноженному на число Pi (π = 3,1415…), таким образом C = d × π .
Если мы подставим выбранное в примере 20 вместо диаметра d, длина окружности будет равна C = 20 дюймов × π = 62,83 дюймов .
Дана круглая площадь A размером 100 дюймов2 . Ищем окружность U.
Расчет
Общая формула площади круга A: A = r² × π . Теперь, используя эту формулу, радиус r можно рассчитать, сначала преобразовав формулу в r. Радиус r равен квадратному корню из площади круга A, деленному на Pi (π = 3,1415…), таким образом r = A / π .
Если мы вставим 100 дюймов², выбранные в примере для площади A, радиус круга будет r = 100 дюймов / π = 5,64 дюймов .
Используя рассчитанный таким образом радиус, теперь можно использовать общую формулу расчета длины окружности: длина окружности C равна удвоенному радиусу r, умноженному на число Pi (π = 3,1415…), таким образом C = 2 × r × π .
Если мы вставим ранее рассчитанное значение радиуса r, длина окружности будет равна C = 2 × 5,64 дюйма × π = 35,45 дюйма .
Калькулятор ↑Содержание ↑
Следующие примеры иллюстрируют вычисление площади круга с использованием радиуса, диаметра и длины окружности.
Дана окружность с радиусом r 10 в . Найдем площадь круга А.
Расчет
Площадь круга A равна квадрату радиуса, т. е. r², умноженному на число Pi (π = 3,1415…), и, следовательно, A = r² × π .
Если 10 дюймов, выбранных в примере, используются для радиуса r, площадь круга будет следующей: A = (10 дюймов)² × π = 314,16 дюйм² .
Дан круг с диаметром d 20 в . Найдем площадь круга А.
Расчет
Площадь A равна половине диаметра в квадрате, т. е. (d / 2)², умноженному на число Pi (π = 3,1415…), и, таким образом, A = (d / 2)² × π .
Если вместо диаметра d подставить выбранные в примере 20, то площадь круга будет равна А = (20 дюймов / 2)² × π = 314,16 дюйм² .
Дан круг с длиной окружности C 30 в . Найдем площадь круга А.
Расчет
Площадь А получается из окружности, например, сначала определяя радиус окружности r на основе окружности.
Затем вы можете использовать общую формулу площади круга, а именно A = r² × π .
Расчет радиуса на основе длины окружности уже получен в примере для преобразования длины окружности в радиус и составляет 4,77 дюйма.
Теперь, если мы вставим значение радиуса r, рассчитанное здесь на основе длины окружности 30 дюймов, выбранной в примере, а именно 4,77 дюйма, площадь круга составит А = (4,77 дюйма)² × π = 71,62 в 90 080 .
Другие онлайн калькуляторы
Преобразование времени, Онлайн калькулятор, Конвертер длины
Оцените наш калькулятор
одним щелчком мыши
(левая звезда несчастна — правая звезда хороша)
5,0 звезды в 3 рейтинги 5 3 Вычислить круг — радиус окружности площади диаметр
ГлавнаяМатематикаCircle
Радианы к Части диаметра | Преобразователь Кайла
- Угол >
- Радиан >
- Радианы в Части диаметра
org/ListItem»> Преобразователь Кайла >| Радианы (рад) | Детали диаметра |
| Точность: 0123456789121518 |
Обратное преобразование?
Диаметр Деталей в Радианы (или просто введите значение в поле «до»)
Пожалуйста, поделитесь, если вы нашли этот инструмент полезным:
| Описание единиц измерения | |
|---|---|
|
|
Один полный оборот составляет 2π радиан.| ТАБЛИЦА | ||
|---|---|---|
| 1 Радиан с диаметрами | 8870 Радиан. | |
| 3 радианы в части диаметра = 180 | 90 радианы в части диаметра = 5400 | |
| 4 Радиан к диаметрам частям = 240 | 100 Радиан к диаметрам частям = 6000 | |
| 5 Радианы до диаметра = 300 | 200 Радианы. 360 | 300 радиан в диаметр детали = 18000 |
| 7 радиан в диаметр детали = 420 | 400 радиан в диаметр детали = 24000 | |
| радиан = диаметр детали 8 | 0388 | 500 Радиан к диаметрам частям = 30000 |
| 9 Радиан к диаметрам частям = 540 | 600 Радиан до диаметра по частям = 36000 | |
| 10 Радианов до диаметра | ||
. | ||