Градус (deg) → Градусы, минуты, секунды (d°m′s″), Общеупотребительные единицы
Перевод величин: Градус (deg) → Градусы, минуты, секунды (d°m′s″), Общеупотребительные единицыEN ES PT RU FR
Ой… Javascript не найден.
Увы, в вашем браузере отключен или не поддерживается JavaScript.
К сожалению, без JavaScript этот сайт работать не сможет. Проверьте настройки браузера, может быть JavaScript выключен случайно?
Перевод величин: градус (deg) → градусы, минуты, секунды (d°m′s″), Общеупотребительные единицы
?Настройки конвертера:
x
Объяснение настроек конвертера
Кстати, пользоваться настройками не обязательно. Вам вполне могут подойти настройки по умолчанию.
Количество значащих цифр
Для бытовых целей обычно не нужна высокая точность,
удобнее получить округлённый результат.
В таких случаях выберите 3 или 4 значащих цифры.
Максимальная точность — 9 значащих цифр.
Точность можно изменить в любой момент.
Разделитель групп разрядов
Выберите, в каком виде вам будет удобно получить результат:
| 1234567.89 | нет |
|---|---|
| 1 234 567.89 | пробел |
| 1,234,567.89 | запятая |
| 1.234.567,89 | точка |
- Значащих цифр: 1 23456789
- Разделитель разрядов: нет пробел запятая точка
градус (deg)
Общеупотребительные единицы
градусы, минуты, секунды (d°m′s″)
Общеупотребительные единицы
На этой странице мы можете сделать онлайновый перевод величин: градус → градусы, минуты, секунды. Эти две единицы относятся к одной и той же системе измерения: Общеупотребительные единицы.
Если вам нужен калькулятор для переводы из единицы градус в другую совместимую единицу, пожалуйста выберете нужную на этой странице ниже.
Вы также можете переключиться на конвертер
градусы, минуты, секунды
→
градус.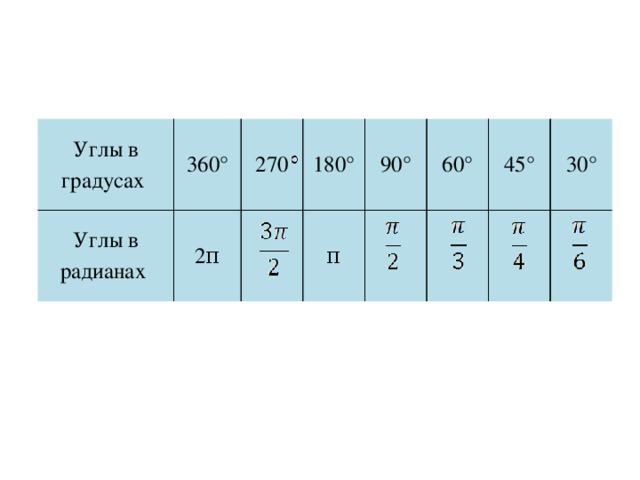
Значения других единиц, равные введённым выше
» открыть »
» свернуть »
Общеупотребительные единицы
Чтобы ввести комбинированную единицу градусы, минуты, секунды, вы можете набрать * или o вместо символа градуса °.
| градус → окружность (circle) | |
| градус → секстант | |
| градус → радиан (rad) | |
| градус → градус (deg) | |
| градус → градусы, минуты, секунды (d°m′s″) | |
| градус → град (grad) | |
| градус → минута (′) | |
| градус → секунда (″) |
Единицы: окружность (circle) / секстант / радиан (rad) / градус (deg) / градусы, минуты, секунды (d°m′s″) / град (grad) / минута (′) / секунда (″)
» открыть »
» свернуть »
Единицы уклона
Уклон в процентах часто используют для обозначения уклона дорог или строительных объектов.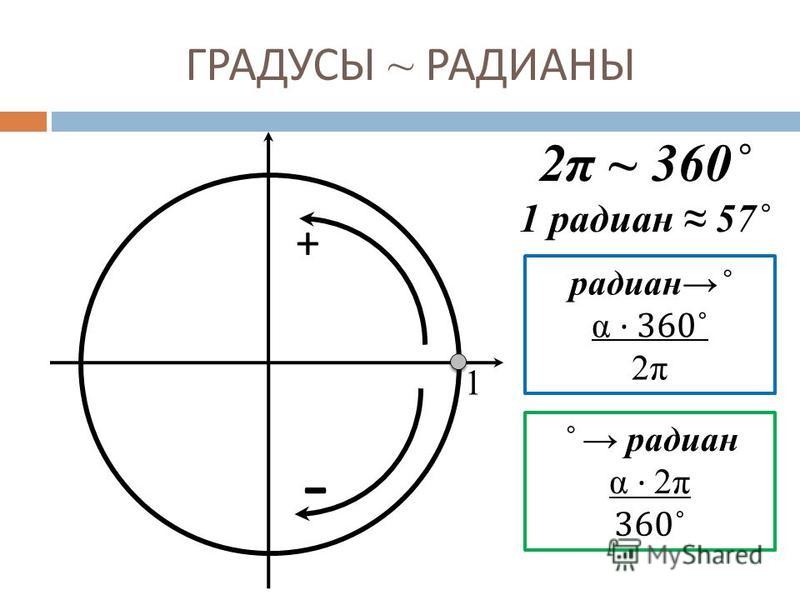
| градус → уклон в процентах (%) | |
| градус → уклон в промилле (‰) |
Единицы: уклон в процентах (%) / уклон в промилле (‰)
» открыть »
» свернуть »
Морские единицы
| градус → румб |
Единицы: румб
» открыть »
» свернуть »
Артиллерийские единицы
Эти шкалы используются в артиллерийских прицелах и некоторых военных приборах. Происхождение названия ‘тысячная’ связано с тем, что величина близка к 1/1000 радиана.
| градус → Русская тысячная | |
| градус → Немецкая тысячная | |
| градус → Угловой мил | |
| градус → Шведская тысячная |
Единицы: Русская тысячная / Немецкая тысячная / Угловой мил / Шведская тысячная
Не можете найти нужную единицу?
Попробуйте поискать:
Другие варианты:
Посмотрите алфавитный список всех единиц
Задайте вопрос на нашей странице в facebook
< Вернитесь к списку всех конвертеров
Надеемся, Вы смогли перевести все ваши величины,
и Вам у нас на Convert-me.
Com понравилось. Приходите снова!
!
Значение единицы приблизительное.
Либо точного значения нет,
либо оно неизвестно. ?
Пожалуйста, введите число. (?)
Простите, неизвестное вещество. Пожалуйста, выберите что-то из списка. ***
Нужно выбрать вещество.
Совет: Не можете найти нужную единицу? Попробуйте поиск по сайту. Поле для поиска в верхней части страницы.
Нашли ошибку? Хотите предложить дополнительные величины? Свяжитесь с нами в Facebook.
Действительно ли наш сайт существует с 1996 года? Да, это так. Первая версия онлайнового конвертера была сделана ещё в 1995, но тогда ещё не было языка JavaScript, поэтому все вычисления делались на сервере — это было медленно. А в 1996г была запущена первая версия сайта с мгновенными вычислениями.
Для экономии места блоки единиц могут отображаться в свёрнутом виде. Кликните по заголовку любого блока, чтобы свернуть или развернуть его.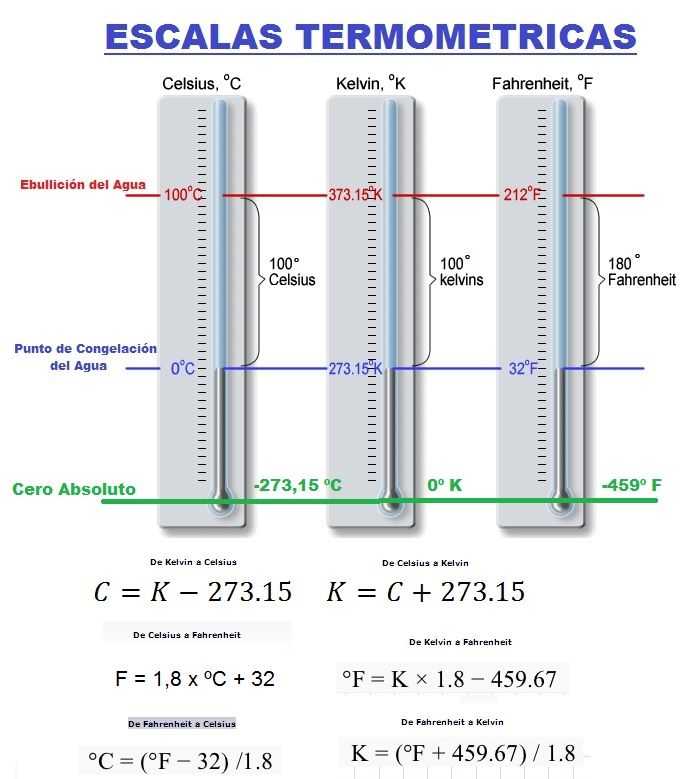
Слишком много единиц на странице? Сложно ориентироваться? Можно свернуть блок единиц — просто кликните по его заголовку. Второй клик развернёт блок обратно.
Наша цель — сделать перевод величин как можно более простой задачей. Есть идеи, как сделать наш сайт ещё удобнее? Поделитесь!
? Пожалуйста, введите градусы, минуты и секунды, например 5°10’5″
Минуточку, загружаем коэффициенты…
Перевод градусов в радианы и обратно, формулы, примеры. Как перевести градусы в радианы
С давних времён люди измеряют углы. Но что такое угол? Геометрия даёт нам ответ: «Угол — это два луча, проведённые из заданной точки» . Углы бывают разные: тупые, острые, прямые , развёрнутые, центральные, смежные . Возьмём точку O и проведём из неё луч O. A. Теперь из этой же точки проведём луч OB, параллельный лучу OA и направленный с ним в одну сторону. Про такие лучи говорят, что угол между ними составляет 0° (ноль градусов).
Если мы теперь направим луч OB параллельно лучу OA, но в противоположную сторону, то получим развёрнутый угол, равный 180°.
Что означают градус и радиан
Так вот, мерой расхождения двух лучей, проведённых из одной точки друг от друга, будет
Вращая один радиус относительно другого против часовой стрелки, мы будем получать разные углы. Когда эти отрезки совпадают, то между ними будет 0°, когда же отрезки отсекают сектор круга, равный одной четверти полного круга, то угол между ними составит 90°.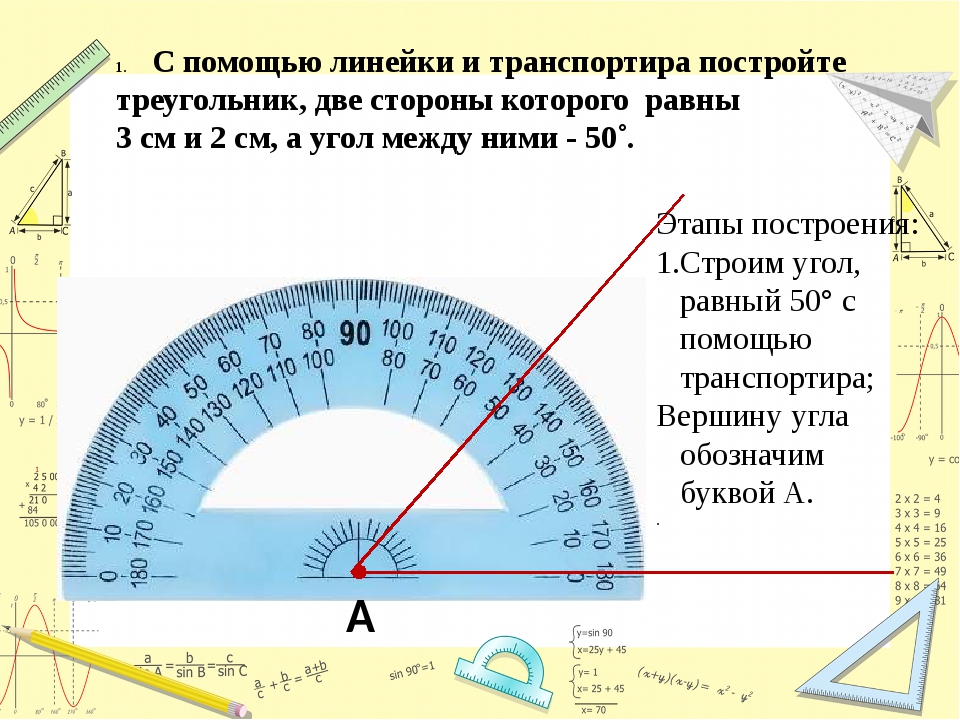
Вращая дальше таким образом, мы получим следующие углы: 180° — радиусы лежат на диаметре круга и делят его пополам, 270° — радиусы отсекают три четверти круга, 360° — радиусы совпадают. Таким образом, полный круг составляет 360°. Для измерения углов существует транспортир .
Кроме градусной меры для измерения углов применяют меру радианную . Радиан — это мера центрального угла. «Радиан» означает «связанный с радиусом». Если из центра окружности радиусом R провести два луча, то они на ней отсекут дугу, длина которой l. Так вот, угол α между указанными лучами называется центральным . Чтобы его измерить, нужно длину дуги окружности разделить на её радиус: α=l/R. Получится значение, выраженное в радианах (рад). Поскольку любому углу на плоскости можно сопоставить такой же центральный угол, то встаёт вопрос, как от обычной градусной меры перейти к радианной.
Как перевести градусы в радианы и обратно
Мы знаем, что центральному углу в 360° соответствует вся окружность, длина которой вычисляется по известной формуле l=2 π R.
- 1 рад=180°/π≈57,2958°;
- 1°=π/180 рад≈0,01745 рад.
Сколько составит 180 градусов в радианах и 90 градусов в радианах? Воспользовавшись полученными выше формулами, придём к таким соотношениям:
- 90°=π/2 рад≈1,571 рад;
- 180°=π рад≈3,142 рад.
Итак, как правильно переводить градусную меру в радианную и обратно? В этом вам поможет следующее правило:
Чтобы найти число радиан, нужно градусную меру умножить на число π и поделить на 180. Чтобы найти число градусов, нужно радианную меру умножить на 180 и поделить на число π .
Примеры решения задач
Задача 1.
Чему равна длина дуги окружности, если R=1 см, α=1 рад?
Решение. По формуле длины дуги найдём: l=R α=1 1=1 см.
Задача 2. Сколько рад в 45°?
Решение. Используя правило, получим: α=45 π/180=π/4 рад.
Задача 3. Сколько град. в π² рад?
Решение. Используя правило, найдём: А=π² 180/π=180π град.≈565,5°.
Задача 4. Чему равен средний угловой размер лунного диска, если среднее расстояние до Луны равно R=384399 км, а диаметр самой Луны D=3476 км?
Решение. Если мысленно на Луну с Земли провести два луча, которые пройдут через крайние точки диаметра её диска, мы получим центральный угол, исходящий из глаз наблюдателя. Поскольку расстояние до Луны намного превышает её диаметр, то этот диаметр можно будет приравнять длине дуги l окружности, образуемой радиусом R, т. е. D≈l=α R. Тогда искомый угловой размер составит: α≈D/R=3476/384399=0,00904268742 рад=0,51810782462°≈31’05”≈0,5°. Итак, видимый угловой диаметр Луны равен полградуса.
Минуты и секунды
Издревле для измерения углов пользовались так называемой шестидесятиричной системой исчисления .
В этой системе вся окружность делится на 360°. Затем каждый градус делят на 60 минут, а каждую минуту — на 60 секунд. Минуты обозначаются значком «»”, а секунды — значком «””. Отсюда пошло измерение времени. Кроме того, циферблат — это символ круга, а стрелки часов отмеряют центральные углы. Для перевода этих единиц используйте следующие соотношения:
- 1°=60’=3600”;
- 1’=(1/60)°=60”;
- 1”=(1/3600)°=(1/60)’;
- 1 рад≈3438′.
Необходимость в измерении углов появилась у людей с тех пор, как цивилизация достигла минимального технического уровня. Всем известна феноменальная точность соблюдения наклона и ориентации по странам света, обеспеченная строителями египетских пирамид. Современную градусную меру углов, как сейчас считается, изобрели древние аккадцы.
Что такое градусы?
Градус — общепринятая единица измерения углов. В полной окружности 360 градусов. Причина выбора именно этого числа неизвестна. Вероятно, аккадцы разделили окружность на сектора, используя угол равностороннего треугольника, а затем полученные сегменты снова разделили на 60 частей согласно своей системе счисления.
Градус тоже делится на 60 минут, а минуты — на 60 секунд. Общепринятыми обозначениями являются:
° — угловые градусы
’ — минуты,
’’ — секунды.
За тысячелетия градусная мера углов прочно вошла во многие сферы человеческой деятельности. Она и сейчас незаменима во всех областях науки и техники — от картографии до расчета орбит искусственных спутников Земли.
Что такое радианы?
Архимеду приписывается открытие постоянства соотношения длины окружности и ее диаметра. Мы называем его числом π. Оно иррационально, то есть не может быть выражено в виде обычной или периодической дроби. Чаще всего используется значение числа π с точностью до двух знаков после запятой — 3,14. Длина окружности L с радиусом R легко вычисляется по формуле: L=2πR.
Окружность радиуса R=1 имеет длину 2π. Это соотношение используется в геометрии как формулировка радианной меры угла.
По определению, радиан — угол с вершиной в центре окружности, опирающийся на дугу с длиной, равной радиусу окружности.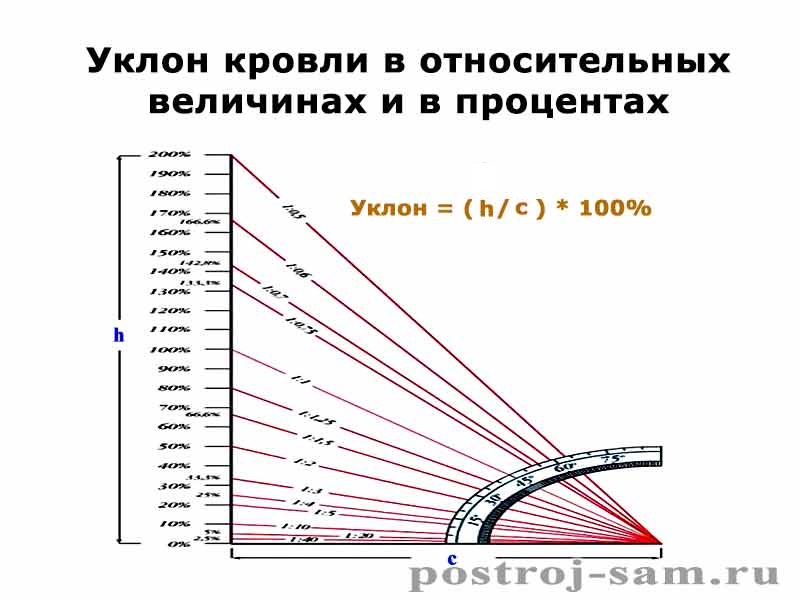
Международное обозначение радиана — rad, отечественное — рад. Размерности он не имеет.
Дуга окружности с радиусом R с угловой величиной α радиан, имеет длину α * R.
Зачем понадобилось вводить новую единицу измерения угла?
Развитие науки и техники привело к появлению тригонометрии и математического анализа, необходимых для точных расчетов механических и оптических устройств. Одной из его задач является измерение длины кривой линии. Самый распространенный случай — определение длины дуги окружности. Использование для этой цели градусной меры углов крайне неудобно. Идея сопоставить длину дуги с радиусом окружности возникала у многих математиков, но сам термин «радиан» был введен в научный обиход только во второй половине XIX века. Сейчас все тригонометрические функции в математическом анализе по умолчанию используют радианную меру угла.
Как переводить градусы в радианы
Из формулы длины окружности вытекает, что в нее укладывается 2π радиусов. Отсюда вытекает, что: 1⁰=2π/360= π/180 рад.
И простая формула перевода из радианов в градусы: 1 рад = 180/π.
Пусть мы имеем угол в N градусов. Тогда формула для перевода из градусов в радианы будет такой: α(радиан) = N/(180/π) = N*π/180.
Остались вопросы?
Ответы на них можно найти , где подробно разъяснены понятия длины окружности, радианной меры углов и на конкретных примерах показан перевод градусов в радианы. Знания упомянутого крайне важны для понимания математики, без которой невозможно существование современной цивилизации.
Конвертер длины и расстояния Конвертер массы Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер площади Конвертер объема и единиц измерения в кулинарных рецептах Конвертер температуры Конвертер давления, механического напряжения, модуля Юнга Конвертер энергии и работы Конвертер мощности Конвертер силы Конвертер времени Конвертер линейной скорости Плоский угол Конвертер тепловой эффективности и топливной экономичности Конвертер чисел в различных системах счисления Конвертер единиц измерения количества информации Курсы валют Размеры женской одежды и обуви Размеры мужской одежды и обуви Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер плотности Конвертер удельного объема Конвертер момента инерции Конвертер момента силы Конвертер вращающего момента Конвертер удельной теплоты сгорания (по массе) Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему) Конвертер разности температур Конвертер коэффициента теплового расширения Конвертер термического сопротивления Конвертер удельной теплопроводности Конвертер удельной теплоёмкости Конвертер энергетической экспозиции и мощности теплового излучения Конвертер плотности теплового потока Конвертер коэффициента теплоотдачи Конвертер объёмного расхода Конвертер массового расхода Конвертер молярного расхода Конвертер плотности потока массы Конвертер молярной концентрации Конвертер массовой концентрации в растворе Конвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяжения Конвертер паропроницаемости Конвертер паропроницаемости и скорости переноса пара Конвертер уровня звука Конвертер чувствительности микрофонов Конвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с возможностью выбора опорного давления Конвертер яркости Конвертер силы света Конвертер освещённости Конвертер разрешения в компьютерной графике Конвертер частоты и длины волны Оптическая сила в диоптриях и фокусное расстояние Оптическая сила в диоптриях и увеличение линзы (×) Конвертер электрического заряда Конвертер линейной плотности заряда Конвертер поверхностной плотности заряда Конвертер объемной плотности заряда Конвертер электрического тока Конвертер линейной плотности тока Конвертер поверхностной плотности тока Конвертер напряжённости электрического поля Конвертер электростатического потенциала и напряжения Конвертер электрического сопротивления Конвертер удельного электрического сопротивления Конвертер электрической проводимости Конвертер удельной электрической проводимости Электрическая емкость Конвертер индуктивности Конвертер Американского калибра проводов Уровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
единицах Конвертер магнитодвижущей силы Конвертер напряженности магнитного поля Конвертер магнитного потока Конвертер магнитной индукции Радиация. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Конвертер радиоактивного распада Радиация. Конвертер экспозиционной дозы Радиация. Конвертер поглощённой дозы Конвертер десятичных приставок Передача данных Конвертер единиц типографики и обработки изображений Конвертер единиц измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева
1 радиан [рад] = 57,2957795130823 градус [°]
Исходная величина
Преобразованная величина
градус радиан град гон минута секунда зодиакальный сектор тысячная оборот окружность оборот квадрант прямой угол секстант
Электрическая проводимость
Общие сведения
Плоский угол — геометрическая фигура образованная двумя пересекающимися линиями. Плоский угол состоит из двух лучей с общим началом, и эта точка называется вершиной луча.
Лучи называются сторонами угла. У углов много интересных свойств, например, сумма всех углов в параллелограмме — 360°, а в треугольнике — 180°.
Виды углов
Прямые углы равны 90°, острые — меньше 90°, а тупые — наоборот, больше 90°. Углы, равные 180° называются развернутыми , углы в 360° называются полными , а углы больше развернутых но меньше полных называются невыпуклыми . Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными смежными , а если же до 360° — то сопряженными
Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными . Если они дополняют друг друга до 180°, они называются смежными , а если же до 360° — то сопряженными . В многоугольниках углы внутри многоугольника называются внутренними, а сопряженные с ними — внешними.
Два угла, образованные при пересечении двух прямых и не являющихся смежными, называются вертикальными .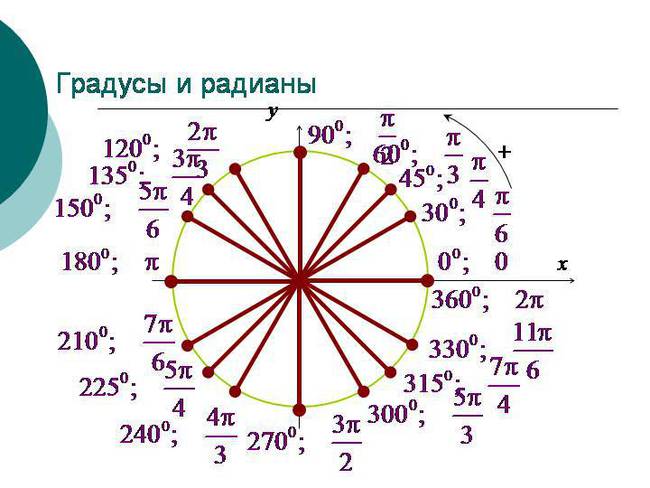
Они равны.
Измерение углов
Углы измеряют с помощью транспортира или вычисляют по формуле, измерив стороны угла от вершины и до дуги, и длину дуги, которая эти стороны ограничивает. Углы обычно измеряют в радианах и градусах, хотя существуют и другие единицы.
Можно измерять как углы, образованные между двумя прямыми, так и между кривыми линиями. Для измерения между кривыми используют касательные в точке пересечения кривых, то есть в вершине угла.
Транспортир
Транспортир — инструмент для измерения углов. Большинство транспортиров имеют форму полукруга или окружности и позволяют измерить углы до 180° и до 360° соответственно. В некоторых транспортирах встроена дополнительная вращающаяся линейка для удобства в измерении. Шкалы на транспортирах наносят чаще в градусах, хотя иногда они бывают и в радианах. Транспортиры чаще всего используют в школе на уроках геометрии, но их также применяют в архитектуре и в технике, в частности в инструментальном производстве.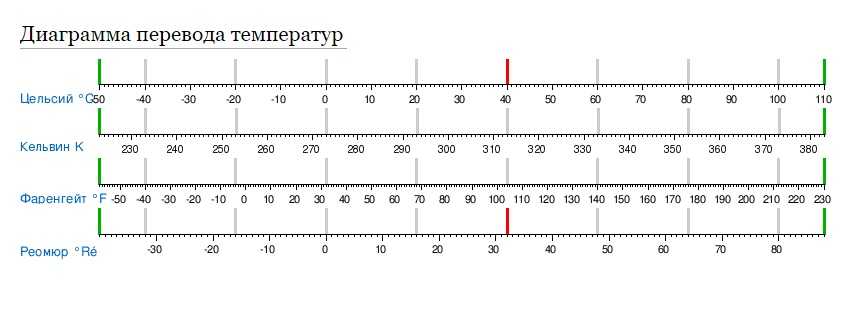
Использование углов в архитектуре и искусстве
Художники, дизайнеры, мастера и архитекторы издавна используют углы для создания иллюзий, акцентов и других эффектов. Чередование острых и тупых углов или геометрические узоры из острых углов часто используются в архитектуре, мозаике и витражах, например в строении готических соборов и в исламской мозаике.
Одна из известных форм исламского изобразительного искусства — украшение с помощью геометрического орнамента гирих. Этот рисунок применяют в мозаике, резьбе по металлу и дереву, на бумаге и на ткани. Рисунок создается с помощью чередования геометрических фигур. Традиционно используют пять фигур со строго определенными углами из комбинаций в 72°, 108°, 144° и 216°. Все эти углы делятся на 36°. Каждая фигура разделена линиями на несколько более маленьких симметричных фигур, чтобы создать более тонкий рисунок. Изначально гирихом назывались сами эти фигуры или кусочки для мозаики, отсюда и пошло название всего стиля.
В Марокко существует похожий геометрический стиль мозаики, зулляйдж или зилидж. Форма терракотовых изразцов, из которых складывают эту мозаику, не соблюдается так строго, как в гирихе, и изразцы часто более причудливой формы, чем строгие геометрические фигуры в гирихе. Несмотря на это, мастера зулляйджа также используют углы для создания контрастных и причудливых узоров.
В исламском изобразительном искусстве и архитектуре часто используется руб аль-хизб — символ в форме одного квадрата, наложенного на другой под углом в 45°, как на иллюстрациях. Он может быть изображен как сплошная фигура, или в виде линий — в этом случае этот символ называется звездой Al-Quds (аль кудс). Руб аль-хизб иногда украшают небольшими кругами на пересечении квадратов. Этот символ используют в гербах и на флагах мусульманских стран, например на гербе Узбекистана и на флаге Азербайджана. Основания самых высоких в мире на момент написания (весна 2013) башен близнецов, башен Петро́нас построены в форме руб аль-хизба.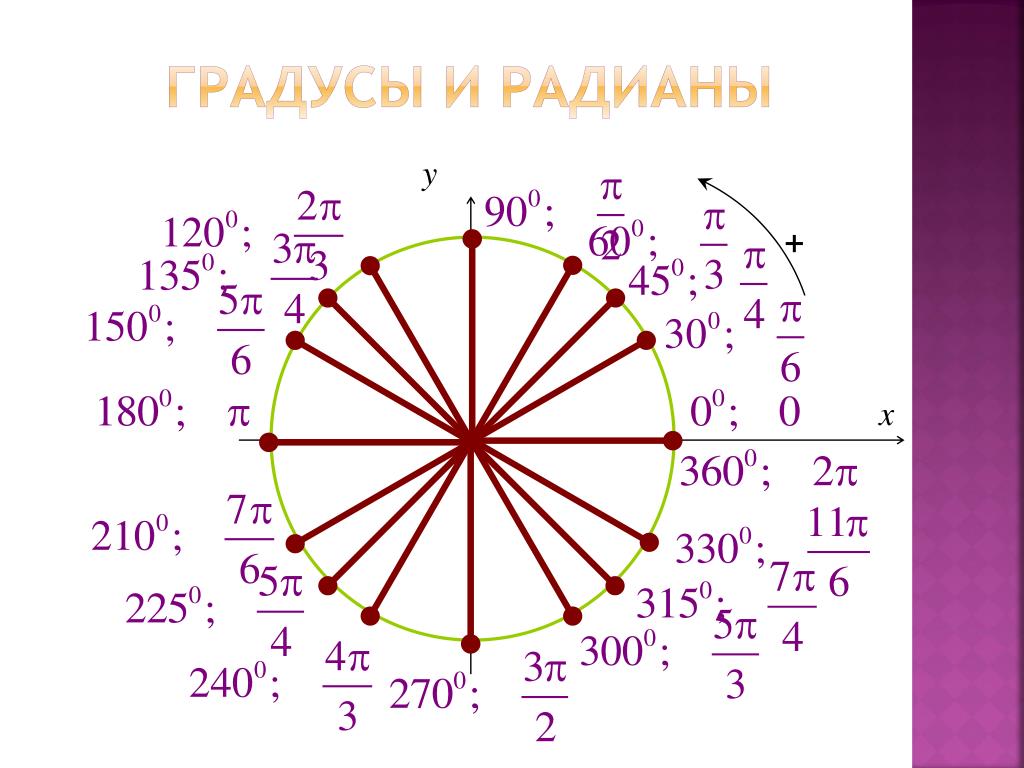
Эти башни находятся в Куала-Лумпуре в Малайзии и в их проектировании участвовал премьер-министр страны.
Острые углы часто используют в архитектуре как декоративные элементы. Они придают зданию строгую элегантность. Тупые углы, наоборот, придают зданиям уютный вид. Так, например, мы восхищаемся готическими соборами и замками, но они выглядят немного печально и даже устрашающе. А вот дом себе мы скорее всего выберем с крышей с тупыми углами между скатами. Углы в архитектуре также используют для укрепления разных частей здания. Архитекторы проектируют форму, размер и угол наклона в зависимости от нагрузки на стены, нуждающиеся в укреплении. Этот принцип укрепления с помощью наклона использовали еще с древних времен. Например, античные строители научились строить арки без цемента и иных связующих материалов, укладывая камни под определенным углом.
Обычно здания строят вертикально, но иногда бывают исключения. Некоторые здания специально строят с наклоном, а некоторые наклоняются из-за ошибок.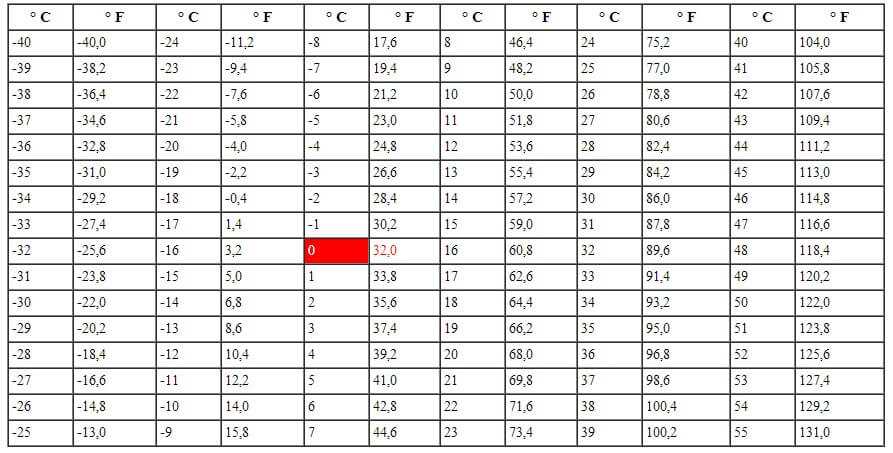
Один из примеров наклонных зданий — Тадж-Махал в Индии. Четыре минарета, которые окружают главное строение, построены с наклоном от центра, чтобы в случае землетрясения они упали не вовнутрь, на мавзолей, а в другую сторону, и не повредили основное здание. Иногда здания строят под углом к земле в декоративных целях. Например, Падающая башня Абу-Даби или Capital Gate наклонена на 18° к западу. А одно из зданий в Мире Головоломок Стюарта Лэндсборо в городе Ванка в Новой Зеландии наклоняется к земле на 53°. Это здание так и называется, «Падающая башня».
Иногда наклон здания — результат ошибки в проектировании, как например наклон Пизанской башни. Строители не учли структуру и качество почвы, на которой ее возводили. Башня должна была стоять прямо, но плохой фундамент не смог поддерживать ее вес и здание осело, покосившись на один бок. Башню много раз реставрировали; самая последняя реставрация в 20-м веке остановила ее постепенное оседание и увеличивающийся наклон. Ее удалось выровнять с 5.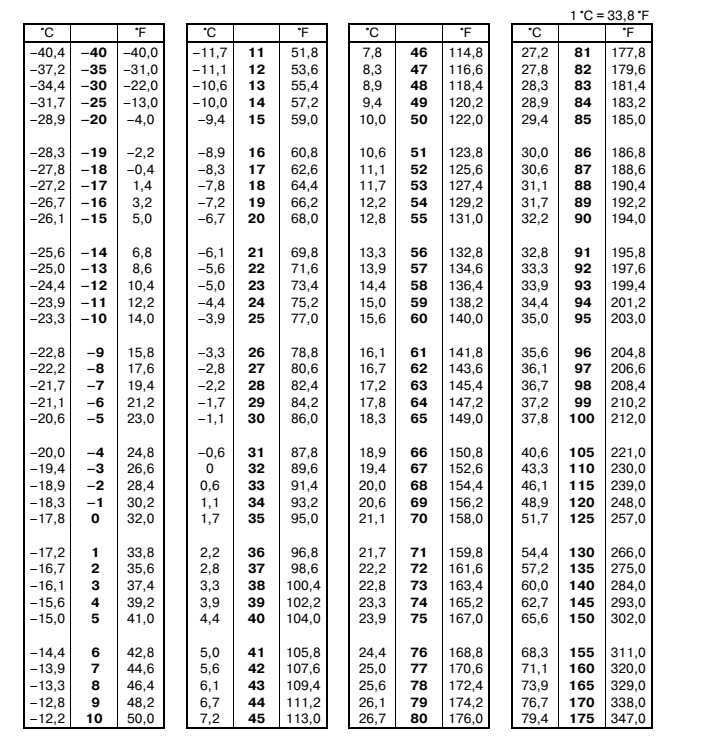
5°до 4°. Башня церкви СуурХусен в Германии тоже наклонена из-за того, что ее деревянный фундамент прогнил с одной стороны после осушения болотистой почвы, на которой она построена. На данный момент эта башня наклонена больше, чем Пизанская — примерно на 5°.
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Калькулятор онлайн выполняет перевод градусов в радианы , перевевод радиан в градусы , перевод дробных градусов (градусы представленные десятичной дробью) в вид градусов, минут и секунд и выводит формулы с подробным решением.
Перевести градусы в радианы : градусы необходимо умножить на π/180. Если градусы заданы в виде «градусов, минут и секунд», то вначале их необходимо перевести в десятичную форму по формуле: градусы + минуты/60 + секунды/3600;
Формула перевода радиан в градусы : если угол равен α rad радиан, то он равен формула перевода радиан в градусы градусов, где π ≈ 3,1415.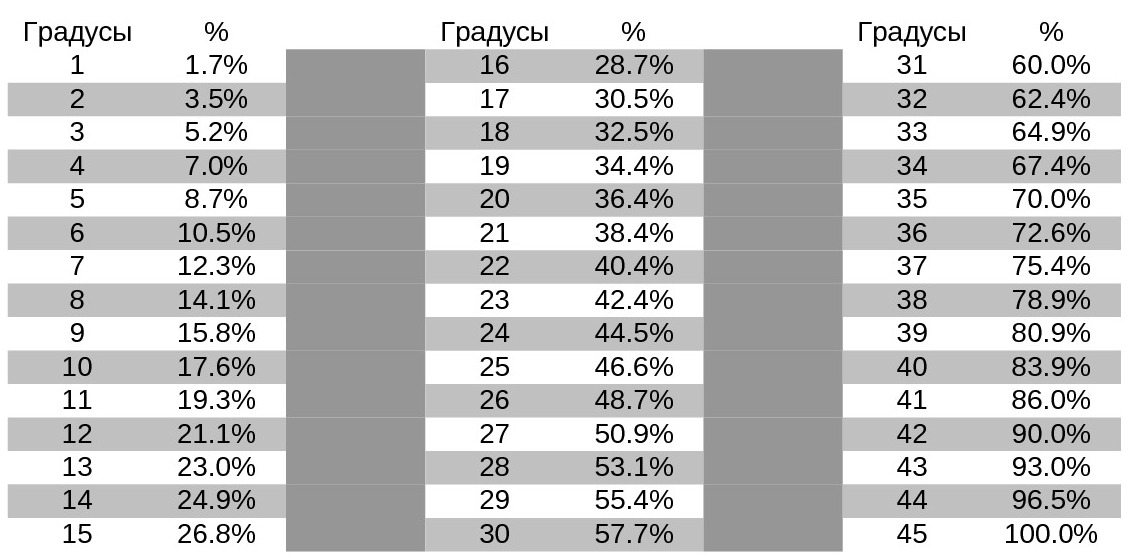
Перевести радианы в градусы : радианы необходимо умножить на 180/π. Целая часть полученного произведения — это количество градусов. Чтобы перевести дробную часть в минуты, необходимо ее умножить на 60. Целая часть полученного произведения — количество минут. Для вычисления секунд необходимо снова умножить дробную часть от предыдущей операции на 60, округлить полученное произведение до ближайшего целого — это количество секунд.
Формула перевода градусов в радианы : если угол равен α deg радиан, то он равен формула перевода градусы в радианы радиан, где π ≈ 3,1415.
| Дано: | Решение: | |
Перевод градусов, минут и секунд в радианы | ||
| α° deg = градусов | перевод градусов в радианы | |
| α» deg = минут | ||
| α» deg = секунд | ||
Перевод радиан в градусы, минуты и секунды | ||
| α rad = радиан | перевод радиан в градусы, минуты и секунды | |
Перевод десятичных градусов в вид градусов, минут и секунд | ||
| α deg = градусов | выделение из десятичных градусов градусов, минут и секунд перевод десятичных градусов в вид градусов, минут и секунд | |
| округление до 1 2 3 4 5 знаков после запятой | ||
Помощь на развитие проекта сайт
Уважаемый Посетитель сайта.
Если Вам не удалось найти, то что Вы искали — обязательно напишите об этом в комментариях, чего не хватает сейчас сайту. Это поможет нам понять в каком направлении необходимо дальше двигаться, а другие посетители смогут в скором времени получить необходимый материал.
Если же сайт оказался Ваме полезен — подари проекту сайт всего 2 ₽ и мы будем знать, что движемся в правильном направлении.
Спасибо, что не прошели мимо!
I. Примечание:
- Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолчанию — округление до десятитысячных).
II. Для справки:
- Градусна мера угла — угловая мера, в которой за единицу принимается угол в 1 градус и показывающая сколько раз градус и его части (минута и секунда) укладывается в данном угле.
- Радианная мера угла — угловая мера, в которой за единицу принимается угол в 1 радиан и показывающая сколько раз радиан укладывается в данном угле.
- Градусы и радианы — единицы измерения плоских углов в геометрии.
- Один градус равен 1/180 части развернутого угла.
- Радиан — угол, соответствующий дуге, длина которой равна ее радиусу.
Номограмма для перевода радиан в градусы и градусов в радианы.
Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.
Yandex.RTB R-A-339285-1
Связь между градусами и радианами
Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности.
Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.
Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.
Связь градусов с радианами
Связь между радианами и градусами выражается формулой
π радиан = 180 °
Формулы перевода радианов в градусы и наоборот
Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.
Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
1 р а д = 180 π ° — градусная мера угла в 1 радиан равна 180 π .
Также можно выразить один градус в радианах.
1 ° = π 180 р а д
Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °
Значит, в одном радиане примерно 57 градусов
1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д
Один градус содержит 0,0175 радиана.
Формула перевода радианов в градусы
x р а д = х · 180 π °
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Рассмотрим пример.
Пример 1. Перевод из радианов в градусы
Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.
Как переводить радианы в градусы
Перевод градусов в радианы, радианов в градусы
Основные единицы измерения плоских углов — градус и радиан.
Онлайн калькулятор позволяет перевести градусы в радианы и радианы в градусы.
Формула перевода радианов в градусы:
xрад = xрад ⋅ 180° π градусов
Т.е. чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Формула перевода из градусов в радианы:
Т.е. чтобы перевести угол из градусов в радианы, нужно значение угла в градусах умножить на пи и разделить на 180.
Онлайн калькуляторы
Calculatorium.ru — это бесплатные онлайн калькуляторы для самых разнообразных целей: математические калькуляторы, калькуляторы даты и времени, здоровья, финансов. Инструменты для работы с текстом. Конвертеры. Удобное решение различных задач — в учебе, работе, быту.
Актуальная информация
Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день. Информация из официальных источников, постоянное обновление.
Что такое один градус? Что такое один радиан? Перевод радианов в градусы и обратно.
В прошлый раз мы с вами ответили на первый вопрос, касаемый работы с углами. А именно — как отсчитываются углы. Рассмотрели положительные и отрицательные углы, а также углы, большие 360 градусов.
И на круге углы порисовали.)
В этом же уроке настал черёд ответить на второй вопрос, связанный с измерением углов. Здесь мы разберёмся с загадочными радианами и особенно — с пресловутым числом «пи», которое будет мозолить нам глаза на протяжении всего дальнейшего изучения тригонометрии. Поймём, что это за число, откуда оно берётся и как с ним работать. И задания порешаем, само собой. Стандартные и не очень…)
Разберёмся? Ну сколько же можно бояться числа «пи», в конце-то концов!)
Итак, в чём же измеряются углы в математике? Начнём с привычного и знакомого. С градусов.
Что такое один градус? Градусная мера угла.
К градусам вы уже попривыкли. Геометрию изучаете, да и в жизни постоянно сталкиваетесь. Например, «повернул на 90 градусов».) Короче, градус — штука простая и понятная.
Вы и вправду так думаете? Тогда сможете сказать мне, что такое градус? Нет, гуглить и потрошить Википедию не надо.
Ну как, слабо с ходу? Вот так-то…
Начнём издалека. С древнейших времён. А именно — с двух очагов древних цивилизаций Вавилона и Египта.)
Градус — это 1/360 часть окружности. И всё!
Придумали градусы в Древнем Вавилоне.) Как? Очень просто! Просто взяли да разбили окружность на 360 равных кусочков. Почему именно на 360? А не на 100 или на 1000? Вроде бы, число 100 поровнее, чем 360… Вопрос хороший.
Основная версия — астрономическая. Ведь число 360 очень близко к числу дней в году! А для наблюдений за Солнцем, Луной и звёздами это было оч-чень удобно.)
Кроме того, в астрономии (а также строительстве, землемерии и прочих смежных областях) очень удобно делить окружность на равные части. А теперь давайте прикинем чисто математически, на какие числа делится нацело 100 и на какие — 360? И в каком из вариантов этих делителей нацело больше? А людям такое деление очень удобно, да…)
Что такое число «пи»? Как оно возникло?
А теперь переместимся из Древнего Вавилона в Древний Египет.
Примерно в то же самое время там разгадывали другую загадку. Не менее интересную, чем вопрос, на сколько частей бить окружность. А именно — во сколько раз длина окружности больше её диаметра? Или по-другому: чему равна длина окружности с диаметром, равным единице?
И так измеряли и сяк… Каждый раз получалось чуть-чуть больше трёх. Но как-то коряво получалось, неровно…
Но они, египтяне, ни в чём не виноваты. После них математики всех мастей продолжали мучиться аж до 18 века! Пока в 1767 году окончательно не доказали, что, как бы мелко ни нарезать окружность на равные кусочки, из таких кусочков сложить точно длину диаметра нельзя. Принципиально нельзя. Только лишь примерно.
Нет, конечно же, во сколько раз длина окружности больше её диаметра установили давным-давно. Но, опять же, примерно… В 3,141592653… раза.
Это число — и есть число «пи» собственной персоной.) Да уж… Корявое так корявое… После запятой — бесконечное число цифр безо всякого порядка, безо всякой логики.
В математике такие числа называются иррациональными. И на сегодняшний день доказательство факта иррациональности числа «пи» занимает аж десять (!) лекций на 4-м курсе мехмата МГУ… Этот факт, кстати, и означает, что из одинаковых кусочков окружности её диаметр точно не сложить. Никак. И никогда…
Конечно, рациональные приближения числа «пи» известны людям ещё со времён Архимеда. Например:
22/7 = 3,14285714…
377/120 = 3,14166667…
355/113 = 3,14159292…
Сейчас, в век суперкомпьютеров, погоня за десятичными знаками числа «пи» не стихает, и на сегодняшний день человечеству известно уже два квадриллиона (!) знаков этого числа…
Но нам для практического применения такая сверхточность совершенно не требуется. Чаще всего достаточно запомнить всего лишь две цифры после запятой.
Вот и всё. Раз уж нам ясно, что длина окружности больше её диаметра в «пи» раз, то можно записать (и запомнить) точную формулу для длины окружности:
Здесь L — длина окружности, а d — её диаметр.
В геометрии всяко пригодится.)
Для общего развития скажу, что число «пи» сидит не только в геометрии или тригонометрии. Оно возникает в самых различных разделах высшей математики. В интегралах, например. Или в теории вероятностей. Или в теории комплексных чисел, а также рядов. Само по себе возникает, хотим мы того или нет… Поступите в ВУЗ — убедитесь лично.)
Ну а теперь снова вернёмся к старым добрым градусам. Как мы помним, один градус — это 1/360 часть окружности. С исторической и практической точек зрения людям такое деление на 360 равных частей оказалось очень даже удобно, но…
Как выяснилось гораздо позже Древнего Вавилона, градусы удобны далеко не всем. Например, высшей математике они ой как неудобны! Высшая математика — дама серьёзная. По законам природы устроена. И она справедливо заявляет: «Сегодня вы на 360 частей круг разбили, завтра — на 100 разобьёте, послезавтра — на 250… А мне что делать? Каждый раз под ваши хотелки подстраиваться?»
Против природы не попрёшь… Пришлось прислушаться и уступить.
И ввести новую меру угла, не зависящую от наших хотелок. )
Итак, знакомьтесь — радиан!
Что такое один радиан? Радианная мера угла.
В основе определения радиана — та же самая окружность. Угол в 1 радиан — это угол, который отсекает от окружности дугу, длина которой (L) равна радиусу окружности (R). И всё!
Причём величина угла в один радиан не зависит от радиуса окружности! Никак. Можно нарисовать очень большую окружность, можно очень маленькую. Но угол, отсекающий от окружности дугу, равную радиусу, никогда не изменит своей величины и будет составлять ровно один радиан. Всегда. Это важно.)
Запоминаем:
Угол в один радиан — это угол, вырезающий из окружности дугу, равную радиусу окружности. Величина угла в 1 радиан не зависит от радиуса окружности.
Кстати говоря, градусная мера угла тоже не зависит от радиуса окружности. Большая окружность, маленькая — углу в один градус без разницы.
Но градус — это величина, искусственно придуманная людьми для их личного удобства! Древними вавилонянами, если мы помним.) 1/360 часть окружности. Так уж сложилось чисто исторически. А если бы по каким-то причинам договорились на 100 частей разбить окружность? Или на 200? Кто знает, что тогда называлось бы градусом сегодня… Вот на сколько частей разобьём окружность, такой «градус» и получим. А вот радиан — штука универсальная!) К способу разбиения окружности никак не привязан. Строго дуга, равная радиусу! И чем больше радиус, тем больше (по длине) будет и соответствующая вырезаемая дуга. И наоборот. Но сама величина угла в один радиан не меняется. И разбиение окружности (любой!) радианами — всегда одинаковое. И сейчас мы в этом лично убедимся.)
Как переводить радианы в градусы и обратно?
К этому моменту вам уже должно быть интуитивно понятно, что один радиан существенно больше одного градуса. Всё-таки непонятно? Тогда смотрим снова на картинку:
Будем считать, что малюсенький красный угол имеет величину примерно один градус.
Совсем крохотный уголок, почти и нет его… А большой зелёный угол — примерно один радиан! Чувствуете разницу?) Конечно же, один радиан сильно больше одного градуса…
А вот теперь начинается самое интересное! Вопрос: а во сколько раз один радиан больше одного градуса? Или сколько градусов в одном радиане? Сейчас выясним!)
Смотрим на очередные картинки:
На картинке слева изображён полукруг. Обычный развёрнутый угол величиной 180°. А вот на картинке справа — тот же самый полукруг, но нарезанный радианами! Видно, что в 180° помещается примерно три с хвостиком радиана.
Вопрос на засыпку: как вы думаете, чему равен этот хвостик?)
Да! Он равен 0,141592653… Привет, число «пи», вот мы про тебя и вспомнили!)
Стало быть, в 180° укладывается 3,141592653… радиан. Понятное дело, что каждый раз писать такое длинное число неудобно, поэтому пишут приближённо:
Вот и всё. Вот и весь секрет тотального присутствия числа «пи» в тригонометрии.
Эту простую формулку надо знать железно. Уловили?)
Так сколько же градусов в одном радиане? Не вопрос! Если в «пи» радианах содержится 180 градусов, то сколько же тогда градусов сидит в одном радиане? Правильно, в «пи» раз меньше! То есть меньше примерно в 3,14 раза.
Вот и делим обе части нашего соотношения на «пи» и получаем один радиан в градусах:
Это приближённое равенство также очень полезно запомнить. В одном радиане примерно 60 градусов. Такой грубой оценки бывает вполне достаточно для ответа на очень многие каверзные вопросы, связанные с углами. Бывает и недостаточно, конечно. В своё время мы такие хитрые задачки рассмотрим.)
Но это не самое главное применение этой формулы!) А самое главное — перевод радианов в градусы и обратно.
Переводим радианы в градусы!
Чаще всего углы в тригонометрии заданы в радианах с числом «пи».
Это — самая стандартная ситуация. Если угол задан в радианах с числом «пи», то всё очень просто. Мы знаем, что «пи» радиан — это 180 градусов. Вот и подставляем вместо «пи» радиан — число 180. Сокращаем всё что сокращается и получаем угол в градусах.
Или более мудрёный угол:
Переводим градусы в радианы!
Обратный перевод градусов в радианы чуть сложнее, но ненамного. Если угол задан в градусах, то сначала нам надо узнать, сколько составляет один градус в радианах. И умножить это значение на количество градусов.) И чему же равен 1° в радианах?
Снова смотрим на нашу формулу и соображаем. Если 180° — это «пи» радиан, то 1° в 180 раз меньше. Вот и делим обе части формулы на 180! Получаем, что 1° в радианах равен:
Вот и все дела. Умножаем дробь π /180 на количество градусов, сокращаем что сокращается и получаем угол в радианах. Например:
Вот и всё. Заменять «пи» на примерно 3,14 никакой необходимости нет: его всегда буквой пишут.
Что правда, то правда: нас же в заданиях обычно точный ответ интересует! А не приближённый.) Кстати, кому интересен приближённый ответ, посчитайте на калькуляторе. Получите примерно 0,628 и 2,356 радиана соответственно.
Итак, в непринуждённой беседе с лирическими отступлениями мы узнали, что радианы — это очень даже просто, не больно и не страшно.) Да и перевод туда-обратно несложен. И «пи» — не кусается… Так откуда же проблемы?
Что ж, вскрою тайну. Всё дело в том, что в тригонометрии значок градусов — пишется. Всегда и везде. Например, cos30° — это косинус 30 градусов! А вот значок радианов («рад») — не пишется! Он — подразумевается. В чём причина — неизвестно. Может, обленились математики, может ещё что… Но договорились не писать. Например, sin5 — это синус пяти радианов!
Это и приводит к казусам. Человек смотрит на пример, видит «пи» и автоматически считает, что это 180°. Везде и всюду.
Кстати, это срабатывает. До поры до времени, пока примеры — типовые. Но любое отклонение примера от шаблона — тут же валит наповал! Почему?
Потому, что само по себе «пи» — это число! А никакие не градусы! Это «пи» радиан = 180°!
Ещё раз запоминаем:
Просто «пи» — это число! «Пи» РАДИАН — это 180°!
Это заклинание надо понимать железно. Причём не просто механически зазубрить, а именно понимать каждое слово и каждый значок! И особенно — слово «радиан». Я не шучу. Ибо, если на вопрос, «Что такое «пи» в тригонометрии?», вы, блистая знаниями, радостно заявляете:
«Пи — это 180 градусов. « ,
то это говорит о том, что вы не понимаете до конца смысла этой зелёной фразы. И все дальнейшие беседы уже бессмысленны, да…
Ещё раз: «пи» — это число! Примерно равное 3,14. Точного значения этого числа не знает никто: оно бесконечно длинное, корявое, иррациональное.
Но — число! Такое же, как 2 или 7. Можно пройти примерно «пи» километров. Три километра и ещё около 140 метров. Можно купить «пи» килограммов картошки. Если продавец образованный встретится.) Можно выпить «пи» литров кока-колы. Если здоровье не жалко… И так далее…
Всё равно непонятна зелёная запись? Хорошо, вот вам простые житейские фразы:
1 километр — это 1000 метров;
3 часа — это 180 минут;
2 года — это 730 дней;
И тому подобное. Точно так же и с градусами/радианами:
«Пи» радиан — это 180 градусов!
Уяснили, что «пи» — это просто число? Или я уже достал вас этой заезженной фразой? Ну ладно, убедили. Тогда вот вам парочка нестандартных вопросов:
Если у вас случился ступор, не беда. Вспоминаем нашу мантру: «Пи» — это число! В первом синусе нам чётко сказано, что угол — в градусах! Следовательно, машинально заменять «пи» на 180° — нельзя.
«Пи» градусов — это примерно 3,14°. Вот и пишем:
Во втором синусе никаких значков нет. Значит, там — радианы. И вот тут замена «пи» на 180° — вполне законна.) Переводим радианы в градусы и получаем:
А теперь сравниваем эти два синуса. Как? По кругу, разумеется! Рисовать углы мы с вами уже умеем, что такое синус угла на круге — тоже знаем. Вперёд! Рисуем круг, углы примерно 0,79 ° и 45° и смотрим какие синусы у этих углов. Даже на самом корявом круге будет видно, что sin45° гораздо больше, чем sin0,79°.
С косинусами — всё то же самое. Рисуем на круге в правильных четвертях углы примерно 5 градусов и 5 радианов (помним, чему примерно равен один радиан в градусах?). Круг нам всё и подскажет. А именно, что cos5 меньше, чем cos5°.
Вообще, задачки с углами в радианах без «пи» (типа определить знак выражения sin10∙cos20) относятся к разряду нестандартных.
В следующем уроке разберём парочку таких.)
Ну что, потренируемся с переводом углов?) Решаем несложные задания.
1. Переведите следующие углы из градусной меры в радианную:
Ответы (по возрастанию):
Как вы думаете, что это были за углы? Да! Это углы, которые попадают на координатные оси! Эти опорные значения надо держать в голове надёжно. До автоматизма! Как в градусах, так и в радианах. Зачем? Да всё за тем же! Для правильного распределения любых углов по четвертям.) Это полезное умение — залог успеха в любом задании по тригонометрии. Любом! От примитивных примеров до вполне себе солидных ЕГЭшных задачек части 2 (уравнения с отбором корней, тригонометрические неравенства и прочие хитрые штучки).
2. Переведите углы в радианную меру:
Ответы (в беспорядке):
Получилось? Рад за вас. Почему я выделил именно эти три угла? По той же самой причине. Эти углы — особые личности в тригонометрии. Потому что именно про эти углы вы обязаны знать всё! И где они находятся и весь комплект их тригонометрических функций.
Скажем, значение sin20° вы знать не обязаны. А вот sin30° — уж будьте так добры! Это обязательные значения, без которых во всей остальной тригонометрии делать вообще нечего. Но об этом — в отдельном уроке.)
Переведите следующие углы из радианной меры в градусную:
Ответы (в беспорядке):
300°; 225°; 120°; 330°; 240°; 135°; 210°; 315°; 150°.
А это что за углы? Правильно! Это углы, в пределах одного оборота, кратные предыдущим трём! Но не попадающие на оси координат. Такие углы вы также обязаны уметь просчитывать! И более того, все углы, кратные 30, 45 или 60 градусам, вы обязаны уметь просчитывать! Как в пределах одного оборота, так и за его пределами. Как положительные, так и отрицательные… В соответствующем уроке мы научимся с вами проделывать такие полезные вещи.
Если и это получилось, то тогда можно считать, что перевод радианов в градусы и обратно — уже не ваша проблема. Но перевод углов из одной размерности в другую — это лишь ещё один шаг вперёд к успешному постижению тригонометрии.
Шаг мощный, но недостаточный. Ведь, чаще всего, с углами надо потом ещё и что-то делать.) Рисовать на круге, например. Или синус/косинус считать. Да и тангенс/котангенс тоже…
Второй серьёзный шаг — это умение правильно определять положение любого угла на тригонометрическом круге. Любого! Как в градусах, так и в радианах. С градусами на круге мы уже плотно поработали в предыдущем уроке. Теперь настал черёд набивать руку в работе с радианами.
Как перевести радиан в градусы?
В единицах измерения под названием «Радиан» измеряются плоские углы в математике и физике.
Для перевода радиан в градусы, необходимо воспользоваться следующей формулой:
Например, у нас есть значение угла А = 3 (это в радианах). Для того, чтобы успешно перевести эту величину в обычные градусы, надо помножить величину радиана на 180 градусов и поделить на число Пи. В данном примере это значит 3*180/3.14 = 171. То есть, 3 радиана — это 171 градусов.
Можно перевести радианы в градусы и наоборот онлайн на этой странице.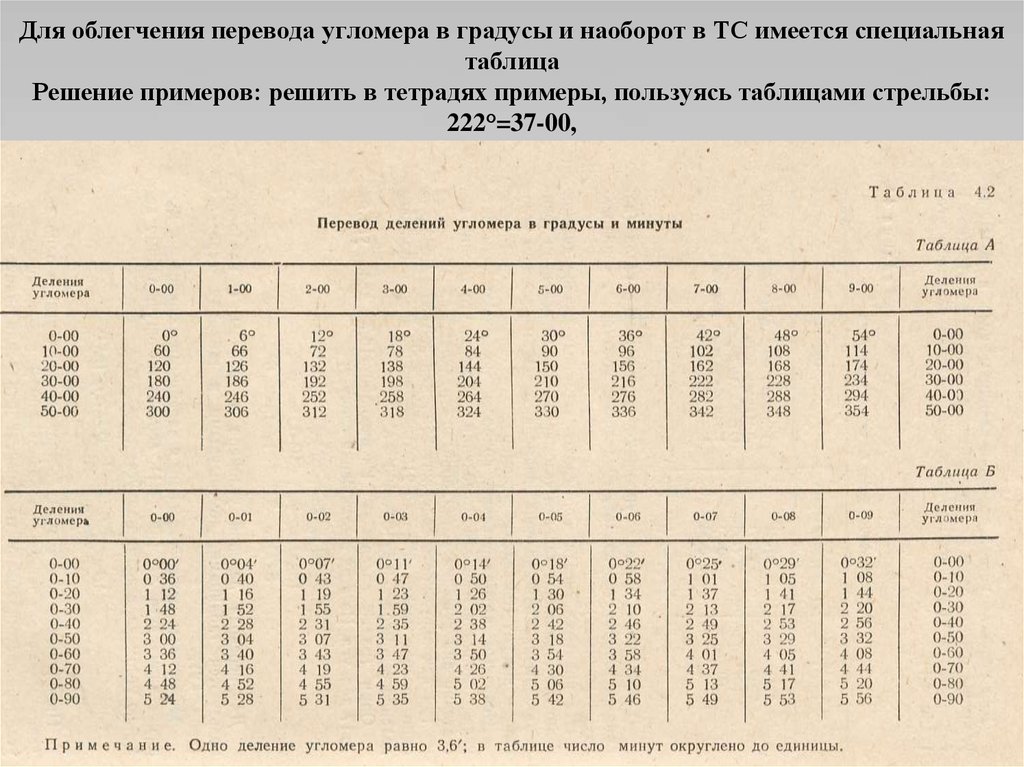
Преобразование температуры: градусы Цельсия в градусы Фаренгейта | от F до C или от C до F
Основное изображение
Подпись
Узнайте, как легко преобразовать градусы Цельсия в градусы Фаренгейта и наоборот.
Преобразуйте F в C или C в F — и выучите формулы!
F в C: Калькулятор преобразования Фаренгейта в Цельсий
| Фаренгейт | по Цельсию |
|---|---|
| °F | °С |
Введите значение для Фаренгейта или Цельсия для конвертации в другое значение.
09 июня 2022 г.
Тело
Хотите изменить градусов по Фаренгейту на градусов по Цельсию или градусов по Фаренгейту на градусов по Фаренгейту? Воспользуйтесь нашим простым конвертером температуры Цельсия в градусы Фаренгейта, нашими таблицами преобразования температуры или рассчитайте C в F или F в C самостоятельно, используя формулы преобразования .
О градусах Фаренгейта и Цельсия
Температурная шкала градусов по Фаренгейту названа в честь немецкого физика Даниэля Габриэля по Фаренгейту и представляет измерение температуры, обычно используемое в Соединенных Штатах (и связанных с ними территориях) и несколькими странами Карибского бассейна. По шкале Фаренгейта вода замерзает при 32°F и кипит при 212°F (на уровне моря).
Температурная шкала по Цельсию — первоначально называвшаяся по Цельсию и позже переименованная в честь шведского астронома Андерса Цельсия – используется почти во всем мире. По шкале Цельсия вода замерзает при 0°C и кипит при 100°C (на уровне моря).
F° в C°: Формула преобразования Фаренгейта в Цельсия
Чтобы преобразовать температуру в градусах Фаренгейта в Цельсия, вычтите 32 и умножьте на 0,5556 (или 5/9).
- Пример: (50°F — 32) x 0,5556 = 10°C
«>Фаренгейтов в Цельсий Таблица преобразования
по Фаренгейту
по Цельсию
C° в F°: формула преобразования градусов Цельсия в градусы Фаренгейта ) + 32 = 86°F
«>градусов Цельсия в градусы Фаренгейта. Таблица преобразования
по Цельсию
9 градусов по Фаренгейту0003
Другие преобразования
- Еще одно интересное преобразование температуры – преобразование крикета крикета в градусы по Фаренгейту. Знаете ли вы, что сверчки могут сказать вам, насколько тепло на улице? Узнайте, как определить температуру по крику сверчков здесь!
- Ищете кулинарные преобразования? На этой странице есть все, что вам нужно знать о простых заменах и преобразованиях на кухне.
- Хотите преобразовать измерение в метрическое (или обратно)? Ознакомьтесь с нашей удобной таблицей преобразования метрической системы.
Знаете ли вы, что сверчки могут сказать вам, насколько тепло на улице? Узнайте, как определить температуру по крику сверчков здесь!Погода
Информация о погоде
Температура
РЕКЛАМА
Еще подобное
Прогноз температуры с помощью Cricket Chirps
Таблица измерений и преобразований
Таблица Windchill для США
Факты о сверчках и содержание домашних сверчков
Советы на открытом воздухе: рыбалка, кемпинг, наблюдение за небом
Таблица возраста собаки: годы собаки к человеческим годам
Получить ежедневное обновление Альманаха
Адрес электронной почты
РЕКЛАМА
Комментарии
РЕКЛАМНОЕ ОБЪЯВЛЕНИЕ
@Recommendation.
Title
Купить сейчас
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус (-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | Найти точное значение 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 пи)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценка | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | коричневый((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценка | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт. )/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | грех((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
градусов в радианы – преобразование и примеры решения
Градусы и радианы — две разные единицы, которые используются для измерения углов.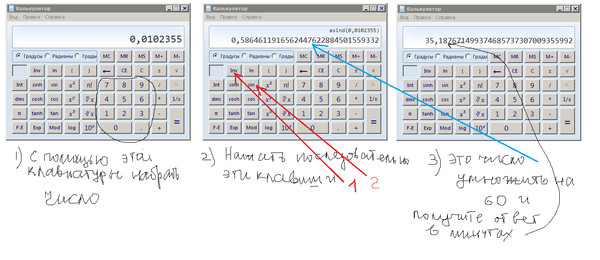
Преобразование градусов в радианы учитывается при измерении углов в геометрии. Меру угла обычно обозначают градусами, имеющими символ °. Угол можно определить двумя разными единицами измерения: градусами и радианами. Вы можете преобразовать одну форму представления любого математического угла в другую, используя простые формулы. Градус также имеет свои составные части, которые представляют собой минуты и секунды. Это преобразование играет важную роль в приложениях тригонометрии. В этой статье мы узнаем, как преобразовать градусы в радианы, градусы в формулу радианов и рассмотрим некоторые решенные примеры, основанные на том, как преобразовать градусы в формулу радианов. Давайте сначала посмотрим на преобразование градусов в радианы.
Преобразование градусов в радианы
Значение 180° равно \[\pi\] радианам. Для преобразования любого заданного угла из его градусов в радианы необходимо умножить значение на \[\frac{\pi}{180}\].
Значение \[\pi\] равно \[\frac{22}{7}\] или 3,14.
Градусы в радианы Формула
Мы уже узнали, как преобразовать градусы в радианы для любого заданного угла. Давайте узнаем, как преобразовать формулу градусов в радианы. Формула для перевода градуса в радиан выглядит следующим образом:
Градус \[\times \frac{\pi}{180}\] = радианы
Как преобразовать градусы в радианы
Теперь рассмотрим пошаговую процедуру преобразования градусов в радианы.
1. Запишите градусы, которые вы хотите преобразовать в радианы. Рассмотрим следующие примеры:
Пример 1: 120°
Пример 2: 30°
Пример 3: 225°
2. Затем умножьте градусы на \[\frac{\pi}{180}\].
Пример 1: \[120 \times \frac{\pi}{180}\]
Пример 2: \[30 \times \frac{\pi}{180}\]
Пример 3: \[225 \times \frac{\pi}{180}\]
3. Затем просто выполните умножение путем умножения градусов на π/180.
Представьте, что вы умножаете две дроби. Первая дробь состоит из степеней в числителе и 1 в знаменателе, а вторая дробь состоит из π в числителе и имеет 180 в знаменателе.
Пример 1:
\[120 \times \frac{\pi}{180}\]
= \[\frac{120\pi}{180}\]
Пример 2:
\[30 \times \frac{\pi}{180}\]
=\[\frac{30\pi }{180}\]
Пример 3:
\[225 \times \frac{\pi}{180}\]
= \[\frac{225\pi}{180}\]
4. Последний шаг — упростить. Теперь вам нужно поставить каждую дробь в наименьшее значение, чтобы получить окончательный ответ. Найдите наибольшее число, которое можно без остатка разделить на числитель и знаменатель каждой дроби, и используйте его для упрощения каждой дроби.
Пример 1:
\[120 \times \frac{\pi}{180}\]
= \[\frac{120\pi}{180} ÷ \frac{60}{60} \]
= \[ \frac{2}{3 \pi} \] радиан
Пример 2:
\[30 \times \frac{\pi}{180}\]
= \[\frac{30\ pi}{180} ÷ \frac{30}{30} \]
= \[\frac{1}{6\pi}\] радиан
Пример 3:
\[225 \times \frac{\ pi}{180}\]
= \[\frac{225\pi}{180} ÷ \frac{45}{45} \]
= \[\frac{5}{4π}\] радиан
Это очень простой метод, с помощью которого можно легко преобразовать градусы в радианы.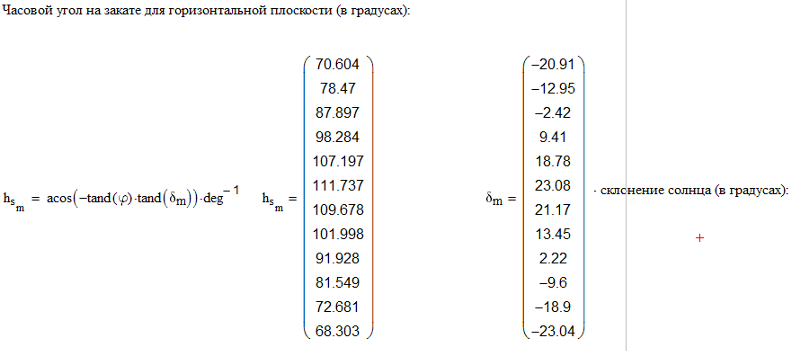
Давайте подробно рассмотрим, как преобразовать углы в радианы.
Как преобразовать углы в радианы
Вы узнали, как преобразовать градусы в радианы. Теперь давайте узнаем, как преобразовать угол в радианы.
Угол, который образуется при обертывании радиуса вокруг окружности, определяется следующим образом:
1 радиан приблизительно равен 57,2958°.
9{0}}{\pi} \] = 57,2958°Если вы хотите преобразовать градус или угол в радианы, просто умножьте угол на , а затем разделите его на 180.
Взгляните на таблицу ниже углы и их перевод в радианы.
градусов | Радиан | .0022 \ [\ frac {\ pi} {6} \] | 0,524 |
45 ° | \ [\ FRAC {\ PI {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 {4 rath wry} | \ | |
60° | \[\frac{\pi}{3}\] | 1. | |
90° | \[\frac{\pi} {2}\] | 1,571 | |
180° | \[\pi\] | 3.142 | |
270° | \[\frac{3\pi}{2}\] | 4.712 | |
360 ° | \ [2 \ PI \] | 6.283 |
047 к измерению получения степени. Умножьте данное значение в градусах на \[\frac{\pi}{180}\]. Это простой шаг, и учащиеся могут использовать его, чтобы найти меру в радианах. Однако в таблице, приведенной выше, указаны радианы и приблизительные значения радианов для наиболее распространенных углов. Студенты могут использовать эту таблицу для более простых и быстрых вычислений. Например, если учащийся хочет вычислить в радианах 30°, 60° и 90°, он или она может обратиться к таблице.
Радианные меры следующих мер в градусах будут \[\frac{\pi}{6}\], \[\frac{\pi}{3}\] и \[\frac{\pi}{2} \] и значения в радианах будут 0,524, 1,047 и 1,571 соответственно.
Использование радиана
Радиан — еще одна единица измерения углов, а также единица измерения углов в системе СИ. Он определяется как угол, образованный в центре окружности дугой, длина которой равна радиусу окружности.
Обозначается «рад» или буквой с. Угол, написанный без единицы измерения, означает, что он записан в радианах. Некоторые примеры: 4 рад, \[\frac{\pi}{2}\] или 90°
В исчислении и других областях математики в качестве единицы измерения используются радианы. Он также используется в областях науки.
Решенные примеры
Давайте теперь посмотрим на некоторые решенные примеры, чтобы вы лучше поняли, как преобразовывать градусы в радианы и радианы в градусы.