Обратная матрица в Excel — TutorExcel.Ru
Обратная матрица в Excel
Подробно рассмотрим особенности вычисления обратной матрицы в Excel и примеры использования функции МОБР.
В первую очередь освежим в памяти, что обратная матрица — это матрица (записывается как A-1), при умножении которой на исходную матрицу (A) дает единичную матрицу (E), другими словами выполняется формула:
Из определения следует важное свойство, что обратная матрица определена только для квадратных (т.е. число строк и столбцов совпадает) и невырожденных матриц (т.е. определитель отличен от нуля).
Как найти обратную матрицу в Excel?
В отличие от транспонированной матрицы, вычислить обратную матрицу технически несколько сложнее.
Посчитать обратную матрицу можно через построение матриц алгебраических дополнений и определителя исходной матрицы.
Однако сложность вычисления по данному алгоритму имеет квадратичную зависимость от порядка матрицы.
К примеру, для обращения квадратной матрицы 3-го порядка нам необходимо будет дополнительно сделать 9 матриц алгебраических дополнений, транспонировать итоговую созданную матрицу и поэлементно разделить на определитель начальной матрицы, что затрудняет возможность подобного расчета в Excel.
Поэтому воспользуемся стандартной функцией МОБР, которая позволит найти обратную матрицу:
Функция МОБР
Синтаксис и описание функции МОБР в Excel:
МОБР(массив)
Возвращает обратную матрицу (матрица хранится в массиве).
- Массив (обязательный аргумент)
Рассмотрим расчет обратной матрицы посредством функции МОБР на конкретном примере.
Предположим у нас имеется следующая квадратная матрица 3-го порядка:
Выделяем диапазон пустых ячеек E2:G4, куда мы в дальнейшем поместим обратную матрицу.
Не снимая выделения ячеек вводим формулу =МОБР(A2:C4) и нажимаем комбинацию клавиш Ctrl + Shift + Ввод для расчета формулы массива по данному диапазону:
При работе с функцией МОБР могут возникнуть следующие ошибки:
- В том случае, когда исходная матрица является вырожденной (определитель равен нулю), то функция вернет ошибку #ЧИСЛО!;
- Если число строк и столбцов в матрице не совпадает, то функция возвратит ошибку #ЗНАЧ!;
- Функция также вернет ошибку #ЗНАЧ!, если хотя бы один из элементов матрицы является пустым или записан в текстовом виде.
Удачи вам и до скорой встречи на страницах блога Tutorexcel.ru!
Поделиться с друзьями:
Поиск по сайту:
Математика,Матрица,Функции
- ← Как пронумеровать страницы в Excel?
- Точка пересечения графиков в Excel →
Нахождение обратной матрицы с примерами решения
Содержание:
- Примеры с решением
Определение 8. 1. Пусть — квадратная матрица порядка . Квадратную матрицу того же порядка называют обратной к , если , где — единичная матрица порядка .
1. Пусть — квадратная матрица порядка . Квадратную матрицу того же порядка называют обратной к , если , где — единичная матрица порядка .
Обратную матрицу обозначают . Она позволяет определить целую отрицательную степень матрицы . А именно, для полагают .
Теорема 8.1. Если квадратная матрица имеет обратную матрицу, то обратная матрица единственная.
Предположим, что матрица имеет две обратные матрицы и . Тогда, согласно определению 8.1 обратной матрицы, выполнены, в частности, равенства . Используя ассоциативность умножения матриц, получаем , т.е. матрицы В и В’ совпадают.
| Квадратная матрица не всегда имеет обратную. |
Установить, имеет ли данная матрица обратную, позволяет следующий критерий.
Теорема 8.2. Для того чтобы квадратная матрица порядка имела обратную, необходимо и достаточно, чтобы .
Необходимость.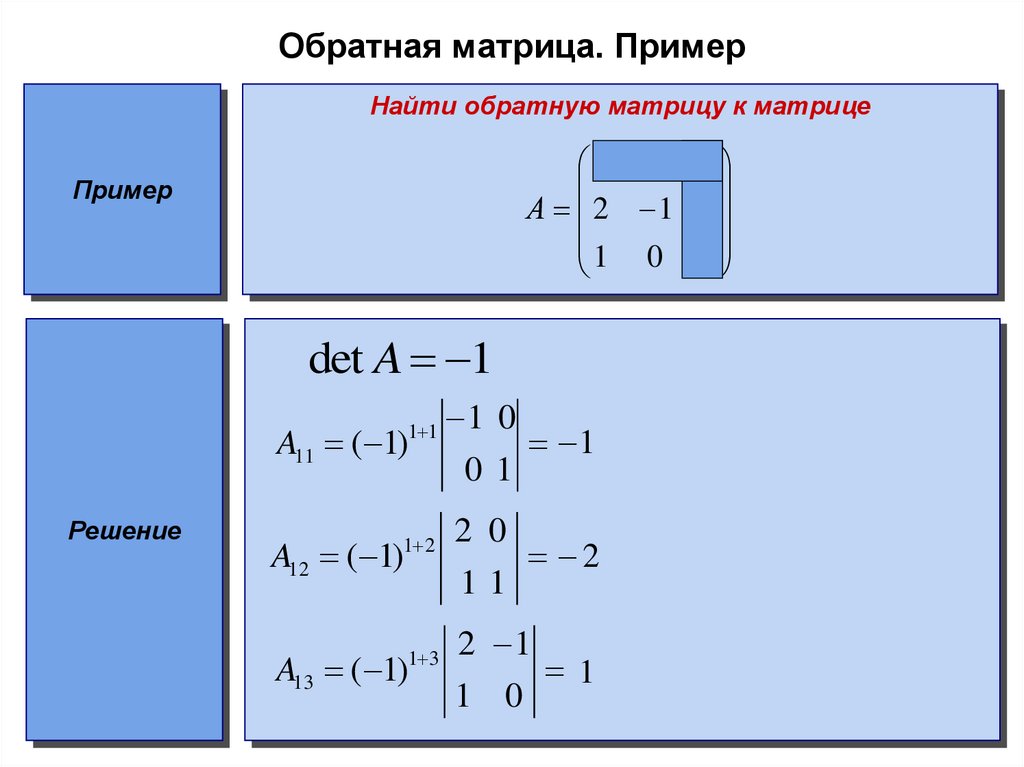 Пусть — матрица, обратная к . Тогда , но, согласно свойству 7.11 определителей, . Поэтому и, следовательно, . Достаточность. Пусть . Рассмотрим алгебраическое дополнение матрицы , соответствующее элементу ( — минор этого же элемента).
Пусть — матрица, обратная к . Тогда , но, согласно свойству 7.11 определителей, . Поэтому и, следовательно, . Достаточность. Пусть . Рассмотрим алгебраическое дополнение матрицы , соответствующее элементу ( — минор этого же элемента).
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Согласно свойству 7.7 определителей, для любого выполнены равенства (7.4) . Согласно свойству 7.9 определителей, для любых индексов выполнены равенства (7.8) . Рассмотрим теперь квадратную матрицу порядка с элементами
.
Матрица имеет элементы т.е. — это единичная матрица. Аналогично матрица имеет элементы следовательно, матрица является единичной. Согласно определению 8.1, матрица является обратной для .
Следствие 8.1. Если квадратная матрица имеет обратную, то . Действительно, .
Действительно, .
| Квадратную матрицу с ненулевым определителем называют невырожденной или неособой. |
В противном случае, когда определитель матрицы равен нулю, ее называют вырожденной. Итак, для существования обратной матрицы необходимо и достаточно, чтобы сама матрица была невырожденной.
Теорема 8.3. Если квадратные матрицы и порядка имеют обратные матрицы, то и их произведение имеет обратную матрицу, причем . В соответствии с определением 8.1 обратной матрицы достаточно доказать два равенства: . Используя ассоциативность умножения матриц (см. 6.4), получаем что и требовалось доказать.
Возможно вам будут полезны данные страницы:
Собственные значения матрицы |
Найти определитель матрицы |
Как найти ранг матрицы: пример решения |
Жорданова форма матрицы |
Теорема 8. 4. Если матрица порядка имеет обратную, то и транспонированная матрица имеет обратную, причем . Нужно убедиться, что и . Используя свойство произведения матриц относительно операции транспонирования, имеем
4. Если матрица порядка имеет обратную, то и транспонированная матрица имеет обратную, причем . Нужно убедиться, что и . Используя свойство произведения матриц относительно операции транспонирования, имеем
Вычисление обратной матрицы
Применяют два основных метода вычисления обратной матрицы. Первый вытекает из теоремы 8.2 и состоит в следующем. Пусть дана квадратная матрица порядка . Матрицу , транспонированную к матрице алгебраических дополнений, называют присоединенной. Как следует из доказательства теоремы 8.2, если — невырожденная матрица, то обратная к ней имеет вид . Таким образом, чтобы для квадратной матрицы порядка найти обратную матрицу, надо вычислить один определитель порядка и составить присоединенную матрицу, т.е. вычислить определителей порядка .
Метод присоединенной матрицы эффективен при или , но при росте становится слишком трудоемким.
Примеры с решением
Пример 8.1.
Выясним, имеет ли матрица
обратную и если имеет, то найдем ее. Поскольку , матрица является невырожденной и, согласно теореме 8.2, имеет обратную. Для ее вычисления последовательно находим
Поскольку , матрица является невырожденной и, согласно теореме 8.2, имеет обратную. Для ее вычисления последовательно находим
Отметим, что для квадратной матрицы второго порядка присоединенная матрица получается перестановкой в диагональных элементов и изменением знака двух других.
Проверка ответа выполняется в соответствии с определением 8.1 обратной матрицы:
Второй метод вычисления обратной матрицы состоит в преобразовании исходной матрицы к более простому виду с помощью элементарных преобразований строк.
Чтобы найти матрицу , обратную к , фактически надо решить матричное уравнение . Отметим, что если над матрицей выполняется какое-либо элементарное преобразование строк, то это же преобразование осуществляется и над матрицей , поскольку любое элементарное преобразование строк матрицы эквивалентно умножению ее слева на соответствующую матрицу специального вида.
Таким образом, если в уравнении над матрицами и одновременно выполнить какое-либо элементарное преобразование строк, т. е. домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное уравнение .
е. домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное уравнение .
Оба эти матричные уравнения имеют одно и то же решение, так как любое элементарное преобразование строк имеет обратное элементарное преобразование строк. Последовательность элементарных преобразований строк надо подобрать так, чтобы на -м шаге матрица превратилась в единичную матрицу. В результате этих шагов получается уравнение , где , т.е. . Итак, поскольку является решением уравнения , которое эквивалентно , то .
Чтобы синхронно выполнять преобразования над матрицами в левой и правой частях матричного уравнения , записывают блочную матрицу и выполняют такие элементарные преобразования строк этой матрицы, чтобы вместо получить единичную матрицу .
Пример 8.2.
Продемонстрируем изложенный метод нахождения обратной матрицы для матрицы из примера 8.1. Для этого записываем матрицу и выполняем элементарные преобразования ее строк в следующем порядке: Таким образом,
.
обратных матриц. На самом деле нет понятия… | Соломон Се | Основы линейной алгебры. Но аналогичным образом мы можем позволить
умножить обратное для достижения той же цели. Обратитесь к 3Blue1Brown: обратные матрицы, пространство столбцов и нулевое пространство
Обратитесь к математике весело: обратная матрица.
ВНИМАНИЕ, СПОЙЛЕР: ДАЖЕ 3×3 ОБРАТНАЯ МАТРИЦА УЖЕ СЛИШКОМ ТЯЖЕЛАЯ ДЛЯ РАСЧЕТА, ПОЭТОМУ ЛУЧШЕ ПРОСТО ЗАПОМНИТЬ 2×2 И ПОЗВОЛИТЬ КОМПЬЮТЕРУ ВЫПОЛНЯТЬ ВСЕ ВЫСШИЕ ИЗМЕРЕНИЯ.
3Blue1Brown видео идеально объяснило интуицию этого, почти все, что вам нужно знать. Ссылка: Обратные матрицы, пространство столбцов и пустое пространство
Потому что Матрица
Авсегда как«Коэффициент»к вектору или какправило преобразованияк вектору, поэтому он всегда слева от вектора (или графика).Это простое, но важное обозначение для деления матрицы.

The
Identity Matrixis the matrix equals to the number of1:It’s very much more intuitive to think a
identity matrixasone unit vector.
- 1-х измерения:
x = 1- 2-х дименсии:
V = (1, 1)- 3-х дименсии:
В = (1, 1, 1)
- это
квадрат(матрица m×m)- Он может быть большим или маленьким (2×2, 3×3, 100×100, … любым)
- Он имеет
1с по диагонали и0с повсюду else- Его символ — заглавная буква
𝗜Что еще более важно, ОН МОЖЕТ ПЕРЕКЛЮЧАТЬСЯ НА СТОРОНУ ПРИ УМНОЖЕНИИ ДРУГОЙ МАТИРКС!
Это очень особенное, и ТОЛЬКО матрица может ИГНОРИРОВАТЬ порядок при умножении другой матрицы.Два условия делают матрицу НЕобратимой:
- Матрица не является квадратной матрицей
(матрица m×m).- Определитель
равен НОЛЬ . Такая матрица также называетсяСингулярной матрицейЕе также называют
Сопряженной матрицейилиКлассическая совмещенная.Обратитесь к математике весело: обратная матрица с использованием миноров, кофакторов и Adjugate.
«Вычислить это для 2×2 довольно просто, 3×3 становится немного сложно, 4×4 займет у вас весь день, 5×5 вы почти наверняка совершите ошибку по невнимательности, если будете делать обратную матрицу». — Сал Хан
С матрицей 2×2 вам действительно не нужно много думать и тратить время на полные шаги, просто следуйте этой формуле
1/Определитель × AdjugateСм.
лекцию Хана.
Мы можем вычислить обратную матрицу следующим образом:
- Шаг 1: вычислить матрицу миноров,
- Шаг 2: затем преобразовать ее в матрицу кофакторов,
- Шаг 3: затем скорректировать и
- Шаг 4: умножьте это на 1/Определитель.
Я склонен не приводить здесь полное содержание, потому что оно бесполезно в обычной математической жизни. Потому что слишком сложно считать даже с матрицей 3×3. Так что просто поймите идею и позвольте компьютеру сделать все остальное.
Решите:
- Формула обратной матрицы:
Adjugate(A) / определитель(A).- Определитель A равен
-3*-5 - 2*6 = 3- Адъюгат A равен
[(-5, -2), (-6, -3)]- Итак, ответ:
Лекция Хана: Решение линейных систем с матричными уравнениями Обратная матрица — это та матрица, которая при умножении на исходную матрицу дает единичную матрицу.
В этой статье я объясню, как использовать обратную матрицу NumPy для вычисления обратной матрицы массива с помощью этой функции.
1. Краткие примеры обратной матрицы
Если вы спешите, ниже приведены несколько кратких примеров использования обратной матрицы Python NumPy.
# Ниже приведены краткие примеры # Пример 1: Используйте numpy.linalg.inv() для получения обратной матрицы массив = np.массив ([[7, 2,], [3, -5]]) обр2 = np.linalg.inv (обр) # Пример 2: получить обратную матрицу с помощью функции scipy.linalg.inv() arr = np.matrix([[7, 2,], [3, -5]]) arr2 = linalg.inv(arr) # Пример 3: Использование функции np.linalg.inv() arr = np.array([[[2., 6.], [5., 8.]], [[3, 7], [4, 1]]]) обр2 = np.linalg.inv (обр)2. Синтаксис функции numpy.linalg.inv()
Ниже приведен синтаксис для создания функции
numpy.linalg.inv().# Синтаксис функции numpy.linalg.inv() numpy.linalg.inv (обработка)2.1 Параметры обратной матрицы
Ниже приведены параметры обратной матрицы.
arr: Этот параметр представляет инвертируемую матрицу.2.2 Возвращаемое значение обратной матрицы
Эта функция возвращает обратную матрицу массива.
3. Использование функции numpy.linalg.inv()
Использование функции Python
numpy.linalg.inv()для обратной матрицы в простой математике может быть определено как матрица.3.1 Используйте функцию numpy.linalg.inv()
Мы можем использовать матрицу как прямоугольное расположение данных или чисел, другими словами, мы можем сказать, что это прямоугольный массив данных, горизонтальные элементы в матрице называются строками, а вертикальные записи называются столбцами. Для обратной функции матрицы нам нужно использовать
Функция np.linalg.inv(). Эта функция будет инвертировать данную матрицу. Python NumPy предоставляет простую функцию для вычисления обратной матрицы. Функция помогает пользователю проверить, чтоnumpy.linalg.inv()доступен в библиотеке Python.импортировать numpy как np # создание входного массива массив = np.массив ([[7, 2,], [3, -5]]) # Используйте numpy.linalg.inv(), чтобы получить обратную матрицу обр2 = np.linalg.inv (обр) печать (обр2) # Выход # [[ 0,12195122 0,04878049] # [0,07317073 -0,17073171]]4. Получить обратную матрицу с помощью функции scipy.linalg.inv()
Мы также можем использовать модуль
scipyдля выполнения различных научных расчетов с использованием его функций. Использование функцииscipy.linalg.inv()используется для возврата заданной квадратной матрицы в NumPy Python. Он работает так же, как функция numpy.linalg.inv() .импортировать numpy как np из scipy import linalg # создание входного массива arr = np.matrix([[7, 2,],[3, -5]]) # получить обратную матрицу с помощью функции scipy.linalg.inv() arr2 = linalg.inv(arr) печать (обр2)Выдает тот же результат, что и выше.
5.

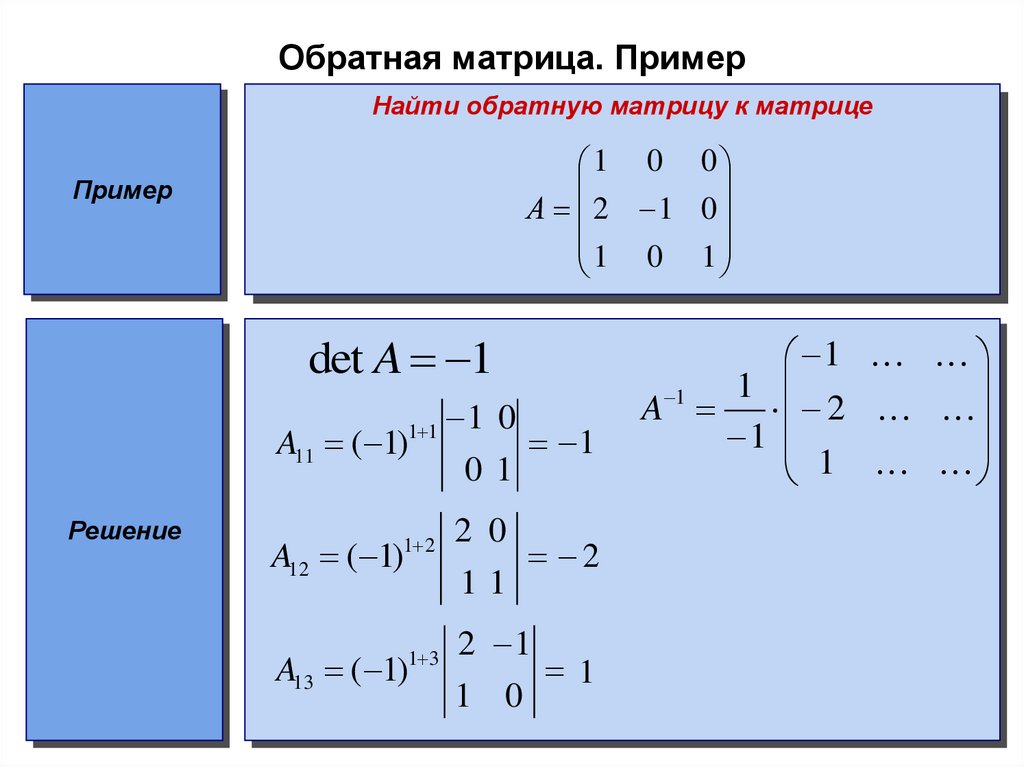

 лекцию Хана.
лекцию Хана. В этой статье я объясню, как использовать обратную матрицу NumPy для вычисления обратной матрицы массива с помощью этой функции.
В этой статье я объясню, как использовать обратную матрицу NumPy для вычисления обратной матрицы массива с помощью этой функции.

